Journal of Modern Physics
Vol. 2 No. 7 (2011) , Article ID: 5825 , 9 pages DOI:10.4236/jmp.2011.27075
Structural and Electronic Properties of BiXO3BiXO3 (X = Mn, Fe, Cr)
1Laboratoire des Matériaux Magnétiques, Faculté des Sciences, Université Djillali Liabes de Sidi Bel Abbès, Algérie
E-mail: *Djizer@yahoo.fr, **Nordine_bt@yahoo.com
Received November 15, 2010; revised February 16, 2011; accepted March 1, 2011
Keywords: Multiferroics, Perovskite, Density Functional Theory, ABO3 Oxide Perovskites
ABSTRACT
The candidate multiferroic BiCrO3 and its chemical neighbors BiMnO3 and BiFeO3 are known to be ferromagnetic and ferroelectric respectively. With structural distortions driven by the strongly polarizable Bi ions, we present results of the first-principles density functional calculations using the (FP-LMTO) method with the spin-orbit coupling for those materials in the pseudo-cubic perovskite phase. The results showed that the valence bands in these compounds are formed by the 6p orbitals of bismuth and 3d orbital’s of the transition metals. Our results indicate that these materials have metallic behavior for spin-up polarization but being a clear tandance for semiconductor spin-down BiMnO3.
1. Introduction
Multiferroic materials, in which both ferromagnetic and ferroelectric orders coexist, have recently attracted significant attention because of their potential use in technological applications as well as for fundamental research. Examples of such a multiferroic material are BiFeO3, BiMnO3 and BiCrO3. The single-phase perovskite BiFeO3 is ferroelectric (TC ~ 1103 K), and antiferromagnetic (AF) (TN ~ 643 K), exhibiting weak magnetism at room temperature due to a residual moment from a canted spin structure [1]. The bulk single crystal form has been extensively studied [2-6] and it has been shown to possess a rhombohedrally distorted perovskite structure (a = b = c = 5.63 Å, α = β = g = 59.4˚) at room temperature. Reports on the properties of BFO in thin film form are quite contradictory, the measured values of the spontaneous magnetization ranging from 0 to 0.5 μB per formula unit [7-10].
The highest values most probably result from the presence of iron oxides foreign phases formed as products during the deposition process [11] or even by the decomposition of BFO under certain external conditions [12].
Another perovskite, BiCrO3 (BCO) was first synthesized in 1968 using very high pressure firing and was reported to be antiferromagnetic (AF) below 123 K with a weak parasitic ferromagnetic moment [13]. A magnetic anomaly was observed around 95 K as an increase of magnetic moment with decreasing temperature, which was interpreted as a consequence of a change in the direction of the magnetic easy axis. A first-order structural phase transition was observed around 410 K. Below this temperature, the structure is triclinic with a = c = 3.906 Å, b = 3.870 Å, α = g = 90.5˚, β = 89.1˚ (at 300 K) while above this transition temperature it is a pseudo-monoclenic with a = c = 3.878 Å, b = 7.765 Å, and β = 88.8˚ (at 460 K).
BiMnO3 with a highly distorted perovskite-type structure has been extensively studied as a multiferroic material. Among ABO3-type multiferroic oxides, BiMnO3 is a unique compound that displays true ferromagnetic behaviors with a Curie temperature (TC) of ~105 K [14-19].
BiMnO3 is also expected to be ferroelectric according to the first-principle calculations [20,21]. Ferroelectricity requires that the crystal structure must be noncentrosymmetric and the ferroelectric transition is directly related to the structural phase transformation. At room temperature, BiMnO3 has a highly distorted perovskitetype structure, and was primitively reported to be of a triclinic lattice with a = c » 3.935 Å, b » 3.989 Å, a = c » 91.47˚, and b » 91.97˚ [12]. Later, an ED observation by Chiba et al. [13] suggested a 4-fold periodicity along the [11] p-direction (where the subscript “p” refers to the fundamental perovskite-type cell). Based on the electron diffraction information, the crystal structure of BiMnO3 was refined from powder neutron diffraction data to be a C2 monoclinic structure with a = 9.53 Å, b = 5.61 Å, c = 9.85 Å, and β = 110.67˚ [14]. This structure was commonly accepted and used as a fundamental model for interpretation of the observed physical phenomena. However, very recently Belik et al. [19]. On the other hand there are no theoretical studies available explaining the ground state and the elastic properties of this compound to compare to our calculations. In the present work we investigate the electronic structure of BiXO3 with emphasis on the ground state properties and elastic properties.
Section 2 deals with the computational details. Results are discussed in Section 3. Finally, conclusions are presented in Section 4.
2. Computational Details
In this work we have used the all-electron full-potential linear muffin tin orbital (FP-LMTO) method to calculate the total energies as well as the basic ground state properties[22], and implementations of density functional theory [23] within the local spin density approximation (LSDA, GGA) with the parameterization of Vosko-WilkNusair [24,25]. We have used the available computer code Lmtart [26].
Here the crystal is divided into two regions: nonoverlapping muffin-tin spheres surrounding each atom and the interstitial region between the spheres.
We used a double κ spdf LMTO basis (each radial function within the spheres is matched to a Hankel function in the in-terstitial region) for describing the valence bands.
The following basis set Bi (6s, 6p, 6d), O (2s, 2p) Cr, Mn, Fe (3s, 3p, 3d) [27-29] were used in the calculations within the spheres, the potential is expanded interims of spherical harmonics, while in the interstitial region, it is expanded in terms of plane waves.
The charge density and potential inside the muffin-tin spheres are represented by spherical harmonics up to lmax = 6. The k integration over Brillouin zone is performed using the tetrahedron method [30].
2.1. Structural Properties BiXO3 (X = Mn, Cr, Fe)
We have performed structural optimizations of lattice constants and bulk modulus in the pseudo cubic ferromagnetic phase. The calculated ground state properties such as equilibrium lattice constant in Table 1. Our results are underestimated compared to the experimental ones. While, typically for DFT/LDA (GGA) implementations, there is a 2.79(3.3)%, 2.84(1.03)%, underestimation of the lattice constant for BiMnO3 and BiCrO3 respectively.
The calculated lattice parameters for BiFeO3 is high 7% of the experimental result with GGA, Likewise the calculated bulk moduli for BiFeO3 is good compared to other calculated.
2.2. Electronic Properties of BiXO3 (X = Mn, Cr, Fe)
2.2.1. Cubic Paramagnetic Structures
We begin by calculating the electronic structure of BiXO3 in the high symmetry pseudo-cubic phase without including magnetic effects First, we present results for BiCrO3, BiMnO3 and BiFeO3 in the highest possible symmetry state, that is the pseudo- cubic structure, without spin polarization (we call this the paramagnetic (PM) phase). Although this phase is experimentally inaccessible, it provides a useful reference for understanding the spin-polarized structures to be discussed later in this paper.
In Figure 1 we compare our calculated band structure of BiCrO3 plotted along the high-symmetry axes of the simple cubic Brillouin zone to that of BiMnO3 and
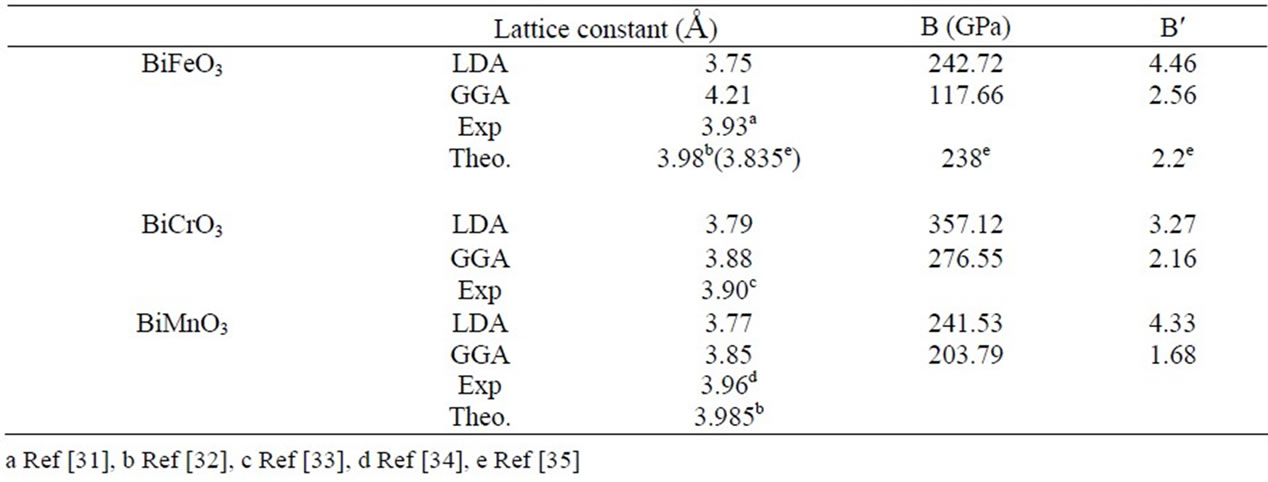
Table 1. The Calculated Lattice Parameter a, the Bulk Modulus B and its Pressure Derivative B′ for Pressure derivative B′ of BiXO3 (X = Fe, Cr, Mn).
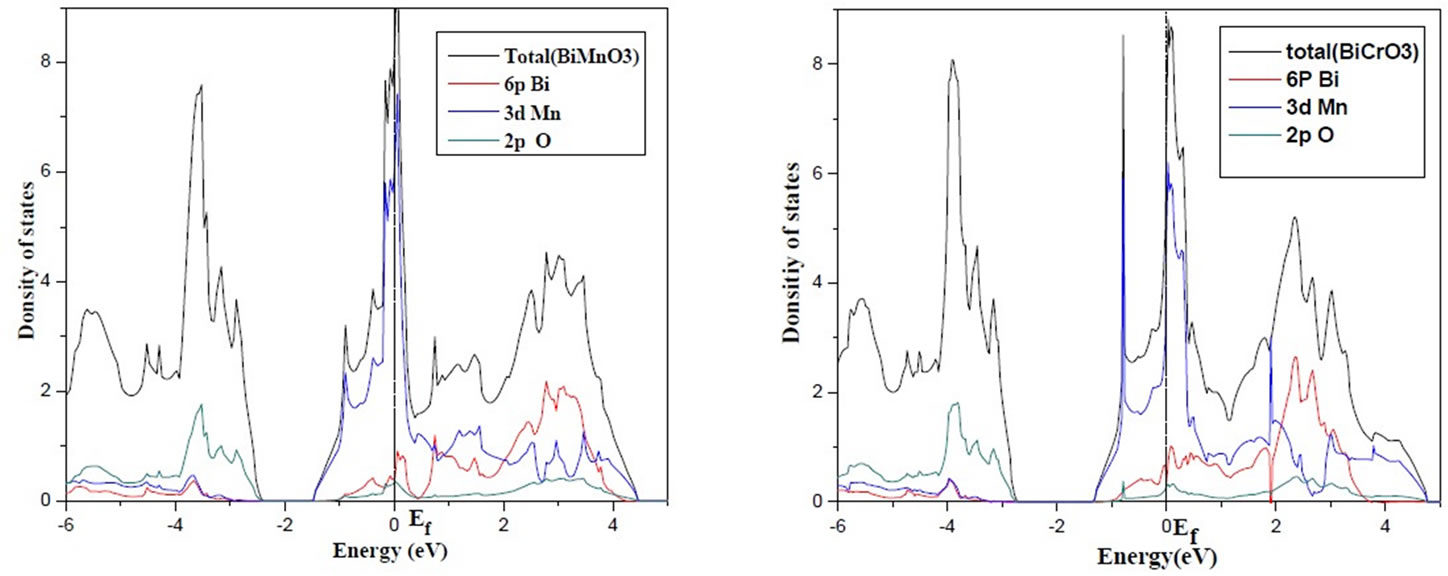
Figure 1. DOS for the cubic paramagnetic BiMnO3 and BiCrO3 calculated within the LDA.
BiFeO3 again the Fermi level is set to 0 eV in both cases. The most striking feature in comparing the band structures of BiCrO3 and BiMnO3 is their similarity.
In Figure 1, the large electronic density of states (DOS) at the Fermi level in the NM configuration suggests that this phase is metallic (which is similar with the result obtained by (FP-LAPW + lo) method [36]) and should be unstable toward spin polarization based on Stoner’s theory [37].
The broad O 2p bands between –3 and –6 eV can be seen to have almost identical structure in both materials(BiCrO3 and BiMnO3), as do the transition metal 3d bands which lie above them. In addition, both the Mn 3d bands in BiMnO3 and the Cr 3d bands in BiCrO3 occupy the same energy
Figure 2 shows the calculated densities of states for cubic paramagnetic BiXO3. The plotted energy range is from –6 eV to 5 eV. Again the broad O 2p bands between –2.5 and –7 eV can be seen clearly, with the Cr and Mn (3d) bands above them for BiCrO3 and BiMnO3 Who must place at the turn of the level of Fermi. A sharp peak at –1 eV corresponding to the Cr 3d states is clearly visible. Hybridization between Cr 3d (Mn 3d) and O 2p is expected between –2.5 and –6 eV band, and of course leads to the well-known super exchange interactions in magnetic perovskites [36].
Again we observe the Bi 6s band, which can be seen to have considerable dispersion suggesting that it is involved in covalent bonding. In addition, the Mn 3d (Cr 3d) bands in BiMnO3 (BiCrO3) overlap with the partially occupied Bi 6p orbital’s.
The large DOS at the Fermi level for the three materials suggests that the cubic PM structure is unstable, and that a lower energy structure could be achieved by allowing spin-polarization and/or structural distortion.
2.2.2. Cubic Ferromagnetic Structures
Next, we present the results of calculations in which the high-symmetry cubic structure is retained, but the electrons are allowed to spin polarize. We find that the ferromagnetic structure has a GGA magnetic moment of (2.78 mB, 2.89 mB, 2.85 mB) for BiXO3 (X = Mn, Cr, Fe) respectively, which is close to the Hund’s rule value of 3 mB expected for the 3d configuration. The slight reduction from the maximum possible magnetization is the result of hybridization between the (Mn, Cr, Fe) 3d and O 2p electrons which is seen clearly in the band structure and is discussed below. The LSDA magnetic moment is slightly lower again, reflecting the well-established over- estimation of p-d hybridization within the local density approximation.
We find that introduction of spin polarization reduces the energy of BiXO3 within the LSDA, The source of the stabilization for BiCrO3 is apparent in the density of states, shown in Figure 2 note that the density of states at the Fermi level is lower than that in the paramagnetic phase who are shown. The DOS at EF is still finite for BiCrO3, and has sizable contributions from both Cr 3d and Bi 6p states. This suggests that either the ferromagnetic phase of BiCrO3 is not the most stable, and that an AFM spin arrangement will further lower the energy of the system, or that the cubic phase is unstable, and a structural distortion will lower the energy.
At first sight the plots in Figures 2(a)-(c) look almost identical for energies below the Fermi level.
The reason of these similarities is simple-all the com pounds studied here have the same crystallographic structure and analogous atomic environments. The O 2p bandlying between –6 and –2.5 eV, is completely filled for the three materials. The electronic structure near the Fermi level is mainly formed by the Mn, Cr and Fe (3d) states. Due to the hybridization, there is also a considerable weight of the Mn (3d) states in the O 2p band. The electronic structure near the Fermi level is further split by the pseudo cubic crystal field into the Mn (eg) and Mn (t2g)
 (a)
(a) (b)
(b)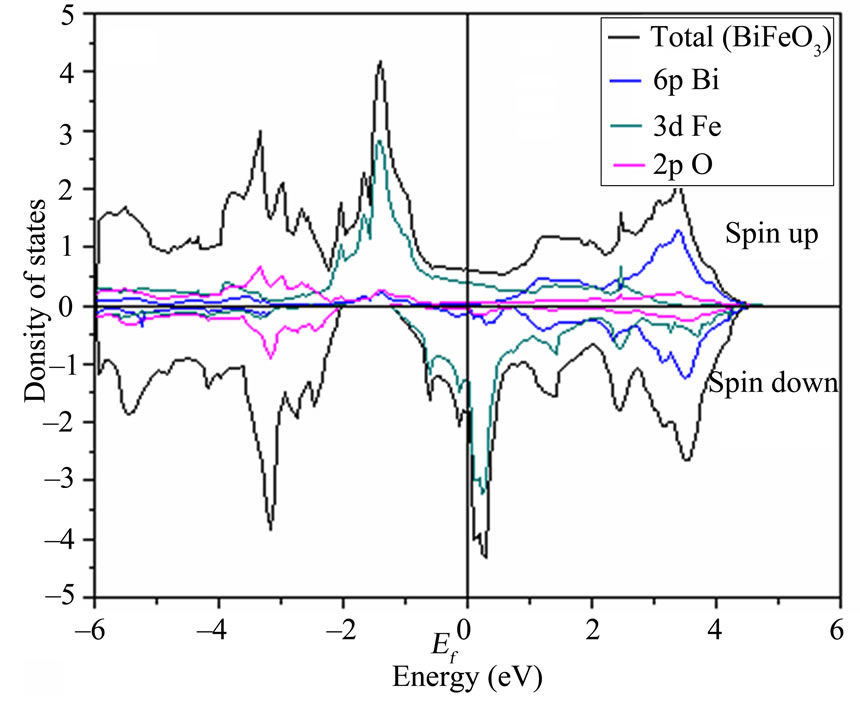 (c)
(c)
Figure 2. DOS for the ferromagnetic BiCrO3, BiMnO3 and BiFeO3 calculated within the LSDA.
bands, although in the highly distorted monoclinic structure there is no unique definition of the “t2g” and “eg” states, which are mixed by the crystal distortion. Leading even to an overlap between the Mn (t2g) and Mn (eg) bands. The Mn (eg) band itself is split into the lowand high-energy subbands, lying at around 2 and 3 eV, respectively. Therefore, according to the formal valence argument, in the fully polarized FM phase In Figure 2(c) the valence band contains O 2p orbitals hybridized with Fe 3d, the larger contribution of Bi 6s to the total DOS just above the Fermi level of the structure suggesting an enhanced role of Bi in chemical bonding. This enhanced chemical activity of Bi (whose lone pair is known to be at the origin of the ferroelectric instability of BiFeO3 and other magnetic perovskites [38])
Figure 3 shows the up and down-spin LSDA band structures for BiMnO3, BiCrO3 and BiFeO3 along the high-symmetry axes of the simple cubic Brillouin zone. The plotted energy range is from –10 eV to 5 eV, and the lower lying semi-core states have been omitted for clarity. The Fermi level is set to zero in both cases. The broad series of bands between –2 and –7 eV in both materials arises from the oxygen 2p orbitals are the (Mn, Cr) 3d bands. The (Mn, Cr) 3d bands are divided into two sub-bands the lower energy t2g bands, and the higher energy eg bands—as a result of crystal field splitting by the octahedral oxygen anions. In both cases the Fermi level lies near the top of the Mn 3d t2g bands and is in a region of high density of states.
The first notable point is that the Fermi energy is now very close to a band gap region for the majority carriers, so that the system is almost half-metallic.
For the minority carriers, EF almost divides the t2g and eg bands, and O 2p bands are almost identical for upand down-spin, and are similar to the corresponding bands in the paramagnetic band structure (not shown) Thus the effect of the exchange splitting is to introduce an almost rigid shift of the Cr 3d bands, with the up-spin bands moving down in energy relative to the PM phase, and the down-spin bands moving up in energy and becoming unoccupied [39].
2.3. Calculated Magnetic Properties of BiXO3 (X = Mn, Cr, Fe)
Our calculated total magnetic moment Jz, i.e., the sum of the spin and orbital moments, at perfect ordering of the Cr. Mn and Fe atoms. Note that a large part of the moment is delocalized into magnetic atom.
The magnetic moment of 2.3 μB (for Cr atoms) was obtained in spin-polarized calculation in good agreement with the value 2.55 μB obtained in neutron diffraction Experiments [40] and even by the LMTO method are found 2.63 μB [41]. The calculated magnetic moment for

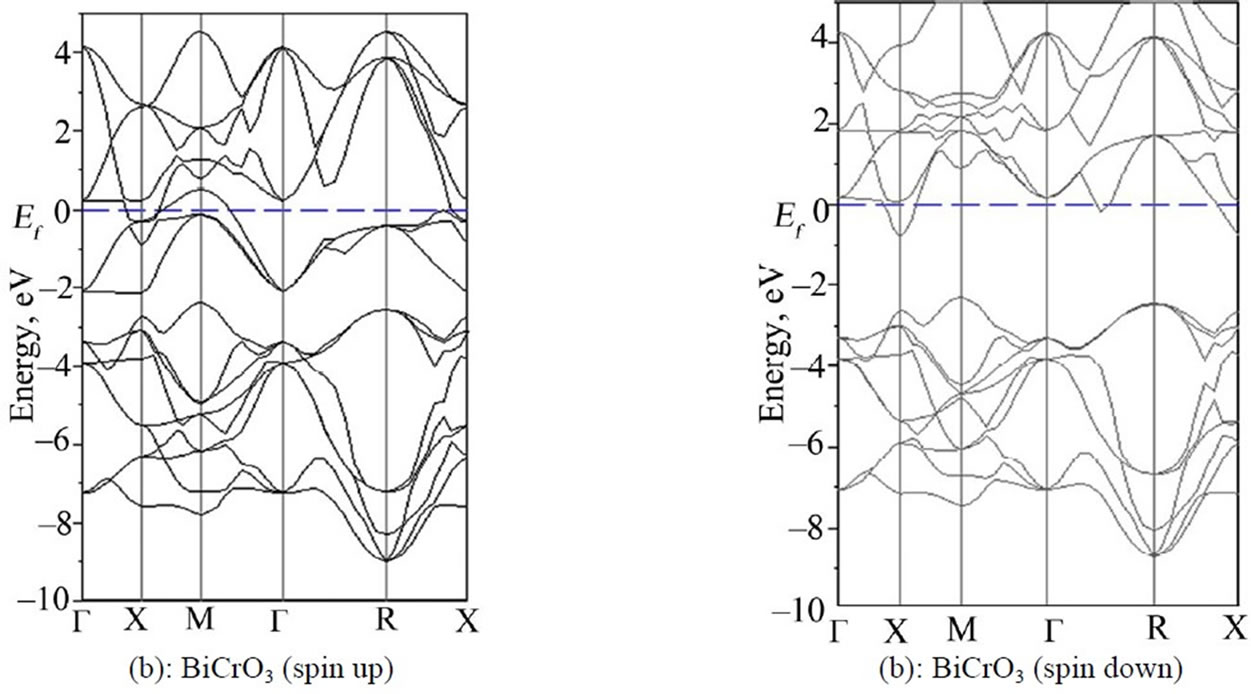

Figure 3. Upand down-spin band structures for pseudo-cubic BiXO3 (X = Cr, Mn, Fe) along the high symmetry axes of the Brillouin Zone.
Mn ions is 2.42 μB which is smaller than the experimental and theoretical values shown in Table 2.
Our calculations a magnetic moment are underestimated with experimental. The majority magnetic moment because of inflience of the atom magnetic as provided in Table 2, but BiFeO3 to see a negative value.
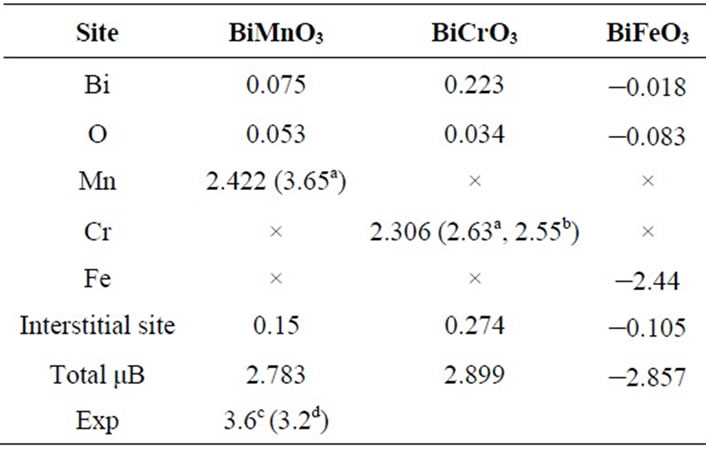
Table 2. Calculated magnetic moments (in Bohr magneto μB) of several sites and for the ferromagnetic BiXO3 (X = Mn, Cr, Fe).
The temperature dependence of magnetization of BiMnO3 are shown in Figure 4(a) which shows that the magnetic moment increased then liniarement varies with the tempratues .the measures exprementals indicates the magnetic moment decreases with temperature [39]. The magnetic moment for BiCrO3 decreases until 124 K then increased in Figure 4(b).
For the origin of ferroelectricity in BiMnO and BiFeO3 from Figure 1 it is clear that the Bi (6s) states in all compounds are not hybridized with the Bi (6p) states, as was supposed in Reference [49], these Bi (6s) lone pairs are slightly hybridized with O 2p states, and can induce dipole moment. However, we could not find any difference in degree of Bi (6s)-O 2p hybridization for BiMnO3 and BiFeO3 compared to that of other BiMeO3 compounds where no ferroelectricity is observed. The stereochemical activity of the Bi lone pair induces the electric moment but if the symmetry of the system includes inversion the net polarization turns to zero. The space group for the monoclinic structure of BiMnO3 contains inversion while the rhombohedral BiFeO3 has R3c symmetry without inversion. Therefore the origin of ferroelectricity in these two compounds seems to be different. In BiMnO3 the emergence of electric moment is connected with inversion symmetry breaking by the AFM order induced by particular orbital order below T = 474 K [42,43]. Another scenario for the onset of electric moment is possible in BiFeO3: an extensive investigation of ferroelectricity in BiFeO3 in the framework of density functional theory was reported in reference [44]. It was mentioned that the driving force of the ferroelectric distortion is the Bi lone pair. The calculated values of polarization agree well with experimental results [45].
2.4. Optical Properties of BiXO3 (X= Mn, Cr, Fe)
Figure 4 shows the calculated dielectric function of BiCrO3. The imaginary part 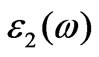 of the dielectric fun- ction has six prominent peaks. Peak A (13.79 eV) corresponds to the transition from O 2p VB to states in CB with a small contribution from Bi 6s states, and peaks B (4.64 eV) and C (9.66 eV) correspond to the transition from O 2p VB to Cr 3d CB. Peaks D (9.43 eV), E (7.82 eV) and F (4.77 aV) are ascribed to the transition of inner electron excitation from O 2s and Bi 6s leve, ls to CB.
of the dielectric fun- ction has six prominent peaks. Peak A (13.79 eV) corresponds to the transition from O 2p VB to states in CB with a small contribution from Bi 6s states, and peaks B (4.64 eV) and C (9.66 eV) correspond to the transition from O 2p VB to Cr 3d CB. Peaks D (9.43 eV), E (7.82 eV) and F (4.77 aV) are ascribed to the transition of inner electron excitation from O 2s and Bi 6s leve, ls to CB.
The energy-loss spectrum describes the energy loss of a fast electron traversing in the material [48].
The electron energy loss spectrum, as given in Figure 4 (c) supports the fact given above. The first peak at 3.33eV for BiCrO3 and another peak at 3.75 eV the calculation of the imaginary part of BiMnO3 and BiFeO3 are simillaire that BiCrO3 which are not indicated in this article .
3. Conclusions
In summary, the importance of structural, magnetic and elctronic propretie of multiferroic is analyzed. And im
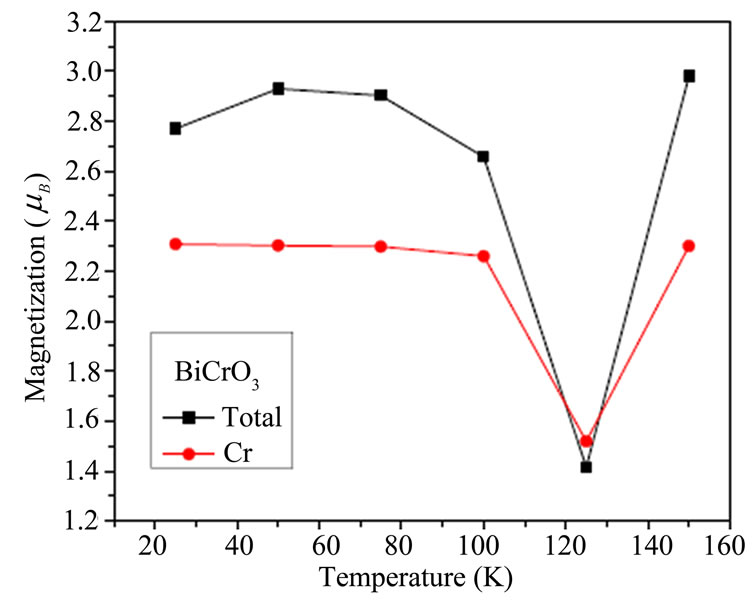

Figure 4 .Temperature dependence of the magnetization of BiCrO3 and BiMnO3.
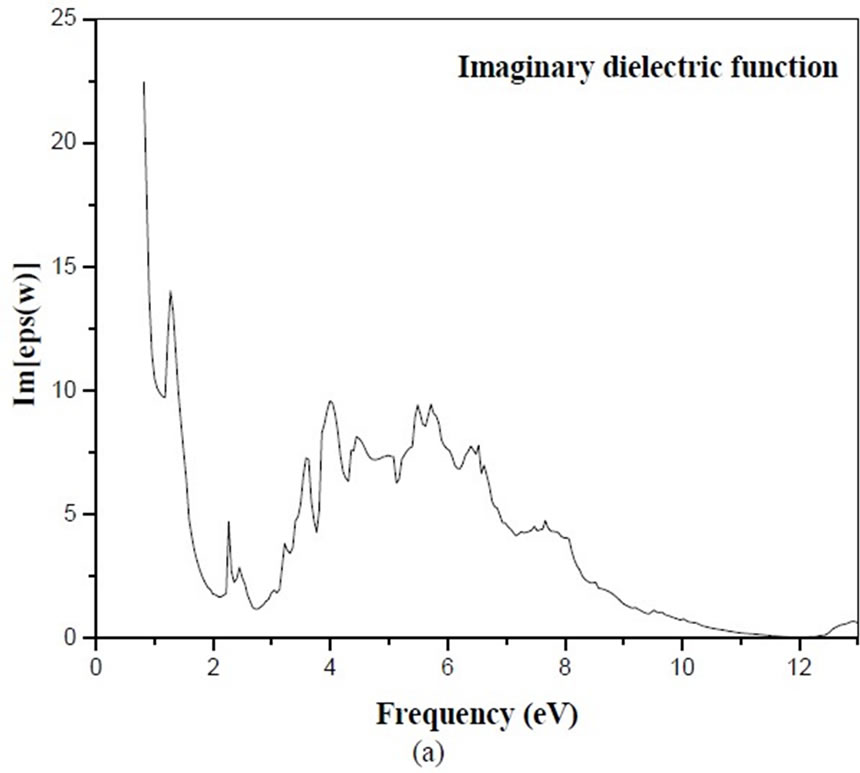

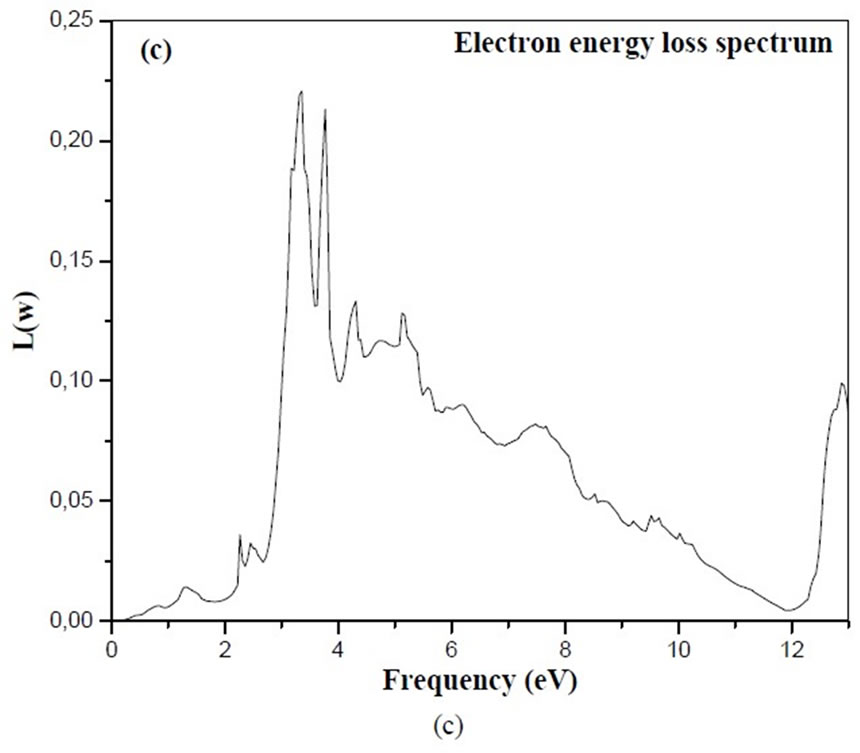
Figure 5. The calculated imaginary part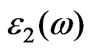 , real part
, real part 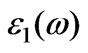 of the dielectric function
of the dielectric function and energy-loss spectrum for cubic BiCrO3.
and energy-loss spectrum for cubic BiCrO3.
portance of the covalent nature due to the orbital hybridization between A-site ion and O has been emphasized based on the first principles Calculations for the typical multiferroic perovskite oxides. It is found that the magnetic and orbital orders are ingeniously cooperated with the lattice distortion and ionic displacements.
In this article, we obtained results of first principle for materials multiferouic in a cubic structure which they do not exist in experiments what a way of studies gives towards other structures.
Our remark for lattice is has agreement good with experimental dated. The DOS calculates that the three materials show has a ferromagnetic order..
REFERENCES
- G. A. Smolenskii and I. E. Chupis, “Ferroelectromagnets,” Soviet Physical Uspekhi, Vol. 25, 1982, p. 475. HHUdoi:10.1070/PU1982v025n07ABEH004570U
- C. Michel, J.-M. Moreau, G. D. Achenbach, R. Gerson and W. J. James, “The Atomic Structure of BiFeO3,” Solid State Communication, Vol. 7, No. 9, 1969, pp. 701- 704. HUdoi:10.1016/0038-1098(69)90597-3U
- J. D. Bucci, B. K. Robertson and W. J. James, “The Precision Determination of the Lattice Parameters and the Coefficients of Thermal Expansion of BiFeO3,”Journal of Applied Crystallograph, Vol. 5, No.3, 1972, pp. 187-191. HHUdoi:10.1107/S0021889872009173U
- J. R. Teague, R. Gerson and W. J. James, “Dielectric Hysteresis in Single Crystal BiFeO3,” Solid State Communication, Vol. 8, No. 13, 1970, pp. 1073-1074. HHUdoi:10.1016/0038-1098(70)90262-0U
- Yu. E. Roginskaya, Yu. Ya. Tomashpol’skii, Yu. N. Venevtsev, V. M. Petrov and G. S. Zhdanov, “Nature of the Dielectric and Magnetic Properties of BiFeO3,” Zhurnal Eksperimental’noi I Teoreticheskoi Fiziki, Vol. 50, 1966, pp. 69-75.
- S. V. Kiselev, R. P. Ozerov and G. S. Zhdanov, “Detection of Magnetic Order in Ferroelectric BiFeO3 by Neutron Diffraction,” Soviet Physics Doklady, Vol. 7, 1963, pp. 742-744.
- W. Eerenstein, F. D. Morrison, J. Dho, J. F. Scott, M. Blamire and N. D. Mathur, “Comment on: Epitaxial BiFeO3 Multiferroic Thin Film Heterostructures,” Science, Vol. 307, No. 5713, 2005, p. 1203. HHUdoi:10.1126/science.1105422U
- J. Wang, J. B. Neaton, H. Zheng, V. Nagarajan, S. B. Ogale, B. Liu, D. Viehland, V. Vaithyanathan, D. G. Schlom, U. V. Waghmare, N. A. Spaldin, K. M. Rabe, M. Wuttig and R. Ramesh, “Epitaxial BiFeO3 Multiferroic Thin Film Heterostructures,” Science, Vol. 299, No. 5613, 2003, pp. 1719-1722. HHUdoi:10.1126/science.1080615U
- H. Bea, M. Bibes and S. Petit, et al. “Structural Distortion and Magnetism of BiFeO3 Epitaxial Thin Films: A Raman Spectroscopy and Neutron Diffraction Study,” Philosophical Magazine Letters, Vol. 87, 2007, pp. 165-174. HHUdoi:10.1080/09500830701235802U
- W. Eerenstein, N. D. Mathur and J. F. Scott, “Multiferroic and Magnetoelectric Materials,” Nature, Vol. 442, 2006, pp. 759-765. HHUdoi:10.1038/nature05023U
- H. Bea, M. Bibes and S. Fusil, et al. “Investigation on the Origin of the Magnetic Moment of BiFeO3 Thin Films by Advanced X-Ray Characterizations,” Physical Review B, Vol. 74, No. 2, 2006, pp. 020101-020105. HHUdoi:10.1103/PhysRevB.74.020101U
- X.-J, Lou, C.-X Yang, T. Tang, Y. Y. Lin, M. Zhang and J. F. Scott, “Phase Decomposition of Bismuth Ferrite Into Magnetite under Dc Voltage Stressing,” Applied Physical Letters, Vol. 90, 2007, p. 262908.
- F. Sugawara, S. Iiida, Y. Syono and S. Akimoto, “Magnetic Properties and Crystal Distortions of BiMnO3 and BiCrO3,” Journal Physical Society Japan, Vol. 25, 1968, pp. 1553-1558. HHUdoi:10.1143/JPSJ.25.1553U
- F. Sugawara, S. Iida, Y. Syono and S. Akimoto, “New Magnetic Perovskites BiMnO3 and BiCrO3,” Journal of Physical Society Japan, Vol. 20, 1965, p. 1529. HHUdoi:10.1143/JPSJ.20.1529U
- H. Faqir, H. Chiba, M. Kikuchi, Y. Syono, M. Mansori, P. Satre and A. Sebaoun, “High-Temperature XRD and DTA of BiMnO3 Perovskite,” Journal of Solid State Chemisty, Vol. 142, No. 1, 1999, pp. 113-119. HHUdoi:10.1006/jssc.1998.7994U
- T. Kimura, S. Kawamoto, I. Yamada, M. Azuma, M. Takano and Y. Tokura, “Magnetocapacitance Effect in Multiferroic BiMnO3,” Physical Review B, Vol. 67, No. 18, 2003, pp. 180401-180405. HHUdoi:10.1103/PhysRevB.67.180s401U
- Z. H. Chi, C. J. Xiao, S. M. Feng, F. Y. Li, C. Q. Jin, X. H. Wang, R. Z. Chen and L. T. Li, “Manifestation of Ferroectromagnetism in Multiferroic BiMnO3,” Journal Applied Physical, Vol. 98, No. 10, 2005, pp. 103519- 103524. HHUdoi:10.1063/1.2131193U
- E. Montanari, L. Righi, G. Calestani, A. Migliori, Gilioli E. and F. Bolzoni, “Room Temperature Polymorphism in Metastable BiMnO3 Prepared by High-Pressure Synthesis,” Chemical Mater, Vol. 17, No. 7, 2005, pp. 1765-1773. HHUdoi:10.1021/cm048250sU
- A. A. Belik, S. Iikubo, T. Yokosawa, K. Kodama, Igawa N, S. Shamoto, M. Azuma, M. Takano, K. Kimoto, Y. Matsui and E. Takayama-Muromachi, “Organicall Modified Silica Nanoparticles Co-encapsulating Photosensitizing Drug and Aggregation-Enhanced Two-Photon Absorbing Fluorescent Dye Aggregates for Two-Photon Photodynamic Therapy,” Journal of the American Chemical Society, Vol. 129, 2007, p. 971. HHUdoi:10.1021/ja0664032UHH
- N. A. Hill and K. M. Rabe, “First-Principles Investigation of Ferromagnetism and Ferroelectricity in Bismuth Manganite,” Physical Review B, Vol. 59, No. 13, 1999, pp. 8759-8769. HHUdoi:10.1103/PhysRevB.59.8759U
- R. Seshadri and N. A. Hill, “Visualizing the Role of Bi 6s ‘Lone Pairs’ in the Off-Center Distortion in Ferromagnetic BiMnO3,” Chemical Mater, Vol. 13, No. 9, 2001, pp. 2892-2899. HHUdoi:10.1021/cm010090mU
- S. Y. Savrasov, “Linear-Response Theory and Lattice Dynamics: A Muffin-Tin-Orbital Approach,” Physical Review B, Vol. 54, No. 23, 1996, pp. 16470-16486. HHUdoi:10.1103/PhysRevB.54.16470U
- H. Hohenberg and W. Kohn, “Inhomogeneous Electron Gas,” Physical Review, Vol. 136, No. 38, 1964, pp. 864- 871. HHUdoi:10.1103/PhysRev.136.B864U
- S. H. Vosko, L. Wilk, M. Nusair and J. Can, “Accurate Spin-Dependent Electron Liquid Correlation Energies for local Spin Density Calculations: a Critical Analysis,” Physical, Vol. 58, 1980, pp. 1200-1211.
- J. P. Perdew, K. Burke and M. Ernzerhof, “Generalized Gradient Approximation Made Simple,” Physical Review Letters, Vol. 77, No. 18, 1996, pp. 3865-3868. HHUdoi:10.1103/PhysRevLett.77.3865U
- S. Y. Savrasov, “Full-potential Program Package ‘Lmtart 6.20’,” User’s Manual, 12 October, 2000.
- D. C. Wallace, “Thermodynamics of Crystals,” Wiley, New York, 1972.
- M. Dacorogna, J. Ashkenazi and M. Peter, “Ab Initio Calculation of the Tatergonal Shear Modli of the Cubic Transition Metals,” Physical Review B, Vol. 26, No. 4, 1982, pp. 1527-1537. HHUdoi:10.1103/PhysRevB.26.1527U
- N. E. Christensen, “Force Thearem and Elastic Constants of Solids,” Solid State Commune, Vol. 49, No. 7, 1984, pp. 701-705. HHUdoi:10.1016/0038-1098(84)90224-2U
- P. Blochl, O. Jepsen and O. K. Andersen, “Improved Tetrahedron Method for Brillouin-Zone Integrations,” Physical Review B, Vol. 49, No. 23, 1994, pp. 16223-16233. HHUdoi:10.1103/PhysRevB.49.16223U
- F. Sugawara, S. Ihda, Y. Syono and S. Akimoto, “Single-Crystal Colloidal Multilayers of Controlled Thickness,” Journal Physical Society, Vol. 25, 1968, p. 1553.
- T. Atou, H. Chiba, K. Ohoyama, Y. Yamaguchi and Y. Syono, “Structure Determination of Ferromagnetic Perovskite BiMnO3,” Journal of Solid State Chemical, Vol. 145, No. 2, 1999, pp. 639-642. HHUdoi:10.1006/jssc.1999.8267U
- R. Nechache, C. Harnagea, L. Gunawan and L. P. Growth, “Structure and Properties of BiFeO3-BiCrO3 Films Obtained by Dual Cross Beam,” Programmable Logic Device, Vol. 54, No. 12, 2007, pp. 2645-2652.
- H. Béa, M. Bibes, S. Cherifi, F. Nolting, B. Warot-Fonrose, S. Fusil, G. Herranz, C. Deranlot, E. Jacquet, K. Bouzehouane and A. Barthélémy, “Tunnel Magnetoresistance and Robust Room Temperature Exchange Bias with Multiferroic BiFeO3 Epitaxial Thin Films,” Applied Physical Letters, Vol. 89, No. 24, 2006, pp. 242114-242117. HHUdoi:10.1063/1.2402204U
- P. Ravindran, R. Vidya, A. Kjekshus, H. Fjellvåg and O. Eriksson, “Thearetical Investigation of Magnetoelectric Behaviour in BiFeO3,” Physical Review B, Vol. 74, No. 22, 2006, pp. 224412-224430. HHUdoi:10.1103/PhysRevB.74.224412U
- Y. H. Xu, X. F. Hao, M. Jian, D. F. Zhou and F. M. Gao, “HJournal of Physics: Condensed MatterH,” IOP Science, Vol. 21, 2009, p. 236006.
- S. F. Matar, “Ab Initio Investigations in Magnetic Oxides,” Programmer Solid State Chemical, Vol. 31, No. 4, 2003, pp. 239-299. HHUdoi:10.1016/j.progsolidstchem.2004.01.001U
- A. N. Hill, P. Battig and C. Daul, Journal Physical Chemical B, Vol. 106, 2002, pp. 3383-3388
- Goodenough, “Theory of the Role of Covalence in the Perovskite-Type Manganites [La, M(ii)]MnO3,” Journal. Physicl Reviews B, Vol. 100, No. 2, 1955, pp. 564-573. HHUdoi:10.1103/PhysRev.100.564U
- A. A. Belik, S. Iikubo, K. Kodama, N. Igawa, S. Shamoto and E. Takayama-Muromachi, “Neutron Powder Diffranction Study on the Crystal and Magnetic Structures of BiCrO3,” Chemical Mater, Vol. 20, No. 11, 2008, pp. 3765- 3769. HHUdoi:10.1021/cm800375dU
- I. V. Solovyev and Z. V. Pchelkina, “Orbital Ordering and Magnetic Interactions BiMnO3,” New Journal Physical Vol. 10, 2008, p. 073021. HHUdoi:10.1088/1367-2630/10/7/073021U
- J. A. McLeod, Z. V. Pchelkina, L. D. Finkelstein, E. Z. Kurmaev, R. G. Wilks, A. Moewes, I. V. Solovyev, A. A. Belik and E. Takayama-Muromachi, “Electronic Structure of BiMnO3 Multiferrocis and Related Oxides,” Physical Review B, Vol. 81, 2010, pp. 144103-144113. HHUdoi:10.1103/PhysRevB.81.144103U
- I. V. Solovyev and Z. V. Pchelkina, “Magnetic Ground State and Multiferroicity in BiMnO3,” Pis’ma v ZhETF. Vol. 89, No. 12, 2009, pp. 597-602.
- J. B. Neaton, C. Ederer, U. V. Waghmare, N. A. Spaldin, and K. M. Rabe, “First-Principles Study of Spontaneous Polarization in Mulferroic BiFeO3,” Physical Review B, Vol. 71, No. 1, 2005, pp. 014113-014121. HHUdoi:10.1103/PhysRevB.71.014113U
- J. Wang, J. B. Neaton, H. Zheng, V. Nagarajan, S. B. Ogale, B. Liu, D. Viehland, V. Vaithyanathan, D. G. Schlom and U. V. Waghmare, et al., “Epitaxial BiFeO3 Mutiferroic Thin Film Heterostructures,” Science, Vol. 299, No. 5613, 2003, pp. 1719-1722. HHUdoi:10.1126/science.1080615U
- R. Seshadri and N. A. Hill, “Visualizing the Role of Bi 6s ‘Lone Pairs’in the off-Center Distortion in Ferromagnetic BiMnO3,” Chemistry of Materials, Vol. 13, No. 9, 2001. pp. 2892-2899. HHUdoi:10.1021/cm010090mU
- Z. W. Chen, M. Y. Lv, L. X. Li, Q. Wang, X. Y. Zhang and R. P. Liu, “Thearetical Investigations on Electronic and Optical Properties of Rock-Salt Gallium Nitride,” Thin Solid Films, Vol. 515, No. 4, 2006, pp. 2433-2436. HHUdoi:10.1016/j.tsf.2006.06.005U
- H. Chiba, T. Atou and Y. Syono, “Magnetic and Electrical Properties of Bi1-xSrxMnO3: Hole-Doping Effect on Ferromagnetic Perovskite BiMnO3,” Journal Solid State Chemical, Vol. 132, No. 1, 1997, pp. 139-143. HHUdoi:10.1006/jssc.1997.7432U
- J. V. D. Brink and D. I. Khomskii, “Multiferroicity Due to Charge Ordering,” Journal of Physical Condensed Matter, Vol. 20, No. 43, 2008, p. 434217. HUdoi:10.1088/0953-8984/20/43/434217UH

