Applied Mathematics
Vol.07 No.18(2016), Article ID:72492,11 pages
10.4236/am.2016.718181
A Semi-Lagrangian Type Solver for Two-Dimensional Quasi-Geostrophic Model on a Sphere
Quanyong Zhu1, Yan Yang2
1Department of Mathematics, Lishui University, Lishui, China
2Jiangsu Key Laboratory for NSLSCS, School of Mathematical Sciences, Nanjing Normal University, Nanjing, China

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: September 12, 2016; Accepted: November 29, 2016; Published: December 2, 2016
ABSTRACT
In this paper, we propose a numerical method based on semi-Lagrangian approach for solving quasi-geostrophic (QG) equations on a sphere. Using potential vorticity and stream-function as prognostic variables, two-order centered difference is suggested on the latitude-longitude grid. In our proposed numerical scheme, advection terms are expressed in a Lagrangian frame of reference to circumvent the CFL restriction. The pole singularity associated with the latitude-longitude grid is eliminated by a smoothing technique for the initial flow. Error analysis is provided for the numerical scheme.
Keywords:
Quasi-Geostrophic Equations, Semi-Lagrangian Methods, Smoothing Technique, Error Analysis, Pole Singularity

1. Introduction
The quasi-geostrophic (QG) equations on a sphere are the major system of interest in weather forecasting and climate prediction [1] , where the horizontal velocities are approximately geostrophic for extratropical synoptic-scale motions. It is important to investigate the QG equations because of both its intrinsic mathematical interest and its potential applications in dynamic meteorology and oceanography. The two-dimensional QG equations are originally established in modeling rotating fluids on the earth surface [2] . Over the years, the study of two-dimensional QG equations has been an active research field; see, e.g., [3] [4] . However, in spite of quite a number of contributions dealing with two-dimensional QG equations, there is little research on the evolution of two-dimensional QG equations on a sphere.
Analytic solutions are rarely available due to the relatively complex nature of QG equations on a sphere; numerical simulations play an important role in the exploration of the QG equations, for example, [5] [6] [7] . The accuracy of numerical investigation on QG models depends on many factors, including the knowledge of the initial state, the numerical methods employed, the resolution and so on. Some numerical methods based on finite difference methods can be applied to solve the QG equations on a spherical coordinate that may suffer from the pole singularity.
Some efforts have made to alleviate the difficulties of the pole singularity. Kurihara [8] proposed a spherical grid system whose grid density on the globe is almost homogeneous, and the number of grid points per line of latitude near the poles is reduced. If the equations written in such coordinates are directly transformed into finite differences, excessive errors are committed in grids [9] [10] . Some slight alteration was made in Kurihara’s grid which alleviated the troubles [10] [11] . On the other hand, in many global atmospheric applications, spatial discretization schemes are based on the spectral transform methods, in which solution fields are expressed as spherical harmonic expansions. Since the spherical harmonics are the natural representation of a two-dimen- sional field on the surface of a sphere, the spectral approach may provide better accuracy for the pole problem. The spectral transform method seems ideal for the spherical domain; however, it is too expensive for long time simulations. Especially at high spatial resolutions, since it requires associated Legendre transforms.
A framework of semi-Lagrangian semi-implicit methods was developed by Robert [12] . It offers another possibility of developing fast numerical schemes for weather forecast models in complex systems. Over the years, researchers have devoted much attention to the further development and application of semi-Lagrangian methods. In [13] [14] , Robert combined the semi-implicit integration scheme with a semi-Lagrangian treatment of the advection terms in a barotropic model. Robert et al. [15] extended this scheme to a multilevel model. They found that the time step could be increased by a further factor over an Eulerian semi-implicit scheme. For improving accuracy, McDonald [16] has incorporated a semi-Lagrangian treatment of advection in an efficient two-time-level integration scheme. The accuracy and stability of the semi-Lagrangian semi-implicit methods were investigated by McDonald [17] . They showed that there is no restriction on the time step when considering the linear advection and following certain rules for the interpolation of functions at the trajectory points. Compared with Eulerian schemes, they have advantages of their own, such as high efficiency and easy to use in problems with nonuniform grids. In addition, semi-Lagrangian methods avoid the leading source of nonlinear instability in most wave-propagation problems since the nonlinear advection terms appearing in the Eulerian form of the momentum equations are eliminated when those equations are expressed in a Lagrangian approach [18] . Semi-Lagrangian methods and semi-implicit approach have become one of the most popular architectures used in numerical weather forecast and lots of other computational fluid dynamical applications; see e.g., [19] [20] [21] .
In this paper, we consider the following non-dimensional 2D QG equations on a sphere:
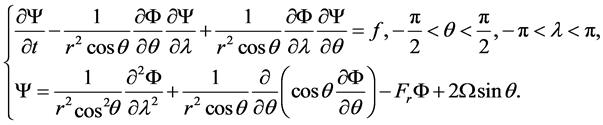 (1)
(1)
where 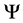 is the potential vorticity;
is the potential vorticity; 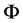 is the stream-function; f is an external force;
is the stream-function; f is an external force; 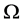 is the rotational speed;
is the rotational speed; 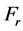 is the planetary Froude number. r is the radius of sphere. It is challenging when initial flow is related to longitude, the discrete equation contains the
is the planetary Froude number. r is the radius of sphere. It is challenging when initial flow is related to longitude, the discrete equation contains the 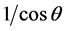 terms. It gives rise to larger truncation errors and reducing the order of convergence by one near the poles when
terms. It gives rise to larger truncation errors and reducing the order of convergence by one near the poles when 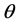 approaches
approaches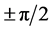 . As the stimulation propagated, these larger errors propagated over the sphere and eventually contaminated the rest of the solution. We provide a smoothing technique for the initial flow to overcome the above difficulty. Numerical experiments demonstrate the performance of our proposed method and investigate behaviors of QG model with geostrophic implications.
. As the stimulation propagated, these larger errors propagated over the sphere and eventually contaminated the rest of the solution. We provide a smoothing technique for the initial flow to overcome the above difficulty. Numerical experiments demonstrate the performance of our proposed method and investigate behaviors of QG model with geostrophic implications.
The rest of paper is structured as follows. In Section 2, we present the semi-Lagrangian discrete scheme of QG equations on a sphere. In Section 3, we carry out the detailed accuracy analysis of the method and explain some details. The conclusions are summarized in Section 4.
2. Discretization Schemes
In this section, we introduce the semi-Lagrangian scheme for QG equations. We will focus on the time discretization and ignore the space variable for the moment. The first equation of QG model is expressed as
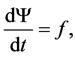 (2)
(2)
where
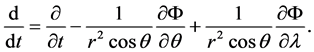
Then the semi-Lagrangian scheme for above equation is
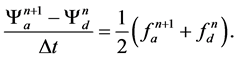
Here subscripts a and d refer to evaluation at an arrival and departure point, respectively. We firstly iteratively calculate departure point using some first guess and an interpolation formula, the order of the interpolation is much less important. So we use linear interpolation here. Secondly, an cubic interpolation formula is adopted to evaluate 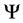 at upstream point [22] . Finally, evaluate
at upstream point [22] . Finally, evaluate 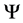 at arrival points at time
at arrival points at time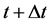 . By doing so, we have
. By doing so, we have
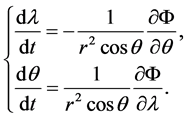 (3)
(3)
Using the two-stage trajectory calculation, Equation (3) can be computed as follows,
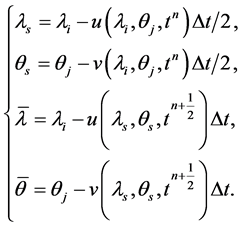 (4)
(4)
where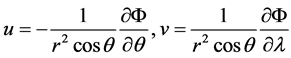 .
. 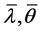 denote the longitude and latitude of
denote the longitude and latitude of
the departure point. Comparing to the classical Runge-Kutta midpoint method, a slight difference is that the first stage uses 



Let us introduce, for example, cubic Lagrange interpolation. Set 


and similarly for q. When

With the propositions above, we have
alternatively, it can be expanded as follows,

In the case
When


and similarly for the case
For spatial approximation, we adopt unstaggered grid that is uniform in longitude and latitude. Stream-function 




More specifically, for fixed 











For the second term of right hand side of Equation (6), we use the following approximation

With the definition of the discrete operators above, the spatial discretization for (6) is defined as follows. When

When


Similarly when

3. Error Analysis
In this section, we will carry out the error estimate of our new algorithm. We let 


Employ Taylor expansion for the terms in the above equation at






Substituting (12)-(17) into (11), notice that 
Similarly, we consider the truncation error of the semi-Lagrangian discrete scheme. The semi-Lagrangian scheme of the first equation in (1) reads
Here subscript d refers to evaluation at an departure point. By expanding 

where 



We first calculate the error of the Runge-Kutta discretization


Similarly
Since the right hand side of Equation (20) matches the Taylor series expansion of 



Now consider the error that generated by Runge-Kutta scheme used to estimate the back-trajectory in semi-Lagrangian approach. The data are available only at discrete
points on a space-time grid in many practical dynamics, 
evaluated by interpolation or extrapolation. Before examining the errors introduced by such interpolation and extrapolation, consider the cases where 

Noticing

Similarly we can get

Employ Taylor expansions of 

Substituting (22) into (23) gives
Which implies that the Runge-Kutta scheme (4) generates an 
Now suppose that the velocity data 

lation between times 


Suppose that the extrapolated velocity field 


Substituting the preceding equation into (20) shows that the use of 


4. Conclusion
In this paper, we present a numerical method which combines semi-Lagrangian method with two-order centered difference scheme for solving two-dimensional quasi- geostrophic equations on a sphere. In our approach, potential vorticity and stream- function are used as prognostic variables. Advection terms are expressed in a Lagrangian frame of reference to avoid the necessity of stable constraint. The pole singularity is eliminated by means of employ a smoothing technique. An error analysis is presented.
Acknowledgements
We thank the Editor and the referee for their comments. This work is supported by the National Natural Science Foundation of China (Nos. 11447017, 11471166 and 11401294).
Cite this paper
Zhu, Q.Y. and Yang, Y. (2016) A Semi-Lagrangian Type Solver for Two-Dimensional Quasi-Geostro- phic Model on a Sphere. Applied Mathematics, 7, 2296-2306. http://dx.doi.org/10.4236/am.2016.718181
References
- 1. Verkley, W.T.M. (2009) A Balanced Approximation of the One-Layer Shallow-Water Equations on a Sphere. Journal of the Atmospheric Sciences, 66, 1735-1748.
https://doi.org/10.1175/2008JAS2837.1 - 2. Pedlosky, J. (1987) Geophysical Fluid Dynamics. Springer-Verlag.
https://doi.org/10.1007/978-1-4612-4650-3 - 3. Wu, J. (2005) Global Solutions of the 2D Dissipative Quasi-Geostrophic Equation in Besov Spaces. SIAM Journal on Mathematical Analysis, 36, 1014-1030.
https://doi.org/10.1137/S0036141003435576 - 4. Mu, M. and Zhang, Z. (2006) Conditional Nonlinear Optimal Perturbations of a Two-Dimensional Quasigeostrophic Model. Journal of the Atmospheric Sciences, 63, 1587-1604.
https://doi.org/10.1175/JAS3703.1 - 5. Wang, Q., Zhang, Z. and Li, Z. (2013) A Fourier Finite Volume Element Method for Solving Two-Dimensional Quasi-Geostrophic Equations on a Sphere. Applied Numerical Mathematics, 71, 1-13.
https://doi.org/10.1016/j.apnum.2013.03.007 - 6. Zhang, Z. and Lu, F. (2012) Quadratic Finite Volume Element Method for the Improved Boussinesq Equation. Journal of Mathematical Physics, 53, Article ID: 013505.
https://doi.org/10.1063/1.3672197 - 7. Wang, Q., Zhang, Z., Zhang, X. and Zhu, Q. (2014) Energy-Preserving Finite Volume Element Method for the Improved Boussinesq Equation. Journal of Computational Physics, 270, 58-69.
https://doi.org/10.1016/j.jcp.2014.03.053 - 8. Kurihara, Y. (1965) Numerical Integration of the Primitive Equations on a Spherical Grid. Monthly Weather Review, 93, 399-415.
https://doi.org/10.1175/1520-0493(1965)093<0399:NIOTPE>2.3.CO;2 - 9. Rao, M. and Umscheidu Jr., L. (1969) Tests of the Effect of Grid Resolution in a Global Prediction Model. Monthly Weather Review, 97, 659-664.
https://doi.org/10.1175/1520-0493(1969)097<0659:TOTEOG>2.3.CO;2 - 10. Shuman, F. (1970) On Certain Truncation Errors Associated with Spherical Coordinates. Journal of Applied Meteorology, 9, 564-570.
https://doi.org/10.1175/1520-0450(1970)009<0564:OCTEAW>2.0.CO;2 - 11. Umscheid, L. and Bannon, P. (1977) A Comparison of Three Global Grids Used in Numerical Prediction Models. Monthly Weather Review, 105, 618-635.
https://doi.org/10.1175/1520-0493(1977)105<0618:ACOTGG>2.0.CO;2 - 12. Robert, A., Henderson, J. and Turnbull, C. (1972) An Implicit Time Integration Scheme for Baroclinic Models of the Atmosphere. Monthly Weather Review, 100, 329-335.
https://doi.org/10.1175/1520-0493(1972)100<0329:AITISF>2.3.CO;2 - 13. Robert, A. (1981) A Stable Numerical Integration Scheme for the Primitive Meteorological Equations. Atmosphere-Ocean, 19, 35-46.
https://doi.org/10.1080/07055900.1981.9649098 - 14. Robert, A. (1982) A Semi-Lagrangian and Semi-Implicit Numerical Integration Scheme for the Primitive Meteorological Equations. Journal of the Meteorological Society of Japan, 60, 319-325.
- 15. Robert, A., Yee, T. and Ritchie, H. (1985) A Semi-Lagrangian and Semi-Implicit Numerical Integration Scheme for Multilevel Atmospheric Models. Monthly Weather Review, 113, 388-394.
https://doi.org/10.1175/1520-0493(1985)113<0388:ASLASI>2.0.CO;2 - 16. McDonald, A. (1986) A Semi-Lagrangian and Semi-Implicit Two Time-Level Integration Scheme. Monthly Weather Review, 114, 824-830.
https://doi.org/10.1175/1520-0493(1986)114<0824:ASLASI>2.0.CO;2 - 17. McDonald, A. (1987) Accuracy of Multiply-Upstream, Semi-Lagrangian Advective Schemes II. Monthly Weather Review, 115, 1446-1450.
https://doi.org/10.1175/1520-0493(1987)115<1446:AOMUSL>2.0.CO;2 - 18. Durran, D. (2010) Numerical Methods for Fluid Dynamics: With Applications to Geophysics. Springer, New York.
https://doi.org/10.1007/978-1-4419-6412-0 - 19. Sun, W., Yeh, K. and Sun, R. (1996) A Simple Semi-Lagrangian Scheme for Advection Equations. Quarterly Journal of the Royal Meteorological Society, 122, 1211-1226.
https://doi.org/10.1002/qj.49712253310 - 20. Pep, M. and Francesco, V. (2013) A Semi-Lagrangian AMR Scheme for 2D Transport Problems in Conservation Form. Journal of Computational Physics, 237, 151-176.
https://doi.org/10.1016/j.jcp.2012.11.039 - 21. Ullrich, P., Lauritzen, P. and Jablonowski, C. (2014) A High-Order Fully Explicit Flux-Form Semi-Lagrangian Shallow-Water Model. International Journal for Numerical Methods in Fluids, 75, 103-133.
https://doi.org/10.1002/fld.3887 - 22. Amato, U. and Carfora, M. (2000) Semi-Lagrangian Treatment of Advection on the Sphere with Accurate Spatial and Temporal Approximations. Mathematical and Computer Modelling, 32, 981-995.
https://doi.org/10.1016/S0895-7177(00)00184-9



















