Applied Mathematics
Vol.07 No.16(2016), Article ID:71222,8 pages
10.4236/am.2016.716157
Existence and Uniqueness of Solution for Cahn-Hilliard Hyperbolic Phase-Field System with Dirichlet Boundary Condition and Regular Potentials
Jean De Dieu Mangoubi, Daniel Moukoko, Fidele Moukamba, Franck Davhys Reval Langa
G.R.A.F.E.D.P, Faculté des Sciences et Techniques, Université Marien NGOUABI, Brazzaville, Congo
Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: August 20, 2016; Accepted: October 11, 2016; Published: October 14, 2016
ABSTRACT
Our aim in this paper is to study the existence and the uniqueness of the solutions for hyperbolic Cahn-Hilliard phase-field system, with initial conditions, Dirichlet boundary condition and regular potentials.
Keywords:
Cahn-Hilliard Hyperbolic Phase-Field System, Regular Potential, Dirichlet Boundary Conditions

1. Introduction
G. Caginalp introduced in [1] the following phase-field system
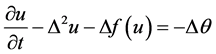 (1)
(1)
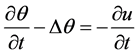 (2)
(2)
where u is the order parameter and 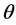 is the (relative) temperature. These equations model phase transition processes such as melting-solidification processes and have been studied, see [2] - [6] , for a similar phase-field model with a nonlinear term.
is the (relative) temperature. These equations model phase transition processes such as melting-solidification processes and have been studied, see [2] - [6] , for a similar phase-field model with a nonlinear term.
These Cahn-Hilliard phase-fiel system are known as the conserved phase-field system (see [7] - [9] ) based on type III heat conduction and with two temperatures (see [10] ). The authors have proved the existence and the uniqueness of the solutions, the existence of global attractor and of exponential attractors with singularly or regular potentials.
In [11] , Ntsokongo and Batangouna have studied the following Cahn-Hilliard phase- field system
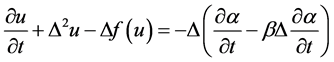 (3)
(3)
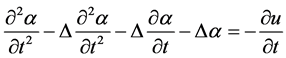 (4)
(4)
where , u is the order parameter and
, u is the order parameter and 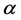 is the (relative) temperature, they have proved the existence and the uniqueness solution with Dirichlet boundary condition and regular potentials.
is the (relative) temperature, they have proved the existence and the uniqueness solution with Dirichlet boundary condition and regular potentials.
In this paper, we consider the following Cahn-Hilliard hyperbolic phase-fiel system
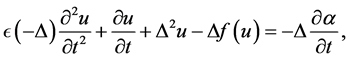 (5)
(5)
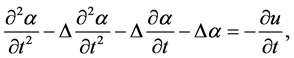 (6)
(6)
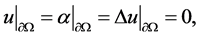 (7)
(7)
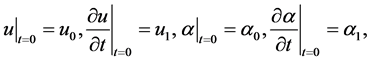 (8)
(8)
which is the perturbed phase-field system of Cahn-Hilliard phase-field system (3)-(4) with . In the above hyperbolic system
. In the above hyperbolic system  is a bounded and regular domain of
is a bounded and regular domain of 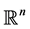 with
with 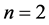 or 3 and f is the nonlinear regular potentials.
or 3 and f is the nonlinear regular potentials.
The hyperbolic system has been extensively studied for Dirichlet boundary conditions and regular or singular potentials (see [12] - [14] ). Whose certain have to end at existence of global attractor or at the existence of exponential attractors (see [15] ).
In this paper we prove the existence and the uniqueness of solutions of (5)-(8). We consider the regular potential 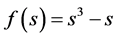 which satisfies the following properties:
which satisfies the following properties:
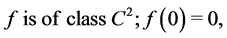 (9)
(9)
 (10)
(10)

2. Notations
We denote by 


boundary conditions. More generally, 
Throughout this paper, the same letters 

3. A Priori Estimates
We multiply (5) by 


where
satisfies
Finaly, we conclude that
and
for all
Multiply (6) by 

Then
In this study, we have three main results; existence theorem, uniqueness theorem and existence theorem with more regularity.
4. Existence and Uniqueness of Solutions
Theorem 4.1. (Existence) We assume 



and

The proof is based on a priori estimates obtained in the previous section and on a standard Galerkin scheme.
Theorem 4.2. (Uniqueness) Let the assumpptions of Theorem 4.1 hold. Then, the system (5) - (8) possesses a unique solution 


and 

Proof. Let 








We multiply (12) by 


Multiplying (13) by 


Now summing (14) and (15) we obtain

where
Lagrange theorem gives a estimates
which implies
Inserting the above estimate into (16), we have
Applying Gronwall’s lemma, we obtain for all
We deduce the continuous dependence of the solution relative to the initial conditions, hence the uniqueness of the solution.
The existence and uniqueness of the solution of problem (5)-(8) being proven in a larger space, we will seek the solution with more regularity.
Theorem 4.3. Assume

then the system (5)-(8) possesses a unique solution 



and

Proof. Following theorems 4.1 and 4.2, the system (5)-(8) possesses the unique solution 


and

Multiply (2.1) by 

we deduce the following inequality

Thanks to use
Since

Multiplying (6) by 


Now summing (18) and (19), we obtain
where
Appling the Gronwall’s lemma, we deduce that
and

Multiplying (5) by 


Thanks to use 

Inserting the above estimate into (20), we obtain
which implies that
Multiplying (6) by 

that implies
5. Conclusion
We have just shown the theorems of existence and uniqueness of the solutions for perturbed Cahn-Hilliard hyperbolic phase-field system with regular potentials.
Cite this paper
De Dieu Mangoubi, J., Moukoko, D., Moukamba, F. and Langa, F.D.R. (2016) Existence and Uniqueness of Solution for Cahn-Hilliard Hyperbolic Phase-Field System with Dirichlet Boundary Condition and Regular Potentials. Applied Mathematics, 7, 1919-1926. http://dx.doi.org/10.4236/am.2016.716157
References
- 1. Caginalp, G. (1988) Conserved-Phase Field System: Implications for Kinetic Undercooling. Physical Review B, 38, 789-791.
http://dx.doi.org/10.1103/PhysRevB.38.789 - 2. Brochet, D., Hilhorst, D. and Novick-Cohen, A. (1996) Maximal Attractor and Inertial Sets for a Conserved Phase-Field Model. Advances in Differential Equations, 1, 547-578.
- 3. Brochet, D. (1993) Maximal Attractor and Inertial Sets for Some Second and Fourth Order Phase-Field Models. In: Pitman Res. Notes Math. Ser, Vol. 296, Longman Sci. Tech., Harlow, 77-85.
- 4. Colli, P., Gilardi, G., Grasselli, M. and Schimperna, G. (2001) The Conserved Phase-Field System with Memory. Adv. Math. Sci Appl., 11, 265-291.
- 5. Gatti, S. and Pata, V. (2004) Exponential Attractor for a Conserved Phase-Field System with Memory. Physica D: Nonlinear Phenomena, 189, 31-48.
http://dx.doi.org/10.1016/j.physd.2003.10.005 - 6. Gilardi, G. (2007) On a Conserved Phase-Field Model with Irregular Potentials and Dynamic Boundary Condition. Rend. Cl. Sci. Mat. Nat., 141, 129-161.
- 7. Miranville, A. (2013) On the Conserved Phase-Field Model. Journal of Mathematical Analysis and Applications, 400, 143-152.
http://dx.doi.org/10.1016/j.jmaa.2012.11.038 - 8. Caginalp, G. (1990) The Dynamic of Conserved Phase Field System: Stefan-Like, Hele-Shaw and Cahn-Hilliard Models as Asymptotic Limits. IMA Journal of Applied Mathematics, 44, 77-94.
- 9. Colli, P., Gilardi, G., Laurenot, Ph. and Novick-Cohen, A. (1999) Uniqueness and Long-Time Behavior for the Conserved Phase-Field System Memory. Discrete and Continuous Dynamical Systems—Series A, 5, 375-390.
http://dx.doi.org/10.3934/dcds.1999.5.375 - 10. Miranville, A. and Quintanilla, R. (2011) A Type III Phase-Field System with a Logarithmic Potential. Applied Mathematics Letters, 24, 1003-1008.
http://dx.doi.org/10.1016/j.aml.2011.01.016 - 11. Ntsokongo, A.J. and Batangouna, N. (2016) Existence and Uniqueness of Solutions for a Conserved Phase-Field Type Model. AIMS Mathematics, 1, 144-155.
http://dx.doi.org/10.3934/Math.2016.2.144 - 12. Goyaud, M.E.I., Moukamba, F., Moukoko, D. and Langa, F.D.R. (2015) Existence and Uniqueness of Solution for Caginalp Hyperbolic Phase Field System with Polynomial Growth Potential. International Mathematical Forum, 10, 477-486.
- 13. Moukoko, D. (2014) Well-Posedness and Longtime Behaviors of a Hyprebolic Caginalp System. Journal of Applied Analysis and Computation, 4, 151-196.
- 14. Moukoko, D. (2015) Etude de Modeles Hyperboliques de champ de phase de Caginalp, These unique, Falculté des Sciences et Techniques, Université Marien NGOUABI.
- 15. Moukoko, D., Moukamba, F. and Reval, L.F.D. (2015) Global Attractor for Caginalp Hyperbolics Field-Phase System with Singular Potential. Journal of Mathematics Research, 7, 165-177.































