Applied Mathematics
Vol.07 No.15(2016), Article ID:70512,25 pages
10.4236/am.2016.715142
A New Approach to Investigate Students’ Behavior by Using Cluster Analysis as an Unsupervised Methodology in the Field of Education
Onofrio Rosario Battaglia1, Benedetto Di Paola2, Claudio Fazio1
1University of Palermo Physics Education Research Group (UOP-PERG), Dipartimento di Fisica e Chimica, Università di Palermo, Palermo, Italia
2Mathematics Education Research Group (GRIM), Dipartimento di Matematica e Informatica, Università di Palermo, Palermo, Italia

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: July 14, 2016; Accepted: September 9, 2016; Published: September 12, 2016
ABSTRACT
The problem of taking a set of data and separating it into subgroups where the elements of each subgroup are more similar to each other than they are to elements not in the subgroup has been extensively studied through the statistical method of cluster analysis. In this paper we want to discuss the application of this method to the field of education: particularly, we want to present the use of cluster analysis to separate students into groups that can be recognized and characterized by common traits in their answers to a questionnaire, without any prior knowledge of what form those groups would take (unsupervised classification). We start from a detailed study of the data processing needed by cluster analysis. Then two methods commonly used in cluster analysis are before described only from a theoretical point a view and after in the Section 4 through an example of application to data coming from an open-ended questionnaire administered to a sample of university students. In particular we describe and criticize the variables and parameters used to show the results of the cluster analysis methods.
Keywords:
Education, Unsupervised Methods, Hierarchical Clustering, Not-Hierarchical Clustering, Quantitative Analysis

1. Introduction
Many quantitative and qualitative research studies involving open- and closed-ended questionnaire analysis have provided instructors/teachers with tools to investigate students’ conceptual knowledge of various fields of physics. Many of these studies examined the consistency of students’ answers in a variety of situations [1] - [3] .
The problem of separating a group of students into subgroups where the elements of each subgroup are more similar to each other than they are to elements not in the subgroup has been studied through the methods of Cluster Analysis (ClA), but the use of the various available techniques have hardly been deepened to reveal their strength and weakness points. ClA can separate students into groups that can be recognized and characterized by common traits in their answers, without any prior knowledge of what form those groups would take (unsupervised classification [4] - [6] ).
ClA, introduced in Psychology by R.C. Tyron in 1939 [7] , has been the subject of research since the beginning of the 1960s, with its first systematic use by Sokal and Sneath [8] in 1963. The application of techniques related to ClA is common in many fields, including information technology, biology, medicine, archeology, econophysics and mar- ket research [9] - [12] . For example, in market research it is important to classify the key elements of the decision-making processes of business strategies as the characteristics, needs and behavior of buyers. These techniques allow the researcher to locate subsets or clusters within a set of objects of any nature that have a tendency to be homogeneous “in some sense”. The results of the analysis should reveal a high homogeneity within each group (intra-cluster), and high heterogeneity between groups (inter-clusters), in line with the chosen criteria.
ClA techniques [13] are exploratory and do not necessarily require a priori assumption about the data. The choice of the criteria of similarity between the data, the choice of clustering techniques, the selection of the number of groups to be obtained and the evaluation of the solution found, as well as the choice between possible alternative solutions, are particularly important. It is also important to bear in mind that the result of ClA, the subgroups of students, is dependent on the criteria used for the analysis of data as it is typical in all the processes of reduction and controlled simplification of information.
Some studies using ClA methods are found in the literature concerning research in education. They group and characterize students’ responses by using open-ended questionnaires [14] - [16] or multiple-choice tests [14] . All these papers show that the use of cluster analysis leads to identifiable groups of students that make sense to researchers and are consistent with previous results obtained using more traditional methods. Particularly, Springuel et al. [14] identify by means of cluster analysis groups of responses in open-ended questions about two-dimensional kinematics. These groups show striking similarity to response patterns previously reported in the literature and also provide additional information about unexpected differences between groups. Fazio et al. [15] [16] analyze students’ responses to specially designed written questionnaires using researcher-generated categories of reasoning, based on the physics education research literature on student understanding of relevant physics content. Through cluster analysis methods groups of students showing remarkable similarity in the reasoning categories are identified and the consistency of their deployed mental models is validated by comparison with researcher-built ideal profiles of student behavior known from previous research. Ding & Beichner [17] study five commonly used approaches to analyzing multiple-choice test data (classic test theory, factor analysis, cluster analysis, item response theory and model analysis) and show that cluster analysis is a good method to point out how student response patterns differ so as to classify student.
ClA can be carried out using various algorithms that significantly differ in their notion of what constitutes a cluster and how to effectively find them. Moreover, a deep ana- lysis of the ClA procedures applied is needed, because they often include approximations strongly influencing the interpretation of results. For this reason, in this paper we start from a detailed analysis of the data setting needed by ClA. Then, two methods com- monly used in ClA are described and the variables and parameters involved are outlined and criticized. Section IV deals with an example of application of these methods to the analysis of data from an open-ended questionnaire administered to a sample of university students, and discusses the significance and validity of information that can be obtained by using the two different solutions to clustering. Finally a comparison of the results obtained by using the two methods is done in order to reveal their coherence.
2. Data Coding
The application of ClA methods to answers to a closed-ended questionnaire does not pose to the researcher difficulties in the classification of student answers, as the categories can be considered the answers themselves.
On the other hand, research in education that uses open-ended questions and aims at performing a quantitative analysis of student answers usually involves the prior development of coding procedures aimed at categorizing student answers in a limited number of “typical” ways to answer each question. However, it is well known that there are inherent difficulties in the classification and coding of student responses. Hammer & Berland [18] point out that researchers “should not treat coding results as data but rather as tabulations of claims about data and that it is important to discuss the rates and substance of disagreements among coders” and proposes guidelines for the presentation of research that “quantifies” individual student answers. Among such guidelines, they focus on the need to make explicit that: “developing a coding scheme requires researchers to articulate definitions of categories well enough that others could interpret them and recognize them in the data”. Chi [19] describes the process of developing a coding scheme in the context of verbal data such as explanations, interviews, problem- solving protocols, and retrospective reports. The method of verbal analyses is deeply discussed with the objective of formulating an understanding of the representation of the knowledge used in cognitive performances.
On the basis of the approach previously described, the logical steps that the researcher can use in a research to process data coming from student answers to an open- or closed-ended questionnaire can be synthesized by the flow chart represented in Figure 1. In the case of open-ended questions, the student answers need to first be categorized by the n researchers involved in the study, by means of an analysis that can reveal patterns, trends, and common themes emerging from them. Through comparison and
Figure 1. Flow chart of the steps involved in processing data coming from student answers to an open- or closed-ended questionnaire
discussion among researchers, these themes are then developed and grouped in a number of categories whose definition take into account as much as possible the words, the phrase, the wording used by students [20] . Such categories actually are the typical “answering strategies” put into action by the N students tackling the questionnaire.
At the end of this phase, the whole set of answers given by students to the open- ended questionnaire is grouped into a limited number, M, of typical answers, i.e. the student answering strategies. M is obtained by adding all the answering strategies used by students when answering to each question.
In the case of closed-ended questions, the preliminary analysis described above is often not necessary, as the answers to each question are often already “classified” in a limited number, that are the explicit options for the respondent to select from.
The next step is unique for both the kind of questionnaire and involves the binary coding of student answers,1 according to the defined categories, generating a binary matrix (as shown in Table 1). So, through categorization (if needed) and coding, each student, i, can be identified by an array, ai, composed of M components 1 and 0, where 1 means that the student used a given answering strategy/answer option to respond to a question and 0 means that he/she did not use it. Then, a M × N binary matrix (the
Table 1. Matrix of data: the N students are indicated as S1, S2, …, SN, and the M answering strategies as AS1, AS2, ..., ASM.
“matrix of answering strategies”) modeled on the one shown in Table 1, is built. The columns in it show the N student arrays, ai, and the rows represent the M components of each array, i.e. the M answering strategies/answer options.
For example, let us say that student S1 used answering strategies AS2, AS3 and AS5 to respond to the questionnaire questions. Therefore, column S1 in Table 1 will contain the binary digit 1 in the three cells corresponding to these strategies, while all the other cells will be filled with 0.
The matrix depicted in Table 1 contains all the basic information needed to describe the sample behavior according to the previously described categorization. However, it needs some elaboration to be used for ClA (step 4 of Figure 1).
Particularly, ClA requires the definition of new quantities that are used to build the grouping, like the “similarity” or “distance” indexes. These indexes are defined by starting from the M × N binary matrix discussed above.
In the literature [7] [11] [13] the similarity between two students i and j of the sample is often expressed by taking into account the distance, dij, between them (which actually expresses their “dissimilarity”, in the sense that a higher value of distance involves a lower similarity).
A distance index can be defined by starting from the Pearson’s correlation coefficient. It allows the researcher to study the correlation between students i and j if the related variables describing them are numerical. If these variables are non-numerical variables (as in our case, where we are dealing with the arrays ai and aj containing a binary symbolic coding of the answers of students i and j, respectively), we need to use a modified form of the Pearson’s correlation coefficient, Rmod, similar to that defined by Tumminello et al. [20] . We define Rmod as,2
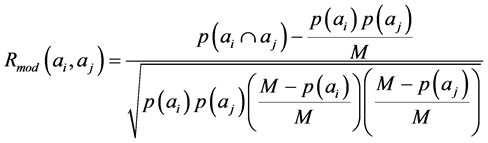 (1)
(1)
where p(ai), p(aj) are the number of properties of ai and aj explicitly present in our students (i.e. the numbers of 1’s in the arrays ai and aj, respectively), M is the total number of properties to study (in our case, the answering strategies) and 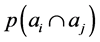 is the number of properties common to both students i and j (the common number of 1’s in the arrays ai and aj).
is the number of properties common to both students i and j (the common number of 1’s in the arrays ai and aj). 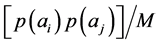 is the expected value of the properties common to ai and aj.
is the expected value of the properties common to ai and aj.
By following Equation (1) it is possible to find for each student, i, the N − 1 correlation coefficients Rmod between him/her and the others students (and the correlation coefficient with him/herself, that is, clearly, 1). All these correlation coefficients can be placed in a N × N matrix that contains the information we need to discuss the mutual relationships between our students.
The similarity between students i and j can be defined by choosing a type of metric to calculate the distance dij. Such a choice is often complex and depends on many factors. If we want two students, represented by arrays ai and aj and negatively correlated, to be more dissimilar than two positively correlated, a possible definition of the distance between ai and aj, making use of the modified correlation coefficient, Rmod(ai, aj), is:
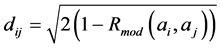 (2)
(2)
This function defines an Euclidean metric [22] , which is required for the following calculations. A distance dij between two students equal to zero means that they are completely similar (Rmod = 1), while a distance dij = 2 shows that the students are completely dissimilar (Rmod = −1). When the correlation between two students is 0 their distance is .
.
By following Equation (2) we can, then build a new N ´ N matrix, D (the distance matrix), containing all the mutual distances between the students. The main diagonal of D is composed by 0s (the distance between a student and him/herself is zero). Moreover, D is symmetrical with respect to the main diagonal.
3. Theoretical Framework of Clustering
Clustering Analysis methods can be roughly distinguished in Non-Hierarchical (or Centroid-Based), and Hierarchical ones (also known as connectivity based clustering methods). The first category of methods basically takes to partitions of the data space into a structure known as a Voronoi Diagram (a number of regions including subsets of similar data). The second one is based on the core idea of building a binary tree of the data that are then merged into similar groups. This tree is a useful summary of the data that are connected to form clusters based on their known distance, and it is sometimes referred to as a dendrogram.
A. Non-Hierarchical Clustering Analysis (NH-ClA)
Non-hierarchical clustering analysis is used to generate groupings of a sample of elements (in our case, students) by partitioning it and producing a smaller set of non-overlapping clusters with not hierarchical relationships between them. Among the currently used NH-ClA algorithms, we will consider k-means, which was first proposed by MacQueen in 1963 [23] .
The starting point is the choice of the number, q, of clusters one wants to populate and of an equal number of “seed points”, randomly selected in the bi-dimensional Cartesian space representing the data. The students are then grouped on the basis of the minimum distance between them and the seed points. Starting from an initial classification, students are iteratively transferred from one cluster to another or swapped with students from other clusters, until no further improvement can be made. The students belonging to a given cluster are used to find a new point, representing the average position of their spatial distribution. This is done for each cluster Clk (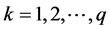 ) and the resulting points are called the cluster centroids Ck. This process is repeated and ends when the new centroids coincide with the old ones. As we said above, the spatial distribution of the set elements is represented in a 2-dimensional Cartesian space, creating what is known as the k-means graph (see Figure 2).
) and the resulting points are called the cluster centroids Ck. This process is repeated and ends when the new centroids coincide with the old ones. As we said above, the spatial distribution of the set elements is represented in a 2-dimensional Cartesian space, creating what is known as the k-means graph (see Figure 2).


Figure 2. A set of 150 hypothetical data partitioned in two (a); three (b) and four (c) clusters. The mean values of the Silhouette function are 0.47, 0.45 and 0.45, respectively.
NH-ClA has some points of weakness and here we will describe how it is possible to overcome them. The first involves the a-priori choice of the initial positions of the centroids. This is usually resolved in the literature [23] [24] by repeating the clustering procedure for several values of the initial conditions and selecting those that lead to the minimum values of the distances between each centroid and the cluster elements. Furthermore, at the beginning of the procedure, it is necessary to arbitrarily define the number, q, of clusters. A method widely used to decide if this number q, initially used to start the calculations, is the one that best fits the sample element distribution is the calculation of the so-called Silhouette Function, S, [25] [26] .
When the k-means clustering method is applied, in order to choose the number of clusters, q, to be initially used to perform the calculations, the so-called Silhouette Function, S, [25] [26] is defined. This function allows us to decide if the partition of our sample in q clusters is adequate, how dense a cluster is, and how well it is differentiated from the other ones.
For each selected number of clusters, q, and for each sample student, i, assigned to a cluster k, with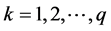 , a value of the Silhouette Function, Si(q), is calculated as
, a value of the Silhouette Function, Si(q), is calculated as

where the first term of the numerator is the average distance of the i-th student in cluster k to l-th student placed in a different cluster p (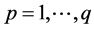 ), minimized over clusters. The second term is the average distance between the i-th student and another student j placed in the same cluster k.
), minimized over clusters. The second term is the average distance between the i-th student and another student j placed in the same cluster k.
Si(q) gives a measure of how similar student i is to the other students in its own cluster, when compared to students in other clusters. It ranges from −1 to +1: a value near +1 indicates that student i is well-matched to its own cluster, and poorly-matched to neighboring clusters. If most students have a high silhouette value, then the clustering solution is appropriate. If many students have a low or negative silhouette value, then the clustering solution could have either too many or too few clusters (i.e. the chosen number, q, of clusters should be modified).
Subsequently, the values Si(q) can be averaged on each cluster, k, to find the average silhouette value in the cluster, 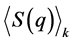 , and on the whole sample to find the total average silhouette value,
, and on the whole sample to find the total average silhouette value, 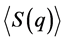 for the chosen clustering solution. Large values of
for the chosen clustering solution. Large values of  are to be related to the cluster elements being tightly arranged in the cluster k, and vice versa [25] [26] . Similarly, large values of
are to be related to the cluster elements being tightly arranged in the cluster k, and vice versa [25] [26] . Similarly, large values of 





The k-means results can be plotted in a 2-dimensional Cartesian space containing points that represent the students of the sample placed in the plane according to their mutual distances. As we said before, for each student, i, we know the N distances, dij between such a student and all the students of the sample (being dii = 0. It is, then, necessary to define a procedure to find two Cartesian coordinates for each student, starting from these N distances. This procedure consists in a linear transformation between a N-dimensional vector space and a 2-dimensional one and it is well known in the specialized literature as multidimensional scaling [28] .
Figure 3 shows an example of the spatial distribution of the results of a k-means analysis on a same hypothetical set of data, represented in a 2-dimensional Cartesian space.3 First three clusters (q = 3 in Figure 3(b)), and then four (q = 4 in Figure 3(b)) have been chosen to start the calculations. The x- and y-axes simply report the values needed to place the points according to their mutual distance. The average silhouette values, 


It is interesting to study how well a centroid geometrically characterizes its cluster. Two parameters affect this: both the cluster density and the number of its elements.4

Figure 3. Clustering of N = 64 hypothetical data using k-means method. Figure 1(a) shows q = 3 possible clusters, Figure 1(b) shows q = 4 clusters.
For this purpose, we propose a coefficient, rk, defined as the centroid reliability. It is calculated as follows:

where nk is the number of students contained in cluster Clk and 
In order to compare the reliability values of different clusters in a given partition the rk values can be normalized according to the following formula
where 

Once the appropriate partition of data has been found, we want to characterize each cluster in terms of the most prominent answering strategies. Such characterizations will help us to compare clusters. To do this, we start by creating a “virtual student” for each of the q clusters, Clk (with



Another way to find the array that describes the centroid of a cluster starts from the coordinates of the centroid in the 2-dimensional Cartesian Plane reporting the results of a k-means analysis. We devised a method that consists of repeating the k-means procedure in reverse, by using the iterative method described as follows. For each cluster, Clk, we define a random array 
where 

By using an iterative procedure that permutes the values of the random array 


B. Hierarchical Clustering Analysis (H-ClA)
Hierarchical clustering is a method of cluster construction that starts from the idea of elements (again students in our case) of a set being more related to nearby students than to farther away ones, and tries to arrange students representing them as being “above”, “below”, or “at the same level as” one another. This method connects students to form clusters based on the presence of common characteristics. As a hierarchy of clusters, which merge with each other at certain distances, is provided, the term “hierarchical clustering” has been used in the literature.
In H-ClA, which is sometimes used in education to analyze the answers given by students to open- and closed-ended questionnaires (see, for example, [14] - [17] ), each student is initially considered as a separate cluster. Then the two “closest” students are joined as a cluster and this process is continued (in a stepwise manner) to join one student with another, a student with a cluster, or a cluster with another cluster, until all the students are combined into one single cluster as one moves up the hierarchy (Agglomerative Hierarchical Clustering) [13] . Another possibility is to build recursive partitions from a single starting cluster that contains all the students observed (Divisive Hierarchical Clustering) [13] . The results of hierarchical clustering are graphically displayed as a tree, referred to as the hierarchical tree or dendrogram. The term “closest” is identified by a specific rule in each of the linkage methods. Hence, in different linkage methods, the corresponding distance matrix after each merger are differently computed.
Among the many linkage methods described in the literature, the following have been taken into account in education studies: Single, Complete, Average and Weighted Average. Each method differs in how it measures the distance between two clusters r and s by means of the definition of a new metric (an “ultrametric”), and consequently influences the interpretation of the word “closest”. Single linkage, also called nearest neighbor linkage, links r and s by using the smallest distance between the students in r and those in s; complete linkage, also called farthest neighbor linkage, uses the largest distance between the students in r and the ones in s; average linkage uses the average distance between the students in the two clusters; weighted average linkage uses a recursive definition for the distance between two clusters. If cluster r was created by combining clusters p and q, the distance between r and another cluster s is defined as the average of the distance between p and s and the distance between q and s.
To better represent the differences and approximations involved in the various linkages, an example is displayed in Figure 4.
Table 3 reports the recurrence relationships applied in order to calculate the ultrametric distances, δ, for the different linkage methods, on the basis of the Euclidean distances, dij, represented in matrix, D, (see Section 2).
Suppose r, p and q are existing clusters and cluster r is the cluster formed by merging p and q (r = p ں q). The distances between the elements of r and the elements of another cluster s are defined for the four linkage methods, as shown in Table 2 [39] , where nr indicates the number of students in cluster r, ns indicates the number of students in cluster s, xri is the i-th student in r and xsj is the j-th student in s.


Figure 4. (a) Dendrograms obtained for single linkage (a), complete linkage (b), average linkage (c) and weighted linkage (d) for the 7 element sample whose distances are reported in Table 3. The δ value on the y-axis is the “ultrametric” distance.
Table 2. Silhouette values for clusters depicted in Figure 3. The confidence intervals are reported according to a significance level (CI) of 95%8.
Single linkage links the two clusters r and s by using the smallest distance between the students in r and those in s; complete linkage uses the largest distance between the students in r and the ones in s; average linkage uses the average distance between the students in the two clusters; weighted average linkage uses a recursive definition for the distance between two clusters. If cluster r was created by combining clusters p and q, the distance between r and another cluster s is defined as the average of the distance between p and s and the distance between q and s.
It is important to note that the difference between dendrograms obtained by using the average and the weighted average methods are evident only when the number of elements is not too low. Here, we report an example for a sample of 7 elements. Table 4 supplies the matrix of distances between the 7 elements and Figure 4(a) and Figure 4(b) show the two dendrograms for the single, complete, average and weighted average linkage, respectively. The figure shows some differences, as for example the values of the highest linkage: δ = 1.08 (a) and δ = 1.2 (b).
Several conditions can determine the choice of a specific linkage method. For instance, when the source data are in binary form (as in our case) the single and complete linkage methods do not give a smooth progression of the distances [14] . For this reason, when the source data are in binary form, the viable linkage methods actually reduce to the average or weighted average ones.
In the specialized literature it is easy to find numerical indexes driving the choice of a specific linkage method, such as the “cophenetic correlation coefficient” [33] [34] .
Table 3. “Ultrametric” distance formulas of commonly used linkages.
Table 4. Matrix of distances of a generic sample of 7 elements.
The cophenetic correlation coefficient, ccoph, gives a measure of the concordance between the two matrixes: matrix D of the distances and matrix Δ of the ultrametric distances. It is defined as
where:
・ dij is the distance between elements i and j in D.
・ δij is the ultrametric distance between elements i and j in Δ, i.e. the height of the link at which the two elements i and j are first joined together.
・ 

High values of ccoph indicate how much the matrix Δ is actually representative of matrix D and, consequently, how much ultrametric distances, δij, are representative of distances, dij.
Its value is based on the correlation (like the Pearson one [35] ) between the original distances, in D, and the ultrametric distances given by the linkage type (contained in a new matrix, Δ), and it evaluates how much the latter are actually representative of the former. More precisely, the cophenetic coefficient is a measure of how faithfully a dendrogram preserves the pair wise distances between the original un-modeled data points. In the cases we analyzed the highest values of the cophenetic coefficient are always obtained by using average or weighted average linkage methods.
Reading a dendrogram and finding clusters in it can be a rather arbitrary process. There is not a widely accepted criterion that can be applied in order to determine the distance values to be chosen for identifying the clusters. Different criteria, named stopping criteria, aimed at finding the optimal number of clusters are discussed in the literature (see, for example, Springuel [35] ). Many of these cannot be applied to non- numerical data, as it is our case. Here we discuss two criteria applicable to our case: the first one involves the calculation of the “inconsistency coefficient” [36] and the second is known as “variation ratio criterion” [37] .
One way to decide if the grouping in a data set is adequate is to compare the height of each link in a cluster tree with the heights of neighboring links below it in the tree. A link that is approximately the same height as the links below it indicates that there are no distinct divisions between the objects joined at this level of the hierarchy. These links are said to exhibit a high level of consistency, because the distance between the objects being joined is approximately the same as the distances between the objects they contain. On the other hand, a link whose height differs noticeably from the height of the links below it indicates that the objects joined at this level in the cluster tree are much farther apart from each other than their components were when they were joined. This link is said to be inconsistent with the links below it.
The relative consistency of each link in a hierarchical cluster tree can be quantified through the inconsistency coefficient, Ik [33] .
The inconsistency coefficient compares the height of each link in a cluster tree made of N elements, with the heights of neighboring links above it in the tree.
The calculations of inconsistency coefficients are performed on the matrix of the ultrametric distances, Δ, generated by the chosen linkage method.
We consider two clusters, s and t, whose distance value is reported in matrix Δ, and that converge in a new link, k, (with
where 


This formula shows that a link whose height differs noticeably from the height of the n links below it indicates that the objects joined at this level in the cluster tree are much farther apart from each other than their n components. Such a link has an high value of Ik. On the contrary, if the link, k, is approximately the same height as the links below it, no distinct divisions between the objects joined at this level of the hierarchy can be identified. Such a link has a low value of Ik.
The higher is the value of this coefficient, the less consistent is the link connecting the students. A link that joins distinct clusters has a high inconsistency coefficient; a link that joins indistinct clusters has a low inconsistency coefficient.
The choice of Ik value to be considered significant in order to define a threshold is arbitrary and involves the choice of the significant number of clusters that can describe the whole sample. Moreover, in the specialized literature [33] the Ik value of a given link is considered by also taking into account the ultrametric distance of the link, in order to avoid a too low or too high fragmentation9 of the sample clusters. This means that, after having disregarded the links that produce a too low fragmentation, the Ik of the links just below are taken into account.
The variation ratio criterion (VRC) [37] is also used in the literature to define the clustering validity.
For a partition of N elements in q cluster, the VRC value is defined as:
where WGSS (Within Group Squared Sum) represents the sum of the distance squares between the elements belonging to a same cluster and BGSS (Between Group Squared Sum), defines the sum of the distance squares between elements of a given cluster group and the external ones.
It measures the ratio between the sum of the squares of the distances between the elements belonging to the same cluster and the sum of the squares of the distances between the elements of a given cluster and the external ones. The larger is the VRC value, the better is the clustering.
It is worth noting that the evaluation of the number of cluster to be consider significant for an education-focused research should also be influenced by pedagogic considerations, related to the interpretation of the clusters that are formed. Although it could be desirable to have a fine grain description of our sample students, this can make the search for common trends in the sample too complicated, and perhaps less interesting if too many “micro-behaviors” related to the various small clusters are found and have to be explained.
As a final consideration, we want to point out that the comparison of different clustering methods (in our case NH-ClA and H-ClA methods) is a relevant point. As Meila et al. [38] point out: “just as one cannot define a best clustering method out of the content, one cannot define a criterion for comparing clusters that fits every problem”. Many coefficients have been identified to compare two partitions of the same data set obtained with different methods, but the majority of them are not applicable to our data that are in binary form. However a criterion, called variation of information (VI), can be applied in our case. It measures the difference in information shared between two particular partitions of data and the total information content of the two partitions. In this sense, the smaller the distance between the two clustering the more these are coherent with each other, and vice versa. VI can be normalized to 0 - 1 range: a value equal to 0 indicates very similar clustering results, and a value equal to 1 corresponds to very different ones. Meila et al. [38] supply all the details for VI calculation as well as examples of its application.
In the following sections we will present an application of the described ClA procedures to the analysis of data from an open-ended questionnaire administered to a sample of university students, and we will discuss the results of the application on these data of the two methods of Cluster Analysis we outlined above. Similarly to what we have done in Figure 1, we report in Figure 5 the flowchart of the logical steps we are going to follow here. This figure should be considered as the continuation of the flow chart shown in Figure 1 and starts from the resources we will use to perform ClA and the subsequent result interpretation, i.e. the Distance Matrix and the Answering Strategy Set shown in Figure 1.
Each set of clusters that is obtained by means of H-ClA and/or NH-ClA is interpreted on the basis of the answering strategy set (as explained in Section IV) and these interpretations, together with a possible comparison of the results obtained by the two methods, leads us to the final results of the study.
4. An Implementation of Cluster Analysis
In this Section we want to describe an application of the methods discussed above to the analysis of the answers to a questionnaire composed by 4 open-ended questions, each with 5 possible answering strategies resulting from the preliminary analysis
Figure 5. Flow chart of the steps involved in elaborating data coming from student answers to a questionnaire.
discussed in Section 2.10 124 students participated in the survey and completed the questionnaire.
A. Non-hierarchical clustering analysis (NH-ClA)
All the clustering calculations were made using a custom software, written in C language, for the NH-ClA (k-means method), as well as for H-ClA where the weighted average linkage method was applied. The graphical representations of clusters in both cases were obtained using the well-known software MATLAB [39] .
In order to define the number q of clusters that best partitions our sample, the mean value of S-function, 


Figure 7 shows the representation of this partition in a 2-dimensional graph. The four clusters show a partition of our sample into groups made up of different numbers of students (see Table 3).
The four clusters Clk (




Figure 6. Average Silhouette values and related 95% confidence intervals (CI) for different cluster partitions of our sample. The two highest values are obtained for partitions in q = 4 clusters (

Figure 7. K-means graph. Each point in this Cartesian plane represents a student. Points labeled C1, C2, C3, C4 are the centroids.
The 

B. Hierarchical clustering analysis (H-ClA)
In order to apply the H-ClA method to our data, we first had to choose what kind of linkage to use. Since we could not use simple or complete linkages (see Section 3(B)), we calculated the cophenetic correlation coefficient for the average and weighted average linkages, which gave a measure of the accordance between the distances calculated by (2) and the ultrametric distances introduced by the linkage. We obtained the values 0.61 and 0.68 for average and weighted average linkages, respectively. We chose to use
Table 5. An overview of results obtained by NH-ClA method.
the weighted average link and Figure 8 shows the obtained dendrogram of the nested cluster structure.
In this figure the vertical axis represents the ultrametric distance between two clusters when they are joined; the horizontal axis is divided in 124 ticks, each representing a student. Furthermore, vertical lines represent students or groups of students and horizontal lines represent the joining of two clusters. Vertical lines are always placed in the center of the group of students in a cluster and horizontal lines are placed at the height which corresponds to the distance between the two clusters that they join.
By describing the cluster tree from the top down, as if clusters are splitting apart, we can see that all the students come together into a single cluster, located at the top of the figure. In this cluster, for each pair of students, i and j, the ultrametric distance is
If we disregard the higher links (δ ≈ 1.8, black, dashed links in Figure 8) because their use would produce a unique, single cluster of our sample, or two big ones, and we also take into account a threshold for the Inconsistency Coefficients equal to 1.6 (i.e. we consider inconsistent all the links that have Ik > 1.6, we can accept all the links just below, including the red, dotted ones in Figure 8 (that have Ik equal to 1.4 and 1.6, respectively). So, we find a partition of our sample into 4 clusters. If, on the other hand, we introduce a lower threshold for the Ik value, but still not producing a too high fragmentation, like for example Ik > 1.25, we must disregard the dotted links in the dendrogram in Figure 8, and obtain 6 clusters. This last representation has a higher significance than the previous one since the links displayed are those that, at equal distances, show a higher consistency.
Figure 8. Dendrogram of our data. Horizontal and vertical axes represent students and ultrametric distances, respectively. Black, dashed links are at ultrametric distances of about 1.8. The Inconsistency Coefficients of the links just below these links are shown. Six clusters, (α, β, γ, δ, ε, ζ) are formed.
Figure 8 shows the 6 distinct clusters α, β, …, ζ above identified. They can be characterized by analyzing the most frequent answers to each of the four questions in the questionnaire (see Section 5).
In order to verify the validity of our choice we also used the VRC (see Section 3). Figure 9 shows the VRC values for different numbers of clusters. The maximum value is obtained for q = 6.
Table 6 provides significant information concerning the H-ClA clustering. By looking at the number of students, and at their identity, we can see that the main results of the new grouping are the redistribution of the students, originally assigned to cluster Cl3 by NH-ClA, into different sub groups, and a redistribution of students located on the edges of cluster Cl4. Furthermore, the students in cluster Cl1 are all located in cluster β and students in cluster Cl2 are all located in cluster γ. This is in accordance with the high values of the 
In conclusion, we can say that although the two partitions of our student sample are different, they are consistent. The characterization via the dendrogram allows us to obtain more detail. This happens in particular, in the case of cluster Cl3, which turns out to be very extensive, with a large number of students and a low value of
In order to better compare the results obtained by NH-ClA and H-ClA methods, we applied the variation of information (VI) criterion (see Section III), that measures the amount of information gained and lost when switching from one type of clustering to another. We calculated the value of VI to compare the 4-clustering results of k-means method with the 4-clustering, 5-clustering and 6-clustering results of H-ClA method and obtained the values of 0.34, 0.38 and 0.28, respectively. We can conclude that the best agreement can be found between the 4-clustering results of k-means method and the 6-clustering results of H-ClA method.
Figure 9. VRC values for some partitions of our sample in different numbers of clusters.
Table 6. An overview of results obtained by H-ClA and comparison with those obtained by NH-ClA method.
*i.e. (14)Cl4+(3)Cl3, means that cluster α contains 14 students part of the cluster Cl4 (in NH-ClA) + 3 students part of cluster Cl3.
5. Conclusions
The use of cluster analysis techniques is common in many fields of research as, for example, information technology, biology, medicine, archeology, econophysics and market research. These techniques allow the researcher to locate subsets or clusters within a set of objects of any nature that have a tendency to be homogeneous “in some sense”. The results of the analysis can reveal a high homogeneity within each group (intra- cluster), and high heterogeneity between groups (inter-clusters), in line with the chosen criteria. However, only a limited number of examples of application of ClA in the field of education are available, and many aspects of the use of the various available techniques have hardly been deepened to reveal their strength and weakness points.
In this paper we started from some preliminary considerations about the problems arising from the coding procedures of student answers to closed- and open-ended questionnaires. These procedures are aimed at categorizing student answers in a limited number of “typical” ways to answer each question. We gave some examples of procedures that can be used according to the questionnaire type (closed- and open-ended), and then we presented and discussed two ClA methodologies that can be sometimes found in the education literature. We started describing a not-hierarchical ClA method, the k-means one that allows the researcher in Education to easily separate students into groups that can be recognized and characterized by common traits in their answers to a questionnaire. It is also possible to easily represent these groups in a 2-dimensional Cartesian graph containing points that represent the students of the sample on the basis of their mutual distances, related to the mutual correlation among students answering the questionnaire. Each of the clusters found by the analysis can be characterized by a point, the “centroid”, representing the answers most frequently given by the students comprised in the cluster. Some functions and parameters useful to carefully evaluate the reliability of the results obtained have also been discussed.
Following this, we described a different method of analysis, based on hierarchical clustering that can also help the researcher to find student groups where the elements (the students) are linked by common traits in their answers to a questionnaire. This method allows the researcher to visualize the clustering results in a graphic tree, called “dendrogram” that easily shows the links between couples and/or groups of students on the basis of their mutual distances. Each cluster can be characterized on the basis of the answers most frequently given by the students in it. Again, functions and parameters useful to evaluate the reliability of the results have been discussed.
Finally, an application of these two methods to the analysis of the answers to a real questionnaire has been given, in order to clearly show what the choices that the researcher must do are, and what parameters he/she must use in order to obtain the best partitions of the whole student groups and check the reliability of the result. In order to study the coherence of the results obtained by using hierarchical and not-hierarchical ClA methods, we compared the results each other. We found that many of the clusters found by NH-ClA are also present in H-ClA; yet some of the clusters found with NH- ClA are further splitted, and can be, so, better characterized, by means of H-ClA.
We can conclude that the H-ClA method we discussed here allows the researcher to easily obtain and visualize in a 2-D graph a global view of the student behaviour with respect to the answers to a questionnaire and to obtain a first characterization of student behaviour in terms of their most frequently used answering strategies. The NH- ClA method, on the other hand, although producing a graph not easy to read as the one produced with the other method (dendrogram vs. Voronoi diagram), allows the researcher to obtain results coherent with the NH-ClA ones and can offer a finer grain detail of student behaviour.
Cite this paper
Battaglia, O.R., Di Paola, B. and Fazio, C. (2016) A New Approach to Investigate Students’ Behavior by Using Cluster Analysis as an Unsupervised Methodology in the Field of Education. Ap- plied Mathematics, 7, 1649-1673. http://dx.doi.org/10.4236/am.2016.715142
References
- 1. Bao, L. and Redish, E.F. (2006) Model Analysis: Representing and Assessing the Dynamics of Student Learning. Physical Review Special Topics—Physics Education Research, 2, Article ID: 010103.
http://dx.doi.org/10.1103/physrevstper.2.010103 - 2. Mestre, J.P. (2002) Probing Adults’ Conceptual Understanding and Transfer of Learning via Problem Posing. Journal of Applied Developmental Psychology, 23, 9-50.
http://dx.doi.org/10.1016/S0193-3973(01)00101-0 - 3. Redfors, A. and Ryder, J. (2001) University Physics Students’ Use of Models in Explanations of Phenomena Involving Interaction between Metals and Electromagnetic Radiation. International Journal of Science Education, 23, 1283-1301.
http://dx.doi.org/10.1080/09500690110038620 - 4. Coates, A. and Ng, A.Y. (2012) Learning Feature Representations with K-Means. In: Montavon, G., Orr, G.B. and Muller, K.R., Eds., Neural Networks: Tricks of the Trade, 2nd Edition, Springer, Berlin, 561-580.
http://dx.doi.org/10.1007/978-3-642-35289-8_30 - 5. Dayan, P. (1999) Unsupervised Learning. In: Wilson, R.A. and Keil, F., Eds., The MIT Encyclopedia of the Cognitive Sciences Wilson, The MIT Press, London, 1-7.
- 6. Sathya, R. and Abraham, A. (2013) Comparison of Supervised and Unsupervised Learning Algorithms for Pattern Classification. International Journal of Advanced Research in Artificial Intelligence, 2, 34-38.
http://dx.doi.org/10.14569/IJARAI.2013.020206 - 7. Tryon, R.C. (1939) Cluster Analysis: Correlation Profile and Orthometric (Factor) Analysis for the Isolation of Unities in Mind and Personality. Edwards Brothers, Ann Arbor.
- 8. Sokal, R.R. and Sneath, P.H.A. (1963) Principles of Numerical Taxonomy. W.H. Freeman & Co., New York.
- 9. Ott, J. (1999) Analysis of Human Genetic Linkage. 3rd Edition, Johns Hopkins University Press, Baltimore.
- 10. Allen, D.N. and Goldstein, G. (Eds.) (2013) Cluster Analysis in Neuropsychological Research: 13 Recent Applications. Springer Science + Business Media, New York.
- 11. Mantegna, R.N. (1999) Hierarchical Structure in Financial Markets. European Physical Journal B, 11, 193-197.
http://dx.doi.org/10.1007/s100510050929 - 12. Cowgill, M.C. and Harvey, R.J. (1999) A Genetic Algorithm Approach to Cluster Analysis. Computers and Mathematics with Applications, 37, 99-108.
http://dx.doi.org/10.1016/S0898-1221(99)00090-5 - 13. Everitt, B.S., Landau, S., Leese, M. and Stahl, D. (2011) Cluster Analysis. John Wiley & Sons Ltd., Chichester.
- 14. Springuel, R.P., Wittmann, M.C. and Thompson, J.R. (2007) Applying Clustering to Statistical Analysis of Student Reasoning about Two-Dimensional Kinematics. Physical Review Special Topics—Physics Education Research, 3, Article ID: 020107.
http://dx.doi.org/10.1103/physrevstper.3.020107 - 15. Fazio, C., Di Paola, B. and Guastella, I. (2012) Prospective Elementary Teachers’ Perceptions of the Processes of Modeling: A Case Study. Physical Review Special Topics—Physics Education Research, 8, Article ID: 010110.
http://dx.doi.org/10.1103/physrevstper.8.010110 - 16. Fazio, C., Battaglia, O.R. and Di Paola, B. (2013) Investigating the Quality of Mental Models Deployed by Undergraduate Engineering Students in Creating Explanations: The Case of Thermally Activated Phenomena. Physical Review Special Topics—Physics Education Research, 9, Article ID: 020101.
http://dx.doi.org/10.1103/physrevstper.9.020101 - 17. Ding, L. and Beichner, R. (2009) Approaches to Data Analysis of Multiple-Choice Questions. Physical Review Special Topics—Physics Education Research, 5, Article ID: 020103.
http://dx.doi.org/10.1103/physrevstper.5.020103 - 18. Hammer, D. and Berland, L.K. (2014) Confusing Claims for Data: A Critique of Common Practices for Presenting Qualitative Research on Learning. Journal of the Learning Sciences, 23, 37-46.
http://dx.doi.org/10.1080/10508406.2013.802652 - 19. Chi, M.T.H. (1997) Quantifying Qualitative Analyses of Verbal Data: A Practical Guide. Journal of the Learning Sciences, 6, 271-315.
http://dx.doi.org/10.1207/s15327809jls0603_1 - 20. Tumminello, M., Micciché, S., Dominguez, L.J., Lamura, G., Melchiorre, M.G., Barbagallo, M. and Mantegna, R.N. (2011) Happy Aged People Are All Alike, While Every Unhappy Aged Person Is Unhappy in Its Own. PLoS ONE, 6, e23377.
http://dx.doi.org/10.1371/journal.pone.0023377 - 21. Lerman, I.C., Gras, R. and Rostam, H. (1981) Elaboration et evaluation d’un indice d’implication pour des données binaires I. Mathématiques et Sciences Humaines, 74, 5-35.
- 22. Gower, J.C. (1966) Some Distance Properties of Latent Root and Vector Methods Used in Multivariate Analysis. Biometrika Trust, 53, 325-338.
http://dx.doi.org/10.1093/biomet/53.3-4.325 - 23. MacQueen, J. (1967) Some Methods for Classification and Analysis of Multivariate Observations. Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability, 1, 281-297.
- 24. Stewart, J., Miller, M., Audo, C. and Stewart, G. (2012) Using Cluster Analysis to Identify Patterns in Students’ Responses to Contextually Different Conceptual Problems. Physical Review Special Topics—Physics Education Research, 8, Article ID: 020112.
http://dx.doi.org/10.1103/physrevstper.8.020112 - 25. Rouseeuw, P.J. (1987) Silhouttes: A Graphical Aid to the Interpretation and Validation of Cluster Analysis. Journal of Computational and Applied Mathematics, 20, 53-65.
http://dx.doi.org/10.1016/0377-0427(87)90125-7 - 26. Saxena, P., Singh, V. and Lehri, S. (2013) Evolving Efficient Clustering Patterns in Liver Patient Data through Data Mining Techniques. International Journal of Computer Applications, 66, 23-28.
- 27. Struyf, A., Hubert, M. and Rousseeuw, P.J. (1997) Clustering in an Object-Oriented Environment. Journal of Statistical Software, 1, 1-30.
- 28. Borg, I. and Groenen, P. (1997) Modern Multidimensional Scaling. Springer, New York.
http://dx.doi.org/10.1007/978-1-4757-2711-1 - 29. Di Paola, B., Battaglia, O.R. and Fazio, C. (2016) Non-Hierarchical Clustering to Analyse an Open-Ended Questionnaire on Algebraic Thinking. South African Journal of Education, 36, 1-13.
http://dx.doi.org/10.15700/saje.v36n1a1142 - 30. Battaglia, O.R. and Di Paola, B. (2015) A Quantitative Method to Analyse an Open Answer Questionnaire: A Case Study about the Boltzmann Factor. GIREP-MPTL 2014 Teching/Learning Physics: Integrating Research into Practice, University of Palermo, 7-12 July 2014.
- 31. Di Ciccio, T.J. and Efron, B. (1996) Bootstrap Confidence Intervals. Statistical Science, 11, 189-228.
http://dx.doi.org/10.1214/ss/1032280214 - 32. Inkley, D.V. (1997) Bootstrap Methods and Their Applications. Cambridge Series in Statistical and Probabilistic Mathematics, Cambridge University Press, Cambridge.
- 33. Sokal, R.R. and Rohlf, F.J. (1962) The Comparison of Dendrograms by Objective Methods. International Association for Plant Taxonomy, 11, 33-40.
http://dx.doi.org/10.2307/1217208 - 34. Saracli, S., Dogan, N. and Dogan, I. (2013) Comparison of Hierarchical Cluster Analysis Methods by Cophenetic Correlation. Journal of Inequalities and Application, 2013, 203.
http://dx.doi.org/10.1186/1029-242X-2013-203 - 35. Springuel, R.P. (2010) Applying Cluster Analysis to Physics Education Research Data. PhD Thesis, the University of Maine, Orono. www.academia.edu
- 36. GhasemiGol, M., Yazdi, H.S. and Monsefi, R. (2010) A New Hierarchical Clustering Algorithm on Fuzzy Data (FHCA). International Journal of Computer and Electrical Engineering, 2, 134-140.
http://dx.doi.org/10.7763/IJCEE.2010.V2.126 - 37. Calinski, T. and Harabasz, J. (1974) A Dendrite Method for Cluster Analysis: Communications in Statistics. Theory and Methods, 3, 1-27.
http://dx.doi.org/10.1080/03610927408827101 - 38. Meila, M. (2007) Comparing Clusterings—An Information Based Distance. Journal of Multivariate Analysis, 98, 873-895.
http://dx.doi.org/10.1016/j.jmva.2006.11.013 - 39. The MathWorks Inc (2015) MATLAB Version 8.6. Natick. www.mathworks.com/products/matlab/
NOTES
1For the sakes of simplicity here we refer to the use of a two-level coding, where 1 means that a given answering strategy/answer option was used and 0 means that that strategy was not used.
2Equation (1) is formally similar to the Similarity Index used by us in [15] [16] . However, Equation (1) is a version of Pearson’s correlation coefficient adapted to the case of non-numerical variables, while the other is an index, defined by Lerman [21] , that defines the similarity between two elements in a probabilistic form and can be directly used to partition a data sample.
3Other examples of use of NH-ClA in Mathematics and Physics Education Research can be found in the literature. See, for example, the recent works of Di Paola et al. [29] and Battaglia & Di Paola [30] .
4For example, two clusters with similar density but different student numbers (i.e. with different variability of student properties) are differently characterized by their centroids: the more populated cluster being less well characterized by its centroid than the other one.
5The term 


6It is worth noting that if some answering strategies are only slightly more frequent than the other ones all those with similar frequencies should also be considered.
7As usual in a procedure to minimize an objective function (in our case, σ), the result may not be unique. In order to be sure to obtain an absolute minimum of σ we repeated the procedure several times, each time changing the initial conditions, i.e. array
8The confidence intervals have been calculated by using the Bootstrap method [30] [31] , as the distribution of the Silhouette values is not a-priori known.
9“Too low” fragmentation is here to be intended as a situation where one or two big clusters are produced, that do not allow us to effectively describe the sample behavior. A “too high” fragmentation means that many small clusters, containing only a few students, are produced.
10So, in the following, 1A, 1B, ..., 1E represent the 5 identified answering strategies used by students to tackle question 1, 2A, 2B, ..., 2E are the 5 answering strategies for question 2, and so on.
11As discussed in Section III, for each value of q the clustering procedure was repeated for several values of the initial conditions. In each case, we selected the cluster solution that leads to the minimum values of the distances between each centroid and the cluster elements.













