Applied Mathematics
Vol.07 No.12(2016), Article ID:68980,14 pages
10.4236/am.2016.712113
Study of Thermally Induced Vibration of Non-Homogeneous Trapezoidal Plate with Parabolically Thickness Variation in Both Directions
Kavita1, Satish Kumar1, Pragati Sharma2*
1Department of Mathematics, M. M. University, Mullana, India
2Department of Mathematics, Haryana College of Technology & Management, Kaithal, India

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 May 2016; accepted 22 July 2016; published 25 July 2016
ABSTRACT
The present analysis demonstrates the thermal effect on vibrations of a symmetric, non-homoge- neous trapezoidal plate with parabolically varying thickness in both directions. The variation in Young’s modulus and mass density is the main cause for the occurrence of non-homogeneity in plate’s material. In this consideration, density varies linearly in one direction. The governing differential equations have been derived by Rayleigh-Ritz method in order to attain fundamental frequencies. With C-S-C-S boundary condition, a two term deflection function has been considered. The effect of structural parameters such as taper constants, thermal gradient, aspect ratio and non-homogeneity constant has been investigated for first two modes of vibration. The obtained numerical results have been presented in tabular and graphical form.
Keywords:
Vibration, Trapezoidal Plate, Taper Constants, Thermal Gradient, Aspect Ratio, Non-Homogeneity, Parabolically Thickness, Linearly Density

1. Introduction
People became interested in vibration when the first musical instruments, probably whistles or drums were discovered. Since then people have applied ingenuity and critical investigation to study the phenomenon of vibration. Many studies in existing period have been aggravated by the engineering applications of vibration, such as design of machines, foundations, structures, engines and turbine systems. Most major movers have vibrational problems because of the inbuilt unbalance in the engines. In spite of its detrimental effects, vibration can be utilized profitably in several industrial and consumer applications.
In many engineering applications different types of plates such as rectangular, parallelogram, circular etc. act as an integral part of the system. In contrast of uniform thickness of plate, the suitable variation in thickness in plate has a significant effect on its vibration. Thus, the choice of material depends on suitable properties of materials. On the whole, non-homogeneity is a significant constituent of any design which occurs as a result of variation in density. Literature shows that the vibration analysis has inspired many researchers to do work in this direction. Out of them few are given under. Kumar and Lal [1] worked on the vibrations of non-homogeneous orthotropic rectangular plates with bilinear thickness variation resting on Winkler foundation. Kumar and Tomar [2] had studied the free transverse vibrations of monoclinic rectangular plates with continuously varying thickness and density. Johri and Johri [3] had worked on the exponential thermal effect on vibration of non-homo- geneous orthotropic rectangular plate having bi-directional linear variation in thickness. Gupta et al. [4] did the vibration analysis of non-homogeneous circular plate of non-linear thickness variation by differential quadrature method. Li and Zhou [5] discussed the shooting method for non-linear vibration and thermal buckling of heated orthotropic circular plates. Chakraverty et al. [6] studied the effect of non-homogeneity on natural frequencies of vibration of elliptic plates. Gupta et al. [7] discussed the vibration of visco-elastic orthotropic parallelogram plate with linear thickness variation in both directions. Chen et al. [8] worked on the free vibration of non-ho- mogeneous transversely isotropic magneto-electro-elastic plates. Gurses et al. [9] analyzed the shear deformable laminated composite trapezoidal plates. Kitipornchai et al. [10] presented a global approach for vibration of thick trapezoidal plates. Sayad and Ghazy [11] studied the rayleigh-ritz method for free vibration of midline trapezoidal plates. Leung et al. [12] had studied the free vibration of laminated composite plates subjected to in-plane stresses using trapezoidal p-element. McGee and Butalia [13] presented the natural vibrations of shear deformable cantilevered skewed trapezoidal and triangular thick plates. Qatu [14] studied the vibrations of laminated composite completely free triangular and trapezoidal plates. Grigorenko et al. [15] used spline functions to solve boundary-value problems for laminated orthotropic trapezoidal plates of variable thickness. Feng and Min [16] worked on the vibrations of axially moving visco-elastic plate with parabolically varying thickness. Gupta and Sharma [17] evaluated the forced axisymmetric response of an annular plate of parabolically varying thickness. Liew and Lim [18] studied the transverse vibration of trapezoidal plates of variable thickness: symmetric trapezoids. Maruyama et al. [19] presented an experimental study of the free vibration of clamped trapezoidal plates. Karami et al. [20] used a differential quadrature method for skewed and trapezoidal laminated plates. Huang et al. [21] carried out experimental and numerical investigations for the free vibration of cantilever trapezoidal plates. Gupta and Sharma [22] studied the effect of thermal gradient on transverse vibration of non-homogeneous orthotropic trapezoidal plate of parabolically varying thickness. Gupta and Sharma [23] observed the effect of linear thermal gradient on vibrations of trapezoidal plates whose thickness varies parabolically. Gupta and Sharma [24] study the thermally induced vibration of non-homogeneous trapezoidal plate with varying thickness and density.
The existing work is an attempt to investigate the thermal effect on vibration of non-homogeneous trapezoidal plate of bi-parabolically varying thickness with linear density variation. To attain the natural frequencies for the first two modes of vibration Rayleigh-Ritz’s method has been applied. The deflection function has been taken to satisfy the C-S-C-S boundary condition. All the obtained results have been presented in tabular and graphical form.
2. Mathematical Formulation
2.1. Geometry of the Plate
For the study of transverse vibration a thin, symmetric, non-homogeneous trapezoidal plate with varying thickness and density has been taken. The geometry of the plate is shown in Figure 1.
2.2. Thickness and Density
The thickness of the plate which varies parabolically in both directions can be expressed as
Figure 1. Geometry of the trapezoidal plate.
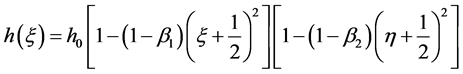 (1)
(1)
The non-homogeneity occurs in the bodies because of imperfection of materials and it is assumed to arise due to the linear variation in density along the length of the plate. So, it can be stated as
 (2)
(2)
It is assumed that the temperature of the non-homogeneous trapezoidal plate varies linearly along x-axis and is of the form
 (3)
(3)
where 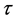 represent the excess above the reference temperature at a distance
represent the excess above the reference temperature at a distance  and
and 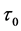 denotes the temperature excess above the reference temperature at the end
denotes the temperature excess above the reference temperature at the end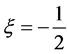 .
.
The temperature dependence of the modulus of elasticity for most of the engineering materials is specified as [25]
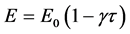 (4)
(4)
where 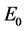 denotes the value of Young’s modulus at reference temperature
denotes the value of Young’s modulus at reference temperature  and
and  is the slope of variation of E with
is the slope of variation of E with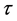 .
.
Using Equation (3) into Equation (4), one obtain
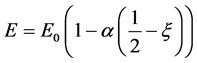 (5)
(5)
where  known as thermal gradient.
known as thermal gradient.
3. Equation of Motion
The governing differential equation for kinetic energy T and strain energy V for a non-homogeneous trapezoidal plate with bi-parabolically varying thickness can be expressed as


where 

Flexural rigidity 

where


On using Equation (9) and (5), Equation (8) gives the value of flexural rigidity as follows

Now after putting Equations (1), (2) into Equation (6) and (10) into Equation (7), kinetic energy and strain energy become

And

Two terms deflection function for a C-S-C-S trapezoidal plate can be defined as,

where 

In this manner, for vibrational analysis a trapezoidal plate whose two sides are clamped and two are simply- supported has been considered. The deflection function which is already discussed by Equation (13) satisfies the boundary conditions and presents an excellent evaluation to the frequency. Thus, the boundaries are given by four straight lines as follows:
and

4. Method of Solution
In addition the frequency is calculated through Rayleigh-Ritz technique which is based on the principle of conservation of energy i.e. the maximum strain energy must be equal to the maximum kinetic energy. Therefore, the resulting equation can be described by

Using boundary condition (14) into Equation (11) and (12), one gets

And

Now Equations (16) and (17) consists the values of T and V so, put these values into Equation (15), we obtain

where


And

is a frequency parameter.
Equation (18) includes two unknowns 


On simplifying (22), we get

where


The quadratic equation in 

5. Results and Discussion
The existing work deals with the vibration behavior of a non-homogeneous trapezoidal plate whose thickness varies bi-parabolically and density varies linearly in one direction. All results acquired by Equation (24) provide the values of frequency parameter for different values of taper constants, thermal gradient, aspect ratios and non-homogeneity constant. The natural frequencies are estimated for first two modes of vibration. The value of Poisson’s ratio is considered as 0.33. With the help of tables and graphs all the results have been displayed.
Table1 includes the values of frequency parameter 







Table 2 contains the values of frequency parameter 








Table 3 depicts the values of frequency parameter 




Table 1. Values of frequency parameter (l) for different values of taper constant (b1) and constant aspect ratios (a/b = 1.0, c/b = 0.5).
Table 2. Values of frequency parameter (l) for different values of taper constant (b2) and constant aspect ratios (a/b = 1.0, c/b = 0.5).
Table 3. Values of frequency parameter (l) for different values of thermal gradient (a) and constant aspect ratios (a/b = 1.0, c/b = 0.5).




Table 4 and Table 5 consist the values of frequency parameter 



a.

b.

c.

d.

The value of non-homogeneity constant


It is obvious from the above discussed Table 4 and Table 5 that the values of frequency parameter 


Table 6 contains the values of frequency parameter 








First mode and second mode of vibrations are presented in Figure 2(a) and Figure 2(b) respectively.
Table 4. Values of frequency parameter (l) for different combinations of thermal gradient (a), taper constants (b1 & b2) fixed value of non-homogeneity constant (b = 0.4) and aspect ratio (a/b = 0.75).
Table 5. Values of frequency parameter (l) for different combinations of thermal gradient (a), taper constants (b1 & b2) fixed value of non-homogeneity constant (b = 0.4) and aspect ratio (a/b = 1.0).
Table 6. Values of frequency parameter (l) for different values of non-homogeneity constant (b) and constant aspect ratios (a/b = 1.0, c/b = 0.5).
Figure 2 depicts the behaviour of frequency parameter 

・ 
・ 
・ 
・ 
・ 
It is evident from the Figure 2 that frequency for both the modes of vibration increases as taper constant 
Figure 2. (a) & (b) Frequency parameter l vs. taper constant b1.
Figure 3 represents the variation of frequency parameter 

・ 
・ 
・ 
・ 
・ 
This figure explicates that as taper constant 
Figure 4 shows the variation of frequency parameter 

・ 
・ 
・ 
・ 
・ 
From the discussed Figure 4 the behaviour of the frequency parameter can be examined. It is found that as thermal gradient increases the values of frequency parameter decreases for both the modes of vibration.
Figure 5 displays the effect of aspect ratio c/b varies from 0.25 to 1.0, on the frequency parameter 



Figure 3. (a) & (b) Frequency parameter l vs. taper constant b2.
・ 

・ 

・ 

・ 

In this case the value of non-homogeneity constant 
Now it can be easily observed from Figure 5 that as aspect ratio c/b increases the frequency parameter decreases for both the modes of vibration. It is also noticed that frequency parameter also increases as taper constant increases. Furthermore when the value of aspect ratio a/b is increased from 0.75 to 1.0 then frequency parameter increases for both the modes of vibration.
Figure 6 demonstrates the effect of non-homogeneity constant 




・ 

・ 

・ 

・ 

The behaviour of the frequency parameter is noticed and found that as non-homogeneity constant 
Figure 4. (a) & (b) Frequency parameter l vs. thermal gradient a.


Figure 5. (a) & (b) Frequency parameter l vs. aspect ratio c/b.
Figure 6. (a) & (b) Frequency parameter l vs. non-homogeneity constant b.
creases for both the modes of vibration as taper constant increases.
6. Conclusion
Study of vibration of plates is an important area owing to its extensive range of engineering applications such as in aeronautical, civil and mechanical engineering. Rayleigh-Ritz method gives a perfect and computationally proficient scheme for finding the vibration characteristics of transverse vibration of trapezoidal plate. Thus the natural frequencies for a symmetric, non-homogeneous trapezoidal plate have been acquired by varying values of taper constants, thermal gradient, aspect ratio and non-homogeneity constant. Tables and graphs state that the frequency increases with the increase of taper constants and decreases with the increase of thermal gradient, aspect ratio and non-homogeneity constant. A design engineer can directly observe the presented plots of figures to have the knowledge about particular mode to finalize the design of the structure. The material should be selected such that the total cost should be minimum and within definite confines.
Cite this paper
Kavita,Satish Kumar,Pragati Sharma, (2016) Study of Thermally Induced Vibration of Non-Homogeneous Trapezoidal Plate with Parabolically Thickness Variation in Both Directions. Applied Mathematics,07,1283-1296. doi: 10.4236/am.2016.712113
References
- 1. Kumar, Y. and Lal, R. (2012) Vibrations of Non-Homogeneous Orthotropic Rectangular Plates with Bilinear Thickness Variation Resting on Winkler Foundation. Meccanica, 47, 893-915.
http://dx.doi.org/10.1007/s11012-011-9459-4 - 2. Kumar, Y. and Tomar, S.K. (2006) Free Transverse Vibrations of Monoclinic Rectangular Plates with Continuously Varying Thickness and Density. International Journal of Applied Mechanics and Engineering, 11, 881-900.
- 3. Johri, T. and Johri, I. (2011) Study of Exponential Thermal Effect on Vibration of Non-Homogeneous Orthotropic Rectangular Plate Having Bi-Directional Linear Variation in Thickness. Proceedings of the World Congress on Engineering (WCE 2011), London, 6-8 July 2011, 807-811.
- 4. Gupta, U.S., Lal, R. and Sharma, S. (2006) Vibration Analysis of Non-Homogeneous Circular Plate of Non-Linear Thickness Variation by Differential Quadrature Method. Journal of Sound and Vibration, 298, 892-906.
http://dx.doi.org/10.1016/j.jsv.2006.05.030 - 5. Li, S.R. and Zhou, Y.H. (2001) Shooting Method for Non-Linear Vibration and Thermal Buckling of Heated Orthotropic Circular Plates. Journal of Sound and Vibration, 248, 379-386.
http://dx.doi.org/10.1006/jsvi.2001.3665 - 6. Chakraverty, S., Jindal, R. and Agarwal, V.K. (2007) Effect of Non-Homogeneity on Natural Frequencies of Vibration of Elliptic Plates. Meccanica, 42, 585-599.
http://dx.doi.org/10.1007/s11012-007-9077-3 - 7. Gupta, A.K., Kumar, A. and Kaur, H. (2011) Vibration of Visco-Elastic Orthotropic Parallelogram Plate with Linear Thickness Variation in Both Directions. International Journal of Acoustics and Vibration, 16, 72-80.
- 8. Chen, W.Q., Lee, K.Y. and Ding, H.J. (2005) On Free Vibration of Non-Homogeneous Transversely Isotropic Magneto-Electro-Elastic Plates. Journal of Sound and Vibration, 279, 237-251.
http://dx.doi.org/10.1016/j.jsv.2003.10.033 - 9. Gurses, M., Civalek,O., Ersoy, H. and Kiracioglu, O. (2009) Analysis of Shear Deformable Laminated Composite Trapezoidal Plates. Materials and Design, 30, 3030-3035.
http://dx.doi.org/10.1016/j.matdes.2008.12.016 - 10. Kitipornchai, S., Xiang, Y., Liew, K.M. and Lim, M.K. (1994) A Global Approach for Vibration of Thick Trapezoidal Plates. Computers & Structures, 53, 83-92.
http://dx.doi.org/10.1016/0045-7949(94)90132-5 - 11. El-Sayad, M.A. and Ghazy, S.S.A. (2012) Rayleigh-Ritz Method for Free Vibration of Midline Trapezoidal Plates. International Journal of Emerging Technology and Advanced Engineering, 2, 271-278.
- 12. Leung, Y.T., Xiao, C., Zhu, B. and Yuan, S. (2005) Free Vibration of Laminated Composite Plates Subjected to In-Plane Stresses Using Trapezoidal P-Element. Composite Structures, 68, 167-175.
http://dx.doi.org/10.1016/j.compstruct.2004.03.011 - 13. McGee, O.G. and Butalia, T.S. (1992) Natural Vibrations of Shear Deformable Cantilevered Skewed Trapezoidal and Triangular Thick Plates. Computers and Structures, 45, 1033-1059.
http://dx.doi.org/10.1016/0045-7949(92)90060-D - 14. Qatu, M.S. (1994) Vibrations of Laminated Composite Completely Free Triangular and Trapezoidal Plates. International Journal of Mechanical Sciences, 36, 797-809.
http://dx.doi.org/10.1016/0020-7403(94)90010-8 - 15. Grigorenko, Y.M., Kryukov, N.N. and Yakovenko, N.S. (2005) Using Spline Functions to Solve Boundary-Value Problems for Laminated Orthotropic Trapezoidal Plates of Variable Thickness. International Applied Mechanics, 41, 413-420.
http://dx.doi.org/10.1007/s10778-005-0104-6 - 16. Feng, Z.Y. and Min, W.Z. (2008) Vibrations of Axially Moving Visco-Elastic Plate with Parabolically Varying Thickness. Journal of Sound and Vibration, 316, 198-210.
http://dx.doi.org/10.1016/j.jsv.2008.02.040 - 17. Gupta, A.P. and Sharma, N. (1999) Forced Axisymmetric Response of an Annular Plate of Parabolically Varying Thickness. International Journal of Mechanical Sciences, 41, 71-83.
http://dx.doi.org/10.1016/S0020-7403(98)00036-8 - 18. Liew, K.M. and Lim, M.K. (1993) Transverse Vibration of Trapezoidal Plates of Variable Thickness: Symmetric Trapezoids. Journal of Sound and Vibration, 165, 45-67.
http://dx.doi.org/10.1006/jsvi.1993.1242 - 19. Maruyama, K., Ichinomiya, O. and Narita, Y. (1983) Experimental Study of the Free Vibration of Clamped Trapezoidal Plates. Journal of Sound and Vibration, 88, 523-534.
http://dx.doi.org/10.1016/0022-460X(83)90654-5 - 20. Karami, G., Shahpari, S.A. and Malekzadeh, P. (2003) DQM Analysis of Skewed and Trapezoidal Laminated Plates. Composite Structures, 59, 393-402.
http://dx.doi.org/10.1016/S0263-8223(02)00188-5 - 21. Huang, C.-H., Hsu, C.-H. and Lin, Y.-K. (2006) Experimental and Numerical Investigations for the Free Vibration of Cantilever Trapezoidal Plates. Journal of the Chinese Institute of Engineers, 29, 863-872.
http://dx.doi.org/10.1080/02533839.2006.9671184 - 22. Gupta, A.K. and Sharma, S. (2011) Study the Effect of Thermal Gradient on Transverse Vibration of Non-Homogeneous Orthotropic Trapezoidal Plate of Parabolically Varying Thickness. Applied Mathematics, 2, 1-10.
http://dx.doi.org/10.4236/am.2011.21001 - 23. Gupta, A.K. and Sharma, P. (2012) Effect of Linear Thermal Gradient on Vibrations of Trapezoidal Plates Whose Thickness Varies Parabolically. Journal of Vibration and Control, 18, 395-403.
http://dx.doi.org/10.1177/1077546311409266 - 24. Gupta, A.K. and Sharma, P. (2012) Study of Thermally Induced Vibration of Non-homogeneous Trapezoidal Plate with Varying Thickness and Density. American Journal of Computational and Applied Mathematics, 2, 265-275.
http://dx.doi.org/10.5923/j.ajcam.20120206.05 - 25. Hoff, N.J. (1958) High Temperature Effect in Air Craft Structures. Pergamon Press, New York.
NOTES
*Corresponding author.











