Applied Mathematics
Vol.07 No.10(2016), Article ID:67236,11 pages
10.4236/am.2016.710090
Dynamic Stiffness Analysis of Repetitive Control System
Wu-Sung Yao
Department of Mechanical and Automation Engineering, National Kaohsiung First University of Science and Technology, Taiwan

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 April 2016; accepted 6 June 2016; published 9 June 2016
ABSTRACT
For dynamic stiffness enhancement, this paper presents a new method for synthesizing repetitive controllers capable of rejecting periodic vibration disturbance. Dynamic stiffness of the control system is analyzed. Direct and quadrature dynamic stiffness are defined for the repetitive controllers’ design. A trade-off method between the determinations of the controller’s parameters is necessary such that both the rejecting performance and stability can be achieved simultaneously. An illustrated example of a twin linear drive system is given to verify the performance of the proposed control design. The control performance of the present method is evaluated in the experimental disturbance rejecting control system, where the real-time control algorithms are implemented using a floating-point digital signal processor. Both computer simulation and experimental results are presented to illustrate the effectiveness of the proposed repetitive controller design.
Keywords:
Dynamic Stiffness, Repetitive Control, Twin Linear Drive System

1. Introduction
Repetitive control [1] is one of the specific control schemes in which its objective is to reduce the steady state errors with the periodic inputs. Figure 1 shows a repetitive control system where r is reference input, d is disturbance, y is system output, u is control output, e is error, and 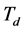 is period of the reference periodic signal. Clearly, the repetitive control system can be achieved for a higher bandwidth with
is period of the reference periodic signal. Clearly, the repetitive control system can be achieved for a higher bandwidth with  and
and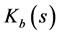 , in which the magnitude of the sensitivity function in Figure 1 can be reduced at the harmonics of the input signal within the certain frequency range, i.e.,
, in which the magnitude of the sensitivity function in Figure 1 can be reduced at the harmonics of the input signal within the certain frequency range, i.e.,  ,
,  , where
, where 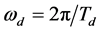 is the fundamental fre-
is the fundamental fre-
Figure 1. Repetitive control system.
quency of the input signal r or d, and  is a designed bandwidth. This should be able to improve the tracking/ rejecting performance for periodic input signals but, as expected, easy cause a degradation at intermediate frequencies. The convenience and simplicity of tuning parameters in the repetitive control scheme make it appearing in many industrial drives. Nevertheless, the classical repetitive control scheme may not easily yield satisfactory stability and performance simultaneously when the system has high order dynamic disturbances. The property of the disturbances rejection is often called dynamic stiffness which is substituted for disturbance response. For a disturbances rejection control system, dynamic stiffness is a measure of how many input force is required to cause a unit output deviation. High dynamic stiffness is essential in the anti-vibration control systems for required disturbance rejection ability. In general, the ability of lower frequency disturbance rejection can be referred to static stiffness. Therefore, to achieve better control performance of the repetitive control, the dynamic stiffness should be considered. Let
is a designed bandwidth. This should be able to improve the tracking/ rejecting performance for periodic input signals but, as expected, easy cause a degradation at intermediate frequencies. The convenience and simplicity of tuning parameters in the repetitive control scheme make it appearing in many industrial drives. Nevertheless, the classical repetitive control scheme may not easily yield satisfactory stability and performance simultaneously when the system has high order dynamic disturbances. The property of the disturbances rejection is often called dynamic stiffness which is substituted for disturbance response. For a disturbances rejection control system, dynamic stiffness is a measure of how many input force is required to cause a unit output deviation. High dynamic stiffness is essential in the anti-vibration control systems for required disturbance rejection ability. In general, the ability of lower frequency disturbance rejection can be referred to static stiffness. Therefore, to achieve better control performance of the repetitive control, the dynamic stiffness should be considered. Let  denote the transfer function from the disturbance force to the velocity/position output of a control system. The dynamic stiffness can be characterized by
denote the transfer function from the disturbance force to the velocity/position output of a control system. The dynamic stiffness can be characterized by 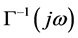 with a frequency
with a frequency . For performance measurement of the dynamic stiffness denoted as,
. For performance measurement of the dynamic stiffness denoted as, 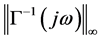 , where
, where  is H-infinite norm. This is the inverse of the maximum magnitude of
is H-infinite norm. This is the inverse of the maximum magnitude of , i.e., the worst case in the frequency response. Thus maximizing the dynamic stiffness measurement implies to minimize
, i.e., the worst case in the frequency response. Thus maximizing the dynamic stiffness measurement implies to minimize 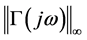 in controller design.
in controller design.
Many design approaches to improve the dynamic stiffness have been proposed, and the related literatures have been found in the following. In [2] , the high static low dynamic stiffness concept is a design strategy for an anti-vibration mount that seeks to increase isolation by lowering the natural frequency of the mount, whilst maintaining the same static load bearing capacity. In [3] , the flutter characteristics of an actuator-fin system are investigated with structural nonlinearity and dynamic stiffness of the electric motor. The component mode substitution method is used to establish the nonlinear governing equations in time domain and frequency domain based on the fundamental dynamic equations of the electric motor and decelerator. The concept of torque-stiff- ness-controlled dynamic walking is proposed by [4] . The disturbance rejection of torque-stiffness-controlled bipedal walking with Central Pattern Generators is analyzed. [5] presents a dynamic analysis of a stiffened cylindrical shell using the dynamic stiffness method This approach is based on the determination of the dynamic stiffness matrix of an unmeshed structure. A finite element model is used in order to validate the numerical results obtained from the method. The high static low dynamic stiffness concept is proposed by [6] , and is used to increase isolation by lowering the natural frequency of the mount, whilst maintaining the same static load bearing capacity. [7] presents a shape-changeable display with dynamic stiffness control. The prototype uses vacuum pressure control on an enclosed volume of particles. Users can mold 3D shapes and apply textures to them while experiencing tactile feedback through dynamically changing stiffness. In practice, high dynamic stiffness often results in large control effort, hence a trade-off should be considered carefully.
For dynamic stiffness enhancement, this paper presents a new method for synthesizing repetitive controllers applied to anti-vibration system for rejecting periodic disturbance. A trade-off to determine the controller’s parameters is often necessary such that both the control performance and stability can be achieved simultaneously. Moreover, an illustrated example of a single-degree-of-freedom anti-vibration system driven by a two linear motor is given to verify the performance of the proposed control design. Dynamic stiffness of the control system is analyzed. Direct and quadrature dynamic stiffness are defined for the controllers’ design. The control performance of the present method is evaluated in the experimental disturbance rejecting control system, where the real-time control algorithms are implemented using a floating-point digital signal processor. Both computer simulation and experimental results are presented to illustrate the effectiveness of the proposed repetitive controller design.
2. Dynamics Stiffness of Control System
Figure 2 shows a single degree-of-freedom (SODF) mass-damping-spring system, where m is equivalent mass, k is spring coefficient, and c is damping coefficient. x denotes the displacement of the object m. f is disturbance force applied to the inertia loading m. The dynamic equation of Figure 2 is given as




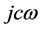


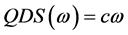
namic stiffness can be obtained, i.e.,
and 
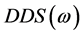






For a stable control system, DDS and QDS are not zero at the same frequency, and the difference in frequency between the zeros of DDS and QDS is referred to as the margin of stability. If both of the direct dynamic stiffness and the quadrature dynamic stiffness are zero at the same frequency, then 









Figure 2. SDOF mass-damping-spring system.
Figure 3. Magnitudes of 

Figure 4. Velocity control loop of the motor with PDF controller.

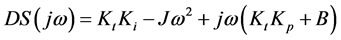

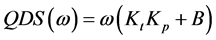



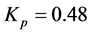








3. Dynamics Stiffness of Repetitive Control System
Figure 6 shows a repetitive control system with the period 

found by 
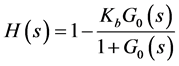

By the small gain theory, the closed-loop system in Figure 7 is stable if 

which is the stability condition of the repetitive control system. Clearly, if 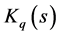

fit the requirement of 

practice, let 

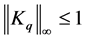
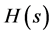
signed for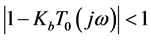
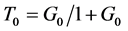



Therefore, for the repetitive control design rule, let 



where 
The dynamic stiffness from the disturbance input 


where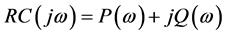








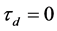



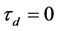






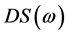

Figure 5. Magnitudes of 


Figure 6. Repetitive control system with the period
Figure 7. A signal regeneration of time delayed system.
Figure 8. Control response of the repetitive control system: Command (solid-line), output (dashed-line), and tracking error (dashed-dotted line).
Figure 9. Error responses of the repetitive control system with 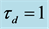

Figure 10. Magnitudes of 


Figure 11. Experimental setup.
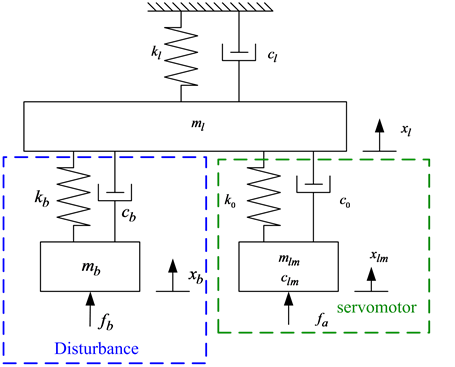
of the two linear servomotors with the mechanical coupling in this study, where a linear motor is given as the target plant and the other one is a disturbance generator. Assume that the velocity of the motor can be estimated or measured by encoder. The control system was purposely developed for experimental study to verify the control performance of the proposed repetitive control scheme. The objective of the control design is to reduce vibrations of the controlled target. In fact, a control system modeling of the experimental setup can be detailed as shown in Figure 12, where the parameters are listed the following.






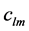








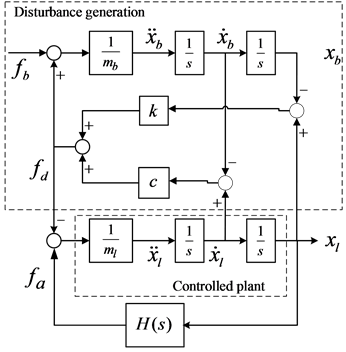
Then, we have the control block diagram of the experimental system as shown in Figure 13. To design an anti-vibration controller, the controlled system in Figure 13 can be simplified to a second-order dynamic systemas depicted in Figure 14. k and c denote the equivalent stiffness and damping effects of the passive anti-vibration elements, respectively. 

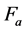





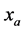

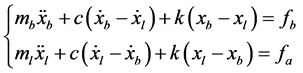
For the requirement of 



appropriate control scheme is adapted to reduce the effect of the disturbance
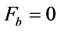


Figure 12. System modeling of experiment setup of Figure 11.
Figure 13. Control block diagram of controlled system.
Figure 14. Block diagram of proposed anti-vibration system.
have
In this paper, an anti-vibration control system can be described with a feedback controller 


required performance. In this case, 
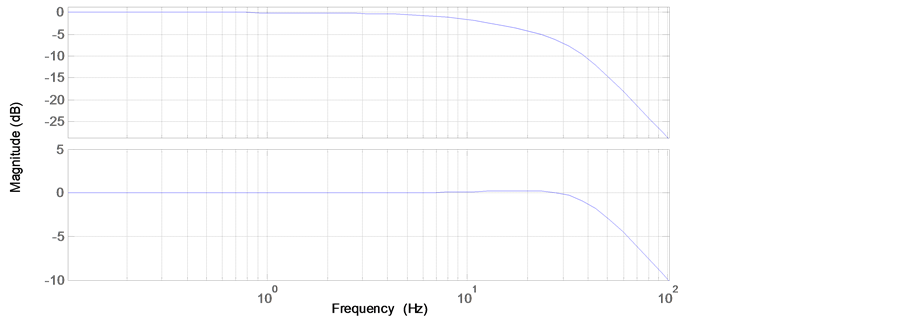
sition loops be set to 40 Hz and 15 Hz respectively, which is just for general requirement of the motion control performance of the linear motor. For the velocity control loop, the control parameters of


Figure 15. Block diagram of the active anti-vibration control system with feedback controller
Figure 16. Block diagram of the anti-vibration control system with repetitive controller and PDF loop controller.
function of the velocity control loop, i.e., 




velocity control loop 





From Figure 16, the controlled plant 
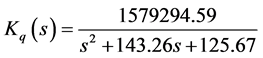
and












4. Conclusion
This paper presented a new method for synthesizing repetitive controllers capable of rejecting periodic vibration disturbance. Dynamic stiffness of the control system is analyzed. Direct and quadrature dynamic stiffness are
Figure 17. Frequency responses of position and velocity control loop.
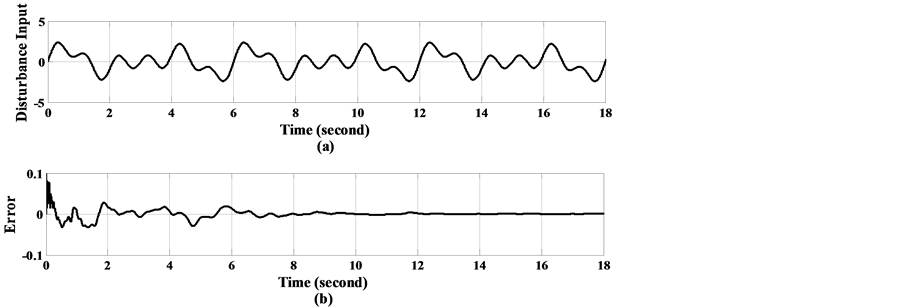
Figure 18. Experimental result: (a) the disturbance input and (b) error response.

Figure 19. Experimental result: (a) the disturbance input and (b) error response.
defined for the repetitive controllers’ design. An illustrated example of a twin linear drive system is given to verify the performance of the proposed control design. The control performance of the present method is evaluated in the experimental disturbance rejecting control system, where the experimental results are given to illustrate that the proposed repetitive control can effectively eliminate steady-state rejecting errors within a few cycles.
Cite this paper
Wu-Sung Yao, (2016) Dynamic Stiffness Analysis of Repetitive Control System. Applied Mathematics,07,1032-1042. doi: 10.4236/am.2016.710090
References
- 1. Tsai, M.C. and Yao, W.S. (2002) Design of a Plug-In Type Repetitive Controller for Periodic Inputs. IEEE Transactions on Control Systems and Technology, 10, 547-555.
http://dx.doi.org/10.1109/TCST.2002.1014674 - 2. Zhou, N. and Liu, K. (2010) A Tunable High-Static-Low-Dynamic Stiffness Vibration Isolator. Journal of Sound and Vibration, 329, 1254-1273.
http://dx.doi.org/10.1016/j.jsv.2009.11.001 - 3. Yang, N., Wu, Z. and Yang, C. (2011) Structural Nonlinear Flutter Characteristics Analysis for an Actuator-Fin System with Dynamic Stiffness. Chinese Journal of Aeronautics, 24, 590-599.
http://dx.doi.org/10.1016/S1000-9361(11)60069-1 - 4. Huang, Y. and Wang, Q. (2015) Disturbance Rejection of Central Pattern Generator Based Torque-Stiffness-Controlled Dynamic Walking. Neurocomputing, 170, 141-151.
http://dx.doi.org/10.1016/j.neucom.2015.04.096 - 5. Tounsi, D., Casimir, J.B., Abid, S., Tawfiq, I. and Haddar, M. (2014) Dynamic Stiffness Formulation and Response Analysis of Stiffened Shells. Computers and Structures, 132, 75-83.
http://dx.doi.org/10.1016/j.compstruc.2013.11.003 - 6. Shaw, A.D., Neild, S.A. and Wagg, D.J. (2013) Dynamic Analysis of High Static Low Dynamic Stiffness Vibration Isolation Mounts. Journal of Sound and Vibration, 332, 1437-1455.
http://dx.doi.org/10.1016/j.jsv.2012.10.036 - 7. Toshiki, S., Jefferson, P., Yasushi, M. and Hideki, K. (2014) Claytric Surface: An Interactive Deformable Display with Dynamic Stiffness Control. IEEE Computer Graphics and Applications, 34, 59-67.
http://dx.doi.org/10.1109/MCG.2014.39