Received 5 January 2016; accepted 15 March 2016; published 18 March 2016

ABSTRACT

In this paper, we establish the existence and uniqueness of fixed points of operator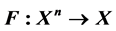, when n is an arbitrary positive integer and X is a partially ordered complete metric space. We have shown examples to verify our work. Our results generalize the recent fixed point theorems cited in [1] - [4] etc. and include several recent developments.

Keywords:

n-Tupled Coincidence Points, n-Tupled Coincidence Fixed Points, Compatible Maps, Fixed Points and Partially Ordered Metric Spaces

1. Introduction

The metric fixed point theory plays a vital role to solve the problems related to variational inequalities, optimization, approximation theory, etc. Many authors (for detail, see [1] - [10] ) have discussed fixed point results in partially ordered metric spaces. In particular, Bhaskar and Lakshmikantham [3] , Nieto and Rodriguez-Lopez [11] , Agarwal et al. [12] and Ran and Recuring [13] proved some new results for contractions in partially ordered metric spaces.

Bhaskar and Lakshmikantham [3] proposed the study of a coupled fixed point in ordered metric spaces and as an application they proved the existence and uniqueness of solutions for a periodic boundary value problem. Nguyen et al. [14] , Berinde and Borcut [15] and Karpinar [8] introduced tripled and quadruple fixed point theorems as a generalization and extension of the coupled fixed point theorem. For comprehensive description of such work, we refer to [16] - [21] . Very recently, Imdad et al. [22] have introduced the concept of n-tupled coincidence point and proved n-tupled coincidence point results for commuting maps in metric spaces. Motivated by the work of M. Imdad, we introduce the notion of compatibility for n-tupled coincidence points and prove n-tupled coincidence point and n-tupled fixed point for compatible maps satisfying different contractive conditions in partially ordered metric spaces.

Jungck [1] obtained common fixed point results for commuting maps in metric spaces. The concept of commuting maps has been generalized in various directions over the years. One such generalization which is weaker than commuting is the concept of compatibility introduced by Jungck [23] .

2. Prilimaries

Definition 2.1 [4] Let 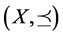be a partially ordered set equipped with a metric d such that 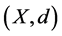is a metric space. Further, equip the product space 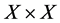with the following partial ordering:

For, define

Definition 2.2 [4] Let 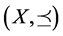be a partially ordered set and 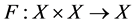then F enjoys the mixed monotone property if 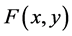is monotonically non-decreasing in x and monotonically non-increasing in y, that is, for any,

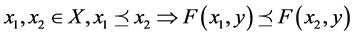and

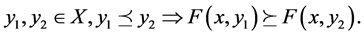
Definition 2.3 [4] Let 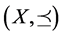be a partially ordered set and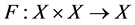, then 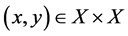is called a coupled fixed point of the mapping F if and

Definition 2.4 [4] Let be a partially ordered set and and then F enjoys the mixed g-monotone property if is monotonically g-non-decreasing in x and monotonically g- non-increasing in y, that is, for any,

Definition 2.5 [4] Let be a partially ordered set and and, then is called a coupled coincidence point of the maps F and g if and

Definition 2.6 [4] Let be a partially ordered set, then is called a coupled fixed point of the maps and if and

3. Main Results

Imdad et al. [22] introduced the concept of n-tupled fixed point and n-tupled coincidence point given by considering n to be an even integer but throughout, we will consider n, a positive integer, in this paper.

Definition 2.7 Let be a partially ordered set and then F is said to have the mixed

monotone property if F is non-decreasing in its odd position arguments and non-increasing in its even positions arguments, that is, if,

1) For all

2) For all

3) For all

For all (if r is odd),

For all (if r is even).

Definition 2.8 Let be a partially ordered set and and be two maps.

Then F is said to have the mixed g-monotone property if F is g-non-decreasing in its odd position arguments and g-non-increasing in its even positions arguments, that is, if,

1) For all

2) For all

3) For all

For all (if r is odd),

For all (if r is even).

Definition 2.9 [22] Let X be a nonempty set. An element is called an r-tupled fixed point of the mapping if

Example 1. Let (R, d) be a partial ordered metric space under natural setting and let be mapping defined by

, for any,

then is an r-tupled fixed point of F.

Definition 2.10 [22] Let X be a nonempty set. An element is called an r-tupled coincidence point of the maps and if

Example 2. Let (R, d) be a partial ordered metric space under natural setting and let and be maps defined by

, ,

for any, then is an r-tupled coincidence point of F and g.

Definition 2.11 [22] Let X be a nonempty set. An element is called an r-tupled fixed point of the maps and if

Now, we define the concept of compatible maps for r-tupled maps.

Definition 2.12 Let be a partially ordered set, then the maps and are called compatible if

whenever, are sequences in X such that

For some

Imdad et al. [22] proved the following theorem:

Theorem 3.1 Let be a partially ordered set equipped with a metric d such that (X, d) is a complete metric space. Assume that there is a function with and for each t > 0. Further, let and be two maps such that F has the mixed g-monotone property satisfying the following conditions:

(i),

(ii) g is continuous and monotonically increasing,

(iii) the pair (g, F) is commuting,

(iv) for all , with, , if r is even and if r is odd. Also, suppose that either

a) F is continuous or

b) X has the following properties:

(i) If a non-decreasing sequence then for all.

(ii) If a non-increasing sequence then for all.

If there exist such that

(iv)

if r is odd,

, if r is even.

Then F and g have a r-tupled coincidence point, i.e. there exist such that

(v)

Now, we prove our main result as follows:

Theorem 3.2 Let be a partially ordered set equipped with a metric d such that (X, d) is a complete metric space. Assume that there is a function with and for each t > 0. Further let and be two maps such that F has the mixed g-monotone property satisfying the following conditions:

(3.1)

(3.2) g is continuous and monotonically increasing,

(3.3) the pair (g, F) is compatible,

(3.4) ,

For all, with, , if r is even and if r is odd. Also, suppose that either

a) F is continuous or

b) X has the following properties:

(i) If a non-decreasing sequence then for all.

(ii) If a non-increasing sequence then for all.

If there exist such that

(3.5)

Then F and g have a r-tupled coincidence point, i.e. there exist such that

(3.6)

Proof. Starting with, we define the sequences in X as follows:

(3.7)

Now, we prove that for all n ≥ 0,

, if r is even and (3.8)

, if r is odd.

(3.9)

So (3.8) holds for n = 0. Suppose that (3.8) holds for some n > 0. Consider

and, if r is odd.

Thus by induction (3.8) holds for all. Using (3.7) and (3.8)

(3.10)

Similarly, we can inductively write

(3.11)

Therefore, by putting

(3.12)

We have,

(3.13)

Since for all t > 0, therefore, for all m so that is a non-increasing sequence. Since it is bounded below, there is some such that

(3.14)

We shall show that. Suppose, if possible. Taking limit as of both sides of (3.13) and keeping in mind our supposition that for all t > 0, we have

(3.15)

this contradiction gives and hence

(3.16)

Next we show that all the sequences are Cauchy sequences. If possible, suppose that at least one of is not a Cauchy sequence. Then there exist and sequences of positive integers and such that for all positive integers k,

(3.17)

and

Now,

(3.18)

Similarly, ,

,

Thus,

(3.19)

Again, the triangular inequality and (3.17) gives

(3.20)

and

i.e., we have

(3.21)

Also,

(3.22)

Using (3.17), (3.19) and (3.22), we have

(3.23)

Letting in above equation, we get

(3.24)

Finally, letting in (3.17) and using (3.19) and (3.23), we get

(3.25)

which is a contradiction. Therefore, are Cauchy sequences. Since the metric space (X, d) is complete, so there exist such that

(3.26)

As g is continuous, so from (2.26), we have

(3.27)

By the compatibility of g and F, we have

(3.28)

Now, we show that F and g have an r-tupled coincidence point. To accomplish this, suppose (a) holds. i.e. F is continuous, then using (3.28) and (3.8), we see that

which gives. Similarly, we can prove

Hence is an r-tupled coincidence point of the maps F and g.

If (b) holds, since is non-decreasing or non-increasing as i is odd or even and as, we have, when i is odd while when i is even. Since g is monotonically increasing, therefore

when i is odd, (3.29)

when i is even.

Now, using triangle inequality together with (3.8), we get

(3.30)

Therefore,. Similarly we can prove

Thus the theorem follows.

Corollary 3.1 Under the hypothesis of theorem 3.2 and satisfying contractive condition as (3.31)

Then F and g have a r-tupled coincidence point.

Proof: If we put with in theorem 3.2, we get the corollary.

Uniqueness of r-tupled fixed point

For all,

.

We say that

Theorem 3.3 In addition to the hypothesis of theorem 3.1, suppose that for every

Then exist such that is comparable to

And

.

Then F and g have a unique r-coincidence point, which is a fixed point of and. That is there exists a unique such that

for all (3.32)

Proof. By theorem 3.2, the set of r-coincidence points is non-empty. Now, suppose that and are two coincidence points of F and g, that is for all and for all.

We will show that for all.

By assumption, there exists such that

is comparable to

and

.

Let for all. Since, we can choose such that for all. By a similar reason, we can inductively define sequences for all such that for all.

In addition, let and for all and in the same way, define the sequences and, for all. Since

And

are comparable, then

for all if i is odd,

for all if i is even.

We have

,

.

Then and are comparable for all. It follows from condition (3.4) of theorem 3.2

Summing, we get

(3.33)

It follows that

For all. Note that for imply that for all Hence from (3.32) we have

for all (3.34)

Similarly, one can prove that

for all (3.35)

Using (3.34), (3.35) and triangle inequality we get

As for all. Hence, , therefore (3.32) is proved.

Since for all, by the commutativity of F and g, we have

(3.36)

Denote for all From (3.36), we have

for all (3.37)

Hence is a r-coincidence point of F and g.

It follows from (3.32) and so

for all

This means that

for all

Now, from (3.37), we have

for all

Hence, is a r-fixed point of F and a fixed point of g.

To prove the uniqueness of the fixed point, assume that is another r-fixed point. Then by (3.32) we have

for all

Thus,. This completes the proof.

Acknowledgements

Authors are highly thankful for the financial support of this paper to Deanship of Scientific Research, Jazan University, K.S.A.

Conflict of Interest

Authors declare that they have no conflict of interest.

Cite this paper

Ibtisam Masmali,Sumitra Dalal, (2016) Study of Fixed Point Theorems for Higher Dimension in Partially Ordered Metric Spaces. Applied Mathematics,07,399-412. doi: 10.4236/am.2016.75037

References