Applied Mathematics
Vol.07 No.01(2016), Article ID:62746,9 pages
10.4236/am.2016.71002
Design and Analysis of Some Third Order Explicit Almost Runge-Kutta Methods
Abdulrahman Ndanusa, Khadeejah James Audu
Department of Mathematics, Federal University of Technology, Minna, Nigeria

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 December 2015; accepted 11 January 2016; published 14 January 2016
ABSTRACT
In this paper, we propose two new explicit Almost Runge-Kutta (ARK) methods, ARK3 (a three stage third order method, i.e., s = p = 3) and ARK34 (a four-stage third-order method, i.e., s = 4, p = 3), for the numerical solution of initial value problems (IVPs). The methods are derived through the application of order and stability conditions normally associated with Runge-Kutta methods; the derived methods are further tested for consistency and stability, a necessary requirement for convergence of any numerical scheme; they are shown to satisfy the criteria for both consistency and stability; hence their convergence is guaranteed. Numerical experiments carried out further justified the efficiency of the methods.
Keywords:
Almost Runge-Kutta, Stability, Consistency, Convergence, Order Conditions, Rooted Trees

1. Introduction
According to [1] the s-stage Runge-Kutta method for solving the initial value problem
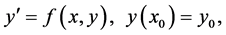 (1)
(1)
is defined by
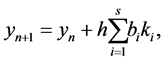 (2)
(2)
where
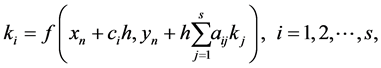 (3)
(3)
and
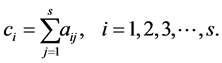 (4)
(4)
Alternative forms of the above equations are:
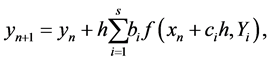 (5)
(5)
where
 (6)
(6)
The two forms of Equations (2) and (5) are equivalent by making the interpretation
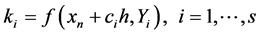 (7)
(7)
where 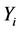 is the inner stages that tend to estimate the solutions at some points; s is the number of stages and
is the inner stages that tend to estimate the solutions at some points; s is the number of stages and  is the points where the function f is computed for a step. ARK methods are a special class of RK methods that arose out of the quest to develop efficient and accurate methods that have advantages over the traditional methods by retaining the simple stability function of RK methods, allowing minimal information to be passed between steps and adjusting stepsize easily. Since the introduction of ARK methods in by [2] , other researchers who have made their input toward the development of this method include [3] - [7] .
is the points where the function f is computed for a step. ARK methods are a special class of RK methods that arose out of the quest to develop efficient and accurate methods that have advantages over the traditional methods by retaining the simple stability function of RK methods, allowing minimal information to be passed between steps and adjusting stepsize easily. Since the introduction of ARK methods in by [2] , other researchers who have made their input toward the development of this method include [3] - [7] .
2. Materials and Methods
2.1. Method ARK3 (s = p = 3)
The general third order three stages Almost Runge-Kutta scheme is of the form:
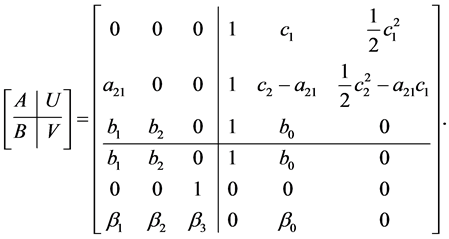 (8)
(8)
We represent the abscissa vector .
.
The order conditions for order three ARK schemes are derived through the standard rooted tree approach used for Runge-Kutta methods [8] .
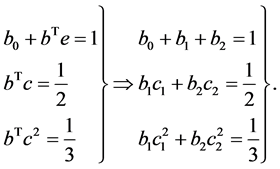 (9)
(9)
The conditions of Runge-Kutta stability for 3rd order, 3 stages are:
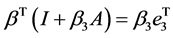 (10)
(10)
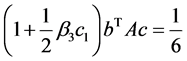 (11)
(11)
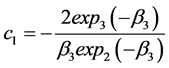 (12)
(12)
where
Acquiring order 2 estimation with respect to 2nd scaled derivative for the 3rd outgoing solution, we need:


From Equation (12) we have,

Solving Equation (9) we obtain



And from Equation (11), we obtain

Evaluating both sides of Equation (10) we obtain

This implies that

Thus Equation (13) becomes

Two free parameters, 


calculating the members of the U matrix we obtain the a scheme for method

2.2. Method ARK34 (s = 4, p = 3)
The third order four stages scheme has the general form:

Its stability function is expressed as

The order conditions are derived using the standard rooted tree approach used for Runge-Kutta methods [8] .






The 

Also,


There is also the additional condition




Thus




From Equation (30) we obtain

Evaluating the stability matrix of a four stage third order method, we arrive at

where Tr is the trace of a matrix and

Hence,


And it follows that:

Since 

We introduce



And from Equations (32) and (33) we obtain respectively


Further simplification produces the following results



Setting 




Thus




And the proposed ARK34 with 

3. Convergence Analysis
For the method ARK3 represented by Equation (24), the matrix

must have bounded powers for the method to be stable.
The characteristic polynomial of V is given as


Thus
Applying Cayley-Hamilton theorem to matrix V


This implies that

Similarly,

for every n greater than 2. It implies 

Similarly, for the ARK34 method of Equation (61), the matrix


And the eigenvalues are evaluated to be
Thus,

And similarly, it implies that


4. Numerical Examples
Considering the problem below:

Source: Rattenbury [3] .
Problem (72) is solved using the proposed ARK34 method. The results are obtained and compared with similar ARK34 methods of [3] and [5] respectively and presented in Figure 1.
Figure 1. Comparison of ARK34 with other methods (h = 0.1).
From Figure 1 it is evident that our Proposed ARK34 method performed better than the methods of [3] and [5] since it exhibits lesser error than the errors of the existing methods.
5. Conclusion
Two ARK methods are proposed, ARK3 

Acknowledgements
The authors would like to thank the reviewer(s) for their constructive criticisms.
Cite this paper
AbdulrahmanNdanusa,Khadeejah JamesAudu, (2016) Design and Analysis of Some Third Order Explicit Almost Runge-Kutta Methods. Applied Mathematics,07,13-21. doi: 10.4236/am.2016.71002
References
- 1. Lambert, J.D. (1991) Numerical Method for Ordinary Differential Systems: The Initial Value Problem. John Wiley & Sons Ltd., New York.
- 2. Butcher, J.C. (1997) An Introduction to Almost Runge-Kutta Methods. Applied Numerical Mathematics, 24, 331-342.
http://dx.doi.org/10.1016/S0168-9274(97)00030-5 - 3. Rattenbury, N. (2005) Almost Runge-Kutta Methods for Stiff and Non-Stiff Problems. Ph.D. Thesis, University of Auckland, Auckland.
- 4. Abraham, O. and Adeboye, K.R. (2009) On the Derivation of Third-Order Almost Runge-Kutta (ARK) Methods with Four Stages (s = 4, p = 3). Proceedings of the 28th Annual Conference of Nigerian Mathematical Society, Ilorin, 23-27 June 2009, 42.
- 5. Abraham, O. (2010) Development of Some New Classes of Explicit Almost Runge-Kutta Methods for Non-Stiff Differential Equations. Ph.D. Thesis, Federal University of Technology, Minna.
- 6. Alimi, O.K. (2014) On the Performance of Richardson’s Extrapolation Technique in Estimating Local Truncation Errors for Explicit Almost Runge-Kutta Methods. Master’s Thesis, Federal University of Technology, Minna.
- 7. Audu, K.J. (2015) Some Explicit Almost Runge-Kutta Methods for Solving Initial Value Problems. Master’s Thesis, Federal University of Technology, Minna.
- 8. Butcher, J.C. (2008) Numerical Methods for Ordinary Differential Equations. 2nd Edition, John Wiley & Sons, Ltd., Chichester.
http://dx.doi.org/10.1002/9780470753767



