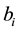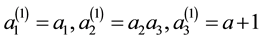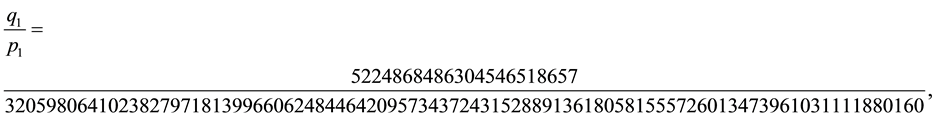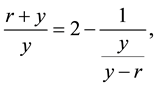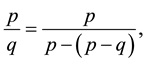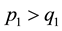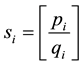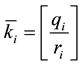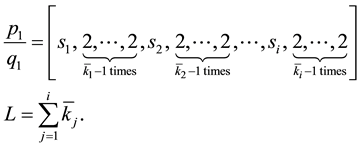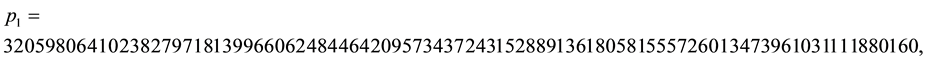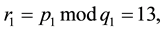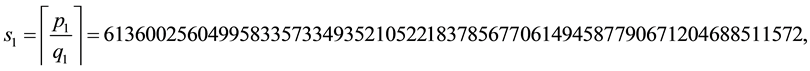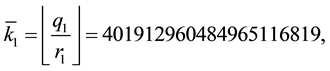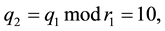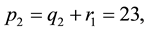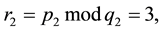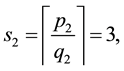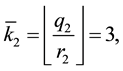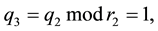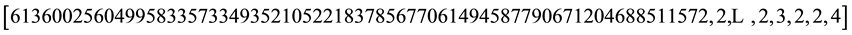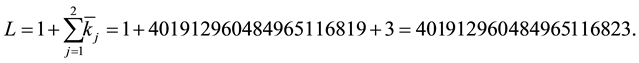Applied Mathematics
Vol.06 No.10(2015), Article ID:59458,8 pages
10.4236/am.2015.610149
Algorithm for Fast Calculation of Hirzebruch-Jung Continued Fraction Expansions to Coding of Graph Manifolds
Fernando I. Becerra López, Vladimir N. Efremov, Alfonso M. Hernández Magdaleno
Department of Mathematics, CUCEI, University of Guadalajara, Guadalajara, México
Email: mail@ferdx.com, efremov@cencar.udg.mx, 137mag@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 6 August 2015; accepted 5 September 2015; published 8 September 2015
ABSTRACT
We present a new algorithm for the fast expansion of rational numbers into continued fractions. This algorithm permits to compute the complete set of integer Euler numbers of the sophisticate tree graph manifolds, which we used to simulate the coupling constant hierarchy for the universe with five fundamental interactions. Moreover, we can explicitly compute the integer Laplacian block matrix associated with any tree plumbing graph. This matrix coincides up to sign with the integer linking matrix (the main topological invariant) of the graph manifold corresponding to the plumbing graph. The need for a special algorithm appeared during computations of these topological invariants of complicated graph manifolds since there emerged a set of special rational numbers (fractions) with huge numerators and denominators; for these rational numbers, the ordinary methods of expansion in continued fraction became unusable.
Keywords:
Hirzebruch-Jung Continued Fraction, Fast Expansion Algorithm, Graph Manifolds

1. Introduction
Hirzebruch-Jung (H-J) continued fractions are widely used in various branches of mathematics as well as in theoretical physics. First of all, HJ-continued fractions arise naturally in the minimal resolution of cyclic quotient (that is, Hirzebruch-Jung) surface singularities of the type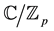 , which is also known as HJ- resolution [1] [2] . This type of resolution gives rise to a smooth 4-dimensional manifold
, which is also known as HJ- resolution [1] [2] . This type of resolution gives rise to a smooth 4-dimensional manifold
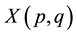 called HJ- space [3] , which is homeomorphic to a plumbing graph manifold
called HJ- space [3] , which is homeomorphic to a plumbing graph manifold
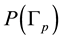 described in [4] [5] . The boundary of HJ-space
described in [4] [5] . The boundary of HJ-space
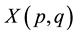 is lens space
is lens space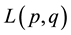 , which can be also obtained as a link of Hirzebruch-Jung surface singularity
, which can be also obtained as a link of Hirzebruch-Jung surface singularity . HJ-continued fractions are used also to describe the plumbing decomposition of the other type of link of surface singularities, namely, Seifert fibered homology spheres (Sfh-spheres), particularly Brieskorn homology spheres (Bh-spheres) [4] [6] [7] .
. HJ-continued fractions are used also to describe the plumbing decomposition of the other type of link of surface singularities, namely, Seifert fibered homology spheres (Sfh-spheres), particularly Brieskorn homology spheres (Bh-spheres) [4] [6] [7] .
In condensed matter theory, the HJ-continued fractions are used to describe fractional quantum Hall (FQH) systems with k levels of hierarchy [8] - [10] . The main numerical characteristic of FQH effect in topological fluids is the filling factor, which is naturally presented in form of a HJ-continued fraction. Also, in topological string theory, the structure of internal space (Calabi-Yau threefold) can be encoded in terms of HJ-continued fraction expansion of positive integers, which are the topological invariants of the internal space and define the mode of interactions between D-branes [3] [11] .
Recently, we have attempted to use the plumbing procedure and corresponding HJ-continued fraction expansion to solve the problems of the coupling constant hierarchy [5] [12] [13] and fine tuning [14] on the base of Kaluza-Klein approach in the multidimensional topological field theory, where plumbing graph manifolds play the role of internal spaces. In the Section 2 we shall explain these ideas. In this way a set of special rational numbers (irreducible fractions) with huge numerators and denominators arise. For these rational numbers, the ordinary methods to find their expansion in continued fraction are impractical due to the number of operations involved; thus in Section 3 we develop an algorithm for fast expansion of HJ-continued fraction. This gives us the possibility to evaluate the number of vertexes of plumbing graphs which can be used to explain the coupling constant hierarchy and the rank of the corresponding Laplacian block matrices [5] . In Section 4, we give an example of calculation of a special continued fraction by means of our algorithm.
2. Continued Fractions and Graph Manifolds
In this section, we review the main concepts of codifying the topology of plumbing graph manifolds by means of continued fraction expansion (for more detales see [1] [2] [5] ). For given coprime integers p and q, the Hirzebruch-Jung modification of euclidean algorithm
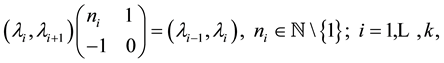 (1)
(1)
leads to HJ-continued fraction
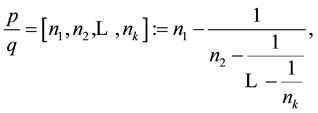 (2)
(2)
if we set the “initial” conditions to
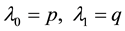 (this expansion is unique under supposition of continued fraction finiteness). The expansion process is finished for k such that
(this expansion is unique under supposition of continued fraction finiteness). The expansion process is finished for k such that . By means of product
. By means of product
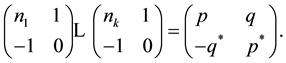 (3)
(3)
Fr. Hirzebruch defined in [1] the plumbing procedure which leads to the 4-dimensional plumbing manifold
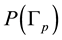 with the boundary
with the boundary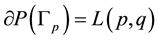 . The plumbing manifold is also known as a graph manifold corresponding to tree graph
. The plumbing manifold is also known as a graph manifold corresponding to tree graph
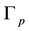 (of type
(of type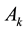 ) shown in Figure 1.
) shown in Figure 1.
With the aim of obtain the coupling constant hierarchy we consider tree plumbing graphs
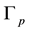 of more general type [5] [13] , whose basic structure blocks are Seifert fibered Brieskorn homology spheres [7] . Let
of more general type [5] [13] , whose basic structure blocks are Seifert fibered Brieskorn homology spheres [7] . Let
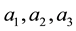
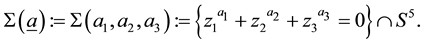
Figure 1. The tree graph
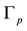
Bh-spheres belong to the class of Seifert fibered homology spheres (Sfh-spheres). On each of these manifolds, there exists a Seifert fibration with unnormalized Seifert invariants
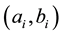
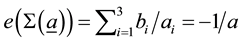
where
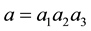
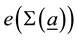
Bh-sphere. If we define continued fraction expansions
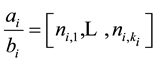
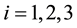
corresponding to Bh-spheres
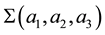
We begin the construction of the principal ensemble of Bh-spheres with definition of a primary sequence (for details see [12] ). Let pi be the ith prime number in the set of positive integers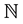
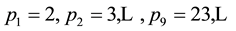
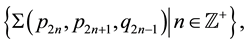
where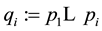
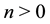
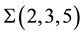
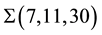
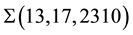
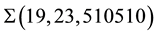
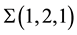
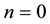
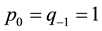
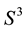
Instead of proceeding with the general consideration (which is rather large and has been realized in [13] [14] ) we want to take up a simplified example, that illustrates in what manner the rational number closed to the experimental value of cosmological constant might appear in our construction. We start considering the term with n = 4 in the primary sequence, that is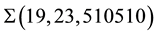
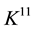
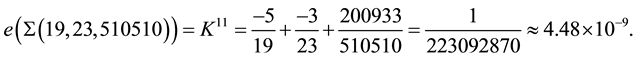
Here we use the classical expression for the rational Euler invariant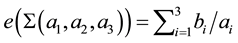
are unnormalized Seifert invariants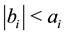
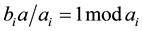
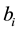
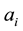
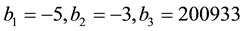
Now we consider the derivative of Bh-sphere [12] defined as
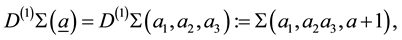
where we can see the result of this operation is the Bh-sphere with Seifert invariants
and the Euler invariant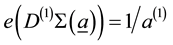
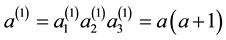
sively, we define by induction the
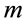
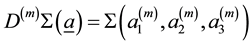
ing 4-th derivative to the Bh-sphere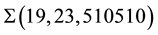
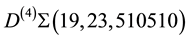
Figure 2. The plumbing graph corresponding to Bh-spheres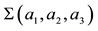
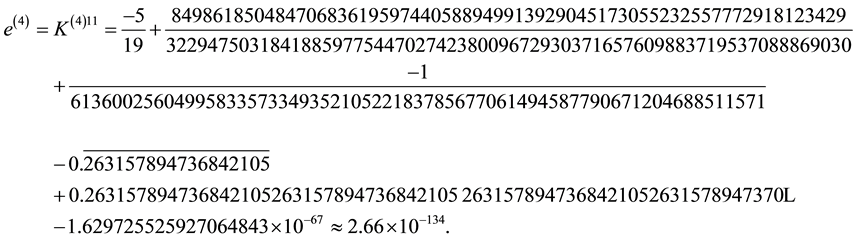
The consequences of these calculations are following. It is possible to interpret the rational linking (1 × 1)- matrix
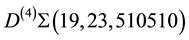
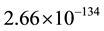
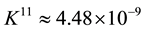
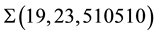
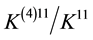
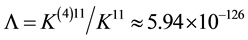
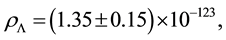
only on three orders. Moreover, the calculations of Euler numbers by the Formulas (6) and (8) lead to the conclusion that the absolute value of each summand is many orders larger that the resulting Euler number which represents the cosmological constant. This fact simulates the fine tuning effect in the modeling scheme, which we have proposed in [14] .
At this point, it emerges the problem of calculate integer Euler numbers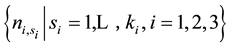
correspond to the plumbing graphs of type shown in Figure 2 which describe Bh-spheres, or equivalently, to calculate the Laplacian matrix for the plumbing graph [5] . (Note that the set of integer Euler numbers is the most important topological invariant of any tree graph manifold.) This problem is reduced to calculate the continued
fraction expansions for all rational numbers
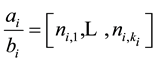
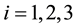
the rational Euler number of a graph manifold. As we can see in the example (8) the second fraction has the huge numerator and denominator, so ordinary methods of expansion in continued fraction represent a lot of operations (as it was mentioned in the Introduction). Note that the same situation occurs for more sophisticated tree graph manifolds which we have to use to describe the coupling constant hierarchy in the universe real [14] . The fact is that our universe contains at least five fundamental interactions (strong, electro-magnetic, weak, gravitational and cosmological) with the corresponding coupling constants. In our model [13] each coupling constant is connected with the rational Euler number of proper Bh-sphere, so to obtain five coupling constants it is necessary to paste together (by plumbing) five certain Bh-spheres. The graph corresponding to this situation is shown in Figure 31. Specific examples are given in [13] [14] . The characteristic feature of all these schemes is the emergence (in the structure of rational Euler invariants) of irreducible fractions with enormous numerators and denominators, which continued fraction expansions are too large to be obtained by classical methods. As an example, in Section 4 we work with the “greatest” fraction which emerges in [14] (Formula (5.12))
Figure 3. The plumbing graph corresponding to the plumbing of five certain Bh-spheres.
whose continued fraction expansion is represented by
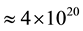
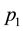
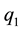
3. Algorithm to Obtain Continued Fraction Expansion
First of all, let’s analyze the fraction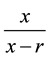
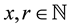

and a direct calculation shows that
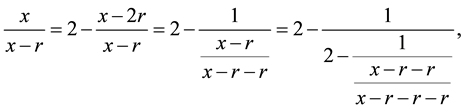
where we observe the difference between the numerator and denominator keeps constant, and so we can repeat
the process k times until obtain the fraction
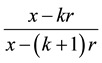
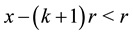
won’t be 1 and we have to restart the process until we get a quotient 1. Moreover, due to condition (10), we can write
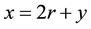
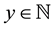
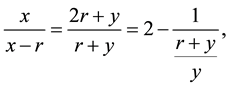
and for the last fraction to satisfy condition (10) we need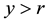
and now we need
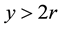
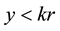
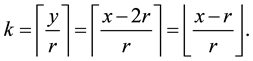
Now, suposse we want the continued fraction expansion for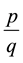
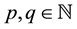
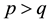
We can observe that this fraction can be rewritten as
that fits with the decomposition in (11) if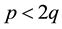
minimum number
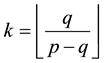
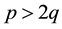
that
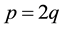
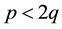
note that the fraction
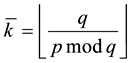
obtained of the previous decomposition to obtain a quotient 1. This is because
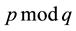
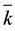
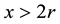
We can obtain all the coefficients of the expansion with these results. Every time we get a quotient 1, we take the value of
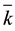
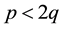
and thus we will get a quotient different to 1. In other words,
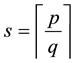
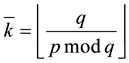
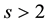
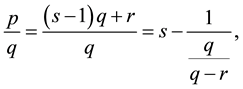
where we note the similarity between the last fraction and (11), so
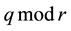
Finally, let
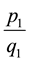
Require:
i = 0
repeat
i = i + 1
ri = pi mod qi
qi + 1 = qi mod ri
pi + 1 = qi + 1 + ri
until ri = 1 or qi + 1 = 1
if ri = 1 then
end if
if qi + 1 = 1 then
end if
In the case
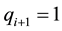
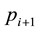
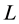
length of the expansion for
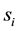
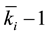
4. Using of the Algorithm to Calculate a Very Long Expansion
Now we show the benefits of the algorithm calculating a special (and long) continued fraction expansion. The algorithm allow us to know the length of expansions even if the number of coefficients is such that it is im- possible to write, by giving us the number of terms equal to 2 in the expansion. Let’s take coprime integers
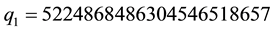
because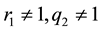
where we stop because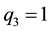
where the suspension points represent
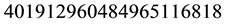
whose quotient is 1. So, the lenght of the continued fraction which represents
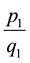
This results clearly shows the benefits of the algorithm against the classical method of the remainders. To illustrate this, the fastest computer over the world at the time, Tianhe-22, would need
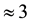
5. Conclusions
The main result of this article is an algorithm for the fast expansion of rational numbers into HJ-continued fractions. This algorithm gives us the possibility to calculate (with a few operations) the complete set of integer Euler numbers (the principal topological invariant) of sophisticate graph manifolds, which we used to simulate the coupling constant hierarchy of the fundamental interactions acting in our universe [13] . Automatically we can explicitly compute the integer Laplacian block matrix associated with any tree plumbing graph [5] . This matrix coincides up to sign with the integer linking matrix of the graph manifold corresponding to the plumbing graph [14] . The rational linking matrix (describing the coupling constants hierarchy) can be obtained from the Laplacian one by means of Gauss-Neumann partial diagonalization procedure described explicitly in [5] [17] . It makes sense to emphasize that the rank of the integer Laplacian block matrix, corresponding to the realistic model coupling constants hierarchy is of order 1020. This gives an idea of the numerical array capacity which is used to simulate the coupling constants hierarchy in the universe, containing five fundamental interactions.
We can make an important physical assumption that the tridiagonal submatrices
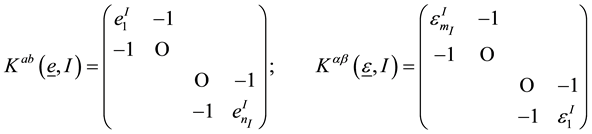
of the integer Laplacian block matrix, corresponding to a plumbing graph shown in Figure 3, describe the low- energy physics of hierarchical topological fluids with
Cite this paper
Fernando I. BecerraLópez,Vladimir N.Efremov,Alfonso M. HernándezMagdaleno, (2015) Algorithm for Fast Calculation of Hirzebruch-Jung Continued Fraction Expansions to Coding of Graph Manifolds. Applied Mathematics,06,1676-1684. doi: 10.4236/am.2015.610149
References
- 1. Hirzebruh, F. (1971) Differentiable Manifolds and Quadratic Forms. Marcel Dekker, New York.
- 2. Popescu-Pampu, P. (2007) The Geometry of Continued Fractions and the Topology of Surface Singularities. Advanced Studies in Pure Mathematics, 46.
- 3. Griguolo, L., Seminara, D., Szabo, R.J. and Tanzini, A. (2007) Black Holes, Instanton Counting on Toric Singularities and q-Deformed Two-Dimensional Yang-Mills Theory. Nuclear Physics B, 772, 1-24.
http://dx.doi.org/10.1016/j.nuclphysb.2007.02.030 - 4. Saveliev, N. (2002) Fukomoto-Furuta Invariants of Plumbed Homology 3-Spheres. Pacific Journal of Mathematics, 205, 465-490.
http://dx.doi.org/10.2140/pjm.2002.205.465 - 5. Becerra, F., Efremov, V. and Hernandez, A. (2014) Block Matrix Representation of a Graph Manifold Linking Matrix Using Continued Fractions. Applied Mathematics, 5, 1894-1902.
http://dx.doi.org/10.4236/am.2014.513183 - 6. Neumann, W. (1981) A Calculus for Plumbing Applied to the Topology of Complex Surface Singularities and Degenerating Complex Curves. Transactions of the American Mathematical Society, 268, 299-344.
http://dx.doi.org/10.1090/S0002-9947-1981-0632532-8 - 7. Saveliev, N. (2002) Invariants for Homology 3-Spheres. Springer, Berlin.
http://dx.doi.org/10.1007/978-3-662-04705-7 - 8. Wen, X.G. and Zee, A. (1992) Classification of Abelian Quantum Hall States and Matrix Formulation of Topological Fluids. Physical Review B, 46, 2290.
http://dx.doi.org/10.1103/PhysRevB.46.2290 - 9. Balachandran, A.P., Chandar, L. and Sathiapalan, B. (1995) Chern-Simons Duality and Quantum Hall Effect. Nuclear Physics B, 443, 465-500.
http://dx.doi.org/10.1016/0550-3213(95)00122-9 - 10. Fujita, M., Li, W., Ryu, S. and Takayanagi, T. (2009) Fractional Quantum Hall Effect via Holography: Chern-Simons, Edge States, and Hierarchy. Journal of High Energy Physics, 2009, JHEP06.
http://dx.doi.org/10.1088/1126-6708/2009/06/066 - 11. Harvey, J.A., Kutasov, D., Martinec, E.J. and Moore, G. (2001) Localized Tachyons and RG Flows. arXiv: hep-th/0111154v2.
- 12. Efremov, V.N., Mitskievich, N.V., Hernandez Magdaleno, A.M. and Serrano Bautista, R. (2005) Topological Gravity on Plumbed V-Cobordism. Classical and Quantum Gravity, 22, 3725.
http://dx.doi.org/10.1088/0264-9381/22/17/022 - 13. Efremov, V.N., Hernandez Magdaleno, A.M. and Moreno, C. (2010) Topological Origin of the Coupling Constants Hierarchy in Kaluza-Klein Approach. International Journal of Modern Physics A, 25, 2699.
http://dx.doi.org/10.1142/S0217751X10048482 - 14. Efremov, V., Hernandez, A. and Becerra, F. (2014) The Universe as a Set of Topological Fluids with Hierarchy and Fine Tuning of Coupling Constants in Terms of Graph Manifolds. arXiv:1309.0690v2.
- 15. Tegmark, M., Aguirre, A., Rees, J. and Wilczek, F. (2006) Dimensionless Constants, Cosmology and Other Dark Matter. Physical Review D, 73, Article ID: 023505.
http://dx.doi.org/10.1103/PhysRevD.73.023505 - 16. Bousso, R. (2007) TASI Lectures on the Cosmological Constant. arXiv: hep-th/0708.4231.
- 17. Neumann, W. (1997) Commensurability and Virtual Fibration for Graph Manifolds. Topology, 36, 355-378.
http://dx.doi.org/10.1016/0040-9383(96)00014-6 - 18. Diamantini, M.C. and Trugenberger, C.A. (2015) Higgsless Superconductivity from Topological Defects in Compact BF Terms. Nuclear Physics B, 891, 401-419.
http://dx.doi.org/10.1016/j.nuclphysb.2014.12.010
NOTES
1In Figure 3 the integer Euler numbers are denoted as
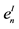
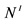
2“TOP #1 SYSTEMS” at Top500 The List, consulted August 5th, 2015. http://www.top500.org/featured/top-systems/