Received 16 June 2015; accepted 2 August 2015; published 6 August 2015

ABSTRACT

Seed dispersal of juniper and pinyon is a process in which frugivorous birds play an important role. Birds either consume and digest seeds or carry and cache them at some distance from the source tree. These transported and settled seeds can be described by a dispersal kernel, which captures the probability that the seed will move a certain distance by the end of the process. To model active seed dispersal of this nature, we introduce handling time probabilities into the dispersal model to generate a seed digestion kernel. In the limit of no variability in handling time the seed digestion kernel is Gaussian, whereas for uniform variability in handling time the kernel approaches a Laplace distribution. This allows us to standardize spatial movement (diffusion) and handling time (peak settling rate) parameters for all three distributions and compare. Analysis of the tails indicates that the seed digestion kernel decays at a rate intermediate between Gaussian and Laplace seed kernels. Using this seed digestion kernel, we create an invasion model to estimate the speed at which juniper and pinyon forest boundaries move. We find that the speed of seed invasion corresponding to the digestion kernel was faster than seeds resulting from Laplace and Gaussian kernels for more rapidly digested seeds. For longer handling times the speeds are bounded between the Laplace (faster) and Gaussian (slower) speeds. Using parameter values from the literature we evaluate the migration potential of pinyon and juniper, finding that pinyon may be able to migrate up to two orders of magnitude more rapidly, consistent with observations of pine migration during the Holocene.

Keywords:

Dispersal Kernel, Invasion Speed, Seed Handling Time, Pinus monophylla, Juniperus osteosperma

1. Introduction

Forest boundaries change over time, and in favorable climates can expand as tree seeds spread beyond the range of the forest and germinate into new trees. Seeds may spread in a variety of ways. Common seed dispersal agents include wind, transportation in water, and transportation via birds and animals (either through being consumed and digested or being carried and cached). Because the diet of birds and some animals is often made up of fleshy-fruited plants, the pattern of seed dispersal and activities of vertebrate dispersers are closely related [1] [2] . Birds in particular contribute heavily to the spread of some plant populations [3] [4] .

A case in point is seed dispersal and forest migration in two southwestern tree species: pinyon (Pinus monophylla) and juniper (Juniperus osteosperma). In both species birds play a major, but different, role. Junipers produce seeds which are available most of the winter, and consequently many birds (particularly American robins, Turdus migratorius, and cedar waxwings, Bombycilla cedrorum) consume juniper berries [5] . The berries are then digested and seeds are deposited some time later by defecation. Digestion does not impede the seeds’ ability to germinate, particularly in the case of robins [6] , and juniper is thus dispersed while robins forage over scores of meters.

By contrast, pinyon seed dispersal by Clark’s nutcracker (Nucifraga columbiana) and pinyon jays (Gymnorhinus cyanocephalus) occurs primarily through seed caching in summer and fall, when the cones mature. Some seeds are consumed immediately, but the majority is placed in a sublingual pouch and carried several kilometers to remote cache sites, where they are buried in small groups [7] [8] . Most of the cache sites are found during the winter, but a substantial percentage of caches are never revisited and the cached seeds are in an ideal situation for germination, which determines pinyon distribution.

Variation in climate also influences the expansion of pinyon-juniper (P-J) woodland via impacts on germination and survival rates. The abundance of summer rainfall and the warming in the winter and spring have caused P-J boundaries to shift northwards [9] [10] . Juniper can sustain more severe drought than pinyon [11] [12] , making pinyon more sensitive to climate than juniper [13] . Although juniper is more drought tolerant than pinyon, both species have declined as their habitat shrinks in the southwestern United States because of accelerated global warming. Recent drought conditions in northern New Mexico, Arizona and southern Utah are more severe than any historic drought. Consequently, P-J habitat boundaries are shifting northwards rapidly [11] [14] [15] . On the other hand, climate change is creating new P-J habitat in central Nevada [12] , the central Great Basin [16] , northeastern Utah [17] and southeastern Oregon [18] . This begs the following research questions: 1) can either pinyon or juniper disperse far enough northward to colonize the new habitat? 2) How rapidly may we expect forest boundaries to move? We will contribute to answering these questions by developing a PDF (Probability Density Function) for seed distribution by active dispersers and using a population-level Integrodifference Equation (IDE) to evaluate the migration potential of these two species.

To model the spread of the seeds, we assume that seed cachers or frugivorous animals collect seeds (through consumption in the case of juniper berries or collection of pinyon seeds to cache at a distance) and then follow a random walk, using the modeling framework introduced by [19] . However, unlike previously considered “failure rates” or “hazard functions” (rates at which seeds are deposited on the ground), we note that the distribution of settling times for seed dispersal by birds should be modeled as distributions in time. Seeds defecated or cached at times sampled from a seed handling PDF will be distributed on the ground in a spatial PDF, or seed digestion kernel (SDK), which is different from any previously-considered dispersal kernel. We will derive the SDK from first principles and find that the mean handling time plays a crucial role in determining its form. The different handlings of juniper and pinyon seeds lead to very different dispersal behaviors. We will compare the SDK with two limiting kernels discussed by [19] , the Laplace and Gaussian kernels; the SDK behaves quite differently in the small handling time limit.

In this paper we numerically calculate the SDK based on PDFs of seed handling times. Once the kernel is determined, we will use it in a generic IDE population model to estimate invasion speeds and compare with speeds generated from Gaussian and Laplace kernels, which are limiting cases. Surprisingly, in some parameter regimes the SDK yields more rapid invasion speeds than either Laplace or Gaussian kernels. Predictions for juniper and pinyon migration rates will be generated using literature values for parameters. We find that pinyon has much higher potential to find and occupy new niches than juniper, consistent with observations of Holocene range expansion for the two species.

2. Methods

2.1. Model for Seed Dispersal

We begin with a common model of dispersal and settling of propagules, (any material that is used for propagating an organism) introduced by [19]

(1)

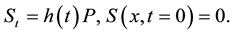(2)

In this model represents the density of seeds during dispersal by frugivorous birds and animals, which are assumed to follow a random walk with diffusion rate D. The function 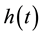represents the hazard function or a failure rate of seeds (i.e. rate at which seeds are placed on the ground by either caching or defectation). The function 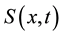is the density of settled seeds (seeds on the ground) at time t. The Dirac delta function, 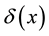, places seeds initially at the origin, with no seeds yet on the ground. Because the system conserves the integral of all seeds at all locations, the sum, 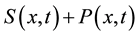, is a PDF for seed location in space at time t. The SDK, K(x), is the long time limit of this process,

.

An important modeling point is that, to be consistent with mechanisms of seed handling by vertebrates, the hazard function, 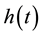, must be a PDF in time. For example, when researchers measure times required for seed digestion and defecation, results are communicated as skewed frequency distributions with a strong mode and tails which decline to zero (e.g. [20] ). This is in direct contrast to failure rates considered in [19] , none of which are modal PDFs. Observed distributions of handling times are asymmetrical, with long tails, and consequently a minimal characterization of such PDFs requires three parameters (one controlling the shape to the left of the mode, one controlling the location of the mode, and one controlling the shape of the tail for large t). We therefore propose

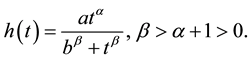(3)

In this distribution the constant b scales the mean digestion time of seeds while a is a normalization constant (not free, since it depends directly on the other three parameters so that integrates to one). The parameters and determine the shape of the tails of 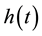(shown in Figure 1 and Figure 2); if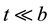, 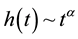while as. The rational form of this hazard function allows us to apply the method of steepest descents to analyze the asymptotic shape of seed digestion kernels below.

2.2. Solution Technique for Calculating SDK

We integrate the PDE directly and then approximate time integrals using the trapezoid rule. To begin, let

. (4)

Equation (1) becomes

. (5)

An integrating factor of can be used to give the solution

. (6)

Using Equation (6) in the model (2) then we get

. (7)

Numerical approximations are then calculated using the trapezoid rule for numerical integration. Solutions generated this way were cross-checked against the (much) more time-consuming finite difference solution of (1) and (2) (see Appendix A) to ensure accuracy. For the same size of time steps we found that direct quadrature of integrals in (7) was substantially more accurate (and rapid) than solution of the PDEs using finite differences.

2.3. Standardizing the Three Kernels for Comparison

We wish to compare the SDK with the Gaussian and Laplace seed. The question is how to standardize the three kernels for comparison? Below we will show that the Laplace and Gaussian kernels arrive from different limiting choices for. We standardize by choosing parameters so that peak seed drop rates occur at the same time for all three handling PDFs (see Figure 3). Since constant seed settling (which leads to the Laplace dispersal kernel) is not a PDF, we instead use a uniform distribution on a bounded interval with mean handling time precisely in the middle to coincide with the modes of the other two handling time distributions. Replacing a constant failure rate with a uniform PDF does not exactly generate the Laplace kernel; however, in Appendix B we show that the SDK generated by a uniform seed handling distribution is well-approximated by the Laplace distribution.

For convenience, we assume in Equation (3) so that is always true. The function is maximal at

. (8)

We will call this time. We wish to standardize the Gaussian and Laplace kernels so that their underlying seed processing PDFs have maxima at. For the Gaussian, let

. (9)

Then

.

This gives

. (10)

To generate a Laplace kernel we assume that the distribution of seed settling is a step function defined by

(11)

As is shown in Appendix B, the solution to (1) and (2) with the step function defined in Equation (11) is approximately the Laplace kernel

. (12)

After this standardization, the Gaussian kernel (10) and the Laplace kernel (12) are ready for comparison with the seed digestion kernel. Figure 4 illustrates the shape of seed distribution on the ground for the standardized kernels. Seeds seem to disperse to the furthest for the Laplace (having fattest tail), , and least for the Gaussian (the thinnest tail),. The pattern of seed dispersal under seed digestion kernel, , is bounded by the other two. This observation will be formalized using the method of steepest descents below.

2.4. Analyzing the Tail of Seed Digestion Kernels

Here, we approximate the tail of the SDK using the steepest descent method [21] to compare tails with Gaussian and Laplace seed kernels. As in the previous section, we assume so that the rate of seed digestion Equation (3) becomes

. (13)

Define the exponent in (7) as

. (14)

The critical point of the function is. Differentiating twice the Equation (14)

with respect to t and evaluating at we get

. (15)

Let us suppose in Equation (7); then

. (16)

Equations (15) and (16) can be used with the generalized steepest descent theorem to approximate (7), giving

. (17)

Analyzing K as gives the asymptotic behavior in the tail (see below).

2.5. Population Model for Evaluating Migration Potential

To determine how the shape of the SDK affects rates of invasion, the kernels must be imbedded in a population model. Below we present a simplification of the model used by [22] to describe the general behavior of an invasion by perennial plants. For xeric-adapted species like pinyon and juniper dispersing into the new regions, competition for water and space occurs primarily among seedlings. We take

, (18)

where N_t represents the population density of adults in generation t. The function is the SDK while is the mortality rate of adults per generation, is the number of seeds produced per adult per generation, and

is the Beverton-Holt model for seed survival and germination in competition with other seeds.

Here M is the maximum number of surviving seeds, g is the germination rate, and is the seedling survival rate. The convolution in Equation (18) is defined by

,

and the integral represents the total number seeds arriving at location x from all possible locations, y. Therefore, the first term on the right hand of the invasion model (18) predicts the distribution of new trees depending on the available sources and the second term provides the surviving number of old trees so that the total is the population of trees in the next generation.

2.6. Analysis of Invasion Speeds

To analyze invasion speeds for models like (18), we follow the analysis of [23] . Because the population density of a tree population approaches zero in advance of the invasion front, we can assume that as

, (19)

with. We assume that the spread of the tree population is a traveling wave with parameter u determining the shape of its leading edge. Introducing a constant, c, to represent the speed of invasion, the traveling wave of population density during an invasion satisfies

. (20)

Combining Equations (19) and (20)

. (21)

Plugging this into Equation (18),

, (22)

Taking only leading order terms,

, (23)

where is the net reproductive rate.

Writing the convolution of Equation (23) in terms of an integral, we have

(24)

where the moment generating function, M(u), is defined by

. (25)

Differentiating Equation (24) with respect to u and setting to zero to find the extremal invasion speed gives

. (26)

Using Equation (26) to eliminate c in (24) gives

. (27)

To find the invasion speed, , we solve Equation (27) numerically for u and then use (26). Both M(u) and M'(u) were approximated for specific u using the trapezoid rule; roots of were found using fzero in MATLAB. Those roots are used in Equation (24) to predict invasion speed.

3. Results

3.1. Shape of Kernels Based on Mean Digestion Time Scaling Parameter

The mean digestion time scaling parameter b plays a major role in determining seed dispersal. Changing the value of b generates different shapes of solutions (see Figure 5) with larger values of b corresponding to broader dispersal, as we expected. If digestion or caching takes longer, birds have more time to travel before depositing seeds, resulting in seeds traveling further from the source.

3.2. Comparison of Tails

We would like to characterize the shape of the tail of the SDK and place it in the context of the well-known Gaussian (10) and Laplace kernels (12). The exponents of the exponential functions for both kernels determine

the shapes of the corresponding tails. To analyze the tails of these kernels, we consider large x and assume other parameter values are bounded. The dominant terms in the exponents of the Gaussian and Laplace kernels are

and, respectively. It follows that the tail of the Gaussian kernel decays to zero much faster

than the tail of the Laplace kernel when.

In the case of the most slowly-decaying PDF of seed handling times, , the SDK derived from the method of steepest descents (17) can be written as:

, (28)

where is given in Equation (13). Note here that branch cuts have not been chosen for the various complex functions in the exponent so we are at liberty to choose branches to keep results on the real axis. Since

is finite, the dominant term in the exponent of (28) is

(29)

and therefore

(30)

The exponents of Gaussian kernel and Laplace kernels are

(31)

and

(32)

Observing

we conclude that the tail of Gaussian kernel decays to zero most rapidly while the tail of Laplace kernel is the slowest. The tail of the SDK is intermediate between the other two.

3.3. Relationship between Invasion Rate and Mean Digestion Time

We have not chosen scales for generation time, population density and space yet. To compare the speeds of invasion from the population IDE (18), we may therefore, without loss of generality, choose mortality, the reproductive rate and the diffusion D = 1. We fix the seed settling parameters and for the longest tail in. Using these values, we estimate the speeds of invasion corresponding to the SDK, , the Gaussian kernel, , and the Laplace kernel,. Speeds of invasion are compared in Figure 6 as a function of the mean digestion time scaling parameter b.

There is a strong relationship between the characteristic handling time, b, and invasion speed, c. The longer it takes to digest a seed, the faster forest migration. For small b, the SDK invasion speed is higher than the speeds corresponding to the Gaussian and Laplace kernels. On the other hand, for bigger b values, the speed of invasion with the Laplace kernel is fastest, the speed with a Gaussian kernel is slowest and the speed corresponding to the SDK stays between the other two, as might be expected from comparing tails.

As, not only does the SDK give faster rates of invasion, but also speeds associated with the Gaussian and Laplace kernels decrease to zero whereas speeds corresponding to the SDK are still positive. This happens because both Gaussian and Laplace kernels approach the delta function, , as, meaning that seeds do not disperse. However, the seed digestion kernel has finite support as (because as). Since mean digestion time is non-zero, the SDK allows for seed dispersal even as b tends to zero.

4. Migration Potential of Pinyon and Juniper

To quantify invasion speeds in terms of yearly distance covered for both pinyon and juniper, we need specific data such as the mean generation time (G), mean dispersal space step, mean dispersal time step, mortality rate and the characteristic handling time (b) for each species. We also need to estimate the reproductive rate and the diffusion rate (D). We are fortunate to have a paired growth rate study on pinyon-juniper in central Utah [24] , in which population growth of both species was tracked dendrochronologically from survivors of a fire in the mid-nineteenth century. This allows us to calculate

, (33)

where G is the generation time (duration from seedling to getting matured tree for producing seeds), n is the initial number of trees and N is the total number of trees at the end of the study. To estimate the diffusion rate D for birds, we use

, (34)

where is the root mean square displacement in a time step of the underlying random walk and τ is the mean time between steps in the walk [25] . A summary of parameters used for the two species, and supporting references, appears in Table 1.

In order to calculate yearly invasion speed, c, we need to rescale both space and time, since we fixed D = 1 (equivalent to nondimensionalized space) in the numerical calculations. Additionally, each step in our IDE is a generation, which must be scaled back to years for comparison purposes. Assuming the dimensional diffusion rate, D, is in m² per minute and the mean handling time is in minutes, the only available space scale in the seed dispersal model (1) and (2) is . Now, if is the speed of invasion associated with the nondimensional dispersal model () then yearly migration rates can be calculated:

(35)

Now we turn to specific parameter values for pinyon and juniper.

For pinyon we use a generation time G ~ 20 years from [26] . To estimate R₀ we refer to [24] , who determined that only 6 pinyon survived the nineteenth-century fire on their site. The number of pinyon pines increased to 1051 over the next 145 years giving R₀ = 2.04/generation for pinyon from equation (33). [7] observed that Clark’s Nutcracker fly from 4000 to 5000 meters while caching seeds, taking 15 - 30 minutes. We therefore take

λ = 4500 meters and use τ = 22.5 minutes, giving. They further observed seed handling in

three phases. Nutcrackers spend 45 minutes collecting seeds to fill their pouch, 15 - 30 minutes to travel to the caching area and 5 - 10 minutes to cache all seeds carried in their pouch. Averaging and summing, we estimate

seed mean handling time to be minutes. This gives a dispersal scale. [27] es-

timate annual mortality at 0.08% - 0.23% for common pinyon. Taking the mean and converting to a rate per generation gives ω = 0.00155. Taken together, these parameters give a minimum speed of 518.97 m/year and a maximum of 946.1 m/year for pinyon, with an average of 773.31 m/year.

On the other hand, for juniper we use a generation time G ~ 50 years from [28] . To estimate R₀ we follow [24] , who observed that only 109 junipers survived the nineteenth-century fire on their site. The number increased to 172 over the next 145 years giving R₀ = 1.17/generation for juniper from Equation (33). [6] observed that American robins forage in the range of 10 - 100 meters with mean 55 meters and average 4 minutes between trees. We therefore take λ = 55 meters and time step τ = 4 minutes, giving D = 189.1 m²/min. [20] report that the cedar waxwing takes between 7.35 and 22.45 minutes to digest red cedar (Juniperus virginiana) seeds; we

therefore use a handling time min. These estimates give a dispersal scale. [27]

estimate annual mortality at 0.01% - 0.07% for Utah juniper (Juniperus osteosperma). Taking the mean and converting to a rate per generation gives ω = 0.0004. Using these parameter ranges we find that juniper spreads with minimum speed 0.42 m/year and maximum speed 7.3 m/year with an average of 3.3 m/year, two orders of magnitude more slowly than pinyon.

These results match up well with what is known about these two species and their relative movements during the Holocene. Juniper seems to have been present in the Great Basin area for at least 30,000 years, based on evidence from fossilized packrat middens [29] . While its range contracted due to climatic shifts there were no significant expansions. By contrast, pinyon pine was limited to Arizona and New Mexico up to 9000 years ago, but migrated up the Wasatch front to the northeastern corner of Utah in the next 1000 - 1500 years [30] , which would have required speeds in excess of 500 m/year.

5. Conclusions

Mechanisms of plant migration vary based on the source plant and the dispersal process delivering seeds to new locations for germination. Juniper berries mainly disperse after being eaten by vertebrates who deposit seeds after digestion. Birds, particularly robins, may be the biggest dispersers. Seeds of pinyon trees, on the other hand, are commonly spread while animals cache, and corvids (jays and nutrcrackers), which cache at large distances, are the largest contributors. In this paper, we introduced a PDF of seed-handling to reflect the effects of digestion/caching on dispersal of pinyon and juniper seeds. We connected this distribution to hazard functions or failure rates in an existing random-walk dispersal model to determine a seed digestion kernel modeling the probable location of seeds after active dispersal. As expected, if birds or animals take more time to handle seeds, those seeds are dispersed further away from the source tree. While no closed-form solution for the SDK is available, it is easy to calculate numerically (and would only have to be calculated once, in advance, for implementation in an IDE model for population invasion).

To evaluate migration potential for pinyon and juniper we introduced an IDE model with competition among seedlings, which is appropriate for desert-adapted trees in the xeric environment of the American Southwest. The SDK was compared with well-known Laplace and Gaussian kernels (L(x) and G(x)). After standardizing the associated PDFs for handling time, the speed of invasion for the SDK was the fastest for shorter handling times (rapidly digesting seeds). As handling times increased, however, the speeds for the SDK fell between the Laplace kernel’s (faster; based on an assumption of constant seed deposition) and the Gaussian kernel’s (slower; based on the assumption of instantaneous seed deposition), as would be expected from the relative behavior of the tails.

Using the SDK and median parameter values estimated from the literature it turned out that pinyon has migration potential at least two orders of magnitude larger than juniper due to avian dispersal. Along with changing temperatures and diminishing moisture levels the favorable environment for P-J is moving northwards through Utah. Over time, these trees will not be able to survive in the southern limits of their current habitat. The large migration potential of pinyon means that it is most likely to occupy new habitats opening to the north.

Of course, juniper already occupies much of the available northern habitat, and with longer generation times and much stronger adaptation to variable moisture regimes juniper can be expected to flourish in northern Utah for the foreseeable future. Moreover, juniper may have much higher migration potential than our analysis indicates. For the slower juniper we can probably not ignore mammalian dispersers [31] and passive dispersal agents (such as runoff and streams for dispersing juniper berries, see [5] ). The two main avian juniper dispersers, American robins and cedar waxwings, both forage and defecate locally and therefore do not seem to make a large contribution to juniper spread. However, mammals such as foxes, bears and coyotes may disperse juniper seeds long distances since they have much longer gut-retention times and can travel more than 10 kilometer per day [32] . Since juniper seeds persist through winter, dispersal by spring runoff can also contribute substantially. Nevertheless, dispersers like pinyon jay and Clark’s nutcracker likely give pinyon the dispersal advantage over juniper.

The largest factor ignored in our study is spatial variability. As [22] pointed out, vertebrate dispersers move rapidly through some habitats and linger in others, and western landscapes are comprised of highly variable habitat, particularly at the leading edge of invasions. One would expect step sizes in the random walks that dispersers follow, and therefore their diffusions rates, to vary strongly with habitat type. Recent advances in the use of homogenization [33] make integration of reaction-diffusion models with highly variable constants surprisingly easy, so building SDKs with variable diffusion and applying asymptotic techniques like homogenization will be our future concentration of research.

Acknowledgements

The authors would like to thank Tom Edwards and Jacob Gibson for discussion of life-history traits of pinyon and juniper and assistance with background literature. Luis Gordillo, Martha Garlick and USU’s MathBio group gave RCN much helpful feedback. RCN was partially supported by a grant from USU’s School of Graduate Studies. JAP would also like to thank the NSF for support under DEB grant 0918756 as well as the Western Wildland Environmental Threat Assessment Center (WWETAC).

Cite this paper

Ram C.Neupane,James A.Powell, (2015) Mathematical Model of Seed Dispersal by Frugivorous Birds and Migration Potential of Pinyon and Juniper in Utah. Applied Mathematics,06,1506-1523. doi: 10.4236/am.2015.69135

References

Appendix A: Finite Difference Approximation

We will use two techniques to solve the dispersal model given by Equations (1) and (2) with corresponding seed digestion rate given by the Equation (3). First, we will solve this PDE numerically using finite difference approximations

(36)

where. We discretize the space derivative with respect to the variable using a second order centered finite difference,

. (37)

Using these discretizations and approximating using a standard normal density,

, (38)

with variance σ chosen to be very small, the system (1) and (2) can be solved numerically provided to ensure numerical stability [34] .

Appendix B: Error Calculation for Seed Digestion Kernel with Step Function h(t)

The Laplace kernel used for comparison in the main text arises from solving Equations (1) and (2) with a con-

stant hazard function. However, since the constant function is not a PDF we must compare the Lap-

lace kernel with the seed digestion kernel with step function defined in Equation (11), which was standardized for comparison. In this appendix, we analyze the difference between the Laplace kernel, used as the

approximation of the systems (1) and (2) with a step function failure rate, and the actual solution.

To calculate the difference between the Laplace and actual kernels, we first find the error in P and use it to calculate the error in S from the models (1) and (2). We denote the actual solution for P (with stepped hazard function) as and the approximate solution (with constant hazard function) for P as. Similarly, the actual and approximate solutions for S are and respectively. Notice that both solutions for P are

equal when and are different when. Plugging in Equation (6) we have

(39)

The solution for at (where) is

, (40)

when and, we have

. (41)

when and, the approximate solution is

, (42)

The error in P as. From Equations (42) and (2) with we get

and,. (43)

Thus, the error in S is

, (44)

Finally we must calculate the error in the kernel () which can be obtained by using the limit in Equation (44). Form Equations (42) and (44) we then have

(45)

We use the trapezoid rule to approximate the integral and note that we have not chosen scalings of time and space, so without loss of generality D = 1 and b = 20. In a spatial domain −30 < x < 30 the estimated and errors are 0.0026 and 0.00052. The two seed dispersal kernels (the Laplace kernel with constant and seed digestion kernel with step function) appear in Figure 7. Pointwise errors are depicted in Figure 8.