Received 20 March 2015; accepted 30 June 2015; published 3 July 2015

ABSTRACT

In the paper, We discussed the matching uniqueness of graphs with degree sequence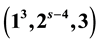. The necessary and sufficient conditions for and its complement are matching unique are given.

Keywords:

Graph, Matching Polynomial, Matching Uniqueness

1. Introduction

All graphs considered in the paper are simple and undirected. The terminology not defined here can be found in [1] . Let G be a graph with n vertices. An r-matching in a graph G is a set of r edges, no two of which have a vertex in common. The number of r-matching in G will be denoted by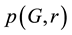. We set 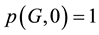and define the matching polynomial of G by

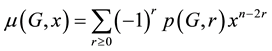
For any graph G, the roots of 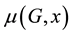are all real numbers. Assume that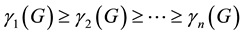, the

largest root 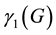is referred to as the largest mathing root of G.

Throughout the paper, we denote by and 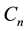the path and the cycle on n vertices, respectively.

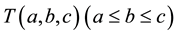denotes the tree with a vertex v of degree 3 such that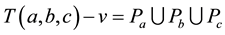, and

denotes the tree obtained by appending a pendant vertex of the path 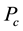in 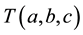to a vertex with degree 2 of. is obtained by appending a cycle to a pendant vertex of a path. Two graphs are matching equivalency if they share the same matching polynomial. A graph G is said to be matching unique if for any graph H, implies that H is isomorphic to G. The study in this ares has made great progress. For details, the reader is referred to the surveys [2] -[6] . In the paper, we prove

and its complement are matching unique if and only if or

.

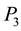2. Basic Results

Lemma 1 [1] The matching polynomial satisfies the following identities:

1).

2) if is an edge of G.

Lemma 2 [1] Let G be a connected graph, and let H be a proper subgraph G.

Then.

Lemma 3 [2] Let, if, then H are precisely the graphs of the following

types:

Lemma 4 1) [1] .

2) [2] .

3) [2] .

4) [3] ,

.

5) [4] .

6) [5] .

Lemma 5 [5] Let G be a tree and let be obtained from G by subdividing the edge uv of G, then

1), if uv not lies on an internal path of G.

2), if uv lies on an internal path of G, and if G is not isomorphic to.

Lemma 6 [6] are matching unique.

Lemma 7.

Proof. Direct computation (using Matlab 8.0), we immediately have the following:

,

.

By Lemma 2, 5, we get

.

3. Main Results

Theorem 1 Let, then G are matching unique if and only if or

.

Proof. The necessary condition follows immediately from Lemma 1. We have

Now suppose that or, H is a graph being matching equivalency with G. We proceed to prove that H must be isomorphic to G. By Lemma 3

Case 1. If. By, we know that. Hence, the component of

in H may be only. By Lemma 4, and

. Let, then, a contradiction. Let. If, then, a contradiction. If, then, a contradic-

tion. If, then, a contradiction. Let. If, then

, a contradiction. If s₂ ≥ 2, then,

a contradiction. Let. If, then, a contradiction. If, then

, a contradiction. Let, then

, a contradiction.

Case 2 If. By, hence the component of in H may be

only. Let. If, then, a contradiction. If, then

, a contradiction. If, then, by Lemma 4, we get, thus. That is,

, then

, by Lemma 6, has at least one equal to 6, a contradiction. If,

by Lemma 4, 6, we have, thus H be isomorphic to G. Let. If,

, a contradiction. If, a contradiction. Let, by

Lemma 4, , a contradiction.

Case 3 If, by, a contradiction. Combing cases 1 - 3, H is isomorphic to G.

The proof is complete. For a graph, its matching polynomial determine the matching polynomial of its Comple-

ment [6] , so the complement of are matching unique if and only if or.

References