Received 9 January 2015; accepted 27 January 2015; published 3 February 2015

ABSTRACT

The paper solves the problem of the variation formulation of the steady-linear oscillations of structurally inhomogeneous viscoelastic plate system with point connections. Under the influence of surface forces, range of motion and effort varies harmonically. The problem is reduced to solving a system of algebraic equations with complex parameters. The system of inhomogeneous linear equations is solved by the Gauss method with the release of the main elements in columns and rows of the matrix. For some specific problems, the amplitude-frequency characteristics are obtained.

Keywords:

Plates, The Ability to Move, The Complex Amplitude

1. Introduction

Currently, in many technical designs there are widely used shell and plate structures. Thin-walled tubes and panels in real conditions usually interact with other structures and bodies, which are based on resilient supports and also have hinge supports and associated masses. As in [1] , we present a generalized interpretation of the statement of the problem of forced oscillations for a certain class of thin deformable bodies, as well as mechanical systems consisting of these elements. Support was adopted from the hinge or of entrapped type that connects elements of the system. The location supports linkages and concentrated masses arbitrarily [2] -[4] . Elements of the system can be both elastic and viscoelastic, on the edge of the elements given by the homogeneous boundary conditions. The case when the operating system on the driving force subordinates to the harmonic law is required to determine the frequency response of the system.

2. The Mathematical Formulation of the Problem of Forced Vibrations Viscoelastic Systems with Point Connections

Consider a homogeneous isotropic a resilient plate of constant thickness h, limited to the size of a rectangular contour a, b. Suppose on the plate is Q dot added mass 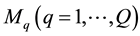and it is elastically and, accordingly, simply supported rigidly in L' and correspondingly S internal points. Swivel bearing plate at the point may be combined with jamming in any direction, layout of point masses and in the plane of the plate arbitrarily. The boundary condition on each side of the plate can be one of the following: hinge-support, jamming or free edge. This paper considers the package of plates (consisting of n-plates (n = 1, ∙∙∙, N)). It is required to determine the steady-linear oscillations of the plate. Assume that the perturbing forces applied to the n-mu body have the same frequency but different amplitude; Then they change the law can be written as

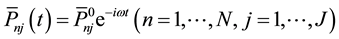, (1)

where ω―given real frequency of the disturbing force,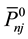―Vector amplitude of the disturbing force directed at j-th component of the displacement vector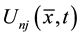, N―the number of elements of the system, J―number of components of the displacement vector. Assuming the validity of Kirchhoff-Love hypotheses, we write the known from the theory of elasticity relationship between displacements and strains [5] :

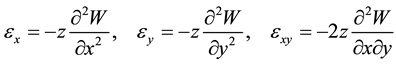
Here z―coordinate of a point in a direction perpendicular to the middle surface, ε_x, ε_y, ε_xy―components of the strain tensor of the plate. To describe the relaxation processes occurring in the viscoelastic elements or point connections system, we adopt a linear Boltzmann theory of heredity:

, (2)

where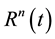―relaxation kernel n-th viscoelastic element or connection point, E_n―instantaneous modulus of elasticity. To stress was periodic function of time, in a ratio heredity (2) the lower limit of integration taken to be negative infinity. If the lower limit is zero, the voltage will contain a periodic additive which decreases with time. On the influence function 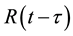the usual requirements imposed inerrability, continuity (except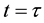), fixed sign and monotonicity:

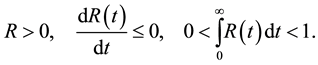
In contrast to the problems of the natural oscillations [1] , the conditions (a little) kernel parameters of relaxation not put.

If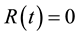, the elastic body. Stress components are equal

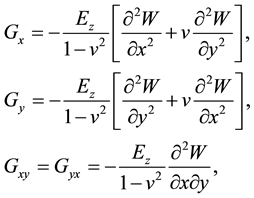(3)

where E―Young’s modulus, and v-Poisson’s ratio, which is assumed to be constant. The normal components G_z transverse rupture is small compared to G_x and G_y, therefore believe G_z = 0. The potential energy stored during the elastic deformation of the plate is given by:

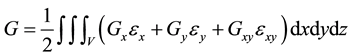, (4)

where V―the volume of the plate. Substituting in (4) the values of the components of deformation and stress (2), (3) and taking into account the potential energy of elastic supports, we obtain

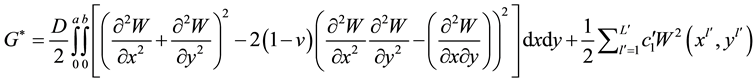, (5)

here―stiffness of the plate cylinder, and,―stiffness and the coordinates of the elastic support. Double integrals in (5) is taken over the surface of the neutral layer. The kinetic energy of the plate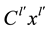, taking into account the added mass is given by

, (6)

where ρ―the density of the plate material, x^q, y^q―coordinates q-th associated mass. We formulate the problem in terms of the method of virtual displacements, according to which the sum of the work of all active forces in the possible displacement δU, satisfies the boundary conditions, is equal to zero:

(7)

here, , ,―virtual work of internal forces shell, elastic supports, inertia forces, taking into account the concentrated loads and virtual work surface forces. These works are calculated by the formulas

(8)

where, h―density and thickness of the shell, M_q-q-I added mass, L'―number-the elastic supports, Q―the number of additional masses, V,―volume and lateral surface of the shell,―components of stress and strain tensors shell, ,―Stress and strain l'-th elastic support, δ―variation on the generalized displacements. All terms in Equations (7) are calculated by the formula (8). Steady-state oscillations of n-th element of the system will be sought in the form

(9)

where―complex amplitude of forced oscillations. It is clear that all the generalized coordinates of the system should be changed with a single frequency equal to (ω real) viscoelastic forces. Transform variation equation (9) as well as in [1] , i.e. substitute in a series of (2), (3), (4), (5), while expressing the deformation of the components of the displacement vector. Contained in the equation of integral expressions of type (2) by replacing the variable into the form [6]

where,―respectively, the cosine and sine Fourier

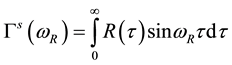
transforms relaxation kernel material. This will eliminate the function of time, which in this case has the form, obtain the variation equation for the displacement vector. Imposed on the system of rigid connection point, as in the problem of the natural vibrations, made under the sign of the variation by the method of Lagrange multipliers. The final form of the variation equation is as follows:

, (10)

where G―total virtual works of the system, and F―kinematic conditions of rigid point constraints imposed on the system.

The task is now formulated as follows:

・ Let the driving force satisfies the relation (1);

・ Required depending on the frequency of the driving force to find a module of the displacement vector (the amplitude of the forced oscillations) satisfying Equation (10) and specify the homogeneous boundary conditions. When studies have established processes, the initial conditions are not put here. If necessary, you can define and Lagrange multipliers, the physical meaning of which - the reaction of hard point connections.

3. Evaluation of the Practical Convergence of the Method

In this paper we do not address the question of convergence of the method with a rigorous mathematical point of view, since it is not crucial for the following reasons. Energy approach used in the formulation of the problem is essentially the Ritz method, the convergence is strictly proved, for example, in [7] [8] . Accounting using Lagrange point constraints imposed on the plate, there is also a well-known method of finding a conditional extremum.

4. Construction of Resolving Equations of Linear Problems of Forced Vibrations of Viscoelastic Systems with Point Connections

The solution of the variation Equation (10) is sought in the form of a superposition of orthogonal basis functions. It is proposed that the elements are free from localized masses and all point connections (poles, posts) are known. Then as the desired displacement field satisfies the variation Equation (10) and specify the homogeneous boundary conditions, we assume a finite sum of these fundamental functions:

, (11)

where―unknown coefficients.

After substituting the sum (11) into Equation (10) coefficients and Lagrange multipliers, , will be the generalized coordinates. The dimensionality of the system is the same as in the case of free oscillation [1] . In matrix for it can be written as

. (12)

Symbols of all the quantities in the left part of the system of equations (12) coincide with the notation of [1] . The program that implements the algorithm, the formation of all the matrices A, , , , B produced by

the same routines that are used in the problem of natural oscillations [1] . Vector-Column structurally con-

sists of two sub vectors. If equation (10) is differentiated with respect Lagrange multiplier first, , ,

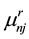
them the upper subvector vector will be zero, and its dimension is equal to the total number of Lagrange multipliers. Lower subvector is the vector amplitude of the driving forces. In formula (9) it is assumed that

the disturbing force is distributed nature. Merits will not change if the applied force is concentrated. Then the virtual work space element is replaced by the virtual work of the concentrated force. Ultimately, the change shall

be subject only vector amplitudes, which, apart from the amplitude of a force filled with zeros. The system

(12) is solved by the Gauss method with the release of the main elements in columns and rows. Note that the initial system of equations (8) has complex coefficients, so the program that implements the algorithm is written for the general case, i.e., for systems with complex numerical coefficients and complex unknowns. Right side of

the system, i.e. vector, must be specified as

,

where,―the real and imaginary parts of the load vector, and,.

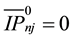
The calculated components of the vector of unknowns, are complex quantities, i.e. vector represented in

the for. To the amplitude of the forced vibrations and reactions bonds had a real sense, it is neces-

sary to take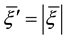, i.e., as generalized coordinates, , , take modules of the corresponding components of the vector. After this, the components of the displacement vector unambiguously be identified through Formula (11). Substituting the last formula the coordinates of any point of the system, we obtain the vibration amplitude for a given driving frequency ω.

5. Numerical Implementation of the Algorithm for Solving Problems of Steady Oscillations with the Analysis of the Results

This part presents the solution of several problems, which are received and analyzed by the frequency-amplitude characteristics for the displacements of individual points of structurally inhomogeneous viscoelastic systems. The purpose of research is to confirm (or refute) the mechanical effects described in [1] . For this purpose, the distribution of forces perturbing is selected so that the resonant cases of components of the displacement field get values close to their own forms. Definition of a sufficient number of basic functions in approximating the sum is as follows. For a selected point of the system builds the frequency-amplitude characteristics at, where K₁―some fixed positive integer. The process ends after the transition from a K + 1 results in a change of the resonance curve, which is not more than 1% of the maximum in the vicinity of the resonance, or in any other region of interest.

Problem 1. Consider the design is a package of two parallel square plates with elastic shock absorber and the associated mass. This task determines the frequency-amplitude characteristics of the mechanical system depending on its geometrical parameters. The system is a package of two elastic square plates connected at the center of a weightless viscoelastic damper. Kernel for relaxation absorber selected as

,

where A, β, α―Kernel parameters.

This corresponds to approximately 60% surge creep contribution to the overall deformation of the viscoelastic body under quasi-static loading process. With the damper stiffness is fixed and taken to be 10.

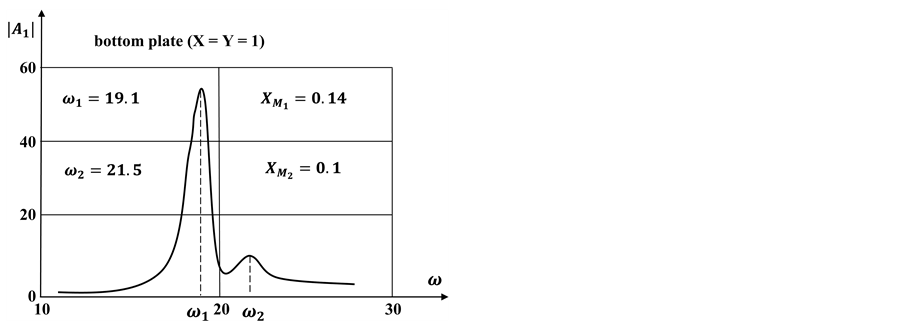
For this case, the kernel parameters as follows: A = 0.078; α = 0.1; β = 0.05 . In both plates has one attached mass. Plate simply supported along a contour similar to mechanical and geometrical parameters, Е = 2 × 10¹¹ н/м²; ρ = 7.8 × 10³ кг/м³; v = 0.3; а = b = 0.2 м; h = 0.001 м . Weights are equal to each other (М₁ = М₂ = 0.05 кг), one of them (М₁) fixed on the bottom plate at a point, , and another (М₂) can move through the central axis of the structure. As the load harmonic excitation is considered uniformly distributed over the area of the two plates driving force vector R. The amplitude of this force is equated to the unit vector. Depending on the position of the load М₂ were the amplitude of forced oscillations of the system of plates. The amplitudes have been constructed for the central points of the two plates (x = y = 0.1 m). Figure 1 shows the case where the mass М₂ located as the point, or, the upper plate. Under these conditions of the masses М₂ frequency-amplitude characteristics of the upper and lower plates are similar and therefore show on the same graph. Given in [1] of Figure 3.1 shows that the damping capacity of the structure at the specified coordinates mass М₂ one and the same. Thus, coincidence plots frequency amplitude characteristics at various locations weight М₂ Figure 3.1 confirms the symmetry [1] . Analysis Figure 1 shows that when the driving frequency coincides with the natural frequencies ω₁, ω₂ a jump in amplitude as that lower and the upper plates, wherein the absolute value of these resonant amplitude lower and upper plates are different. Here and further the equality of natural and forced frequencies relative, since due to the dissipative properties of the structure of the jump amplitude maximum shifted somewhat to the left of their own (and hence disturbing) frequency. Let us analyze the behavior of the graphs in Figure 1. Resonant amplitude of the central points of the two plates takes large values in the case of the first resonance compared to the second. This is because the load applied to the plates at the first resonance is in phase oscillations. Thus, when forced oscillations qualitatively identical displacement field of the central points of the plates at ω = ω₁ и ω = ω₂ differ in terms of quantity, i.e. in the resonance amplitude. This fact is also consistent with Figure 3.1 [1] , in which all and, in particular, in these points,. Figure 2 shows the case when the mass М₂

located at, , i.e., in the center.

The behavior of the resonant amplitudes for the top and bottom plates is qualitatively different from Figure 1. However, in the latter case, the resonant amplitude of the first two plates is greater than the corresponding amplitudes shown in Figure 1. This is also consistent with the results obtained in [1] , namely, the fact that these positions weight М₂ damping coefficients of the first global forms are different. It should be noted that here, as in the previous embodiments, the task number for the resonance amplitude plates plays a determinant role oscillation phase relative to each other, the first resonance occurs when the two plates oscillations in phase (with different or equal amplitudes), the second resonance occurs when vibrations of plates are in antiphase (shift for the period). Displacement field at forced oscillations separate plate within these resonant frequencies qualitatively unchanged―it is close to its own form.

Task 2. Two identical mechanical properties elastic plate (E = 28; ρ = 4; v = 0.3) are connected in the center of one weightless viscoelastic damper (spring). The mass of the spring M₀ = 0.05, square plate (a = b = 1), supported along the contour, the thickness of the lower plate h₁ = 0.1; and upper h₂ = 0.046 on the bottom plate is attached at the center point mass. Recall that we consider two parallel hinged plates connected at the center of a viscoelastic damper. Plates are elastic square and thicknesses. On one of them (thicker) is fixed in the center of the concentrated mass. Parameters his relaxation kernel absorber (spring) determines the value A = 0.078; α = 0.1; β = 0.05 (higher viscosity). The design is distributed over the area of the two plates of the disturbing nature of the harmonic load. Vector amplitudes of these forces have components equal to one. For the case of forced oscillations is required to evaluate the dissipative properties of structurally inhomogeneous viscoelastic system in general, depending on the magnitude of the instantaneous stiffness of the shock absorber. Assessment methodology is as follows. Selected characteristic point of the system and for her with fixed parameter instantaneous damping built―frequency amplitude characteristic. In this case, the damping capacity of the system is determined by the maximum of the resonance amplitude. Then the parameter varies, and with all the defining (maximum) resonance amplitude is selected minimum. This parameter value and will fit most case dissipation system. As the feature points are selected as two of the central (x = y = 0.5) point on the bottom and top plates. Point to other coordinates gives qualitatively the same results. In [1] , it was shown that the natural frequency of the global damping factor reaches its maximum. Thus, the effect of the interaction of natural forms is confirmed once again the problem of forced oscillations [1] [3] [4] . The difference in the optimal values of the instantaneous damping for forced and natural (С^* = 3.4 × 10⁻³ и С^* = 5.4 × 10⁻³) explains the difference between the viscosities of shock absorbers.

References