Applied Mathematics
Vol.05 No.20(2014), Article ID:51585,8 pages
10.4236/am.2014.520303
Infinite Number of Disjoint Chaotic Subsystems of Cellular Automaton Rule 106
Gaocang Zhao1, Fangyue Chen1, Weifeng Jin2
1School of Science, Hangzhou Dianzi University, Hangzhou, China
2College of Pharmaceutical Sciences, Zhejiang Chinese Medical University, Hangzhou, China
Email: gaoluncangcang@qq.com, fychen@hdu.edu.cn, jin.weifeng@hotmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 24 August 2014; revised 20 September 2014; accepted 8 October 2014
ABSTRACT
In this paper, the dynamics of rule 106, a Chua’s hyper Bernoulli cellular automata rule, is studied and discussed from the viewpoint of symbolic dynamics. It is presented that rule 106 defines a chaotic subsystem which is topologically mixing and possesses the positive topologically entropy. An effective method of constructing its chaotic subsystems is proposed. Indeed, it is interesting to find that this rule is filled with infinitely many disjoint chaotic subsystems. Special attention is paid to each subsystem on which rule 106 is topologically mixing and possesses the positive topologically entropy. Therefore, it is natural to argue that the intrinsic complexity of rule 106 is high from this viewpoint.
Keywords:
Cellularautomata, Chaos, topologically Entropy, Topologically mixing, subsystem

1. Introduction
Cellular Automata (CA), first conceived around 1950 by von Neumann [1] , are a class of spatially and temporally discrete mathematical structure by local interactions and an inherently parallel form of evolution. The whole structure is able to produce complex and interesting dynamical phenomena by means of designing simple transition rule. Due to their simple mathematical constructions and distinguishing features, CA have drawn a great deal of attention from various scientists. In 1969, the study of topological dynamics of CA was developed by Hedlund [2] , who viewed one-dimensional CA in the context of symbolic dynamics as endo- morphisms of the shift dynamical system, where the main results are the characterizations of surjective and open CA. In 1970, Conway proposed game of life [3] , which received widespread interests among researchers in different fields. In the early 1980s, Wolfram proposed CA as models for physical systems exhibiting complex or even chaos behaviors and elementary CA (ECA) that consist of a one-dimensional array of finite binary cells, each interacting only with the two nearest neighbors [4] - [6] . He classified 256 ECA rules informally into four classes using dynamical concepts like periodicity, stability and chaos. In 2002, Wolfram introduced his work A New Kind of Science [6] . Based on this work, Chua et al. have concluded the dynamics of ECA from a nonlinear dynamics perspective [7] - [10] . And he divided 256 ECA rules into four classes: period- rules
rules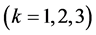 , Bernoulli-shift rules, complex Bernoulli-shift rules and hyper Bernoulli-shift rules.
, Bernoulli-shift rules, complex Bernoulli-shift rules and hyper Bernoulli-shift rules.
Gratefully, the research of CA has drawn more and more scientists’ attention in the last 20 years. Many concepts of topological dynamics have been used to describe and classify them [11] - [15] . And the dynamical properties of some robust Bernoulli-shift rules have been studied in the bi-infinite symbolic sequence space [14] , [15] . Rule 106 belonging to hyper Bernoulli-shift rules possesses complex and distinctive dynamical behaviors. In a paper [16] , the authors introduced the notion of permutivity of a map in a certain variable. Then they proved that every one-dimensional CA based on the local rule which is permutive either in the leftmost or rightmost variable is Devaney chaotic. Rule 106 is in this situation. Presently, this work is devoted to an in-depth study of rule 106 from the perspective of nonlinear dynamics under the framework of bi-infinite symbolic sequence space, and mainly studies the complex dynamics on its infinite number of subsystems.
The rest of the paper is organized as follows: Section 2 presents the basic concepts of one-dimensional CA and symbolic dynamics. Based on these concepts, it shows a subsystem of rule 106. Section 3 explores the complex dynamical behaviors of rule 106. Section 4 describes that there exist infinitely many disjoint chaotic subsystems in this chaotic subsystem. Finally, Section 5 concludes this paper.
2. Preliminaries
For a finite symbol , a word over
, a word over 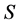 is finite sequence
is finite sequence 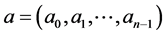 of elements of
of elements of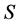 . The length
. The length
of a is denoted by . Denote the set of all words of length
. Denote the set of all words of length  by
by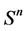 . If
. If 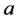 is a finite or infinite word
is a finite or infinite word
and 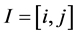 is an interval of integers on which
is an interval of integers on which  is defined, put
is defined, put  and
and
 .
. 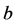 is a subword of
is a subword of , denoted by
, denoted by


denoted









space.
By a theorem of Hedlund, a map 
shift map



radius 





A set 





and 




of some finite words over






For bi-infinite ECA, 


function. For example, the Boolean function of rule 106 is


Thus the global map of rule 106 is induced as follows: for any





Based exclusively on this truth table, a subsystem of rule 106 in 
Proposition 1. For rule 106, there exists a subset 





Proof: (Necessity) Suppose that there exists a subset 



of rule 106, one has 



not be 1 simultaneously,


must satisfy that 


determinative block system of 

(Sufficiency) The proof of sufficiency can be verified directly, the details are omitted here. The proof of the proposition is completed.
For illustration, simulations of the spatial and temporal evolution of rule 106 with a random initial configuration and an initial configuration of 
3. Complex Dynamics of
In this section, the dynamical behaviors of 

definitions from [17] . A matrix A is positive if all of its entries are nonnegative; irreducible if 
that



Table 1. Logical table of rule 106.

Figure 1. (a) The evolution of rule 106 from random initial configuration, (b) The evolution of rule 106 from an initial configuration of
then the associated transition matrix 




Denote a 2-order subshift of finite type by 
topologically mixing if and only if its transition matrix is irreducible and aperiodic [17] [18] .
The nonlinear dynamical behavior of 

relationship between 

set, where


symbolic space 


Then, the 2-order subshift 


matrix A of the subshift 
Theorem 1. 1) 

2) 
3) the topological entropy of 


radius of the transition matrix
Proof: 1) Define a map from 

where






Hence, 

2) 



topologically mixing on

and Proposition 1.
3) As







It is noted that a positive topological entropy is an important signature of the complexity of the system. It follows from [18] that the positive topological entropy implies chaos in the sense of Li-Yorke. And the topologically mixing is a very complex property of dynamical systems. A system with topologically mixing property has many chaotic properties in different senses. Therefore, the above mathematical analysis provides the following result.
Theorem 2. 1) 
2) 

4. Infinitely Many Chaotic subsystems of 
It is helpful to review some definitions and basic properties of releasing transformation before we discuss the
dynamics of 






matric “

where
Proposition 2. [19] Releasing transformation 
Let













Proposition 3. For each


Proposition 4. For each


Proof: It is clear that the following diagram is commutative. The rest of proof can be completed by applying Proposition 2.
Theorem 3. For each


2) the topologically entropy of 





Proof: 1) It is clear to check that 







mixing on each 


3.
2) Since

matrix


topologically entropy of 


on each 

Theorem 4. For each


2) 

Proof: 1) One can use the definition of the topologically mixing to prove that 
on each




Case 1.

open sets




Case 2.


homeomorphism. Since 











continuous map. 

implies that 


2) It is easily deduced by Theorem 3 (2) and Theorem 4 (1).
Note that







closed and 


Remark 1. It is important to point out that the topologically entropy of 



infinite disjoint chaotic subsystems
hyper Bernoulli-shift rule 106 is full of infinite “small” chaotic subsystems in a “big” subsystem, demonstrating its very rich and complex dynamics.
5. Conclusion
One of the main challenges is to explore the quantitative dynamics in cellular automata evolution. Hyper Bernoulli-shift rules possess very interesting and complicated dynamical behaviors [19] [20] , for example, rule 180 possesses infinitely many generalized sub-shifts [20] [21] . This paper is devoted to an in-depth study of cellular automaton rule 106 in the framework of symbolic dynamics. Indeed, rule 106 actually is topologically mixing and possesses positive topological entropy on a subsystem. Furthermore, in this chaotic subsystem, rule 106 defines infinitely number of chaotic subsystems with rich and complex dynamical behaviors, such as topologically mixing, positive topological entropies and chaos in the sense of Li-Yorke and Devaney. Although in this work, one obtains some interesting results, to rule 106, it still needs much deeper research in the future.
Acknowledgements
This research was supported by the NSFC (Grant No. 11171084).
Cite this paper
Gaocang Zhao,Fangyue Chen,Weifeng Jin, (2014) Infinite Number of Disjoint Chaotic Subsystems of Cellular Automaton Rule 106. Applied Mathematics,05,3256-3263. doi: 10.4236/am.2014.520303
References
- 1. von Neumann, J. and Burks, A.W. (1966) Theory of Self-Reproducing Automata. University of Illinois Press, Urbana and London.
- 2. Hedlund, G.A. (1969) Endomorphisms and Automorphism of the Shift Dynamical System. Theory of Computing Systems, 3, 320-375.
- 3. Gardner, M. (1970) The Fantastic Combinations of John Conway’s New Solitaire Game Life. Scientific American, 223, 120-123.
http://dx.doi.org/10.1038/scientificamerican1070-120 - 4. Wolfram, S. (1984) Universality and Complexity in Cellular Automata. Physica D, 10, 1-35.
http://dx.doi.org/10.1016/0167-2789(84)90245-8 - 5. Wolfram, S. (1986) Theory and Application of Cellular Automata. Word Scientific, Singapore.
- 6. Wolfram, S. (2002) A New Kind of Science. Wolfram Media, Inc., Champaign.
- 7. Chua, L.O., Sbitnev, V.I. and Yoon, S. (2004) A Nonlinear Dynamics Perspective of Wolfram’s New Kind of Science, Part III: Predicting the Unpredictable. International Journal of Bifurcation and Chaos, 14, 3689-3820.
http://dx.doi.org/10.1142/S0218127404011764 - 8. Chua, L.O., Guan, J., Sbitnev, V.I. and Jinwook, S. (2007) A Nonlinear Dynamics Perspective of Wolfram’s New Kind of Science, Part VII: Isles of Eden. International Journal of Bifurcation and Chaos, 17, 2839-3012.
http://dx.doi.org/10.1142/S0218127407019068 - 9. Chua, L.O., Karacs, K., Sbitnev, V.I., Guan, J. and Jinwook, S. (2007) A Nonlinear Dynamics Perspective of Wolfram’s New Kind of Science, Part VIII: More Isles of Eden. International Journal of Bifurcation and Chaos, 17, 3741-3894.
http://dx.doi.org/10.1142/S0218127407019901 - 10. Chua, L.O. and Pazienza, G.E. (2010) A Nonlinear Dynamics Perspective of Wolfram’s New Kind of Science, Part XIV: More Bernoulli -Shift Rules. International Journal of Bifurcation and Chaos, 20, 2253-2425.
http://dx.doi.org/10.1142/S0218127410027155 - 11. Guan, J.B., Shen, S.W., Tang, C.B. and Chen, F.Y. (2007) Extending Chua’s Global Equivalence Theorem on Wolfram’s New Kind of Science. International Journal of Bifurcation and Chaos, 17, 4245-4259.
http://dx.doi.org/10.1142/S0218127407019925 - 12. Chen, F.Y., Jin, W.F., Chen, G.R., Chen, F.F. and Chen, L. (2009) Chaos of Elementary Cellular Automata Rule 42 of Wolfram’s Class II. Chaos, 19, Article ID: 013140.
- 13. Chen, F.Y., Chen, G. and Jin, W.F. (2013) Transitivity and Chaoticity in 1-D Cellular Automata. International Journal of Modern Nonlinear Theory and Application, 2, 69-73.
http://dx.doi.org/10.4236/ijmnta.2013.21A008 - 14. Jin, W.F., Chen, F.Y., Chen, G.R., Chen, L. and Chen, F.F. (2010) Extending the Symbolic Dynamics of Chua’s Bernoulli-Shift Rule 56. Journal of Cellular Automata, 5, 121-138.
- 15. Chen, G.R., Chen, F.Y., Guan, J.B. and Jin, W.F. (2010) Symbolic Dynamics of Some Bernoullif-Shift Cellular Automata Rules. 2010 International Symposium on Nonlinear Theory and Its Applications, 595-598.
- 16. Cattaneo, G., Finelli, M. and Margara, L. (2000) Investigating Topological Chaos by Elementary Cellular Automata Dynamics. Theoretical Computer Science, 244, 219-241.
http://dx.doi.org/10.1016/S0304-3975(98)00345-4 - 17. Kitchens, B. (1998) Symbolic Dynamics: One-Sided, Two-Sided and Countable State Markov Shifts. Springer-Verlag, Berlin.
http://dx.doi.org/10.1007/978-3-642-58822-8 - 18. Blanchard, F., Glasner, E. and Kolyada, S. (2002) On Li-Yorke Pairs. Journal fur reine und angewandte Mathematik, 547, 51-68.
- 19. Jin, W.F. and Chen, F.Y. (2011) Topological Chaos of Universal Elementary Cellular Automata Rule. Nonlinear Dynamics, 63, 217-222.
http://dx.doi.org/10.1007/s11071-010-9798-z - 20. Chen, W., Chen, F.Y., Bian, Y.F. and Chen, J. (2011) Infinite Number of Chaotic Generalized Sub-Shifts of Cellular Automaton Rule 180. 2011 International Conference on Scientific Computing, 226-230.
- 21. Cattaneo, G. and Margara, L. (1998) Generalized Sub-Shifts in Elementary Cellular Automata: The “Strange Case” of Chaotic Rule 180. Theoretical Computer Science, 201, 171-187.
http://dx.doi.org/10.1016/S0304-3975(97)00210-7













