Received 21 July 2014; revised 20 August 2014; accepted 8 September 2014

ABSTRACT

We consider two problems from stability theory of matrix polytopes: the existence of common quadratic Lyapunov functions and the existence of a stable member. We show the applicability of the gradient algorithm and give a new sufficient condition for the second problem. A number of examples are considered.

Keywords:

Stable Matrix, Matrix Family, Common Quadratic Lyapunov Functions, Switched System, Gradient Method

1. Introduction

Consider the switched system

(1)

where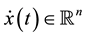,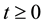. In Equation (1), the matrix 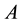switches among 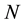matrices.

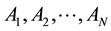Switching signal 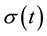is piecewise continuous from the right function 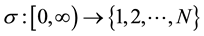and the switching times are arbitrary. For the switched system (1) with initial condition 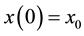and with switching signal denotes the solution by.

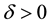Definition 1. The origin is uniformly asymptotically stable (UAS) for the system (1) if for every there exists such that for every signal 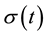and initial state 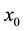with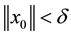, the inequality is satisfied for all and uniformly on

If all systems in (1) share a common quadratic Lyapunov function (CQLF) then the switched

system is UAS (T denotes the transpose).

In this case there exists a common such that

(2)

and is called a common solution to the set of Lyapunov matrix inequalities (2).

The problem of existence of common positive definite solution of (2) has been studied in a lot of works (see [1] -[9] and references therein). Numerical solution for common via nondifferentiable convex optimization has been discussed in [10] .

In the first part of the paper, the problem of existence of CQLF is investigated by Kelley’s method. This method is applied when CQLF problem is treated as a convex optimization problem.

Second part of the paper is devoted to the following question:

Let be a compact, for the matrix is a real matrix. Is there a Hurwitz stable member (all eigenvalues lie in the open left half plane) in the family

or equivalently is there such that is stable? This problem is one of the hard and important problems in control theory (see [11] ). Numerical solution of this problem is considered in [12] . In this paper we reduce this problem to a non-convex optimization problem.

2. Common Quadratic Lyapunov Function

For the switched system

consider the problem of determination of CQLF where. We are going to investigate it by Kelley’s cutting-plane method. This method gives new sufficient condition (Theorem 2) and new algorithm (Algorithm 1) which is more effective in comparison with the algorithm from [10] .

Consider the problem of existence of a common such that

. (3)

Let be and be an symmetric matrix defined as

Define

(4)

If there exists such that and then the matrix is required solution. This problem can be reduced to the minimization of a convex function under convex constraints.

Consider the following convex minimization problem

(5)

Let be a convex set and be convex function. The vector is said to be a subgradient of at if for all

.

The set of all subgradients of at is denoted by. If is an interior point of then the set is nonempty and convex. The following proposition follows from nondifferentiable optimization theory.

Proposition 1. Let be defined as

(6)

where is compact, is continuous and differentiable in. Then

where is the set of all maximizing elements in (6), i.e.

.

If for a given the maximizing element is unique, i.e. then is differentiable at and its gradient is

In the case of the Function (4)

If for the given the maximizing is unique and is a simple eigenvalues, the differentiability of at the point is guaranteed [13] .

We investigate problem (5) by Kelley’s cutting-plane method.

This method converts the problem (5) to the problem

(7)

where, , ,.

Let be a starting point and be distinct points.

At the th iteration, the cutting-plane algorithm solves the following LP problem

(8)

where denotes a subgradient of at.

Let be the minimizer of the problem (8).

If satisfies the inequality, where is a tolerance then is an approx-

imate solution of the problem (7).

Otherwise define as the index for the most negative, update the constraints in (8) by including the linear constraint

and repeat the procedure.

Recall that our aim is to find such that and, but not the solution of the minimization problem (5), (7).

Theorem 2. If there exists such that

where is the minimizer of the problem (8), then the matrix is a common solution to (3).

Proof:

and by (5), is a common solution to (3).

For the problem (5), (7) Kelley’s method gives the following

Algorithm 1.

Step 1. Take an initial point. Compute and. If and stop; otherwise continue.

Step 2. Determine by solving LP problem in (8). If and then stop; otherwise continue. Set, update the constraints in (8) and repeat the procedure.

Example 1. Consider the switched system

where

are Hurwitz stable matrices.

Choose the initial point, then

, and

We obtain by solving LP problem in (8). Calculations give the following Table 1, and

Since and,

is a common positive definite solution for

3. Stable Member in a Polytope

This part is devoted to the following question: Given a matrix family where is a compact, is there a stable matrix in this family?

In [12] , a numerical algorithm has been proposed for a stable member in the affine matrix family. In this algorithm the uncertainty vector varies in the whole space. On the other hand we consider the case where varies in a box and use the gradient algorithm for minimization of the nonconvex maximum eigenvalue function. By choosing appropriate step-size, we obtain the convergence.

Let be a basis for the subspace of symmetric matrices and

where,.

Consider the problem

Theorem 3. There is a stable matrix in the family if and only if

Proof:

By Lyapunov theorem, the matrix is stable.

Example 2. Consider the family of matrices

where

For, is unstable. We apply the gradient algorithm to find a stable member in the family.

Let and. So

Then

Maximum eigenvalue of this matrix and its corresponding unit eigenvector are

respectively. Gradient of the function at is

The first tencomponent of the vector should be on the ten dimensional unit sphere. Therefore and

After 4 steps, we get

and. Therefore is stable.

4. Conclusion

Two important problems from control theory are considered: the existence of common quadratic Lyapunov functions for switched linear systems and the existence of a stable member in a matrix polytope. We obtain new conditions which give new effective computational algorithms.

References

NOTES

^*Corresponding author.