Applied Mathematics
Vol.5 No.16(2014), Article
ID:49367,16
pages
DOI:10.4236/am.2014.516234
Pricing Study on Two Kinds of Power Options in Jump-Diffusion Models with Fractional Brownian Motion and Stochastic Rate
Jin Li, Kaili Xiang, Chuanyi Luo
School of Economic Mathematics, Southwestern University of Finance and Economics, Chengdu, China
Email: lcy@swufe.edu.cn
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 2 July 2014; revised 5 August 2014; accepted 18 August 2014
ABSTRACT
In this paper, under the assumption that the exchange rate follows the extended Vasicek model, the pricing of the reset option in FBM model is investigated. Some interesting themes such as closed-form formulas for the reset option with a single reset date and the phenomena of delta of the reset jumps existing in the reset option during the reset date are discussed. The closed-form formulae of pricing for two kinds of power options are derived in the end.
Keywords:Stochastic Rate, Fractional Jump-Diffusion Process, Fractional Brown Motion, Power Option

1. Introduction
The pricing of exotic options is often an optimal stochastic problem, in which the stochastic process sometimes follows jump-diffusion process. The issue gets more complicated because the distribution of the maximum is difficult to derive. There is no doubt that we should use jump-diffusion process instead of diffusion process to describe the changing behaviors of financial markets, but the pricing process is more complex. Market quotations, trade practices and information dissemination are three important factors which effect trade speed and transaction volume. Therefore, a reasonable pricing is the premise which will make the exchange market active.
In recent years, with the exception of European and American options, a large number of new financial derivatives are derived in the international financial derivative market. Among them, the power option is one of the new typical options. The research of the power options is critically significant in both theoretical aspect and practical area. The BS [1] model has become an indispensable tool for option pricing and hedging in the finance industry. However, it is well documented that the Geometric Brownian Motion (GBM) assumption for the underlying asset’s price dynamics in the BS model fails to reflect the real facts: market return data display excess kurtosis (peaked and fat-tailed distributions), skewness, volatility clustering, long-range dependence and large, sudden movements, etc. These observations reveal that a simple GBM assumption misses some important features of the data. Therefore, many different option valuation models with realistic price dynamics have been currently proposed and tested. Some of these models include jump-diffusion model, sub-ordinated processes, pure jump processes, Lévy processes, stochastic volatility model, regime-switching model, GARCH model, processes driven by FBM and others. Except for FBM, these models give rise to incomplete market. Hu and Oksendal [2] , Elliott and van Hoek [3] have proved that there is no arbitrage in the FBM market if the wick product is used in the definition of stochastic integration. Compared with the traditional efficient market theory, the fractional market theory is more appropriate and accurate. Pricing option with stochastic interest rate under jump-diffusion models is an important field in recent years.
In the FBM market, very little work on the options valuation is considered. Hu and Oksendal [2] have derived a formula for the price at time 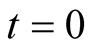 of a European option. Necula [4] has extended the formula in [2] for every time
of a European option. Necula [4] has extended the formula in [2] for every time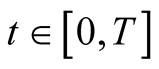 . Liu and Yang [5] [6] considered the European contingent claim and compound option for the ease of a non constant but deterministic volatility using the quasi-conditional expectation. Xue and Wang [7] also consider the pricing of the extremum options for the two risky-assets types. Elliott and Chan [8] obtained a closed-from solution for perpetual American options whose maturity goes to infinity by applying quadratic approximation. Peng [9] also obtained an explicit price of perpetual American put for a fractional O-U model. Deng and Lin [10] considered the approximate valuation for the American put option with finite maturity date using compound option approach.
. Liu and Yang [5] [6] considered the European contingent claim and compound option for the ease of a non constant but deterministic volatility using the quasi-conditional expectation. Xue and Wang [7] also consider the pricing of the extremum options for the two risky-assets types. Elliott and Chan [8] obtained a closed-from solution for perpetual American options whose maturity goes to infinity by applying quadratic approximation. Peng [9] also obtained an explicit price of perpetual American put for a fractional O-U model. Deng and Lin [10] considered the approximate valuation for the American put option with finite maturity date using compound option approach.
In this paper, under the assumption that the exchange rate obeys the expanding Vasicek models, we obtain the pricing formulas of two kinds of power options under fractional jump-diffusion models.
The rest of this paper is organized as follows. Some notations and Lemma are introduced in Section 2. Section 3 describes the model discussed in this paper. Section 4 gives the pricing formulae for the first kind of power option and the second kind of option in FBM model with fractional jump diffusion. Finally, some conclusions are summarized in Section 5.
2. Preliminary
Before the introduction of our model, we firstly state several preliminary theorems and lemmas presented in [11] .
Theorem 2.1. Let . Then, it has
. Then, it has
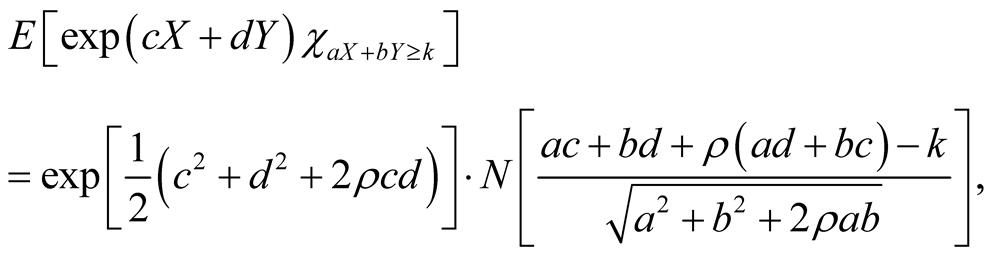 (1)
(1)
where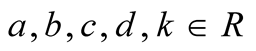 .
.
Lemma 2.1. Let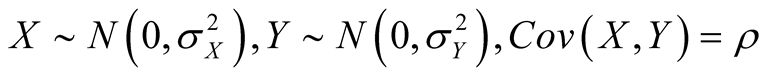 . Then, it gets
. Then, it gets
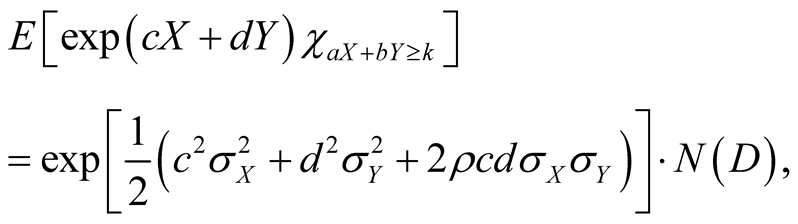 (2)
(2)
where 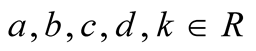 and
and
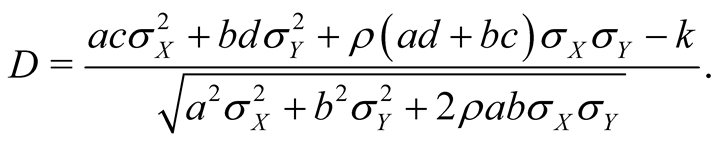
Definition 2.1. Some notations are given as follows
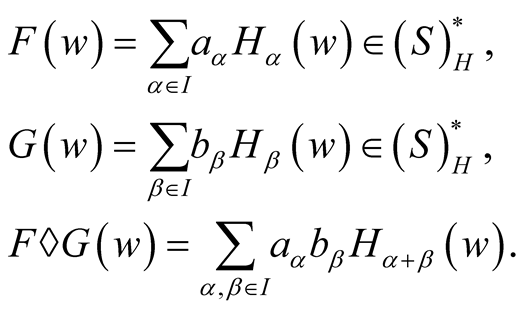
Definition 2.2. We define the stochastic integration of ![]() about
about 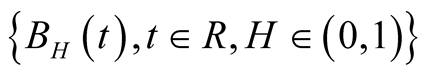 as
as
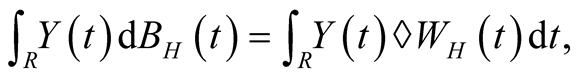 (3)
(3)
where, the function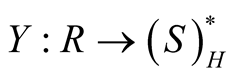 , s.t.
, s.t. 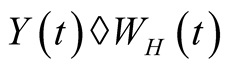 is integrated in
is integrated in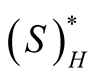 .
. 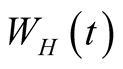 means fractional noise and
means fractional noise and ![]() means wick integral.
means wick integral.
3. Description of Our Models
1) We assume that the interest rate follows the extended Vasicek model. That means it has the following form
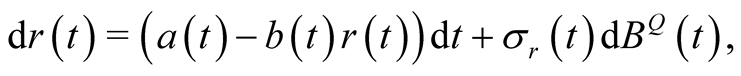 (4)
(4)
where 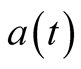 affects long-term average interest rate;
affects long-term average interest rate; 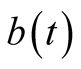 is the average recovery rate which adjusts the relationship of short-term and long-term;
is the average recovery rate which adjusts the relationship of short-term and long-term;  is fluctuation ratio.
is fluctuation ratio.
In order to find out the discounted factor, we need to find out the discount rate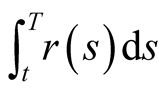 . From the It
. From the It 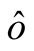 theorem, we have,
theorem, we have,
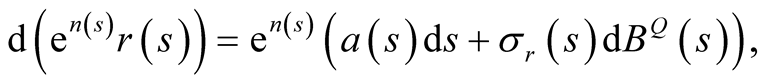
where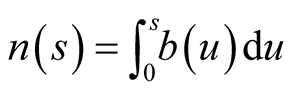 . Integrating both sides of the equation above on
. Integrating both sides of the equation above on , we have
, we have
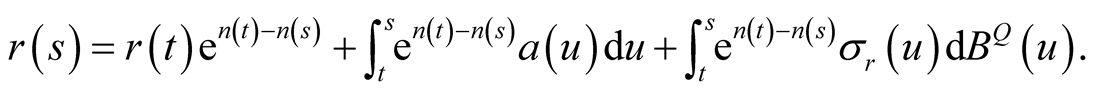
Furthermore,
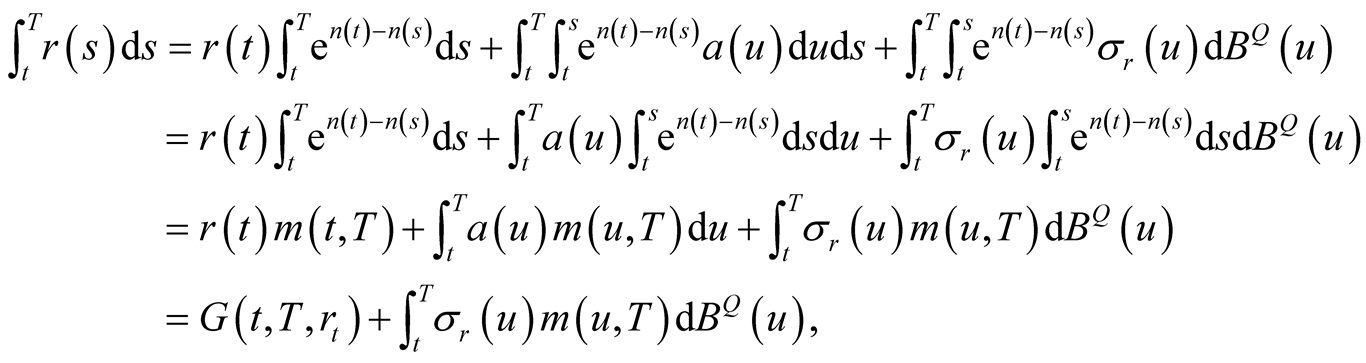 (5)
(5)
where
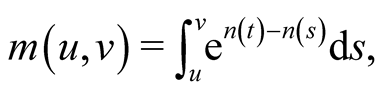 (6)
(6)
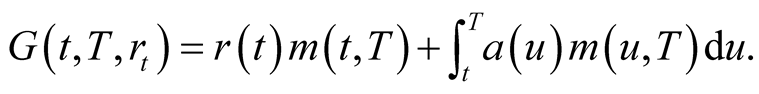 (7)
(7)
2) We assume the market is a full market with continuous time, and there exist two kinds of continuous trading assets, one of which is risk-free bonds. The price process of bonds M(t) satisfies the following equation
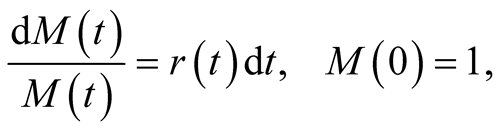 (8)
(8)
where 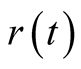 is a continuous function of time
is a continuous function of time![]() ; The other trading asset is the risk asset
; The other trading asset is the risk asset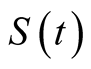 , the price process of
, the price process of 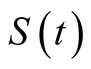 satisfies the following equation
satisfies the following equation
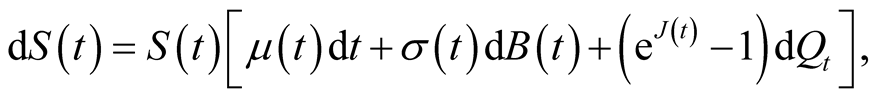 (9)
(9)
where 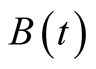 is Brownian motion;
is Brownian motion; 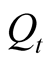 is the number of random jumps of underlying asset price within
is the number of random jumps of underlying asset price within 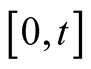 and it follows the Poisson process with the parameter
and it follows the Poisson process with the parameter![]() ;
; 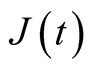 is the random variable which follows the normal distribution
is the random variable which follows the normal distribution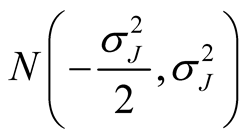 ;
; 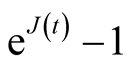 is the height of the stock price jump;
is the height of the stock price jump; 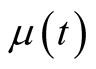 is the expected rate of return;
is the expected rate of return; 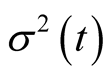 is the volatility. Solving the Equation (9), we have
is the volatility. Solving the Equation (9), we have
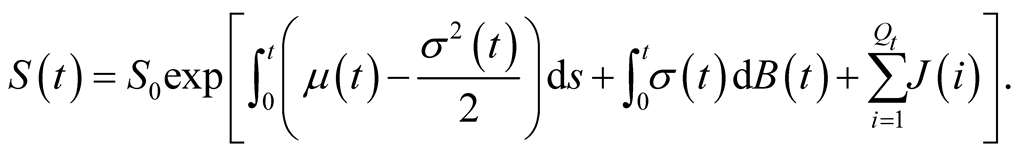 (10)
(10)
3) In addition, the jump-diffusion model is independent of the risk appetite, so risk-free interest rate 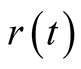 can be used to take place of the expected rate of return
can be used to take place of the expected rate of return 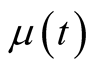 according to the risk-neutral valuation principles. Consequently, the Formula (10) can be rewritten as follow
according to the risk-neutral valuation principles. Consequently, the Formula (10) can be rewritten as follow
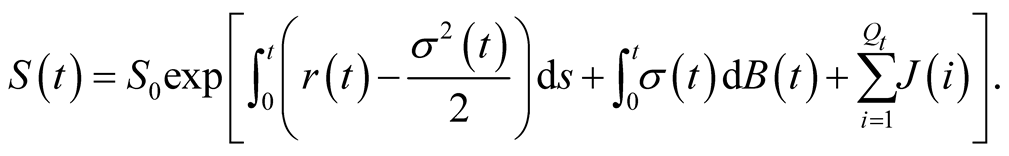 (11)
(11)
4) Fractional Jump-Diffusion assumption. On the basis of assumption of (3), we replace the Brownian motion 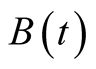 with fractional Brownian motion
with fractional Brownian motion 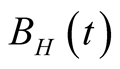 in (9), i.e., the risk-neutral dynamics of the underlying asset is given as
in (9), i.e., the risk-neutral dynamics of the underlying asset is given as
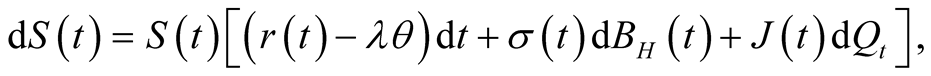 (12)
(12)
where 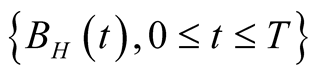 is the fractional Brownian motion in probability space
is the fractional Brownian motion in probability space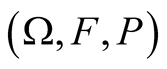 ;
; 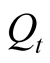 is the number of random jumps of underlying asset price within
is the number of random jumps of underlying asset price within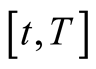 , which follows Poisson process with the parameter
, which follows Poisson process with the parameter
![]() ;
; 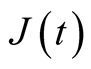 is the height of the jump on stock price, satisfying
is the height of the jump on stock price, satisfying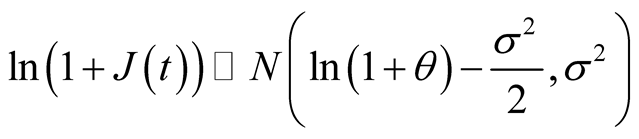 ;
;  is the expected rate of return;
is the expected rate of return; 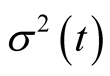 is the volatility.
is the volatility.
From Equation (12), we have
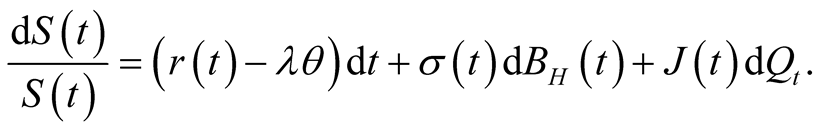 (13)
(13)
According to the definitions and properties of stochastic calculus and function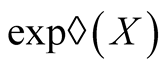 , we get
, we get
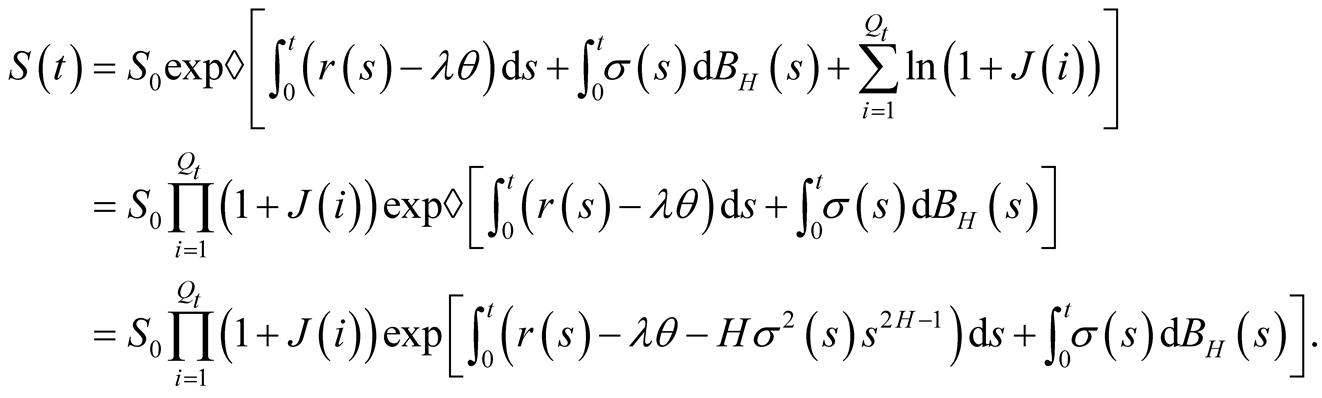 (14)
(14)
4. Pricing Formulae of Two Kinds of Power Options
Under stochastic rate and Jump-Diffusion assumptions, we obtain pricing formulae of two kinds of power options.
4.1. Pricing of the First Kind of Power Option
From Equations (5), we have
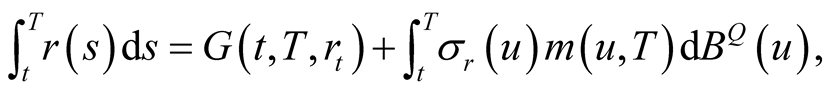
where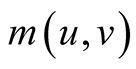 ,
, 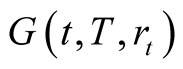 are given by (6) and (7) respectively.
are given by (6) and (7) respectively.
Suppose that underlying assets jump ![]() times during
times during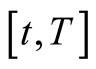 , then
, then
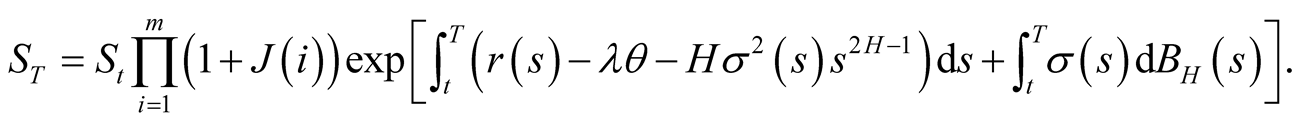 (15)
(15)
Thus, we have the following conclusion.
Theorem 4.1. The formula of the first kind of call power option with exercise price K at exercise date T is
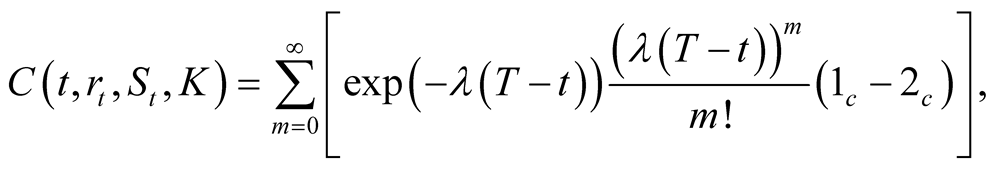 (16)
(16)
where
 (17)
(17)
Proof. According to the No-Arbitrage pricing theory, we get
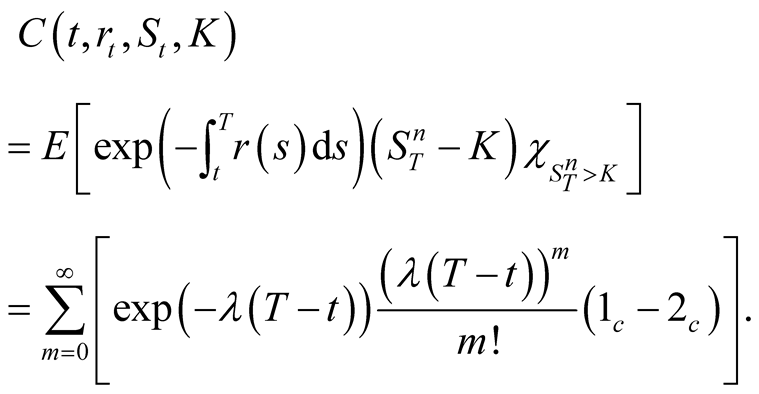 (18)
(18)
Let 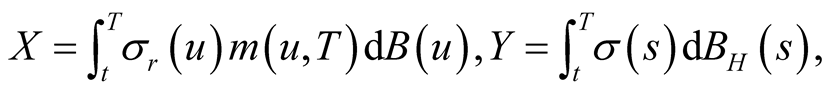 then we have
then we have
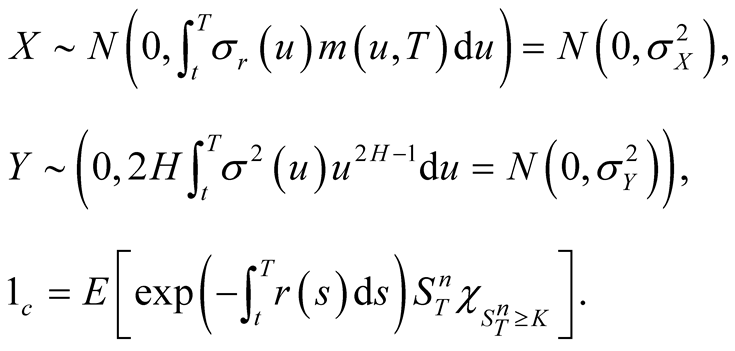
Since
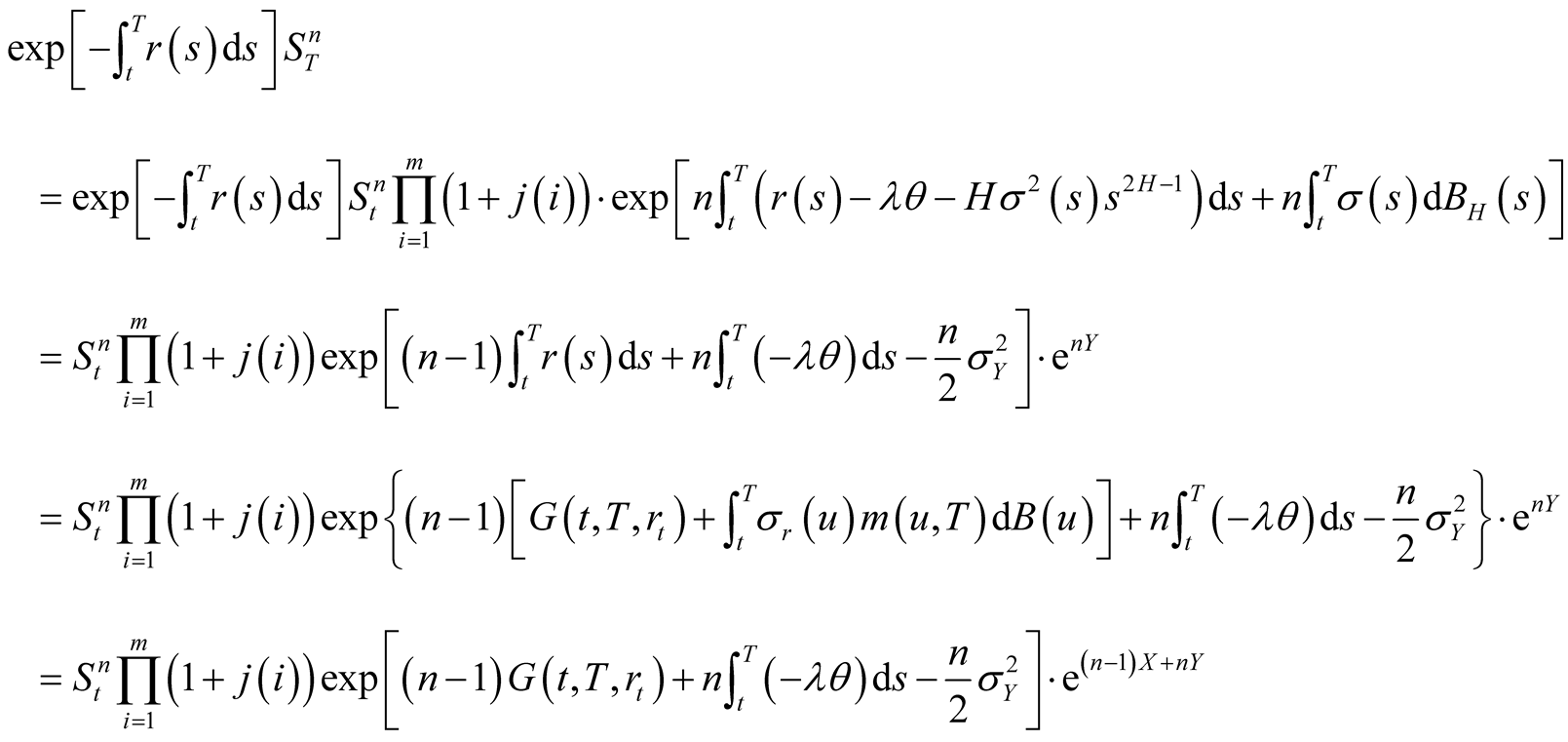 (19)
(19)
and
 (20)
(20)
which means
 (21)
(21)
Thus we obtain
 (22)
(22)
and
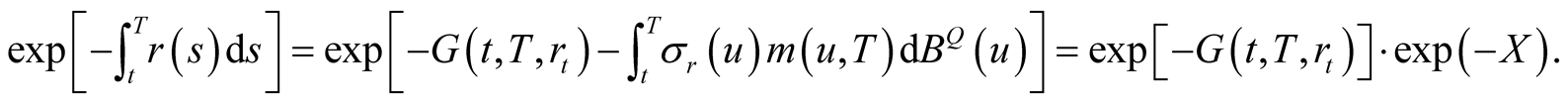 (23)
(23)
In the similar way, we have
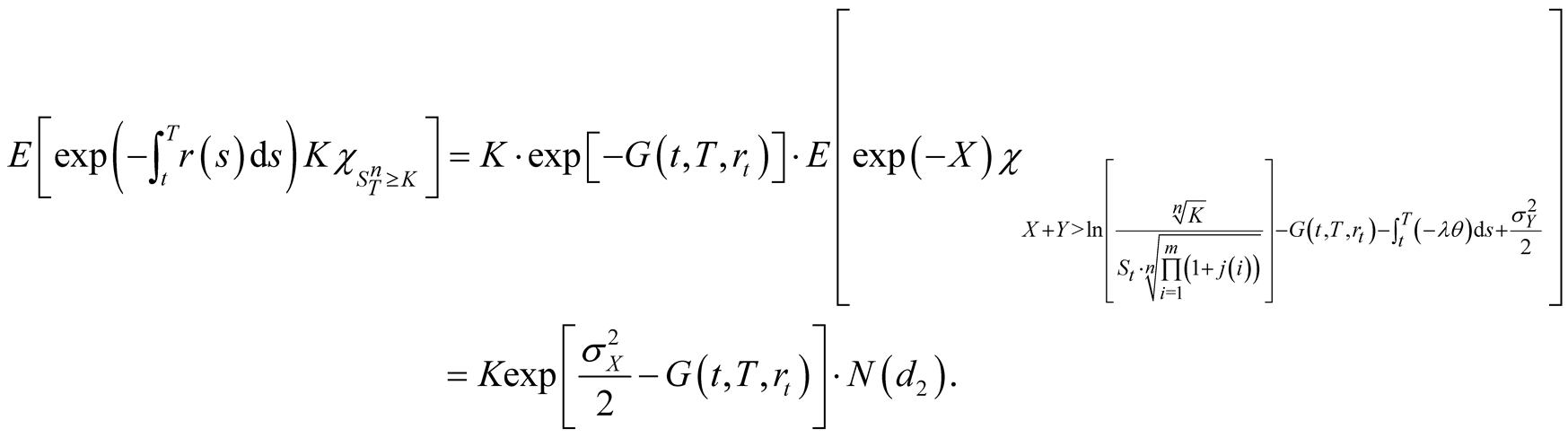 (24)
(24)
Theorem 4.2. The formula of the first kind of put power option with exercise price K at exercise dateT is
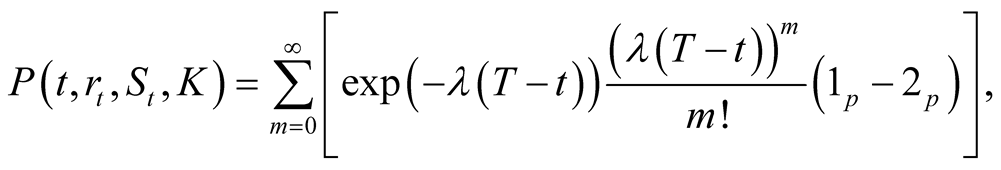 (25)
(25)
where
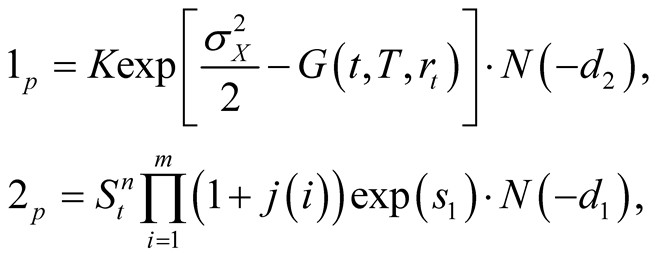
Proof. Similar to the proof procedure in the first kind of call power option, we have
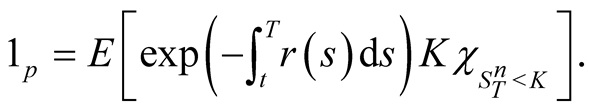
Since
 (26)
(26)
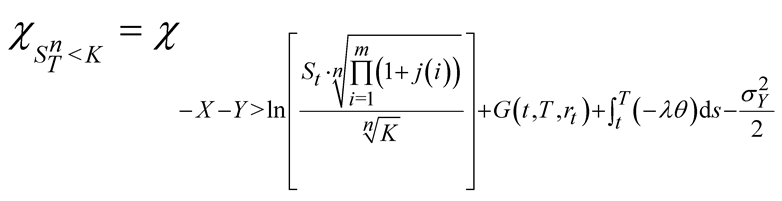 (27)
(27)
and
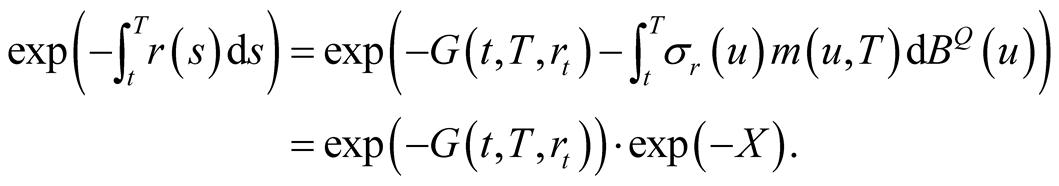 (28)
(28)
We obtain
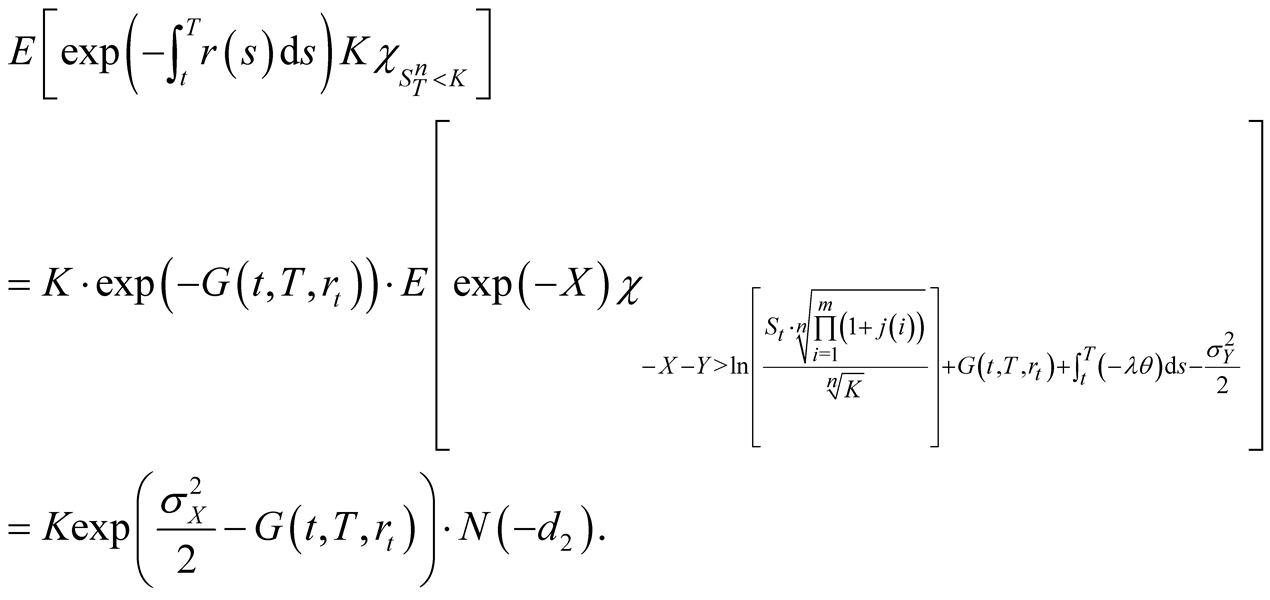
Also
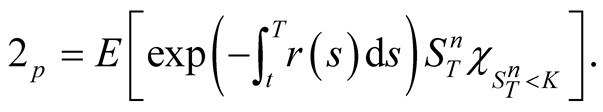
Since
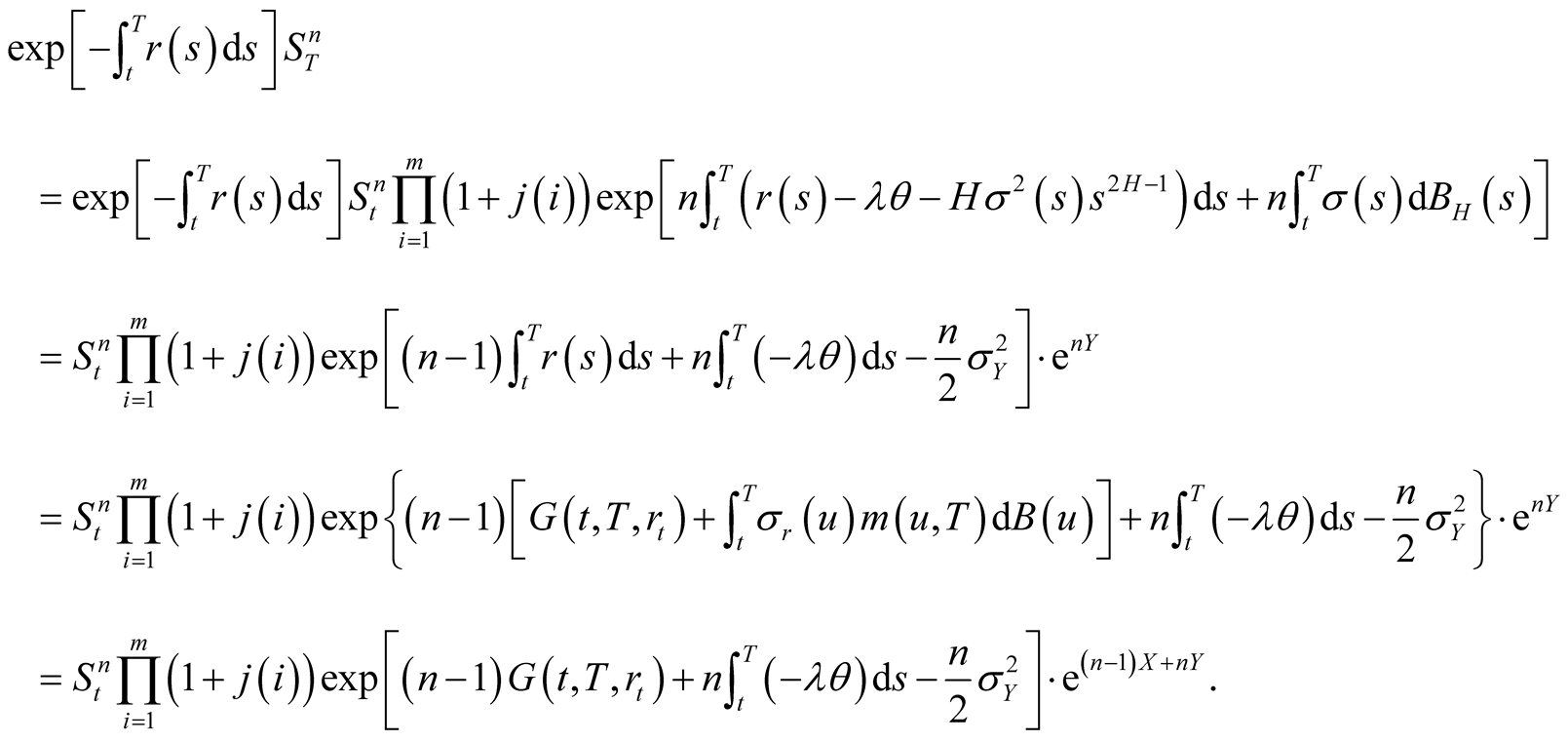 (29)
(29)
and
 (30)
(30)
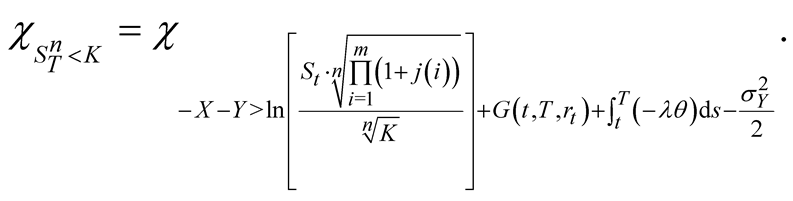 (31)
(31)
We get
 (32)
(32)
4.2. Pricing of the Second Kind Power Option
Theorem 4.3. The formula of the second kind call power option with exercise price![]() , exercise date
, exercise date ![]() is
is
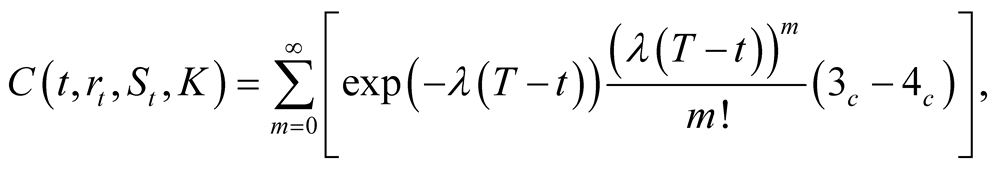 (33)
(33)
where
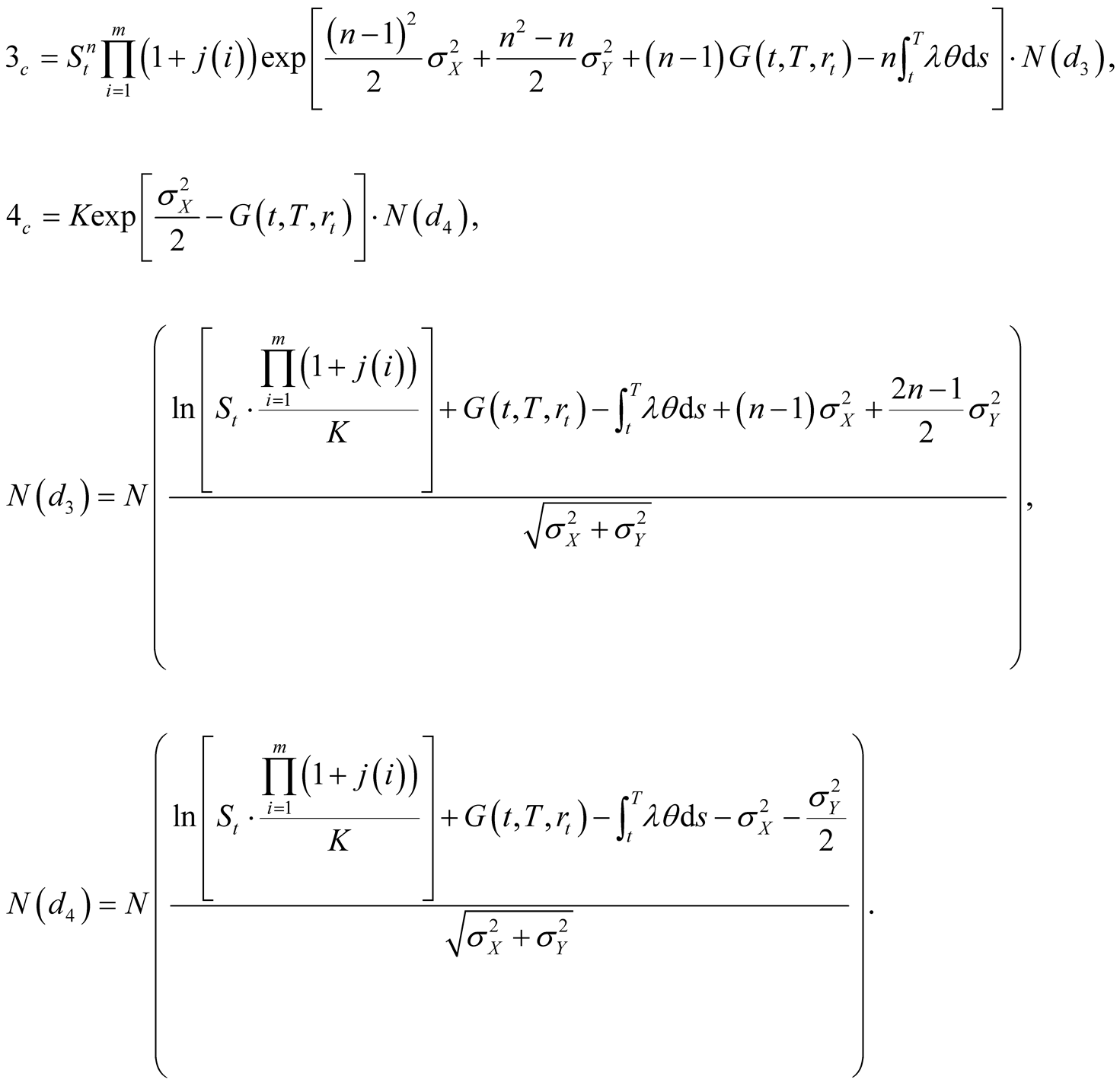
Proof. Similarly, we have
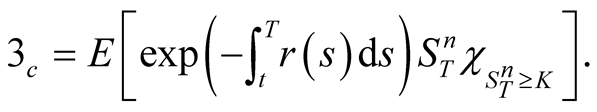
Since
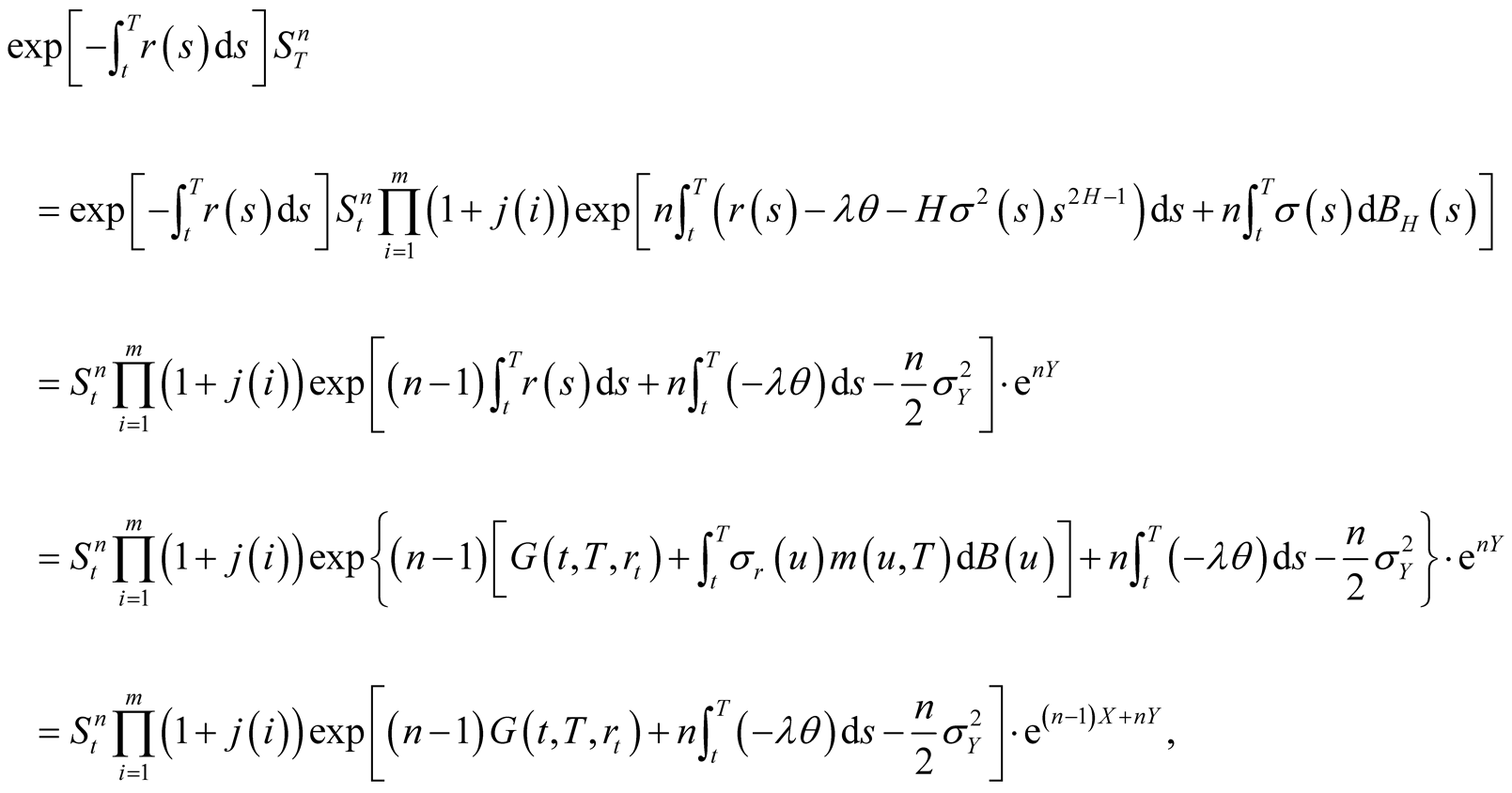 (34)
(34)
and
 (35)
(35)
We obtain
 (36)
(36)
Also,

where
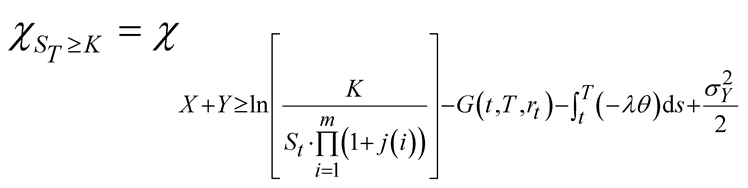 (37)
(37)
and
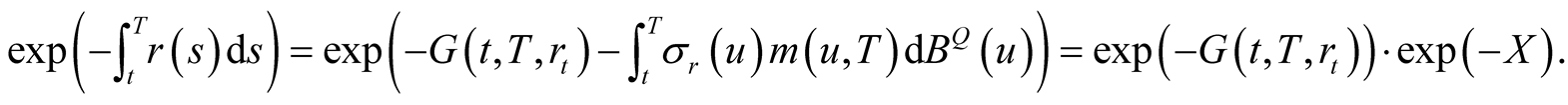 (38)
(38)
In the similar way, we have
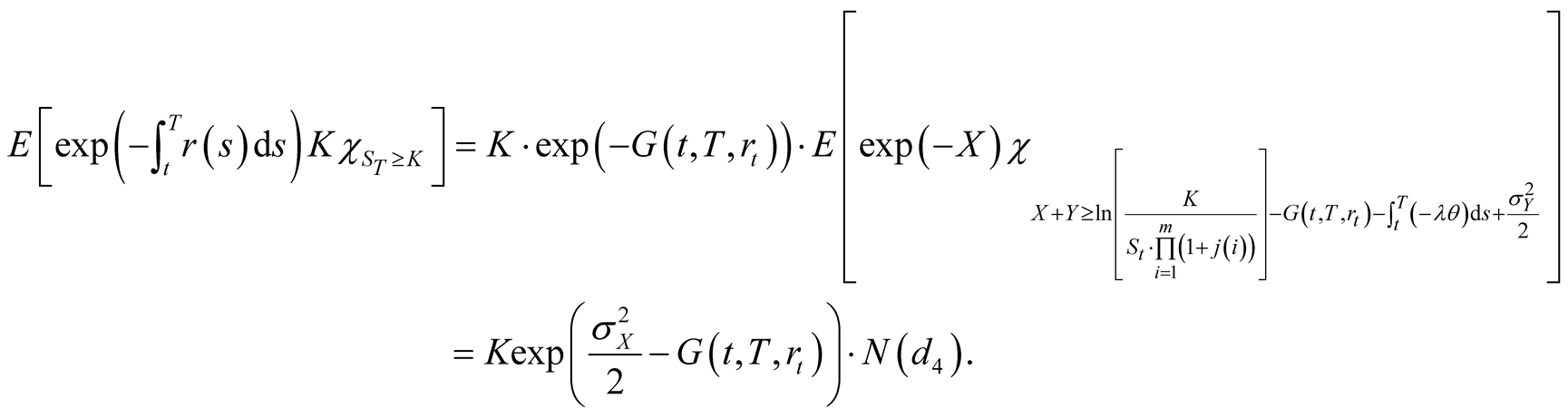 (39)
(39)
Theorem 4.4. The formula of the second kind put power option with exercise price![]() , exercise date
, exercise date ![]() is
is
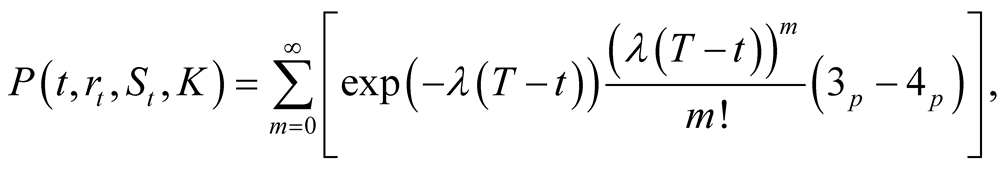 (40)
(40)
where
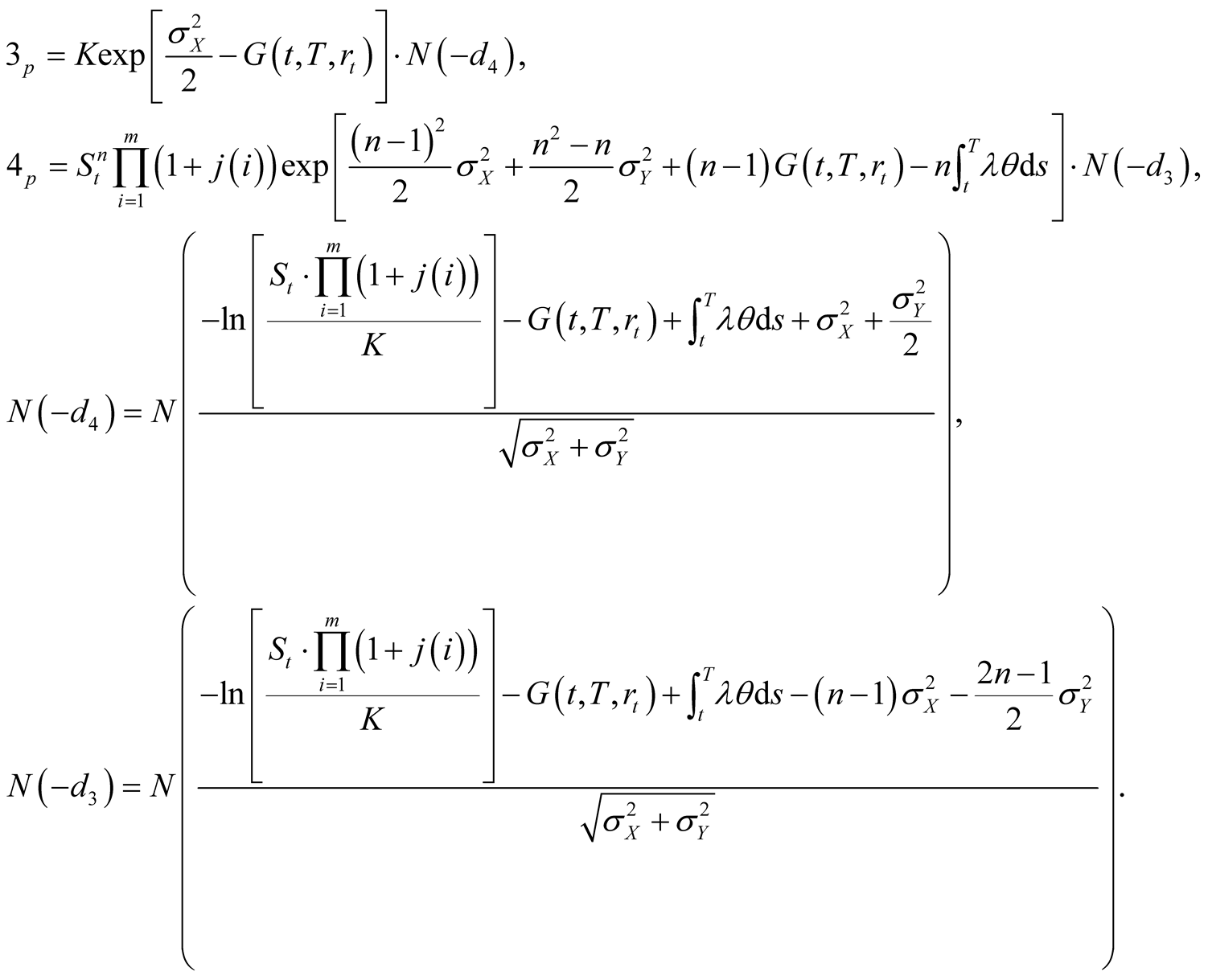
Proof. Similarly, we have
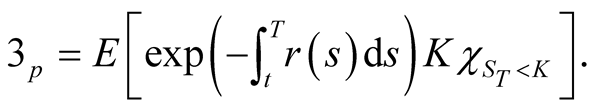
Since
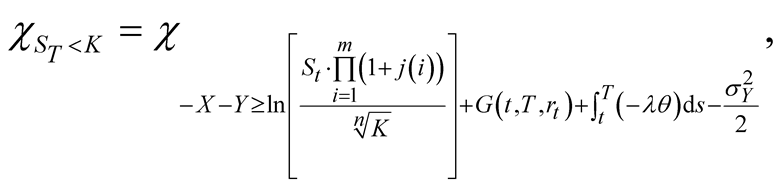 (41)
(41)
and
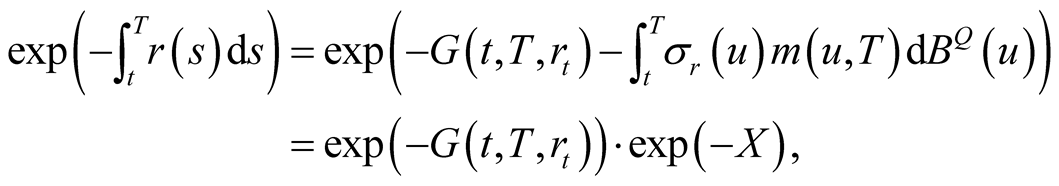 (42)
(42)
we obtain
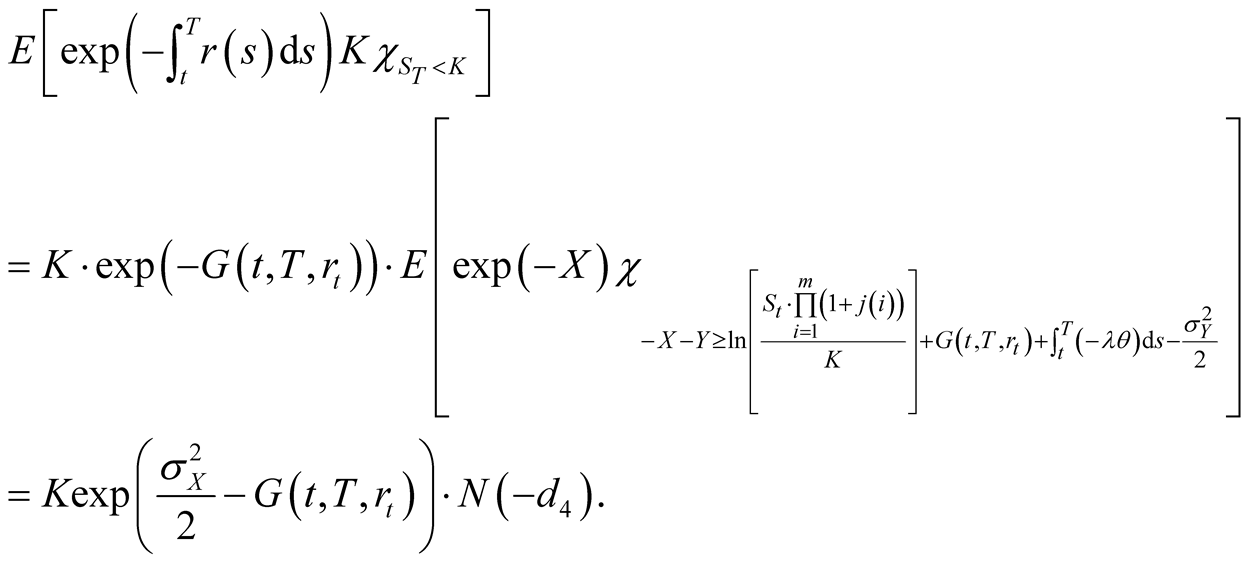 (43)
(43)
Also,
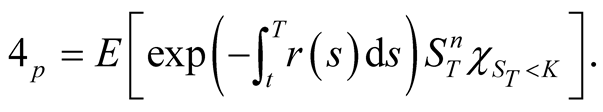
Since
 (44)
(44)
and
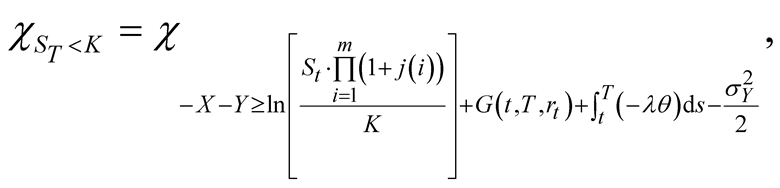 (45)
(45)
we obtain
 (46)
(46)
5. Conclusion
In this paper, we investigate the issue of pricing the reset option in FBM model, closed-form formulas for the reset option with an single reset date, and the phenomena of delta of the reset jumps existing in the reset option during the reset date. Under the assumption that the exchange rate follows the extended Vasicek model, we obtain the closed-form of the pricing formulas for two kinds of power options under fractional Brownian Motion (FBM) jump-diffusion models.
Acknowledgements
Thanks are due to the referees whose meaningful suggestions are very helpful to revise the paper. This work is supported by the Fundamental Research Funds for the Central Universities (JBK140924).
References
- Black, F. and Scholes, M. (1973) The Pricing of Options and Corporate Liabilities. Journal of Political Economy, 81, 637-654. http://dx.doi.org/10.1086/260062
- Hu, Y. and Oksendal, B. (2000) Fractional White Noise Calculus and Application to Finance. Infinite Dimensional Analysis, Quantum Probability and Related Topics, 6, 1-32. http://dx.doi.org/10.1142/S0219025703001110
- Elliott, R. and Hoek, J. (2003) A General Fractional White Noise Theory and Applications to Finance. Mathematical Finance, 13, 301-330. http://dx.doi.org/10.1111/1467-9965.00018
- Necula, C. (2002) Option Pricing in a Fractional Brownian Motion Environment. Pure Mathematics, 2, 63-68.
- Liu, S.Y. and Yang, X.Q. (2004) Pricing of European Contingent Claim in Fractional Brownian Motion Environment. Chinese Journal of Applied Probability and Statistics, 20, 429-434.
- Liu, S.Y. and Yang, X.Q. (2006) Pricing Compound Option in a Fractional Brownian Motion Environment. Chinese Journal of Engineering Mathematics, 23, 153-157.
- Xue, H. and Wang, L.S. (2008) Pricing of Maximum Option in the Fractional Brownian Motion Environment. Chinese Journal of Engineering Mathematics, 25, 843-850.
- Elliott, R.J. and Chan, L.L. (2004) Perpetual American Options with Fractional Brownian Motion. Quantative Finance, 4, 123-128. http://dx.doi.org/10.1080/14697680400000016
- Peng, D.H. (2007) Pricing of Perpetual American Put with Fractional O-U Process. Mathematica Acta Scienta, 27A, 1141-1147.
- Deng, G.H. and Lin, H.Y. (2008) Pricing American Put Option in a Fractional Black-Scholes Model via Compound Option Approximation. Advance in Systems Science and Applications, 8, 447-456.
- Deng, X.H. (2009) Option Pricing under Stochastic Rate in Fractional Brownian Motion. Chongqing University, Chongqing.

