Applied Mathematics
Vol.5 No.11(2014), Article
ID:47059,10
pages
DOI:10.4236/am.2014.511158
The Future Human Lifespan: A Study on Italian Population
Maria Russolillo
Department of Economics and Statistics, Campus di Fisciano, University of Salerno, Salerno, Italy
Email: mrussolillo@unisa.it
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 9 April 2014; revised 9 May 2014; accepted 17 May 2014
ABSTRACT
In the latter part of the 20th century, continued improvements in living standards, health behaviors, and medical care reduced mortality and produced amazing advances in life expectancy. These trends, followed by all industrial nations, decidedly affect the financial position of an insurance company, interested in the construction of updated life tables. The approach to this problem is faced in this paper by using the Lee-Carter methodology. In particular, in the present work, we are interested in modeling and forecasting mortality and life expectancy on a period basis through the use of a stochastic forecasting method which uses time-series models to make long-term forecasts.
Keywords:Lee Carter Model, Mortality Forecasting, Time Series, Survival Analysis

1. Introduction
In the twentieth century many industrialized countries have experimented downwards trends in mortality rates. A number of extremely important developments have contributed to this rapid mortality improvement. Among the others, we can highlight for example the improved healthcare provided to mothers and babies, improvements in motor vehicle safety, safer and more nutritious foods. Other factors are expected to contribute more to annual rates of mortality improvement in the future. We can highlight among the others an improvement in the education regarding health, the development and application of new diagnostic, surgical and life sustaining techniques and the general change in our conception of the value of life.
These improvements are undoubtedly favourable from our point of view, because we live longer than the past. Otherwise from the insurance companies’ point of view, these changes clearly affect pricing and reserve allocation for life annuities. The financial position of an insurance company is indeed affected by the downwards trends in mortality. For this reason it is necessary to create updated life tables in order to produce financial estimates for an insurance company. A life table shows the probabilities of a member of a particular population living to or dying at a particular age. If the life tables do not take the trends into account, there is also the risk of underestimating the survival probability, thus determining inappropriate premiums by the insurance company. This risk is known in the actuarial literature as longevity risk.
In this study, we construct life tables in order to examine the mortality changes in the Italian population over time. In particular, starting from the Italian mortality experience of the past half-century, we extrapolate forecast for the future mortality. To consistently predict the trends [1] , we have to use reasonable mortality forecasting techniques. Our analysis bases on the Lee Carter model [2] , a milestone in the actuarial literature of mortality projections. Following the methodology of Renshaw and Haberman [3] , we fit the Lee-Carter model and obtain forecasts of the time trend parameter. The main goal of this contribution is to construct life tables on a period basis for the Italian population by calendar year and gender.
The paper is organized as follows: in Section 2, we describe the mortality model; Section 3 refers to the SVD approximation technique; Section 4 is devoted to describe the modelling of the mortality index, used to generate associated life table values. Section 5 shows the findings of the empirical analysis on Italian population. Concluding remarks are presented in Section 6.
2. The Mortality Model
Among various forecasting methodologies, in this contribution we focus on the Lee Carter (LC) model which makes use of the past mortality experience in order to forecast future mortality. The authors described a methodology to forecast mortality which combines demographic model with statistical time series method. The model used for mortality bases on the central mortality rates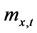 , for age x in year t, defined as the ratio between the number of deaths
, for age x in year t, defined as the ratio between the number of deaths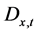 , recorded during the calendar year t for people aged x and the exposure to risk
, recorded during the calendar year t for people aged x and the exposure to risk . The simple bilinear model was defined as:
. The simple bilinear model was defined as:
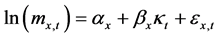 (1)
(1)
where on the right hand side of the equation, we find an age-specific component , independent of time, another component given by the product of a time-varying parameter
, independent of time, another component given by the product of a time-varying parameter  and an age-specific component
and an age-specific component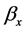 . In particular, the
. In particular, the 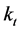 parameter is a time-trend index of the general mortality level and the component
parameter is a time-trend index of the general mortality level and the component 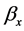 indicates the pattern of deviations from the age profile when the general level of mortality changes.
indicates the pattern of deviations from the age profile when the general level of mortality changes.  is the residual term at age x and time t.
is the residual term at age x and time t.
In their original paper, in order to fit the model, Lee and Carter [2] , suggested a close approximation to the Singular Value Decomposition (SVD) method based on a two-stage estimation procedure. In the course of time, different alternative criteria have been proposed to overcome this method. Wilmoth [4] , for example, developed two alternative one-stage estimation strategies, a weighted least square (WLS) and a maximum likelihood (MLE) technique. Nevertheless, there are still several advantages to use the SVD which has become, together with the WLS and the MLE, the most used method for estimating the model’s parameters. In a study by Koissi, Shapiro and Högnäs [5] , they compared these three methods and showed that SVD is the best alternative for the mortality index k. Moreover, another advantage of SVD is that can be easily represented by using the Biplot [6] .
3. The SVD Approximation
In order to find a least squares solution to the Equation (1), we use a close approximation to the SVD method, assuming that the errors are homoscedastic. Following [2] , the components  and
and  can be estimated according to the SVD [7] with proper normality constraints: we impose the sum of
can be estimated according to the SVD [7] with proper normality constraints: we impose the sum of 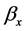 coefficients equal to one and the sum of the
coefficients equal to one and the sum of the 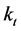 parameters equal to zero. Under these assumptions, we run the following steps:
parameters equal to zero. Under these assumptions, we run the following steps:
• the 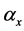 coefficients are the average values over time t of the
coefficients are the average values over time t of the  values for each x:
values for each x:
• 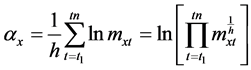
•  must equal the sum over age of
must equal the sum over age of 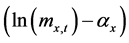
• each 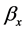 is estimated from
is estimated from 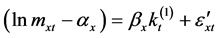 (where
(where 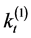 refers to the
refers to the 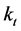 estimated above) using the least squares estimation, i.e. choosing
estimated above) using the least squares estimation, i.e. choosing  to minimize
to minimize
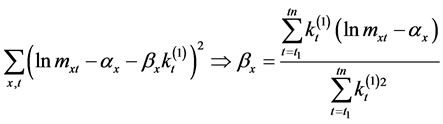 .
.
In Section 2, we stated that the approximation to the SVD method is built on a two-stage estimation procedure. This happens because the first stage estimation is based on logs of death rates rather than the death rates themselves, thus causing possible discrepancies between predicted and actual deaths. To guarantee that the fitted death rates will lead to the actual numbers of deaths, when applied to given population age distribution, we re-estimate 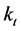 in a second step, taking the
in a second step, taking the 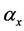 and
and 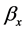 estimates from the first step. To correct for this, we apply the methodology from Section 3 of [2] . We thereby find a new estimate for
estimates from the first step. To correct for this, we apply the methodology from Section 3 of [2] . We thereby find a new estimate for  by an iterative searchadjusting the estimated
by an iterative searchadjusting the estimated 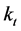 so that the actual total observed deaths
so that the actual total observed deaths 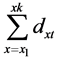 equal the total expected deaths
equal the total expected deaths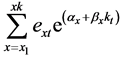 , for each year t (we remind the interested reader to [8] for a deeper insight in the iterative procedure). There are several advantages to make a second stage estimate of the
, for each year t (we remind the interested reader to [8] for a deeper insight in the iterative procedure). There are several advantages to make a second stage estimate of the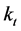 : it can be useful in the life table presentation of the data and especially in cases where only the total, rather than age-specific, death rates are known in certain years.
: it can be useful in the life table presentation of the data and especially in cases where only the total, rather than age-specific, death rates are known in certain years.
4. The Procedure
4.1. Modelling the Time-Varying Parameter
The mortality trend of a country is captured by the time-varying parameter 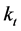 of the LC model. Once we fit the LC on a mortality dataset of a specific population, we obtain the
of the LC model. Once we fit the LC on a mortality dataset of a specific population, we obtain the  for the specific country. Then, we arrange the
for the specific country. Then, we arrange the 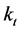 time series in a vector in which the single units are represented by the time-varying parameter
time series in a vector in which the single units are represented by the time-varying parameter 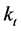 in the different years. In this phase, the estimated time-dependent parameter
in the different years. In this phase, the estimated time-dependent parameter  is modelled as a stochastic process. We use the standard Box and Jenkins methodology (identification-estimation-diagnosis) to generate an appropriate ARIMA (p, d, q) model for the mortality index
is modelled as a stochastic process. We use the standard Box and Jenkins methodology (identification-estimation-diagnosis) to generate an appropriate ARIMA (p, d, q) model for the mortality index 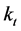 ([9] [10] ). The ARIMA model is then used to generate forecasted mortality index
([9] [10] ). The ARIMA model is then used to generate forecasted mortality index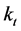 .
.
4.2. Projecting Life Tables
Once we have projected the index of mortality, we can generate associated life table values. Mortality experience is usually represented in the form of a life table. There are two basic type of life tables to be represented, period-based tables and cohort-based tables. In this study, we focus on period life table in order to analyse changes in the mortality experienced by a population through time. Let’s start from the formula:
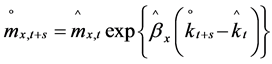 (2)
(2)
for computing forecasted mortality rates by alignment to the latest available empirical mortality rates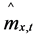 . In the formula we inserted the projected
. In the formula we inserted the projected ,
, 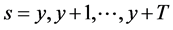 , with y being the first time and T the length of the period considered for the projections.
, with y being the first time and T the length of the period considered for the projections.
A life table treats the mortality experience upon which it is based as though it represents the experience of a single birth cohort consisting of 100,000 births who experience, at each age x of their lives, the probability of death, denoted 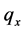 [11] . Thus, we convert the life table death rates,
[11] . Thus, we convert the life table death rates,  , into probabilities of death,
, into probabilities of death,  [12] . In particular, we compute
[12] . In particular, we compute 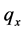 from
from 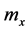 and
and  according to the formula:
according to the formula:
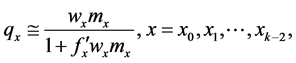 (3)
(3)
where 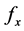 is the average number of years lived within the age interval
is the average number of years lived within the age interval 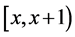 for people dying at that age and
for people dying at that age and . As in [3] , we assume that
. As in [3] , we assume that  for all age groups except age 0 (for x = 0 we fix
for all age groups except age 0 (for x = 0 we fix 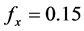
for males and 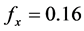 for females). For the sake of completeness, we formulate
for females). For the sake of completeness, we formulate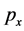 , the probability of surviving from age x to
, the probability of surviving from age x to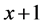 , as:
, as:
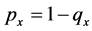 (4)
(4)
The entry  in the life table shows the number of survivors of that birth cohort at each succeeding exact integral age, while
in the life table shows the number of survivors of that birth cohort at each succeeding exact integral age, while 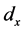 shows the number of deaths that would occur between succeeding exact integral ages among members of the cohort. Thus we working down the column of l’s and d’s in the life tables, applying the recurrence equations:
shows the number of deaths that would occur between succeeding exact integral ages among members of the cohort. Thus we working down the column of l’s and d’s in the life tables, applying the recurrence equations:
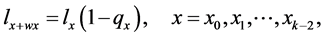 (5)
(5)
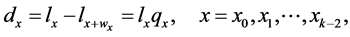 (6)
(6)
where 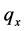 is calculated as in (3) and
is calculated as in (3) and  is arbitrary (in our case is put equal to 100,000).
is arbitrary (in our case is put equal to 100,000).
The number of person-years  lived between consecutive exact integral ages x and
lived between consecutive exact integral ages x and  are:
are:
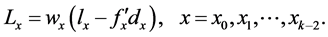 (7)
(7)
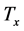 gives the total number of person-years lived beyond each exact integral age x, by all members of the cohort, while the final entry in the life table,
gives the total number of person-years lived beyond each exact integral age x, by all members of the cohort, while the final entry in the life table, 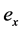 , called life expectancy, represents the average number of years of life remaining for members of the cohort still alive at exact integral age x.
, called life expectancy, represents the average number of years of life remaining for members of the cohort still alive at exact integral age x.
In this case, the person-years remaining for individuals of age x equal
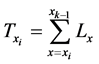 (8)
(8)
imply that life expectancy is given by
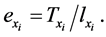 (9)
(9)
5. Numerical Application
This study presents period life tables by gender from 2001 up to 2025 reflecting projected mortality. The fundamental step in constructing a life table from population data is that of developing probabilities of death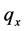 , that accurately reflect the underlying pattern of mortality experienced by the population [11] . In this contribution, the method used for developing the rates is based on the LC model and described in Section 3. Actual data permit the computation of central death rates, which are then converted into probabilities of death. Tabulations of death rates by age and gender are based on information supplied by the Human Mortality Database [13] available on the web at www.mortality.org or www.humanmortality.de). Deaths and exposure to risk for the Italian population are provided by five year age groups for ages 0 through 99 divided by gender. Death rates are calculated as the ratio between deaths and exposure to risk.
, that accurately reflect the underlying pattern of mortality experienced by the population [11] . In this contribution, the method used for developing the rates is based on the LC model and described in Section 3. Actual data permit the computation of central death rates, which are then converted into probabilities of death. Tabulations of death rates by age and gender are based on information supplied by the Human Mortality Database [13] available on the web at www.mortality.org or www.humanmortality.de). Deaths and exposure to risk for the Italian population are provided by five year age groups for ages 0 through 99 divided by gender. Death rates are calculated as the ratio between deaths and exposure to risk.
Usually the procedure for projecting mortality begins with an analysis of past trends. In this study, we fit the LC model to the matrix of Italian death rates from year 1950 to 2000, following the SVD approximation described in Section 3.
An accurate analysis of the autocorrelations and partial autocorrelations, together with related diagnostics, drive us to the choice of the ARIMA model for the re-estimated time-varying parameter 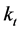 [8] . On the basis of this model, we generate the forecasted index of mortality for the 25 years onwards and produce associated life table values at five-year intervals from 2001 through 2025.
[8] . On the basis of this model, we generate the forecasted index of mortality for the 25 years onwards and produce associated life table values at five-year intervals from 2001 through 2025.
Tables 1-4 show values for the functions qx, lx, dx, Lx by age and gender for quinquennial years 2010 through 2025. The method used to produce the values shown in these tables has been described in Section 4.1.
By looking at Tables 1-4, we notice that for each calendar year the probabilities of death 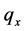 are relatively high at birth, decline to a low point until age-group 10 - 14, and thereafter rise up to age-group 95 - 99. Moreover, all of the four period tables show higher values of
are relatively high at birth, decline to a low point until age-group 10 - 14, and thereafter rise up to age-group 95 - 99. Moreover, all of the four period tables show higher values of 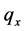 for male than for female. It is relevant to notice also the drop of the probabilities of death as the calendar year increase, thus highlighting the improvement in the mortality, experienced by the industrialised countries.
for male than for female. It is relevant to notice also the drop of the probabilities of death as the calendar year increase, thus highlighting the improvement in the mortality, experienced by the industrialised countries.
Finally, in Table 5 we have compared forecasted life expectancy at birth for male and female as well as life expectancy at 60. As regards life expectancy at age 0, by gender and calendar year, we can notice rapid gains in
Table 5. Forecasted life expectancy at birth and life expectancy at 60.
life expectancy at age 0 from 2001 through 2025 more for female than for male. This trend is confirmed also for life expectancy at 60, even if the pace of improvement is lower than for life expectancy at birth. However, this gender gap diminished during the last decades, is projected to decrease only slightly in the future.
6. Concluding Remarks
Insurance companies often request mortality projections for forecasting and facing their financial position. With this study we suggest that relatively simple information can be used to make accurate risk assessments for the companies. In order to confirm risk specific premiums and to avoid acceptance at standard risk of persons with different life expectancy it is necessary to predict the risk. The paper deals with the projections of mortality for the Italian population. The analysis we propose bases on an application of the model underpinning the LC method for forecasting life table values. In the framework of the LC model, we consider a close approximation to the SVD method, in order to estimate the model’s parameters. The objective of the research is in particular to forecast period life tables, by taking into account time-series-based forecast procedure. The results are life table values at five-year intervals from 2001 through 2025. Obviously, the difference in results is evident for both genders. Our results support the thesis that mortality predictions are necessary to estimate the costs of insurances and to calculate optimal premiums.
References
- Brouhns, N., Denuit, M. and Vermunt, J.K. (2002) A Poisson Log-Bilinear Regression Approach to the Construction of Projected Life Tables. Insurance: Mathematics and Economics, 31, 373-393. http://dx.doi.org/10.1016/S0167-6687(02)00185-3
- Lee, R.D. and Carter, L.R. (1992) Modelling and Forecasting U.S. Mortality. Journal of the American Statistical Association, 87, 659-671.
- Renshaw, A. and Haberman, S. (2003) Lee-Carter Mortality Forecasting: A Parallel Generalised Linear Modelling Approach for England and Wales Mortality Projections. Applied Statistics, 52, 119-137. http://dx.doi.org/10.1111/1467-9876.00393
- Wilmoth, J.R. (1993) Computational Methods for Fitting and Extrapolating the Lee-Carter Model of Mortality Change. Technical Report, University of California, Berkeley.
- Koissi, M.C., Shapiro, A. and H?gn?s, G. (2005) Fitting and Forecasting Mortality Rates for Nordic Countries Using the Lee-Carter Method. Department of Mathematics, Abo Academy University, Finland.�
- Giordano, G., Russolillo, M. and Haberman, S. (2008) Comparing Mortality Trends via Lee Carter Method in the Framework of Multidimensional Data Analysis. Mathematical and Statistical Methods in Insurance and Finance. Springer Verlag, Berlin, 131-138.
- Eckart, C. and Young, G. (1936) The Approximation of One Matrix by Another of Lower Rank. Psychometrika, 1, 211-218. http://dx.doi.org/10.1007/BF02288367
- Haberman, S. and Russolillo, M. (2005) Lee-Carter Mortality Forecasting: Application to the Italian Population. Actuarial Research Paper No. 167, City University.
- Box, G.E.P. and Jenkins, G.M. (1976) Time Series Analysis for Forecasting and Control. Holden-Day, San Francisco.
- Hamilton, J.D. (1994) Time Series Analysis. Princeton University Press, Princeton.
- Bell, F.C. and Miller, M.L. (2005) Life Tables for the United States Social Security Area 1900-2100.
- Keyfitz, N. (1977) Introduction to the Mathematics of Population with Revisions. Addison-Wesley Publishing Co., Reading.
- (2009) Human Mortality Database. University of California, Berkeley (USA), and Max Planck Institute for Demographic Research (Germany). www.mortality.org or www.humanmortality.de


