Received 8 September 2014; revised 28 September 2014; accepted 12 October 2014

ABSTRACT

Duration dependence affects the dynamics of multi sate time to event outcomes. In this paper we are testing if a contraction or an expansion state for the housing price is duration dependent on previous states lengths. This test has implications for explaining the dynamics and the predictability of the housing prices in subsequent spells of contraction/expansion. The test is carried on using a discrete time duration model. This research shows that federal fund rate has strong effect on duration of both expansion and contraction. The analysis is also showing that while for both contraction and expansion spells we observe duration dependence, the risk of exiting from either spell at the beginning of the spell is practically flat for the first five to six years in the expansion spells and between seven and eight years in the contraction spells. After these periods the risk of exiting an expansion spell is increasing but in a non-monotone way, while for the contraction spell the risk of exiting the state is increasing in a monotone way, making the contraction periods easier to predict than the expansion periods.

Keywords:

Discrete Hazard Model, Duration Dependence, Housing Price Market

1. Introduction

There is extensive work about the contribution of the housing market to the economic growth of a given economy. The importance of this sector for the US economy was pointed out by Belsky and Prakken [1] . They showed that over the past 50 years, housing expenditures have accounted for more than one fifth of the US’s gross domestic product and that indirect spillovers in the economy are also happening when housing wealth increases and consumers are spending more. As this indirect contribution to economic growth plays a role on the business cycles, the economic growth of a specific economy becomes dependent on the dynamics of the housing prices. An increase of the demand for housing or in the price of housing may lead to higher growth rates, while a decrease on the above mentioned measures has an opposite effect.

As a consequence, after a period where we experienced both a sustainable expansion and an increase in the housing pricing at limits that were not sustainable by the market, the recent downturn was abrupt with serious consequences for the economies dependent on the development of this sector and to the world economy in general.

An important question about housing price dynamics and their predictability is whether the length of a contraction or an expansion state is duration dependent on previous states lengths. In this regard, positive duration dependence implies an increase in the probability of an exit as the time passes, while negative duration dependence means a decrease in the probability of an exit with time. Therefore, duration dependence, if present in a market and, if properly identified can be used to make predictions about possible turning points in the housing prices. Alternatively, if there is no duration dependence, or in other words turning points in prices are independent on the length of a given state, it becomes hard to make predictions about the lengths of a given state. It becomes evident that to understand the duration dynamics of the housing market one needs to properly identify if duration dependence is present, and if it is present, to identify the type and the magnitude of this dependence.

There are many papers that investigate the factors that are important for the housing prices, some of them focusing on long run models for housing prices. Using data on owner-occupied housing cost in the US metro areas, Himmelberg et al. [2] investigated if housing market was overvalued during the last expansion phase. With the exception of Boston, San Francisco and New York, they did not find any evidence to support that housing prices were out of line with most fundamental factors that are important for the housing prices. At the macro level, Ahearn et al. [3] , with the help of the data from eighteen major industrial countries, showed that housing prices were pro-cyclical and were commoving with most macroeconomics variables. In other line of research, Martin [4] , with the help of a simple Lucas asset pricing model and by focusing on baby boomers, showed the importance of demographic changes on the housing price index and the interest rates in United States. Using a dynamic factor model, Del Negro and Otrok [5] investigated the importance of local shocks versus an aggregated shock for the housing prices dynamics, suggesting that although most past movements were mainly driven by the regional factors, recent housing price boom is a national phenomenon. Ceron and Suarez [6] applied a Markov switching model to a panel of fourteen developed countries to capture changes in the volatility of real housing price. They showed that housing cycles have high and low volatility phases with about the same unconditional frequency over the time.

In this paper, a multiple spells duration model is used with the purpose to properly identify the presence and the type of the duration dependence for the prices in the housing market in both contraction and expansion cycles.

Duration dependence was previously identified in the housing market using different methods. Durland and McCurdy [7] added a duration length as an explanatory variable in a discrete-state Markov switching model used to explain business cycles dynamics and found support of duration dependence for contractions but not for expansions.

Mills [8] applied a non-parametric model and tested the presence of cyclical asymmetry and duration dependence in business cycles. He pointed out towards duration dependence in expansions and whole cycles, but to independence in contractions. Lam [9] extends the Durland and McCurdy’s model by introducing mean growth rate in addition to transition probabilities to depend on the age of current phase. His findings show that expansions are negative duration dependent whilst recessions are positive duration dependent. Layton and Smith [10] in a Markov switching process framework consider duration and movements in two leading indexes as explanatory variables for business cycles. Using a state-dependent multinomial Logit model, they find duration is a significant determinant of transition out of recessions and weakly significant in case on expansions. Cunningham and Kolet [11] estimate a discrete time survival with a probit specification to test the existence of duration dependence in housing price cycles by focusing on survival function. They use a metro level data set and conclude there is positive duration dependence in expansion phases whilst contractions seem to have no duration dependence.

The results of previous research were mixed about the issue of duration dependence. A natural way of identifying duration dependence is by using duration analysis, in particular hazard models, as they are flexible in specification and can account for different types of censoring in the data. Our analysis is showing that while for both contraction and expansion spells we observe duration dependence, the risk of exiting from either spell at the beginning of the spell is practically flat for the first five to six years in the expansion spells and between seven and eight years in the contraction spells. After these periods the risk of exiting an expansion spell is increasing but in a non-monotone way, while for the contraction spell the risk of exiting the state is increasing in a monotone way, making the contraction periods easier to predict than the expansion periods.

The paper is organized as follows. Section 2 discusses the methodology, Section 3 discusses the Data, Section 4 analyzes the results while Section 5 concludes the analysis.

2. Methodology

This paper uses duration modeling to investigate whether there is duration dependence in housing price cycles or not. The type of duration model used is conditioned on the frequency and length of the available duration data. While continuous models are relevant for high frequency data, discrete duration models may be more appropriate for lower frequency durations. An additional advantage of using discrete duration modeling is that they are more tractable as it is easier to incorporate time-varying covariates.

Jenkins [12] shows that it is possible to consider a discrete-time survival model as a binary dependent variable model, which can be estimated using standard probability models a Logit or Probit.

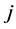The following notation is used: denotes cities, is used to count spells. Therefore 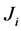is the number of spells observed by city. Within the spell, discrete periods are observed. The last period when the city 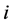is observed in spell 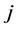is denoted by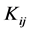. The maximum number of periods observed by a city in spell

is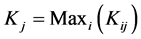. is a discrete random variable, which indicates the time period within spell when a

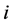terminating event occurs. The distribution of our duration outcome variable is modeled using the probability of having a spell that ends at each of the observed time interval. In this case, the probability that -th spell of city will terminate in the -th time period of that spell given it didn’t terminate earlier, or in other words the discrete hazard function can be written as:

,

where is a vector of time-varying explanatory variables. In this case the distribution of is of primary interest, and can be shown to be expressed as:

with its survival defined as:

.

Under the assumption of independent spells, the total likelihood generated by the discrete hazards can be expressed as:

where if city continues to remain in the current spell and if city exits the current spell. To ease our estimation, this likelihood can be simplified. By defining the dependent binary variable as for all the years an individual city is experiencing a turning point in the prices of houses and with for the years where we have the same trend in prices within a price spell, the total likelihood changes to:

.

Since is one only for the last period, it is possible to change the likelihood function as:

.

The corresponding log-likelihood function is:

,

which is similar to the standard log-likelihood function for a regression analysis with a binary variable with the unit of analysis defined as a spell of time. By using the appropriate probability function, this model can be easily estimated.

The expectation of the dichotomous event indicator equals the probability that a terminating event occurs to an individual from a period of a spell:

.

We have that is equal to 1 in period only if city did not experience the turning point in prices in all earlier periods of spell. If equals 1, then through must equal 0, and

.

Thus, the values of the event indicator are observed realizations of hazard probability. The above probability model can be conditioned on observables of the form, which is a vector of period specific explanatory variables. A dummy variable is created for each period, and the initial discrete hazard model is changed to a binary discrete choice model that can be estimated by panel logit or probit. In this case a panel logit specification is used for the estimation as it is more robust to misspecifications of the error distribution and allows for correlated unobserved heterogeneity, in other words allows for fixed effects.

3. Data Description

The analysis is from the Office of Federal Housing Enterprise Oversight (OFHEO) housing price indices (HPI) and is based on an annual data collected for the largest 110 cities in the United States during the period 1975- 2007. However, for some cities the housing price index is available after 1975. Also, to deal with the potential left censoring of a given spell, the data is trimmed to include only complete spells. The adjustments made the panel to be unbalanced. Consumer Price Index (CPI) is used to transform the nominal data to real data, where CPI was collected from Bureau of Labor Statistics of United States. As covariates, the model includes the Effective Federal Funds Rate (EFFR), which is a good variable to capture the policy makers’ effect on the housing price. The source of these data is St. Louis Federal Reserve. Other fundamental economic variables that are entered in the model are Population Size (PS) and Personal Income (PI). The data at metro level was collected from the Bureau of Economic Analysis. Like other nominal variables in the model, the PI was deflated by CPI.

Fundamental variables are tested for stationarity. PS is stationary in level, while the Real PI and EFFR are not stationary in level but are stationary in the difference. To test PI and PS, Levin-Lin-Chu Unit root test for panel data is used (see Table 1). Alternative panel unit root tests were used to test the robustness of the results. The EFFR is city invariant variable, therefore a Dicky-Fuller unit root test was used (see Table 2). Given the results of the test statistics, the difference of fundamental variables is used in the model.

4. Using the Template (Heading 4)

The estimation was done separately for the expansion and the contraction of the housing cycle spells. As there is no formal test for the type of unobserved heterogeneity, both fixed effects and random effects panel logit models are employed. Both models are consistent under the null of random effects, but if there are significant differences in the parameter estimates between the two models, the random effects estimates are biased. As the results of the random effects model show some differences when they are compared with the fixed effects model, the fixed effects panel logit results are chosen to be reported.

The parameter estimates of the expansion spells are presented in Table 3, while for contraction spells are presented in Table 4. The sign and of the parameter estimates are as expected for both expansion and contraction

Notes: Standard errors are in parentheses. ^*, ^**, and ^*** denote 1%, 5%, and 10% level of significance, respectively.

spells, which means that PS and PI may have negative effect on probability of exiting from the expansion spells, whilst EFFR may have a positive effect on the exiting probability from the expansion spells. The opposite effects are recorded for the contraction spells (see Table 4). PS in contraction model and PI in expansion model are not significant but EFFR is significant in both models at 5 percent significance level.

The dummy variables of each period are capturing the time effects or the baseline hazards patterns. The results for the expansion spells are to some extent mixed, which means that the risk of leaving an expansion spell does not have a stable pattern. The conditional (estimated) plots of first, second and third expansion spells are presented in Figure 1.

The plots suggest that the estimated hazards are mimicking very closely the empirical hazard nonparametric estimates, which suggest a very good fit obtained with the proposed conditional analysis. The graphs also suggest that within the three analyzed categories there are structural differences, with the first and third expansion spells having the highest hazard (probability of exiting the state in the next observed period) in the middle of the period, while for the second expansion spell the hazard is looking more exponential (increasing towards the end of the spell). The first and third spells are also showing increasing hazards towards the end of the spells, but not as high as the increase in the hazard for the second spell.

The conditional (estimated) plots of first, second and third contraction spells are presented in Figure 2.

The plots suggest that the estimated hazards are mimicking very closely the empirical hazard nonparametric estimates as in the case of the expansion spells, and in contractions periods the behavior of the price is similar across different spells. If we pool all the information form all the spells for the expansion and separately for the contraction spells we generate an equivalent of an average expansion/contraction spell. Figure 3 presents the

Notes: Standard errors are in parentheses. ^*, ^**, and ^*** denote 1%, 5%, and 10% level of significance, respectively.

empirical and estimated hazard results for the polled Expansion and Contraction Spells.

Again, both the empirical and the conditional estimated hazards are moving very closely to each other, suggesting a very good fit of the estimated model. We also see that the average expansion spell is more heterogeneous and longer than the average contraction spell. To look at the issue of duration dependence we followed the estimated year dummies. If there is to be no duration dependence, then the period specific dummies should not be significantly different, regardless of the duration of time spent in the spell. The fact that we observe significantly different period dummy variables ensures that there is duration dependence in both expansion and contraction

spells. The forms of duration dependence for both phases are mixed. While the pattern for a contraction spell is clearer. The risk of ending the spell declines between second and fourth year, while it increases after that, for the expansion spell we again observe more heterogeneity in the baseline hazard which suggest less evidence of duration dependence. Therefore, it becomes clearer that while contraction spells are easier to predict, the expansion spells are harder to predict.

5. Conclusion

The main goal of this research is testing duration dependence in housing price market using discrete time duration models. By transforming the main model to a binary discrete choice model a fixed effects panel logit is used for the estimation, while assuming independence between the contraction and expansion spells. This research shows that federal fund rate has strong effect on duration of both expansion and contraction. So policy makers can influence duration by this instrument. The analysis is also showing that while for both contraction and expansion spells we observe duration dependence, the risk of exiting from either spell at the beginning of the spell is practically flat for the first five to six years in the expansion spells and between seven and eight years in the contraction spells. After these periods the risk of exiting an expansion spell is increasing but in a non-monotone way, while for the contraction spell the risk of exiting the state is increasing in a monotone way, making the contraction periods easier to predict than the expansion periods.

References