Applied Mathematics
Vol.5 No.13(2014), Article
ID:47595,7
pages
DOI:10.4236/am.2014.513179
Measuring Dependence Risk of Funds with Copula in China
Jiaqi Tang1, Guohua Sun2
1School of Management, Guilin University of Technology, Guilin, China
2College of Science, Guilin University of Technology, Guilin, China
Email: 262605708@qq.com, 296231428@qq.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/
![]()
![]()

Received 24 April 2014; revised 3 June 2014; accepted 15 June 2014
ABSTRACT
The aim of this paper is to measure dependence risk of fund market with copulas in China. Firstly, we introduce several common copula functions, then estimate parameters of copula function, and discuss how to select the optimal copula function. Finally, according to Shanghai and Shenzhen fund data, empirical analysis was done. Different combinations of risk values were obtained.
Keywords:Copula, Dependence Risk, Monte Carlo Simulation, Parameter Estimation

1. Introduction
Copula research originated in Sklar [1] , and Nelsen systematically introduced the definition, construction method, and dependency [2] , Bouye E, Durrleman V and Nikeghbali A systematically introduced some applications of copula in finance [3] . Currently, the copula function has been widely used in the financial field, especially in the financial market risk management, portfolio selection, asset pricing, etc., and it has become a powerful tool to solve the financial problems. In the actual study, to describe the joint distribution of financial assets is a very important issue. In general, the distribution of financial assets showed fat tail characteristics, if the joint distribution of financial assets yield sequence of most risk management modes obey the multivariate normal distribution, and the linear correlation hypothesis of every single asset in the portfolio, can produce very big deviation and mislead to the empirical results [4] . The copula function can be used to connect marginal distributions of random variables with the joint distribution, and it does not require that the distribution of marginal distributions have the same form, and so it can flexibly construct practical multivariate distribution. The applications of copula in the financial sector have made a lot of meaningful results. In the study of many scholars, there are few to use copula functions to research China fund market, so in this paper, taking Shanghai and Shenzhen fund yields for examples, we analyzed copula functions and their characteristics of the application on correlation analysis, then selected the appropriate copula function and got different combinations of risk values.
2. Introduction to the Theory of Copulas
2.1. The Definition and Properties of Copulas
In 1959, Abe Sklar first proposed copula function, but financial experts didn’t pay attention to copula function until the 1990s. As a method to research associated structures of random variables, copula has its unique properties, namely multivariate distribution function can be described by univariate marginal functions and multivariate correlation structure functions.
Sklar Theorem [1] : Set 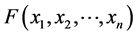 as N-dimensional distribution function whose marginal distribution is
as N-dimensional distribution function whose marginal distribution is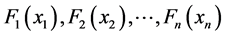 , then there exists a function
, then there exists a function  which has only copula expression:
which has only copula expression:
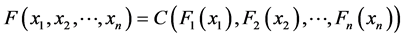 (1)
(1)
According to Sklar theorem, we can through copula function 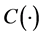 and marginal distributions to build multivariate joint distribution. Since the marginal distribution function arbitrary value
and marginal distributions to build multivariate joint distribution. Since the marginal distribution function arbitrary value 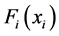
 can be regarded as uniformly distributed random variable values of
can be regarded as uniformly distributed random variable values of 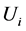 on
on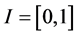 , denoted
, denoted 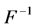 is inverse function of F, namely
is inverse function of F, namely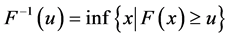 , assuming marginal distributions
, assuming marginal distributions 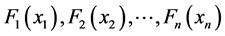 are continuous, then by the Sklar’s theorem, there exists a unique copula function
are continuous, then by the Sklar’s theorem, there exists a unique copula function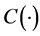 , making
, making
 (2)
(2)
Use type (2), we could start with the marginal distribution and the dependency structure processing, respectively, to integrate, can more effectively and to explore the common changes of relationship between variables, and then get more suitable joint probability distribution and risk assessment as a portfolio or commodity pricing.
2.2. Several Kinds of Commonly Used Copulas Function
There are many kinds of copulas function, basically we are commonly used is Elliptic Copulas and Archimedean Copulas. And in each group, there are a number of specific copulas connect functions. Different copulas connect functions have different nature. In practical application, how to choose the right copulas connect function needs to follow the two principles below: one is copulas connect model should be easy to operate and understand, avoid the phenomenon of unknown parameters of significance [5] ; the other one is to select the copula function which can adapt to related structures of the sample data. The Elliptic Copulas has the property of symmetric tail dependence, it violates the fat-tailed distribution of financial data. Currently, the most widely applied in the field of financial category is the Archimedean Copula function. What’s more, its structure and computation are simple. Therefore, here are several kinds of commonly used Archimedean copulas connect function, this paper just considers the binary case.
1) Gumbel Copula Function The distribution function is expressed as follows:
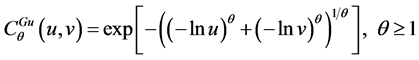 (3)
(3)
The Gumbel Copula function is very sensitive to the changes of the variables at the up-tail of the distribution, so it can fast capture the variations which dependent on the up-tail. It can be used to describe the dependencies between financial variables with relevant characteristics of the up-tail. The Parameter ![]() describes the extent of their dependency, when
describes the extent of their dependency, when![]() , the variable will be independent. When
, the variable will be independent. When![]() , the Variable tends to completely dependent.
, the Variable tends to completely dependent.
2) Clayton Copula Function The distribution function is expressed as follows:
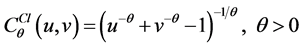 (4)
(4)
The Clayton Copula function is very sensitive to the changes of the variables at the down-tail of the distribution, so it can fast capture the variations which dependent on the down-tail. It can be used to describe the dependencies between financial variables with relevant characteristics of the down-tail. When![]() , it represents independent variables ;When
, it represents independent variables ;When![]() , it represents that the variables are completely dependent.
, it represents that the variables are completely dependent.
3) A12 Copula Function The distribution function is expressed as follows:
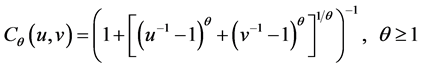 (5)
(5)
The Gumbel Copula function only with the up-tail dependence, on the contrary, the Clayton Copula function only with the down-tail dependence. But the A12 Copula function owns these two characters at the same time.
4) Frank Copula Function The distribution function is expressed as follows:
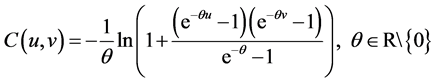 (6)
(6)
The density function’s distribution of Frank Copula function was “U” shaped and its distribution has symmetry. So we cannot capture the asymmetric dependencies between random variables [6] .
The above selected some kinds of Copula function with different characteristics in Archimedean Copula function family. In fact, it can make great influence on the structure of joint distribution when we select different Copulas functions and marginal distribution.
2.3. The Parameter Estimation Method and Selection Principle of Copula Function
For parameter estimation of the specific copula function, we can use the parametric approach and the nonparametric approach averagely: 1) The EML method and the IFM method are more commonly used in the parametric approach. The EML method can estimate the marginal distribution and the parameters in copula function simultaneously. The estimation process is divided into two steps by the IFM method. Firstly, to estimate the parameters of marginal distribution function. Then we need to estimate the parameters of copula function. 2) The Genest and Rivest method are more commonly used in the nonparametric approach [7] . If there are too many parameters in the marginal distributions and copula functions, it is very hard to calculate the exact value of EML. Because of this fact, we use the IFM to estimate the parameter ![]() of copula function in this paper. The estimation principle of IFM is to make the parameters of marginal distribution function and copula function estimated in two steps, it is usually also called two-stage estimation method.
of copula function in this paper. The estimation principle of IFM is to make the parameters of marginal distribution function and copula function estimated in two steps, it is usually also called two-stage estimation method.
First of all, we need to estimate the marginal distribution functions 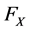 and
and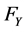 ,
, 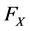 and
and 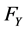 can use the parameter model, such as the Normal distribution, the Students-t distribution, the generalized Pareto distribution and so on. Set the estimation is
can use the parameter model, such as the Normal distribution, the Students-t distribution, the generalized Pareto distribution and so on. Set the estimation is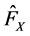 ,
,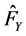 . Then, for this
. Then, for this ,
, 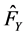 , to construct pseudo samples from the copula below [8] :
, to construct pseudo samples from the copula below [8] :
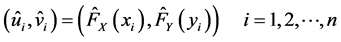 (7)
(7)
Secondly, for the copula 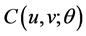 which has the distribution density function
which has the distribution density function 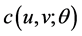 and unknown parameter
and unknown parameter![]() , we need to construct the logarithm likelihood function
, we need to construct the logarithm likelihood function
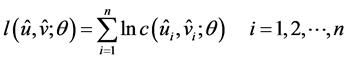 (8)
(8)
In the end, through standard numerical calculation to find the maximum value, we can get the estimate value of the parameter![]() .
.
3. The Selection of Copula Function
3.1. The Statistical Description and Analysis of Fund Yield
This paper selects the day’s closing price which came from the fund of Shanghai and Shenzhen fund from November 3, 2008 to December 4, 2012 as the raw data. The sample size was 997. For the convenience of calculation, by its logarithmic transformation, we can get a corresponding logarithmic revenue rate is 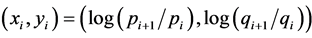 [9] . First of all, the basic statistics of the Shanghai fund yield and Shenzhen fund yield were calculated, the results are shown in Table1
[9] . First of all, the basic statistics of the Shanghai fund yield and Shenzhen fund yield were calculated, the results are shown in Table1
From Table 1, we can see that normality assumption is not appropriate for two kinds of index of yield. Come back now we discuss the two funds dependent risk measurement problem, to analyze their gap between joint distribution and normal distribution. Firstly, we calculate the degree of dependency of these two funds quantitatively. Set ![]() represents the Shanghai stock market fund yields and
represents the Shanghai stock market fund yields and 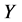 represents the Shenzhen stock market fund yields, it is easy to calculate the correlation coefficient
represents the Shenzhen stock market fund yields, it is easy to calculate the correlation coefficient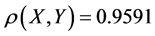 , rank correlation coefficient
, rank correlation coefficient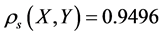 , Kendall
, Kendall![]() . This illustrates that there is a strong linear correlation in the yield of these two kinds of funds. What’s more,
. This illustrates that there is a strong linear correlation in the yield of these two kinds of funds. What’s more, 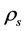 and
and 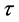 are smaller than classical linear correlation coefficient. In order to further illustrate the gap between the joint distribution and the normal distribution of these two kinds of yield, we made the scatterplot of these two kinds of yield. In addition, we also made the simulation diagram of the bivariate normal distribution which structured by the mean and covariance of these two yields, as shown in Figure 1 and Figure 2.
are smaller than classical linear correlation coefficient. In order to further illustrate the gap between the joint distribution and the normal distribution of these two kinds of yield, we made the scatterplot of these two kinds of yield. In addition, we also made the simulation diagram of the bivariate normal distribution which structured by the mean and covariance of these two yields, as shown in Figure 1 and Figure 2.
From Figure 1 and Figure 2, it’s easy to see that the difference is quite obvious in the tail of the two distribution of data. It shows that using bivariate normal distribution to describe the distribution of these two funds yield is obviously inaccurate. It also suggests that using classical linear correlation coefficient to measure dependency is not enough. So, we use the copula function to measure the dependent risks of this two yields.
3.2. The Selection of Copula Function
Now let’s consider the problem how to select copulas function . Based on the marginal distribution extrapolation, first of all, to structure the sample points which based on the following change:
. Based on the marginal distribution extrapolation, first of all, to structure the sample points which based on the following change:
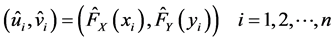
When considering the risk management is only interested in the distribution of the tail, but a large number of studies have shown that yields on the tail of the distribution is the generalized Pareto distribution (GPD), so

Figure 1. The scatter of Shanghai and Shenzhen fund yields.

Figure 2. The simulation diagram of the bivariate normal distribution of Shanghai fund and Shenzhen fund.
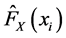 ,
, 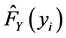 will be taken for the GPD distribution function of the two yields, then according to the marginal distribution extrapolation method to estimate the parameters in the function [8] . Meanwhile, as we care about its risk, so take x, y for the opposite number of its yield. We select Gumbel, Clayton, A12 and Frank Copula to estimate and fitting respectively, after that, according to the AIC and BIC rules to select the most appropriate copulas and its parameters [10] . The specific results are shown in Table2
will be taken for the GPD distribution function of the two yields, then according to the marginal distribution extrapolation method to estimate the parameters in the function [8] . Meanwhile, as we care about its risk, so take x, y for the opposite number of its yield. We select Gumbel, Clayton, A12 and Frank Copula to estimate and fitting respectively, after that, according to the AIC and BIC rules to select the most appropriate copulas and its parameters [10] . The specific results are shown in Table2
From Table 2, it can be seen that the AIC and BIC of Clayton Copulas function are minimal. In view of this, we choose Clayton Copulas function to measure the dependent risks of Shanghai, Shenzhen fund yields.
4. The Dependent Risk Measure in Two Kinds of Fund Portfolio
Assuming in a period of time, to invest in assets 1 and 2, set ![]() and
and 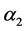 represent the proportion of two kinds of asset investment respectively, X and Y represent the logarithmic yield of this two kinds of asset respectively. Then, the logarithmic yield of this two kinds of asset portfolio can be expressed as below:
represent the proportion of two kinds of asset investment respectively, X and Y represent the logarithmic yield of this two kinds of asset respectively. Then, the logarithmic yield of this two kinds of asset portfolio can be expressed as below:

Due to the nonlinear transformation of combination between X and Y is R, and it is impossible to know the distribution of R. So, it is hard to calculate the dependent risk directly. But, we can use copulas connection function to measure the risk. Here we use copula method to do the Monte Carlo simulation. The algorithm of simulation method is as follows [4] :
1) Generate two uniform random numbers u, w;
2) Make the first random number for asking is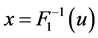 ;
;
3) Through the selected copulas connect function to obtain the random number on uniform distribution which is located in the second sequence 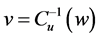 (Among
(Among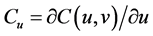 );
);
4) By calculating to obtain the second random number, it is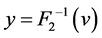 .
.
For the Combination yields R, the VaR and ES which gave them the confidence probability q are
 (9)
(9)
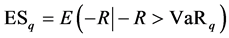 (10)
(10)
Now we try to measure the dependent risk of Shanghai and Shenzhen fund yields. According to the previous analysis, select the corresponding GPD distribution of these two kinds of yields as the marginal distribution, select the Clayton Copula function as the connection function. At the same time, we use the random number which was generated by simulation, then according to formula (9) and (10) above, we can get the risk value of different combinations, as shown in Table3
Table 2. The parameter estimation under the different copulas function.
5. Conclusion
In recent years, the copulas function technology applied in the financial aspects has achieved great development, But the study of copulas connect function is still in its infancy in China at present. This article first introduced several kinds of commonly used copulas connect function, then used the marginal distribution extrapolation for parameter estimation, and selected the optimal copula function. Finally, the VaR and ES values of different combinations between Shanghai fund logarithm yield and Shenzhen fund logarithm yield were calculated by using the copula function theory and combining with Monte Carlo simulation method. By this way, we can measure the dependent risk of fund market well. With the research on copula function being increasingly mature, the copula function will become a powerful tool in the field of finance to greatly promote the stable development of the financial sector.
Fund Project
The national natural science fund project (11061012); The projects of spatial information and surveyingmapping key laboratory in guangxi (GKN 1103108-20); The research projects of Guilin technology bureau (20110120-5).
References
- Sklar, A. (1959) Functions de Repartition an Dimension Set Leursmarges. Publications de L’In-stitut de Statistique de L’Universite de Paris.
- Nelsen, R.B. (2006) An Introduction to Copulas. Springer-Verlag, New York.
- Bouye, E., Durrleman, V., Nikeghbali, A., et al. (2000) Copulas for Finance: A Reading Guide and Some Application. Working Paper, City University Business School-Financial Econometrics Research Centre, Londres.
- Chen, S.D., Hu, Z.Y. and Kong, F.L. (2006) Using Copula Function to Measure the Monte Carlo of Risk Value. Social Science Journal of Jilin University, 46, 85-91.
- Rosenberg, J.V. and Schuermann, T. (2006) A General Approach to Integrated Risk Management with Skewed, Fat-tailed Risks. Journal of Financial Economics, 79, 569-614. http://dx.doi.org/10.1016/j.jfineco.2005.03.001
- Li, S. and Lu, Z.D. (2008) The Copulas Connect Function in the Application of the Measure on Risk Value. The Financial Management, 20, 10-16.
- Genest, C. and Rivest, L.P. (1993) Statistical Inference Procedures for Bivariate Archimedean Copula. Journal of the American Statistical Association, 8, 1034-1043. http://dx.doi.org/10.1080/01621459.1993.10476372
- Ouyang, Z.S. and Wang, F. (2008) The Dependent Risk Measure of the Treasury Bonds Market Which Based on Copulas Connect Method. Statistical Research, 25, 82-85.
- Li, Y. and Cheng, X.J. (2006) The Copulas Connect Tail Correlation Analysis of the Shanghai Composite Index and Hang Seng Index. Systems Engineering, 24, 88-92.
- Liu, W. and Yang, A.L. (2011) The Finite Mixture Model Unsupervised Learning Algorithm Which Based on BIC Criterion and Gibbs Sampling. Electronic Journals, 39, 134-139.


