Applied Mathematics
Vol.5 No.9(2014), Article ID:46143,14 pages DOI:10.4236/am.2014.59126
Coincidence and Common Fixed Point of Weakly Compatible Maps in Fuzzy Metric Space
Saurabh Manro1*, Sumitra2
1School of Mathematics and Computer Applications, Thapar University, Patiala, India
2Department of Mathematics, Faculty of Science, Jazan University, Jazan, KSA
Email: *sauravmanro@yahoo.com, *sauravmanro@hotmail.com, mathsqueen_d@yahoo.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 24 February 2014; revised 24 March 2014; accepted 1 April 2014
Abstract
The aim of this paper is to establish some new common fixed point theorems for generalized contractive maps in fuzzy metric space by using property (E.A.), common property (E.A.), JCLRST property and CLRS property. Our results improve and extend the results of Chauhan et al. [1] and Sedghi et al. [2] besides several known results. We also furnish an illustrative example in support of our results.
Keywords:FM-Space, Weakly Compatible Maps, CLRg Property, Property (E.A.), The Common Property (E.A.), JCLRST Property and Common Fixed Point

1. Introduction
Aamri et al. [3] generalized the concept of non compatibility by defining the notion of property (E.A.) and proved common fixed point theorems under strict contractive conditions. Many authors have proved common fixed point theorems in different settings for different contractive conditions. For details, we refer to [4] -[13] .
In 2005, Liu et al. [14] further improved it by common property (E.A) while proving common fixed point theorems under strict contractive conditions. Recently, Sintunavarat et al. [13] , defined the notion of (CLRg) property which is more general than (E.A) property.
Very recently, Manro et al. [15] introduced the notion of (CLRS) property and Chauhan et al. [4] introduced the notion of (JCLRST) property.
The aim of this paper is to establish some new common fixed point theorems for generalized contractive maps in fuzzy metric space by using property (E.A.), common property (E.A.), JCLRST property and CLRS property. Our results improve and extend the results of Chauhan et al. [1] and Sedghi et al. [2] besides several known results.
2. Preliminaries
Definition 2.1. [16] Let X be any set. A fuzzy set in X is a function with domain X and values in [0,1].
The concept of triangular norms (t-norms) is originally introduced by Menger [17] in study of statistical metric spaces.
Definition 2.2. [18] A binary operation*: 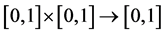 is continuous t-norm if * satisfies the following conditions:
is continuous t-norm if * satisfies the following conditions:
i) * is commutative and associative;
ii) * is continuous;
iii) a * 1 = a for all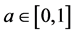 ;
;
iv) a * b £ c * d whenever a £ c and b £ d for all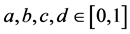 .
.
Examples of t-norms are:
a * b = min{a,b}, a * b = ab and a * b = max{a+b–1, 0} for all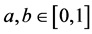 .
.
Definition 2.3. [6] A 3-tuple 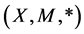 is a fuzzy metric space if X is an arbitrary set, * is a continuous t-norm and M is a fuzzy set on X2 × [0, ∞) satisfying the following conditions for all
is a fuzzy metric space if X is an arbitrary set, * is a continuous t-norm and M is a fuzzy set on X2 × [0, ∞) satisfying the following conditions for all 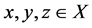 and s, t > 0 i) M(x, y, t) > 0;
and s, t > 0 i) M(x, y, t) > 0;
ii) M(x, y, t) = 1 for all t > 0 if and only if x = y;
iii)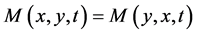 ;
;
iv)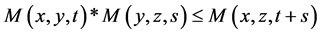 ;
;
v) 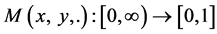 is continuous.
is continuous.
The function M(x, y, t) denote the degree of nearness between x and y with respect to t.
In all that follows 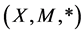 is a fuzzy metric space with the following property:
is a fuzzy metric space with the following property:
vi) 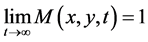 for all
for all 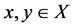 and t > 0.
and t > 0.
Now we give some interesting examples of FM-spaces:
Example 2.1. Let (X, d) be a metric space. Define a * b = a + b, for all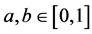 ;
; 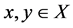 and t > 0.
and t > 0.
Define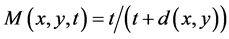 . Then (X, M, *) is a FM-space.
. Then (X, M, *) is a FM-space.
Moreover, fuzzy metric M induced by a metric d is often referred to as the Standard fuzzy metric.
Definition 2.4. [6] . A sequence {xn} in fuzzy metric space 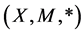 is i) convergent to a point
is i) convergent to a point 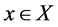 if
if
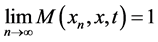 for all t > 0ii) Cauchy sequence if
for all t > 0ii) Cauchy sequence if
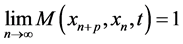
for all t > 0 and p > 0.
Definition 2.5. A pair of self maps (S, T) of a fuzzy metric space 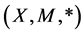 is i) compatible [19] if
is i) compatible [19] if
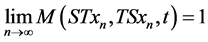
for all t > 0, whenever 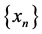 is a sequence in X such that
is a sequence in X such that 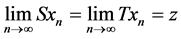 for some
for some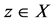 .
.
ii) non-compatible if there exists at least one sequence 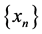 in X such that
in X such that 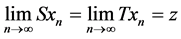 for some
for some 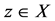 but either
but either 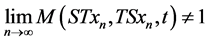 or non-existent.
or non-existent.
iii) weakly compatible [20] if S and T commute at coincidence points, that is, STx = TSx whenever Sx = Tx.
iv) satisfy the property (E.A) [3] if there exist a sequence 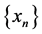 in X such that
in X such that 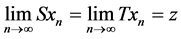 for some
for some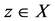 .
.
v) satisfies the common limit in the range of T property (CLRT) [13] if there exist a sequence {xn} in X such that 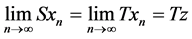 for some
for some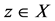 .
.
Definition 2.6. Two pairs of self maps (A, S) and (B, T) of fuzzy metric space 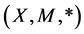 is i) satisfy the common property (E.A) [14] if there exist two sequences
is i) satisfy the common property (E.A) [14] if there exist two sequences 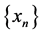 and
and 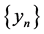 in X such that
in X such that
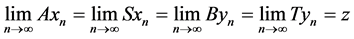 for some
for some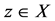 .
.
ii) satisfy the (JCLRST) property (with respect to maps S and T) [4] if there exist two sequences {xn} and {yn} in X such that
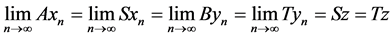 for some
for some 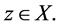
iii) satisfy the (CLRS) property (with respect to maps S) [15] if there exist two sequences {xn} and{yn} in X such that
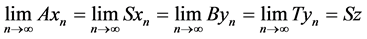
for some 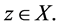
Lemma 2.1. [7] If for all 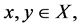 t > 0 and for a number
t > 0 and for a number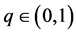 ,
, 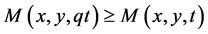 then x = y.
then x = y.
3. Main Results
Let ![]() be the set of all increasing and continuous functions
be the set of all increasing and continuous functions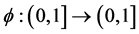 such that
such that  for all
for all 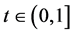 .
.
Example 3.1: Let 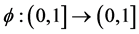 defined by
defined by 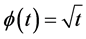 for all
for all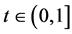 . Clearly,
. Clearly,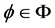 .
.
Theorem 3.1: Let A, B, S and T be self mappings of a fuzzy metric space (X, M, *) satisfying the following:
(3.1)
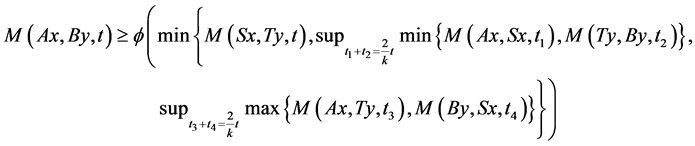
for all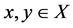 , t > 0 and for some
, t > 0 and for some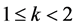 ,
,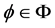 ;
;
(3.2) 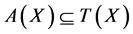 and
and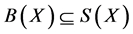 ;
;
(3.3) pair (A,S) or (B,T) satisfies the property (E.A);
(3.4) the range of one of the maps A, B, S or T is a closed subset of X.
Then pairs (A, S) and (B, T) have coincidence point. Further if (A, S) and (B, T) be weakly compatible pairs of self maps of fuzzy metric space (X, M, *) then A, B, S and T have a unique common fixed point in X.
Proof: If the pair (B,T) satisfies the property (E.A.), then there exist a sequence {xn} in X such that
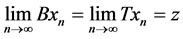 for some
for some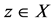 .
.
Since, 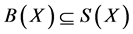 , therefore, there exist a sequence {yn} in X such that
, therefore, there exist a sequence {yn} in X such that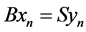 . Hence,
. Hence,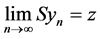 . Also, since
. Also, since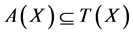 , there exist a sequence
, there exist a sequence 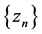 in X such that
in X such that . Hence,
. Hence,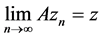 .
.
Suppose that S(X) is a closed subset of X. Then z = Su for some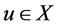 . Therefore,
. Therefore,
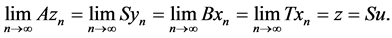
We first claim that Au = z.
If Au ≠ z, then there exist t0 > 0 such that
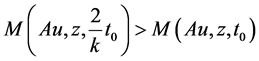 . (3.5)
. (3.5)
The inequality (3.5) is always true when Au ≠ z. To support our claim, we suppose on contrary that (3.5) is not true all t > 0, i.e.,
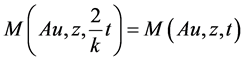 . (3.6)
. (3.6)
Now, using equality (3.6) repeatedly, we get
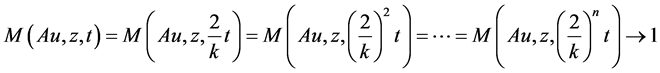
as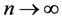 . This gives,
. This gives, 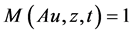 for all t > 0. Hence, Au = z, which gives contradiction.
for all t > 0. Hence, Au = z, which gives contradiction.
Therefore, inequality (3.5) is always true for some t0 > 0.
Using (3.1), take x = u, y = yn, we get
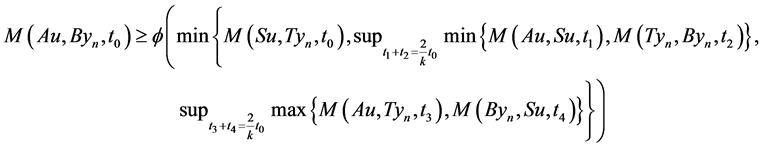
let 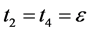 then
then 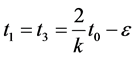 where
where 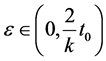 and
and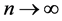 , we get
, we get

As , we get
, we get
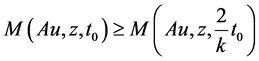
which gives contradiction, hence Au = z.
Therefore, Au = z = Su which shows that u is a coincidence point of the pair (A, S). As A and S are weakly compatible. Therefore, ASu = SAu and then AAu = ASu = SAu = SSu.
On the other hand, since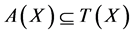 , there exist v in X such that Au = Tv.
, there exist v in X such that Au = Tv.
Now, we show that Bv = z.
If Bv ≠ z, then again, as done above, there exist t0 > 0 such that
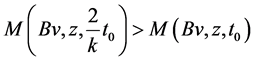 . (3.7)
. (3.7)
The inequality (3.7) is always true when Bv ≠ z.
Using (3.1), take x = u, y = v, we have
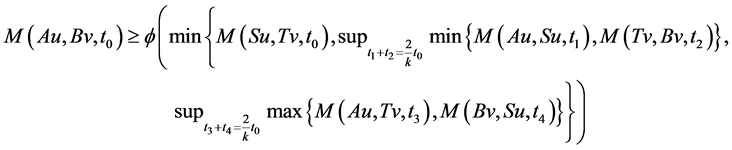
let 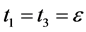 then
then 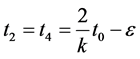 where
where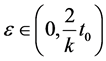 , we get
, we get
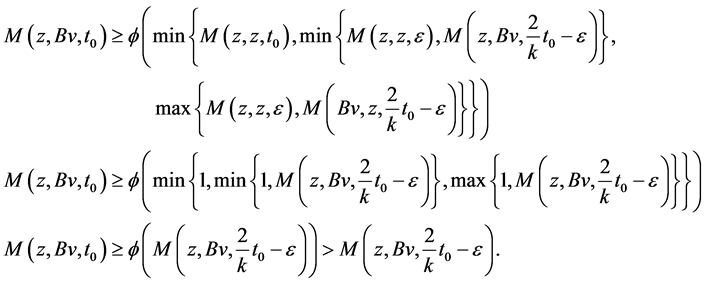
As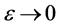 , we get
, we get
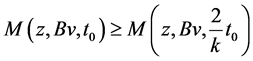
which gives contradiction, hence Bv = z.
Therefore, Bv = z = Au = Tv which shows that Bv = Tv, i.e., v is a coincidence point of the pair (B, T). As B and T are weakly compatible, therefore, BTv = TBv and hence, BTv = TBv = TTv = BBv.
Next, we show that AAu = Au, if not, then again as done above, there exist t0 > 0 such that
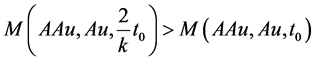 . (3.8)
. (3.8)
Using (3.1), take x = Au, y = v, we have
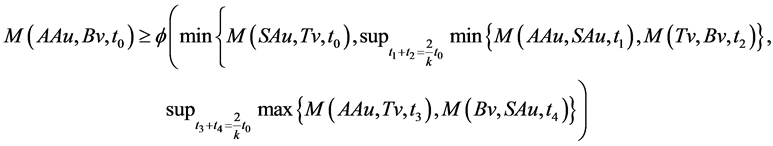
let 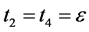 then
then 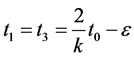 where
where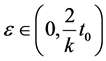 , we get
, we get
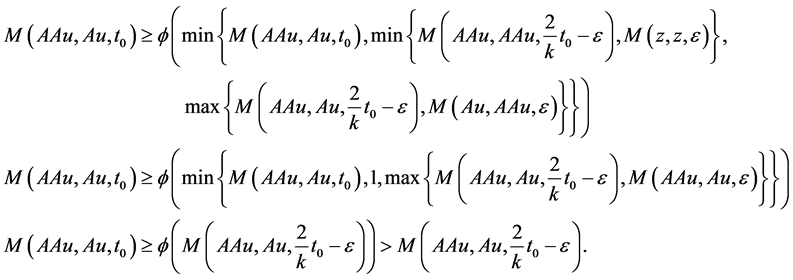
As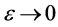 , we get
, we get 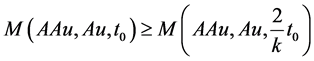 which gives contradiction, hence AAu = Au.
which gives contradiction, hence AAu = Au.
Therefore, AAu = Au = SAu and Au are a common fixed point of A and S. Similarly, we can prove that Bv is a common fixed point of B and T. As Au = Bv, we conclude that Au is a common fixed point of A, B, S and T.
The proof is similar when T(X) is assumed to be a closed subset of X. The cases in which A(X) or B(X) is a closed subset of X are similar to the cases in which T(X) or S(X) respectively, is closed since
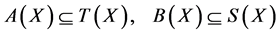 .
.
For uniqueness; let w be another fixed point of A, B, S and T. Then by (3.1), we have
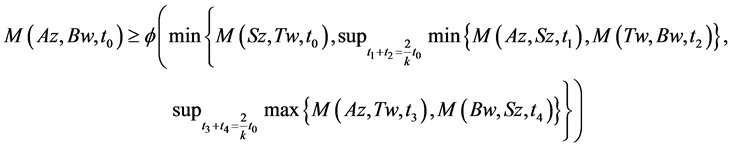
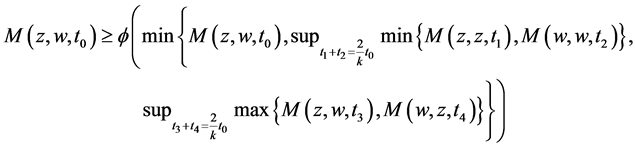
let 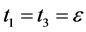 then
then 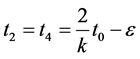 where
where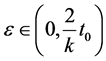 ,
,
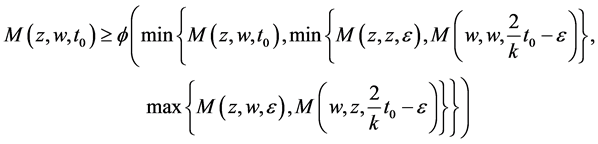
as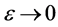 , we get
, we get
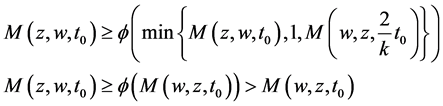
a contradiction, hence, w = z. It implies that A, B, S and T have unique common fixed point in X.
Hence the result.
Now we attempt to drop containment of subspaces by replacing property (E.A.) by a weaker condition common property (E.A.) in Theorem 3.1.
Theorem 3.2: Let A, B, S and T be self mappings of a fuzzy metric space (X, M, *) satisfying condition (3.1) of Theorem 3.1 and the following:
(3.9) the pair (A, S) and (B, T) share the common (E.A.) property;
(3.10) S(X) and T(X) are closed subsets of X.
Then the pairs (A, S) and (B, T) have a point of coincidence each. Moreover, A, B, S and T have a unique common fixed point provided both the pairs (A, S) and (B, T) are weakly compatible.
Proof: In view of (3.2), there exist two sequences {xn} and {yn} in X such that
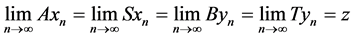
for some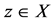 .
.
Since S(X) is a closed subset of X, therefore, there exists a point u in X such that z = Su.
We claim that Au = z. If Au ≠ z, then there exist t0 > 0 such that
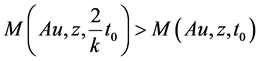 . (3.11)
. (3.11)
The inequality (3.11) is always true when Au ≠ z. To support our claim, we suppose on contrary that (3.11) is not true all t > 0, i.e.,
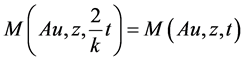 . (3.12)
. (3.12)
Now, using equality (3.12) repeatedly, we get
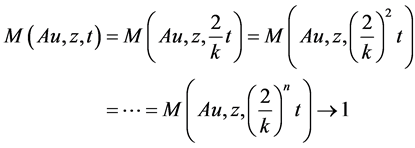
as . This gives,
. This gives, 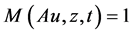 for all t > 0. Hence, Au = z, which gives contradiction.
for all t > 0. Hence, Au = z, which gives contradiction.
Therefore, inequality (3.11) is always true for some t0 > 0. Using (3.1), take x = u, y = yn, we get
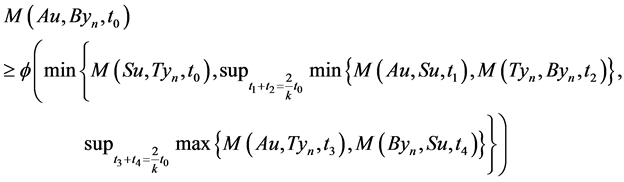
let 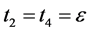 then
then 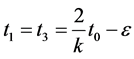 where
where 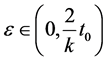 and
and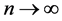 , we get
, we get
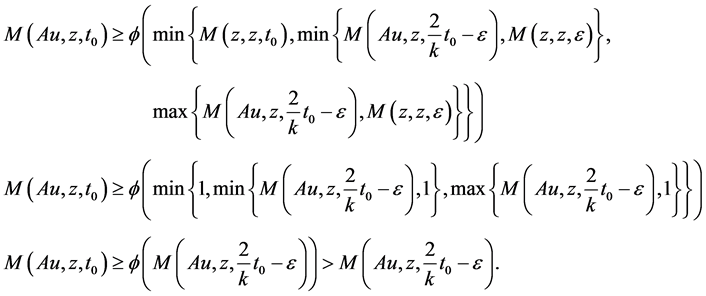
As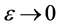 , we get
, we get 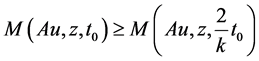 which gives contradiction, hence Au = z.
which gives contradiction, hence Au = z.
Therefore, Au = z = Su which shows that u is a coincidence point of the pair (A, S).
Since T(X) is also a closed subset of X, therefore 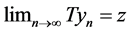 in T(X) and hence there exists v in X such that Tv = z = Au = Su. Now, we show that Bv = z.
in T(X) and hence there exists v in X such that Tv = z = Au = Su. Now, we show that Bv = z.
If Bv ≠ z, then again as done above, there exist t0 > 0 such that
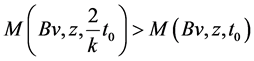 . (3.13)
. (3.13)
The inequality (3.13) is always true when Bv ≠ z.
Using (3.1), take x = u, y = v, we have
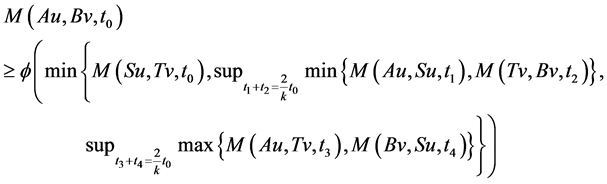
let 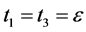 then
then 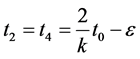 where
where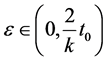 , we get
, we get
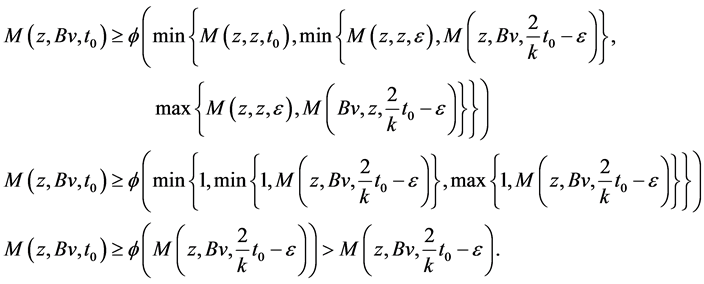
As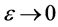 , we get
, we get
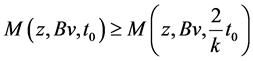
which gives contradiction, hence Bv = z.
Therefore, Bv = z = Tv which shows that v is a coincidence point of the pair (B, T).
Since the pairs (A, S) and (B, T) are weakly compatible and Au = Su, Bv = Tv, therefore, Az = ASu = SAu = Sz, Bz = BTv = TBv = Tz.
If Az ≠ z, then again as done above, there exist t0 > 0 such that
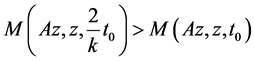 . (3.14)
. (3.14)
Using (3.1), take x = z, y = v, we have
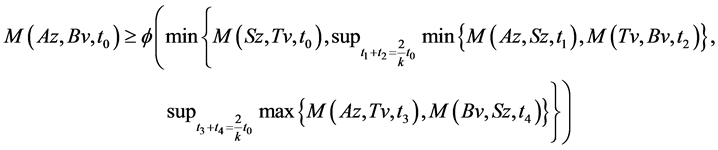
let 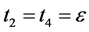 then
then 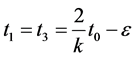 where
where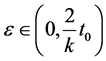 , we get
, we get
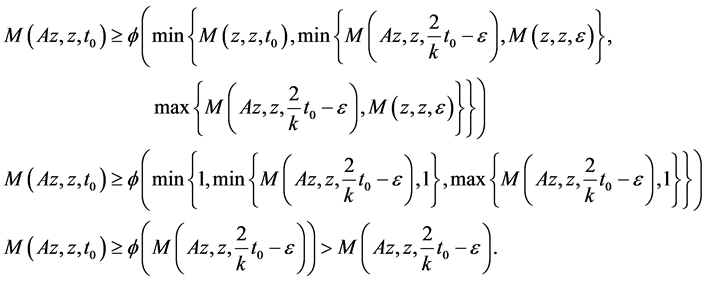
As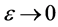 , we get
, we get
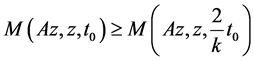
which gives contradiction, hence Az = z.
Therefore, Az = z = Sz.
Similarly, one can prove that Bz = Tz = z. Hence, Az = Bz = Sz = Tz, and z is common fixed point of A, B, S and T.
Uniqueness easily follows by the use of inequality (3.1).
Hence the result.
Now we attempt to drop containment of subspaces by using weaker condition JCLRST property in Theorem 3.2.
Theorem 3.3: Let A, B, S and T be four selfmaps in fuzzy metric space 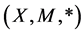 satisfying condition (3.1) of Theorem 3.1 and (3.15) (A, S) and (B, T) shares the JCLRST property.
satisfying condition (3.1) of Theorem 3.1 and (3.15) (A, S) and (B, T) shares the JCLRST property.
Then pairs (A, S) and (B, T) have coincidence point. Further if (A, S) and (B, T) be weakly compatible pair of self maps of X then A, B, S and T have a unique common fixed point in X.
Proof: The pairs (A, S) and (B, T) satisfy the (JCLRST) property, then there exist two sequences {xn} and {yn}
in X such that 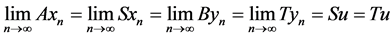 for some
for some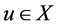 .
.
Firstly, we claim that Tu = Bu. Suppose not, then there exist t0 > 0 such that
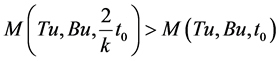 . (3.16)
. (3.16)
The inequality (3.16) is always true when Tu ≠ Bu. To support our claim, we suppose on contrary that (3.16) is not true all t > 0, i.e.,
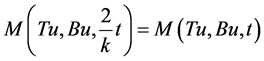 (3.17)
(3.17)
Now, using equality (3.17) repeatedly, we get
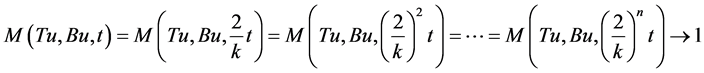
as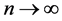 . This gives,
. This gives, 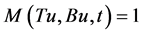 for all t > 0. Hence, Tu = Bu, which gives contradiction.
for all t > 0. Hence, Tu = Bu, which gives contradiction.
Therefore, inequality (3.16) is always true for some t0 > 0.
Using (3.1), take x = xn, y = u, we get
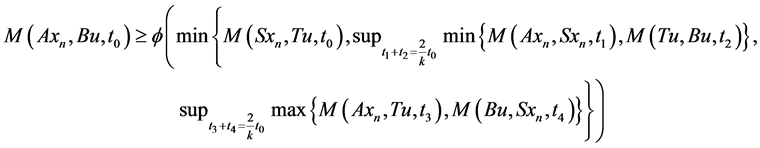
let 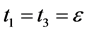 then
then 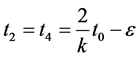 where
where 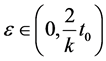 and
and , we get
, we get
As , we get
, we get
which gives contradiction, hence Tu = Bu.
Next, we show that Au = Tu. Suppose not, then again as done above, there exist t0 > 0 such that
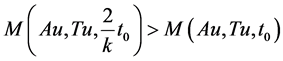 . (3.18)
. (3.18)
Using (3.1), take x = u, y = yn, we get
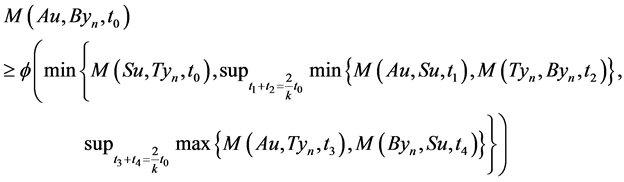
let 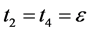 then
then 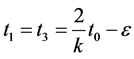 where
where 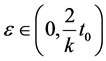 and
and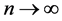 , we get
, we get
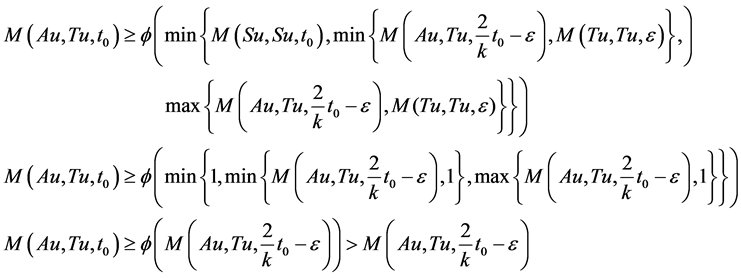
As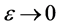 , we get
, we get 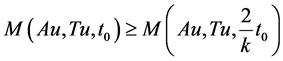 which gives contradiction, hence Au = Tu. Hence, Au
which gives contradiction, hence Au = Tu. Hence, Au
= Bu = Su = Tu = z (say). Since the pair (A, S) is weakly compatible, ASu = SAu and then Az = Sz. Similarly, as the pair (B, T) is weakly compatible, BTu = TBu and then Tz = Bz.
Next, we claim that Az = z, suppose not. Then by (3.1), take x = z, y = u, we get
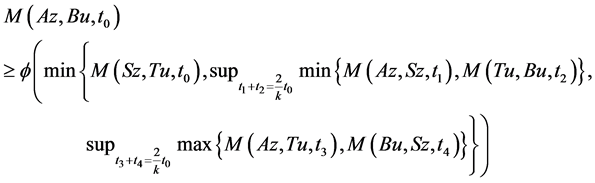
let 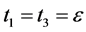 then
then 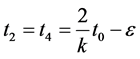 where
where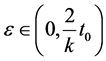 ,
,
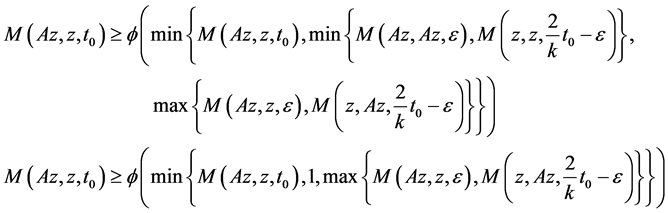
As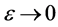 , we get
, we get
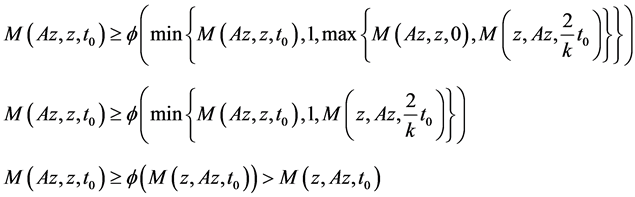
a contradiction, hence, Az = Bz = z. Therefore, z is a common fixed point of A and B. Similarly, we prove that Sz = Tz = z by taking x = u, y = z in (3.1). Therefore, we conclude that z = Az = Bz = Sz = Tz this implies that A, B, S and T have common fixed point in X.
Uniqueness easily follows by the use of inequality (3.1).
Next we attempt to drop closedness of range of maps and relax containment of two subspaces to one subspace by replacing property (E.A.) by a weaker condition CLRS property in Theorem 3.1.
Theorem 3.4: Let A, B, S and T be four selfmaps fuzzy metric space (X, M, *) satisfying condition (3.1) of Theorem 3.1 and
(3.19) (A, S) and (B, T) shares the CLRS property (CLRT property)
(3.20)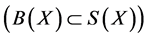
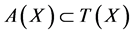 .
.
Then pairs (A, S) and (B, T) have coincidence point. Further if (A, S) and (B, T) be weakly compatible pair of self maps of X then A, B, S and T have a unique common fixed point in X.
Proof: Proof of this theorem easily follows on same lines of Theorem 3.2.
On taking A = B and S = T in Theorem 3.1 then we get the following interesting result which is improved version of Theorem 1 of Sedghi et al. [2] .
Corollary 3.1: Let A and S be self mappings of a fuzzy metric space (X, M, *) satisfying the following:
(3.21)
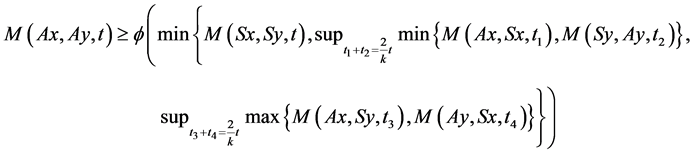
for all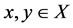 , t > 0 and for some
, t > 0 and for some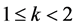 ,
,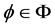 ;
;
(3.22)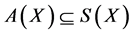 ;
;
(3.23) pair (A, S) satisfies the property (E.A)
(3.24) A(X) or S(X) is a closed subset of X.
Then pair (A, S) has a coincidence point. Further, if pair A and S be weakly compatible self maps of fuzzy metric space (X, M, *), then A and S have a unique common fixed point in X.
On taking A = B and S = T in Theorem 3.4 then we get the following interesting result which is improved version of Theorem 3.3 of Chauhan et al. [3] .
Corollary 3.2: Let A and S be self mappings of a fuzzy metric space (X, M, *) satisfying the following:
(3.25) (A, S) satisfies the CLRS property.
Then pair (A, S) has a coincidence point. Further if pair A and S be weakly compatible self maps of X then A and S has a unique common fixed point in X.
Finally, we conclude this paper by furnishing example to demonstrate Theorem 3.3 besides exhibiting its superiority over earlier relevant results.
Example 3.2. Let 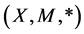 be a fuzzy metric space where a * b = a. b for all
be a fuzzy metric space where a * b = a. b for all 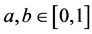 and X = [3, 19). Let
and X = [3, 19). Let 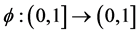 be defined as
be defined as 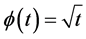 for all
for all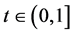 , Clearly,
, Clearly,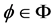 . Define A, B, S and T by
. Define A, B, S and T by
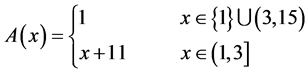 ,
, 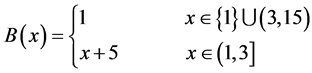 ,
,
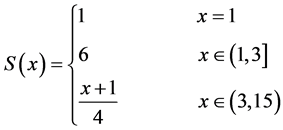
and
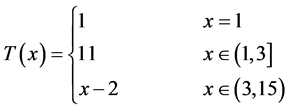 .
.
Take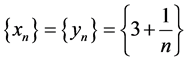 , clearly
, clearly
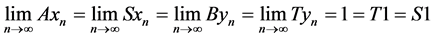
for some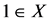 .
.
Thus, (A, S) and (B,T) satisfies JCLRST property.
Also, 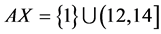 ,
, 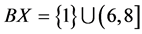 ,
, 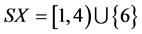 , TX = (1, 13) and condition (3.1) is satisfied by maps A, B, S and T. Thus, the maps A, B, S and T satisfy all conditions of Theorem 3.3. Hence, A, B, S and T have a unique common fixed point x = 1.Moreover it should be noted that AX, BX, SX and TX are not closed subsets of X. Also,
, TX = (1, 13) and condition (3.1) is satisfied by maps A, B, S and T. Thus, the maps A, B, S and T satisfy all conditions of Theorem 3.3. Hence, A, B, S and T have a unique common fixed point x = 1.Moreover it should be noted that AX, BX, SX and TX are not closed subsets of X. Also, 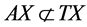 and
and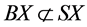 . Also, A, B, S and T are all discontinuous maps at fixed point x = 1.
. Also, A, B, S and T are all discontinuous maps at fixed point x = 1.
Definition 3.1 [21] Two families of self mappings 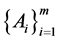 and
and 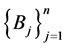 are said to be pairwise commuting if i)
are said to be pairwise commuting if i)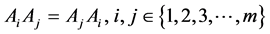 ii)
ii)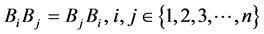 iii)
iii) 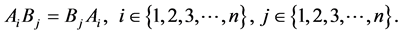
As an application of Theorem 3.2, we prove a common fixed point theorem for four finite families of mappings on fuzzy metric spaces. While proving our result, we utilize Definition 3.1 which is a natural extension of commutativity condition to two finite families.
Theorem 3.4: Let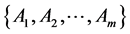 ,
, 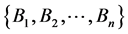 ,
, 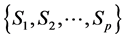 and
and 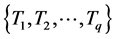 be four finite families of self mappings of a fuzzy metric space (X, M, *) such that
be four finite families of self mappings of a fuzzy metric space (X, M, *) such that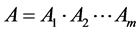 ,
, 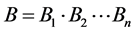 ,
, 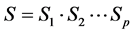 and
and 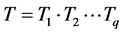 satisfying the conditions (3.1), (3.9), (3.10) and (3.26) the pairs of families
satisfying the conditions (3.1), (3.9), (3.10) and (3.26) the pairs of families 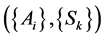 and
and 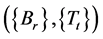 commute pairwise.
commute pairwise.
Then the pairs 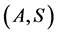 and
and 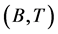 have a point of coincidence each. Moreover,
have a point of coincidence each. Moreover, 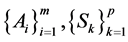 ,
, 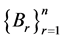 and
and 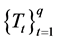 have a unique common fixed point.
have a unique common fixed point.
Proof: By using (3.26), we first show that AS = SA as
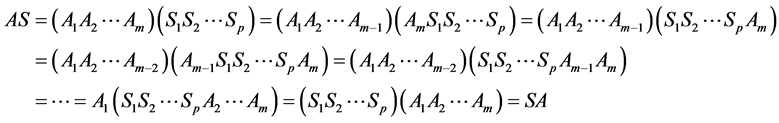 .
.
Similarly one can prove that BT = TB. And hence, obviously the pair (A, S) is compatible and (B, T) is weakly compatible. Now using Theorem 3.1, we conclude that A, S, B and T have a unique common fixed point in X, say z.
Now, one needs to prove that z remains the fixed point of all the component mappings.
For this consider
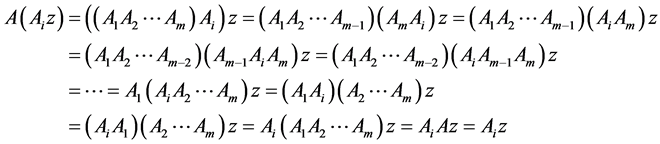 .
.
Similarly, one can prove that
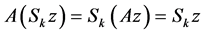 ,
,
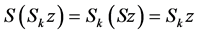 ,
,
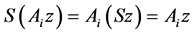 ,
,
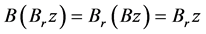 ,
,
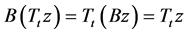 ,
,
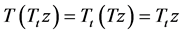
and
 which show that (for all i, r, k and t) Aiz and Skz are other fixed point of the pair (A, S) whereas Brz and Ttz are other fixed points of the pair (B, T). As A, B, S and T have a unique common fixed point, so, we get
which show that (for all i, r, k and t) Aiz and Skz are other fixed point of the pair (A, S) whereas Brz and Ttz are other fixed points of the pair (B, T). As A, B, S and T have a unique common fixed point, so, we get
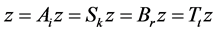 for all
for all 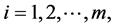
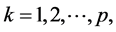
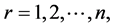
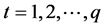 . which shows that z is a unique common fixed point of
. which shows that z is a unique common fixed point of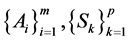 ,
, 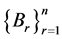 and
and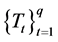 .
.
Remark 3.2: Theorem 3.4 is a slight but partial generalization of Theorem 3.2 as the commutativity requirements in this theorem are slightly stronger as compared to Theorem 3.1.
Remark 3.3. From the above results, it is asserted that for the existence of common fixed point of two pairs of self maps in fuzzy metric spaces satisfying JCLRST property the following conditions are never required:
a) the containment of ranges amongst the involved maps;
b) the completeness of the whole space/subspace;
c) the closedness of space/subspaces;
d) continuity requirement amongst the involved maps.
Acknowledgements
The first author wishes to thank Dr. B. E. Rhoades, Dr. Sanjay Kumar and Dr. S. S. Bhatia and the referees for their very helpful suggestions and many kind comments. The second author wishes to thank DSR, Jizan University, Saudi Arabia for financial support for the publication of this research.
References
- Chauhan, S., Bhatnagar, S. and Radenovic, S. (2013) Common Fixed Point Theorem for Weakly Compatible Mappings in Fuzzy Metric Spaces. Le Matematiiche, 68, 87-98.
- Sedghi, S., Shobe, N. and Aliouche, A. (2010) A Common Fixed Point Theorem for Weakly Compatible Mappings in Fuzzy Metric Spaces. General Mathematics, 18, 3-12.
- Aamri, M. and El Moutawakil, D. (2002) Some New Common Fixed Point Theorems under Strict Contractive Conditions. Journal of Mathematical Analysis and Applications, 270, 181-188. http://dx.doi.org/10.1016/S0022-247X(02)00059-8
- Chauhan, S., Sintunavarat, W. and Kumam, P. (2012) Common Fixed Point Theorems for Weakly Compatible Mappings in Fuzzy Metric Spaces Using (JCLR) Property. Applied Mathematics, 3, 976-982. http://dx.doi.org/10.4236/am.2012.39145
- Fang, J.X. and Gao, Y. (2009) Common Fixed Point Theorems under Strict Contractive Conditions in Menger Spaces. Nonlinear Analysis, 70, 184-193. http://dx.doi.org/10.1016/j.na.2007.11.045
- George, A. and Veeramani, P. (1994) On Some Results in Fuzzy Metric Spaces. Fuzzy Sets and Systems, 64, 395-399. http://dx.doi.org/10.1016/0165-0114(94)90162-7
- Grabiec, M. (1988) Fixed Points in Fuzzy Metric Spaces. Fuzzy Sets and Systems, 27, 385-389. http://dx.doi.org/10.1016/0165-0114(88)90064-4
- Gregori, V., Morillas, S. and Sapena, A. (2011) Examples of Fuzzy Metrics and Applications. Fuzzy Sets and Systems, 170, 95-111. http://dx.doi.org/10.1016/j.fss.2010.10.019
- Kramosil, I. and Michalek, J. (1975) Fuzzy Metric and Statistical Spaces. Kybernetica, 11, 336-344.
- Kumar, S. and Fisher, B. (2010) A Common Fixed Point Theorem in Fuzzy Metric Space Using Property (E. A.) and Implicit Relation. Thai Journal of Mathematics, 8, 439-446.
- Mihet, D. (2010) Fixed Point Theorems in Fuzzy Metric Spaces Using Property E.A. Nonlinear Analysis, 73, 2184- 2188. http://dx.doi.org/10.1016/j.na.2010.05.044
- Shostak, A.P. (1989) Two Decades of Fuzzy Topology; Basic Ideas, Notions and Results. Russian Math Surveys, 44, 123-186. http://dx.doi.org/10.1070/RM1989v044n06ABEH002295
- Sintunavarat, W. and Kumam, P. (2011) Common Fixed Point Theorems for a Pair of Weakly Compatible Mappings in Fuzzy Metric Spaces. Journal of Applied Mathematics, 2011, Article ID: 637958.
- Liu, W., Wu, J. and Li, Z. (2005) Common Fixed Points of Single-Valued and Multivalued Maps. International Journal of Mathematics and Mathematical Sciences, 19, 3045-3055. http://dx.doi.org/10.1155/IJMMS.2005.3045
- Manro, S., Kumar, S. and Bhatia, S.S. Common Fixed Point Theorems in Fuzzy Metric Spaces Using Common Range Property. Journal of Advanced Research in Applied Mathematics.
- Zadeh, L.A. (1965) Fuzzy Sets. Information and Control, 8, 338-353. http://dx.doi.org/10.1016/S0019-9958(65)90241-X
- Menger, K. (1942) Statistical Metrics. Proceedings of the National Academy of Sciences (USA), 28, 535-537. http://dx.doi.org/10.1073/pnas.28.12.535
- Schweizer, B. and Sklar, A. (1983) Probabilistic Metric Spaces. Amsterdam.
- Jungck, G. (1986) Compatible Mappings and Common Fixed Points. International Journal of Mathematics and Mathematical Sciences, 9, 771-779. http://dx.doi.org/10.1155/S0161171286000935
- Jungck, G. and Rhoades, B.E. (1998) Fixed Points for Set Valued Functions without Continuity. Indian Journal of Pure and Applied Mathematics, 29, 227-238.
NOTES

*Corresponding author.

