Applied Mathematics
Vol.5 No.5(2014), Article ID:44066,9 pages DOI:10.4236/am.2014.55076
Application of Multiple Linear Regression and Manova to Evaluate Health Impacts Due to Changing River Water Quality
Sudevi Basu1, K. S. Lokesh2
1Department of Biotechnology, Sir M. Visvesvaraya Institute of Technology, Bangalore, India
2Department of Environmental Engineering, Sri Jayachamarajendra College of Engineering (Autonomuos), Mysore, India
Email: sudevi@rediffmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 November 2013; revised 20 December 2013; accepted 7 January 2014
ABSTRACT
Rivers are important systems which provide water to fulfill human needs. However, excessive human uses over the years have led to deterioration in quality of river causing, causing health problems from contaminated water. This study focuses on the application of statistical techniques, Multiple Linear Regression model and MANOVA to assess health impacts due to pollution in Cauvery river stretch in Srirangapatna. In this study, using Multiple Linear Regression, it is found that health impact level is 60.8% dependent on water quality parameters of BOD, COD, TDS, TC and FC. The t-statistics and their associated 2-tailed p-values indicate that COD and TDS produces health impacts compared to BOD, TC and FC, when their effects are put together across all the six sampling stations in Srirangapatna. Further Pearson correlation Matrix shows highly significant positive correlation amongst parameters across all stations indicating possibility of common sources of origin that might be anthropogenic. Also graphs are plotted for individual parameters across all stations and it reveals that COD and TDS values are significant across all sampling stations, though their values are higher in impact stations, causing health impacts.
Keywords:Multiple Linear Regression Model; MANOVA; t-Statistics; BOD; COD; TDS; TC; FC

1. Introduction
River systems form the lifeline on which human civilization thrives. These are vital freshwater bodies of strategic importance across the world, providing main water resources for domestic, industrial, agricultural and recreational purposes. Rivers play a major role in assimilating industrial and municipal wastewater and runoff from agricultural fields. However, in recent years, rivers are amongst the most vulnerable water bodies to pollution as a consequence of unprecedented development. Thus the water quality of these water resources is a subject of ongoing concern and has resulted in an increasing demand for monitoring river water quality. The quality of water is described by its physical, chemical and microbiological characteristics. Therefore, a regular monitoring of river water quality not only prevents outbreak of diseases and checks water from further deterioration, but also provides a scope to assess the current pollution prevention and control measures.
In this study, Multiple Regression Analysis and MANOVA are applied to find the chemical and biological parameters that affect health of people in Cauvery river stretch in Srirangapatna town in Karnataka.
2. Materials and Methods
2.1. Study Area
Srirangapatna is an island town, situated between the North and South branches of river Cauvery. It is located to the northeast of Mysore city at a distance of 15 Kms on the Bangalore—Mysore highway. The town has developed in two areas consisting of Patna area, which is like an urban area, and Ganjam, which resembles a typical village.
Though it is a town of medium population, the temples and historically significant monuments of this town attracts a large number of tourist people resulting in a very high floating population. Because of this reason the river Cauvery along Srirangapatna town stretch is prone to anthropogenic activities such as bathing, washing and disposal of wastes.
River Cauvery in this town divides into two major branches—north branch and south branch. There exists another small stream branch called Paschima Vahini river, almost parallel to south branch. These branches unite at a place called Sangama. The ground level in the town slopes from south branch towards north branch so that most of the storm and sewerage drains discharge into branch of river Cauvery. There are four stream monitoring stations and two drains located in this town stretch. Three of these stations are on the north branch of the river and one station after the point of confluence of these branches. Two bathing ghats exist in this stretch. The stations are shown in Figure 1.
2.2. Monitoring Stations
There are basically three types of monitoring locations for analyzing samples. These are the baseline, impact and
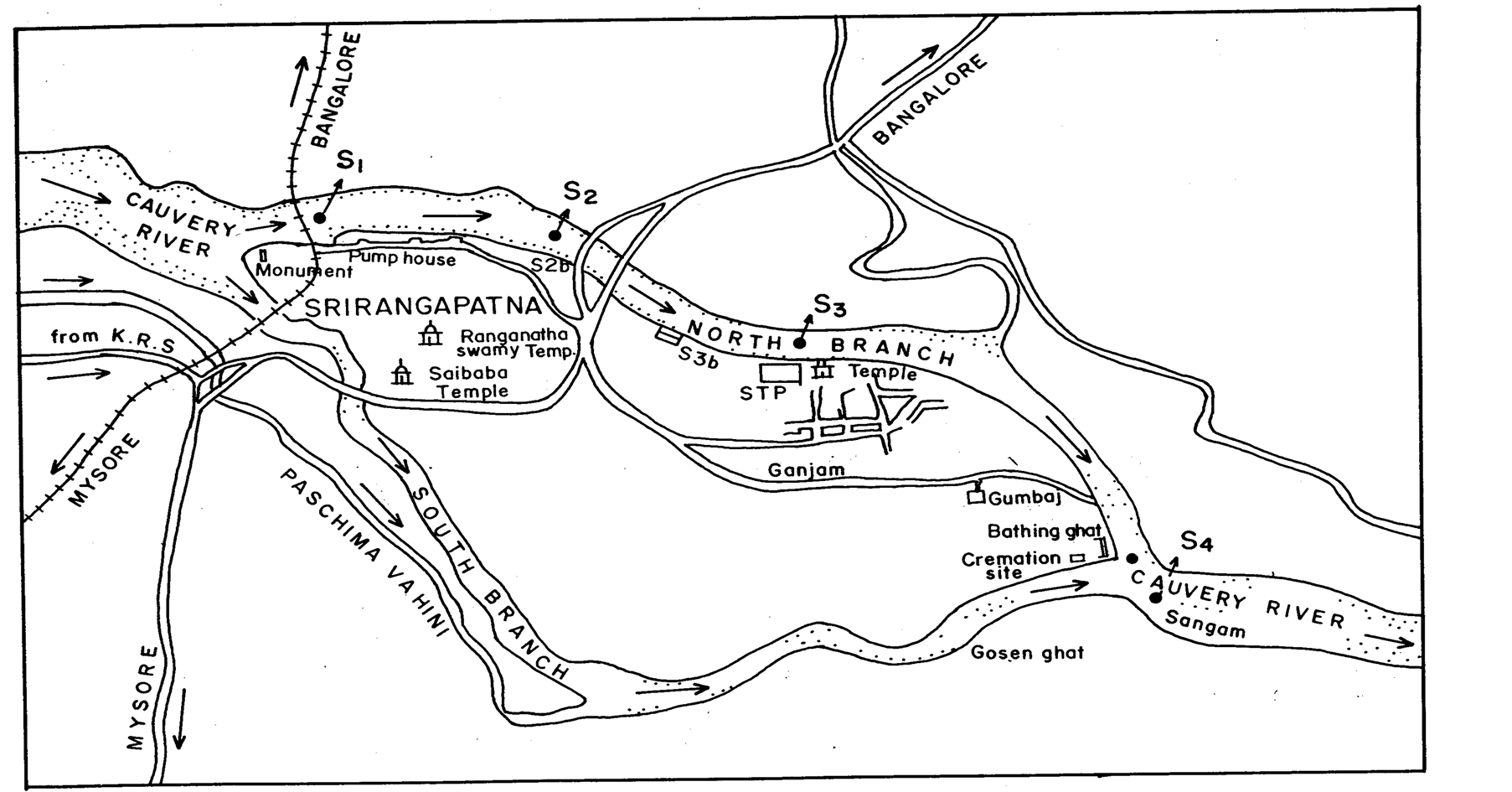
Figure 1.Map of water quality monitoring stations at Srirangapatna town.
trend stations. Baseline locations are concerned with natural and unpolluted state of the river basin. In these stations there is no influence of human activities on water quality. Impact stations are used for measuring the quantity of pollutant and extent of pollution due to human interference. The trend stations show how a particular point on the water course varies over time due to the influence of human activities. These stations not located on main river systems are sited on major tributaries and points just upstream of confluence with the main river.
2.2.1. Baseline Stations—S1 and S2a
Station S1 is located on the north branch of the river, near the Bangalore—Mysore railway bridge. It is an upstream station and near this station water is being drawn for supply to the town. The station S2a is located at a distance of about 150 m upstream of the Wellesly road bridge on the north branch of the river. This station is about 300 m downstream of station S1.
2.2.2. Impact Stations—S2b and S3b
The station S2b is located on a drain that enters the river from the right bank just downstream of S2a. The flow in the drain is mainly comprised of sullage from Srirangapatna town. The station S3b is located on a relatively small drain that enters the river downstream of station S3a. The flow in the drain comprises mainly of wastewater from Ganjam village area of the town.
2.2.3. Trend Stations—S3a and S4
The station S3a is an impact station and is positioned near the Nimishamba temple. It is downstream of the sewage disposal point, approximately 500 m from the station S2a. A bathing ghat exists near this Station. Station S4 is a downstream station, located after the confluence of the north and south branches of the river Cauvery. A bathing ghat exists upstream of this station.
2.3. Data Preparation
The data sets of 6 water quality monitoring stations of Srirangapatna is obtained from the water Quality Monitoring work of Cauvery River Basin in Mysore District, Karnataka State assigned to Sri Jayachamarajendra College of Engineering, Mysore under a nationwide River Water Quality Monitoring Project of the National River Conservation Directorate (NRCD), Ministry of Environment and Forests, Government of India, under its National River Conservation Project (NRCP). The data comprising of 5 selected water quality parameters, monitored monthly over 12 years (2000-2011), include Biochemical Oxygen Demand (BOD), Chemical Oxygen Demand (COD), Total Dissolved Solids (TDS), Total Coliform (TC) and Faecal Coliform (FC). These parameters are chosen as these determine the impact of pollution with respect to health of people.
2.4. Multiple Linear Regression and MANOVA
Multiple linear regressions is a statistical tool for understanding the relationship between a dependent variable and one or more independent variables ([1] -[5] ). According to the researchers, Multiple linear regressions can be expressed using the equation:
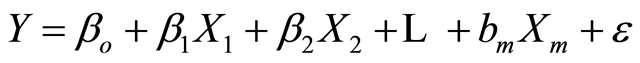 (1)
(1)
where Y represent the dependent variable;
X1, ×××, Xm represent the several independent variables;
β0, ×××, βm represent the regression coefficient and;
ε represent the random error.
Multivariate analysis of variance (MANOVA) is simply an ANOVA with several dependent variables.
MANOVA deals with the multiple dependent variables by combining them in a linear manner to produce a combination which best separates the independent variable groups. MANOVA is applied by researchers in water quality assessment ([6] [7] ).
3. Results and Discussions
In the present study, Multiple Linear Regression analysis and MANOVA were applied to the five parameters (BOD, COD, TDS, TC and FC) for 12 years at six different sampling stations in Srirangapatna, each station consisting of 60 data. The data was analyzed using SPSS version 19, Software Package. The table 1 shows the R2 value which gives the percentage of variability in the Dependent Variable accounted by all the Independent Variables together. In this study the percentage of dependent variable is 60.8 % and accounts for all the independent variables (BOD, COD, TDS, TC and FC) of the six sampling stations (Baseline S1 and Baseline S2a, Impact S2b and Impact S3b and Trend S4 and Trend S3a). This is an overall measure of the strength of association and does not reflect the extent to which any particular independent variable is associated with the dependent variable.
The table 2 gives the F-test to determine whether the model is a good fit for the data. According to this, p-value of the F-test is used to see if the overall model is significant. The p-value is compared to alpha level of 0.05 in testing the null hypothesis that all of the model coefficients are 0. The null hypothesis is not accepted as p-value is smaller than 0.05.
The table 3 gives the β coefficients, one to go with each predictor. The “unstandardized coefficients” are used because the constant β0 is included. Also standardization of the coefficient is usually done to find which of the independent variables have a greater effect on the dependent variable in a multiple regression analysis, when the variables are measured in different units of measurement. Standardizing a variable removes the unit of measurement from its value, a standardized coefficient for a given relationship only represents its strength relative to the variation in the distributions. This invites bias due to sampling error when one standardizes variables using means and standard deviations based on small samples. Based on this table, using unstandardized coefficients, the equation (1) for the regression line for this study is:
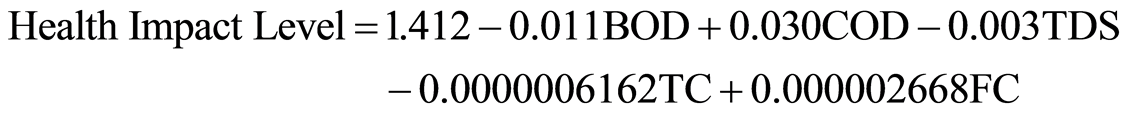 (2)
(2)
In table 3, it is seen from the unstandardized coefficient that for every unit increase in BOD, -0.011 unit decrease in the Health Impact Level is predicted, holding all other variables constant. Similarly, for every unit increase in COD, a 0.030 unit increase in Health Impact Level is predicted, holding all other variables constant. Also for every unit increase in TDS, a 0.003 unit decrease in the Health Impact Level is predicted, holding all other variables constant. Further for every unit increase in TC and FC, −0.0000006162 unit decrease and 0.000002668 unit increase, respectively, in the Health Impact Level is predicted, holding all other variables constant. However the actual interpretation is possible by standardizing the variables before running the regression where all the variables are on the same scale, and it is easy to compare the magnitude of the coefficients to see which one has more of an effect. Further it is found that the larger β values are associated with the larger t-values and lower p-values. It is seen from table 3 that COD and FC have positive effects on health impact in the predicted model which is cause for concern as these are indicators of pollution by human activities on water quality. Further the t-statistics and their associated 2-tailed p-values are used in testing whether a given coefficient is significantly different from zero, using an alpha of 0.05. In this study, the parameters BOD, TC and FC are not significantly different from 0 because their p-values are larger than 0.05. However, the parameters COD and TDS are significantly different from 0 because their p-values are smaller than 0.05. Also the intercept is significantly different from 0 at the 0.05 alpha level. This means that three water quality parameters, BOD, TC and FC do not produce significant health impacts while COD and TDS produces health impacts when their effects are put together across all the six sampling stations in Srirangapatna. However individual parameters across all stations can have significant health impacts as seen from table 4.
Table 4 shows the Pearsons Correlation Matrix of the parameters across Baseline, Trend and Impact stations in Srirangapatna. The highly significant positive correlation amongst parameters across all stations indicates possibility of common sources of origin that might be anthropogenic. Similar study on correlation analysis was carried out on physico-chemical parameters by researcher [7] .
The Multivariate Tests table gives the actual result of the one-way MANOVA. To determine whether the one-way MANOVA was statistically significant, Wilks' Lambda row needs to be looked at along with the Significance column. Wilk’s lambda is a measure of how well each function separates cases into groups. It is equal to the proportion of the total variance in the discriminate scores not explained by differences among the groups. Smaller values of Wilk’s lambda tests indicate greater discriminatory ability of the function [8] . From the table 5, Wilk’s lambda value of 0.27 with a significance of 0.000 is obtained at p < 0.05. This indicates the health impact level was significantly dependent on BOD, COD, TDS, TC and FC across all sampling stations and exhibits
aPredictors: (Constant), FC, TDS, BOD, COD, TC.
aPredictors: (Constant), FC, TDS, BOD, COD, TC; bDependent variable: health impact level.
aDependent variable: health impact level.
Table 4. Pearson correlation matrix.
good discriminatory ability with the water quality parameters.
To determine how the dependent variables interact with the independent variables, the Tests of BetweenSubjects Effects is shown in table 6. This table clearly shows that there is a significant interaction effect of BOD, COD, TDS, TC and FC with health impact level across all sampling stations in Srirangapatna as p-values are less than 0.05.
Further the significant ANOVAs are determined with LSD post-hoc tests, as shown in the Multiple Comparisons table 7. The table 7 shows that BOD values were statistically significantly different between baseline and impact stations (p < 0.05), trend and impact stations (p < 0.05) and impact and baseline stations as well as impact and trend stations (p < 0.05), but not between baseline and trend stations (p = 0.937). This is because baseline stations describe unpolluted state of river while impact stations measure pollution due to human activities. Trend stations are not located on rivers but on tributaries joining river and show how the water quality varies over time due to human influence. Thus the mean difference between baseline and trend or impact stations is negative whereas the mean difference between impact and baseline or trend stations is positive. Also the mean difference between trend and baseline stations is positive due to the relativity of pollution levels in these stations. Similar trends are observed with other parameters like COD, TDS, TC and FC as well.
The graphs of individual parameters are plotted for all stations using Microsoft Excel 2007 and are shown in figures 2-6. It is seen from figure 2 that the BOD values are less for all 12 years in baseline and trend stations whereas it is more in impact stations. Similar trend is seen with TC and FC in figures 5 and 6 respectively. This is the same trend observed with multiple linear regression where BOD, TC and FC do not produce significant health impacts in combined strength. However, it is seen in figures 3 and 4 that COD and TDS values are significant across all sampling stations, though their values are higher in impact stations. Hence these two parameters produce significant health impacts and is also validated in regression equation.
aExact statistic; bComputed using alpha = 0.05; cThe statistic is an upper bound on F that yields a lower bound on the significance level; dDesign: intercept + health impact level.
aR squared = 0.354 (adjusted R squared = 0.335); bComputed using alpha = 0.05; cR squared = 0.621 (adjusted R squared = 0.610); dR squared = 0.182 (adjusted R squared = 0.159); eR squared = 0.094 (adjusted R squared = 0.068); fR squared = 0.099 (adjusted R squared = 0.072).
Based on observed means. The error term is mean square (error) = 22830394234.140. *The mean difference is significant at the 0.05 level.

Figure 2.Trend of BOD for 12 years across the sampling stations at Srirangapatna.
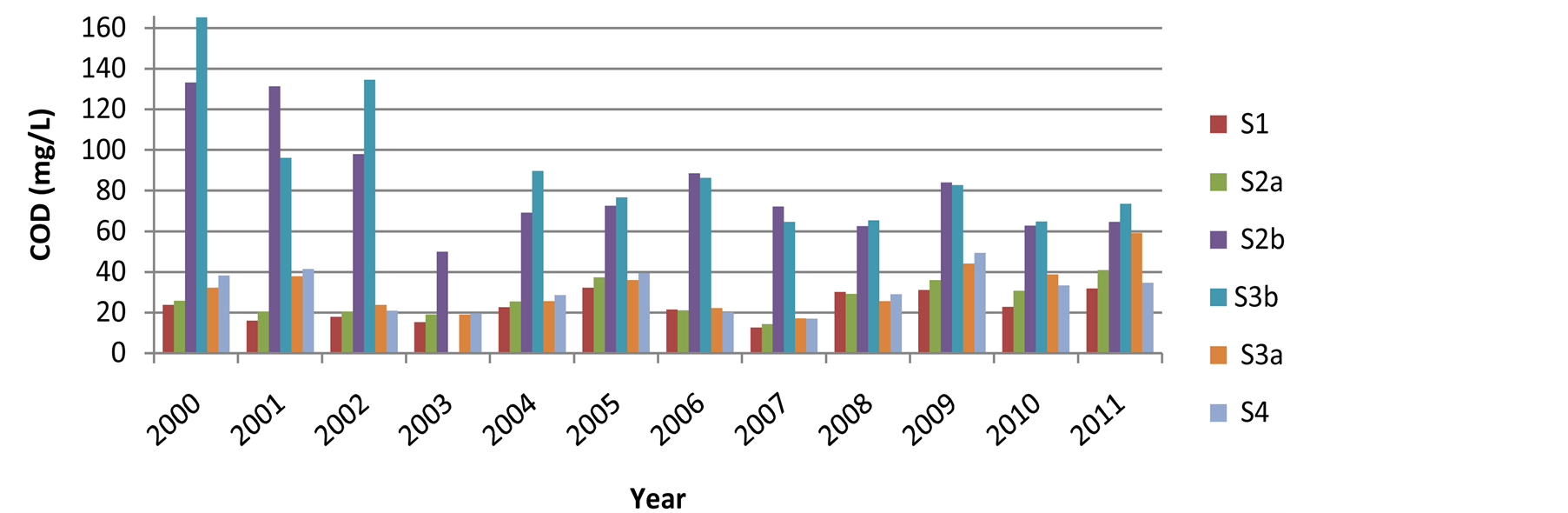
Figure 3.Trend of COD for 12 years across the sampling stations at Srirangapatna.
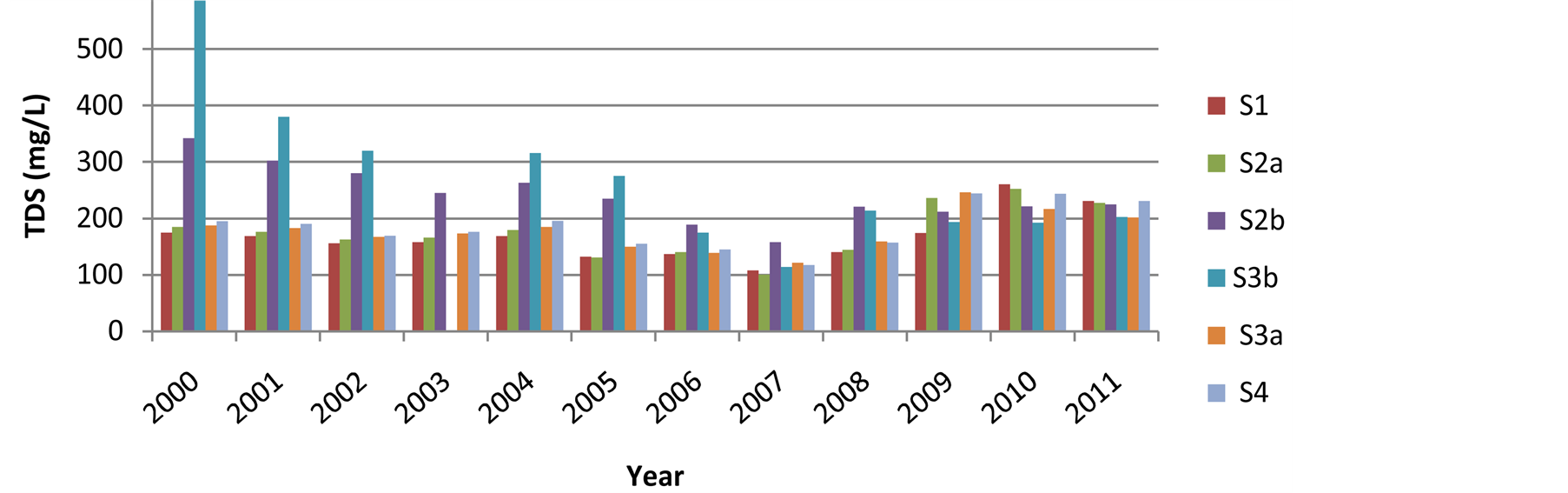
Figure 4.Trend of TDS 12 years across the sampling for stations at Srirangapatna.

Figure 5.Trend of TC for 12 years across the sampling stations at Srirangapatna.
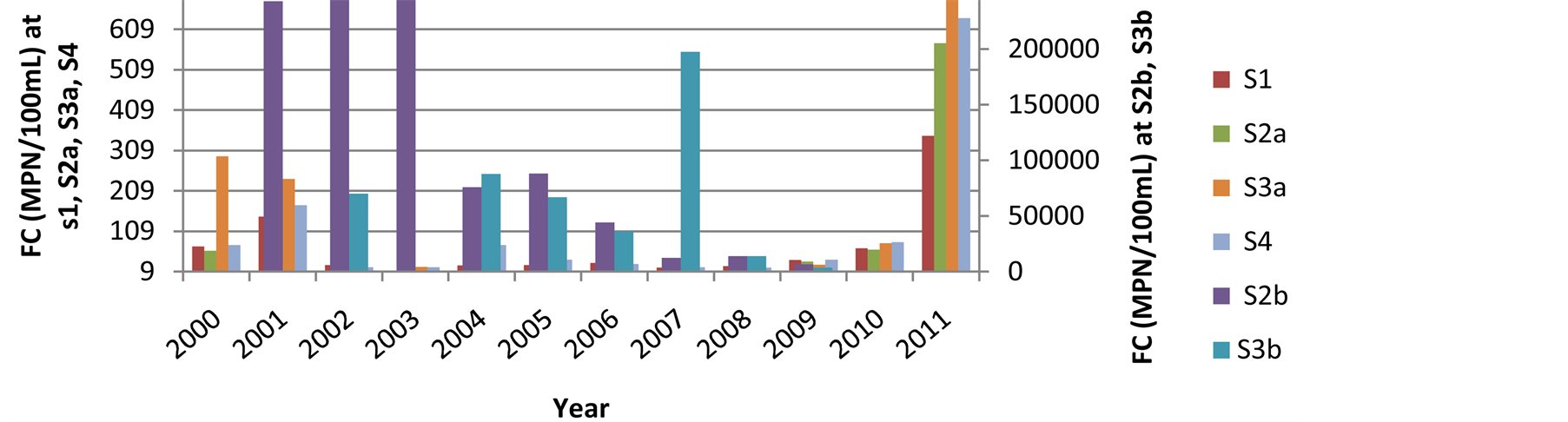
Figure 6.Trend of FC for 12 years across the sampling stations at Srirangapatna.
4. Conclusion
River water pollution is a cause for concern because excessive human uses over the years have led to deterioration in quality of river causing, causing health problems from contaminated water. In this study, using Multiple Linear Regression, it is found that health impact level is 60.8% dependent on water quality parameters of BOD, COD, TDS, TC and FC. The t-statistics and their associated 2-tailed p-values indicate that COD and TDS produces health impacts compared to BOD, TC and FC, when their effects are put together across all the six sampling stations in Srirangapatna. Further Pearson correlation Matrix shows highly significant positive correlation amongst parameters across all stations indicating possibility of common sources of origin that might be anthropogenic. LSD post-hoc tests show that the mean difference of parameters between baseline and trend or impact stations is negative whereas the mean difference between impact and baseline or trend stations is positive. Also the mean difference between trend and baseline stations is positive due to the relativity of pollution levels in these stations. Further graphs are plotted for individual parameters across all stations and it reveals that COD and TDS values are significant across all sampling stations, though their values are higher in impact stations, causing health impacts. Therefore, this research reveals that anthropogenic activities cause water pollution in rivers and this can have serious health impacts and hence pollution must be curtailed to maintain pristine river water quality.
Acknowledgements
The authors thank the National River Conservation Directorate (NRCD), Ministry of Environment and Forests MoEF, Government of India for the financial support under National River Conservation Directorate Project.
References
- Koklu, R., Sengorur, B. and Topal, B. (2010) Water Quality Assessment Using Multivariate Statistical Methods—A Case Study: Melen River System (Turkey). Water Resource Management, 24, 959-978. http://dx.doi.org/10.1007/s11269-009-9481-7
- Mustapha, A. and Abdu, A. (2012) Application of Principal Component Analysis & Multiple Regression Models in Surface Water Quality Assessment. Journal of Environment and Earth Science, 2, 16-23.
- Mustapha, A. and Aris, A.Z. (2012) Multivariate Statistical Analysis and Environmental Modeling of Heavy Metals Pollution by Industries. Polish Journal of Environmental Studies, 21, 1359-1367.
- Pathak, H. (2012) Evaluation of Ground Water Quality Using Multiple Linear Regression and Mathematical Equation Modeling. Annals of the University of Oradea—Geography Series, 2, 304-307.
- Pathak, H. (2013) Water Quality Studies of Two Rivers at Bundelkhand Region, MP, India: A Case Study. U.P.B. Science Bulletin, Series B, 75, 81-90.
- Mohansingh, R., Fernandez, G.C.J. and Dennett, K.E. (2006) Using SAS for Statistical Modeling of Nutrient Removal and Water Quality Aspects from Constructed Wetlands. Statistics and Data Analysis, SUGI 31 Proceedings, 1-11.
- Gyawali, S., Techato, K., Yuangyai, C. and Musikavong, C. (2013) Assessment of Relationship Between Land Uses of Riparian Zone and Water Quality of River for Sustainable Development of River Basin, A Case Study of U-Tapao River Basin, Thailand. The 3rd International Conference on Sustainable Future for Human Security SUSTAIN 2012, Procedia Environmental Sciences, 17, 291-297.
- Eneji, I.S., Onuche, A.P. and Ato, R.S. (2012) Spatial and Temporal Variation in Water Quality of River Benue, Nigeria. Journal of Environmental Protection, 3, 915-921. http://dx.doi.org/10.4236/jep.2012.328106


