Applied Mathematics
Vol.4 No.12A(2013), Article ID:40967,6 pages DOI:10.4236/am.2013.412A002
On the Solutions of Difference Equation Systems with Padovan Numbers*
1Department of Mathematics, Faculty of Science and Art, Nevsehir University, Nevsehir, Turkey
2Department of Mathematics-Computer Sciences, Science Faculty, Necmettin Erbakan University, Konya, Turkey
3Department of Mathematics, Science Faculty, Selcuk University, Konya, Turkey
Email: yyazlik@nevsehir.edu.tr, dttollu@konya.edu.tr, ntaskara@selcuk.edu.tr
Copyright © 2013 Yasin Yazlik et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2013 are reserved for SCIRP and the owner of the intellectual property Yasin Yazlik et al. All Copyright © 2013 are guarded by law and by SCIRP as a guardian.
Received November 1, 2013; revised December 1, 2013; accepted December 8, 2013
Keywords: Rational Difference Equation System; Padovan Numbers; Plastic Number
ABSTRACT
In this study, we investigate the form of the solutions of the following rational difference equation systems 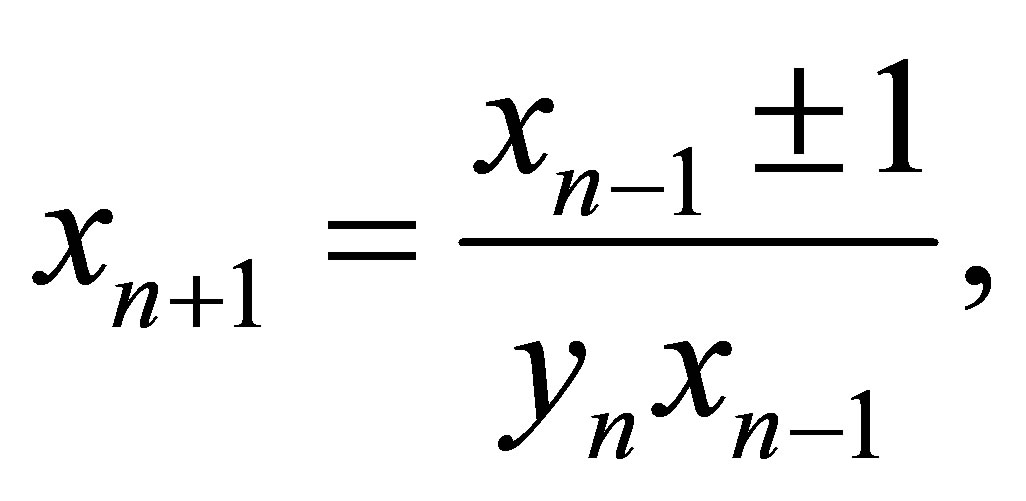
 such that their solutions are associated with Padovan numbers.
such that their solutions are associated with Padovan numbers.
1. Introduction
Nonlinear difference equations have long interested researchers in the field of mathematics as well as in other sciences. They play a key role in many applications such as the natural model of a discrete process. There are many recent investigations and interest in the field of nonlinear difference equations from several authors [1-15]. For example, Tollu et al. [14] investigated the solutions of two special types of Riccati difference equations

such that their solutions are associated with Fibonacci numbers. In [2], Aloqeili investigated the stability properties and semi-cycle behavior of the solutions and the form of solutions of the difference equation
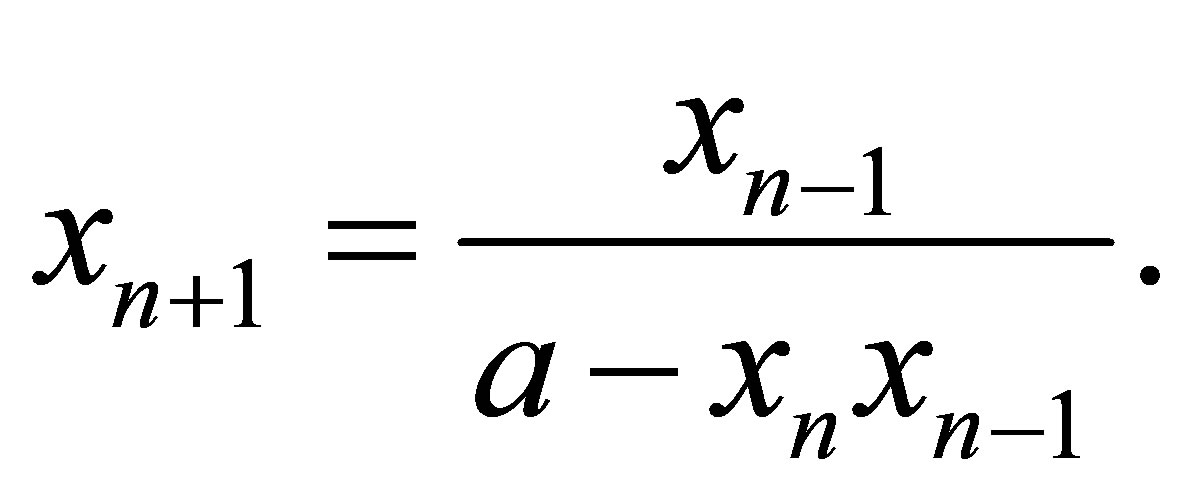
In [4], author obtained the formulae of solutions of the difference equations
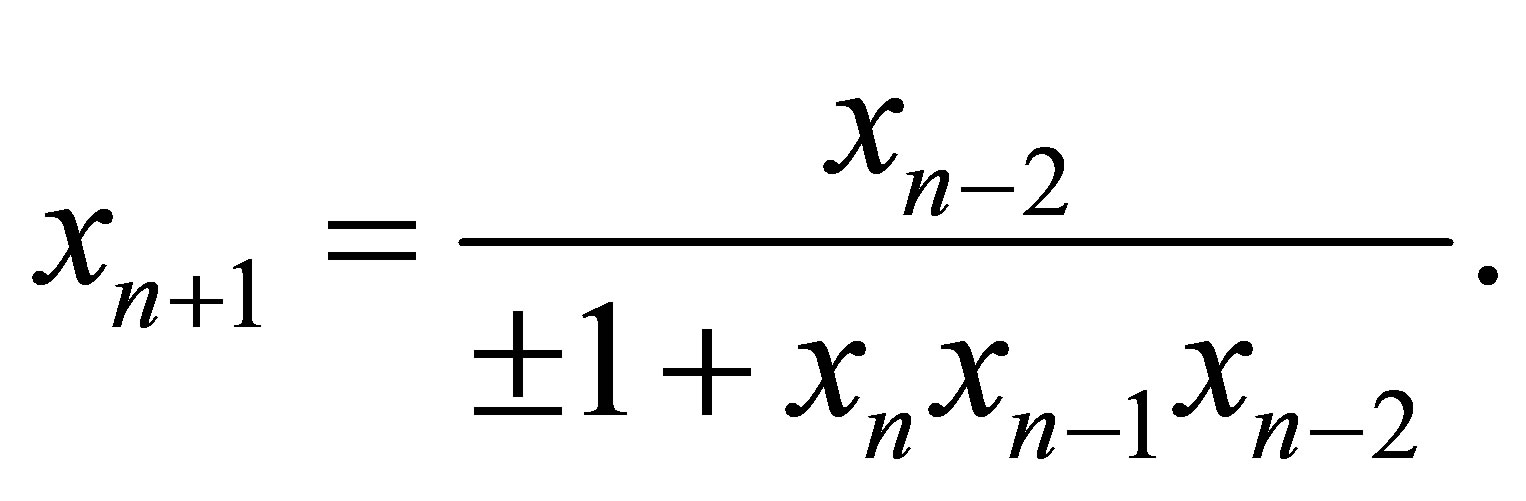
Also, he studied the global asymptotic stability of the equilibrium points of these equations via the formulae. In [5], Elabbasy et al obtained Fibonacci sequence in solutions of some special cases of the following difference equation
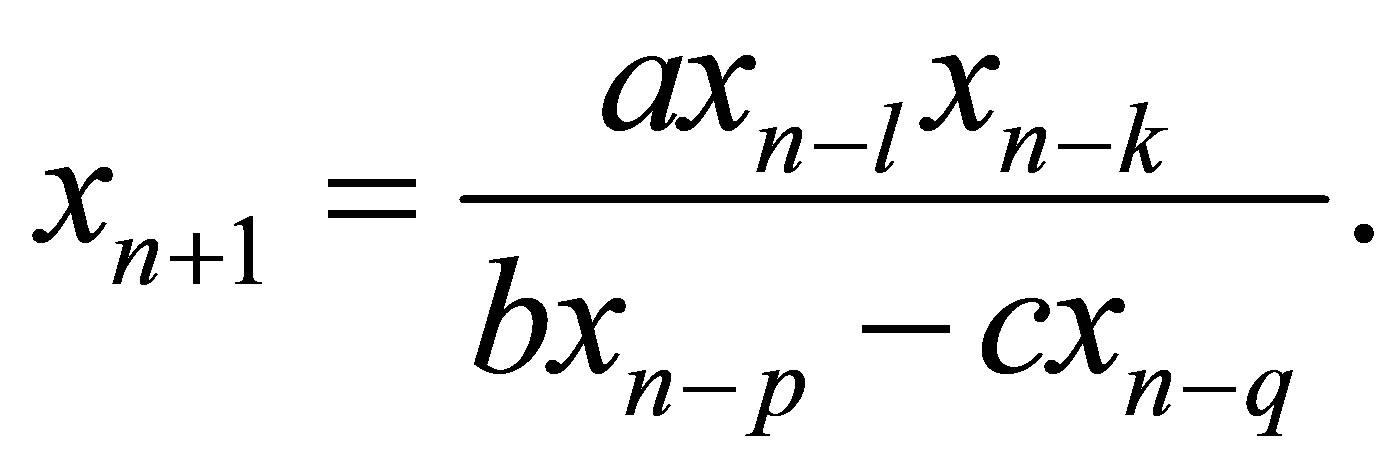
In [6], author deals with the behavior of the solution of the following nonlinear difference equation
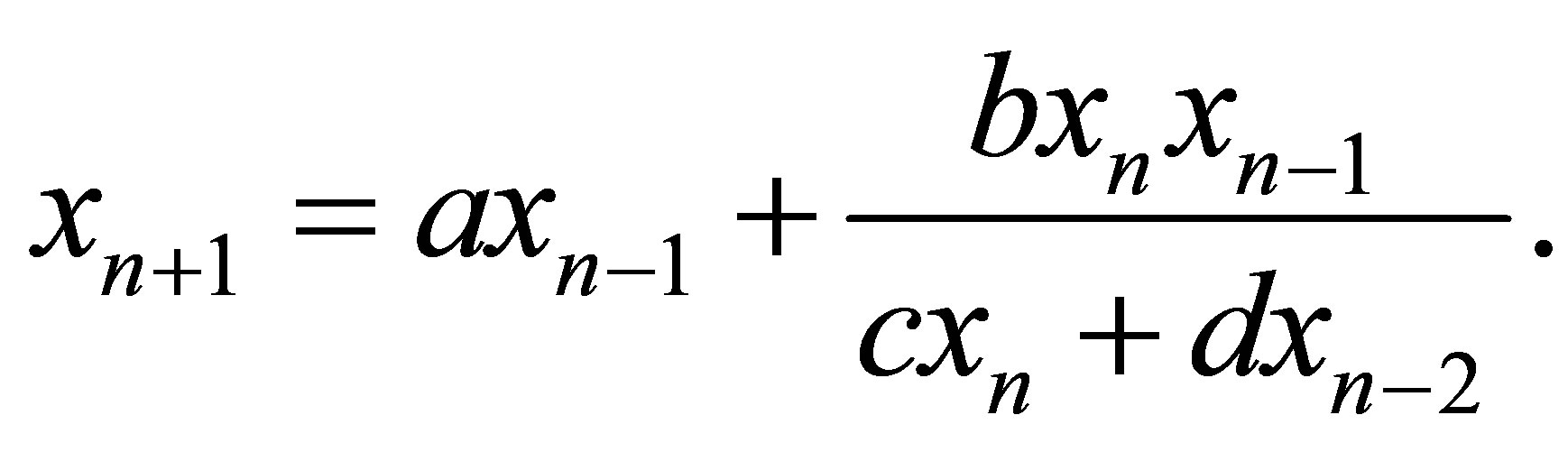
Also, he gives specific forms of the solutions of four special cases of this equation. These specific forms also contain Fibonacci numbers. In [7], Cinar studied the positive solutions of the following difference equation system

In [10], Elsayed obtained the form of the solutions of the following rational difference system

In [12], Stevic examined the solutions of the following system of difference equations

Now, we give information about Padovan numbers that establish a large part of our study. The Padovan sequence , named after Richard Padovan, is defined by
, named after Richard Padovan, is defined by
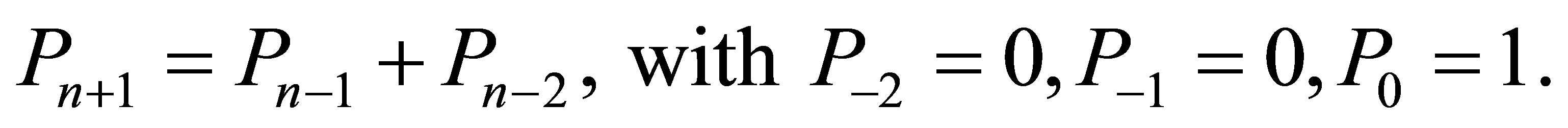 (1.1)
(1.1)
It can be easily obtained that the characteristic equation of (1.1) has the form
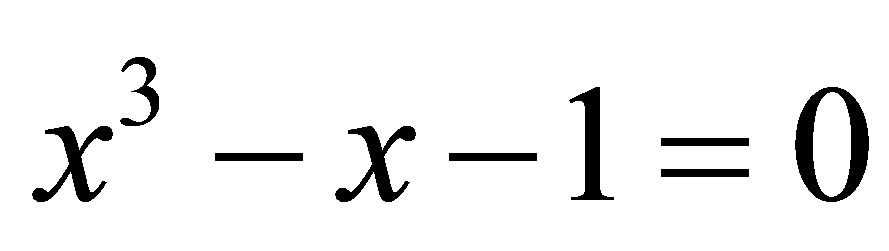 (1.2)
(1.2)
having the roots
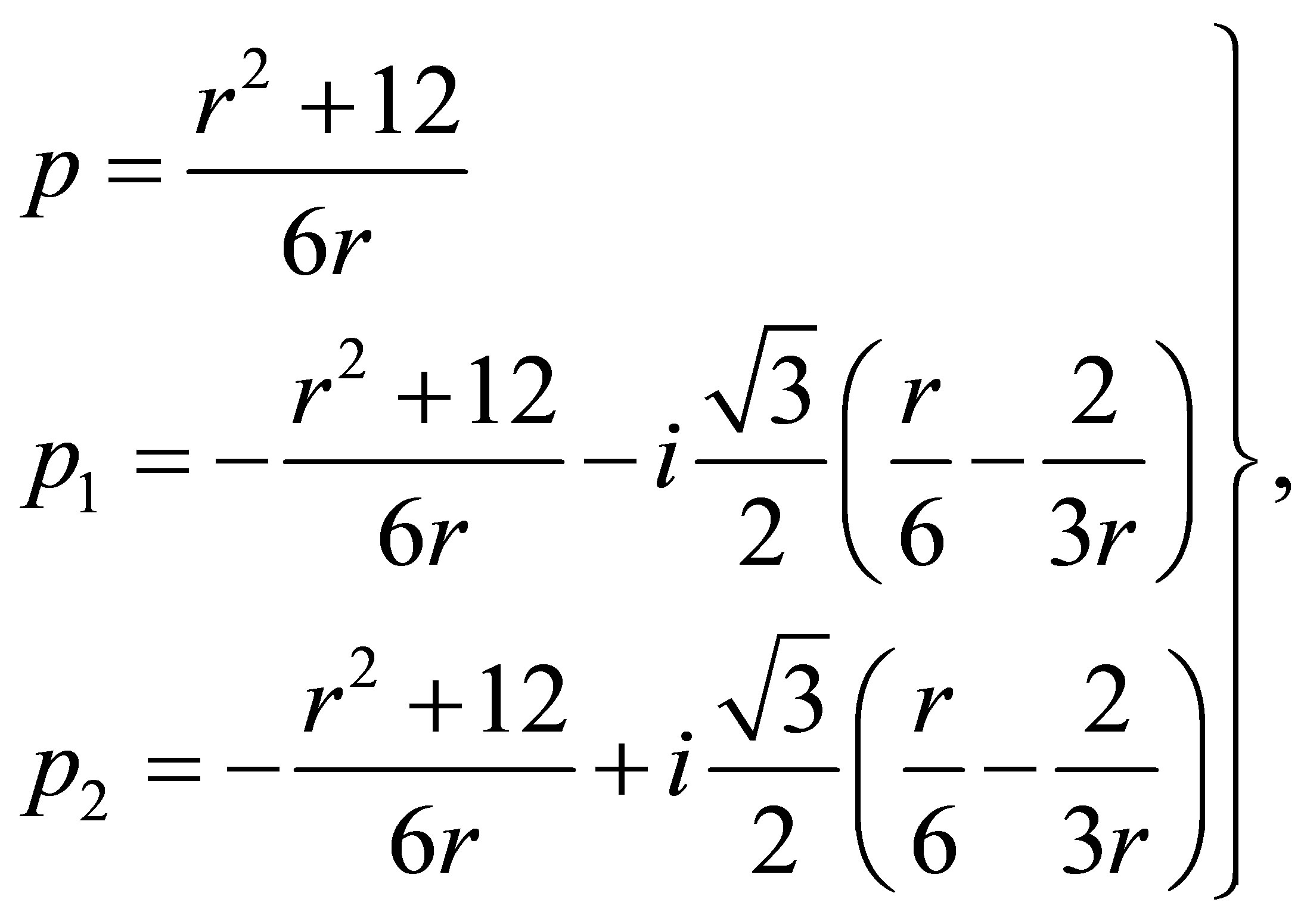
where 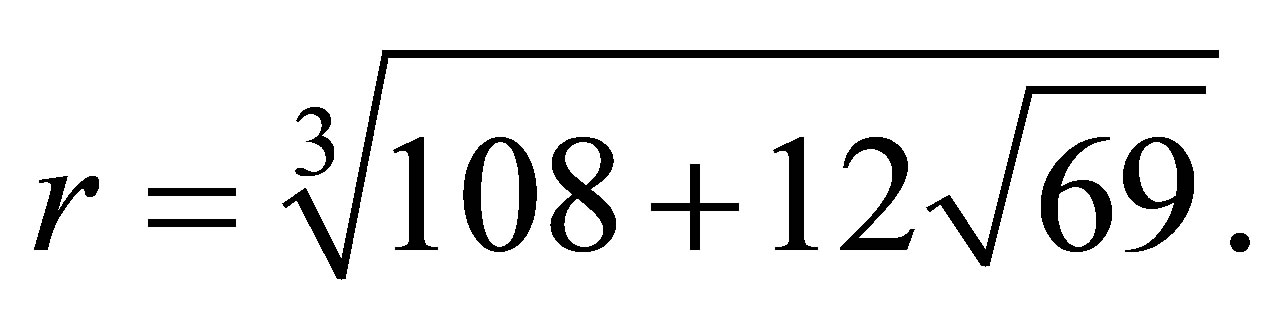 Furthermore, the unique real root
Furthermore, the unique real root  is named as plastic number. Also there exists the following limit
is named as plastic number. Also there exists the following limit
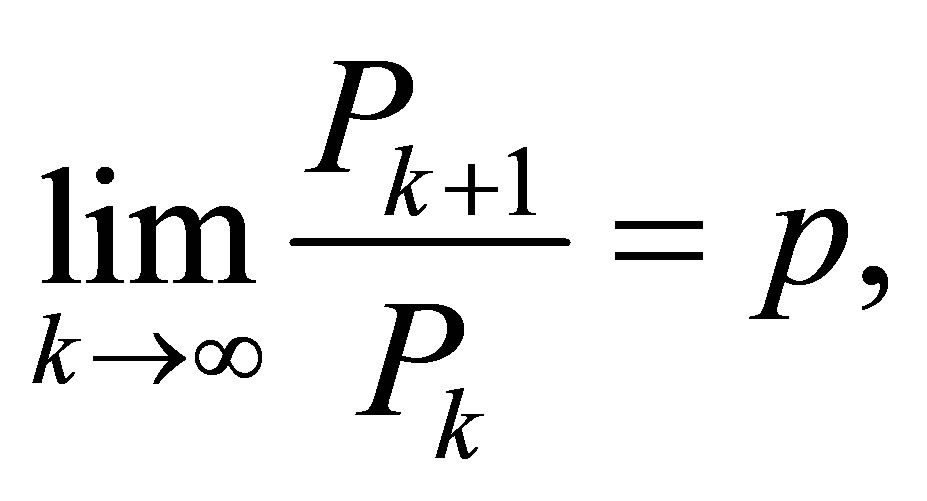
where 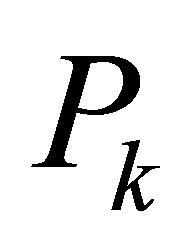 kth Padovan number. One can find more information associated with this sequence in [16,17].
kth Padovan number. One can find more information associated with this sequence in [16,17].
We will need the following definition in the sequel.
Definition 1.1 [18] Let 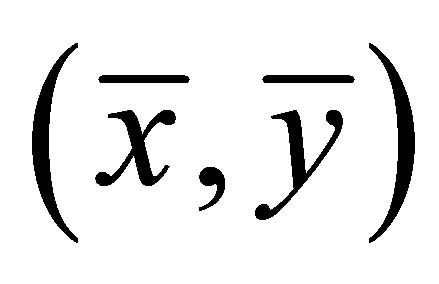 be an equilibrium point of a map
be an equilibrium point of a map , where
, where  and
and  are continuously differentiable functions at
are continuously differentiable functions at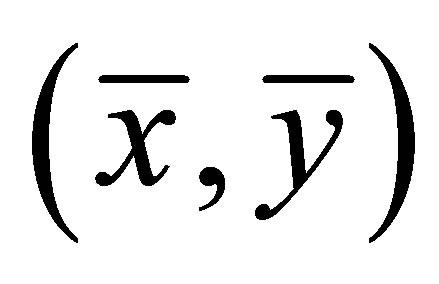 . The Jacobian matrix of
. The Jacobian matrix of  at
at 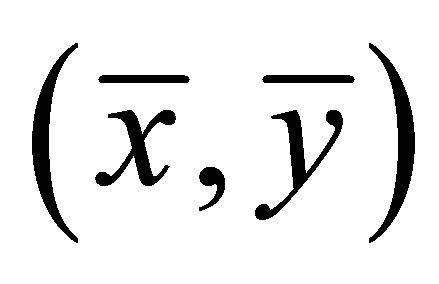 is the matrix
is the matrix

Also, suppose that 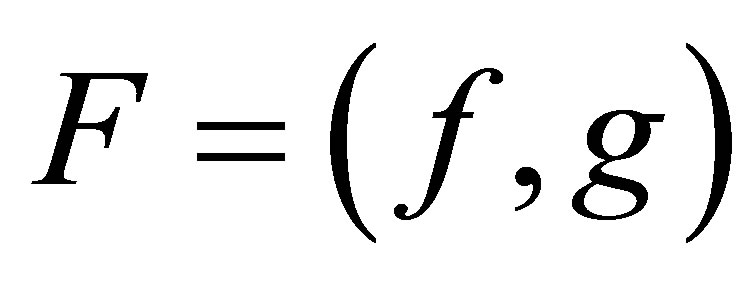 is continuously differentiable on an open set
is continuously differentiable on an open set  in
in . Equilibrium point
. Equilibrium point 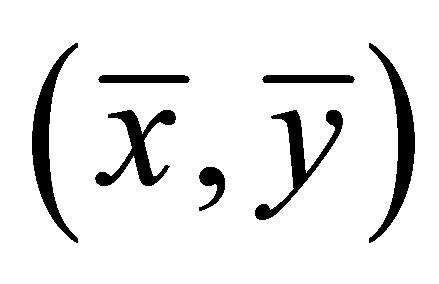 is called a saddle point if one of the eigenvalues of
is called a saddle point if one of the eigenvalues of  is larger and another is less than 1 in absolute value.
is larger and another is less than 1 in absolute value.
In this study, we consider the solutions of the following two difference equation systems
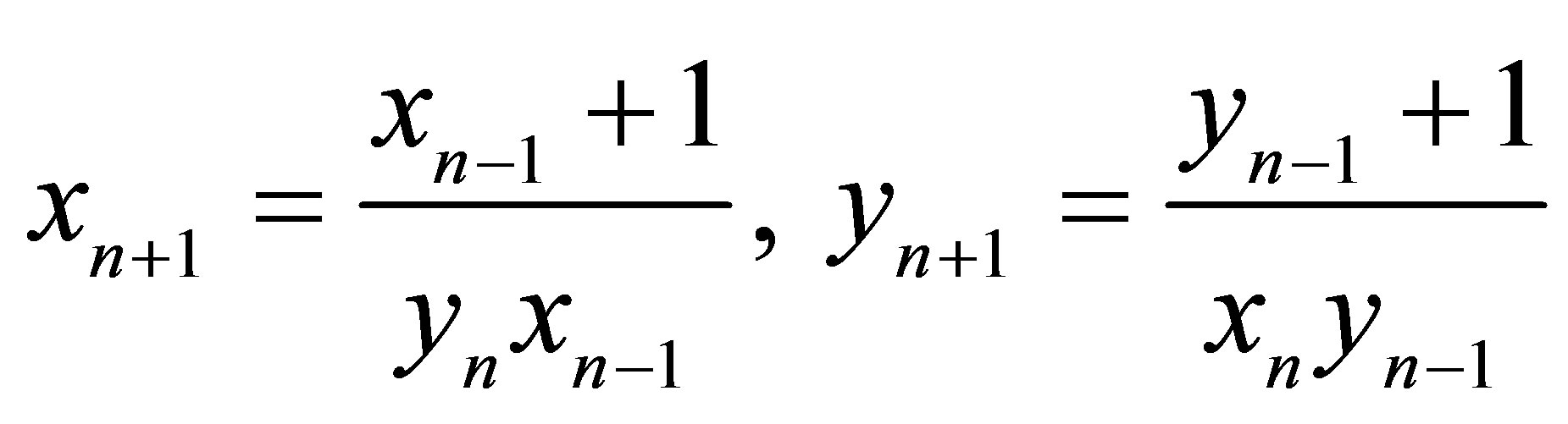 (1.3)
(1.3)
and
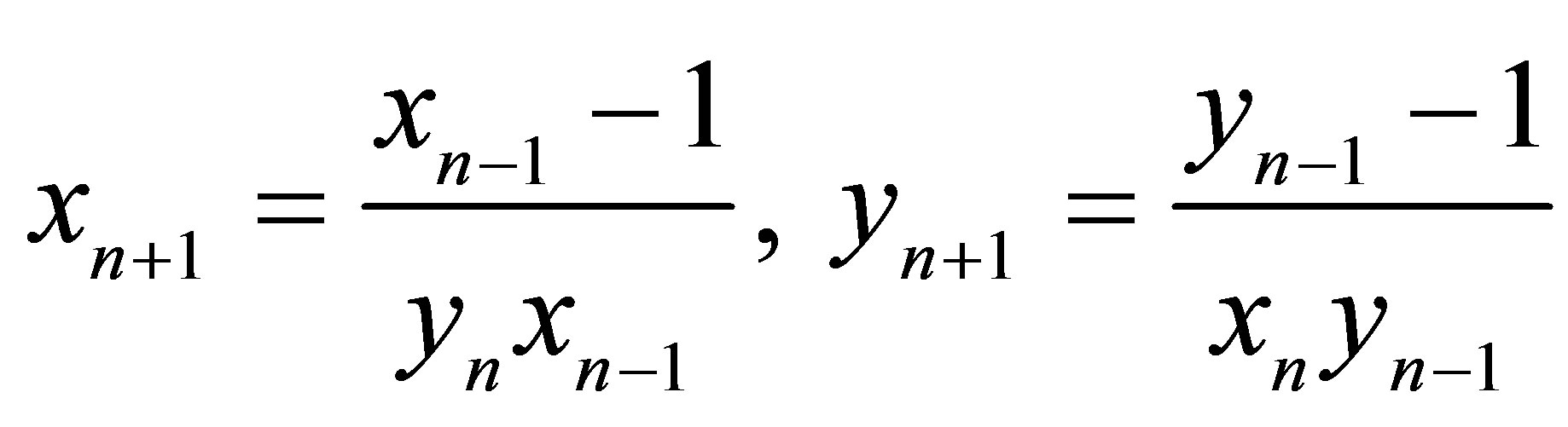 (1.4)
(1.4)
such that their solutions are associated with Padovan numbers. We also establish a relationship between Padovan numbers and the solutions of systems (1.3) and (1.4).
2. Main Results
In this section, we prove our main results. The following theorem studies the formulae of the solutions of systems (1.3) and (1.4) with initial conditions not making the denominator zero.
Teorem 2.1 Let 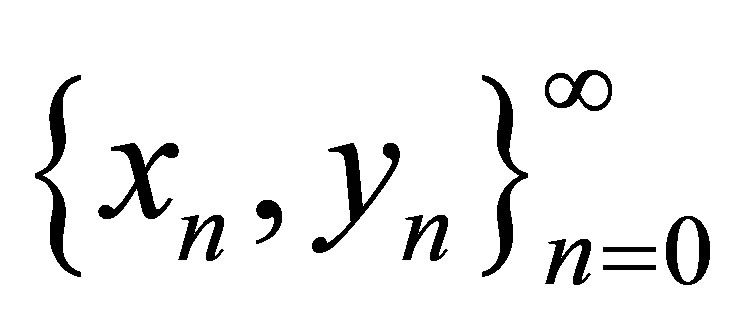 denote the solutions of systems (1.3) and (1.4). Then, the forms of solutions
denote the solutions of systems (1.3) and (1.4). Then, the forms of solutions
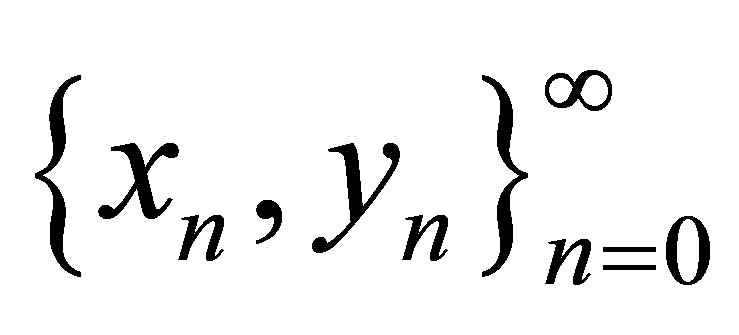 are given by
are given by
 (2.1)
(2.1)
and
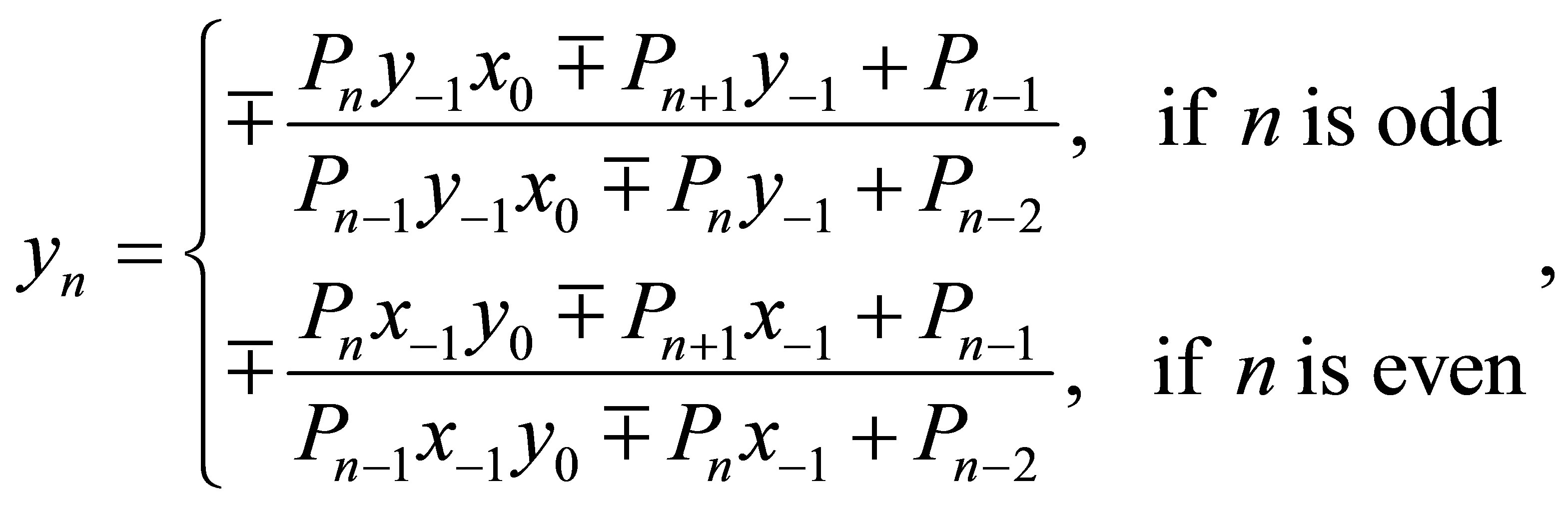 (2.2)
(2.2)
where 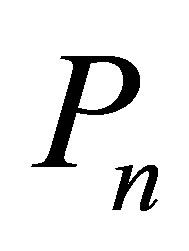 be the nth Padovan number.
be the nth Padovan number.
The following lemma is necessary for determining the initial conditions of the well-defined solutions of systems (1.3) and (1.4).
Lemma 2.2 (Forbidden Set) Forbidden sets of systems (1.3) and (1.4) are given by
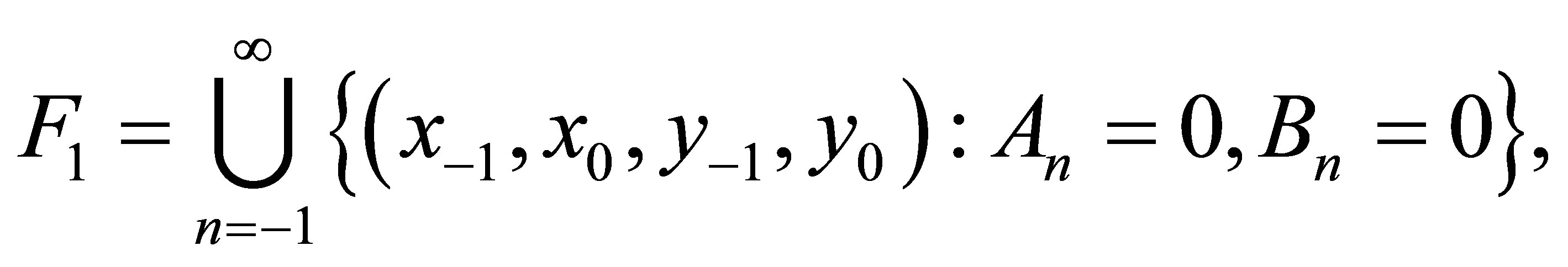
and
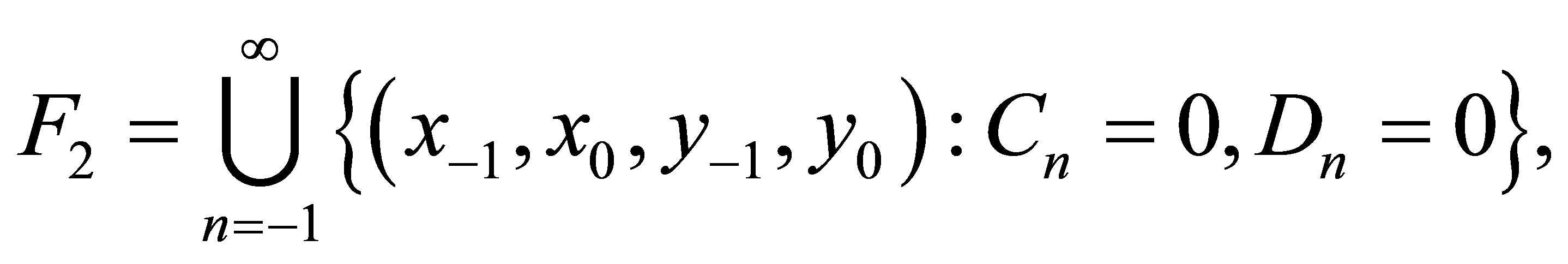
where

respectively.
Proof of Theorem 2.1 We will just prove for system (1.3) since the other part can be proved in the same manner. We use the method of induction on k. For k = 0, we have

For k = 1, we obtain
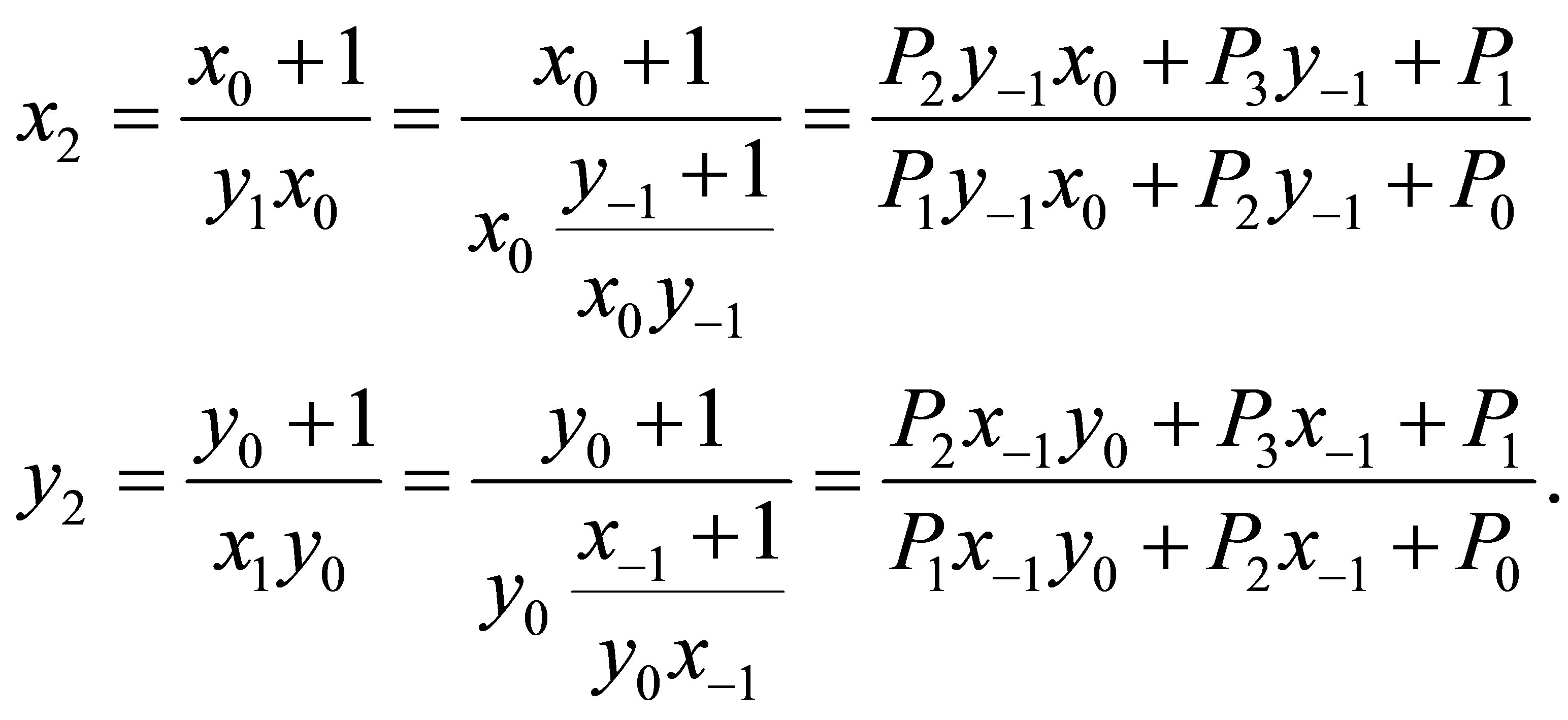
Now, suppose that our assumption holds for 2k - 1. That is;

From Equation (1.3), we can write for 2k,
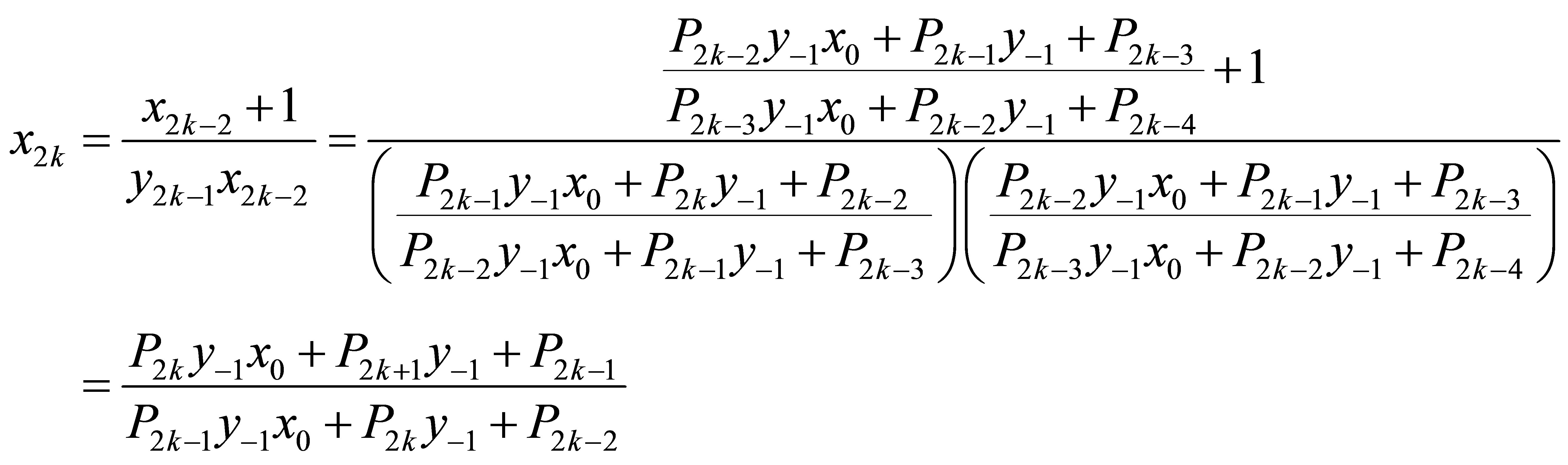
and
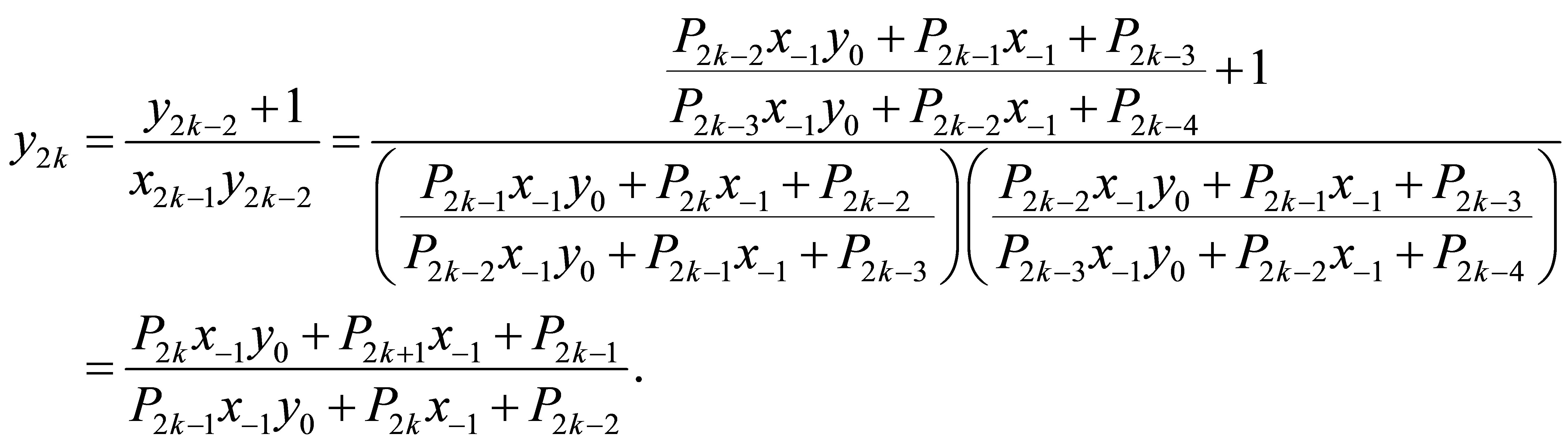
Similarly, from Equation (1.3), we obtain for 2k + 1,
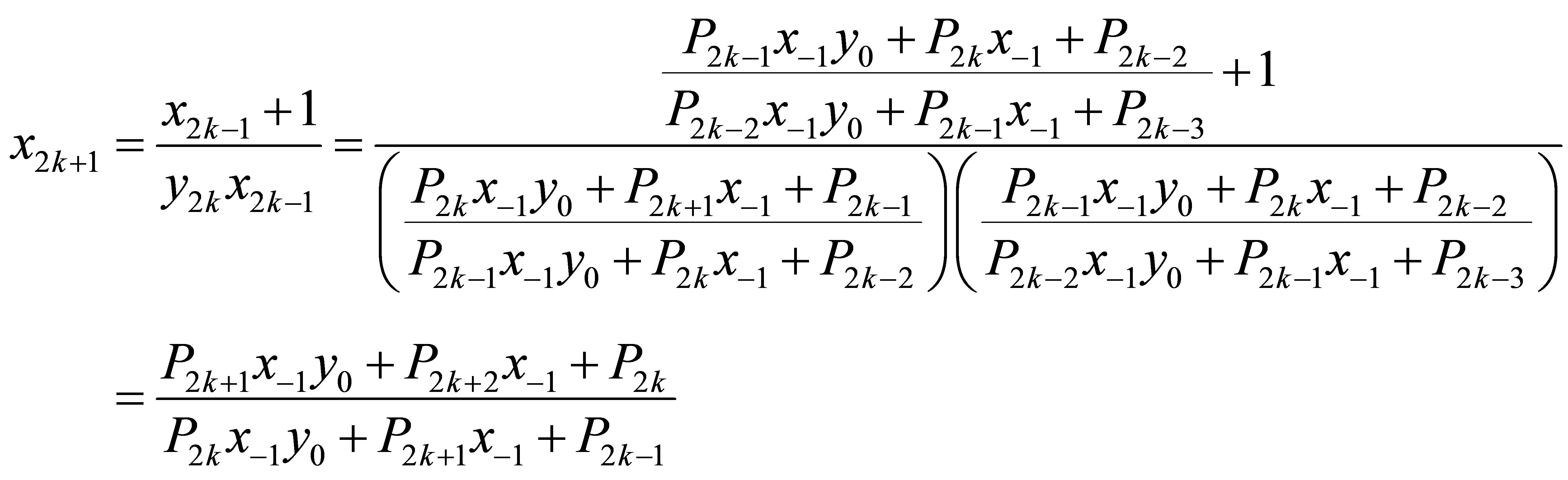
and
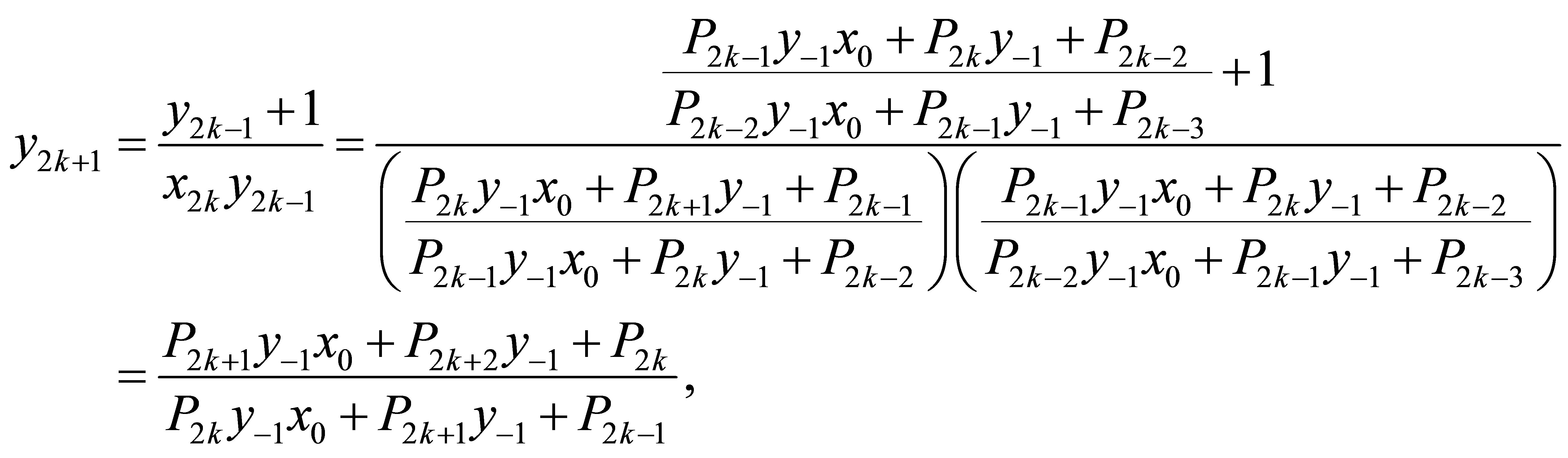
which completes the proof ■.
Theorem 2.3 The following statements hold:
1) System (1.3) has unique real equilibrium point  and
and  is a saddle point2) System (1.4) has unique real equilibrium point
is a saddle point2) System (1.4) has unique real equilibrium point 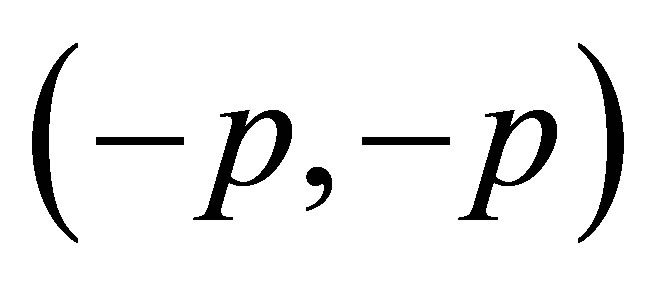 and
and  is a saddle pointwhere p is the plastic number.
is a saddle pointwhere p is the plastic number.
Proof
1) Equilibrium point  of system (1.3) satisfy the system of equations
of system (1.3) satisfy the system of equations
 (2.3)
(2.3)
In (2.3), by subtracting the second equation from the first equation and after some operations, we have
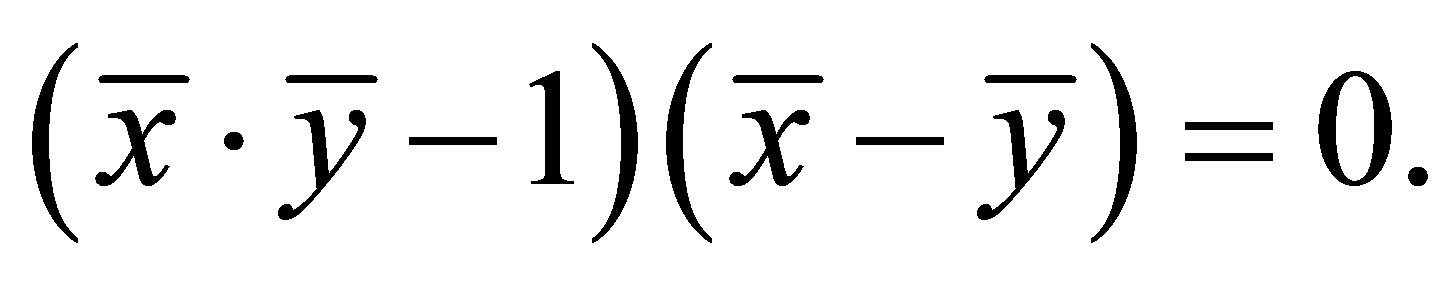
For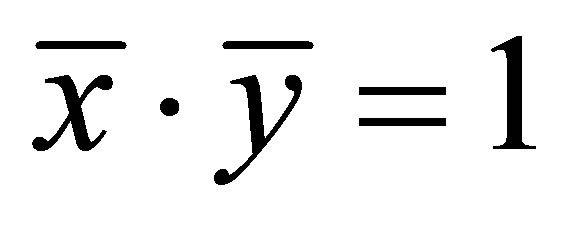 , the equations of (2.3) cannot be satisfied and so
, the equations of (2.3) cannot be satisfied and so . Consequently, we obtain the following cubic equation
. Consequently, we obtain the following cubic equation

The above cubic equation is the characteristic equation of the recurrence relation of the Padovan numbers in (1.2) having the unique real root 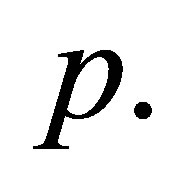 Hence the unique equilibrium point of system (1.3) is point
Hence the unique equilibrium point of system (1.3) is point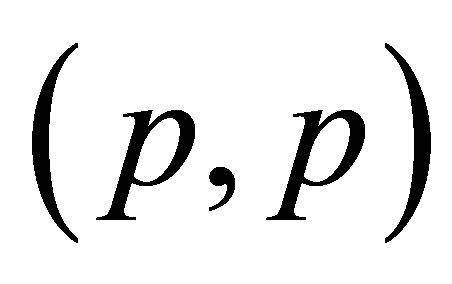 . Now, we show that the equilibrium point is a saddle point. Firstly, system (1.3) is a special case of the general system of the form
. Now, we show that the equilibrium point is a saddle point. Firstly, system (1.3) is a special case of the general system of the form
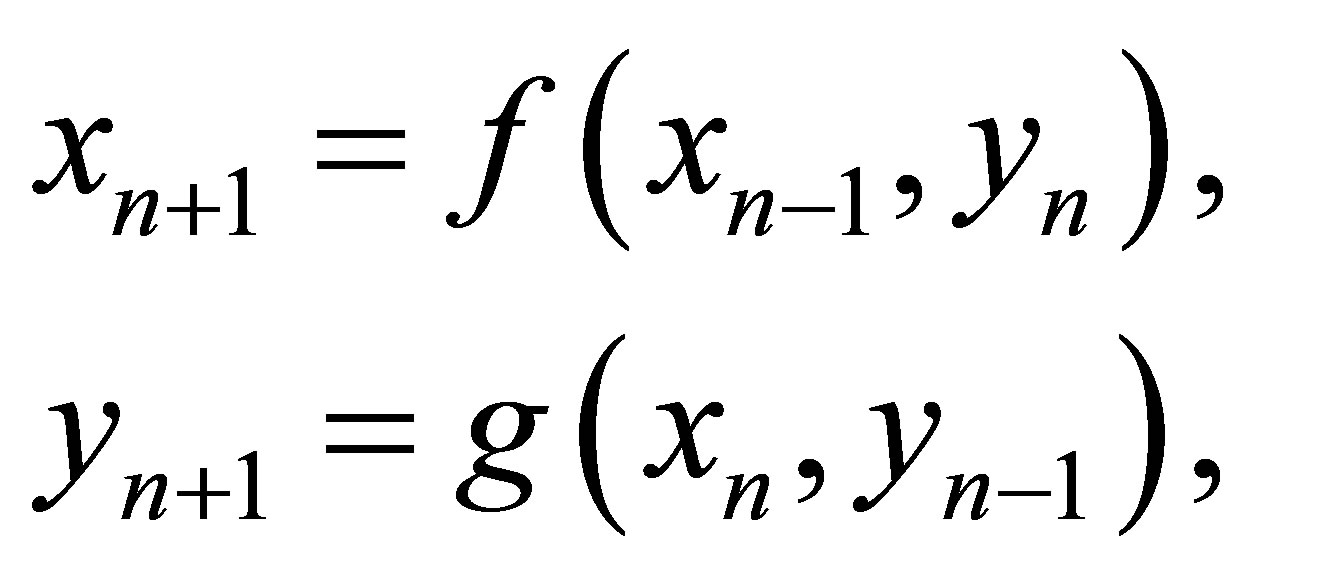
where 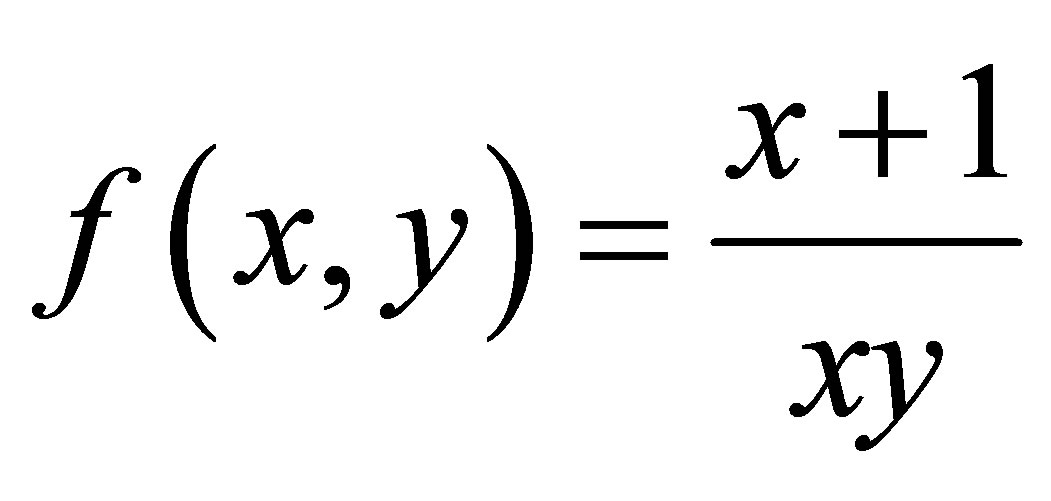 and
and . Then, we calculate the Jacobian of the corresponding map
. Then, we calculate the Jacobian of the corresponding map

We get
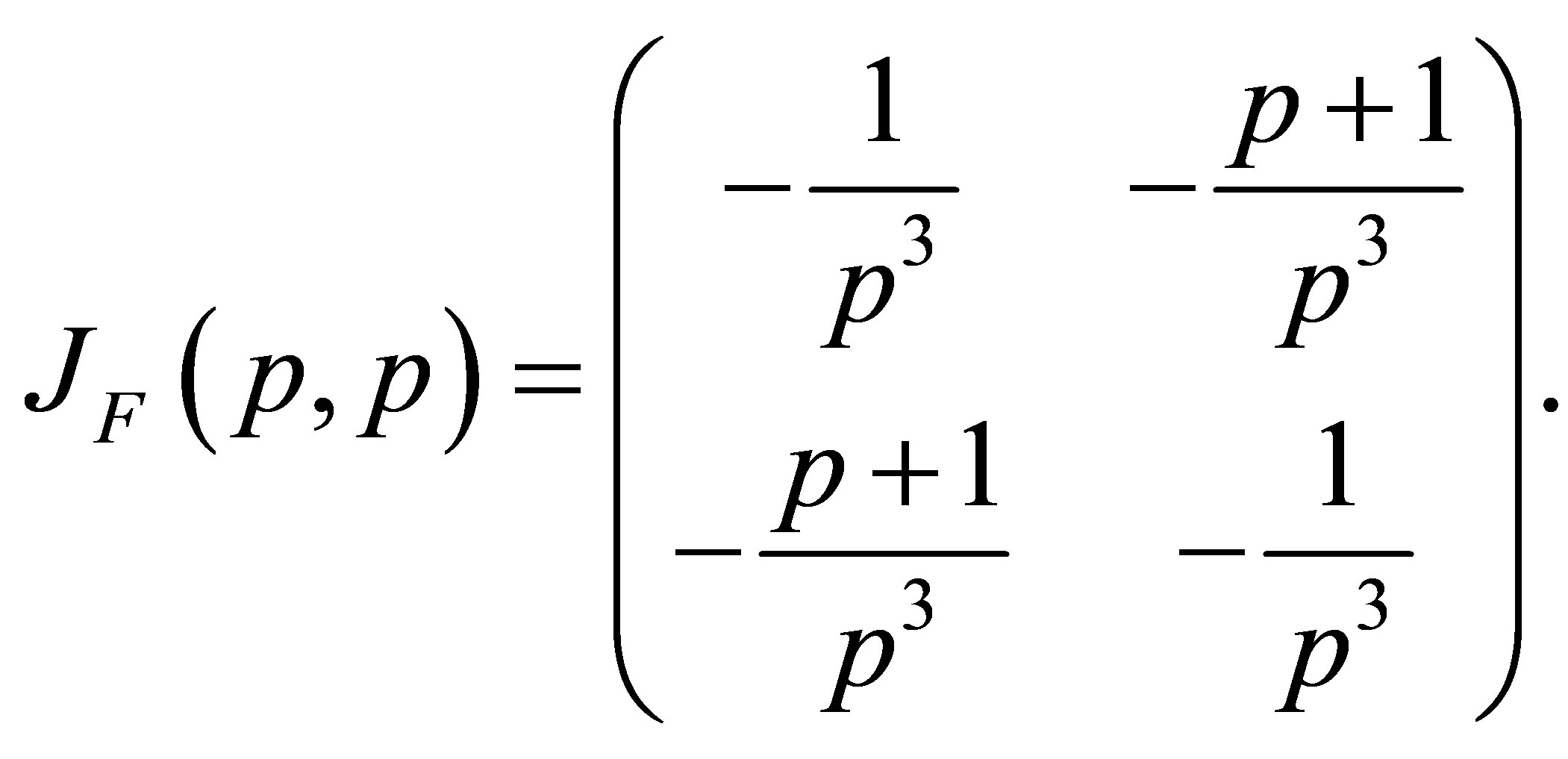
By taking into consideration (1.2), we obtain the characteristic equation of the Jacobian Matrix 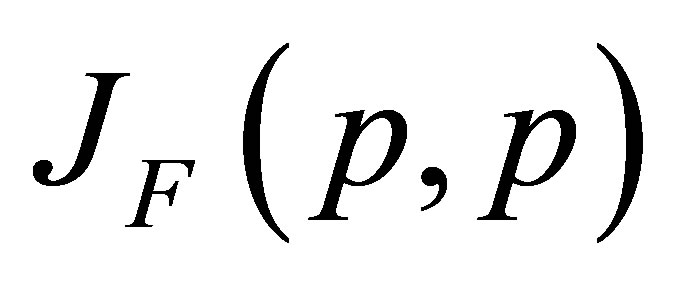 as
as
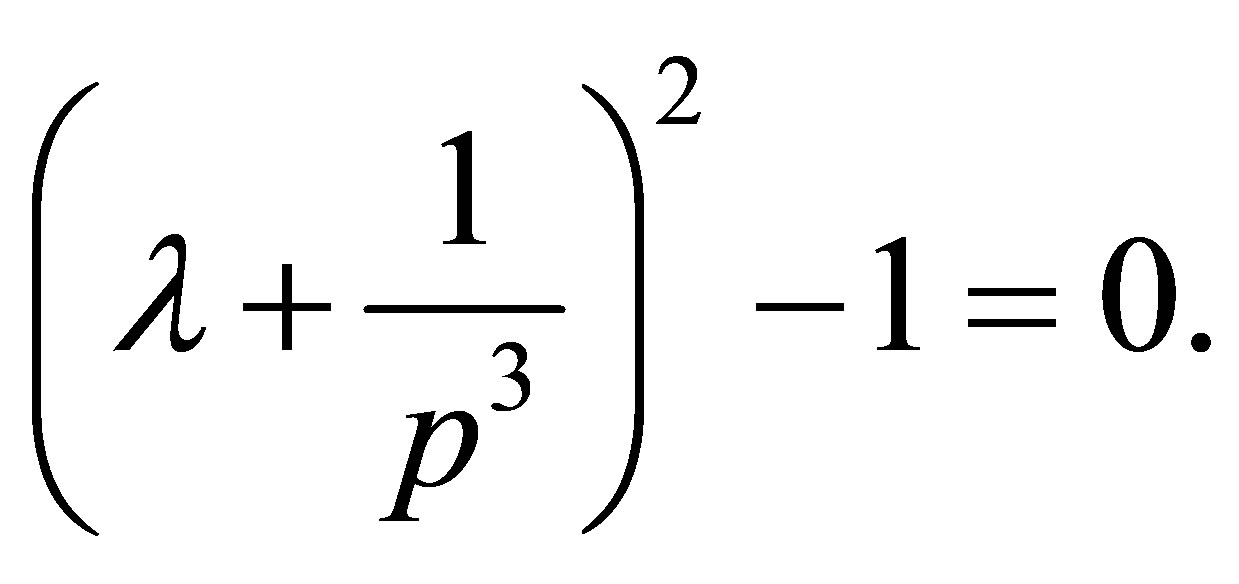
Hence, it is clearly seen that 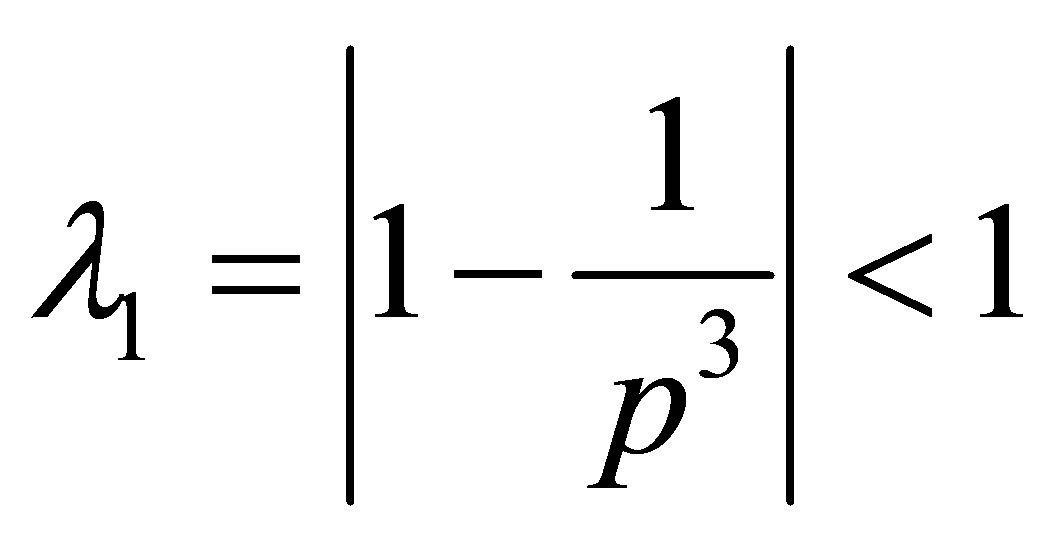 and
and  as desired ■.
as desired ■.
2) It can be proved in a similar manner.
Theorem 2.4 Let the initial conditions of the systems (1.3) and (1.4) be 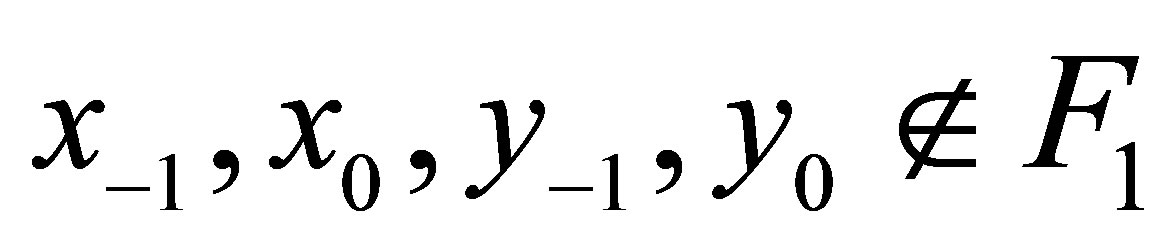 and
and , respectively. Then the following statements hold:
, respectively. Then the following statements hold:
1) The every solution of the system (1.3) converges to point .
.
2) The every solution of the system (1.4) converges to point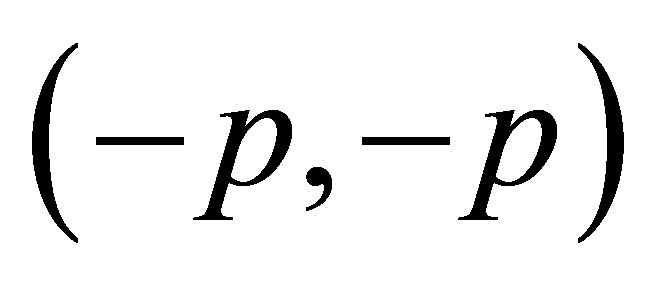 .
.
Proof We will only prove for even-subscripted terms of . Since the other parts of the proof are quite similar, they will be omited.
. Since the other parts of the proof are quite similar, they will be omited.
1) Let us take n = 2k in (2.1). Then, we can write
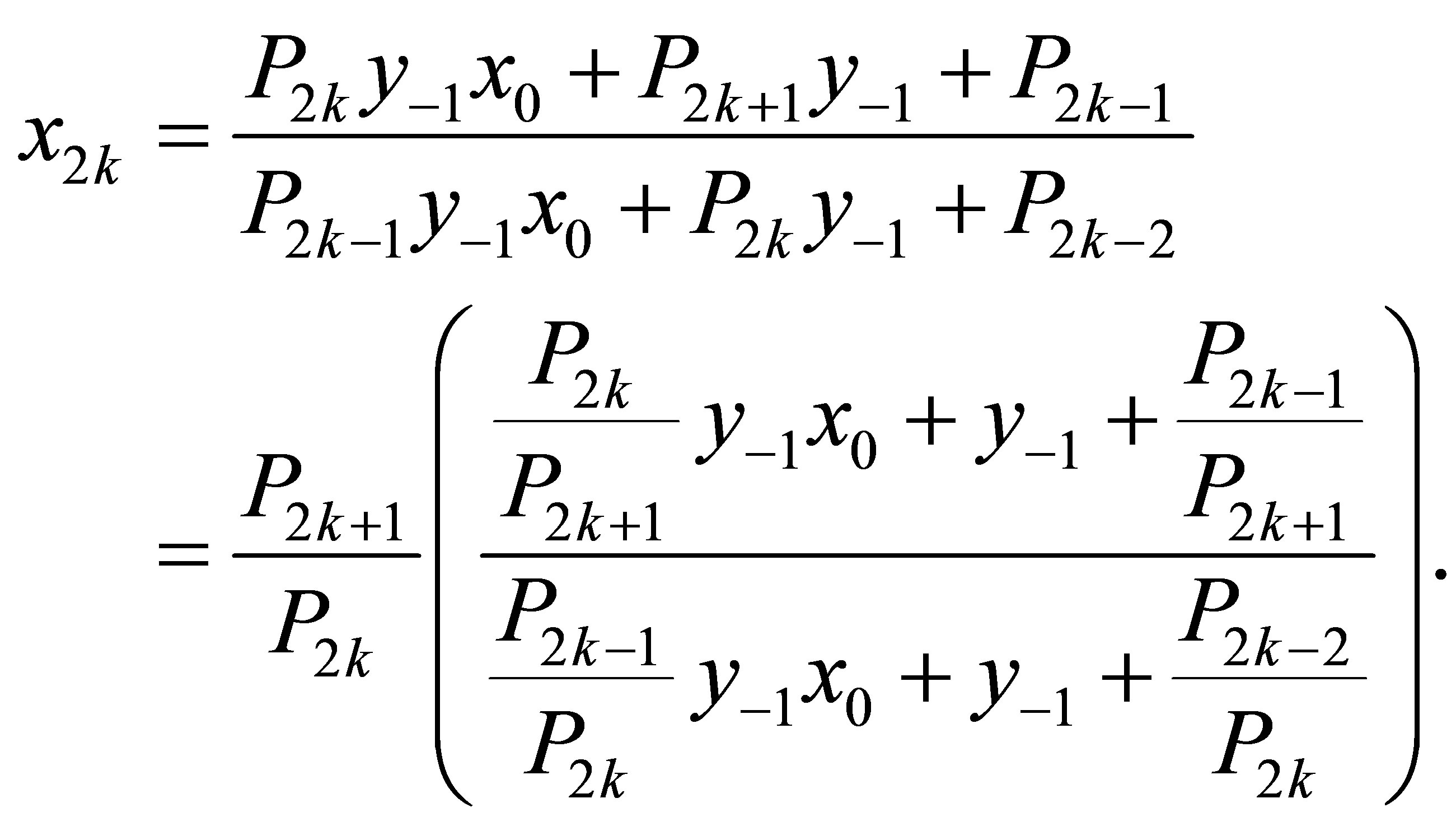
Also, by taking into account 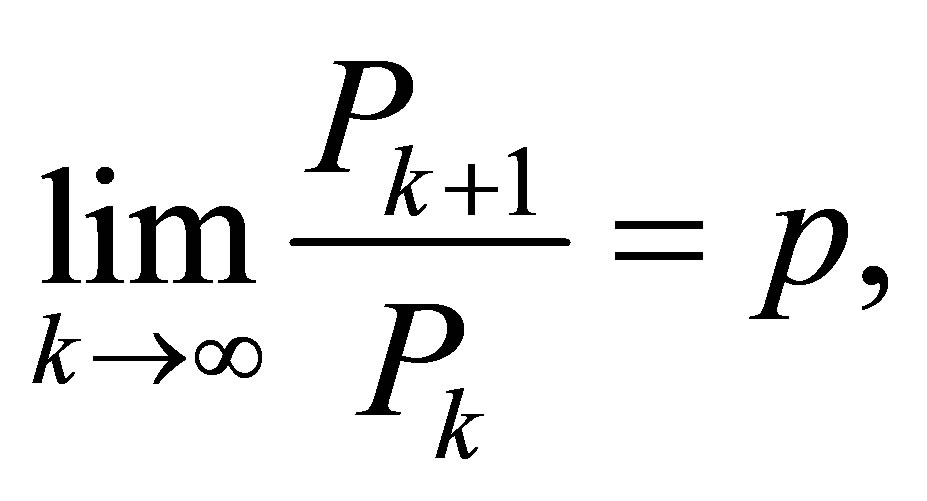 we obtain the following equality
we obtain the following equality
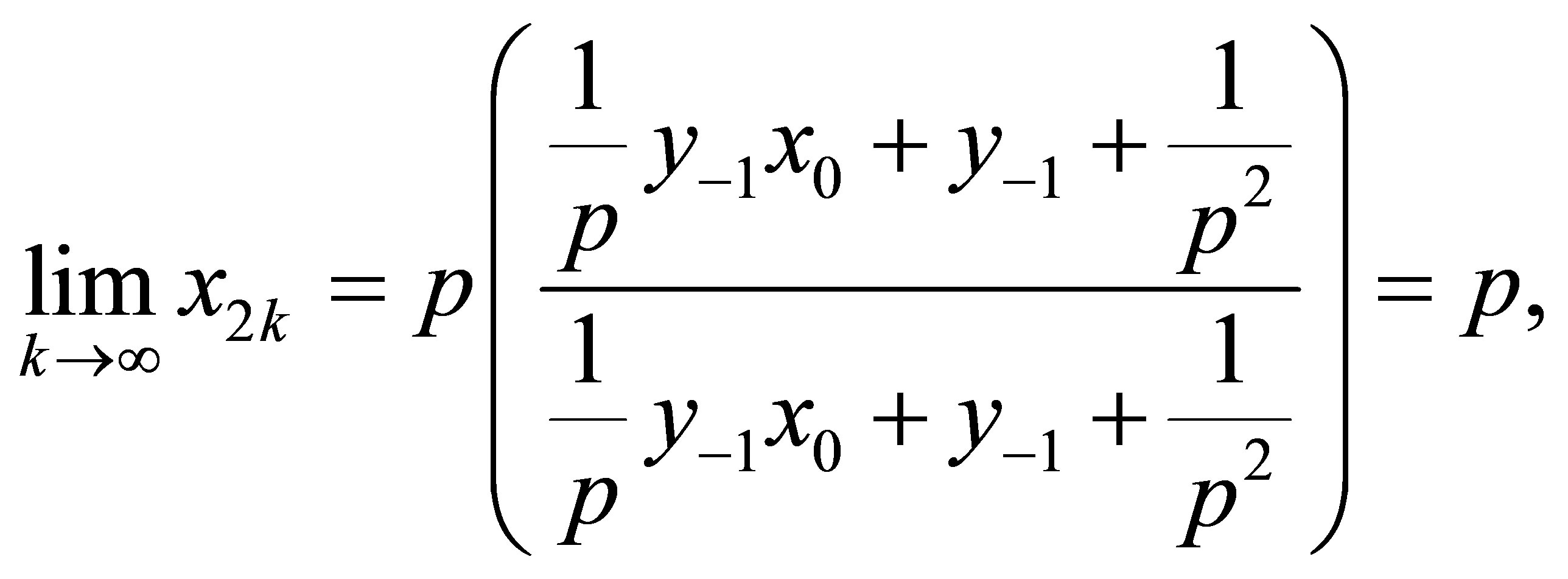
as desired ■.
3. Numerical Examples
In order to illustrate and support theoretical results of the previous section, we consider several examples in this section. These examples represent the qualitative behavior of solutions of the mentioned nonlinear difference equation systems.
Example 3.1 Consider system (1.3) with the inital conditions  (See Figure 1).
(See Figure 1).
Example 3.2 Consider system (1.4) with the inital conditions 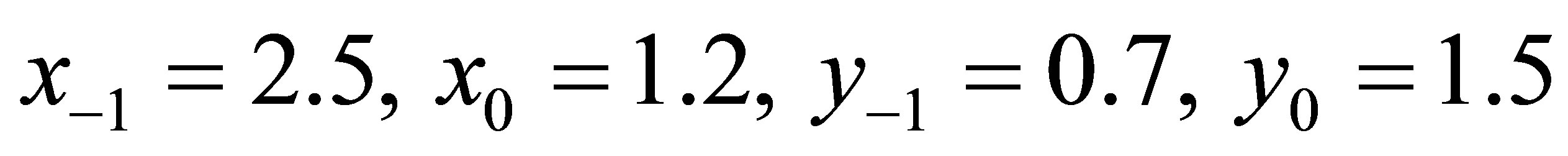 (See Figure 2).
(See Figure 2).
4. Conclusion
In this study, we formulated the solutions of equation systems (1.3) and (1.4) and determined their forbidden sets. Obtained formulae are given by means of Padovan numbers. Also, for  and
and , all the solutions of (1.3) and (1.4) interestingly tend to
, all the solutions of (1.3) and (1.4) interestingly tend to

Figure 1. Plot of ,
, .
.
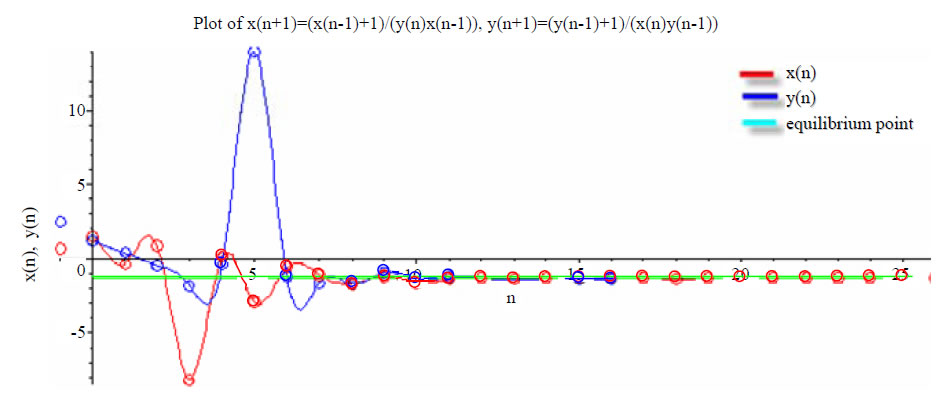
Figure 2. Plot of ,
, .
.
their equilibrium points 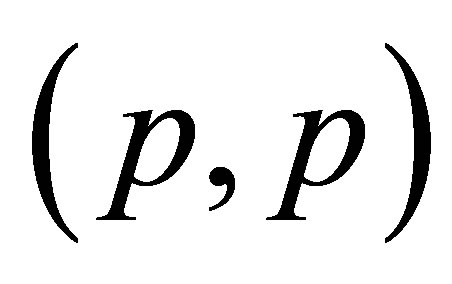 and
and , respectively, where
, respectively, where  is the plastic number.
is the plastic number.
REFERENCES
- R. P. Agarwal, “Difference Equations and Inequalities,” Marcel Dekker, New York, 2000
- M. Aloqeili, “Dynamics of a Rational Difference Equation,” Applied Mathematics and Computation, Vol. 176, No. 2, 2006, pp. 768-774. http://dx.doi.org/10.1016/j.amc.2005.10.024
- T. F. Ibrahim, “On the Third Order Rational Difference equation
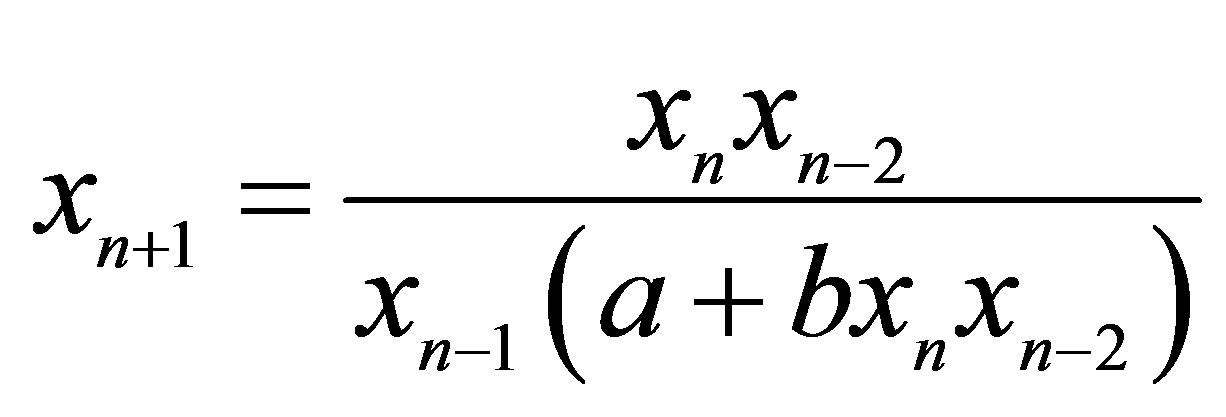 ,” International Journal of Contemporary Mathematical Sciences, Vol. 4, No. 25-28, 2009, pp. 1321-1334.
,” International Journal of Contemporary Mathematical Sciences, Vol. 4, No. 25-28, 2009, pp. 1321-1334. - R. Khalaf-Allah, “Asymptotic Behaviour and Periodic Naturel of Two Difference Equations,” Ukrainian Mathematical Journal, Vol. 61, No. 6, 2009, pp. 988-993. http://dx.doi.org/10.1007/s11253-009-0249-2
- E. M. Elabbasy, H. A. El-Metwally and E. M. Elsayed, “Global Behavior of the Solutions of Some Difference Equations,” Advances in Difference Equations, Vol. 2011, 2011, p. 28. http://dx.doi.org/10.1186/1687-1847-2011-28.
- E. M. Elsayed, “Solution and Attractivity for a Rational Recursive Sequence,” Discrete Dynamics in Nature and Society, Vol. 2011, 2011, Article ID: 982309.
- C. Cinar, “On the Positive Solutions of the Difference Equation System
 ,” Applied Mathematics and Computation, Vol. 158, No. 2, 2004, pp. 303- 305. http://dx.doi.org/10.1016/j.amc.2003.08.073
,” Applied Mathematics and Computation, Vol. 158, No. 2, 2004, pp. 303- 305. http://dx.doi.org/10.1016/j.amc.2003.08.073 - X. Yang, Y. Liu and S. Bai, “On the System of High Order Rational Difference Equations
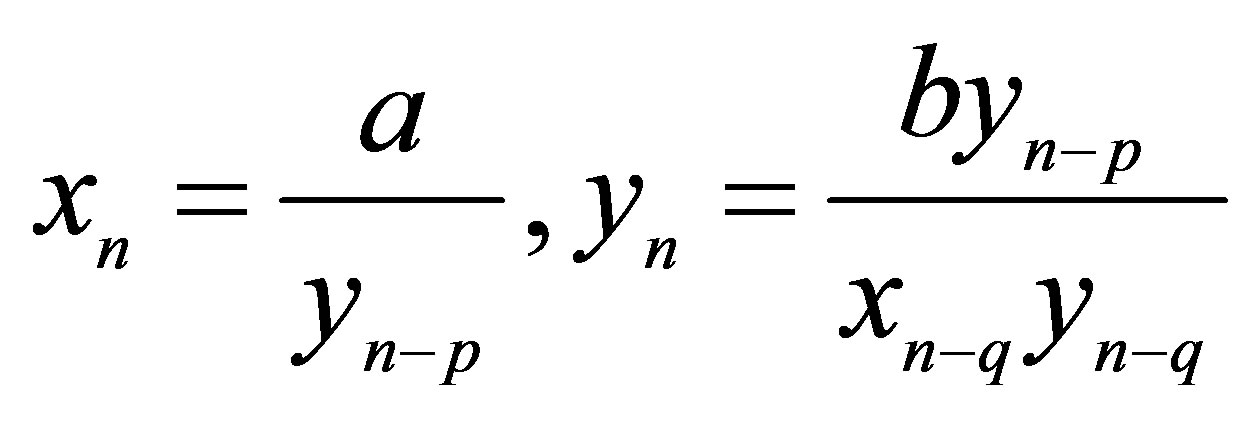 ,” Applied Mathematics and Computation, Vol. 171, No. 2, 2005, pp. 853-856. http://dx.doi.org/10.1016/j.amc.2005.01.092
,” Applied Mathematics and Computation, Vol. 171, No. 2, 2005, pp. 853-856. http://dx.doi.org/10.1016/j.amc.2005.01.092 - A. S. Kurbanli, C. Cinar and I. Yalcinkaya, “On the Behavior of Positive Solutions of the System of Rational Difference Equations,” Mathematical and Computer Modelling, Vol. 53, No.5-6, 2011, pp. 1261-1267. http://dx.doi.org/10.1016/j.mcm.2010.12.009
- E. M. Elsayed, “Solutions of Rational Difference Systems of Order Two,” Mathematical and Computer Modelling, Vol. 55, No. 3-4, 2012, pp. 378-384. http://dx.doi.org/10.1016/j.mcm.2011.08.012
- M. Mansour, M. M. El-Dessoky and E. M. Elsayed, “The Form of the Solutions and Periodicity of Some Systems of Difference Equations,” Discrete Dynamics in Nature and Society, Vol. 2012, 2012, Article ID: 406821.
- S. Stevic, “On a System of Difference Equations,” Applied Mathematics and Computation Vol. 218, No. 7, 2011, pp. 3372-3378. http://dx.doi.org/10.1016/j.amc.2011.08.079
- S. Stevic, “On Some Solvable Systems of Difference Equations,” Applied Mathematics and Computation, Vol. 218, No. 9, 2012, pp. 5010-5018. http://dx.doi.org/10.1016/j.amc.2011.10.068
- D. T. Tollu, Y. Yazlik and N. Taskara, “On the Solutions of Two Special Types of Riccati Difference Equation via Fibonacci Numbers,” Advances in Difference Equations, Vol. 2013, 2013, p. 174. http://dx.doi.org/10.1186/1687-1847-2013-174
- A. S. Kurbanli, C. Cinar and D. Simsek, “On the Periodicity of Solutions of the System of Rational Difference Equations
 ,” Applied Mathematics, Vol. 2, No. 4, 2011, pp. 410-413. http://dx.doi.org/10.4236/am.2011.24050
,” Applied Mathematics, Vol. 2, No. 4, 2011, pp. 410-413. http://dx.doi.org/10.4236/am.2011.24050 - A. G. Shannon, P. G. Anderson and A. F. Horadam, “Properties of Cordonnier, Perrin and Van der Laan Numbers,” International Journal of Mathematical Education in Science and Technology, Vol. 37, No. 7, 2006, pp. 825-831. http://dx.doi.org/10.1080/00207390600712554
- Benjamin M. M. De Weger, “Padua and Pisa are Exponentially Far Apart,” Publicacions Matematiques, Vol. 41, No. 2, 1997, pp. 631-651. http://dx.doi.org/10.5565/PUBLMAT_41297_23
- M. R. S. Kulenovic and O. Merino, “Discrete Dynamical Systems and Difference Equations with Mathematica,” A CRC Press Company, NewYork, 2002.

