Applied Mathematics
Vol.5 No.10(2014), Article ID:46191,12 pages DOI:10.4236/am.2014.510132
Diophantine Equations and the Freeness of Möbius Groups
Marin Gutan
Laboratoire de Mathématiques, Université Blaise-Pascal, Clermont-Ferrand, France
Email: marin.gutan@math.univ-bpclermont.fr
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 16 March 2014; revised 16 April 2014; accepted 23 April 2014
Abstract
Let 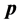 and
and  be two fixed non zero integers verifying the condition
be two fixed non zero integers verifying the condition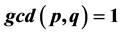 . We check solutions in non zero integers
. We check solutions in non zero integers  and
and 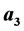 for the following Diophantine equations: (B1)
for the following Diophantine equations: (B1)  (B2)
(B2) 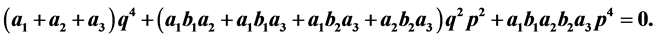 The equations (B1) and (B2) were considered by R.C. Lyndon and J.L. Ullman in [1] and A.F. Beardon in [2] in connection with the freeness of the Möbius group
The equations (B1) and (B2) were considered by R.C. Lyndon and J.L. Ullman in [1] and A.F. Beardon in [2] in connection with the freeness of the Möbius group 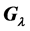 generated by two matrices of
generated by two matrices of 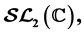 namely
namely 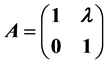 and
and  where
where 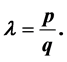 They proved that if one of the equations (B1) or (B2) has solutions in non zero integers then the group
They proved that if one of the equations (B1) or (B2) has solutions in non zero integers then the group 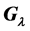 is not free. We give algorithms to decide if these equations admit solutions. We obtain an arithmetical criteria on
is not free. We give algorithms to decide if these equations admit solutions. We obtain an arithmetical criteria on  and
and 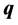 for which (B1) admits solutions. We show that for all
for which (B1) admits solutions. We show that for all 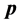 and
and 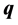 the equations (B1) and (B2) have only a finite number of solutions.
the equations (B1) and (B2) have only a finite number of solutions.
Keywords:Diophantine Equation, Möbius Groups, Free Group

1. Introduction
Let  and
and 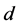 be two positive integers with
be two positive integers with 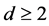 and
and  be matrices of the group
be matrices of the group 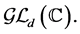
Denote 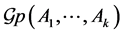 the group, respectively
the group, respectively 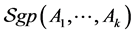 the semigroup, generated by the matrices
the semigroup, generated by the matrices 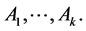
The following problem  has been studied in several papers:
has been studied in several papers:
 Instance:
Instance: 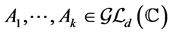
 Question:
Question: 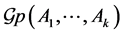 or
or  are they free with
are they free with  as generators?
as generators?
Recall that in 1991 D. Klarner, J.-C. Birget and W. Satterfield in [3] proved that if 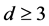 then the problem
then the problem 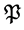 is not decidable. Moreover in 1999 J. Cassaigne, T. Harju and J. Karhümaki in [4] proved that the same result is true if we suppose that all the matrices
is not decidable. Moreover in 1999 J. Cassaigne, T. Harju and J. Karhümaki in [4] proved that the same result is true if we suppose that all the matrices  are lower triangular.
are lower triangular.
The case 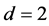 is open and seems difficult. In [5] and [6] results concerning the freeness of the semigroups and groups generated by two matrices are established. In this paper we are studying this problem restricted to the case of Möbius groups.
is open and seems difficult. In [5] and [6] results concerning the freeness of the semigroups and groups generated by two matrices are established. In this paper we are studying this problem restricted to the case of Möbius groups.
Let 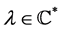 and
and . The Möbius group
. The Möbius group 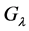 is the subgroup of
is the subgroup of 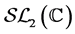 generated by
generated by  and
and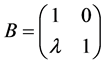 .
.
The problem of characterization of the set of complex values of 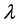 or
or  for which the group
for which the group 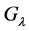 is free, was studied in several papers. Thus in [1] it is proved that if
is free, was studied in several papers. Thus in [1] it is proved that if 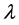 is transcendental or
is transcendental or  then
then 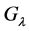 is free.
is free.
R.C. Lyndon and J.L. Ullman in [1] remarked that 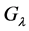 is not free if and only if there exists a word
is not free if and only if there exists a word  whose
whose 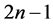 letters are non zero integers so that the product of the powers of matrices
letters are non zero integers so that the product of the powers of matrices 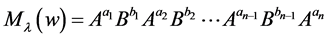 is a lower triangular matrix. The element in the right upper corner of the matrix
is a lower triangular matrix. The element in the right upper corner of the matrix  is of the form
is of the form 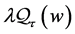 where
where 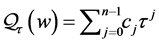 is a polynomial in
is a polynomial in 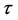 of degree
of degree 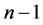 with coefficients
with coefficients 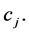 Moreover
Moreover  are polynomials with integers coefficients in the variables
are polynomials with integers coefficients in the variables 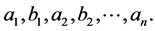
Results concerning the set of algebraic values of 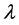 or
or 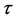 for which the group
for which the group  is not free were obtained in [1] [2] [7] -[11] .
is not free were obtained in [1] [2] [7] -[11] .
Deciding if for 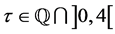 the group
the group 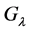 is not free seems very difficult. Let us recall some important results in this direction.
is not free seems very difficult. Let us recall some important results in this direction.
The group 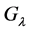 is not free if
is not free if 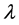 belongs to one of the following sets:
belongs to one of the following sets: 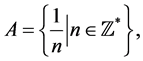

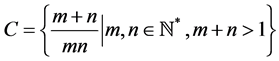 (see [1] [2] [7] [8] [10] [11] ).
(see [1] [2] [7] [8] [10] [11] ).
In this paper we check if for a given  there exists a non trivial word of non zero integers
there exists a non trivial word of non zero integers  such that
such that 
The main results of our paper concern the freeness of Möbius groups:
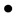 We prove that if the length of
We prove that if the length of 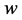 is small then the problem is decidable (cases
is small then the problem is decidable (cases 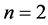 and
and ) (see Theorems 1, 2 and 3).
) (see Theorems 1, 2 and 3).
 We give algorithms which solve the problem for
We give algorithms which solve the problem for  (see Corollary 1 and the proof of Theorem 3). Moreover, we give an arithmetical criteria for this problem when
(see Corollary 1 and the proof of Theorem 3). Moreover, we give an arithmetical criteria for this problem when  (see 2 of Theorem 1).
(see 2 of Theorem 1).
 We give a lower bound numerical function
We give a lower bound numerical function 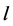 defined from
defined from 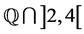 to
to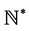 , increasing and unbounded, such that for each
, increasing and unbounded, such that for each 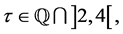 if
if 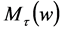 is a lower triangular matrix then the length of
is a lower triangular matrix then the length of  is bigger than
is bigger than 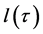 (see Theorem 4 and Corollary 3).
(see Theorem 4 and Corollary 3).
As proved by A.F. Beardon ([2] ) in these two cases 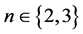 we have to find solutions for the equations (B1) and (B2). In fact in our paper we consider and study two more general equations:
we have to find solutions for the equations (B1) and (B2). In fact in our paper we consider and study two more general equations:
(B'1) 
(B'2) 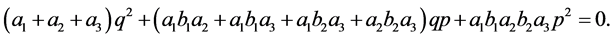
2. Sequences of Polynomials Associated to Matrices
In this section, we study the properties of some sequences of polynomials in a fixed 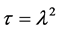 associated to matrices of the group
associated to matrices of the group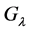 .
.
We consider 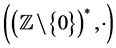 the free monoid of words on non zero integers with the concatenation operation. We denote by
the free monoid of words on non zero integers with the concatenation operation. We denote by 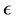 the empty word of the free monoid
the empty word of the free monoid 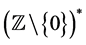 and a non empty word
and a non empty word  by
by , where
, where 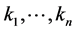 are non zero integers. Then
are non zero integers. Then 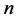 is called the length of
is called the length of 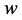 and is denoted by
and is denoted by . The reversal of a word
. The reversal of a word  is
is 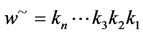 and the opposite of
and the opposite of 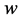 is
is 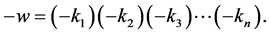
For every word 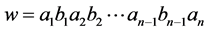 of
of 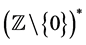 of length
of length 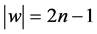 we consider the matrix product
we consider the matrix product
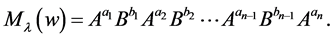
For instance, for 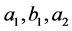 non zero integers we have:
non zero integers we have:
 and
and 
We use the notation:
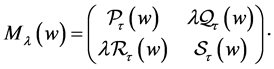
We remark that 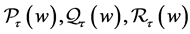 and
and 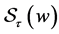 are polynomials in
are polynomials in  with coefficients in
with coefficients in 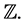 We also have
We also have  and
and 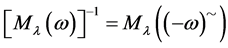
If 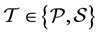 then
then  and if
and if 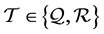 then
then  Also
Also  and if
and if 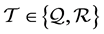 then
then 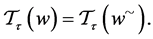
We use the notation 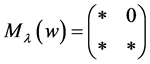 to indicate that
to indicate that  is a lower triangular matrix or that
is a lower triangular matrix or that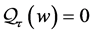 .
.
From now on, in order to simplify the notation we write:
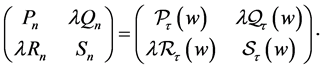
For instance, 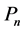 is an abbreviation for the polynomial in
is an abbreviation for the polynomial in  with parameters
with parameters 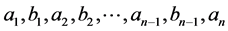 defined by:
defined by:

Using the fact that 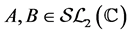 we have:
we have:
 (1)
(1)
The sequences of polynomials in ,
, 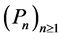 ,
, 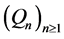 ,
, 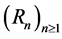 and
and 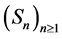 verify the following relations:
verify the following relations:
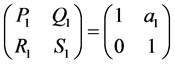 (2)
(2)
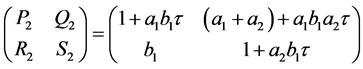 (3)
(3)
 (4)
(4)
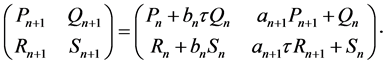 (5)
(5)
The relations (4) and (5) follow from the equality
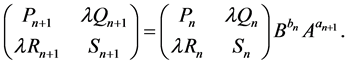
In the following sections, we also use the following two relations:
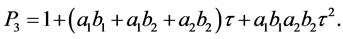 (6)
(6)
 (7)
(7)
Using the previous relations we obtain Proposition 1 The sequences  and
and 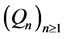 of polynomials in
of polynomials in 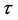 verify the following identities:
verify the following identities:
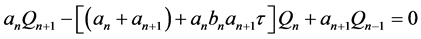 (8)
(8)
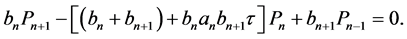 (9)
(9)
Proof. From (5) we have
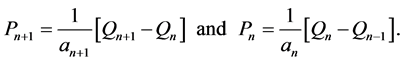
These identities and the equation 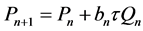 give the equation (8). The equation (9) can be similarly obtained .
give the equation (8). The equation (9) can be similarly obtained .
Let us suppose that 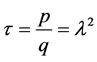 where
where 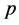 and
and 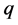 are non zero integers and
are non zero integers and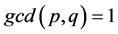 .
.
If 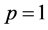 the group
the group 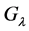 is not free because in this case
is not free because in this case 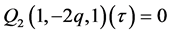 (see [1] ).
(see [1] ).
In the following we consider that . Then
. Then , and
, and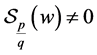 . Indeed, if
. Indeed, if 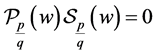 then using the fact that
then using the fact that 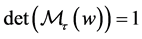 we deduce
we deduce 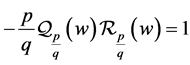 which is in contradiction with the fact that
which is in contradiction with the fact that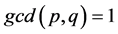 .
.
This remark allows us to define a new sequence 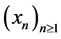 by
by  This sequence satisfies the following relation:
This sequence satisfies the following relation:
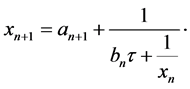 (10)
(10)
Thus we obtain
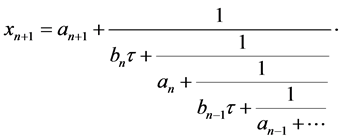
These relations are similar with formulas for continued fractions. The properties of these sequences will be used in the next sections of our paper.
Let us also consider the sequence 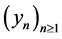 defined by:
defined by:
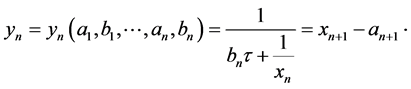
We remark that 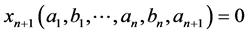 if and only if
if and only if

The following lemma is the key element of Section 5.
Lemma 1 Let 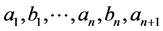 be
be 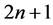 non zero integers and suppose that
non zero integers and suppose that . If
. If
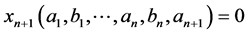 then
then 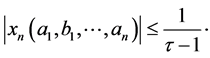
Proof. If 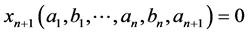 we have
we have

Let  such that
such that 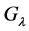 is not free. We define the following numerical function:
is not free. We define the following numerical function:
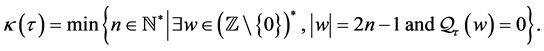 The number
The number 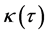 will be called the calibre of the group
will be called the calibre of the group .
.
Hence 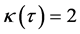 if and only if there are non zero integers
if and only if there are non zero integers  such that
such that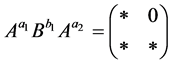 . Also we have
. Also we have 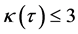 if and only if there are non zero integers
if and only if there are non zero integers 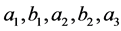 such that
such that 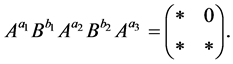
3. The Diophantine Equation (B1)
In the next three sections, we consider the following problem , where
, where ,
, :
:
 Instance: Two non zero integers
Instance: Two non zero integers 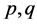 with
with 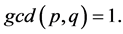
 Question: Is there a word of length
Question: Is there a word of length  of non zero integers
of non zero integers 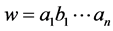 such that
such that
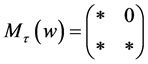 , where
, where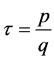 ?
?
So we check solutions in non zero integers  for the diophantine equation
for the diophantine equation
 (11)
(11)
The set of  for which the Möbius group
for which the Möbius group 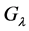 is not free coincides with the set of
is not free coincides with the set of 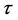 for which there exists
for which there exists 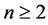 such that the Equation (11) admits solutions.
such that the Equation (11) admits solutions.
In this section, we consider the case 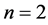 and in the next section the case
and in the next section the case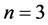 . The relation
. The relation 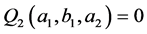 is equivalent to the Equation (B'1) and the relation
is equivalent to the Equation (B'1) and the relation 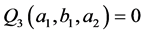 is equivalent to the equation (B'2). If
is equivalent to the equation (B'2). If 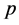 and
and 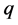 are perfect squares we obtain the equations (B1) and (B2).
are perfect squares we obtain the equations (B1) and (B2).
We will prove that the problem 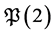 is decidable. The decidability of the problem
is decidable. The decidability of the problem 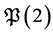 has already been established by A.F. Beardon (Theorem 2, [2] ) for the case when
has already been established by A.F. Beardon (Theorem 2, [2] ) for the case when 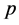 and
and 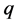 are perfect squares. Our algorithm is simpler and allows us to give an arithmetical criteria for integers
are perfect squares. Our algorithm is simpler and allows us to give an arithmetical criteria for integers  and
and 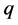 for which the problem
for which the problem 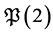 has solutions (see Theorem 1 below).
has solutions (see Theorem 1 below).
First, we prove a result concerning the equation (B'1).
Proposition 2 Let  and
and 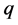 be two integers with
be two integers with 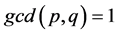 and
and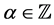 . Denote
. Denote
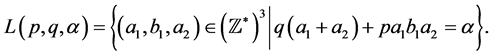
Then:
1. If 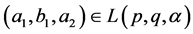 and
and  we have
we have
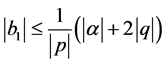
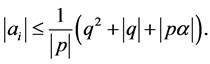
2. The set 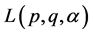 is finite.
is finite.
Proof.
1) Let 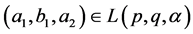 and for
and for 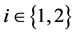 put
put . Then
. Then ,
, 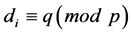 and
and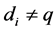 .
.
As 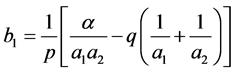 we deduce
we deduce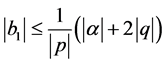 . Because
. Because  and
and 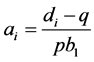 we have
we have
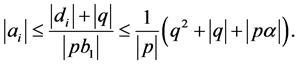
2) results from 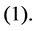
Using the previous proposition we can obtain the decidability of the problem .
.
Theorem 1 Let  and
and 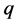 be two integers with
be two integers with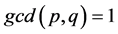 . The following sentences are equivalent:
. The following sentences are equivalent:
1. The equation  has solutions in non zero integers.
has solutions in non zero integers.
2. There exists a divisor 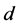 of
of ,
, 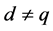 such that
such that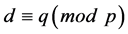 .
.
3.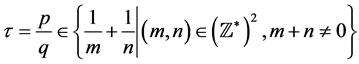 .
.
Proof. The equivalence between (1) and (2) results from the Proposition 2. It is enough to consider  in that proposition. The equivalence between (1) and (3) is obvious.
in that proposition. The equivalence between (1) and (3) is obvious.
Remark 1 Let 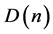 be the set of all divisors of the integer
be the set of all divisors of the integer . If
. If 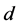 is like in (2) of the previous Theorem 1 then a solution
is like in (2) of the previous Theorem 1 then a solution 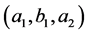 to the equation (B'1) can be obtained by taking
to the equation (B'1) can be obtained by taking
•  and
and
• 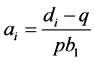 for
for 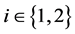
where  and
and 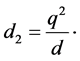 Moreover any solution
Moreover any solution 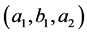 of the equation (B'1) can be obtained by this method. We can write
of the equation (B'1) can be obtained by this method. We can write 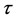 as in (3) of the Theorem 1
as in (3) of the Theorem 1
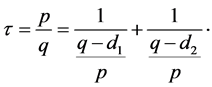
The results of A.F. Beardon ([2] , theorem 2) concerning the problem 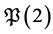 for the case when
for the case when  and
and 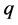 are perfect squares (or equivalently when
are perfect squares (or equivalently when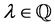 ) result immediately from the next corollary.
) result immediately from the next corollary.
Corollary 1 Let 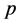 and
and  be two non zero integers with
be two non zero integers with 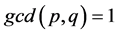 and
and 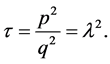 The group
The group
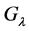 is not free with the calibre
is not free with the calibre 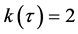 if and only if there exists a divisor
if and only if there exists a divisor  of
of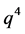 ,
,  such that
such that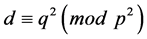 .
.
From the previous theorem it also follows:
1) The equation (B'1) has no solution if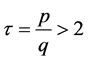 .
.
2) 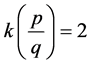 in the following cases: a)
in the following cases: a)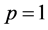 ; b)
; b) 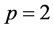 ; c)
; c) 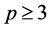 and
and 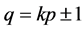 with
with 
Below we present another form of the Theorem 1 in which we use the decomposition of  as a product of prime numbers.
as a product of prime numbers.
Theorem 2 Let 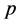 and
and  be two integers with
be two integers with 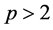 and
and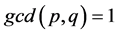 . Let us suppose that the decomposition of
. Let us suppose that the decomposition of 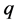 as a product of powers of distinct prime numbers
as a product of powers of distinct prime numbers 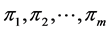 is
is 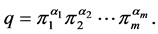
Then 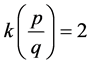 if and only if there exist:
if and only if there exist:
• two disjoint subsets 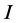 and
and  of
of 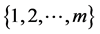 with
with 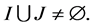
• a set of integers 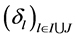 with
with 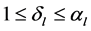 for every
for every 
• 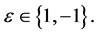
such that 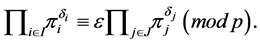
Proof. Let 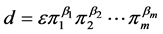 be a divisor of
be a divisor of  We can drop the case
We can drop the case  because
because 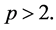 Hence
Hence 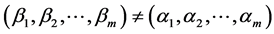 and
and 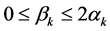 for every
for every 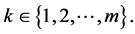 We put
We put 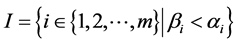 and
and  Then
Then 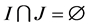 and
and 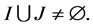 Let:
Let:
 .
.
We have  for every
for every 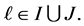 The condition
The condition 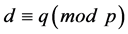 is equivalent to
is equivalent to
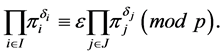
Corollary 2 Let  and
and 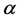 be two non zero integers and
be two non zero integers and  be a prime number. Suppose that
be a prime number. Suppose that
 Then
Then  if and only if there exists an integer
if and only if there exists an integer  with
with 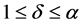 such that
such that
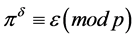 where
where 
Proof. We take 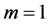 in the previous theorem.
in the previous theorem.
Example: Using the previous results and an example from ([7] ) we have  and
and 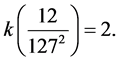
4. The Beardon Diophantine Equation (B2)
Now we consider the problem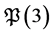 . We mention that the equation
. We mention that the equation 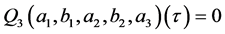 has been considered in several papers (see [2] [8] [10] ) for the case when
has been considered in several papers (see [2] [8] [10] ) for the case when 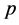 and
and 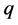 are perfect squares.
are perfect squares.
From now on, we suppose that  for every
for every 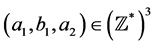 i.e. following Theorem 1,
i.e. following Theorem 1, 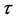 does not belong to
does not belong to 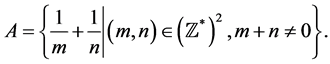 Hence we can define a function
Hence we can define a function 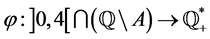 by
by  We remark that
We remark that 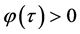 and a)
and a) 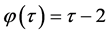 if
if 
b)  if
if 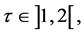 where
where 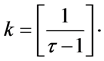
Using the relations (8) for the sequence of polynomials 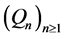 we prove that the problem
we prove that the problem 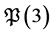 is decidable.
is decidable.
Theorem 3 Let  such that
such that 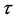 does not belong to the set
does not belong to the set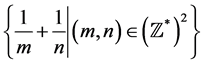 . Then the equation
. Then the equation
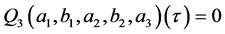
has a finite number of solutions 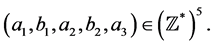
Proof. Using the relations (8) we deduce that
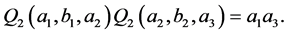
Hence 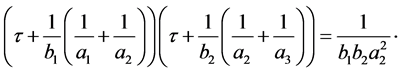 Using the function
Using the function 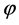 we have:
we have:
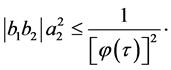
We obtain a finite number of possibilities for 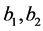 and
and 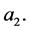 So
So 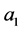 and
and 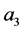 remain to be studied. From the equation
remain to be studied. From the equation

it follows that
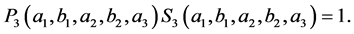
Hence there exists  such that
such that
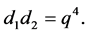

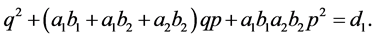
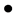
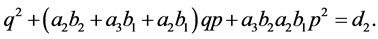

Thus there exists a finite number of possibilities for 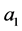 and
and 
If 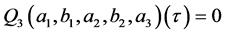 from the inequality
from the inequality 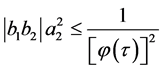 we obtain a) If
we obtain a) If 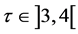 then
then 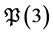 has no solution.
has no solution.
b) If  then
then 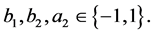
We also remark that the equation (B'2) is equivalent to the following equation
 (12)
(12)
This enables us to obtain some explicit expressions for the rationals 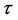 such that equation (B'2) has solutions in
such that equation (B'2) has solutions in 
Proposition 3 Let 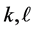 be two non zero integers and
be two non zero integers and  be two divisors of
be two divisors of 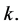 If
If 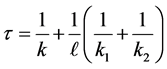
then the equation (B'2) has solutions in 
Proof. Let 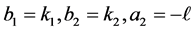 and
and  Then (10) is equivalent to
Then (10) is equivalent to 
Note that if in equation (B'2) we have 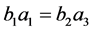 then
then 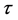 is exactly given by the above expression.
is exactly given by the above expression.
Using once again (10) we obtain Proposition 4 Let 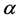 and
and 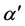 be in
be in 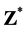 with
with  If
If
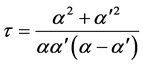
then the equation (B'2) has solutions in 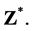
Proof. Consider (10) for 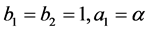 and
and  Then
Then 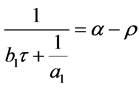 and
and 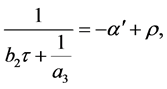 where
where 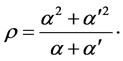 It follows that if we take
It follows that if we take 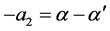 then (10) is verified.
then (10) is verified.
In the next proposition we give another method to obtain solutions of Equation (B'2). It is similar to those presented in [8] and [10] .
Proposition 5 Let 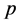 and
and  be two integers with
be two integers with 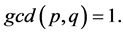 Suppose that there exist
Suppose that there exist 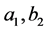 and
and 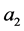
in 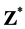 such that
such that 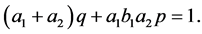 If
If 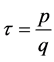 then the equation (B'2) has solutions in
then the equation (B'2) has solutions in 
Proof. Let  and
and  Then
Then 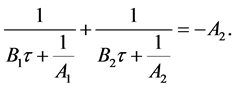 Hence the equation (B'2) has solutions.
Hence the equation (B'2) has solutions.
We end this section with the following open questions:
wang#title3_4:spQuestions:
1) Find all the solutions of (B2).
2) Find arithmetical characterizations (similar to those given in Theorem 1 for the positive integers  and
and 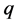 for which the problem
for which the problem 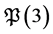 has solutions.
has solutions.
5. Increasing Unbounded Lower Bound Function for (
In this section, we prove that in order to show that the group  is not free for a rational
is not free for a rational 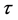 with
with  and
and 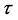 close to 4, we have to consider longer and longer words in
close to 4, we have to consider longer and longer words in 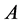 and
and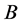 . Similar remarks (without any proof) have been made by A.F. Beardon in [2] and S.P. Farbman in [7] .
. Similar remarks (without any proof) have been made by A.F. Beardon in [2] and S.P. Farbman in [7] .
Everywhere in this section, we consider that  is a rational number in the open interval
is a rational number in the open interval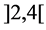 .
.
From the Lemma 1, Section 2, if 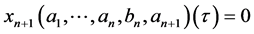 then
then 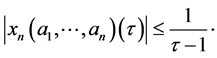 For this reason we consider the sequence
For this reason we consider the sequence 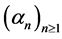 of rational functions in the variable
of rational functions in the variable ,
, 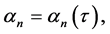 defined by:
defined by:
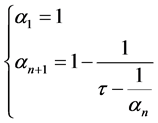
For example
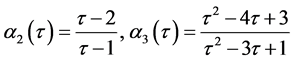 and
and 
We also define the function 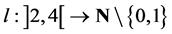 by the formula:
by the formula:
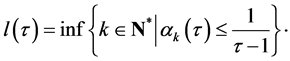
Thus one has 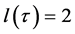 if and only if
if and only if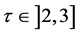 ,
, 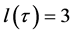 if and only if
if and only if 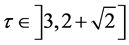 and
and 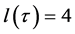 if and only if
if and only if 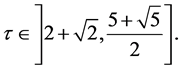
Now we will calculate .
.
Note that 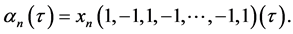 For this reason we find the matrix
For this reason we find the matrix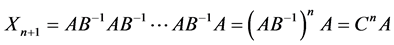 , where
, where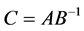 . We suppose now that
. We suppose now that 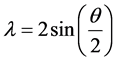 with
with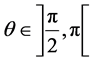 , so
, so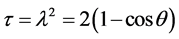 . As
. As 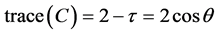 the matrix
the matrix 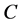 verifies the equation:
verifies the equation:

Using this relation we find that
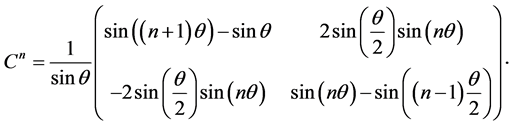
Hence 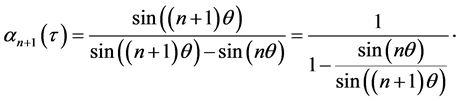
Lemma 2 Let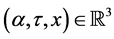 ,
,  be such that
be such that . Then for every
. Then for every 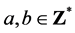 we have
we have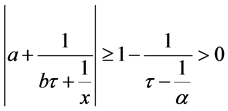 .
.
Proof. Since 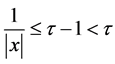 we obtain that
we obtain that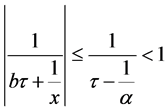 . Hence
. Hence 
The previous expression for  and Lemma 2 show that
and Lemma 2 show that 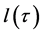 is well defined and
is well defined and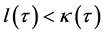 , for every
, for every  in the open interval
in the open interval . So
. So 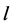 is a lower bound numerical function for the function
is a lower bound numerical function for the function  restricted to
restricted to 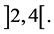
Theorem 4 For any 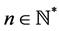 and
and  one has
one has  if and only if there exists
if and only if there exists
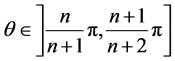 such that
such that 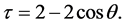
Proof. Let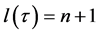 , where
, where 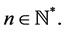 From the definition of the function
From the definition of the function 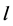 this previous equality holds if and only if
this previous equality holds if and only if 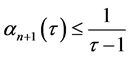 and
and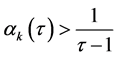 , for all
, for all . But
. But 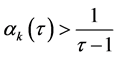 if and only if
if and only if 
Thus we obtain the system of two inequalities 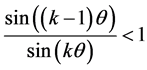 and
and .
.
Finally, 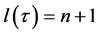 if and only if we have
if and only if we have 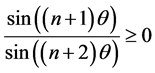 and
and 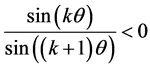 for all
for all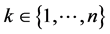 . These inequalities give
. These inequalities give 
Corollary 3 The function 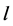 is increasing and unbounded.
is increasing and unbounded.
Therefore

Example: We consider the sequence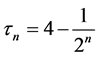 , for
, for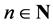 .
.
• For  we have
we have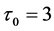 . So
. So , hence
, hence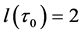 . As
. As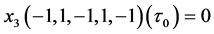 , it follows that
, it follows that 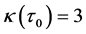 .
.
• For 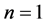 we have
we have  and
and ,
,  ,
, 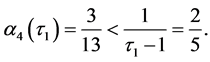 Hence
Hence 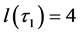 and since
and since
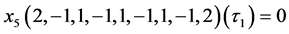
we have 
• For  we have
we have 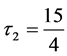 and
and ,
, 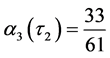 ,
, 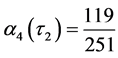 ,
, 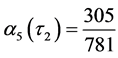 ,
, 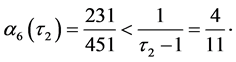 Hence
Hence 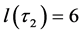 and
and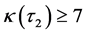 . From [7] we have
. From [7] we have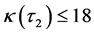 .
.
wang#title3_4:spQuestions:
1) Is it true that for every 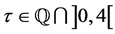 and
and , the problem
, the problem 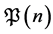 is decidable?
is decidable?
2) Is it true that for every 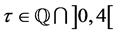 there exists
there exists 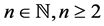 such that the problem
such that the problem 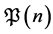 is decidable?
is decidable?
3) Is it true that for every 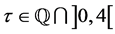 there exists
there exists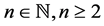 , such that the problem
, such that the problem  has solutions?
has solutions?
4) Find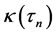 , for
, for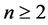 .
.
Acknowledgements
I thank Elias Tahhan (University S. Bolivar, Caracas) and Jerzy Tomasik (Universite d’Auvergne, ClermontFerrand) for discussion concerning some logical aspects of my paper.
References
- Lyndon, R.C. and Ullman, J.L. (1969) Groups Generated by Two Linear Parabolic Transformations. Canadian Journal of Mathematics, 21, 1388-1403. http://dx.doi.org/10.4153/CJM-1969-153-1
- Beardon, A.F. (1993) Pell’s Equation and Two Generator Möbius Groups. Bulletin of the London Mathematical Society, 25, 527-532. http://dx.doi.org/10.1112/blms/25.6.527
- Klarner, D., Birget, J.-C. and Satterfield, W. (1991) On the Undecidability of the Freeness of Integer Matrix Semigroups. International Journal of Algebra and Computation, 1, 223-226. http://dx.doi.org/10.1142/S0218196791000146
- Cassaigne, J., Harju, T. and Karhumaki, J. (1999) On the Undecidability of the Freeness of Matrix Semigroups. International Journal of Algebra and Computation, 9, 295-305. http://dx.doi.org/10.1142/S0218196799000199
- Cassaigne, J. and Nicolas, F. (2012) On the Decidability of Semigroup Freeness. RAIRO—Theoretical Informatics and Applications, 46, 355-399. http://dx.doi.org/10.1051/ita/2012010
- Gawrychowski, P., Gutan, M. and Kisielewicz, A. (2010) On the Problem of Freness of Multplicative Matrix Semigroups. Theoretical Computer Science, 411, 1115-1120. http://dx.doi.org/10.1016/j.tcs.2009.12.005
- Farbman, S.P. (1995) Non-Free Two-Generator Subgroups of
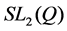 . Publicacions Mathemàtiques, 39, 379-391. http://dx.doi.org/10.5565/PUBLMAT_39295_13
. Publicacions Mathemàtiques, 39, 379-391. http://dx.doi.org/10.5565/PUBLMAT_39295_13 - Tan, E.-C. and Tan, S.-P. (1996) Quadratic Diophantine Equations and Two Generators Möbius Groups. Journal of the Australian Mathematical Society, 61, 360-368. http://dx.doi.org/10.1017/S1446788700000434
- de la Harpe, P. (2000) Topics in Geometric Group Theory. Chicago Lectures in Mathematics. University of Chicago Press, Chicago.
- Grytczuk, A. and Wojtowicz, M. (2000) Beardon’s Diophantine Equations and Non-Free Möbius Groups. Bulletin of the London Mathematical Society, 32, 305-310. http://dx.doi.org/10.1017/S1446788700000434
- Bamberg, J. (2000) Non-Free Points for Groups Generated by a Pair of 2 × 2 Matrices. Journal of the London Mathematical Society, 62, 795-801. http://dx.doi.org/10.1112/S0024610700001630

