Applied Mathematics
Vol.4 No.10(2013), Article ID:37368,5 pages DOI:10.4236/am.2013.410185
Mathematical Neurolaw of Crime and Punishment: The q-Exponential Punishment Function
Department of Behavioral Science, Center for Experimental Research in Social Science, Faculty of Letters, Hokkaido University, Sapporo, Japan
Email: taikitakahashi@gmail.com
Copyright © 2013 Taku Yokoyama, Taiki Takahashi. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received August 13, 2013; revised September 13, 2013; accepted September 20, 2013
Keywords: Neurolaw; Neuroeconomics; Econophysics; Tsallis’ Statistics; Hyperbolic Punishment Function
ABSTRACT
Whether people tend to punish criminals in a socially-optimal manner (i.e., hyperbolic punishment) or not is unknown. By adopting mathematical models of probabilistic punishment behavior (i.e., exponential, hyperbolic, and q-exponential probability discounting model based on Tsallis thermodynamics and neuroeconomics, Takahashi, 2007, Physica A; Takahashi et al., 2012, Applied Mathematics), we examined 1) fitness of the models to behavioral data of uncertain punishment, and 2) deviation from the socially optimal hyperbolic punishment function. Our results demonstrated that, the q-exponential punishment function best fits the behavioral data, and people overweigh the severity of punishment at small punishing probabilities and underweigh the severity of punishment at large punishing probabilities. In other words, people tend to punish crimes too severely and mildly with high and low arrest rate (e.g., homicide vs. excess of speed limit), respectively. Implications for neuroeconomics and neurolaw of crime and punishment (Takahashi, 2012, NeuroEndocrinology Letters) are discussed.
1. Introduction
Crime and punishment in law and economics have been attracting attention [1-3], in addition to neuroeconomics [4,5] and econophysics [6]. Although 1) criminals’ decision making has been examined with mathematical models developed in expected utility theory [1] and non-expected utility theory (prospect theories) in behavioral economics [7] and 2) socially optimal punishment behavior has been mathematically determined for criminals whose decision making is following expected [1] and non-expected utility theories [3], no study to date examines the mathematical characteristics of non-criminal citizen punisher’s decision making. In this study, we experimentally assessed people’s probabilistic punishment behavior and analyzed the behavioral data with the q-exponential probability discounting model [8,9] inspired by Tsallis thermostatistics [10] to examine the deviation of the punishing behavior from the socially optimal punishment function [3].
This paper is organized in the following manner: In Section 1, probabilistic punishment functions (including the q-exponential model) are introduced and the objectives of the present study are addressed. In Section 2, the experimental procedure and analytical strategies based on the q-exponential probability discounting framework are denoted. In Section 3, main experimental findings are presented and mathematical analysis is conducted. In Section 4, some conclusions and implications for mathematical neurolaw and neuroeconomics are addressed.
Mathematical Model of Probabilistic Punishment
In order to mathematically model human probabilistic choice, several models were proposed: exponential discounting; hyperbolic discounting, and q-exponential discounting inspired by the development of deformed algebra in Tsallis’ thermodynamics [8,10]. Because, according to Rachlin et al. (1991) [11] and Takahashi (2011) [12], delay and probability discounting (i.e., decision over time and under risk) shares common psychophysical processing, we can adopt mathematical functions utilized in delay discounting (i.e., exponential, simple hyperbolic, qexponential models [13-17] for probabilistic punishment behavior in terms of, not probability per se, but “odds against” = 1/probability − 1. Note that in this study, the probability corresponds to arrest rate due to criminal behavior, which is a fixed given variable (controlled by, for instance, police officers) and uncontrollable by the citizen punishers themselves.
The exponential probabilistic punishment model is now proposed to be:
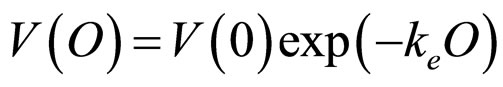 , (1)
, (1)
where V(O) is a subjective value (severity) for a noncriminal citizen punisher of uncertain punishment imposed on a criminal; i.e., a fine which a criminal pays with “odds-against”, O = (1 − probability of punishment)/(probability of punishment), and 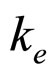 is an exponential punishment rate
is an exponential punishment rate 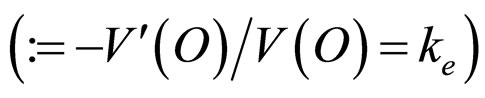 at all O (>0). The exponential punishment rate is constant over certain odds against. It is now to be noted that odds against corresponds to waiting time until being arrested in repeated criminal behaviors in which the fine (punishment)could be imposed at probability p. Therefore, the probabilistic punishment rate k indicates the punisher’s tendency to impose more immediate (i.e., more guaranteed) punishment on habitual criminals who repeatedly conduct crimes.
at all O (>0). The exponential punishment rate is constant over certain odds against. It is now to be noted that odds against corresponds to waiting time until being arrested in repeated criminal behaviors in which the fine (punishment)could be imposed at probability p. Therefore, the probabilistic punishment rate k indicates the punisher’s tendency to impose more immediate (i.e., more guaranteed) punishment on habitual criminals who repeatedly conduct crimes.
The simple hyperbolic punishment model is then proposed to be:
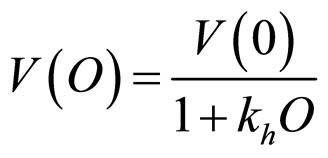 , (2)
, (2)
where V(O) is a subjective value (severity) for the (noncriminal) citizen punisher of an uncertain fine imposed on the criminal with odds against = 1/probability − 1. The important point here is that the socially optimal “hyperbolic punishment function” is obtained when 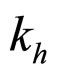 is fixed at 1 (see [3]), for a mathematical proof of the social optimality of this hyperbolic punishment function with
is fixed at 1 (see [3]), for a mathematical proof of the social optimality of this hyperbolic punishment function with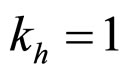 ). The social optimality here indicates the best trade-off between an increase in arrest rate (by, for instance, increasing the number of police officers) and severity of punishment (note that both are socially costly), which is a key concept in law and economics which examines the social efficiency of legal systems [1,3].
). The social optimality here indicates the best trade-off between an increase in arrest rate (by, for instance, increasing the number of police officers) and severity of punishment (note that both are socially costly), which is a key concept in law and economics which examines the social efficiency of legal systems [1,3].
In order to generalize and unify these probabilistic punishment models, we now propose the q-exponential punishment function based on deformed algebra developed in Tsallis’ non-extensive thermostatistics [10,18]. The qexponential probabilistic punishment function is:
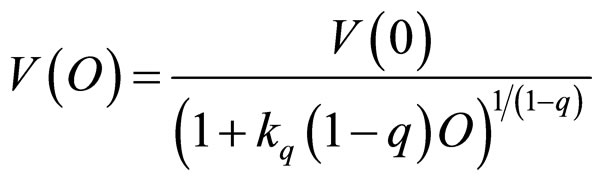 , (3)
, (3)
where V(O) is, again, a subjective value (severity) for the (non-criminal) citizen punisher of an uncertain fine imposed on the criminal with odds against = 1/probability − 1, 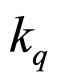 is a q-exponential punishment rate
is a q-exponential punishment rate 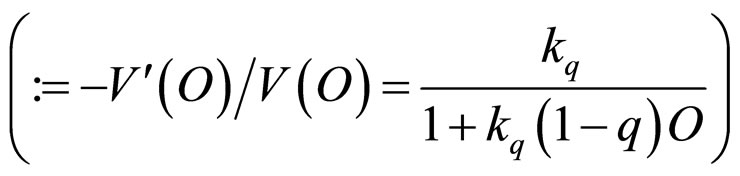 at odds against O = 0, and 1 − q indicates the degree of the deviation of the non-criminal punisher’s probabilistic punishment behavior from exponential punishment. Namely, when q = 0, the q-exponential model is equivalent to the simple hyperbolic model, and when
at odds against O = 0, and 1 − q indicates the degree of the deviation of the non-criminal punisher’s probabilistic punishment behavior from exponential punishment. Namely, when q = 0, the q-exponential model is equivalent to the simple hyperbolic model, and when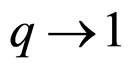 , the q-exponential model is equivalent to the exponential model.
, the q-exponential model is equivalent to the exponential model.
The objectives of the present study are 1) to establish a probabilistic punishment task; 2) to determine non-criminal citizen’s punishment functions; and 3) to examine the deviations of the citizen punisher’s probabilistic punishing behavior from the socially optimal “hyperbolic punishment function”. These examinations may help future investigations in mathematical psychology, neuroeconomics and econophysics in addition to law and economics. It is to be noted that although the q-exponential discounting function has been utilized in neuroeconomics [15], this study is the first to apply the q-exponential function to mathematical neurolaw.
2. Method
2.1. Participants
Twenty-seven (20 male and 7 female) students were recruited from Hokkaido University in Japan to take part in the experiment. The mean age was 19.22 years old (standard deviation = 0.84). In our experiment, participants were isolated and did not interact with each other.
2.2. Procedure
The participants were asked to perform probabilistic punishment task (conceptually similar to a probability discounting task of loss for a hypothetical criminal, not for a decision maker herself). They were seated individually in a quiet room, facing the experimenter across a table. Then they received a simple instruction that they were asked to choose from a series of alternatives of monetary loss imposed on a criminal with certain probabilities and imagine them, though hypothetical, as real money in this experiment.
The hypothetical monetary amounts of punishment (fine) and the probabilities were printed on each A4 size page. Each page included each probability (in the order of 95%, 90%, 70%, 50%, 30%, 10%, 5%) of uncertain loss (fine) that the criminal would hypothetically be forced to pay. Two columns of hypothetical money amounts were listed. The right column (standard amount of fine imposed upon the criminal) presented 40 rows of a fixed magnitude of monetary amount (=10,000 yen); the left column (adjusted amount) presented 40 rows of ascending or descending magnitudes of monetary amounts in 2.5% increments (=10,000 ´ 0.025 = 250 yen) of the alternative in the right column. The participants were asked to choose between the two alternatives (i.e. either standard amount on the right or adjusted amount on the left) in each row of the questionnaire.
2.3. Data Analysis
We adopted the analytical strategy, on the standard probability discounting task [9,19,20] in our previous study, for the newly established probabilistic punishment task in the present study. More specifically, switching points of the probabilistic punishment tasks were defined as the means of the largest adjusting amount in which the standard alternative choice and the smallest adjusting amount in which the adjusting alternative choice. Indifference points of individuals were calculated by averaging the switching point in the ascending and descending adjusting conditions. The indifference points of the group data were obtained by calculating the medians of individuals’ indifference points in order to compare the goodnessof-fit among the exponential, the hyperbolic and the qexponential models at the group level.
We employed probability discounting (i.e., uncertain punishment behavioral) parameters introduced in the probability discounting models (see Equations (1)-(3)). For estimating the parameters (i.e. ke in the exponential discounting, kq and q in the q-exponential discounting, kh in the hyperbolic discounting), we fitted the three types of the probability discounting model equations (i.e. Equations (1)-(3)) to group median behavioral data of indifference points with the Gauss-Newton algorithm (using R statistical language, non-linear modeling package). The goodness-of-fit of each probability discounting model was assessed with AIC (Akaike Information Criterion) values, which is the most standard criterion for the fitness of mathematical model to observed data. It should be noted that the comparison between the R-square values of equations with different numbers of free parameters are statistically irrelevant (note that an increase in the numbers of free parameters in a fitting equation always yield a larger R-square value). The AIC is defined as 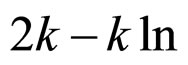 (L), where k is the number of parameters in the statistical model and L is the maximized value of the likelihood function for the fitted model. Given a set of candidate models for the data, the preferred model is the one with the smallest AIC value. AIC includes a penalty that is an increasing function of the number of free parameters in the model. This penalty discourages overfitting. Therefore, better fitting in terms of smaller AIC indicates a better trade-off between over fitting and poor fitting.
(L), where k is the number of parameters in the statistical model and L is the maximized value of the likelihood function for the fitted model. Given a set of candidate models for the data, the preferred model is the one with the smallest AIC value. AIC includes a penalty that is an increasing function of the number of free parameters in the model. This penalty discourages overfitting. Therefore, better fitting in terms of smaller AIC indicates a better trade-off between over fitting and poor fitting.
3. Result
First, we estimated the parameters of three types of probability discounting models (i.e., exponential, simple hyperbolic, and q-exponential models) in terms of odds against = 1/probability − 1 (proportional to waiting time until the realization of punishment in repeated crimes) by fitting the three types of equations to group median data of the indifference points at the seven punishment probabilities (see Figure 1). After fitting each model to the group median behavioral data, we calculated AIC with best-fit parameters as an index of goodness-of-fit (see Table 1 for estimated parameters and AICs of the group data). The orders of the AICs for group median data were [q-exponential discounting function < Simple hyperbolic discounting function < Exponential discounting function]. We can see that the q-exponential punishment function best fitted the behavioral data (i.e. smallest AIC for the q-exponential function), indicating that the q-exponential probability discounting function is the best model even when uncertain loss is imposed upon criminals rather than decision maker herself. This is consistent with our previous study on probability discounting of gain and loss [9].
As noted earlier, the socially-optimal punishment function is the simple hyperbolic function with k = 1 (“hyperbolic punishment function”). In order to examine the deviation of participants’ punishment behavior from the socially optimal punishment function (i.e., the hyperbolic
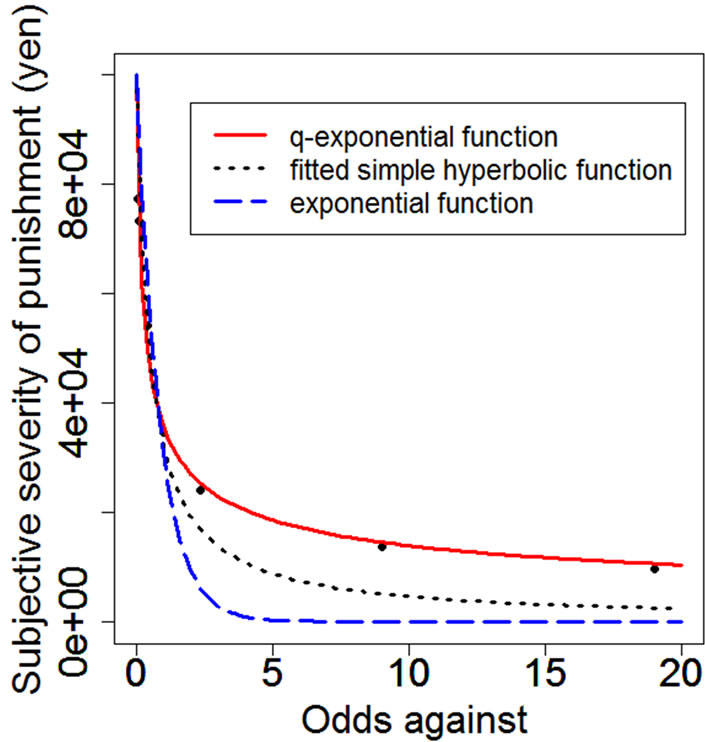
Figure 1. Punishment functions in terms of odds against = 1/probability − 1. The vertical axis is the subjective value (severity) of uncertain punishment. The horizontal axis is the odds against = (1/probability) − 1. The red solid curve is the q-exponential function (the best-fitting model); the blue dashed curve is the exponential function; the black dotted curve is the fitted simple hyperbolic function.

Table 1. Parameters and AICs for the three punishment functions.
punishment function), we plotted the probability-discounted values for the seven probabilities with the best fit q-exponential function and the hyperbolic punishment function (i.e., the simple hyperbolic function with k = 1) (Figure 2). We can see that, people overweigh the severity of punishment at small probabilities (large odds against) and underweigh the severity of punishment at large probabilities (small odds against), indicating that people tend to “under-punish” crimes with small arrest rates (e.g., exceeding the speed limit) and “over-punish” crimes with large arrest rates (e.g., homicide) in terms of social welfare maximization (i.e., utilitarian) ethics which is typically adopted in the discipline of “law and economics” [1,3,21].
4. Discussion
As far as we know, this study is the first to experimentally examine the mathematical characteristics of people’s punishing behavior, by utilizing the q-exponential discounting model based on deformed algebra developed in Tsallis’ thermostatistics. Our results demonstrated that the q-exponential punishment function best fitted human punishment behavior. Furthermore, it was observed that people overweigh and underweigh the severity of punishment imposed on criminals whose criminal conducts are with small and large arrest rates, respectively, in terms of socially optimal punishment behavior which is characterized with the hyperbolic punishment function (i.e., the simple hyperbolic function with k = 1). It can therefore be stated that when based on peoples’ natural psy-

Figure 2. Socially optimal hyperbolic punishment function and the q-exponential punishment function in terms of odds against = 1/probability − 1. The vertical axis is the subjective value (severity) of uncertain punishment. The horizontal axis is the odds against = (1/probability) − 1. The red solid curve is the q-exponential function (the best-fitting model); the green dashed curve is the socially optimal hyperbolic punishment function (k = 1). Note that people overweigh the severity of punishment at small probabilities (large odds against) and underweigh the severity of punishment at large probabilities (small odds against).
chological tendencies, crimes with high arrest rates (e.g., homicide) and low arrest rates (e.g., excess of speed limits) would be punished too severely and mildly in comparison to socially optimal severity of the punishments, respectively.
Psychophysically, the observed deviation of participants’ punishment behavior from the exponential discounting could be attributed to nonlinear (logarithmic) psychophysical effect on the perception of waiting time [12,14,17,22] until arrested by criminals who repeatedly conduct crimes, in a similar vein to the non-exponential probability discounting [9,12] and nonlinear probability weighting function due to distorted waiting time perception in repeated gambles [12,23]. This possibility should be examined in future studies in behavioral and psychophysical neuroeconomics and mathematical psychology.
Regarding the implications for neuroeconomics of crime and punishment [5], previous studies on crime and punishment in behavioral economics and neuroeconomics mainly focused on criminals’ decision making patterns [1,3,7], rather than the mathematical characteristics of punisher’s decision making. Therefore, future studies in law and neuroeconomics should investigate into the mathematical models of punisher’s decision making, which could contribute to design and establish more sociallyefficient legal systems based on quantitative empirical findings guided by mathematically rigorous analytical formalism.
5. Acknowledgements
The research reported in this paper was supported by a grant from the Grant-in-Aid for Scientific Research (Global COE and on Innovative Areas, 23118001; Adolescent Mind & Self-Regulation) from the Ministry of Education, Culture, Sports, Science and Technology of Japan.
REFERENCES
- G. S. Becker, “Crime and Punishment: An Economic Approach,” Journal of Political Economy, Vol. 76, No. 2, 1968, pp. 169-217. http://dx.doi.org/10.1086/259394
- N. Garoupa, “Optimal Magnitude and Probability of Fines,” European Economic Review, Vol. 45, No. 9, 2001, pp. 1765-1771. http://dx.doi.org/10.1016/S0014-2921(00)00084-2
- A. Al-Nowaihi and S. Dhami, “Hyperbolic Punishment Functions,” Review of Law and Economics, Berkeley Electronic Press Journals, Vol. 8, No. 3, 2012, pp. 759- 787.
- K. Prehn, F. Schlagenhauf, L. Schulze, C. Berger, K. Vohs, M. Fleischer, K. Hauenstein, P. Keiper, G. Domes and S. C. Herpertz, “Neural Correlates of Risk Taking in Violent Criminal Offenders Characterized by Emotional Hypoand Hyper-Reactivity,” Social Neuroscience, Vol. 8, No. 2, 2013, pp. 136-147. http://dx.doi.org/10.1080/17470919.2012.686923
- T. Takahashi, “Molecular Neuroeconomics of Crime and Punishment: Implications for Neurolaw,” Neuro Endocrinology Letters, Vol. 33, No. 7, 2012, pp. 667-673.
- L. G. A. Alves, H. V. Ribeiro and R. S. Mendes, “Scaling Laws in the Dynamics of Crime Growth Rate,” Physica A: Statistical Mechanics and Its Applications, Vol. 392, No. 11, 2013, pp. 2672-2679.
- T. Pachur, Y. Hanoch and M. Gummerum, “Prospects behind Bars: Analyzing Decisions under Risk in a Prison Population,” Psychonomic Bulletin and Review, Vol. 17, No. 5, 2010, pp. 630-636. http://dx.doi.org/10.3758/PBR.17.5.630
- T. Takahashi, “A Comparison of Intertemporal Choices for Oneself versus Someone Else Based on Tsallis’ Statistics,” Physica A: Statistical Mechanics and Its Applications, Vol. 385, No. 2, 2007, pp. 637-644.
- T. Takahashi, R. Han, H. Nishinaka, T. Makino and H. Fukui, “The q-Exponential Probability Discounting of Gain and Loss,” Applied Mathematics, Vol. 4, No. 6, 2013, pp. 876-881.
- C. Tsallis, C. Anteneodo, L. Borland and R. Osorio, “Nonextensive Statistical Mechanics and Economics,” Physica A: Statistical Mechanics and Its Applications, Vol. 324, No. 1-2, 2003, pp. 89-100.
- H. Rachlin, A. Raineri and D. Cross, “Subjective Probability and Delay,” Journal of Experimental: Analysis of Behavior, Vol. 55, No. 2, 1991, pp. 233-244. http://dx.doi.org/10.1901/jeab.1991.55-233
- T. Takahashi, “Psychophysics of the Probability Weighting Function,” Physica A: Statistical Mechanics and Its Applications, Vol. 390, No. 5, 2011, pp. 902-905.
- D. O. Cajueiro, “A Note on the Relevance of the q-Exponential Function in the Context of Intertemporal Choices,” Physica A: Statistical Mechanics and Its Applications, Vol. 364, 2006, pp. 385-388.
- T. Takahashi, H. Oono and M. H. B. Radford, “Psychophysics of Time Perception and Intertemporal Choice Models,” Physica A: Statistical Mechanics and Its Applications, Vol. 387, No. 8-9, 2008, pp. 2066-2074.
- T. Takahashi, “Theoretical Frameworks for Neuroeconomics of Intertemporal Choice,” Journal of Neuroscience, Psychology, and Economics, Vol. 2, No. 2, 2009, pp. 75-90. http://dx.doi.org/10.1037/a0015463
- T. Takahashi, T. Hadzibeganovic, S. A. Cannas, T. Makino, H. Fukui and S. Kitayama, “Cultural Neuroeconomics of Intertemporal Choice,” Neuroendocrinology Letters, Vol. 30, No. 2, 2009, pp. 185-191.
- R. Han and T. Takahashi, “Psychophysics of Valuation and Time Perception in Temporal Discounting of Gain and Loss,” Physica A: Statistical Mechanics and Its Applications, Vol. 391, No. 24, 2012, pp. 6568-6576.
- C. Tsallis, “Nonadditive Entropy Sq and Nonextensive Statistical Mechanics: Applications in Geophysics and Elsewhere,” Acta Geophysica, Vol. 60, No. 3, 2012, pp. 502-525. http://dx.doi.org/10.2478/s11600-012-0005-0
- T. Takahashi, H. Oono and M. H. Radford, “Comparison of Probabilistic Choice Models in Humans,” Behavioral and Brain Functions, Vol. 3, No. 1, 2007, p. 20. http://dx.doi.org/10.1186/1744-9081-3-20
- T. Takahashi, K. Ikeda and T. Hasegawa, “A Hyperbolic Decay of Subjective Probability of Obtaining Delayed Rewards,” Behavior and Brain Functions, Vol. 3, 2007, p. 52. http://dx.doi.org/10.1186/1744-9081-3-52
- J. Bentham, “An Introduction to the Principles of Morals and Legislation,” In: The Utilitarians, Anchor Books, Garden City, 1973.
- T. Takahashi, “Loss of Self-Control in Intertemporal Choice May Be Attributable to Logarithmic Time-Perception,” Medical Hypotheses, Vol. 65, No. 4, 2005, pp. 691-693. http://dx.doi.org/10.1016/j.mehy.2005.04.040
- T. Takahashi, R. Han and F. Nakamura, “Time Discounting: Psychophysics of Intertemporal and Probabilistic Choices,” Journal of Behavioral Economics and Finance, Vol. 5, 2012, pp. 10-14.

