Applied Mathematics
Vol.4 No.10B(2013), Article ID:37455,15 pages DOI:10.4236/am.2013.410A2002
Dale’s Principle Is Necessary for an Optimal Neuronal Network’s Dynamics
Instituto de Matemática y Estadstica “Prof. Ing. Rafael Laguardia”, Universidad de la República, Montevideo, Uruguay
Email: eleonora@fing.edu.uy
Copyright © 2013 Eleonora Catsigeras. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 21, 2013; revised July 21, 2013; accepted July 28, 2013
Keywords: Neural Networks; Impulsive ODE; Discontinuous Dynamical Systems; Directed & Weighted Graphs; Mathematical Model in Biology
ABSTRACT
We study a mathematical model of biological neuronal networks composed by any finite number  of non-necessarily identical cells. The model is a deterministic dynamical system governed by finite-dimensional impulsive differential equations. The statical structure of the network is described by a directed and weighted graph whose nodes are certain subsets of neurons, and whose edges are the groups of synaptical connections among those subsets. First, we prove that among all the possible networks such as their respective graphs are mutually isomorphic, there exists a dynamical optimum. This optimal network exhibits the richest dynamics: namely, it is capable to show the most diverse set of responses (i.e. orbits in the future) under external stimulus or signals. Second, we prove that all the neurons of a dynamically optimal neuronal network necessarily satisfy Dale’s Principle, i.e. each neuron must be either excitatory or inhibitory, but not mixed. So, Dale’s Principle is a mathematical necessary consequence of a theoretic optimization process of the dynamics of the network. Finally, we prove that Dale’s Principle is not sufficient for the dynamical optimization of the network.
of non-necessarily identical cells. The model is a deterministic dynamical system governed by finite-dimensional impulsive differential equations. The statical structure of the network is described by a directed and weighted graph whose nodes are certain subsets of neurons, and whose edges are the groups of synaptical connections among those subsets. First, we prove that among all the possible networks such as their respective graphs are mutually isomorphic, there exists a dynamical optimum. This optimal network exhibits the richest dynamics: namely, it is capable to show the most diverse set of responses (i.e. orbits in the future) under external stimulus or signals. Second, we prove that all the neurons of a dynamically optimal neuronal network necessarily satisfy Dale’s Principle, i.e. each neuron must be either excitatory or inhibitory, but not mixed. So, Dale’s Principle is a mathematical necessary consequence of a theoretic optimization process of the dynamics of the network. Finally, we prove that Dale’s Principle is not sufficient for the dynamical optimization of the network.
1. Introduction
Based on experimental evidence, Dale’s Principle in Neuroscience (see for instance [1,2]) postulates that most neurons of a biological neuronal network send the same set of biochemical substances (called neurotransmitters) to the other neurons that are connected with them. Most neurons release more than one neurotransmitter, which is called the co-transmission” phenomenon [3,4], but the set of neurotransmitters is constant for each cell. Nevertheless, during plastic phases of the nervous systems, the neurotransmitters are released by certain groups of neurons change according to the development of the neuronal network. This plasticity allows the network perform diverse and adequate dynamical responses to external stimulus: Evidence suggests that during both development (in utero) and the postnatal period, the neurotransmitter phenotype of neurons is plastic and can be adapted as a function of activity or various environmental signals [4]. Also a certain phenotypic plasticity occurs in some cells of the nervous system of mature animals, suggesting that a dormant phenotype can be put in play by external inputs [4].
Some mathematical models of the neuronal networks represent them as deterministic dynamical systems (see for instance [5-8]). In particular, the dynamical evolution of the state of each neuron during the interspike intervals, and the dynamics of the bursting phenomenon, can be modelled by a finite-dimensional ordinary differential equation (see for instance [8,9] and in particular [10] for a mathematical model of a neuron as a dynamical system evolving on a multi-dimensional space). When considering a network of many neurons, the synaptical connections are frequently modelled by impulsive coupling terms between the equations of the many cells (see for instance [7,11-13]). In such a mathematical model, Dale’s Principle is translated into the following statement:
Dale’s Principle: Each neuron is either inhibitory or excitatory. We recall that a neuron 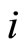 is called inhibitory (resp. excitatory) if its spikes produce, through the electro-biochemical actions that are transmitted along the axons of
is called inhibitory (resp. excitatory) if its spikes produce, through the electro-biochemical actions that are transmitted along the axons of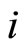 , only null or negative (resp. positive) changes in the membrane potentials of all the other neurons
, only null or negative (resp. positive) changes in the membrane potentials of all the other neurons 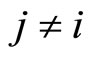 of the network. The amplitudes of those changes may depend on many variables. For instance, they may depend on the membrane instantaneous permeability of the receiving cell
of the network. The amplitudes of those changes may depend on many variables. For instance, they may depend on the membrane instantaneous permeability of the receiving cell . But the sign of the postsynaptical actions is usually only attributed to the electro-chemical properties of the substances that are released by the sending cell
. But the sign of the postsynaptical actions is usually only attributed to the electro-chemical properties of the substances that are released by the sending cell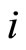 . In other words, the sign depends only on the set of neurotransmitters that are released by
. In other words, the sign depends only on the set of neurotransmitters that are released by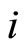 . Since this set of substances is fixed for each neuron
. Since this set of substances is fixed for each neuron 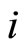 (if
(if 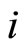 satisfies Dale’s Principle), the sign of its synaptical actions on the other neurons
satisfies Dale’s Principle), the sign of its synaptical actions on the other neurons  is fixed for each cell
is fixed for each cell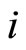 , and thus, independent of the receiving neuron
, and thus, independent of the receiving neuron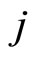 .
.
In this paper we adopt a simplified mathematical model of the neuronal network with a finite number 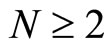 of neurons, by means of a system of deterministic impulsive differential equations. This model is taken from [11,13], with an adaptation that allows the state variable
of neurons, by means of a system of deterministic impulsive differential equations. This model is taken from [11,13], with an adaptation that allows the state variable 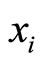 of each cell
of each cell  be multidimensional. Precisely
be multidimensional. Precisely 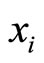 is a vector of finite dimension, or equivalently, a point in a finite-dimensional manifold of an Euclidean space. The finite dimension of the state variable
is a vector of finite dimension, or equivalently, a point in a finite-dimensional manifold of an Euclidean space. The finite dimension of the state variable 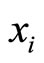 is larger or equal than 1, and besides, may depend on the neuron
is larger or equal than 1, and besides, may depend on the neuron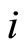 . The dynamical model of the network is the solution of a system of impulsive differential equations. This dynamics evolves on a product manifold whose dimension is the sum of the dimensions of the state variables of its
. The dynamical model of the network is the solution of a system of impulsive differential equations. This dynamics evolves on a product manifold whose dimension is the sum of the dimensions of the state variables of its 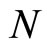 neurons.
neurons.
We do not assume a priori that the neurons of the network satisfy Dale’s Principle. In Theorem 16 we prove this principle a posteriori, as a necessary final consequence of a dynamical optimization process. We assume that during this process, a plastic phase of the neuronal network occurs, eventually changing the total numbers of neurons and synaptical connections, but such that the graph-scheme of the synaptic connections among groups of mutually identical cells remains unchanged. We assume that a maximal amount of dynamical richness is pursued during such a plastic development of the network. Then, by means of a rigourous deduction from the abstract mathematical model, we prove that, among all the mathematically theoretic networks  of such a model, those exhibiting an optimal dynamics (i.e. the richest or the most versatile dynamics) necessarily satisfy Dale’s Principle (Theorem 16).
of such a model, those exhibiting an optimal dynamics (i.e. the richest or the most versatile dynamics) necessarily satisfy Dale’s Principle (Theorem 16).
The mathematical criteria to decide the dynamical optimization is the following: First, in Definition 9, we classify all the theoretic neuronal networks (also those that hypothetically do not satisfy Dale’s Principle) into non countably many equivalence classes. Each class is a family of mutually equivalent networks, with respect to their internal synaptical connections among groups of cells (we call those groups of cells synaptical units in Definition 6). Second, in Definitions 11 and 14, we agree to say that a network  has an optimal dynamics conditioned to its class, if the dynamical system modelling any other network
has an optimal dynamics conditioned to its class, if the dynamical system modelling any other network 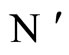 in the same class as
in the same class as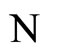 , has a space of orbits in the future that is a subset of the space of orbits of
, has a space of orbits in the future that is a subset of the space of orbits of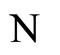 . In other words,
. In other words, 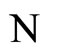 is the network capable to perform the richest dynamics, namely, the most diverse set of possible evolutions in the future among all the networks that are in the same class.
is the network capable to perform the richest dynamics, namely, the most diverse set of possible evolutions in the future among all the networks that are in the same class.
RESULTS TO BE PROVED
In Theorem 15 we prove that the theoretic dynamical optimum exists in any equivalence class of networks that have isomorphic synaptical graphs.
In Main Theorem 16 we prove that such an optimum is achieved only if the network  satisfies Dale’s Principle.
satisfies Dale’s Principle.
In Main Theorem 17 we prove that the converse of Theorem 16 is false: Dale’s Principle is not sufficient for a network exhibit the optimal dynamics within its synaptical equivalence class.
The results are abstract and theoretically deduced from the mathematical model. They are epistemologically suggestive since they give a possible answer to the following question:
Epistemological question: Why does Dale’s Principle hold for most cells in the nervous systems of animals?
Mathematically, the hypothesis of searching for an optimal dynamics implies (through Theorem 16) that at some step of the optimization process all the cells must satisfy Dale’s Principle. In other words, this principle would be a consequence, instead of a cause, of an optimization process during the plastic phase of the network. This conclusion holds under the hypothesis that the dynamical optimization (i.e. the maximum dynamical richness) is one of the natural pursued aims during a certain changeable development of the network.
Finally, we notice that the converse of Theorem 16 is false: there exist mathematical examples of simple abstract networks whose cells satisfy Dale’s Principle but are not dynamically optimal (Theorem 17). Thus, Dale’s Principle is necessary but not sufficient for the dynamical optimization of the network.
Structure of the paper and purpose of each section: In Section 2, we write the hypothesis of Main Theorems 16 and 17. This Section is necessary because the proofs of the theorems are deduced from the hypothesis. In other words, their statements could be false if not all the hypothesis holded.
From Section 3 to 6 we prove Main Theorem 16. The proof is developed in four steps, one in each separate section. The first step (Section 3) is devoted to prove the intermediate result of Proposition 7. The second step (Section 4) is deduced from Proposition 7. The third step (Section 5) is logically independent from the first and second steps, and is devoted to obtain the two intermediate results of Proposition 13 and Theorem 15. Section 6 exposes the fourth step (the end) of the proof of Main Theorem 16, from the logic junction of the previous three steps, using the intermediate results (Propositions 7 and 13, and Theorem 15).
On the one hand, the intermediate results (Propositions 7 and 13, and Theorem 15) are necessary stages in the logical process of our proof of Main Theorem 16 which ends in Section 6. In fact, Theorem 16 establishes that, if there exists a dynamical optimum within each synaptical equivalence class of networks, this optimal network necessarily satisfy Dale’s Principle. But this result would be void if we did not prove (as an intermediate step), that a dynamically optimal network exists (Theorem 15). It would be also void if we did not prove that the synaptical equivalence classes of networks exist (Definition 9). The synaptical equivalence classes of networks could not been defined if the inter-units graph of the network did not existed (Definition 8). And these graphs exist as an immediate corollary of Proposition 7. So, Proposition 7 must be proved as an intermediate step for our final purpose. Finally, the end of the proof of Main Theorem 16 argues by contradiction: if the dynamically optimal network did not satisfy Dale’s Principle, then Proposition 13 would be false. So, we need first, also as an intermediate step, to prove Proposition 13.
On the other hand, to prove all the required intermediate results, we need some other (previous) mathematical statements from which we deduce the intermediate results. So, we start posing all the previous mathematical statements (obtaining them from the general hypothesis of Section 2), in a series of mathematical definitions, comments and remarks that are at the beginning of Sections 3, 4 and 5.
In Section 7, we end the proof of Main Theorem 17 stating that Dale’s Principle is not sufficient for the dynamical optimization. Its final statement is proved by applying directly some of the definitions, intermediate results and examples of Sections 3, 4 and 5 (in particular, those of Figures 1-3).
Finally, in Section 8 we write the conclusions obtained from all the mathematical results that are proved along the paper.
2. The Hypothesis (The Model by a System of Impulsive Differential Equations)
We assume a simplified (but very general) mathematical model of the neuronal network which is defined along this section. The model, up to an abstract reformulation, and a generalization that allows any finite dimension for the impulsive differential equation governing each neuron, is taken from [11] and [13]. In the following subsections we describe the mathematical assumptions of this model:
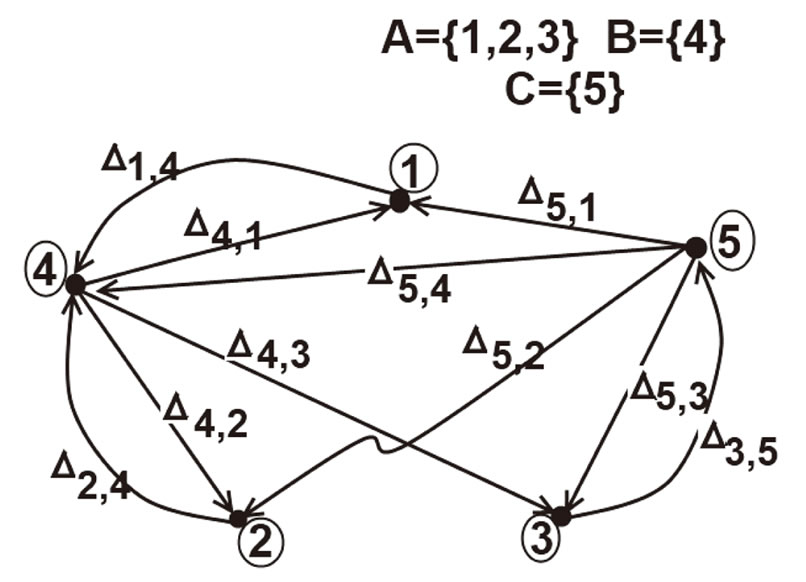
Figure 1. The graph of a network . The directed and weighted edges correspond to the nonzero synaptical interactions
. The directed and weighted edges correspond to the nonzero synaptical interactions  among the neurons
among the neurons .
.
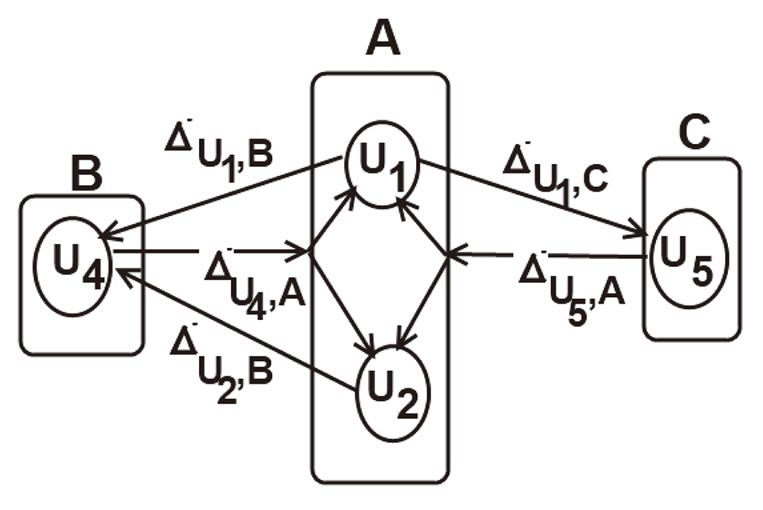
Figure 2. The inter-units graph of the network  of Figure 0. It is composed by three homogeneous parts
of Figure 0. It is composed by three homogeneous parts ,
, 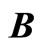 and
and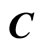 . The part
. The part 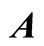 is composed by two synaptical units
is composed by two synaptical units  and
and , the part
, the part  is the single unit
is the single unit  and the part
and the part  is the single unit
is the single unit .
.
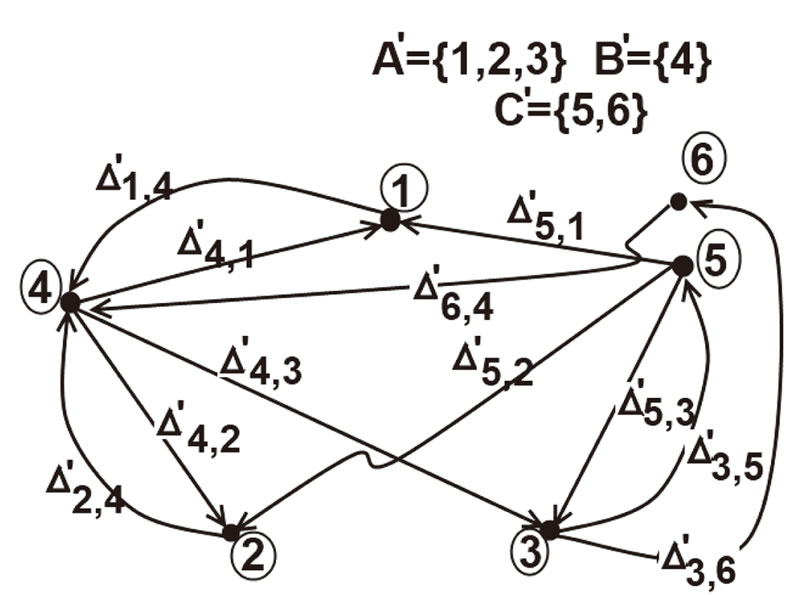
Figure 3. The graph of a network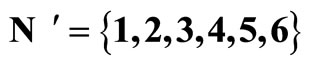 . It is composed by three homogeneous parts
. It is composed by three homogeneous parts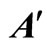 ,
, 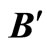 and
and . This network
. This network 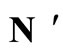 is synaptically equivalent to the network
is synaptically equivalent to the network 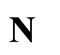 of Figure 1.
of Figure 1.
2.1. Model of an Isolated Neuron
Each neuron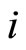 , while it does not receive synaptical actions from the other cells of the network, and while its membrane potential is lower than a (maximum) threshold level
, while it does not receive synaptical actions from the other cells of the network, and while its membrane potential is lower than a (maximum) threshold level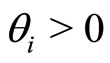 , and larger than a lower bound
, and larger than a lower bound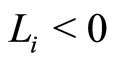 , is assumed to be governed by a finite-dimensional differential equation of the form
, is assumed to be governed by a finite-dimensional differential equation of the form
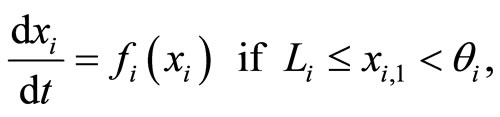 (1)
(1)
where 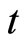 is time,
is time, 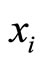 is a finite-dimensional vector
is a finite-dimensional vector 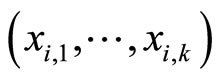 whose components are real variables that describe the instantaneous state of the cell
whose components are real variables that describe the instantaneous state of the cell , and
, and 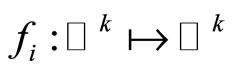 is a Lipschitz continuous function giving the velocity vector
is a Lipschitz continuous function giving the velocity vector 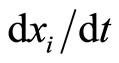 of the changes in the state of the cell
of the changes in the state of the cell , as a function of its instantaneous vectorial value
, as a function of its instantaneous vectorial value . The function
. The function 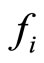 is the so called vector field in the phase space of the cell
is the so called vector field in the phase space of the cell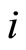 . This space is assumed to be a finite dimensional compact manifold. The advantages of considering that
. This space is assumed to be a finite dimensional compact manifold. The advantages of considering that 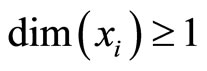 (not necessarily 1) are, among others, the possibility of showing dynamical bifurcations between different rythms and oscillations that appear in some biological neurons [10], that would not appear if the mathematical model of all the neurons were necessarily onedimensional.
(not necessarily 1) are, among others, the possibility of showing dynamical bifurcations between different rythms and oscillations that appear in some biological neurons [10], that would not appear if the mathematical model of all the neurons were necessarily onedimensional.
One of the components of the vectorial state variable 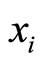 (which with no loss of generality we take as the first component
(which with no loss of generality we take as the first component ) is the instantaneous membrane potential
) is the instantaneous membrane potential 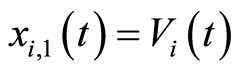 of the cell
of the cell .
.
In the sequel, we denote  and
and 
In addition to the differential equation (1), it is assumed the following spiking condition [9]: If there exists an instant 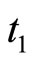 such that the potential
such that the potential 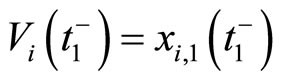 equals the threshold level
equals the threshold level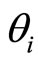 , then
, then . In brief, the following logic assertion holds, by hypothesis:
. In brief, the following logic assertion holds, by hypothesis:
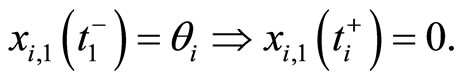 (2)
(2)
Here, 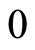 is the reset value. It is normalized to be zero after a change of variables, if necessary, that refers the difference of membrane potential of the cell
is the reset value. It is normalized to be zero after a change of variables, if necessary, that refers the difference of membrane potential of the cell 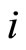 to the reset value. A more realistic model would consider a positive relatively short time-delay
to the reset value. A more realistic model would consider a positive relatively short time-delay 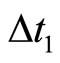 between the instant
between the instant 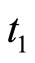 when the membrane potential arrives to the threshold level
when the membrane potential arrives to the threshold level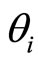 , and the instant
, and the instant  for which the potential takes its reset value
for which the potential takes its reset value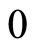 . During this short time-delay, the membrane potential shows an abrupt pulse of large amplitude, which is called spike of the neuron
. During this short time-delay, the membrane potential shows an abrupt pulse of large amplitude, which is called spike of the neuron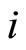 . The impulsive simplified model approximates the spike to an abrupt discontinuity jump, by taking the time-delay
. The impulsive simplified model approximates the spike to an abrupt discontinuity jump, by taking the time-delay 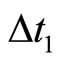 equal to zero. Then, the spike becomes an instantaneous jump of the membrane potential
equal to zero. Then, the spike becomes an instantaneous jump of the membrane potential 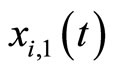 from the level
from the level  to the reset value
to the reset value 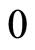 which occurs at
which occurs at 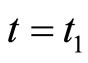 according to condition (2).
according to condition (2).
We denote by 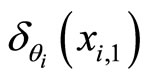 the Dirac delta supported on
the Dirac delta supported on . Namely
. Namely 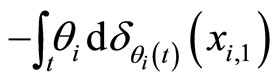 (via the abstract integration theory with respect to the Dirac delta probability measure) denotes a discontinuity step
(via the abstract integration theory with respect to the Dirac delta probability measure) denotes a discontinuity step 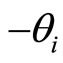 that occurs on the potential
that occurs on the potential 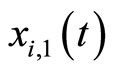 at each instant
at each instant 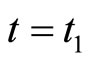 such that
such that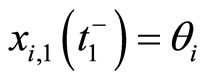 . In other words:
. In other words:
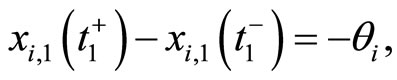
and so
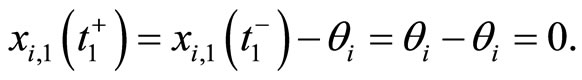
After the above notation is adopted, the dynamics of each cell 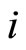 (while isolated from the other cells of the network) is modelled by the following impulsive differential equation:
(while isolated from the other cells of the network) is modelled by the following impulsive differential equation:
 (3)
(3)
In the above equality 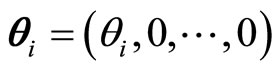 is the jump vector with dimension equal to the dimension of the state variable
is the jump vector with dimension equal to the dimension of the state variable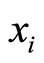 . Namely, at each spiking instant, only the first component
. Namely, at each spiking instant, only the first component 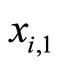 (the membrane potential) is abruptly reset, since the jump vector has all the other components equal to zero.
(the membrane potential) is abruptly reset, since the jump vector has all the other components equal to zero.
Strictly talking, the Equation (3) is not a differential equation, but the hybrid between the differential equation 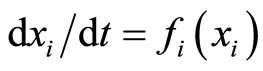 plus a rule, denoted by
plus a rule, denoted by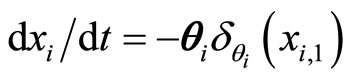 . This impulsive rule imposes a discontinuity jump of amplitude vector
. This impulsive rule imposes a discontinuity jump of amplitude vector 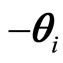 in the dependence of the state variable
in the dependence of the state variable 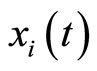 on
on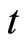 . Therefore,
. Therefore,  is not continuous, and thus it is not indeed differentiable. It is in fact discontinuous at each instant
is not continuous, and thus it is not indeed differentiable. It is in fact discontinuous at each instant 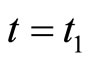 such that
such that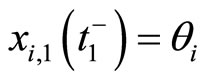 , i.e. when the Dirac delta
, i.e. when the Dirac delta 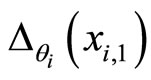 is not null.
is not null.
Nevertheless, the theory of impulsive differential equations follows similar rules than the theory of ordinary differential equations. It was early initiated by Milman and Myshkis [14], cited in [15]. In particular, the existence and uniqueness of solution for each initial condition, and theorems of stability, still hold for the impulsive differential Equation (3), as if it were an ordinary differential equation [14,15].
2.2. Model of the Synaptical Interactions among the Neurons
The synaptical interactions are modelled by the following rule: If the membrane potential 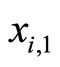 of some neuron
of some neuron 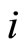 arrives to (or exceeds) its threshold level
arrives to (or exceeds) its threshold level  at instant
at instant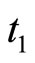 , then the cell
, then the cell 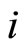 sends an action
sends an action  to the other neurons
to the other neurons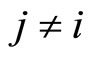 . In particular
. In particular 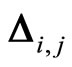 may be zero if no synaptical connection exists from the cell
may be zero if no synaptical connection exists from the cell 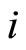 to the cell
to the cell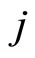 . This action produces a discontinuity jump in the membrane potential
. This action produces a discontinuity jump in the membrane potential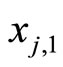 . We denote by
. We denote by 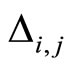 the signed amplitude of the discontinuity jump on the membrane potential
the signed amplitude of the discontinuity jump on the membrane potential 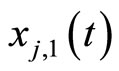 of the neuron
of the neuron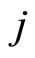 , which is produced by the synaptical action from the neuron
, which is produced by the synaptical action from the neuron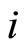 , when
, when 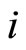 spikes. The real value
spikes. The real value 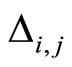 may depend on the instantaneous state
may depend on the instantaneous state 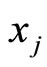 of the receiving neuron
of the receiving neuron 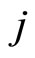 just before the synaptic action from neuron
just before the synaptic action from neuron 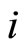 arrives. For simplicity we do not explicitly write this dependence. Thus, the symbol
arrives. For simplicity we do not explicitly write this dependence. Thus, the symbol  denotes a real function of
denotes a real function of , which we assume to be either identically null or with constant sign.
, which we assume to be either identically null or with constant sign.
We denote by  the discontinuity jump vector, with dimension equal to the dimension of the variable state
the discontinuity jump vector, with dimension equal to the dimension of the variable state 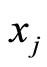 of the cell
of the cell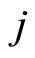 . In other words, the discontinuity jump in the instantaneous vector state
. In other words, the discontinuity jump in the instantaneous vector state 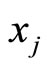 of the cell
of the cell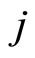 , that is produced when the cell
, that is produced when the cell 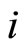 spikes, is null on all the components of
spikes, is null on all the components of  except the first one
except the first one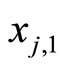 , i.e. except on the membrane potential of the neuron
, i.e. except on the membrane potential of the neuron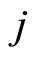 . In formulae:
. In formulae:
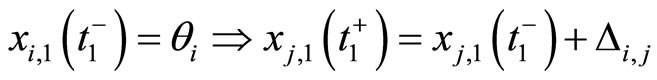
 (4)
(4)
Thus, the dynamics of the whole neuronal network is modelled by the following system of impulsive differential equations:
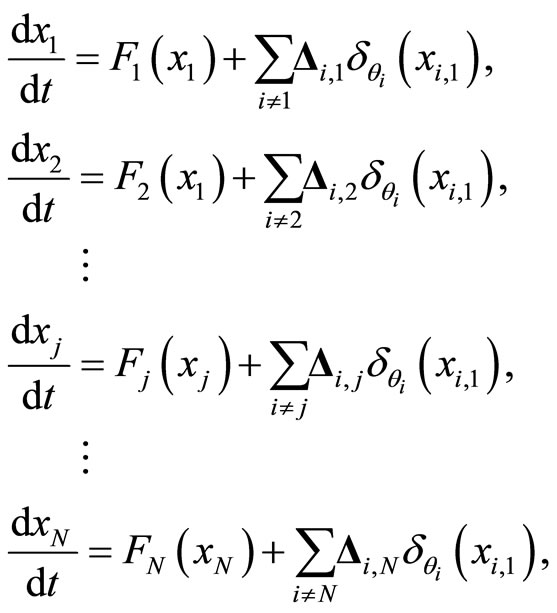 (5)
(5)
where 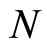 is the number of cells in the network.
is the number of cells in the network.
Definition 1 (Excitatory, inhibitory and mixed neurons) The synapses from cell 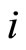 to
to 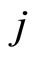 is called excitatory if
is called excitatory if  and it is called inhibitory if
and it is called inhibitory if . If
. If 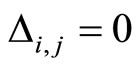 then there does not exist synaptical action from the cell
then there does not exist synaptical action from the cell  to the cell
to the cell . A neuron
. A neuron  is called excitatory (resp. inhibitory) if
is called excitatory (resp. inhibitory) if 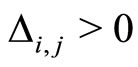 (resp.
(resp.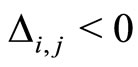 ) for all
) for all  such that
such that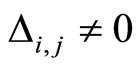 . The cell
. The cell 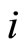 is called mixed if it is neither excitatory nor inhibitory. Dale’s Principle (which we do not assume a priori to hold) states that no neuron is mixed.
is called mixed if it is neither excitatory nor inhibitory. Dale’s Principle (which we do not assume a priori to hold) states that no neuron is mixed.
Remark 2 It is not restrictive to assume that no cell 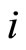 is indifferent, namely no cell
is indifferent, namely no cell  sends null synaptical actions to all the other cells, i.e.
sends null synaptical actions to all the other cells, i.e.
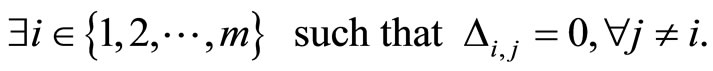
In fact, if there existed such a cell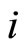 , it would not send any action to the other cells of the network
, it would not send any action to the other cells of the network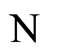 . So, the global dynamics of the network is not modified (except for having one less variable) if we take out the cell
. So, the global dynamics of the network is not modified (except for having one less variable) if we take out the cell  from
from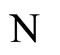 .
.
All along the paper we assume that the network 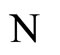 has at least 2 neurons and no neuron is indifferent.
has at least 2 neurons and no neuron is indifferent.
2.3. The Refractory Rule
To obtain a well defined deterministic dynamics from the system (5), other complementary assumptions are adopted by the model. First, a refractory phenomenon (see for instance [16, page 725]) is considered as follows: If some fixed neuron 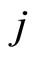 spikes at instant
spikes at instant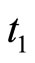 , then its potential
, then its potential  is reset to zero becoming indifferent to the synaptical actions that it may receive (at the same instant
is reset to zero becoming indifferent to the synaptical actions that it may receive (at the same instant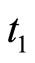 ) from the other neurons. Second, if for some fixed neuron
) from the other neurons. Second, if for some fixed neuron 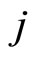 at some instant
at some instant , the sum
, the sum 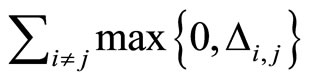 of the excitatory actions that
of the excitatory actions that 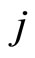 simultaneously receives from the other neurons of the network, is larger or equal than
simultaneously receives from the other neurons of the network, is larger or equal than , then
, then 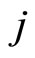 itself spikes at instant
itself spikes at instant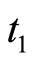 , regardless whether
, regardless whether  or not. In this case, at instant
or not. In this case, at instant  the cell
the cell 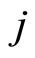 sends synaptical actions
sends synaptical actions 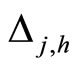 to the other neurons
to the other neurons 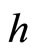 of the network, and then, the respective potentials
of the network, and then, the respective potentials  will suffer a jump
will suffer a jump  at instant
at instant . This process may make new neurons
. This process may make new neurons 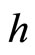 to spike in an avalanche process (see [13]). This avalanche is produced instantaneously, when some excitatory neuron spontaneously arrived to its threshold level. But due to the refractory rule, once each neuron spikes, its membrane potential refracts all the excitations or inhibitions that come at the same instant. So, the avalanche phenomenon is produced instantaneously, but includes each neuron
to spike in an avalanche process (see [13]). This avalanche is produced instantaneously, when some excitatory neuron spontaneously arrived to its threshold level. But due to the refractory rule, once each neuron spikes, its membrane potential refracts all the excitations or inhibitions that come at the same instant. So, the avalanche phenomenon is produced instantaneously, but includes each neuron  at most once. Then, each interaction term
at most once. Then, each interaction term 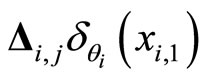 in the sum at right of Equation (5) is added only once at each spiking instant
in the sum at right of Equation (5) is added only once at each spiking instant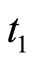 .
.
3. First Step of the Proof (Graphs, Parts and Units)
The purpose of this section is to prove Proposition 7 and to state the existence of an Inter-units Graph (Definition 8). These are intermediate results (the first step) of the proof of Main Theorems 16 and 17. We will prove these intermediate results by logical deduction from several previous statements and hypothesis. So, we start by including the needed previous statements in the following series of mathematical definitions:
Let  be a network of
be a network of 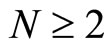 neurons, according to the model defined in Section 2.
neurons, according to the model defined in Section 2.
Definition 3 (The Network’s Graph) We call a directed and weighted graph 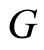 the graph of the network
the graph of the network  if the vertices of
if the vertices of 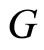 are the cells
are the cells  of
of , each edge
, each edge 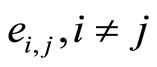 of
of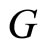 , corresponds to each nonzero synaptical action from the cell
, corresponds to each nonzero synaptical action from the cell 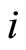 to the cell
to the cell 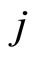 and conversely, and
and conversely, and 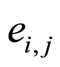 has weight
has weight . (See the example of Figure 1.)
. (See the example of Figure 1.)
To unify the notation, we agree:
•  denotes either the network or its graph;
denotes either the network or its graph;
• 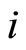 is either a cell of
is either a cell of  or a node of the graph;
or a node of the graph;
•  denotes either the synaptical action from
denotes either the synaptical action from  to
to , or the weight of the edge
, or the weight of the edge  in the graph, or this edge itself.
in the graph, or this edge itself.
Definition 4 (Structurally identical cells) Two different cells  are structurally identical if
are structurally identical if  in the respective differential Equations (3),
in the respective differential Equations (3), 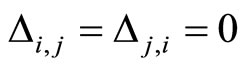 , and
, and 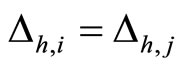 for all
for all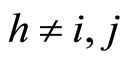 . These conditions imply that the dynamical systems that governs neurons
. These conditions imply that the dynamical systems that governs neurons 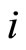 and
and 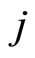 are the same. So, their future dynamics may differ only because their initial states
are the same. So, their future dynamics may differ only because their initial states 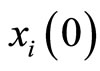 and
and 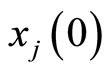 may be different. Note that, if
may be different. Note that, if  and
and  are structurally identical, then by definition, the edges of the graph at the receiving nodes
are structurally identical, then by definition, the edges of the graph at the receiving nodes 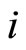 and
and  (from any other fixed sending node
(from any other fixed sending node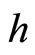 ) are respectively equally weighted by
) are respectively equally weighted by . Nevertheless, the edges from
. Nevertheless, the edges from 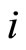 and
and , as sending nodes of the network, are not necessarily identically weighted, i.e.
, as sending nodes of the network, are not necessarily identically weighted, i.e.  may be different from
may be different from .
.
In Figure 1 we represent a graph 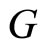 with three mutually identical cells 1, 2 and
with three mutually identical cells 1, 2 and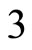 , provided that
, provided that 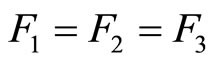 in the Equation (3) and
in the Equation (3) and  for
for . Besides, the graph
. Besides, the graph 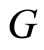 has two other nodes, which corresponds to the neurons
has two other nodes, which corresponds to the neurons  and
and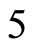 . The cells
. The cells  and
and 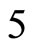 are not mutually identical because the synaptical actions that they receive from the other cells are not equal.
are not mutually identical because the synaptical actions that they receive from the other cells are not equal.
The above definitions and the following ones are just mathematical tools, with no other purpose than enabling us to prove Theorems 16 and 17. They are not aimed to explain physiological or functional roles of subsets of real biological neurons in the brain or in the nervous system. Nevertheless, it is rather surprising that the following abstract mathematical tools, which we include here just to prove Theorems 16 and 17, have indeed a resemblance with concepts or phenomena that are studied by Neuroscience. In particular, the following Definitions 5 and 6 of homogeneous part and synaptical unit of a neuronal network, are roughly analogous to the concepts of regions, subnetworks or groups of many similar neurons, characterized by a certain structure and a collective physiological role. For instance some subnetworks or layers of biological or artificial neurons are defined according to the role of their synaptical interactions with other subnetworks or layers [17].
Definition 5 (Homogeneous Part) An homogeneous part of the neuronal network is a maximal subset of cells of the network that are mutually pairwise identical (cf. Definition 4). As a particular case, we agree to say that an homogeneous part is composed by a single neuron  when no other neuron is structurally identical to
when no other neuron is structurally identical to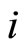 . In Figure 1 we draw the graph of a network composed by three homogeneous parts
. In Figure 1 we draw the graph of a network composed by three homogeneous parts 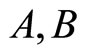 and
and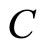 . The homogeneous part
. The homogeneous part 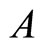 is composed by the three identical neurons 1, 2 and 3, provided that
is composed by the three identical neurons 1, 2 and 3, provided that 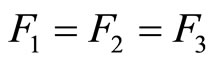 and
and 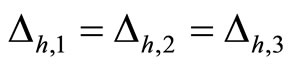 for
for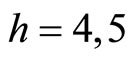 . The homogeneous parts
. The homogeneous parts 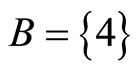 and
and  have a single neuron each because
have a single neuron each because 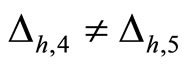 for some
for some  (for instance for
(for instance for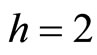 ).
).
Definition 6 Synaptical Unit A synaptical unit is a subset  of an homogeneous part
of an homogeneous part 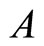 of a neuronal network such that:
of a neuronal network such that:
• For any neuron 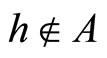 there exists at most one neuron
there exists at most one neuron 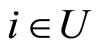 such that
such that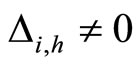 .
.
• 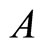 is partitioned in a minimal number of sets
is partitioned in a minimal number of sets 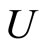 possessing the above property.
possessing the above property.
In particular, a synaptical unit may be composed by a single neuron. This occurs, for instance, when for some neuron 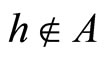 and for any neuron
and for any neuron 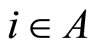 the synaptical interaction
the synaptical interaction 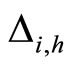 from
from  to
to  is nonzero. In Figure 1 we draw the graph of a network composed by three homogeneous parts
is nonzero. In Figure 1 we draw the graph of a network composed by three homogeneous parts ,
, 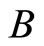 and
and 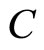 such that:
such that: 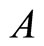 is composed by three identical neurons 1, 2 and 3, that form two synaptical units
is composed by three identical neurons 1, 2 and 3, that form two synaptical units  and
and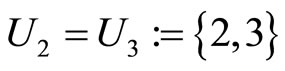 . In fact, the cells
. In fact, the cells 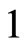 and
and 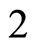 can not belong to the same unit because there exist nonzero actions departing from both of them to neuron
can not belong to the same unit because there exist nonzero actions departing from both of them to neuron . One can also form the two synaptical units of
. One can also form the two synaptical units of  by defining
by defining 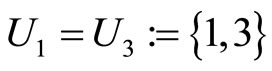 and
and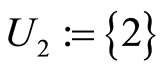 . The homogeneous part
. The homogeneous part 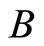 is composed by a single neuron
is composed by a single neuron , and thus, it is a singe synaptical unit
, and thus, it is a singe synaptical unit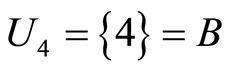 . Analogously
. Analogously 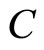 is composed by a single neuron
is composed by a single neuron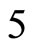 , and thus it is a single synaptical unit
, and thus it is a single synaptical unit . The total number of neurons of the network in Figure 1 is 5, the total number of synaptical units is 4, the total number of homogeneous parts is 3, the total number of nonzero synaptical interactions among the neurons is 9, but the total number of synaptical interactions among different homogeneous parts is only 5 (see Figure 2).
. The total number of neurons of the network in Figure 1 is 5, the total number of synaptical units is 4, the total number of homogeneous parts is 3, the total number of nonzero synaptical interactions among the neurons is 9, but the total number of synaptical interactions among different homogeneous parts is only 5 (see Figure 2).
When a synaptical unit 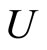 has more neurons, the following quotient
has more neurons, the following quotient 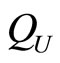 diminishes:
diminishes: 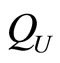 is the number of synaptical connections departing from the cells of
is the number of synaptical connections departing from the cells of 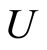 divided by the total number of neurons of
divided by the total number of neurons of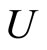 . In fact, by Definition 6, for each synaptical unit
. In fact, by Definition 6, for each synaptical unit 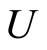 there exists at most one nonzero synaptical action to any other fixed neuron
there exists at most one nonzero synaptical action to any other fixed neuron 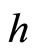 of the network, regardless how many cells compose
of the network, regardless how many cells compose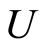 . So, if we enlarge the number of cells in
. So, if we enlarge the number of cells in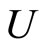 , the number of nonzero synaptical actions departing from the cells of
, the number of nonzero synaptical actions departing from the cells of 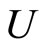 remains constant. Thus, the quotient
remains constant. Thus, the quotient 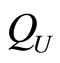 diminishes. Although this quotient
diminishes. Although this quotient  becomes smaller when the number of neurons of the synaptical unit
becomes smaller when the number of neurons of the synaptical unit 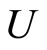 enlarges, in Theorem 15 we will rigourously prove the following result:
enlarges, in Theorem 15 we will rigourously prove the following result:
The dynamical system governing a neuronal network 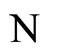 with the maximum number of neurons in each of its synaptical units, is the richest one, i.e.
with the maximum number of neurons in each of its synaptical units, is the richest one, i.e. 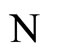 will exhibit the largest set of different orbits in the future, and so it will be theoretically capable to perform the most diverse set of processes.
will exhibit the largest set of different orbits in the future, and so it will be theoretically capable to perform the most diverse set of processes.
The following result proves that any neuronal network, according to the mathematical model of Section 2, is decomposed as the union of at least two homogeneous parts, and each of these parts is decomposed into pairwise disjoint synaptical units. It also states the existence of an upper bound for the number of neurons that any synaptical unit can have.
Proposition 7 (Intermediate result in the proof of Main Theorems 16 and 17)
Let  be any network according to the mathematical model defined in Section 2. Then:
be any network according to the mathematical model defined in Section 2. Then:
1) The set of neurons of 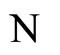 is the union of exactly
is the union of exactly 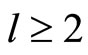 pairwise disjoint homogeneous parts.
pairwise disjoint homogeneous parts.
2) Each homogeneous part 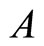 is the union of a positive finite number of pairwise disjoint synaptical units.
is the union of a positive finite number of pairwise disjoint synaptical units.
3) The total number of neurons of each synaptical unit is at least one and at most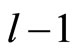 .
.
4) For each synaptical unit 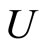 and for each homogeneous part
and for each homogeneous part  there exists a unique real number
there exists a unique real number 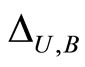 that satisfies the following properties:
that satisfies the following properties:
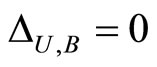 if and only if
if and only if  for all
for all  and for all
and for all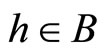 . In particular
. In particular  if
if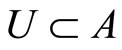 .
.
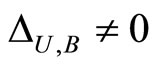 if and only if
if and only if 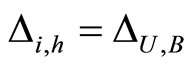 for one and only one neuron
for one and only one neuron 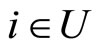 and for all
and for all , and
, and 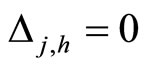 for all
for all 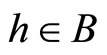 and all
and all  such that
such that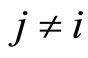 .
.
Proof: 1) We denote 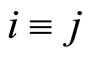 if the cells
if the cells 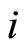 and
and 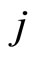 are structurally identical according to Definition 4. We add the rule
are structurally identical according to Definition 4. We add the rule 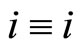 for any cell
for any cell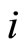 . Thus,
. Thus, 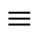 is an equivalence relation. From Definition 5 the
is an equivalence relation. From Definition 5 the 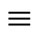 classes of neurons are the homogeneous parts of the network.
classes of neurons are the homogeneous parts of the network.
Since the equivalence classes of any equivalence relation in any set determine a partition of this set, then the network, as a set of neurons, is the union of its pairwise disjoint homogeneous parts. Denote by  the total number of different homogeneous parts that compose the network. Let us prove that
the total number of different homogeneous parts that compose the network. Let us prove that . In fact, if
. In fact, if  were equal to 1, then, by Definition 4,
were equal to 1, then, by Definition 4, 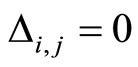 for any pair of cells, contradicting the assumption that no cell is indifferent (see the end of Remark 2). We have proved Assertion 1).
for any pair of cells, contradicting the assumption that no cell is indifferent (see the end of Remark 2). We have proved Assertion 1).
2) Fix an homogeneous part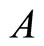 , and fix some neuron
, and fix some neuron . Consider the set of neurons
. Consider the set of neurons . The set
. The set 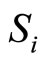 is nonempty because the cell
is nonempty because the cell 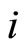 is not indifferent (see Remark 2). Choose and fix a neuron
is not indifferent (see Remark 2). Choose and fix a neuron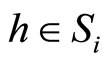 . We discuss two cases: either
. We discuss two cases: either 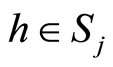 for all
for all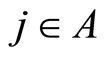 , or the set
, or the set 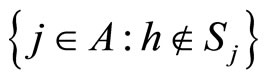 is nonempty.
is nonempty.
In the first case, for each neuron 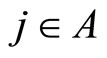 the singleton
the singleton 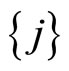 (formed by the single element
(formed by the single element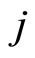 ), satisfies Definition 6. Thus,
), satisfies Definition 6. Thus,  is a synaptical unit for all
is a synaptical unit for all 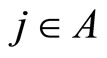 and assertion 2) is proved.
and assertion 2) is proved.
In the second case, consider the set 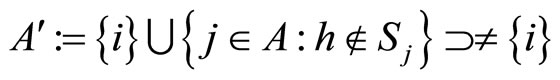 . Consider also (if they exist) all the singletons
. Consider also (if they exist) all the singletons 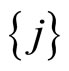 where
where 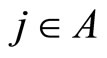 is such that
is such that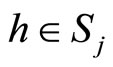 . These latter sets
. These latter sets 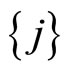 satisfy Definition 6 and, thus, they are pairwise disjoint synaptical units, which are also disjoint with
satisfy Definition 6 and, thus, they are pairwise disjoint synaptical units, which are also disjoint with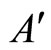 . Besides, their union with
. Besides, their union with 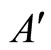 compose
compose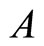 . So, it is now enough to prove that
. So, it is now enough to prove that  is also the union of pairwise disjoint synaptical units.
is also the union of pairwise disjoint synaptical units.
Now, we choose and fix a neuron  such that
such that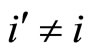 . (Such a neuron exists because
. (Such a neuron exists because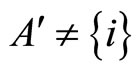 ). By construction of the set
). By construction of the set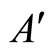 , we have
, we have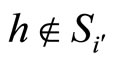 . But, since the neuron
. But, since the neuron 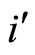 is not indifferent, there exists
is not indifferent, there exists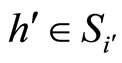 . So, we can repeat the above argument putting
. So, we can repeat the above argument putting 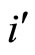 in the role of
in the role of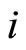 ,
, 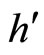 in the role of
in the role of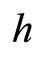 , and
, and 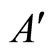 in the role of
in the role of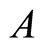 .
.
Since the number of neurons is finite, after a finite number of steps (repeating the above argument at each step), we obtain a decomposition of  into a finite number of pairwise disjoint sets that are synaptical units, ending the proof of Assertion 2).
into a finite number of pairwise disjoint sets that are synaptical units, ending the proof of Assertion 2).
3) Let 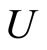 be a synaptical unit. By Definition 6,
be a synaptical unit. By Definition 6, 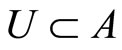 where
where  is an homogeneous part of the set of neurons. By Assertion 1) there are exactly
is an homogeneous part of the set of neurons. By Assertion 1) there are exactly 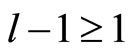 other homogeneous parts
other homogeneous parts . From Definitions 4 and 5, for any fixed
. From Definitions 4 and 5, for any fixed 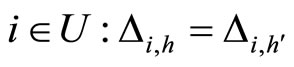 for all
for all . So, for each
. So, for each  we denote
we denote
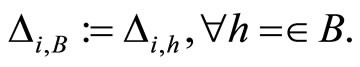
Since any neuron 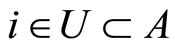 is not indifferent, there exists at least one homogeneous part
is not indifferent, there exists at least one homogeneous part  such that
such that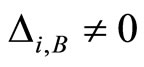 . Besides, applying Definition 6, for each homogeneous part
. Besides, applying Definition 6, for each homogeneous part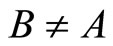 , there exists at most one neuron
, there exists at most one neuron 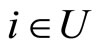 such that
such that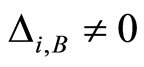 . The last two assertions imply that there is a one-to-one correspondence (which is not necessarily surjective) from the set of neurons in
. The last two assertions imply that there is a one-to-one correspondence (which is not necessarily surjective) from the set of neurons in 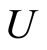 to the set of homogeneous parts that are different from
to the set of homogeneous parts that are different from . Then, the number of neurons in
. Then, the number of neurons in 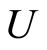 is not larger than the number of existing homogeneous parts
is not larger than the number of existing homogeneous parts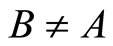 , i.e. it is not larger than
, i.e. it is not larger than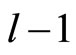 . We have proved Assertion 3).
. We have proved Assertion 3).
4) Fix an arbitrary synaptical unit  (where
(where  is the homogeneous part that contains
is the homogeneous part that contains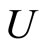 ) and an arbitrary homogeneous part
) and an arbitrary homogeneous part 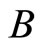 (in particular,
(in particular, 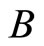 may be
may be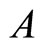 ). As in the above proof of Assertion 3), for each neuron
). As in the above proof of Assertion 3), for each neuron  it is defined
it is defined 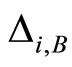 such that
such that  for all
for all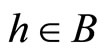 . By Definition 6, either
. By Definition 6, either 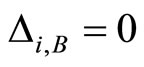 for all
for all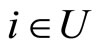 , or
, or 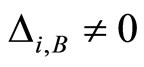 for one and only one cell
for one and only one cell . In the first case we define
. In the first case we define 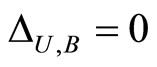 and in the second case we define
and in the second case we define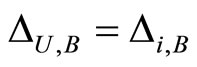 . By construction, Assertion (iv) holds: in particular, from Definitions 4 and 5, we have
. By construction, Assertion (iv) holds: in particular, from Definitions 4 and 5, we have 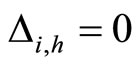 for all
for all  and for all
and for all . So,
. So, 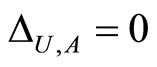 if
if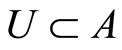 .□
.□
Definition 8 (Inter-units graph—Intermediate result in the proof of Theorems 16 and 17) As a consequence of Proposition 7 the graph of a neuronal network 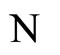 can be represented by a simpler one, which we call the inter-units graph. This is, by definition, the graph whose nodes are not the cells but the synaptical units. Each directed and weighted edge in the inter-units graph, links a synaptical unit
can be represented by a simpler one, which we call the inter-units graph. This is, by definition, the graph whose nodes are not the cells but the synaptical units. Each directed and weighted edge in the inter-units graph, links a synaptical unit 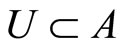 with the synaptical unit
with the synaptical unit 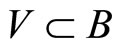
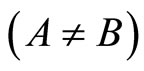 . It is weighted by the synaptical action
. It is weighted by the synaptical action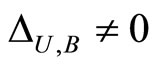 . For instance, the network
. For instance, the network 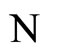 of Figure 1 is represented by the inter-units graph of Figure 2.
of Figure 1 is represented by the inter-units graph of Figure 2.
Interpretation: The inter-units graph of a neuronal network, according to Definition 8, recovers the essential anatomy of the spatial distribution of the synaptical connections of the network, among groups of mutually identical cells (the so called synaptical units). This description, by means of the inter-units graph, recalls experimental studies on the synaptical activity of some neuronal subnetworks of the brain. For instance, in [17], Megas et al. study the spatial distribution of inhibitory and excitatory synapses inside the hippocampus.
Each synaptical unit acts, in the inter-units graph, as if it were a single neuron. The spatial statical structure of groups of synaptical connections is the only observed object by this graph. Besides, the inter-units graph does not change if the number of neurons composing each of the many synaptical units, change. In the following section, we will condition the study of the networks to those that have mutually isomorphic inter-units graphs, i.e. they have the same statical structure of synaptical connections among groups of identical cells.
In Section 5, we will look on the dynamical responses of the network that have the same (statical) inter-units graph of synaptical connections. Any change in the number of neurons will change the space of possible initial states, and so the space of possible orbits and the global dynamics. So, among all the networks that have isomorphic inter-units graphs, the network with more neurons should, a priori, exhibit a larger diversity of theoretic possible dynamical responses to external stimulus.
For instance, two identical neurons  and
and 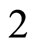 in a synaptical unit
in a synaptical unit  define a space of initial states (and so of orbits) that is composed by all the pairs
define a space of initial states (and so of orbits) that is composed by all the pairs 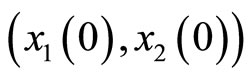 of vectors in the phase space of each neuron. But three identical neurons
of vectors in the phase space of each neuron. But three identical neurons ,
, 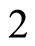 and
and 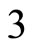 in
in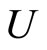 , define a space of initial states composed by all the triples
, define a space of initial states composed by all the triples 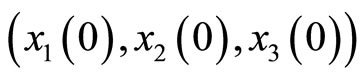 of vectors. So, the diversity of orbits that a neuronal network can exhibit, enlarges if the number of neurons of each synaptical unit enlarges. In Section 5, we will study the theoretical optimum in the dynamical response of a family of networks that are synaptical equivalent. We will prove that this optimum exists and that it is achieved when the network has the maximum number of cells (Theorem 15).
of vectors. So, the diversity of orbits that a neuronal network can exhibit, enlarges if the number of neurons of each synaptical unit enlarges. In Section 5, we will study the theoretical optimum in the dynamical response of a family of networks that are synaptical equivalent. We will prove that this optimum exists and that it is achieved when the network has the maximum number of cells (Theorem 15).
4. Second Step of the Proof (Synaptical Equivalence between Networks)
The purpose of this section is to prove the existence of an equivalence relation (Definition 9) in the space of all the neuronal networks modelled by the mathematical hypothesis of Section 2. This is the intermediate result in the second step of the proof of Main Theorems 16 and 17. We will deduce this intermediate result from the previous ones obtained in Section 3.
Let  and
and  be two neuronal networks according to the model defined in Section 2. Denote:
be two neuronal networks according to the model defined in Section 2. Denote:
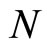 and
and  the numbers of neurons of
the numbers of neurons of  and
and 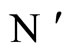 respectively,
respectively,
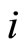 and
and 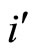 a (general) neuron of
a (general) neuron of 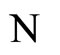 and
and 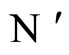 respectively,
respectively,
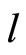 and
and 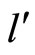 the respective numbers of homogeneous parts of
the respective numbers of homogeneous parts of 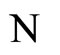 and
and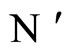 , according to Definition 5.
, according to Definition 5.
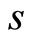 and
and  the respective numbers of synaptical units according to Definition 6.
the respective numbers of synaptical units according to Definition 6.
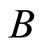 and
and 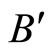 a (general) homogeneous part of
a (general) homogeneous part of 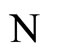 and
and 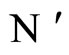 respectively.
respectively.
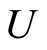 and
and 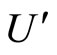 a (general) synaptical unit of
a (general) synaptical unit of 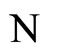 and
and  respectively.
respectively.
 the synaptical weights, according to part (iv) of Proposition 7, of
the synaptical weights, according to part (iv) of Proposition 7, of  and
and  respectively.
respectively.
Definition 9 (Synaptically equivalent networks— Intermediate result in the proof of Main Theorems 16 and 17)
We say that 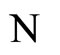 and
and  are synaptically equivalent if:
are synaptically equivalent if:
• 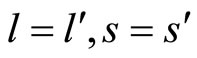 , according to the above notation.
, according to the above notation.
• There exists a one-to-one and surjective correspondence 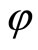 from the set of synaptical units
from the set of synaptical units 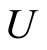 of
of 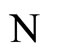 and the set of synaptical units
and the set of synaptical units  of
of  such that
such that

where 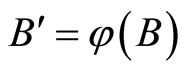 is the homogeneous part of the network
is the homogeneous part of the network 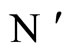 whose synaptical units are the images by
whose synaptical units are the images by 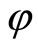 of the synaptical units that compose
of the synaptical units that compose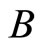 .
.
• For any synaptical unit  of
of 
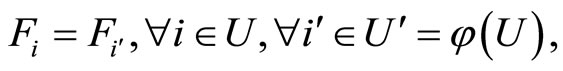
where 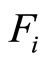 and
and 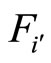 are the second terms of the impulsive differential Equations (3) that govern the dynamics of the neurons
are the second terms of the impulsive differential Equations (3) that govern the dynamics of the neurons  and
and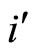 , respectively.
, respectively.
In other words, the networks 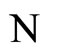 and
and  are synaptically equivalent, if there exists an isomorphism
are synaptically equivalent, if there exists an isomorphism 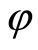 between their respective inter-units graphs such that all the neurons in the unit
between their respective inter-units graphs such that all the neurons in the unit  of the network
of the network  are structurally identical to all the neurons in the unit
are structurally identical to all the neurons in the unit  of the network
of the network .
.
For example, let us consider the network  of Figure 3. Assume that
of Figure 3. Assume that ,
,  in the respective impulsive differential equations (3). Also assume that
in the respective impulsive differential equations (3). Also assume that  for
for 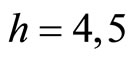 and
and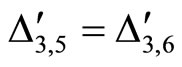 . Then, the network
. Then, the network  has
has  homogeneous parts
homogeneous parts 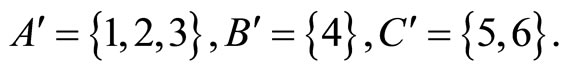 Analogously to the example of Figure 1, the part
Analogously to the example of Figure 1, the part 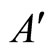 of the network
of the network 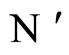 is composed by two synaptical units
is composed by two synaptical units 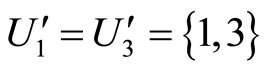 and
and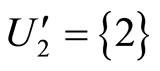 , and the part
, and the part  is composed by a single synaptical unit
is composed by a single synaptical unit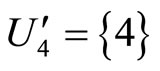 . Finally, the part
. Finally, the part 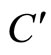 of the network of Figure 3 is composed by a single synaptical unit
of the network of Figure 3 is composed by a single synaptical unit .
.
Assume that the interactions  and
and 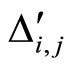 of the networks
of the networks 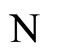 and
and 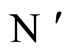 of Figures 1 and 3 respectively, satisfy the following properties:
of Figures 1 and 3 respectively, satisfy the following properties:
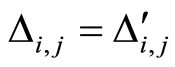 for all
for all  such that
such that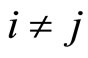 ,
,
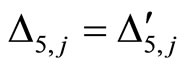 for all
for all 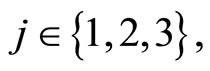
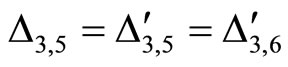 ,
,
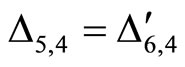 .
.
Then, the inter-units graph of Figure 2 also corresponds to the network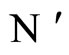 . So, the networks
. So, the networks  and
and  of Figures 1 and 3 are synaptically equivalent.
of Figures 1 and 3 are synaptically equivalent.
We note that, for synaptically equivalent networks, the number of neurons, and also the number of nonzero synaptical interactions, may vary. For instance, the networks of Figures 1 and 3 are synaptically equivalent, but their respective total numbers of of neurons and of synaptical interactions are mutually different.
Comments: The equivalence relation between networks 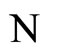 and
and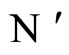 , according to Definition 9, implies that both
, according to Definition 9, implies that both 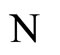 and
and 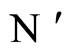 will have exactly the same dynamical response (i.e. they will follow the same orbit), provided that, for any dynamical unit
will have exactly the same dynamical response (i.e. they will follow the same orbit), provided that, for any dynamical unit  of
of , the initial states of all the neurons in
, the initial states of all the neurons in 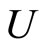 are mutually equal and also equal to the initial states of all the neurons in the dynamical unit
are mutually equal and also equal to the initial states of all the neurons in the dynamical unit 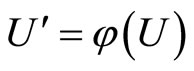 of the other network. In fact, since the impulsive differential Equations (3) that govern the dynamics of all those neurons coincide, and since the synaptical jumps that each of those neurons receive from the other neurons of its respective network also coincide, their respective deterministic orbits in the future must coincide if the initial states are all the same.
of the other network. In fact, since the impulsive differential Equations (3) that govern the dynamics of all those neurons coincide, and since the synaptical jumps that each of those neurons receive from the other neurons of its respective network also coincide, their respective deterministic orbits in the future must coincide if the initial states are all the same.
Nevertheless, if not all those initial states are mutually equal, for instance if some external signal changes the instantaneous states of some but not all the neurons in a synaptical unit, then their respective orbits will differ, during at least some finite interval of time. In this sense, each synaptical unit with more than one neuron, is a group of identical cells that distributes the dynamical process among its cells, i.e. it has the capability of dynamically distributing the information.
In brief, two synaptically equivalent networks have, as a common feature, the same statical configuration or anatomy of the synaptical interactions between their units (i.e. between groups of identical cells, equally synaptically connected). Then, both networks would evolve equally, under the hypothetical assumption that all the initial states of the neurons of their respective synaptical units coincided. But the two networks may exhibit qualitatively different dynamical responses to external perturbations or signals, if these signals make different the instantaneous states of different neurons in some synaptical unit. Such a difference produces a diverse distribution of the dynamical response among the cells.
5. Third Step of the Proof (Dynamically Optimal Networks)
The purpose of this section is to prove Proposition 13 and Theorem 15. These are intermediate results (the third step) of the proof of Main Theorems 16 and 17. We will prove these intermediate results by logical deduction from several previous statements and hypothesis. So, we start by including the needed previous statements in the following series of mathematical definitions, remarks and notation agreements:
We condition the study to the networks of any fixed single class, which we denote by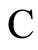 , of synaptically equivalent networks according to Definition 9. In this section we search for networks exhibiting an optimum dynamics conditioned to
, of synaptically equivalent networks according to Definition 9. In this section we search for networks exhibiting an optimum dynamics conditioned to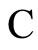 .
.
Notation:
We consider the mathematical model of a general neuronal network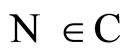 , given by the system (5) of impulsive differential equations. We denote by
, given by the system (5) of impulsive differential equations. We denote by

the instantaneous state of the network  at instant
at instant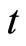 , where
, where 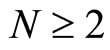 is the number of neurons of the network, and
is the number of neurons of the network, and 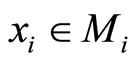 is the instantaneous state of the neuron
is the instantaneous state of the neuron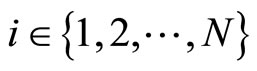 . Since by hypothesis
. Since by hypothesis 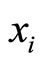 evolves on a finite-dimensional compact manifold
evolves on a finite-dimensional compact manifold , the state
, the state 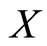 of the network evolves on the finite-dimensional compact product manifold
of the network evolves on the finite-dimensional compact product manifold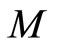 , defined by the following equality:
, defined by the following equality:

In other words, 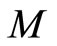 is the cartessian product of the manifolds
is the cartessian product of the manifolds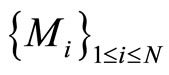 . Then
. Then
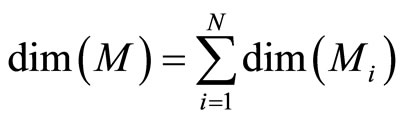 (6)
(6)
Definition 10 (Dynamics of the network) Consider any initial state

of the network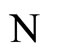 , i.e.
, i.e.  is the state of the neuron
is the state of the neuron 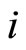 at the instant
at the instant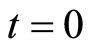 .
.
The solution  of the system (5) of impulsive differential equations that govern the dynamics of
of the system (5) of impulsive differential equations that govern the dynamics of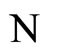 , exists and is unique, provided that the initial condition
, exists and is unique, provided that the initial condition  is given (see for instance [14], cited in [15]). We denote:
is given (see for instance [14], cited in [15]). We denote:
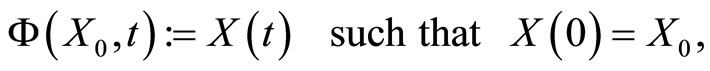
and call  the (deterministic) dynamical system (or, in brief, the dynamics) associated to the network
the (deterministic) dynamical system (or, in brief, the dynamics) associated to the network . It is an autonomous deterministic dynamical system.
. It is an autonomous deterministic dynamical system.
For any autonomous deterministic dynamical system (also if it were not modelled by differential equations), we have the following properties:
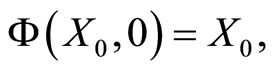
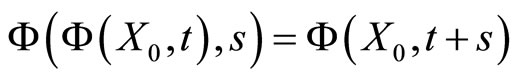

So, for any fixed instant 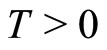 the state
the state  plays the role of a new initial state, from which the orbit
plays the role of a new initial state, from which the orbit
 evolves for time
evolves for time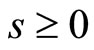 . This orbit coincides with the piece of orbit
. This orbit coincides with the piece of orbit 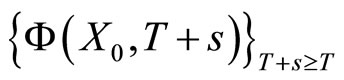 (for time
(for time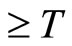 ) that had the initial state
) that had the initial state .
.
Definition 11 (Partial Order in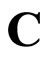 )
)
Let 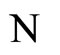 and
and 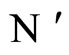 be two networks in
be two networks in 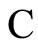 and denote by
and denote by 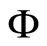 and
and 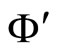 the dynamics of
the dynamics of 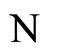 and
and 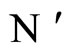 respectively. Denote by
respectively. Denote by  and
and 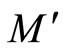 the compact manifolds where
the compact manifolds where  and
and  respectively evolve.
respectively evolve.
We say that 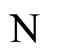 is dynamically richer than
is dynamically richer than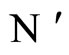 , and write
, and write

if there exists a continuous and one-to-one (non necessarily surjective) mapping

such that
 (7)
(7)
for any initial state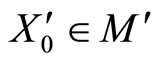 .
.
In other words,  if and only if the dynamical system
if and only if the dynamical system 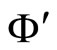 of
of  is a subsystem of the dynamical system
is a subsystem of the dynamical system 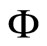 of
of , up to the continuous change
, up to the continuous change 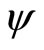 of the state variables.
of the state variables.
From Definition 11 it is immediately deduced the following assertion:
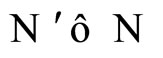 and
and  if and only if their respective dynamical systems
if and only if their respective dynamical systems 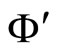 and
and  are topologically conjugated.
are topologically conjugated.
This means that the dynamics of 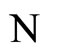 and
and  are the same topological dynamical system, up to an homeomorphic change in their variables which is called a conjugacy. So, we deduce:
are the same topological dynamical system, up to an homeomorphic change in their variables which is called a conjugacy. So, we deduce:
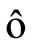 is a partial order in the class
is a partial order in the class 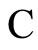 of synaptically equivalent networks up to conjugacies.
of synaptically equivalent networks up to conjugacies.
As an example, assume that the numbers 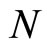 and
and 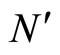 of neurons of
of neurons of 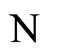 and
and  satisfy
satisfy . Then
. Then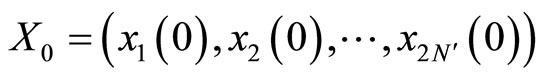 ,
,  . Define the function
. Define the function 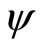 by:
by:
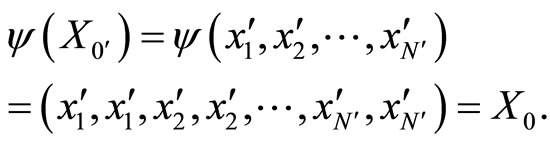
If this function 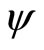 satisfies Equality (7), then each orbit
satisfies Equality (7), then each orbit 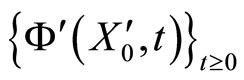 of the dynamical system of
of the dynamical system of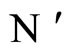 , is identified with one orbit
, is identified with one orbit 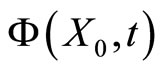 of the dynamics of
of the dynamics of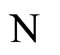 . Along this orbit
. Along this orbit , each two consecutive identical neurons have the same initial states, and thus also have coincident instantaneous states for all
, each two consecutive identical neurons have the same initial states, and thus also have coincident instantaneous states for all . Nevertheless, the whole dynamics
. Nevertheless, the whole dynamics  of the network
of the network  also includes many other different orbits, which are obtained if the initial states of some pair of consecutive identical neurons of
also includes many other different orbits, which are obtained if the initial states of some pair of consecutive identical neurons of 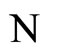 are mutually different.
are mutually different.
Remark 12 From Definition 11, since 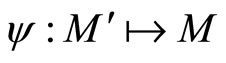 is continuous and one-to-one, we deduce that the image
is continuous and one-to-one, we deduce that the image 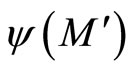 is a submanifold of
is a submanifold of  which is homeomorphic to
which is homeomorphic to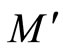 . This is a direct application of the Domain Invariance Theorem (see for instance [18]). Therefore:
. This is a direct application of the Domain Invariance Theorem (see for instance [18]). Therefore:
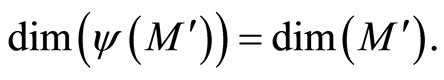
Besides,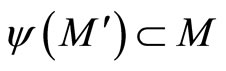 . So,
. So,  contains the submanifold
contains the submanifold 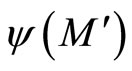 that has the same dimension than
that has the same dimension than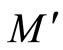 . We deduce the following statement:
. We deduce the following statement:
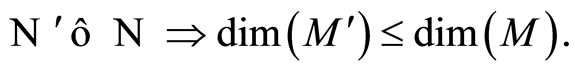 (8)
(8)
In extensum:
If the dynamics of 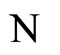 is richer than the dynamics of
is richer than the dynamics of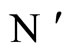 , then the dimension of the manifold
, then the dimension of the manifold  where the dynamics of
where the dynamics of 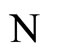 evolves, is larger or equal than the dimension of the manifold
evolves, is larger or equal than the dimension of the manifold 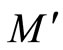 where the dynamics of
where the dynamics of 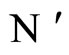 evolves.
evolves.
From the above remark we deduce the following result:
Proposition 13 (Intermediate result in the proof of Main Theorems 16 and 17)
If 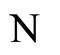 and
and 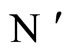 are synaptically equivalent and if
are synaptically equivalent and if , then the number of neurons of
, then the number of neurons of 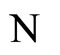 is larger or equal than the number of neurons of
is larger or equal than the number of neurons of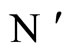 .
.
Proof: Both networks are synaptically equivalent; so, each neuron 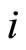 of
of 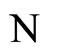 is structurally identical to some neuron (which we still call
is structurally identical to some neuron (which we still call ) of
) of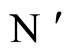 . This implies that the finite dimension of the variable
. This implies that the finite dimension of the variable 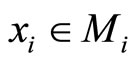 in the network
in the network  is equal to the finite dimension of the corresponding variable
is equal to the finite dimension of the corresponding variable 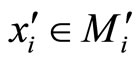 in the network
in the network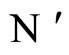 . Thus,
. Thus,
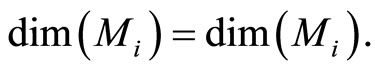 (9)
(9)
After Equality (6) applied to the networks  and
and 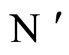 respectively, we obtain:
respectively, we obtain:
 (10)
(10)
 (11)
(11)
where  and
and 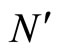 are the number of neurons of
are the number of neurons of  and
and 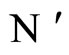 respectively. From Inequality (8) we have:
respectively. From Inequality (8) we have:
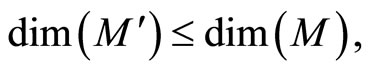
Finally, substituting (10) and (11), we obtain:
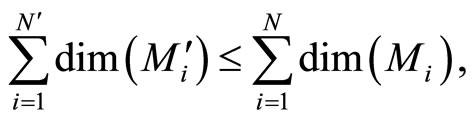
and joining with (9) we conclude , as wanted.
, as wanted.
Definition 14 (Dynamically optimal networks) We say that a network 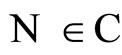 is a dynamical optimum conditioned to the synaptical equivalence class
is a dynamical optimum conditioned to the synaptical equivalence class  (i.e. within the class
(i.e. within the class ) if
) if 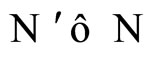 for all
for all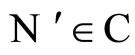 .
.
Theorem 15 (Existence of the dynamical optimum
Intermediate result in the proof of Main Theorems 16 and 17)
For any class 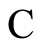 of synaptically equivalent neuronal networks there exists a dynamical optimum network conditioned to
of synaptically equivalent neuronal networks there exists a dynamical optimum network conditioned to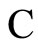 . This optimal network has the maximum number of cells among all the networks of the class
. This optimal network has the maximum number of cells among all the networks of the class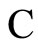 .
.
Proof: The class 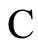 of synaptically equivalent networks is characterized by the numbers
of synaptically equivalent networks is characterized by the numbers 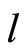 and
and  of homogeneous parts and synaptical units respectively, and by the real values
of homogeneous parts and synaptical units respectively, and by the real values  of the synaptical connections between the dynamical units
of the synaptical connections between the dynamical units 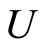 and the homogeneous classes
and the homogeneous classes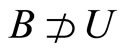 .
.
For each dynamical unit , we denote by
, we denote by 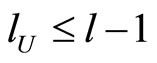 the number of homogeneous classes
the number of homogeneous classes  such that
such that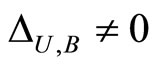 . Thus,
. Thus, 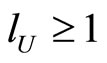 because each cell
because each cell  is not indifferent, and so, there exists at least one nonzero synaptical action departing from
is not indifferent, and so, there exists at least one nonzero synaptical action departing from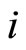 . (Recall that by Definitions 4 and 5, the nonzero synaptical actions only exist between cells belonging to different homogeneous parts.)
. (Recall that by Definitions 4 and 5, the nonzero synaptical actions only exist between cells belonging to different homogeneous parts.)
Construct a network 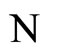 as follows:
as follows:
First, compose each dynamical unit  with exactly
with exactly 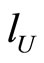 cells. Then, there exists a surjective one-to-one correspondence
cells. Then, there exists a surjective one-to-one correspondence 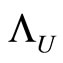 between the set of cells
between the set of cells 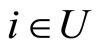 and the set of homogeneous parts
and the set of homogeneous parts 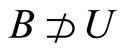 satisfying
satisfying 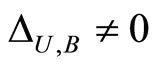 .
.
Second, define the synaptical connections departing from each cell 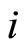 of each dynamical unit
of each dynamical unit , by the following equalities:
, by the following equalities:
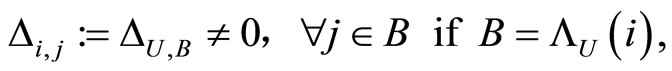 (12)
(12)
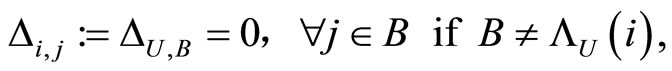 (13)
(13)
We will prove that the network  such constructed is dynamically optimal within the class
such constructed is dynamically optimal within the class :
:
Fix any network . Consider the dynamical systems
. Consider the dynamical systems  and
and 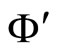 corresponding to the networks
corresponding to the networks 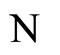 and
and 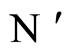 respectively. Denote by
respectively. Denote by 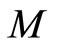 and
and  the compact manifolds where
the compact manifolds where 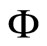 and
and 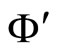 respectively evolve. According to Definition 11, to prove that
respectively evolve. According to Definition 11, to prove that 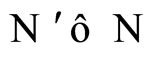 it is enough to construct a continuous oneto-one mapping
it is enough to construct a continuous oneto-one mapping 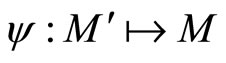 satisfying Equality (7).
satisfying Equality (7).
Let . For any cell
. For any cell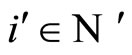 , the initial state
, the initial state 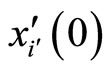 is a component of
is a component of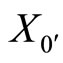 . Let us define
. Let us define 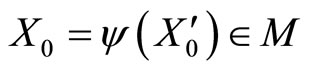 satisfying Equality (7). To do so, we must define the initial state
satisfying Equality (7). To do so, we must define the initial state 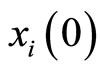 of any cell
of any cell 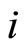 of the network
of the network .
.
So, fix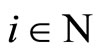 . Denote by
. Denote by 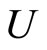 the synaptical unit to which
the synaptical unit to which 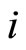 belongs, and denote by
belongs, and denote by  the unique homogeneous class of the network
the unique homogeneous class of the network  satisfying (12). We denote
satisfying (12). We denote
 (14)
(14)
where 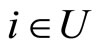 and
and 
Since 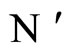 is synaptical equivalent to
is synaptical equivalent to 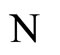 (because both networks
(because both networks 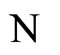 and
and 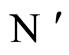 belong to the same class
belong to the same class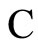 ), we apply Definition 9 to deduce the following equalities:
), we apply Definition 9 to deduce the following equalities:
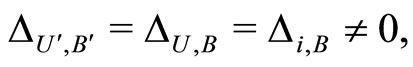 (15)
(15)
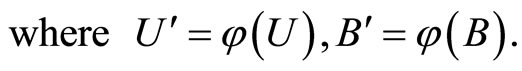
From Definition 6, there exists a unique cell  such that
such that
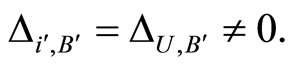 (16)
(16)
Summarizing, for any fixed neuron 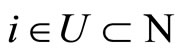 we have constructed a unique cell
we have constructed a unique cell 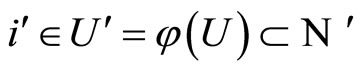 such that Equalities (14), (15) and (16) hold. In other words, we have constructed a mapping
such that Equalities (14), (15) and (16) hold. In other words, we have constructed a mapping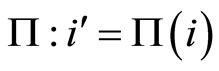 , defined from the synaptical equivalence between the networks
, defined from the synaptical equivalence between the networks 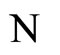 and
and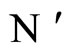 , such that:
, such that:
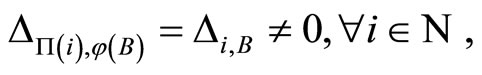 (17)
(17)
where 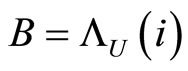 is the unique homogeneous class in
is the unique homogeneous class in  satisfying (12).
satisfying (12).
Assertion A: The mapping  transforms each cell
transforms each cell  of the network
of the network 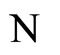 into the cell
into the cell 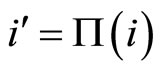 in the network
in the network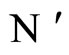 , which is structurally identical to
, which is structurally identical to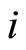 .
.
In fact, assertion A follows from the fact that 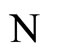 and
and 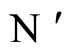 are synaptically equivalent (cf. Definition 9) and from Equality (17).
are synaptically equivalent (cf. Definition 9) and from Equality (17).
Let us prove that  is surjective. In fact, for each
is surjective. In fact, for each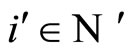 , there exists at least one homogeneous part
, there exists at least one homogeneous part 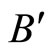 such that
such that , because
, because 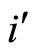 is not indifferent. By Definition 9,
is not indifferent. By Definition 9, 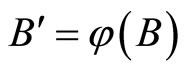 where
where 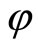 is a one-to-one and surjective transformation between the homogeneous parts of
is a one-to-one and surjective transformation between the homogeneous parts of  and
and . Therefore, there exists a unique homogeneous part
. Therefore, there exists a unique homogeneous part  of
of  such that
such that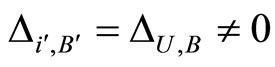 , where
, where ,
, 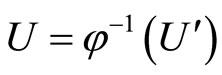 and
and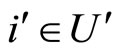 . By construction of the network
. By construction of the network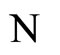 , if
, if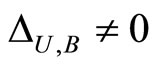 , then there exists a unique
, then there exists a unique  such that
such that . Then, we deduce that
. Then, we deduce that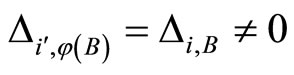 . Joining with (17), and recalling that for each synaptical unit
. Joining with (17), and recalling that for each synaptical unit  there exists at most one cell
there exists at most one cell  such that
such that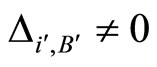 , we deduce
, we deduce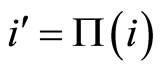 . This proves that
. This proves that  is surjective.
is surjective.
We define the initial state 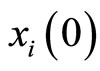 of the cell
of the cell  by
by
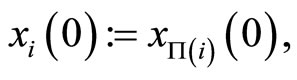
and the mapping 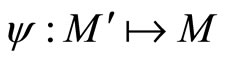 by
by
 (18)
(18)
The mapping  is continuous because the components
is continuous because the components 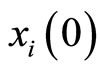 of
of 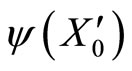 are components
are components 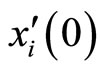 of
of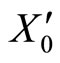 . Thus, small increments in the components
. Thus, small increments in the components  of
of 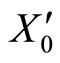 imply small increments in the components
imply small increments in the components 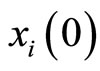 of
of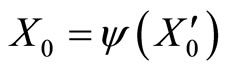 . Besides, the mapping
. Besides, the mapping  is one-to-one (but non necessarily surjective). In fact, if
is one-to-one (but non necessarily surjective). In fact, if 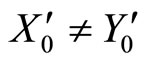 then, at least one component
then, at least one component 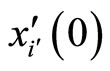 of
of 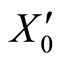 differs from the respective component
differs from the respective component 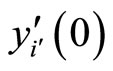 of
of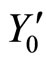 . Since
. Since  is surjective, there exists
is surjective, there exists  such that
such that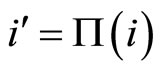 . So, applying Equality (18) we obtain
. So, applying Equality (18) we obtain , where
, where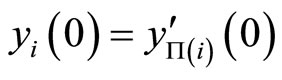 . Thus
. Thus  proving that
proving that  is one-to-one.
is one-to-one.
To end the proof of the first part of Theorem 15, it is now enough to check that the mapping  satisfies Equality (7):
satisfies Equality (7):
From Equality (18) and from the surjectiveness of , for each initial state
, for each initial state 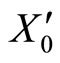 of the network
of the network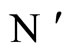 , and for each neuron
, and for each neuron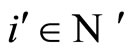 , the corresponding set of neurons
, the corresponding set of neurons 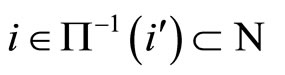 have initial states
have initial states 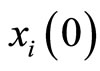 which equal
which equal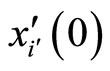 . Besides, from Assertion A,
. Besides, from Assertion A, 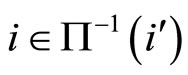 and
and 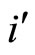 are structurally identical. Now, we consider Equalities (14), (15) and (17), applied to any neuron
are structurally identical. Now, we consider Equalities (14), (15) and (17), applied to any neuron 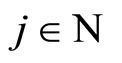 and
and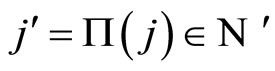 , in the respective roles of
, in the respective roles of 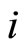 and
and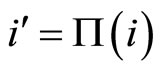 . We deduce that the synaptical interaction jumps
. We deduce that the synaptical interaction jumps  that
that  receives from any other neuron
receives from any other neuron 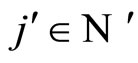 coincides with the synaptical interaction jumps
coincides with the synaptical interaction jumps 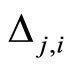 that
that 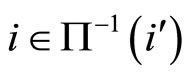 receives from
receives from 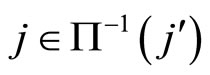 in the network
in the network . Therefore, both
. Therefore, both 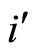 and
and  satisfy the same impulsive differential equation (5). Besides, their respective initial conditions
satisfy the same impulsive differential equation (5). Besides, their respective initial conditions  and
and 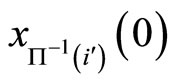 coincide, due to Equality (18). Since the solution of the impulsive differential Equation (5) that satisfies a specified initial condition is unique, we deduce the following statement:
coincide, due to Equality (18). Since the solution of the impulsive differential Equation (5) that satisfies a specified initial condition is unique, we deduce the following statement:
For any instant 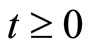 the state
the state 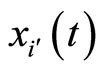 coincides with the instantaneous state
coincides with the instantaneous state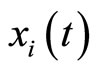 , where
, where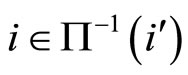 .
.
Recalling Definition 10 of the dynamics 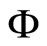 and
and 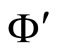 of the networks
of the networks 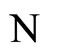 and
and 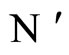 respectively, we deduce:
respectively, we deduce:
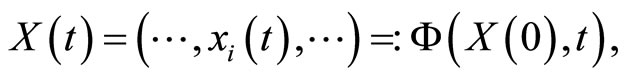

Applying again Equality (18), which defines the mapping 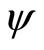 for each fixed instant
for each fixed instant 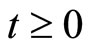 as the new initial state, we conclude
as the new initial state, we conclude
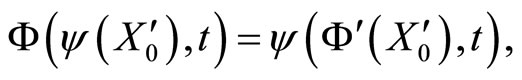
proving Equality (7), as wanted.
We have proved that  for all
for all . Thus, in each synaptical equivalence class
. Thus, in each synaptical equivalence class  there exists a network
there exists a network  that is the dynamical optimum conditioned to
that is the dynamical optimum conditioned to .
.
Now, let us prove the second part of Theorem 15. We have to show that the number 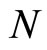 of neurons in
of neurons in  is the maximum number of neurons of all the networks in the class
is the maximum number of neurons of all the networks in the class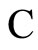 . In fact, since
. In fact, since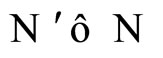 , after Proposition 13 we get
, after Proposition 13 we get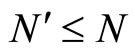 , where
, where 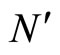 is the number of neurons of
is the number of neurons of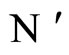 , for all
, for all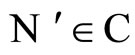 .
.
6. End of the Proof of Dale’s Principle
Let  be the set of all the neuronal networks according to the mathematical model defined in Section 2. Let
be the set of all the neuronal networks according to the mathematical model defined in Section 2. Let 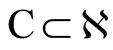 be a fixed class of synaptically equivalent networks. The purpose of this section is to end the proof of the following Main Theorem of the paper:
be a fixed class of synaptically equivalent networks. The purpose of this section is to end the proof of the following Main Theorem of the paper:
Theorem 16 (Dale’s Principle is necessary for the dynamical optimization)
If  is the dynamical optimum network conditioned to
is the dynamical optimum network conditioned to , then all the neurons of
, then all the neurons of  satisfy Dale’s Principle.
satisfy Dale’s Principle.
Namely, any neuron of  is either inhibitory or excitatory.
is either inhibitory or excitatory.
End of the proof of Theorem 16: Let  be the dynamical optimum among the networks in
be the dynamical optimum among the networks in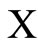 . Therefore,
. Therefore,

Thus, applying Proposition 13, the numbers 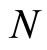 and
and  of neurons in
of neurons in 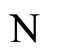 and
and 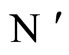 respectively, satisfy
respectively, satisfy
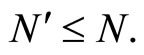 (19)
(19)
Denote by  the synaptical action from the neuron
the synaptical action from the neuron 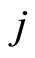 to the neuron
to the neuron 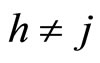 in
in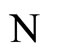 , for any
, for any  Assume by contradiction that there exists a neuron
Assume by contradiction that there exists a neuron 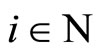 which is mixed, according to Definition 1. Let us fix such a value of
which is mixed, according to Definition 1. Let us fix such a value of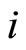 . Now, we construct a new network
. Now, we construct a new network  as follows:
as follows:
First, include in  all the neurons
all the neurons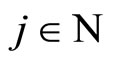 , in particular
, in particular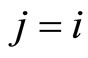 . Define in
. Define in  the synaptical interactions
the synaptical interactions 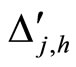 as follows:
as follows:

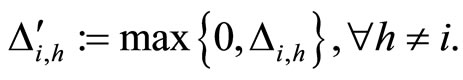
Second, add one more neuron in , say the
, say the 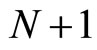 - th. neuron, which we make, by construction, structurally identical to the
- th. neuron, which we make, by construction, structurally identical to the  -th. neuron. Define
-th. neuron. Define
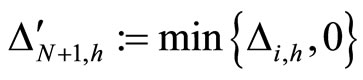
The new neuron 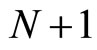 is not indifferent in the network
is not indifferent in the network 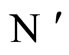 because
because  is mixed in
is mixed in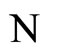 . (So, there exists
. (So, there exists 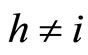 such that
such that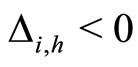 .)
.)
It is immediate to check that 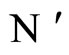 is synaptically equivalent to
is synaptically equivalent to . In fact, all the neurons, except the added one
. In fact, all the neurons, except the added one  -th. cell in
-th. cell in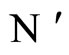 , are respectively structurally identical in the networks
, are respectively structurally identical in the networks 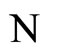 and
and . Besides, all the synaptical interactions, except those that depart from
. Besides, all the synaptical interactions, except those that depart from 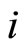 and
and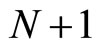 , are the same in both networks. Finally, also the nonzero synaptical interactions that depart from
, are the same in both networks. Finally, also the nonzero synaptical interactions that depart from  in the network
in the network , are equal, either to the synaptical interactions that depart from
, are equal, either to the synaptical interactions that depart from  in
in 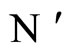 (if positive), or to those that depart from the new neuron
(if positive), or to those that depart from the new neuron 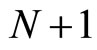 in
in 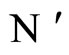 (if negative). So,
(if negative). So,  is synaptically equivalent to
is synaptically equivalent to . In other words,
. In other words,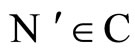 . To end the proof, we note that the number
. To end the proof, we note that the number 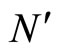 of neurons of
of neurons of  is
is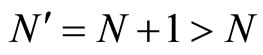 , contradicting Inequality (19).□
, contradicting Inequality (19).□
7. Counter Example
The purpose of this section is to exhibit a counter-example that shows that the converse of Main Theorem 16 is false (Theorem 17).
Theorem 17 is the second Main Theorem of the paper. Its proof is deduced from the intermediate results that were previously obtained along the paper, and is ended by showing the explicit counter-example from Figures 1-3.
Theorem 17 (Dale’s Principle is not sufficient for the dynamical optimization)
There exist neuronal networks according to the mathematical model of Section 2 that satisfy Dale’s Principle and are not dynamically optimal conditioned to their respective synaptical equivalence classes.
End of the proof of Theorem 17: We will show an explicit example of a dynamical suboptimal network  within a synaptical equivalence class
within a synaptical equivalence class , such that
, such that  satisfies Dale’s Principle. We will exhibit such an example with
satisfies Dale’s Principle. We will exhibit such an example with  neurons, but it can be repeated (after obvious adaptations) with any arbitrarily chosen number
neurons, but it can be repeated (after obvious adaptations) with any arbitrarily chosen number .
.
Consider the network  of Figure 1. Assume, for instance, the following signs for the nonzero synaptical interactions:
of Figure 1. Assume, for instance, the following signs for the nonzero synaptical interactions:

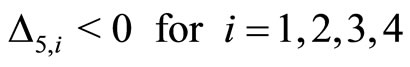
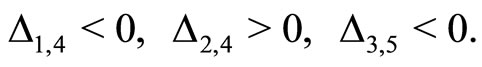
Then, the neurons 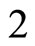 and
and  are excitatory and the neurons 1, 3 and
are excitatory and the neurons 1, 3 and 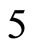 are inhibitory. Thus, all the neurons of the network
are inhibitory. Thus, all the neurons of the network 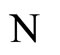 satisfy Dale’s Principle.
satisfy Dale’s Principle.
As shown in Section 4, the network 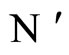 of Figure 3 is synaptically equivalent to the network
of Figure 3 is synaptically equivalent to the network 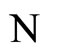 of Figure 1. In other words, both networks
of Figure 1. In other words, both networks 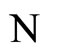 and
and 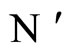 belong to the same equivalence class
belong to the same equivalence class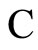 . Since
. Since 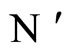 has exactly 6 neurons and
has exactly 6 neurons and 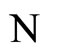 has 5 neurons, applying Proposition 13 we deduce that
has 5 neurons, applying Proposition 13 we deduce that . Thus
. Thus 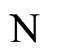 is not the optimal network of its class
is not the optimal network of its class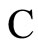 .
.
8. Final Comments
In Section 2 we posed the mathematical simplified (but general) model of biological neuronal networks, by a system (5) of deterministic impulsive differential equations. In its essence, this model was taken from [11] (some particular conditions of the model were also taken from [8-10,12,13] and from the bibliography therein).
On the one hand, the mathematical model is an idealized simplification of the network, because the spiking of each neuron is reduced to an instantaneous reset, without delay, of its membrane potential. Also the synaptical actions are assumed to be instantaneous and have no delay.
On the other hand, the abstract mathematical model is general, since we require neither particular formulae, nor numerical specification, nor computational algorithms for the functions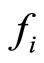 ,
, 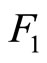 and
and 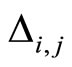 of Equations (1), (3) and (5), nor specific values for the parameters.
of Equations (1), (3) and (5), nor specific values for the parameters.
In Section 3 we defined the homogeneous parts of the network, composed by mutually identical cells. The groups of neurons, which we call synaptical units, are formed by structurally identical and synaptically representative neurons. In Proposition 7 we proved that any neuronal network, according to the mathematical model described in Section 2, is decomposable in more than one homogeneous part, and that each homogeneous part is decomposable into pairwise disjoint dynamical units. Then, a simplified graph, which we called inter-units graph mathematically represents the statical structure of the synaptical connections among the groups of neurons in the network. This theoretical approach have rough similitudes with empirical research in Neuroscience [17], for which the structure of synaptical connections among groups of neurons or regions in the brain is studied, regardless how many neurons exactly compose each region.
In Section 4 we conditioned the study to a fixed family of networks that are mutually synaptically equivalent. We denote this family by , and call it a class. Even if this condition may appear as a restriction, it is not. In fact, first, any neuronal network (provided that it is mathematically modelled by the equations of Section 2), belongs to one such a class
, and call it a class. Even if this condition may appear as a restriction, it is not. In fact, first, any neuronal network (provided that it is mathematically modelled by the equations of Section 2), belongs to one such a class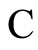 . Second, all the results that we proved along the paper stand for any arbitrarily chosen class
. Second, all the results that we proved along the paper stand for any arbitrarily chosen class 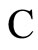 of synpatically equivalent networks.
of synpatically equivalent networks.
Each class  of synaptically equivalent networks gives a particular specification for the number of synaptical units and for the inter-units graph. This specification implies a particular statical anatomy in the synaptical structure of the network, described by the different groups of mutually identical neurons (and not by the neurons themselves). Each group of neurons is a synaptical unit that has a characteristic functional role in the complex synaptical structure of the network.
of synaptically equivalent networks gives a particular specification for the number of synaptical units and for the inter-units graph. This specification implies a particular statical anatomy in the synaptical structure of the network, described by the different groups of mutually identical neurons (and not by the neurons themselves). Each group of neurons is a synaptical unit that has a characteristic functional role in the complex synaptical structure of the network.
Roughly speaking, a class 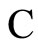 of mutually synaptically equivalent neuronal networks works as an abstraction of the following analogous example: When a Neuroscientist studies the nervous system of certain species of animals, he is investigating a class of neuronal networks composed by a relatively large amount of particular cases that are indeed different networks (one particular case for each individual of the same species). But all the neuronal networks in that class share a certain structure, which is given, for instance, by the genetic neurological characteristics of the species. Some type of synaptical connections between particular groups of neurons with specific physiological roles, is shared by all the healthy individuals of the species. However, the exact number of neurons, and the exact number and weight of synaptical connections between particular neurons, may vary from one individual to another of the same species, or from an early age to a mature age of the same individual.
of mutually synaptically equivalent neuronal networks works as an abstraction of the following analogous example: When a Neuroscientist studies the nervous system of certain species of animals, he is investigating a class of neuronal networks composed by a relatively large amount of particular cases that are indeed different networks (one particular case for each individual of the same species). But all the neuronal networks in that class share a certain structure, which is given, for instance, by the genetic neurological characteristics of the species. Some type of synaptical connections between particular groups of neurons with specific physiological roles, is shared by all the healthy individuals of the species. However, the exact number of neurons, and the exact number and weight of synaptical connections between particular neurons, may vary from one individual to another of the same species, or from an early age to a mature age of the same individual.
In Section 5 we studied the abstract dynamical system of any neuronal network defined by the mathematical model of Section 2, and conditioned to a certain fixed class  of mutually synaptically equivalent networks. In Theorem 15 we proved that (theoretically) a dynamically optimal network exists in each class
of mutually synaptically equivalent networks. In Theorem 15 we proved that (theoretically) a dynamically optimal network exists in each class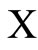 .
.
The proof of Theorem 15 is constructive: first, we defined a particular network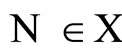 , and second, we proved that
, and second, we proved that  is the richest network of its class. This means that
is the richest network of its class. This means that  would potentially exhibit the most diverse set of dynamical responses (orbits in the future) when external signals change the instantaneous state of some of its neurons.
would potentially exhibit the most diverse set of dynamical responses (orbits in the future) when external signals change the instantaneous state of some of its neurons.
Since the system is assumed to be deterministic, any network according to this model will reproduce a unique response if the same instantaneous state occurs for all its neurons. So, the space of responses is represented by the space of instantaneous states (or initial states, if time 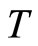 is translated to become 0). Nevertheless, this space may change from one network to another of the same synaptical equivalence class
is translated to become 0). Nevertheless, this space may change from one network to another of the same synaptical equivalence class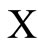 . If we assumed that the natural pursued aim in the development of a biological neuronal network were to optimize the space of dynamical responses under stimulus, preserving the same characteristic and functional structure between groups of cells, then, theoretically, the final (but maybe never arrived) network would be
. If we assumed that the natural pursued aim in the development of a biological neuronal network were to optimize the space of dynamical responses under stimulus, preserving the same characteristic and functional structure between groups of cells, then, theoretically, the final (but maybe never arrived) network would be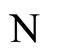 , constructed in the proof of Theorem 15.
, constructed in the proof of Theorem 15.
In Section 6 we proved Theorem 16, which is one of the main results of the paper. It states that the dynamically optimal network 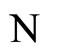 in the class
in the class 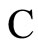 must satisfy Dale’s Principle (i.e. all its neurons are either excitatory or inhibitory but not mixed). So, if the natural pursued aim in the development of the neuronal network were to optimize the space of possible dynamical responses, the tendency of the network during its plastic phases will provoke as many neurons as possible to satisfy Dale’s Principle. From this point of view, Theorem 16 shows that Dale’s Principle is a consequence of an optimization process. So, it gives a mathematically possible answer to the following epistemological question:
must satisfy Dale’s Principle (i.e. all its neurons are either excitatory or inhibitory but not mixed). So, if the natural pursued aim in the development of the neuronal network were to optimize the space of possible dynamical responses, the tendency of the network during its plastic phases will provoke as many neurons as possible to satisfy Dale’s Principle. From this point of view, Theorem 16 shows that Dale’s Principle is a consequence of an optimization process. So, it gives a mathematically possible answer to the following epistemological question:
Why does Dale’s Principle hold for most neurons of most biological neuronal networks?
Mathematical answer: Because maybe biological networks evolve pursuing the theoretical optimum or richest dynamics, conditioned to preserve the synaptical connections among its different homogeneous groups of neurons.
Finally, in Theorem 17 we proved that Dale’s Principle is not enough for the neuronal network to be a dynamical optimum within its synaptically equivalence class. In other words, Dale’s Principle would be just a stage of a plastic optimization process of the neuronal network, but its validity does not ensure that the end of hypothetical process of optimization has been arrived.
9. Acknowledgements
The author thanks the anonymous referees for their valuable comments and suggestions, Agencia Nacional de Investigación e Innovación (ANII) and Comisión Sectorial de Investigación Cientfica (CSIC) of the Universidad de la República, both institutions of Uruguay, and the Editorial Office of the Journal Applied Mathematics.
REFERENCES
- P. Strata and R. Harvey, “Dale’s Principle,” Brain Research Bulletin, Vol. 50, No. 5-6, 1999, pp. 349-350. http://dx.doi.org/10.1016/S0361-9230(99)00100-8
- M. F. Bear, B. W. Connors and M. A. Paradiso, “Neuroscience—Exploring the Brain,” 3rd Edition, Lippincott Williams & Wilkins, Philadelphia, 2007
- G. Burnstock, “Cotransmission,” Current Opinion in Pharmacology, Vol. 4, No. 1, 2004, pp. 47-52. http://dx.doi.org/10.1016/j.coph.2003.08.001
- L. E. Trudeau and R. Gutiérrez, “On Cotransmission & Neurotransmitter Phenotype Plasticity,” Molecular Interventions, Vol. 7, No. 3, 2007, pp. 138-146. http://dx.doi.org/10.1124/mi.7.3.5
- R. E. Mirollo and S. H. Strogatz, “Synchronization of Pulse Coupled Biological Oscillators,” SIAM Journal on Applied Mathematics, Vol. 50, No. 6, 1990, pp. 1645- 1662. http://dx.doi.org/10.1137/0150098
- L. Gómez and R. Budelli, “Two-Neuron Networks II: Leaky Integrator Pacemaker Models,” Biological Cybernetics, Vol. 74, No. 2, 1996, pp. 131-137. http://dx.doi.org/10.1007/BF00204201
- W. Mass and C. M. Bishop, “Pulsed Neural Networks,” MIT Press, Cambridge, 2001.
- G. B. Ermentrout and D. H. Terman, “Mathematical Foundations of Neuroscience,” In: Interdisciplinary Applied Mathematics, Springer, New York, 2010. http://link.springer.com/book/10.1007/978-0-387-87708-2/page/1
- W. Gerstner and W. Kistler, “Spiking Neuron Models,” Cambridge University Press, Cambridge, 2002. http://dx.doi.org/10.1017/CBO9780511815706
- K. K. Lin, K. C. A. Wedgwood, S. Coombes and L.-S. Young, “Limitations of Perturbative Techniques in the Analysis of Rhythms and Oscillations,” Journal of Mathematical Biology, Vol. 66, No. 1-2, 2013, pp. 139-161. http://dx.doi.org/10.1007/s00285-012-0506-0
- E. M. Izhikevich, “Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting,” MIT Press, Cambridge, 2007.
- A. J. Catllá, D. G. Schaeffer, T. P. Witelski, E. E. Monson and A. L. Lin, “On Spiking Models for Synaptic Activity and Impulsive Differential Equations,” SIAM Review, Vol. 50, No. 3, 2008, pp. 553-569. http://dx.doi.org/10.1137/060667980
- E. Catsigeras and P. Guiraud, “Integrate and Fire Neural Networks, Piecewise Contractive Maps and Limit Cycles,” Journal of Mathematical Biology, 2013, in Press. http://dx.doi.org/10.1007/s00285-012-0560-7
- V. D. Milman and A. D. Myshkis, “On the Stability of Motion in the Presence of Impulses (in Russian),” Siberian Mathematical Journal, Vol. 1, No. 2, 1960, pp. 233- 237.
- G. T. Stamov and I. Stamova, “Almost Periodic Solutions for Impulsive Neural Networks with Delay,” Applied Mathematical Modelling, Vol. 31, No. 7, 2007, pp. 1263- 1270. http://dx.doi.org/10.1016/j.apm.2006.04.008
- R. F. Schmidt and G. Thews, “Human Physiology,” SpringerVerlag, Berlin, 1983.
- M. Megas, Z. S. Emri, T. F. Freund and A. I. Gulyas, “Total Number and Distribution of Inhibitory and excitatory Synapses on Hippocampal CA1 Pyramidal Cells,” Neuroscience, Vol. 102, No. 3, 2001, pp. 527-540. http://dx.doi.org/10.1016/S0306-4522(00)00496-6
- J. Van Mill, “Domain Invariance,” In: M. Hazewinkel, Ed., Encyclopedia of Mathematics, Springer, Berlin, 2001- 2003. http://www.springer.com/mathematics/book/978-1-4020-0609-8

