Applied Mathematics
Vol.5 No.3(2014), Article ID:42640,5 pages DOI:10.4236/am.2014.53034
Generalizations of a Matrix Inequality
1School of Mathematics and Information Technology, Nanjing Xiaozhuang University, Nanjing
2College of Teacher Education, Nanjing Xiaozhuang University, Nanjing
3College of Science, Nanjing University of Posts and Telecommunications, Nanjing
Email: yuanjun_math@126.com
Received June 16, 2013; revised July 16, 2013; accepted July 23, 2013
ABSTRACT
In this paper, some new generalizations of the matrix form of the Brunn-Minkowski inequality are presented.
Keywords:Brunn-Minkowski Inequality; Positive Definite Matrix; Determinant Differences
1. Introduction
The well-known Brunn-Minkowski inequality is one of the most important inequalities in geometry. There are many other interesting results related to the Brunn-Minkowski inequality (see [1-8]). The matrix form of the Brunn-Minkowski inequality (see [9,10]) asserts that if 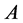 and
and  are two positive definite matrices of order
are two positive definite matrices of order 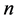 and
and , then
, then
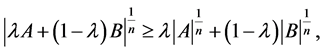 (1)
(1)
with equality if and only if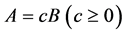 , where
, where 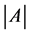 denotes the determinant of
denotes the determinant of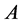 .
.
Let 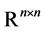 denote the set of
denote the set of  real symmetry matrices. Let
real symmetry matrices. Let 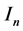 denote
denote 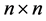 unit matrix. We use the notation
unit matrix. We use the notation 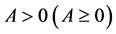 if
if 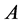 is a positive definite (positive semi-definite) matrix, and
is a positive definite (positive semi-definite) matrix, and  denotes the transpose of
denotes the transpose of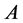 . Let
. Let , then
, then 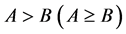 if and only if
if and only if 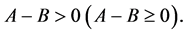
If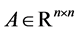 , then there exists a unitary matrix
, then there exists a unitary matrix  such as
such as
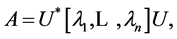
where 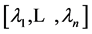 is a diagonal matrix
is a diagonal matrix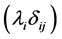 , and
, and  are the eigenvalues of
are the eigenvalues of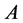 , each appearing as its multiplicity. Assume now that
, each appearing as its multiplicity. Assume now that 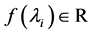 is well defined. Then
is well defined. Then 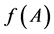 may be defined by (see e.g. [11, p. 71] or [12, p. 90])
may be defined by (see e.g. [11, p. 71] or [12, p. 90])
 (2)
(2)
In this paper, some new generalizations of the matrix form of the Brunn-Minkowski inequality are presented. One of our main results is the following theorem.
Theorem 1.1. Let ,
, 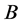 be positive definite commuting matrix of order
be positive definite commuting matrix of order  with eigenvalues in the interval
with eigenvalues in the interval . If
. If 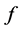 is a positive concave function on
is a positive concave function on 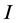 and
and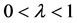 , then
, then
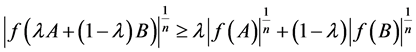 (3)
(3)
with equality if and only if 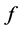 is linear and
is linear and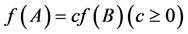 .
.
Let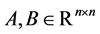 , if
, if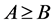 . We can define the determinant differences function of
. We can define the determinant differences function of 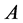 and
and 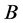 by
by
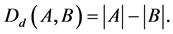
The following theorem gives another generalization of (1).
Theorem 1.2. Let ,
,  be positive definite commuting matrix of order
be positive definite commuting matrix of order  with eigenvalues in the interval
with eigenvalues in the interval 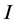 and
and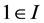 . Let
. Let 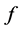 be a positive function on
be a positive function on  and a and b be two nonnegative real numbers such that
and a and b be two nonnegative real numbers such that

Then
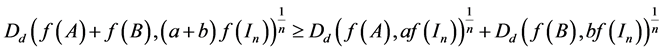 (4)
(4)
with equality if and only if 
Remark 1. Let  in Theorem 1.1 or let
in Theorem 1.1 or let 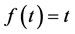 and
and 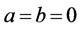 in Theorem 1.2. We can both obtain (1). Hence Theorem 1.1 and Theorem 1.2 are generalizations of (1).
in Theorem 1.2. We can both obtain (1). Hence Theorem 1.1 and Theorem 1.2 are generalizations of (1).
2. Proofs of Theorems
To prove the theorems, we need the following lemmas:
Lemma 2.1. ([13], p.472) Let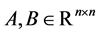 ,
,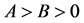 . Then
. Then
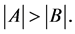
Lemma 2.2. ([13], p.50) Let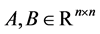 ,
,  ,
,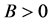 . If
. If 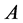 and
and 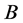 are commute, then exists a unitary matrix
are commute, then exists a unitary matrix 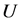 such that
such that
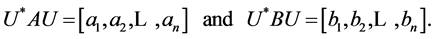
Lemma 2.3. ([14], p.35) Let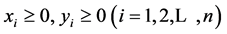 . Then
. Then

with equality if and only if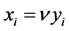 , where
, where 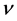 is a constant.
is a constant.
This is a special case of Maclaurin’s inequality.
Proof of Theorem 1.1.
Since 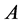 and
and 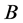 are commuted, by lemma 2.2, there exists a unitary matrix
are commuted, by lemma 2.2, there exists a unitary matrix 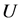 such that
such that

Hence,
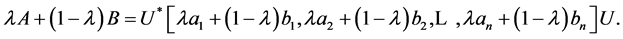
By (2), we have
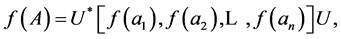
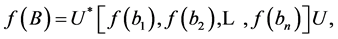
and
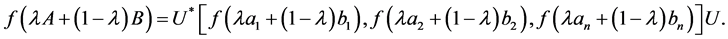
Since 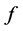 is a concave function, by lemma 2.3, we get
is a concave function, by lemma 2.3, we get

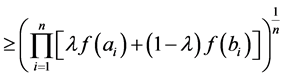 (5)
(5)
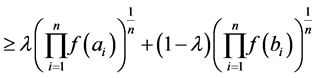 (6)
(6)

Now we consider the conditions of equality holds. Since 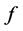 is a concave function, the equality of (5) holds if and only if
is a concave function, the equality of (5) holds if and only if  is linear. By the equality of Lemma 2.3, the equality of (6) holds if and only if
is linear. By the equality of Lemma 2.3, the equality of (6) holds if and only if 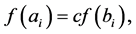 which means
which means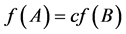 . So the equality of (3) holds if and only if
. So the equality of (3) holds if and only if 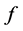 is linear and
is linear and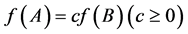 . This completes the proof of the Theorem 1.1.
. This completes the proof of the Theorem 1.1.
Applying the arithmetic-geometric mean inequality to the right side of (3), we get the following corollary.
Corollary 2.4. Let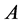 ,
, 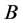 be positive definite commuting matrix of order
be positive definite commuting matrix of order  with eigenvalues in the interval
with eigenvalues in the interval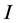 . If
. If 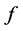 is a positive concave function on
is a positive concave function on 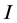 and
and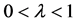 , then
, then
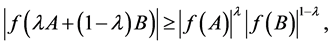
with equality if and only if 
Taking for 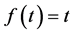 in Corollary 2.4, we obtain the Fan Ky concave theorem.
in Corollary 2.4, we obtain the Fan Ky concave theorem.
Proof of Theorem 1.2.
As in the proof of Theorem 1.1, since 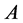 and
and 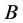 are commuted, by lemma 2.2, there exists a unitary matrix
are commuted, by lemma 2.2, there exists a unitary matrix  such that
such that
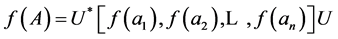
and
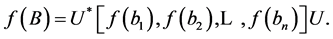
So
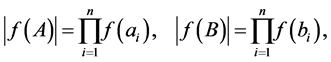
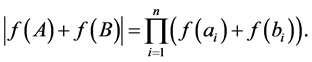
It is easy to see that (4) holds if and only if
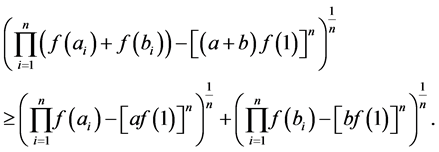 (7)
(7)
Since , by Lemma 2.1, we have
, by Lemma 2.1, we have
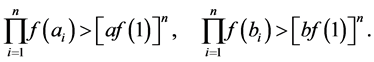
Now we prove (7). Put
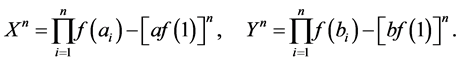
Then

Applying Minkowski inequality, we have
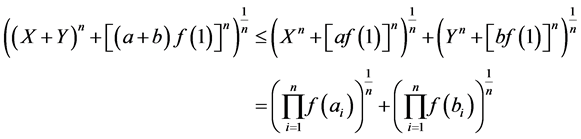
Using the Lemma 2.3 to the right of the above inequlity, we obtain

which implies that
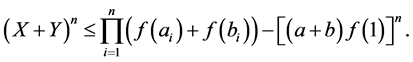
It follows that
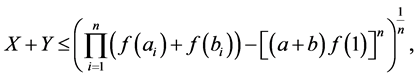
which is just the inequality (7).
By the equality conditions of Minkowski inequality and Lemma 2.3, the equality (1.4) holds if and only if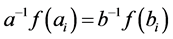 , which means
, which means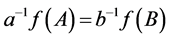 . Thus we complete the proof of Theorem 1.2.
. Thus we complete the proof of Theorem 1.2.
Taking for 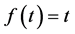 in Theorem 1.2, we obtain the following corollary.
in Theorem 1.2, we obtain the following corollary.
Corollary 2.5. [7] Let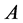 ,
,  be positive definite commuting matrix of order
be positive definite commuting matrix of order 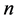 and a and b be two nonnegative real numbers such that
and a and b be two nonnegative real numbers such that
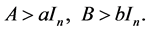
Then
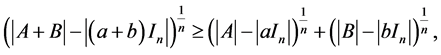
with equality if and only if .
.
Acknowledgements
The authors are most grateful to the referee for his valuable suggestions. And the authors would like to acknowledge the support from the National Natural Science Foundation of China (11101216,11161024), Qing Lan Project and the Nanjing Xiaozhuang University (2010KYQN24, 2010KYYB13).
REFERENCES
- I. J. Bakelman, “Convex Analysis and Nonlinear Geometric Elliptic Equations,” Springer, Berlin, 1994. http://dx.doi.org/10.1007/978-3-642-69881-1
- C. Borell, “The Brunn-Minkowski Inequality in Gauss Space,” Inventiones Mathematicae, Vol. 30, No. 2, 1975, pp. 202-216. http://dx.doi.org/10.1007/BF01425510
- C. Borell, “Capacitary Inequality of the Brunn-Minkowski Inequality Type,” Mathematische Annalen, Vol. 263, No. 2, 1993, pp. 179-184. http://dx.doi.org/10.1007/BF01456879
- K. Fan, “Some Inequality Concerning Positive-Denite Hermitian Matrices,” Mathematical Proceedings of the Cambridge Philosophical Society, Vol. 51, No. 3, 1958, pp. 414-421. http://dx.doi.org/10.1017/S0305004100030413
- R. J. Gardner and P. Gronchi, “A Brunn-Minkowski Inequality for the Integer Lattice,” Transactions of the American Mathematical Society, Vol. 353, No. 10, 2001, pp. 3995-4024. http://dx.doi.org/10.1090/S0002-9947-01-02763-5
- R. J. Gardner, “The Brunn-Minkowski Inequality,” Bulletin of the American Mathematical Society, Vol. 39, No. 3, 2002, pp. 355-405. http://dx.doi.org/10.1090/S0273-0979-02-00941-2
- G. S. Leng, “The Brunn-Minkowski Inequality for Volume Differences,” Advances in Applied Mathematics, Vol. 32, No. 3, 2004, pp. 615-624. http://dx.doi.org/10.1016/S0196-8858(03)00095-2
- R. Osserman, “The Brunn-Minkowski Inequality for Multiplictities,” Inventiones Mathematicae, Vol. 125, No. 3, 1996, pp. 405-411. http://dx.doi.org/10.1007/s002220050081
- E. V. Haynesworth, “Note on Bounds for Certain Determinants,” Duke Mathematical Journal, Vol. 24, No. 3, 1957, pp. 313- 320. http://dx.doi.org/10.1215/S0012-7094-57-02437-7
- E. V. Haynesworth, “Bounds for Determinants with Positive Diagonals,” Transactions of the American Mathematical Society, Vol. 96, No. 3, 1960, pp. 395-413. http://dx.doi.org/10.1090/S0002-9947-1960-0120242-1
- M. Marcus and H. Minc, “A Survey of Matrix Theory and Inequalities,” Allyn and Bacon, Boston, 1964.
- R. Bellman, “Introduction to Matrix Analysis,” McGraw-Hill, New York, 1960.
- R. Horn and C. R. Johnson, “Matrix Analysis,” Cambridge University Press, New York, 1985. http://dx.doi.org/10.1017/CBO9780511810817
- E. F. Beckenbach and R. Bellman, “Inequalities,” Springer, Berlin, 1961. http://dx.doi.org/10.1007/978-3-642-64971-4

