Applied Mathematics
Vol. 4 No. 9A (2013) , Article ID: 36442 , 7 pages DOI:10.4236/am.2013.49A002
Fixed Point of a Countable Family of Uniformly Totally Quasi- -Asymptotically Nonexpansive Multi-Valued Mappings in Reflexive Banach Spaces with Applications
-Asymptotically Nonexpansive Multi-Valued Mappings in Reflexive Banach Spaces with Applications
School of Science, Southwest University of Science and Technology, Mianyang, China
Email: liyi@swust.edu.cn
Copyright © 2013 Yi Li. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received April 23, 2013; revised May 23, 2013; accepted June 1, 2013
Keywords: Multi-Valued Mapping; Totally Quasi- -Asymptotically Nonexpansive; Countable Family of Uniformly Totally Quasi-
-Asymptotically Nonexpansive; Countable Family of Uniformly Totally Quasi-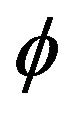 -Asymptotically Nonexpansive Multi-Valued Mappings; Firmly Convergence
-Asymptotically Nonexpansive Multi-Valued Mappings; Firmly Convergence
ABSTRACT
The purpose of this article is to discuss a modified Halpern-type iteration algorithm for a countable family of uniformly totally quasi-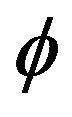 -asymptotically nonexpansive multi-valued mappings and establish some strong convergence theorems under certain conditions. We utilize the theorems to study a modified Halpern-type iterative algorithm for a system of equilibrium problems. The results improve and extend the corresponding results of Chang et al. (Applied Mathematics and Computation, 218, 6489-6497).
-asymptotically nonexpansive multi-valued mappings and establish some strong convergence theorems under certain conditions. We utilize the theorems to study a modified Halpern-type iterative algorithm for a system of equilibrium problems. The results improve and extend the corresponding results of Chang et al. (Applied Mathematics and Computation, 218, 6489-6497).
1. Introduction
Throughout this paper, we denote the strong convergence and weak convergence of the sequence 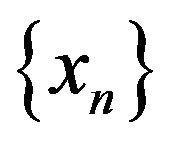 by
by 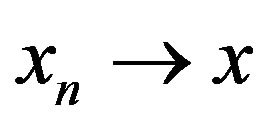 and
and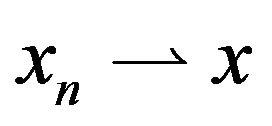 , respectively. We denote by N and R the sets of positive integers and real numbers, respectively. Let
, respectively. We denote by N and R the sets of positive integers and real numbers, respectively. Let  be a nonempty closed subset of a real Banach space
be a nonempty closed subset of a real Banach space . A mapping
. A mapping 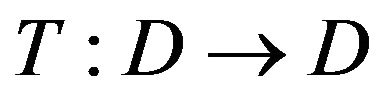 is said to be nonexpansive if
is said to be nonexpansive if , for all
, for all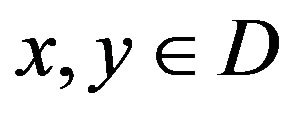 . Let
. Let 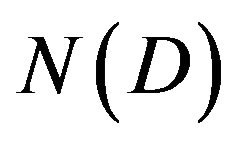 and
and  denote the family of nonempty subsets and nonempty bounded closed subsets of
denote the family of nonempty subsets and nonempty bounded closed subsets of , respectively.
, respectively.
Let  be a real Banach space with dual
be a real Banach space with dual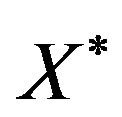 . We denote by
. We denote by ![]() the normalized duality mapping from
the normalized duality mapping from 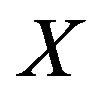 to
to  which is defined by
which is defined by
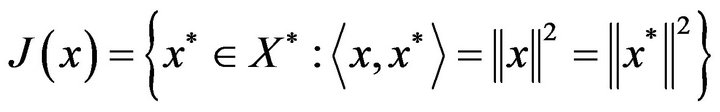 , where
, where 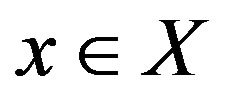
and  denotes the generalized duality pairing. The Hausdorff metric on
denotes the generalized duality pairing. The Hausdorff metric on  is defined by
is defined by
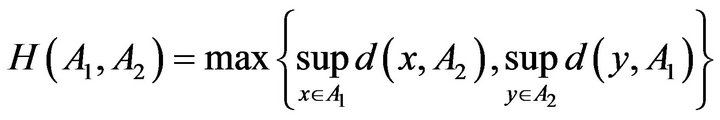 , for
, for
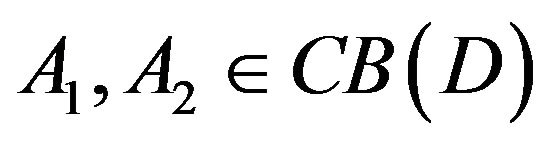 , where
, where . The multi-valued mapping
. The multi-valued mapping 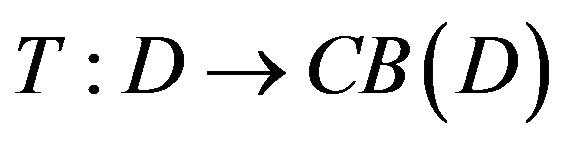 is called nonexpansive if
is called nonexpansive if 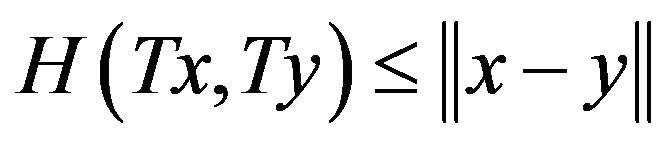 for all
for all . An element
. An element  is called a fixed point of
is called a fixed point of
 if
if . The set of fixed points of
. The set of fixed points of ![]() is represented by
is represented by . In the sequel, denote
. In the sequel, denote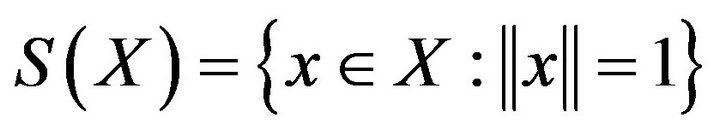 . A Banach space
. A Banach space  is said to be strictly convex if
is said to be strictly convex if  for all
for all 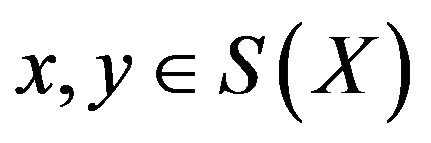
and . A Banach space is said to be uniformly convex if
. A Banach space is said to be uniformly convex if 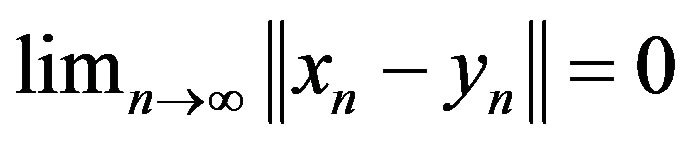 for any two sequences
for any two sequences
 and
and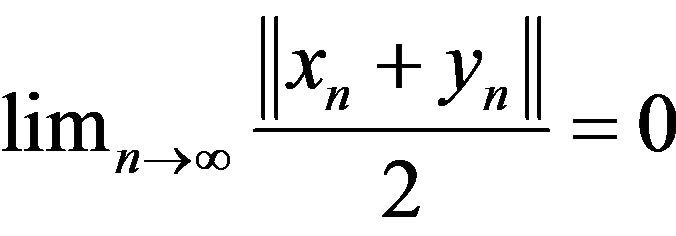 . The norm of Banach space
. The norm of Banach space 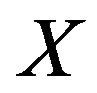 is said to be Gâteaux differentiable if for each
is said to be Gâteaux differentiable if for each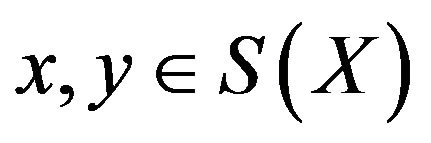 , the limit
, the limit
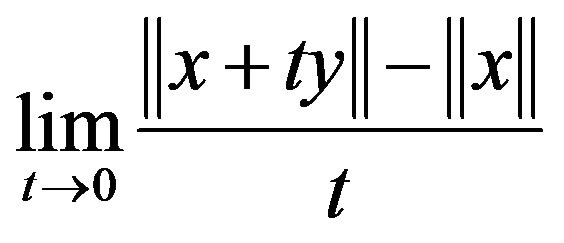 (1.1)
(1.1)
exists. In this case,  is said to be smooth. The norm of Banach space
is said to be smooth. The norm of Banach space  is said to be Fréchet differentiable, if for each
is said to be Fréchet differentiable, if for each , the limit (1.1) is attained uniformly for
, the limit (1.1) is attained uniformly for 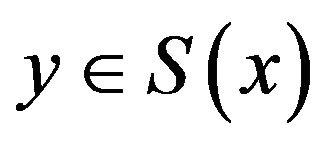 and the norm is uniformly Fréchet differentiable if the limit (1.1) is attained uniformly for
and the norm is uniformly Fréchet differentiable if the limit (1.1) is attained uniformly for . In this case,
. In this case, 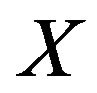 is said to be uniformly smooth.
is said to be uniformly smooth.
The following basic properties for Banach space X and for the normalized duality mapping ![]() can be found in Cioranescu [1].
can be found in Cioranescu [1].
(1) 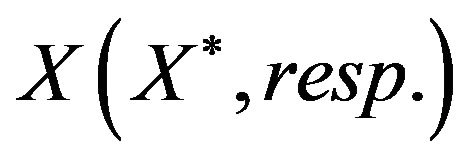 is uniformly convex if and only if
is uniformly convex if and only if 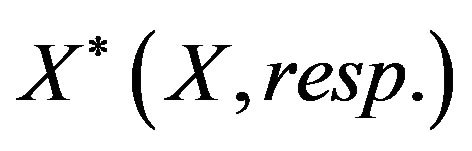 is uniformly smooth.
is uniformly smooth.
(2) If 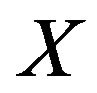 is smooth, then
is smooth, then ![]() is single-valued and norm-to-weak* continuous.
is single-valued and norm-to-weak* continuous.
(3) If 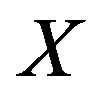 is reflexive, then
is reflexive, then ![]() is onto.
is onto.
(4) If 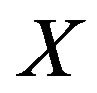 is strictly convex, then
is strictly convex, then 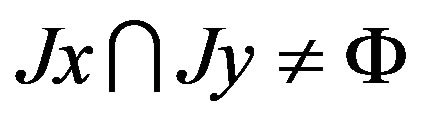 for all
for all .
.
(5) If 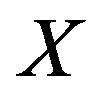 has a Fréchet differentiable norm, then
has a Fréchet differentiable norm, then ![]() is norm-to-norm continuous.
is norm-to-norm continuous.
(6) If 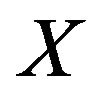 is uniformly smooth, then
is uniformly smooth, then ![]() is uniformly norm-to-norm continuous on each bounded subset of
is uniformly norm-to-norm continuous on each bounded subset of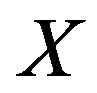 .
.
(7) Each uniformly convex Banach space  has the Kadec-Klee property, i.e., for any sequence
has the Kadec-Klee property, i.e., for any sequence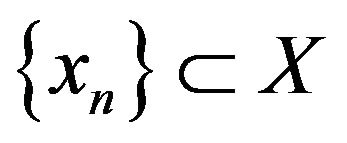 , if
, if  and
and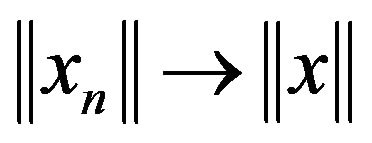 , then
, then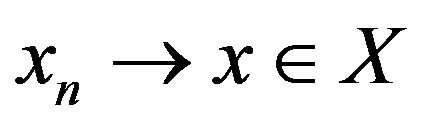 .
.
In 1953, Mann [2] introduced the following iterative sequence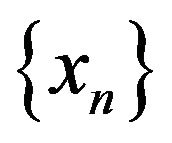 ,
,
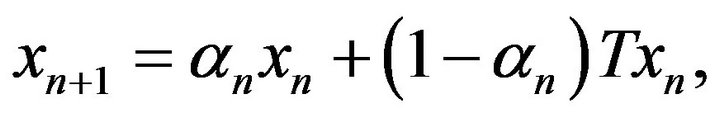
where the initial guess 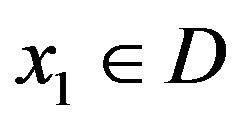 is arbitrary and
is arbitrary and 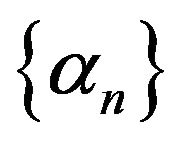 is a real sequence in
is a real sequence in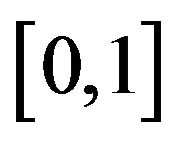 . It is known that under appropriate settings the sequence
. It is known that under appropriate settings the sequence 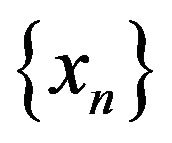 converges weakly to a fixed point of
converges weakly to a fixed point of![]() . However, even in a Hilbert space, Mann iteration may fail to converge strongly [3]. Some attempts to construct iteration method guaranteeing the strong convergence have been made. For example, Halpern [4] proposed the following so-called Halpern iteration,
. However, even in a Hilbert space, Mann iteration may fail to converge strongly [3]. Some attempts to construct iteration method guaranteeing the strong convergence have been made. For example, Halpern [4] proposed the following so-called Halpern iteration,
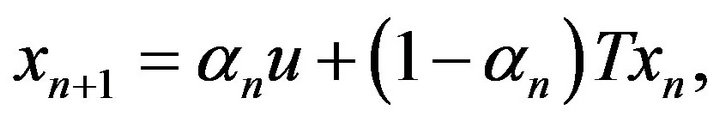
where 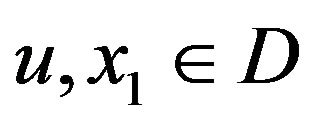 are arbitrary given and
are arbitrary given and 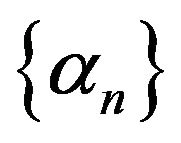 is a real sequence in
is a real sequence in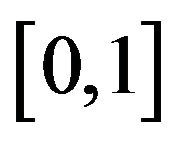 . Another approach was proposed by Nakajo and Takahashi [5]. They generated a sequence as follows,
. Another approach was proposed by Nakajo and Takahashi [5]. They generated a sequence as follows,
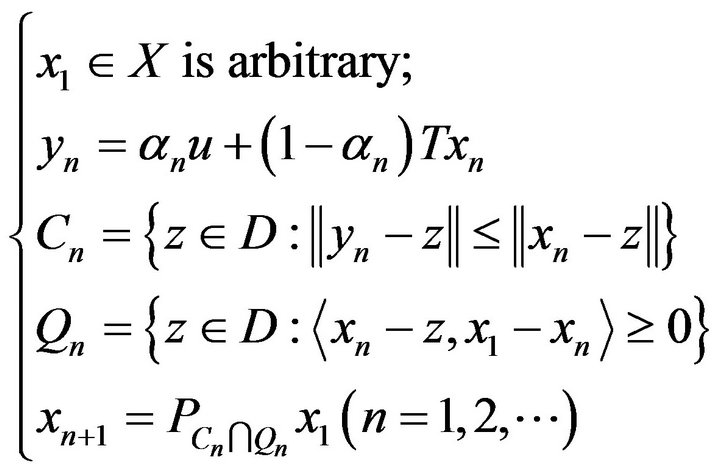 (1.2)
(1.2)
where 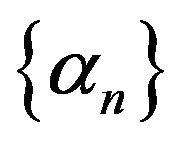 is a real sequence in
is a real sequence in  and
and  denotes the metric projection from a Hilbert space H onto a closed convex subset K of H. It should be noted here that the iteration above works only in Hilbert space setting. To extend this iteration to a Banach space, the concept of relatively nonexpansive mappings and quasi-
denotes the metric projection from a Hilbert space H onto a closed convex subset K of H. It should be noted here that the iteration above works only in Hilbert space setting. To extend this iteration to a Banach space, the concept of relatively nonexpansive mappings and quasi-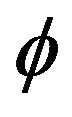 -nonexpansive mappings are introduced by Aoyama et al. [6], Chang et al. [7,8], Chidume et al. [9], Matsushita et al. [10-12], Qin et al. [13], Song et al. [14], Wang et al. [15] and others.
-nonexpansive mappings are introduced by Aoyama et al. [6], Chang et al. [7,8], Chidume et al. [9], Matsushita et al. [10-12], Qin et al. [13], Song et al. [14], Wang et al. [15] and others.
Inspired by the work of Matsushita and Takahashi, in this paper, we introduce modifying Halpern-Mann iterations sequence for finding a fixed point of a countable family of uniformly totally quasi- -asymptotically nonexpansive multi-valued mappings in reflexive Banach spaces
-asymptotically nonexpansive multi-valued mappings in reflexive Banach spaces  and some strong convergence theorems are proved. The results presented in the paper improve and extend the corresponding results in [7].
and some strong convergence theorems are proved. The results presented in the paper improve and extend the corresponding results in [7].
2. Preliminaries
In the sequel, we assume that 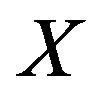 is a smooth, strictly convex, and reflexive Banach space and
is a smooth, strictly convex, and reflexive Banach space and  is a nonempty closed convex subset of
is a nonempty closed convex subset of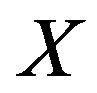 . In the sequel, we always use
. In the sequel, we always use  to denote the Lyapunov bifunction defined by
to denote the Lyapunov bifunction defined by
 . (2.1)
. (2.1)
It is obvious from the definition of the function 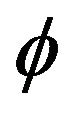 that
that
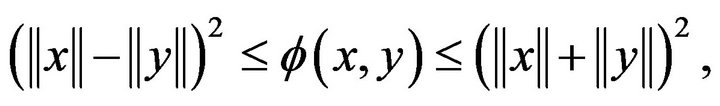 (2.2)
(2.2)
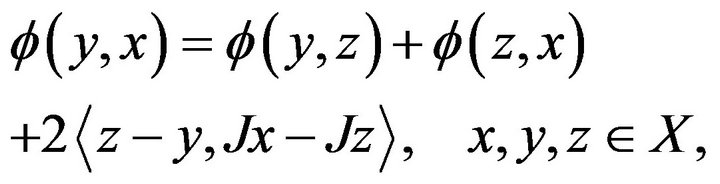 (2.3)
(2.3)
and
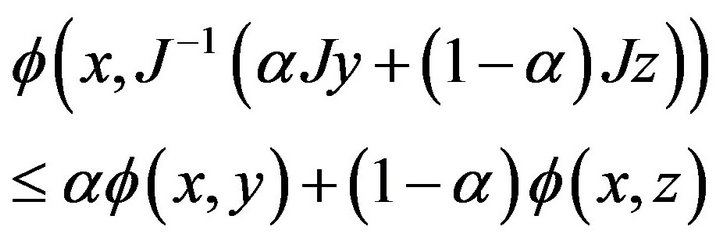 (2.4)
(2.4)
for all 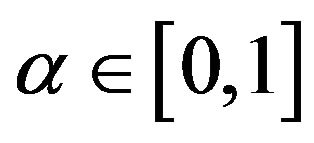 and
and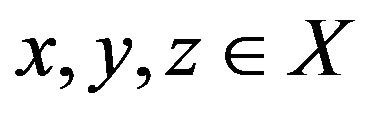 .
.
Following Alber [16], the generalized projection  is defined by
is defined by
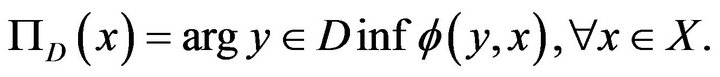
Many problems in nonlinear analysis can be reformulated as a problem of finding a fixed point of a nonexpansive mapping.
Remark 2.1 (see [17]) Let  be the generalized projection from a smooth, reflexive and strictly convex Banach space
be the generalized projection from a smooth, reflexive and strictly convex Banach space 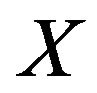 onto a nonempty closed convex subset
onto a nonempty closed convex subset  of
of , then
, then 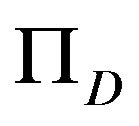 is a closed and quasi-
is a closed and quasi-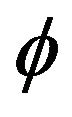 -nonexpansive from
-nonexpansive from  onto
onto .
.
Lemma 2.1 (see [16]) Let 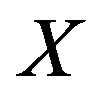 be a smooth, strictly convex and reflexive Banach space and
be a smooth, strictly convex and reflexive Banach space and  be a nonempty closed convex subset of
be a nonempty closed convex subset of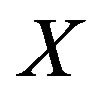 . Then the following conclusions hold(a)
. Then the following conclusions hold(a) 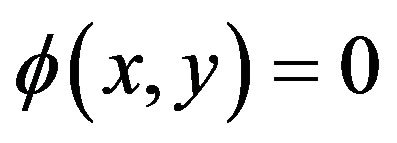 if and only if
if and only if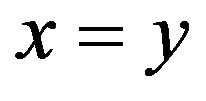 .
.
(b)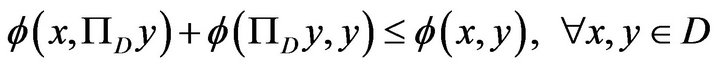 .
.
(c) If 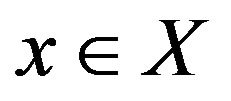 and
and , then
, then 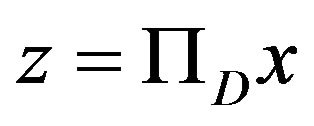 if and only if
if and only if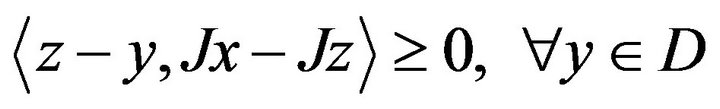 .
.
Lemma 2.2 (see [7]) Let 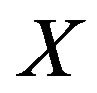 be a real uniformly smooth and strictly convex Banach space with KadecKlee property, and
be a real uniformly smooth and strictly convex Banach space with KadecKlee property, and  be a nonempty closed convex subset of
be a nonempty closed convex subset of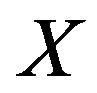 . Let
. Let  and
and 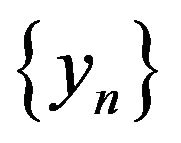 be two sequences in
be two sequences in  such that
such that  and
and  where
where 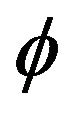
is the function defined by (1.2), then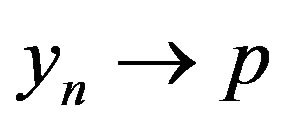 .
.
Definition 2.1 A point 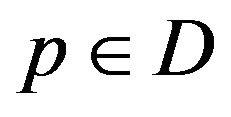 is said to be an asymptotic fixed point of multi-valued mapping
is said to be an asymptotic fixed point of multi-valued mapping
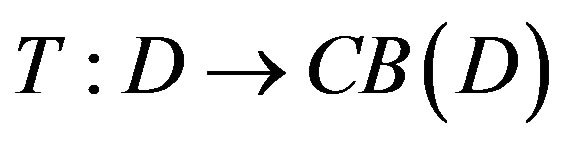 , if there exists a sequence
, if there exists a sequence  such that
such that 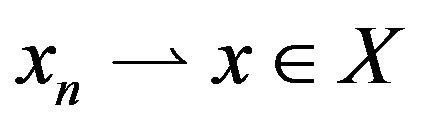 and
and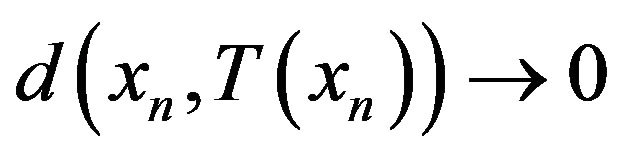 . Denote the set of all asymptotic fixed points of
. Denote the set of all asymptotic fixed points of ![]() by
by .
.
Definition 2.2
(1) A multi-valued mapping 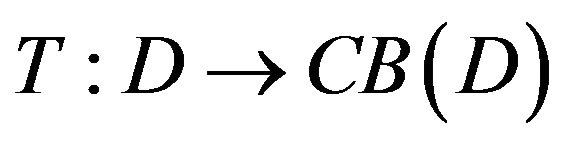 is said to be relatively nonexpansive, if
is said to be relatively nonexpansive, if ,
,
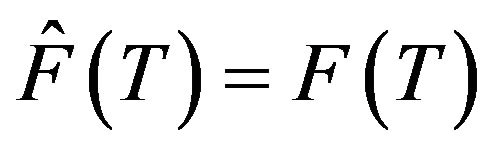 , and
, and 
 .
.
(2) A multi-valued mapping 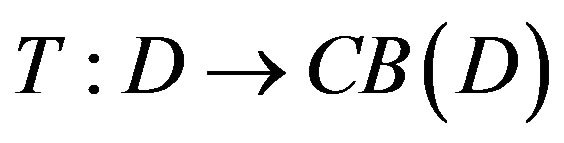 is said to be closed, if for any sequence
is said to be closed, if for any sequence  with
with  and
and , then
, then
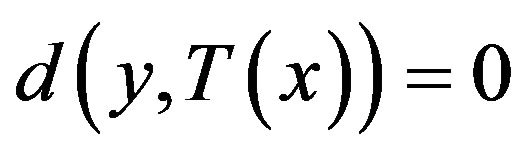 .
.
Remark 2.2 If  is a real Hilbert space, then
is a real Hilbert space, then 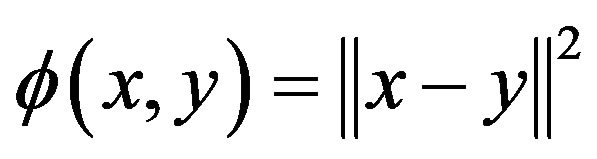 and
and 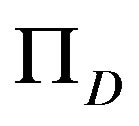 is the metric projection
is the metric projection 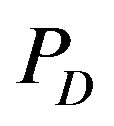 of
of  onto
onto .
.
Next, We present an example of relatively nonexpansive multi-valued mapping.
Example 2.1 (see [18]) Let 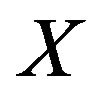 be a smooth, strictly convex and reflexive Banach space,
be a smooth, strictly convex and reflexive Banach space,  be a nonempty closed and convex subset of
be a nonempty closed and convex subset of  and
and  be a bifunction satisfying the conditions:
be a bifunction satisfying the conditions:
(A1)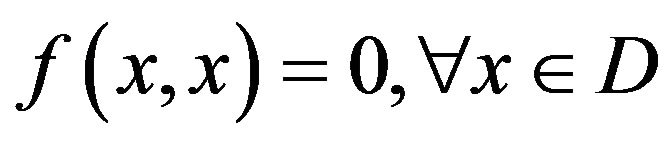 ;
;
(A2) ;
;
(A3) for each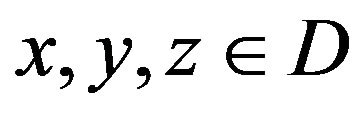 ,
,
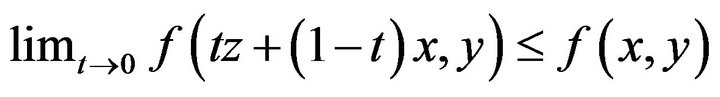 ;
;
(A4) for each given , the function
, the function  is convex and lower semicontinuous.
is convex and lower semicontinuous.
The “so-called” equilibrium problem for f is to find a  such that
such that . The set of its solutions is denoted by
. The set of its solutions is denoted by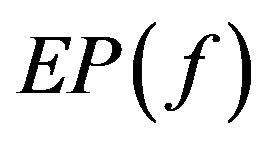 .
.
Let 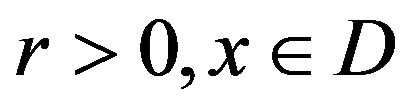 and define a multi-valued mapping
and define a multi-valued mapping 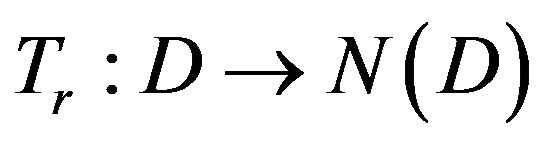 as follows,
as follows,
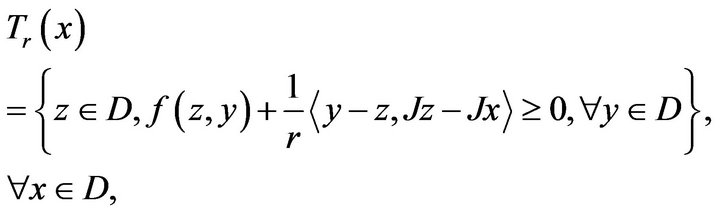 (2.5)
(2.5)
then (1) 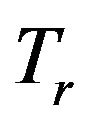 is single-valued, and so
is single-valued, and so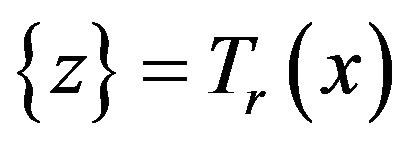 ; (2)
; (2) 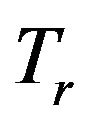 is a relatively nonexpansive mapping, therefore, it is a closed quasi-
is a relatively nonexpansive mapping, therefore, it is a closed quasi-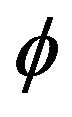 -nonexpansive mapping; (3)
-nonexpansive mapping; (3)  .
.
Definition 2.3
(1) A multi-valued mapping 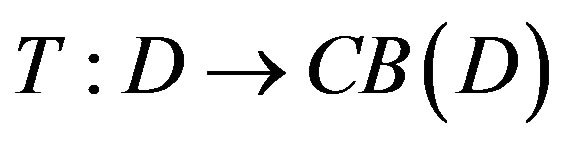 is said to be quasi-
is said to be quasi- -nonexpansive, if
-nonexpansive, if , and
, and .
.
(2) A multi-valued mapping 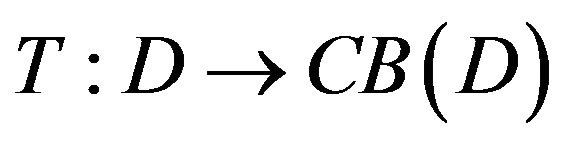 is said to be quasi-
is said to be quasi-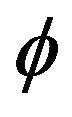 -asymptotically nonexpansive, if
-asymptotically nonexpansive, if 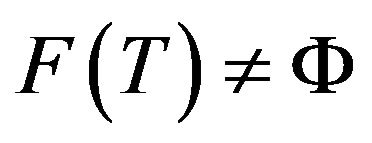 and there exists a real sequence
and there exists a real sequence 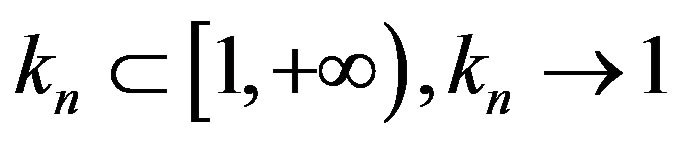 such that
such that
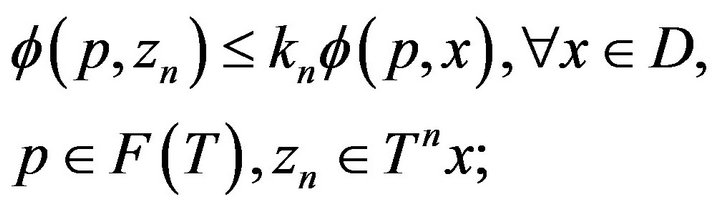 (2.6)
(2.6)
(3) A multi-valued mapping  is said to be totally quasi-
is said to be totally quasi- -asymptotically nonexpansive, if
-asymptotically nonexpansive, if 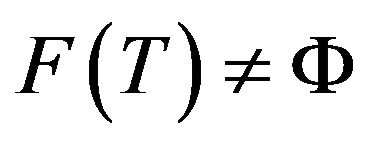 and there exist nonnegative real sequences
and there exist nonnegative real sequences , with
, with 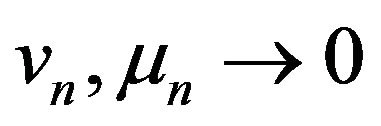 (as
(as![]() ) and a strictly increasing continuous function
) and a strictly increasing continuous function  with
with 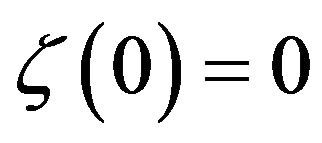 such that
such that
 (2.7)
(2.7)
Remark 2.3 From the definitions, it is obvious that a relatively nonexpansive multi-valued mapping is a quasi-  -nonexpansive multi-valued mapping, and a quasi-
-nonexpansive multi-valued mapping, and a quasi- - nonexpansive multi-valued mapping is a quasi-
- nonexpansive multi-valued mapping is a quasi-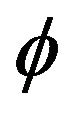 -asymptotically nonexpansive multi-valued mapping, and a quasi-
-asymptotically nonexpansive multi-valued mapping, and a quasi- -asymptotically nonexpansive multi-valued mapping is a total quasi-
-asymptotically nonexpansive multi-valued mapping is a total quasi- -asymptotically nonexpansive multi-valued mapping, but the converse is not true.
-asymptotically nonexpansive multi-valued mapping, but the converse is not true.
Lemma 2.3 Let 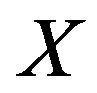 and
and  be as in Lemma 2.2.
be as in Lemma 2.2. 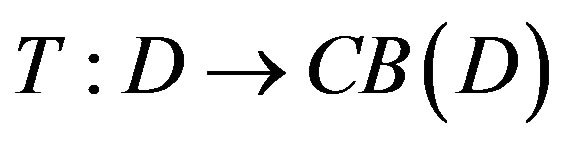 be a closed and totally quasi-
be a closed and totally quasi-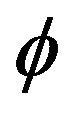 -asymptotically nonexpansive multi-valued mapping with nonnegative real sequences
-asymptotically nonexpansive multi-valued mapping with nonnegative real sequences 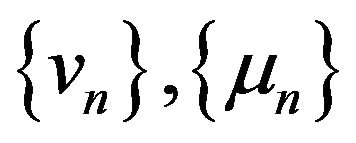 and a strictly increasing continuous function
and a strictly increasing continuous function 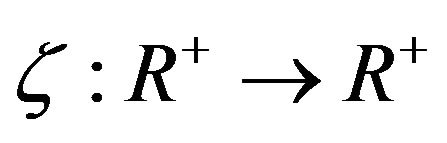 with
with 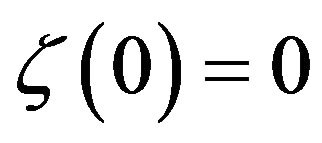 ,if
,if  (as
(as![]() ) and
) and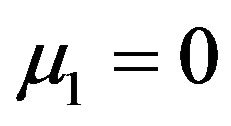 , then
, then 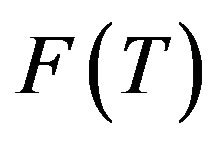 is a closed and convex subset of
is a closed and convex subset of .
.
Proof. Let 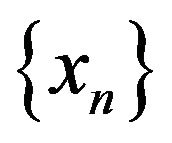 be a sequence in
be a sequence in , such that
, such that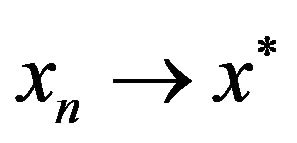 . Since
. Since ![]() is totally quasi-
is totally quasi-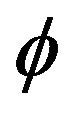 -asymptotically nonexpansive multi-valued mapping, we have
-asymptotically nonexpansive multi-valued mapping, we have
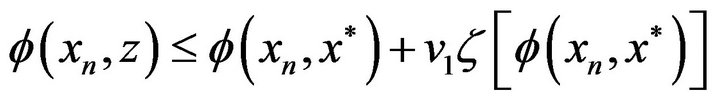
for all 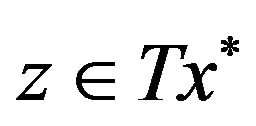 and for all
and for all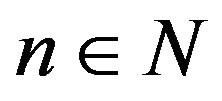 . Therefore,
. Therefore,

By Lemma 2.1(a), we obtain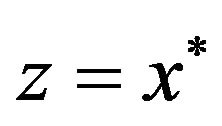 . Hence,
. Hence,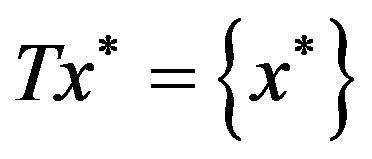 . So, we have
. So, we have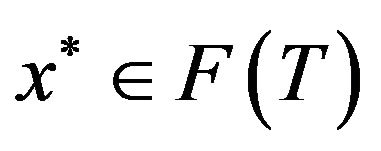 . This implies
. This implies  is closed.
is closed.
Let  and
and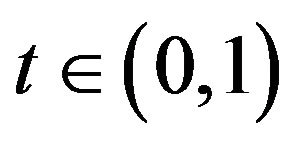 , and put
, and put 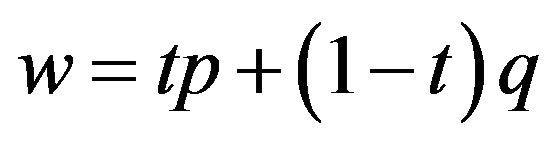 . Next we prove that
. Next we prove that . Indeed, in view of the definition of
. Indeed, in view of the definition of , letting
, letting , we have
, we have
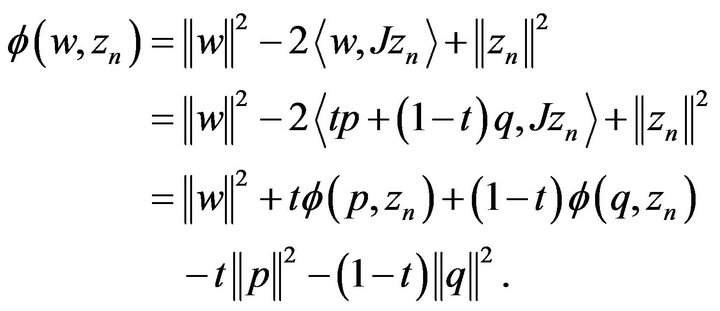 (2.8)
(2.8)
Since
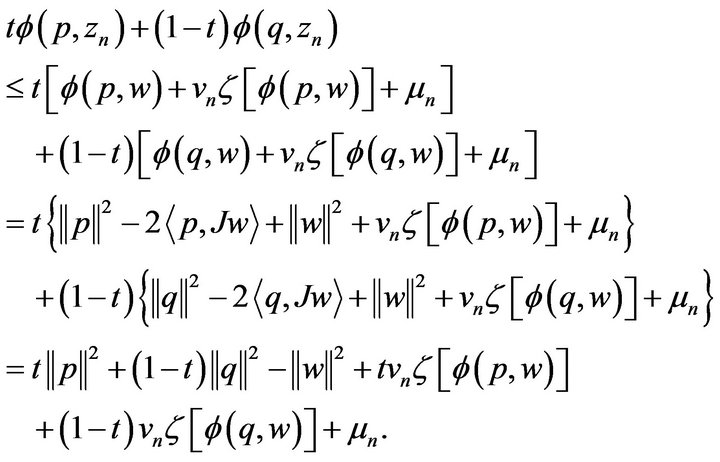 (2.9)
(2.9)
Substituting (2.8) into (2.9) and simplifying it, we have
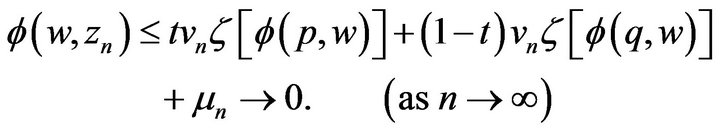
By Lemma 2.2, we have . This implies that
. This implies that . Since
. Since ![]() is closed, we have
is closed, we have  , i.e.,
, i.e., . This completes the proof of Lemma 2.3. □
. This completes the proof of Lemma 2.3. □
Definition 2.4 A mapping 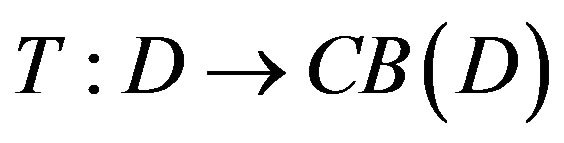 is said to be uniformly
is said to be uniformly ![]() -Lipschitz continuous, if there exists a constant
-Lipschitz continuous, if there exists a constant 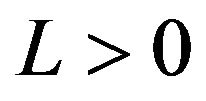 such that
such that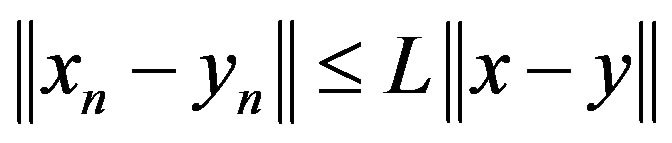 , where
, where .
.
Definition 2.5
(1) A countable family of mappings 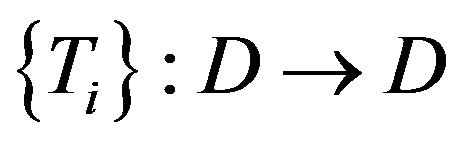 is said to be uniformly quasi-
is said to be uniformly quasi- -nonexpansive, if
-nonexpansive, if ![]() , and
, and
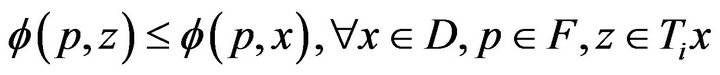 .
.
(2) A countable family of mappings 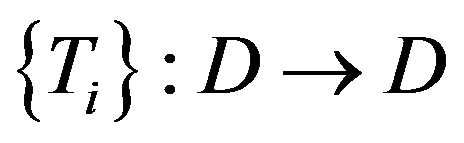 is said to be uniformly quasi-
is said to be uniformly quasi-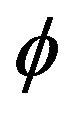 -asymptotically nonexpansive, if
-asymptotically nonexpansive, if![]() , and there exists a real sequence
, and there exists a real sequence  such that,
such that,
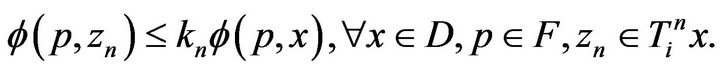 (2.10)
(2.10)
(3) A countable family of mappings 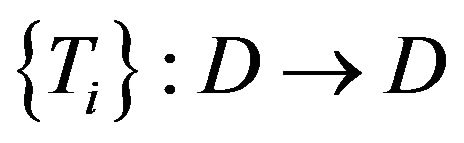 is said to be totally uniformly quasi-
is said to be totally uniformly quasi-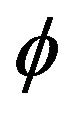 -asymptotically nonexpansive multi-valued, if
-asymptotically nonexpansive multi-valued, if ![]() and there exists nonnegative real sequences
and there exists nonnegative real sequences 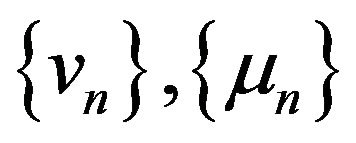 with
with 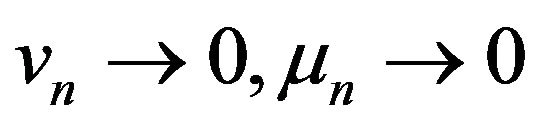 (as
(as![]() ) and a strictly increasing and continuous function
) and a strictly increasing and continuous function 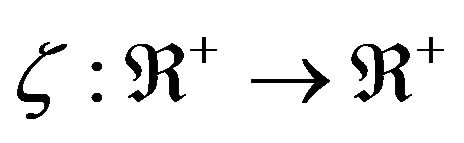 with
with 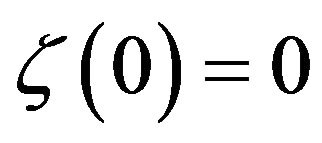 such that
such that
 (2.11)
(2.11)
Remark 2.4 From the definitions, it is obvious that a countable family of uniformly quasi- -nonexpansive multi-valued mappings is a countable family of uniformly quasi-
-nonexpansive multi-valued mappings is a countable family of uniformly quasi-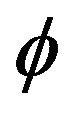 -asymptotically nonexpansive multi-valued mappings, and a countable family of uniformly quasi-
-asymptotically nonexpansive multi-valued mappings, and a countable family of uniformly quasi-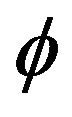 -asymptotically nonexpansive multi-valued mappings is a countable family of totally uniformly quasi-
-asymptotically nonexpansive multi-valued mappings is a countable family of totally uniformly quasi-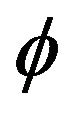 -asymptotically multi-valued mappings, but the converse is not true.
-asymptotically multi-valued mappings, but the converse is not true.
3. Main Results
Theorem 3.1 Let  be a real uniformly smooth and strictly convex Banach space with Kadec-Klee property, D be a nonempty closed convex subset of X,
be a real uniformly smooth and strictly convex Banach space with Kadec-Klee property, D be a nonempty closed convex subset of X, 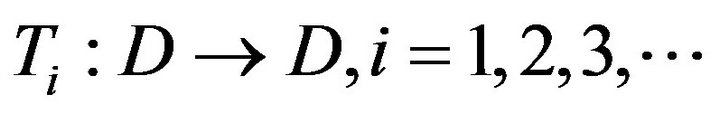 be a closed and uniformly
be a closed and uniformly 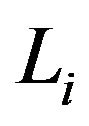 - Lipschitz continuous and a countable family of uniformly totally quasi-
- Lipschitz continuous and a countable family of uniformly totally quasi- -asymptotically nonexpansive multi-valued mappings with nonnegative real sequences
-asymptotically nonexpansive multi-valued mappings with nonnegative real sequences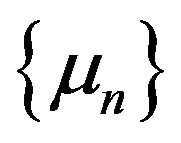
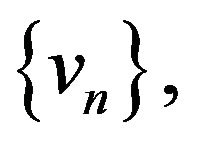 ,
,  (as
(as![]() ) and a strictly increasing continuous function
) and a strictly increasing continuous function 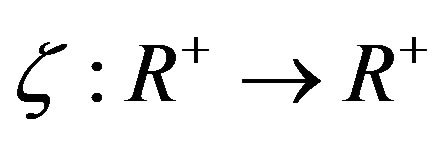 with
with 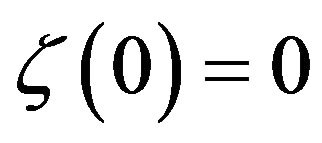 satisfying condition (2.11). Let
satisfying condition (2.11). Let 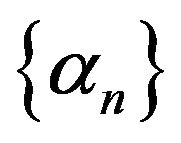 be a sequence in
be a sequence in 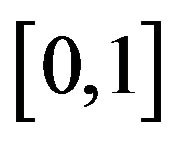 such that
such that . If
. If 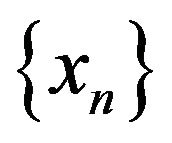 is the sequence generated by
is the sequence generated by
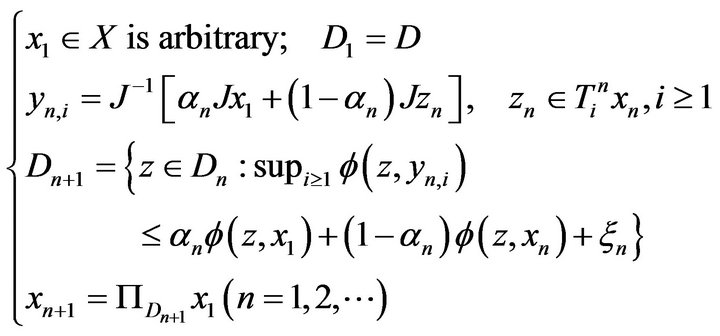 (3.1)
(3.1)
where ,
, 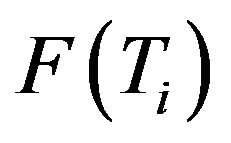 is the fixed point set of
is the fixed point set of![]() , and
, and 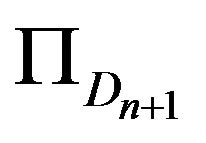 is the generalized projection of
is the generalized projection of 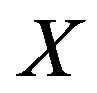 onto
onto![]() .
.
If ![]() and
and 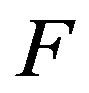 is bounded and
is bounded and
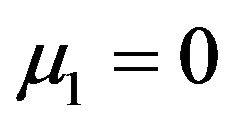 , then
, then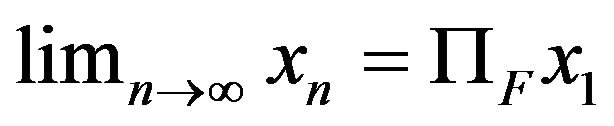 .
.
Proof. (I) First, we prove that F and 
 are closed and convex subsets in
are closed and convex subsets in . In fact, it follows from Lemma 2.3 that
. In fact, it follows from Lemma 2.3 that 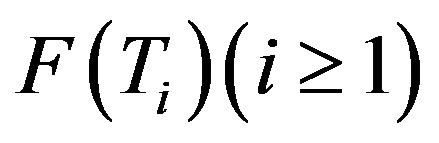 is a closed and convex subsets in D. therefore F is closed and convex subsets in D. Again by the assumption,
is a closed and convex subsets in D. therefore F is closed and convex subsets in D. Again by the assumption, 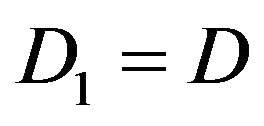 is closed and convex. Suppose that
is closed and convex. Suppose that  is closed and convex for some
is closed and convex for some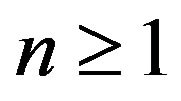 . In view of the definition of
. In view of the definition of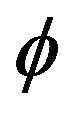 , we have
, we have

This shows that ![]() is closed and convex. The conclusions are proved.
is closed and convex. The conclusions are proved.
(II) Next, we prove that , for all
, for all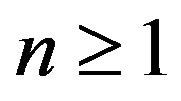 .
.
In fact, it is obvious that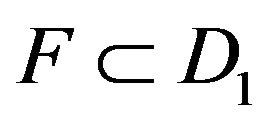 . Suppose that
. Suppose that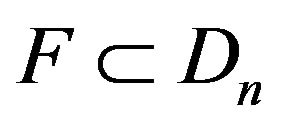 . Hence for any
. Hence for any , by (2.4), we have
, by (2.4), we have
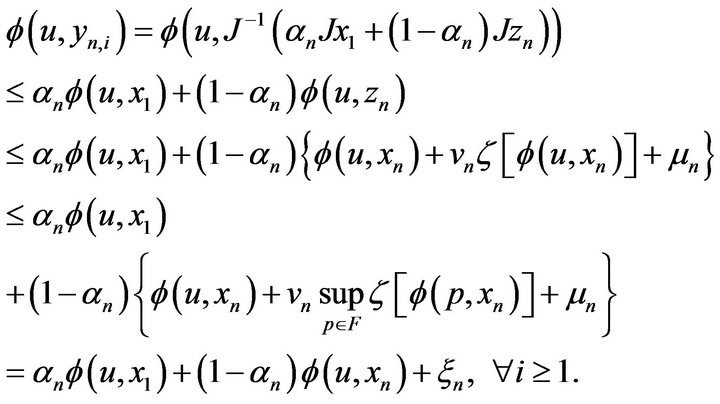 (3.2)
(3.2)
Therefore we have
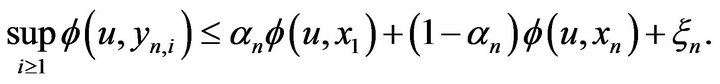 (3.3)
(3.3)
This shows that 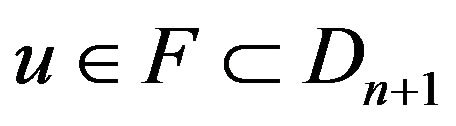 and so
and so . The conclusions are proved.
. The conclusions are proved.
(III) Now we prove that 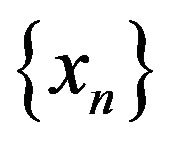 converges strongly to some point
converges strongly to some point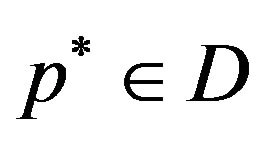 .
.
In fact, since , from Lemma 2.1(c), we have
, from Lemma 2.1(c), we have 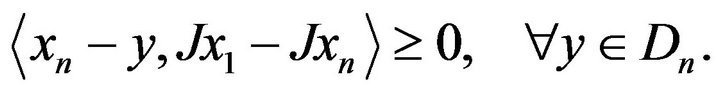 Again since
Again since  , we have
, we have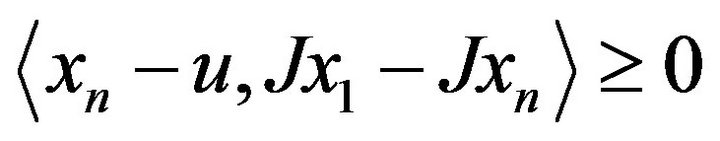 ,
,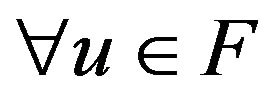 . It follows from Lemma 2.1(b) that for each
. It follows from Lemma 2.1(b) that for each 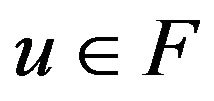 and for each
and for each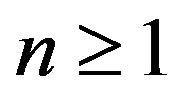 ,
,
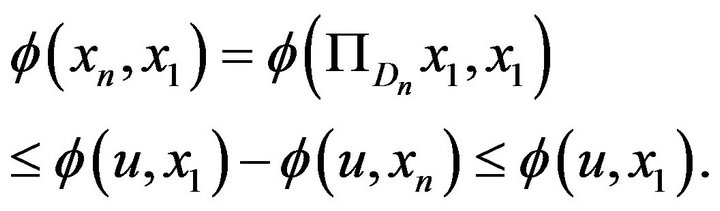 (3.4)
(3.4)
Therefore,  is bounded, and so is
is bounded, and so is . Since
. Since 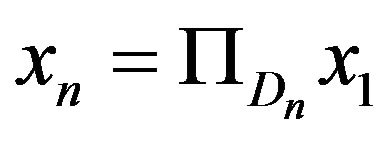 and
and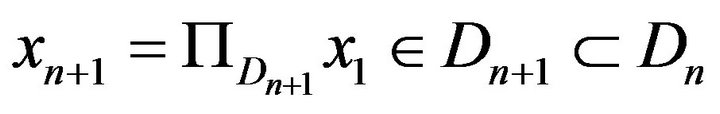 , we have
, we have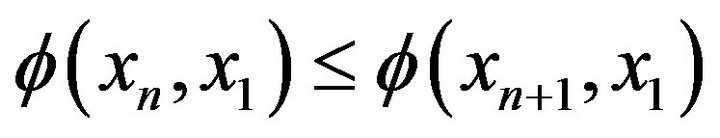 .
.
This implies that 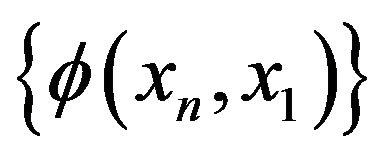 is nondecreasing. Hence
is nondecreasing. Hence
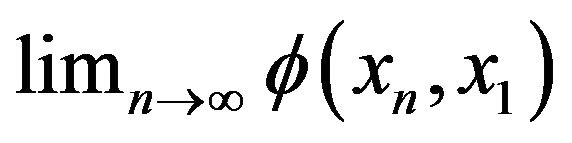 exists. Since X is reflexive, there exists a subsequence
exists. Since X is reflexive, there exists a subsequence  such that
such that 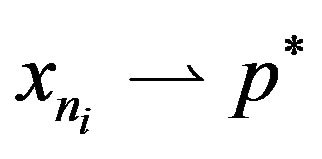 (some point in
(some point in ). Since
). Since 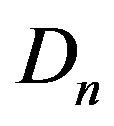 is closed and convex and
is closed and convex and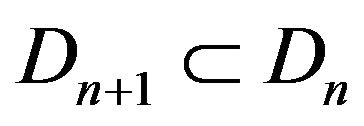 . This implies that
. This implies that 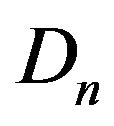 is weakly closed and
is weakly closed and 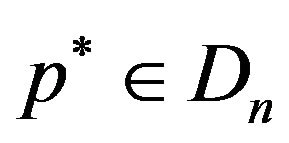 for each
for each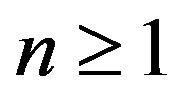 . In view of
. In view of
 , we have
, we have 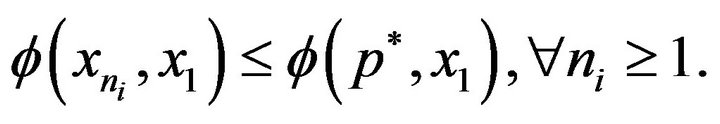 Since the norm
Since the norm  is weakly lower semi-continuous, we have
is weakly lower semi-continuous, we have

and so

This shows that 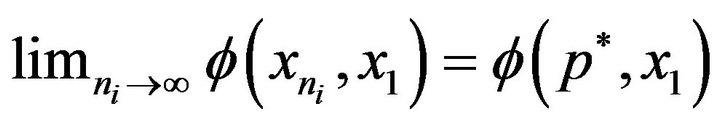 and we have
and we have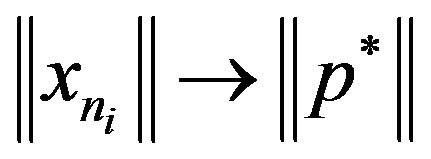 . Since
. Since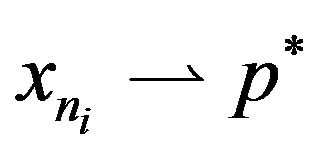 , by virtue of KadecKlee property of
, by virtue of KadecKlee property of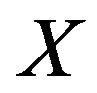 , we obtain that
, we obtain that 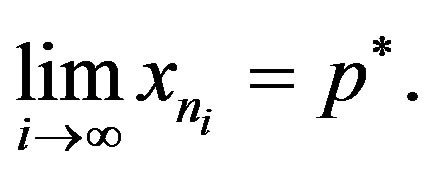 Since
Since 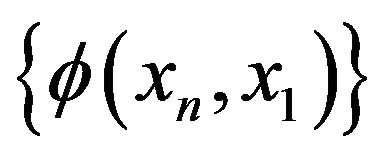 is convergent, this together with
is convergent, this together with
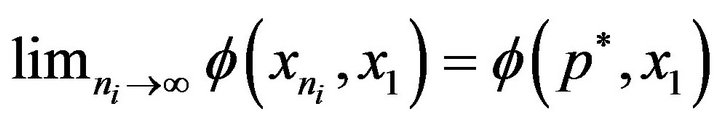 shows that
shows that
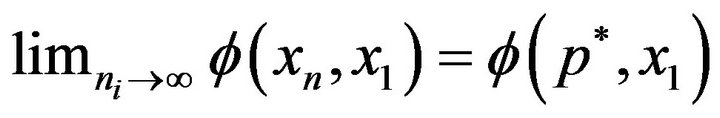 . If there exists some subsequence
. If there exists some subsequence  such that
such that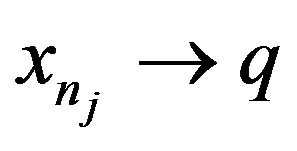 , then from Lemma 2.1, we have
, then from Lemma 2.1, we have
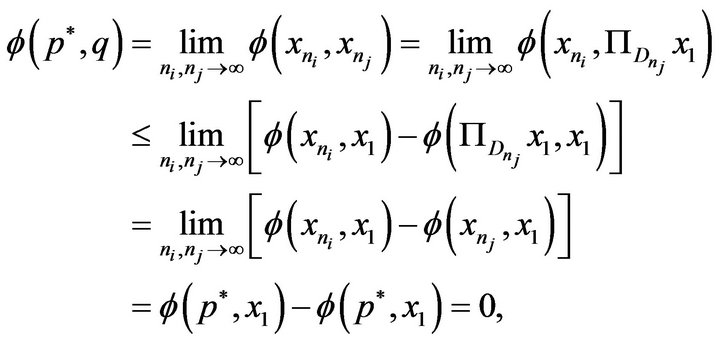
i.e., 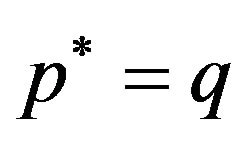 and hence
and hence
 (3.5)
(3.5)
By the way, from (3.4), it is easy to see that
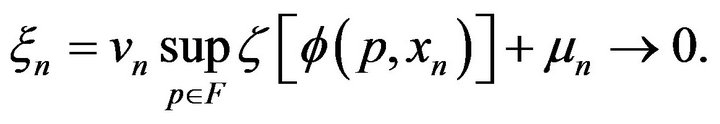 (3.6)
(3.6)
(IV) Now we prove that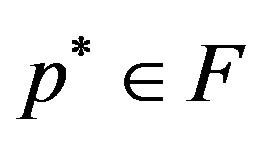 .
.
In fact, since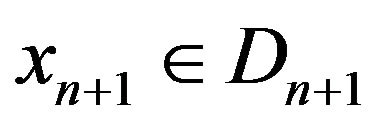 , from (3.1), (3.4) and (3.5), we have
, from (3.1), (3.4) and (3.5), we have
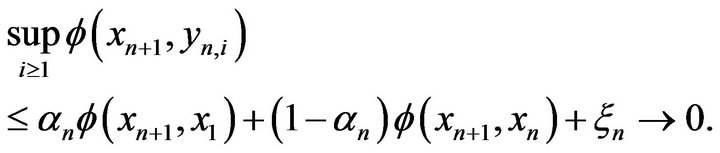 (3.7)
(3.7)
Since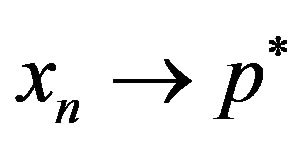 , it follows from (3.6) and Lemma 2.2 that
, it follows from (3.6) and Lemma 2.2 that
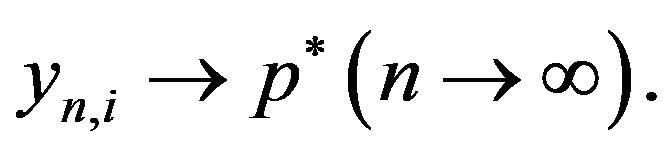 (3.8)
(3.8)
Since 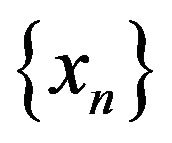 is bounded and
is bounded and  is a countable family of uniformly totally quasi-
is a countable family of uniformly totally quasi- -asymptotically nonexpansive multi-valued mappings,
-asymptotically nonexpansive multi-valued mappings, 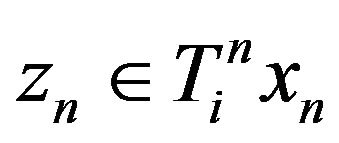 is bounded. In view of
is bounded. In view of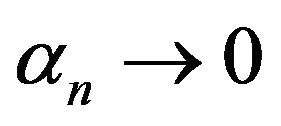 , from (3.1), we have
, from (3.1), we have
 (3.9)
(3.9)
Since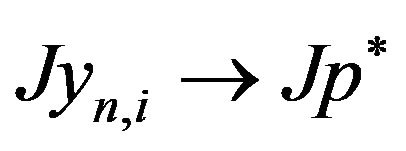 , this implies
, this implies . From Remark 2.1, it yields that
. From Remark 2.1, it yields that
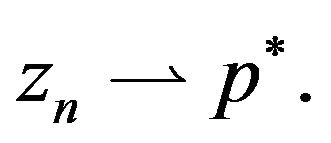 (3.10)
(3.10)
Again since
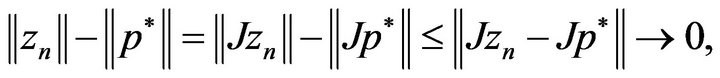 (3.11)
(3.11)
this together with (3.9) and the Kadec-Klee-property of  shows that
shows that
 (3.12)
(3.12)
On the other hand, by the assumptions that ![]() is
is 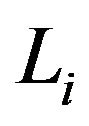 -Lipschitz continuous for each
-Lipschitz continuous for each![]() , we have
, we have
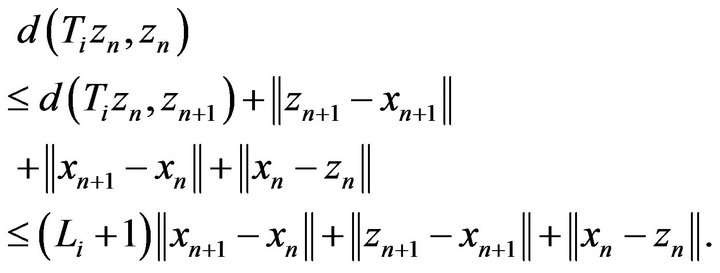 (3.13)
(3.13)
From (3.12) and , we have that
, we have that
 . In view of the closeness of
. In view of the closeness of![]() , it yields that
, it yields that , which implies that
, which implies that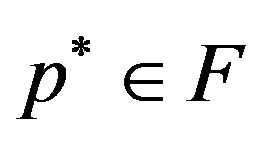 .
.
(V) Finally we prove that 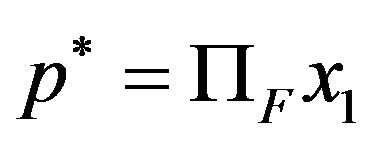 and so
and so  .
.
Let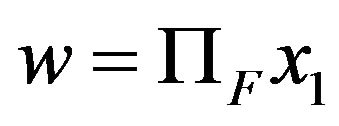 . Since
. Since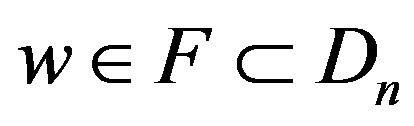 , we have
, we have 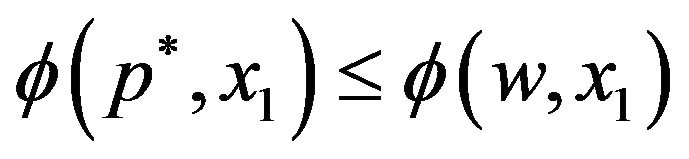 . This implies that
. This implies that
 (3.14)
(3.14)
which yields that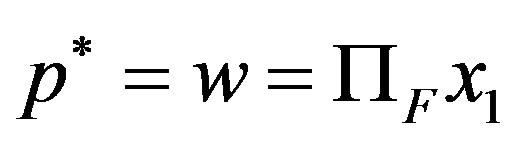 . Therefore,
. Therefore,  . The proof of Theorem 3.1 is completed.
. The proof of Theorem 3.1 is completed.
By Remark 2.4, the following corollaries are obtained. □
Corollary 3.1 Let X and  be as in Theorem 3.1, and a countable family of mappings
be as in Theorem 3.1, and a countable family of mappings 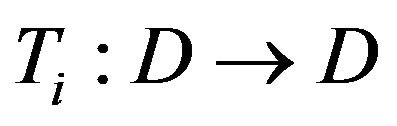
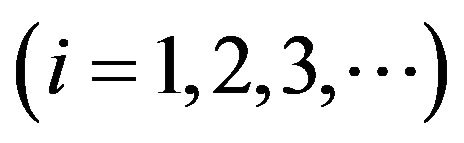 be a closed and uniformly
be a closed and uniformly 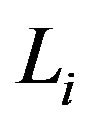 -Lipschitz continuous a relatively nonexpansive multi-valued mappings. Let
-Lipschitz continuous a relatively nonexpansive multi-valued mappings. Let  in
in 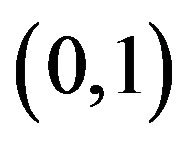 with
with . Let
. Let 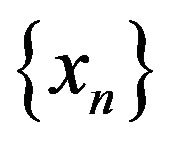 be the sequence generated by
be the sequence generated by
 (3.15)
(3.15)
where  is the set of fixed points of
is the set of fixed points of![]() , and
, and 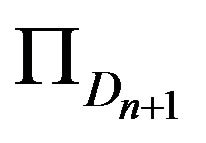 is the generalized projection of
is the generalized projection of 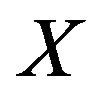 onto
onto![]() , If
, If
![]() and F is bounded, then
and F is bounded, then 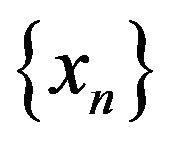 converges strongly to
converges strongly to .
.
Corollary 3.2 Let  and
and  be as in Theorem 3.1, and a countable family of mappings
be as in Theorem 3.1, and a countable family of mappings 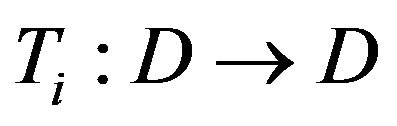
 be a closed and uniformly
be a closed and uniformly  -Lipschitz continuous quasi-phi-asymptotically nonexpansive multivalued mappings with nonnegative real sequences
-Lipschitz continuous quasi-phi-asymptotically nonexpansive multivalued mappings with nonnegative real sequences
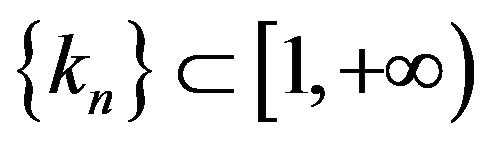 and
and 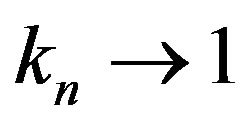 satisfying condition (2.1). Let
satisfying condition (2.1). Let  be a sequence in
be a sequence in  and satisfy
and satisfy
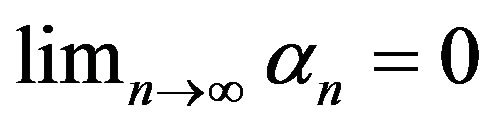 . If
. If 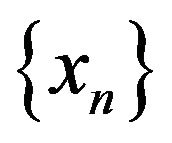 is the sequence generated by
is the sequence generated by
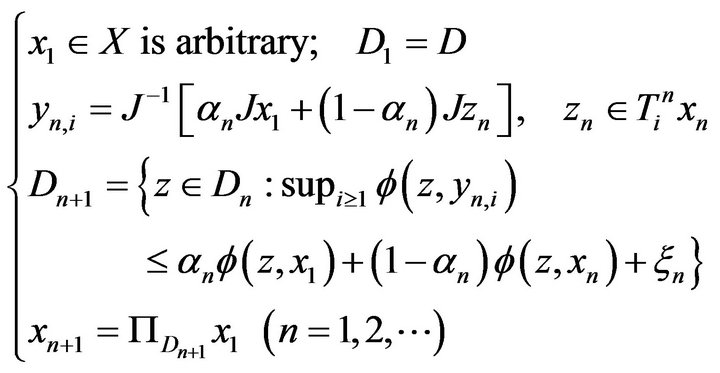 (3.16)
(3.16)
where  is the set of fixed points of
is the set of fixed points of![]() , and
, and  is the generalized projection of
is the generalized projection of 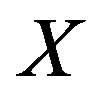 onto
onto![]() , and
, and 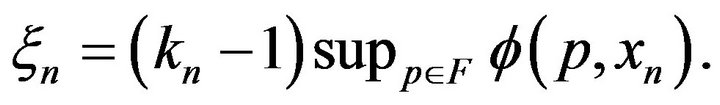
If ![]() and F is bounded, then
and F is bounded, then 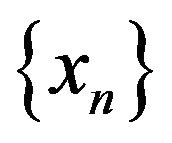
converges strongly to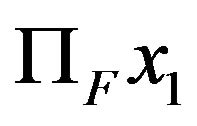 .
.
4. Application
We utilize Corollary 3.2 to study a modified Halpern iterative algorithm for a system of equilibrium problems.
Theorem 4.1 Let ,
, 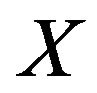 and
and  be the same as in Theorem 3.1. Let
be the same as in Theorem 3.1. Let 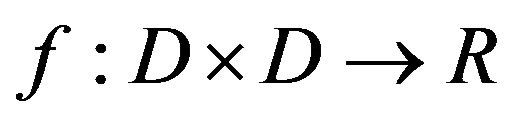 be a bifunction satisfying conditions (A1)-(A4) as given in Example 2.6.
be a bifunction satisfying conditions (A1)-(A4) as given in Example 2.6.
Let  be a mapping defined by (2.5), i.e.,
be a mapping defined by (2.5), i.e.,

Let  be the sequence generated by
be the sequence generated by
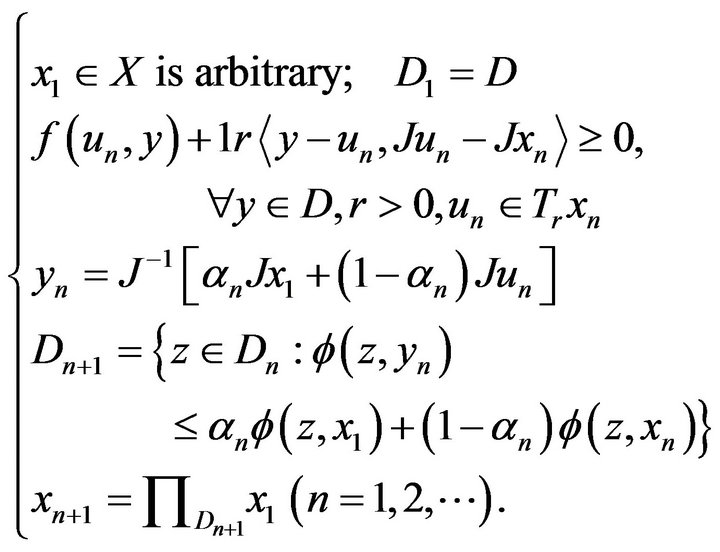 (4.1)
(4.1)
If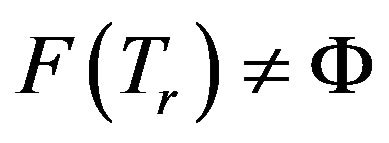 , then
, then 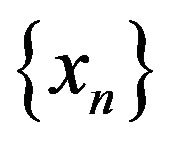 converges strongly to
converges strongly to
 which is a common solution of the system of equilibrium problems for
which is a common solution of the system of equilibrium problems for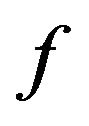 .
.
Proof. In Example 2.6, we have pointed out that ,
, 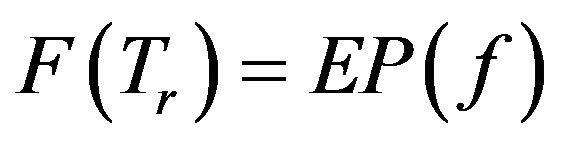 and
and 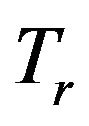 is a closed quasi-
is a closed quasi- -nonexpansive mapping. Hence (4.1) can be rewritten as follows:
-nonexpansive mapping. Hence (4.1) can be rewritten as follows:
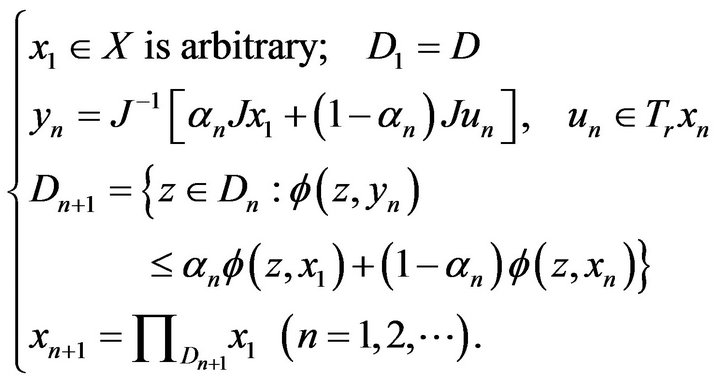
Therefore the conclusion of Theorem 4.6 can be obtained from Corollary 3.2.
REFERENCES
- I. Cioranescu, “Geometry of Banach Spaces, Duality Mappings and Nonlinear Problems,” Kluwer Academic, Dordrecht, 1990. doi:10.1007/978-94-009-2121-4
- W. R. Mann, “Mean Value Methods in Iteration,” Proceedings of the American Mathematical Society, Vol. 4, No. 3, 1953, pp. 506-510. doi:10.1090/S0002-9939-1953-0054846-3
- A. Genel and J. Lindenstrauss, “An Example Concerning Fixed Points,” Israel Journal of Mathematics, Vol. 22, No. 1, 1975, pp. 81-86.
- B. Halpren, “Fixed Points of Nonexpansive Maps,” Bulletin of the American Mathematical Society, Vol. 73, 1967, pp. 957-961. doi:10.1090/S0002-9904-1967-11864-0
- K. Nakajo and W. Takahashi, “Strong Convergence Theorems for Nonexpansive Mappings and Nonexpansive Semigroups,” Journal of Mathematical Analysis and Applications, Vol. 279, No. 2, 2003, pp. 372-379. doi:10.1016/S0022-247X(02)00458-4
- K. Aoyama and Y. Kimura, “Strong Convergence Theorems for Strongly Nonexpansive Sequences,” Applied Mathematics and Computation, Vol. 217, No.19 , 2011, pp. 7537-7545. doi:10.1016/j.amc.2011.01.092
- S. S. Chang, H. W. J. Lee, C. K. Chan and W. B. Zhang, “A Modified Halpern-Type Iteration Algorithm for Totally Quasi-
 -Asymptotically Nonexpansive Mappings with Applications,” Applied Mathematics and Computation, Vol. 218, No. 11, 2012, pp. 6489-6497. doi:10.1016/j.amc.2011.12.019
-Asymptotically Nonexpansive Mappings with Applications,” Applied Mathematics and Computation, Vol. 218, No. 11, 2012, pp. 6489-6497. doi:10.1016/j.amc.2011.12.019 - S. S. Chang, L. Yang and J. A. Liu, “Strong Convergence Theorem for Nonexpansive Semi-Groups in Banach Space,” Applied Mathematics and Mechanics, Vol. 28, No. 10, 2007, pp. 1287-1297. doi:10.1007/s10483-007-1002-x
- C. E. Chidume and E. U. Ofoedu, “Approximation of Common Fixed Points for Finite Families of Total Asymptotically Nonexpansive Mappings,” Journal of Mathematical Analysis and Applications, Vol. 333, No. 1, 2007, pp. 128-141. doi:10.1016/j.jmaa.2006.09.023
- S. Matsushita and W. Takahashi, “Weak and Strong Convergence Theorems for Relatively Nonexpansive Mappings in a Banach Space,” Fixed Point Theory and Applications, Vol. 2004, 2004, pp. 37-47. doi:10.1155/S1687182004310089
- S. Matsushita and W. Takahashi, “An Iterative Algorithm for Relatively Nonexpansive Mappings by Hybrid Method and Applications,” Proceedings of the 3rd International Conference on Nonlinear Analysis and Convex Analysis, Tokyo, 2004, pp. 305-313.
- S. Matsushita and W. Takahashi, “A Strong Convergence Theorem for Relatively Nonexpansive Mappings in a Banach Space,” The Journal of Approximation Theory, Vol. 134, No. 2, 2005, pp. 257-266. doi:10.1016/j.jat.2005.02.007
- X. L. Qin, Y. J. Cho, S. M. Kang and H. Y. Zhou, “Convergence of a Modified Halpern-Type Iterative Algorithm for Quasi-
 -Nonexpansive Mappings,” Applied Mathematics Letters, Vol. 22, No. 7, 2009, pp. 1051-1055. doi:10.1016/j.aml.2009.01.015
-Nonexpansive Mappings,” Applied Mathematics Letters, Vol. 22, No. 7, 2009, pp. 1051-1055. doi:10.1016/j.aml.2009.01.015 - Y. Song, “New Strong Convergence Theorems for Nonexpansive Nonself-Mappings without Boundary Conditions,” Computers and Mathematics with Applications, Vol. 56, No. 6, 2008, pp. 1473-1478. doi:10.1016/j.camwa.2008.03.004
- Z. M. Wang, Y. F. Su, D. X. Wang and Y. C. Dong, “A Modified Halpern-Type Iteration Algorithm for a Family of Hemi-Relative Nonexpansive Mappings and Systems of Equilibrium Problems in Banach Spaces,” The Journal of Computational and Applied Mathematics, Vol. 235, No. 8, 2011, pp. 2364-2371. doi:10.1016/j.cam.2010.10.036
- Y. I. Alber, “Metric and Generalized Projection Operators in Banach Spaces: Properties and Applications,” In: A. G. Kartosator, Ed., Theory and Applications of Nonlinear Operators of Accretive and Monotone Type, Dekker, New York, 1996, pp. 15-50.
- S. S. Chang, C. K. Chan and H. W. J. Lee, “Modified Block Iterative Algorithm for Quasi-
 -Asymptotically Nonexpansive Mappings and Equilibrium Problem in Banach Spaces,” Applied Mathematics and Computation, Vol. 217, No. 18, 2011, pp. 7520-7530. doi:10.1016/j.amc.2011.02.060
-Asymptotically Nonexpansive Mappings and Equilibrium Problem in Banach Spaces,” Applied Mathematics and Computation, Vol. 217, No. 18, 2011, pp. 7520-7530. doi:10.1016/j.amc.2011.02.060 - E. Blum and W. Oettli, “From Optimization and Variational Inequalities to Equilibrium Problems,” Mathematical Studies, Vol. 63, No. 1/4, 1994, pp. 123-145.

