Applied Mathematics
Vol.4 No.7A(2013), Article ID:33967,4 pages DOI:10.4236/am.2013.47A002
Study for System of Nonlinear Differential Equations with Riemann-Liouville Fractional Derivative
Department of Mathrmatics, Taiyuan Normal University, Taiyuan, China
Email: *zhengyanping2003@126.com
Copyright © 2013 Yanping Zheng, Wenxia Wang. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received April 19, 2013; revised May 19, 2013; accepted May 29, 2013
Keywords: Riemann-Liouville Fractional Derivative; Weighted Cauchy-Type Problem; Fractional Differential Equations
ABSTRACT
In this work, we study existence theorem of the initial value problem for the system of fractional differential equations 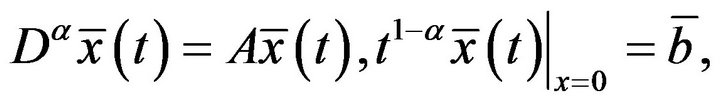 where
where 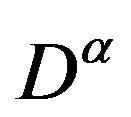 denotes standard Riemann-Liouville fractional derivative,
denotes standard Riemann-Liouville fractional derivative, 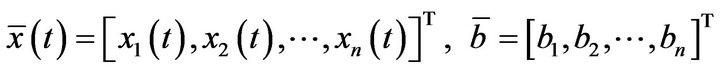
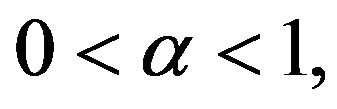 and
and  is a square matrix. At the same time, power-type estimate for them has been given.
is a square matrix. At the same time, power-type estimate for them has been given.
1. Introduction
Let 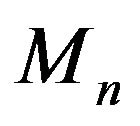 denote the
denote the 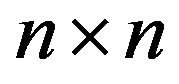 matrix over real fields
matrix over real fields 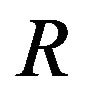 or complex fields
or complex fields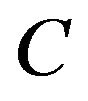 . For
. For 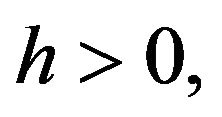
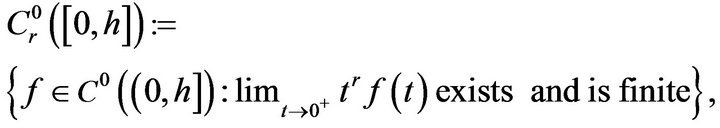
here 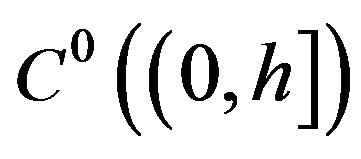 is the usual space of continuous functions on
is the usual space of continuous functions on 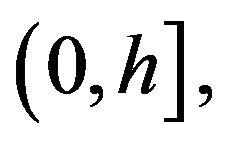 which is a Banach space with the norm
which is a Banach space with the norm
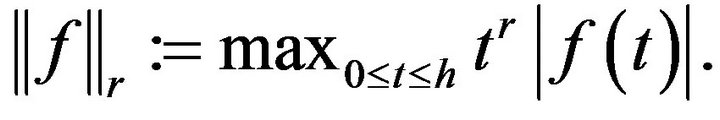
The space 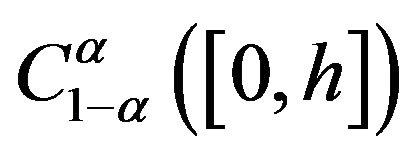 is defined by
is defined by
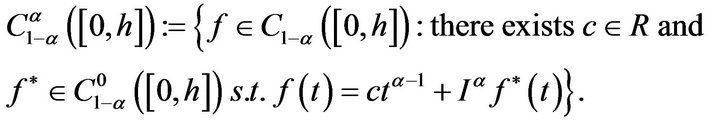
(see [1]).
The existence of solution of initial value problems for fractional order differential equations have been studied in many literatures such as [1-4]. In this paper, we present the analysis of the system of fractional differential equations
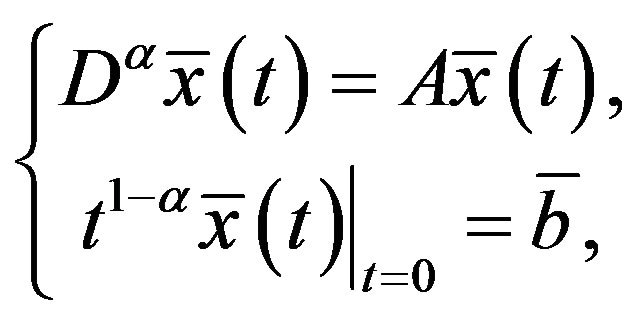 (*)
(*)
where  denotes standard Riemann-Liouville fractional derivative, where
denotes standard Riemann-Liouville fractional derivative, where
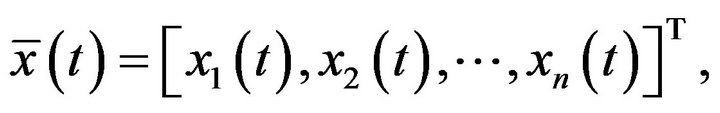
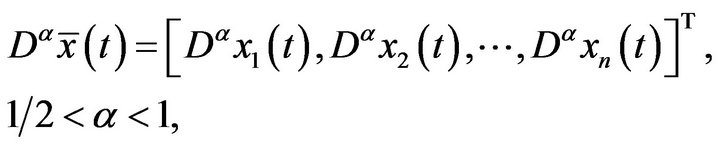
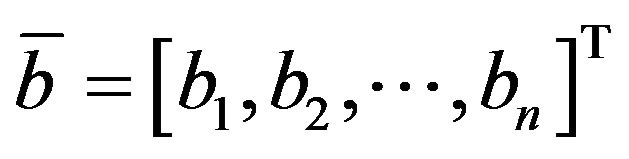 and
and  is a square.
is a square.
To prove the main result, we begin with some definitions and lemmas. For details, see [1-5].
Definition 1.1 Let 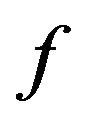 be a continuous function defined on
be a continuous function defined on 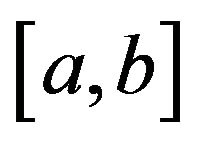 and
and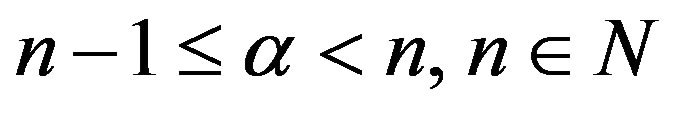 . Then the expression
. Then the expression
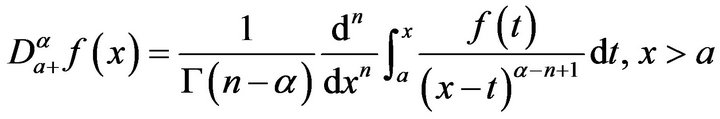
is called left-sided fractional derivatives of order 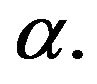
Definition 1.2 Let 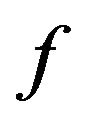 be a continuous function defined on
be a continuous function defined on 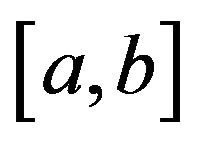 and
and 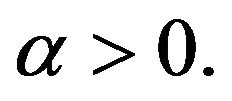 Then the expression
Then the expression
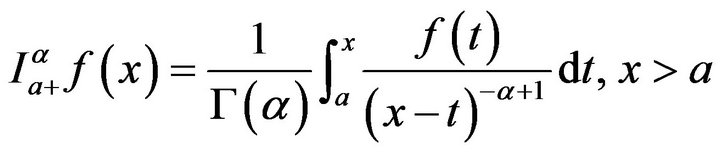
is called left-sided fractional integral of order 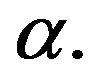
Lemma 1.3 Given 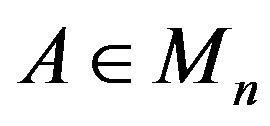 with eigenvalues
with eigenvalues
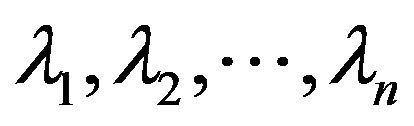 in any prescribed order, there is a unitary matrix
in any prescribed order, there is a unitary matrix 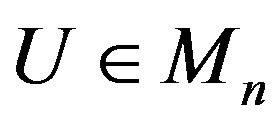 such that
such that 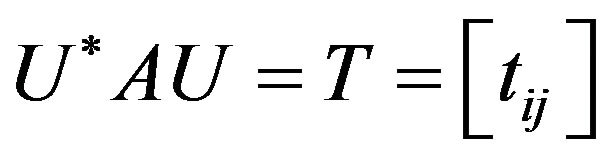 is upper triangular with diagonal entries
is upper triangular with diagonal entries 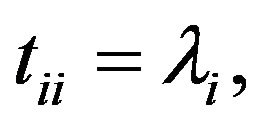
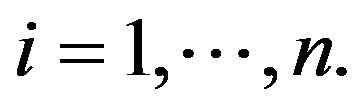 That is, every square matrix
That is, every square matrix  is unitarily equivalent to triangular matrix whose entries are the eigenvalues of
is unitarily equivalent to triangular matrix whose entries are the eigenvalues of  in a prescribed order. Further more, if
in a prescribed order. Further more, if 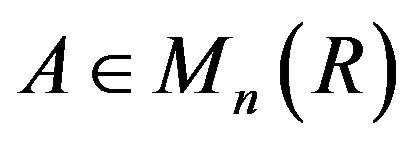 and if all the eigenvalues of
and if all the eigenvalues of  are real, then
are real, then 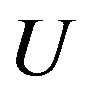 may be chosen to be real and orthogonal.
may be chosen to be real and orthogonal.
Lemma 1.4 Assume that 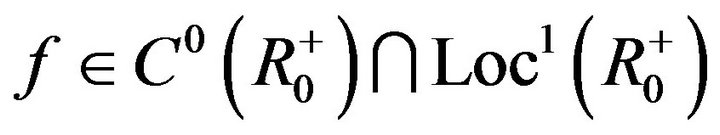 with fractional derivative of order
with fractional derivative of order 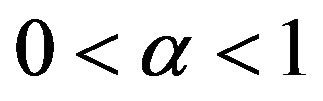 that belongs to
that belongs to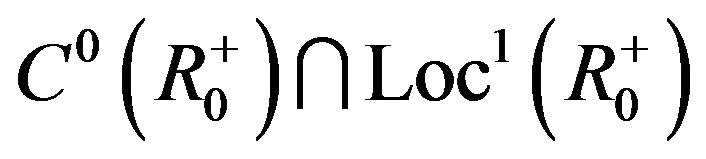 . Then
. Then
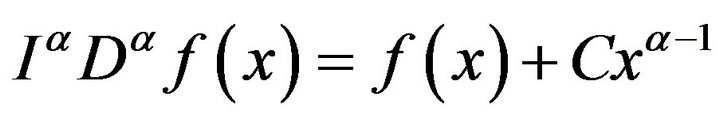
for some  When the function
When the function 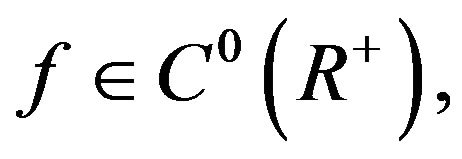 then
then
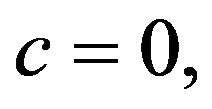 where
where
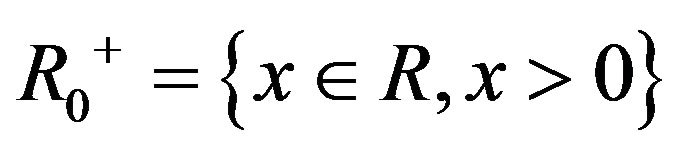 and
and 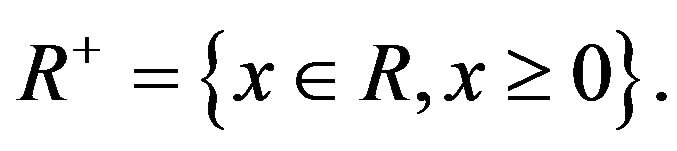
Lemma 1.5 (Schauder’s fixed theorem) Assume  is a relative subset of a convex set
is a relative subset of a convex set 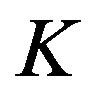 in a normed space
in a normed space 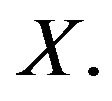 Let
Let 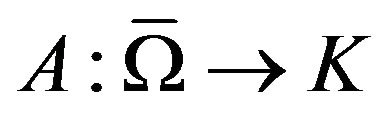 be a compact map with
be a compact map with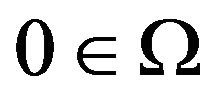 . Then either
. Then either
(A1)  has a fixed point in
has a fixed point in , or
, or
(A2) there is a 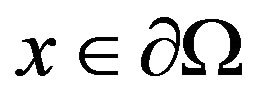 and a
and a 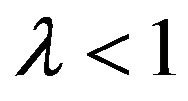 such that
such that 
Now, let’s us give some hypotheses:
H1: 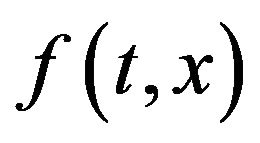 is continuous on
is continuous on  and is such that
and is such that
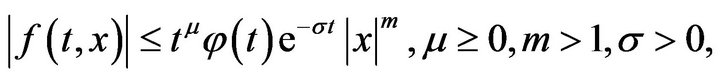 (1)
(1)
where 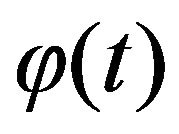 is a continuous function on
is a continuous function on 
H2: 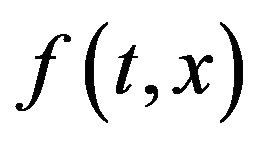 is continuous on
is continuous on 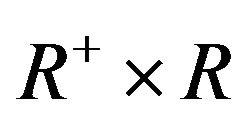 and is such that
and is such that
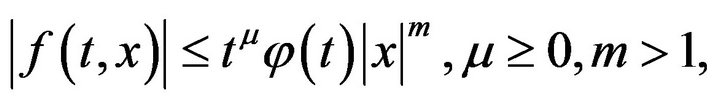 (2)
(2)
where  is a continuous function on
is a continuous function on 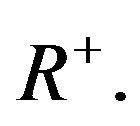
Lemma 1.6 Let 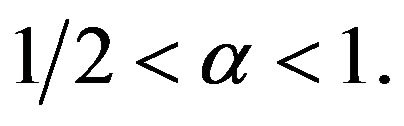 If we assume that
If we assume that 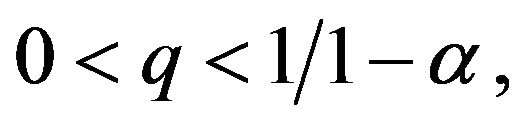 then the initial value problem
then the initial value problem
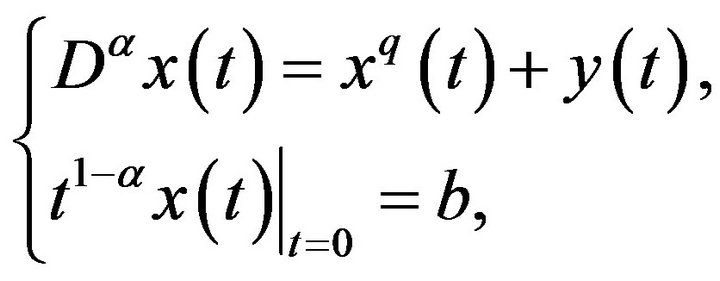 (3)
(3)
where
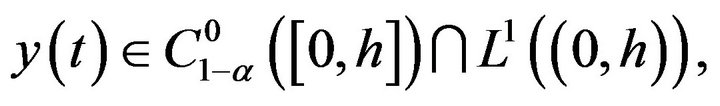
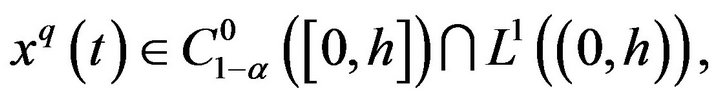
has at least a solution 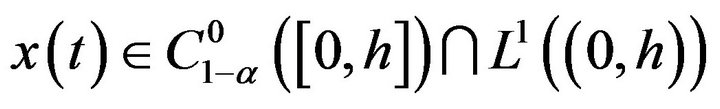 for
for  sufficiently small.
sufficiently small.
Proof. If
 then
then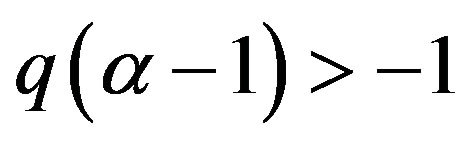 , by Lemma 1.4, We are therefore reduced the initial problem to the nonlinear integral equation
, by Lemma 1.4, We are therefore reduced the initial problem to the nonlinear integral equation
 (4)
(4)
The existence of a solution to Problem (3) can be formulated as a fixed point equation 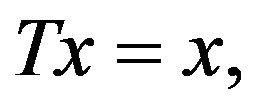 where
where
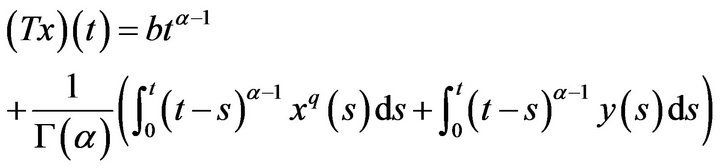 (5)
(5)
in the space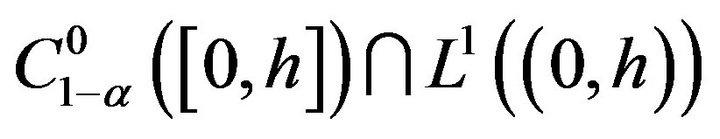 .
.
Define
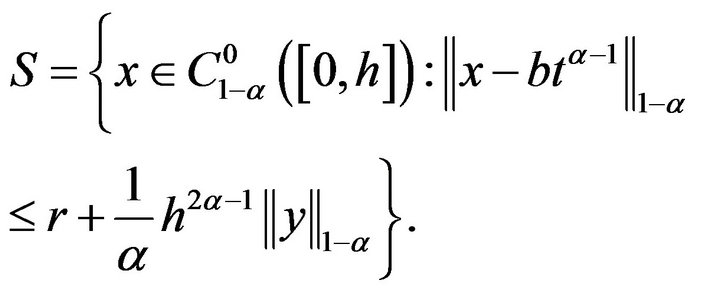
Clearly, it is closed, convex and nonempty.
Step I. We shall prove that we note that 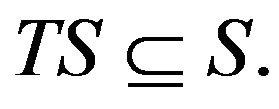
We note that
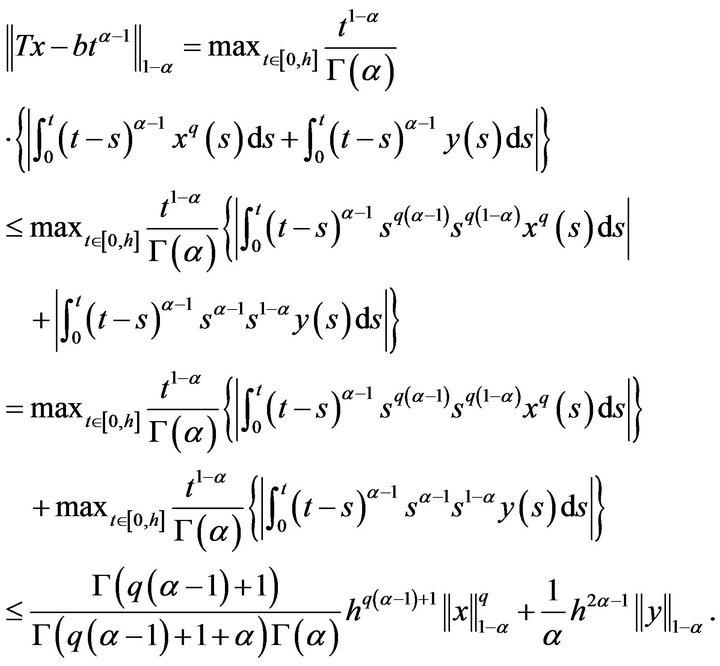
Since 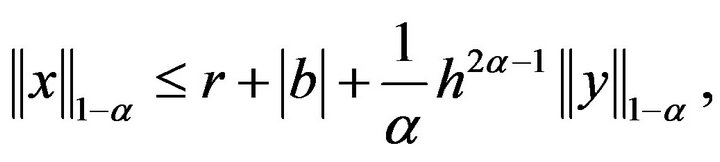 it will be sufficient to impose
it will be sufficient to impose
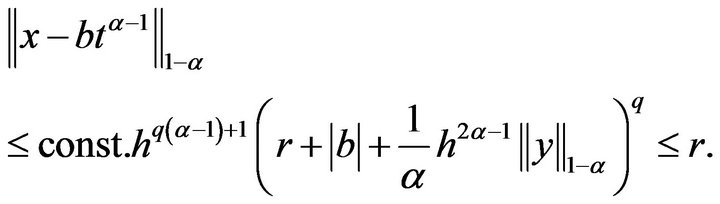
In view of the assumption 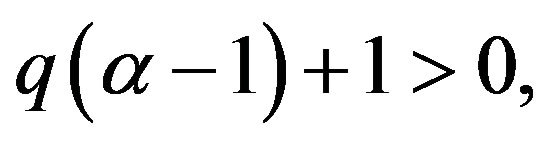 the second estimate is satisfied if say
the second estimate is satisfied if say 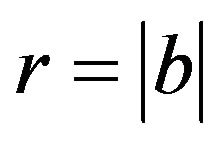 and
and  is chosen sufficiently small.
is chosen sufficiently small.
Step II. We shall prove that the operator  is compact. To prove the compactness of
is compact. To prove the compactness of
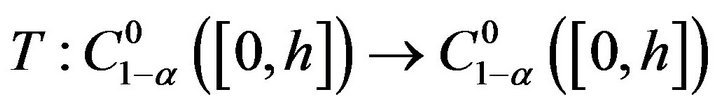
defined by (5), it will be sufficient to argue on the operator
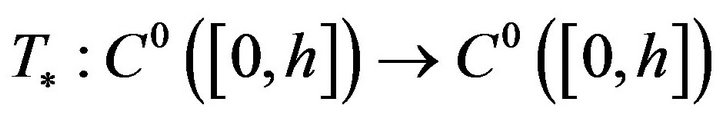
defined in this way:
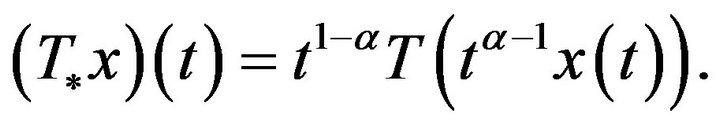
We have 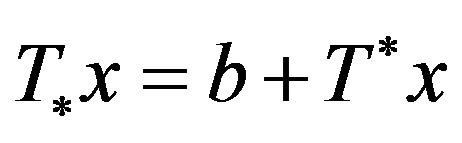 where the operator
where the operator

Turn out to be compact from classical sufficient conditions, since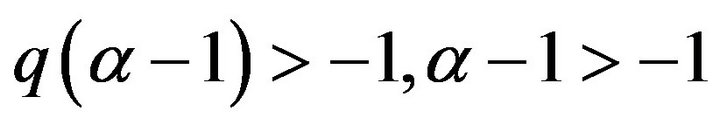 . By Lemma 1.5, we have that Problem (3) has least a solution.
. By Lemma 1.5, we have that Problem (3) has least a solution.
The proof is complete.
Lemma 1.7 Suppose that 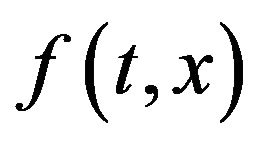 satisfies H1,
satisfies H1,
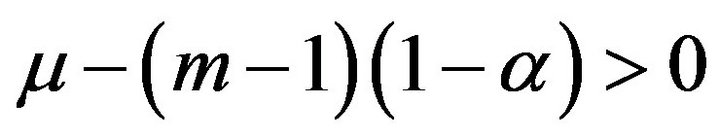 and
and 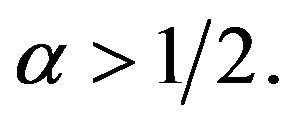 If
If 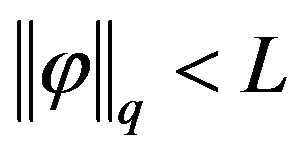 for some
for some 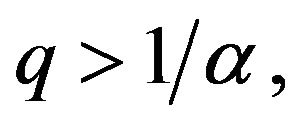 then the problem
then the problem
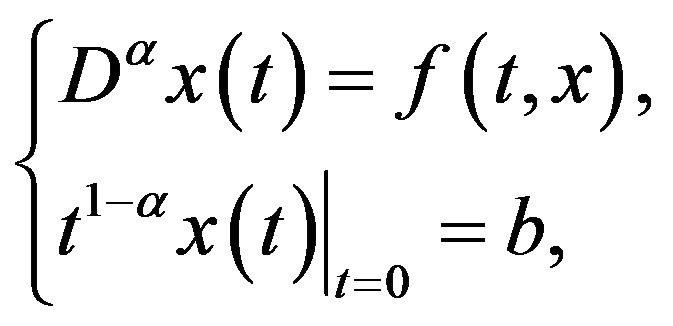 (6)
(6)
exists a positive constant 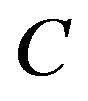 such that
such that 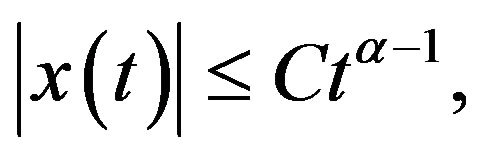
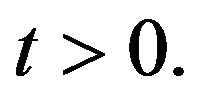
Lemma 1.8 Let  with
with 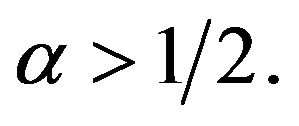 Suppose further that
Suppose further that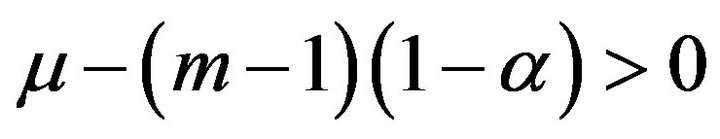 . Then Problem (6) and its associated integral equation
. Then Problem (6) and its associated integral equation
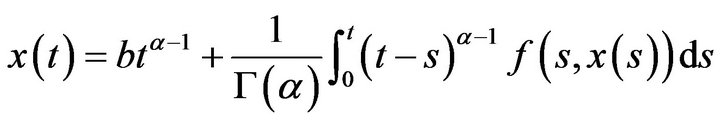 (7)
(7)
are equivalent.
Lemma 1.9 Assume that 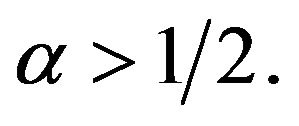
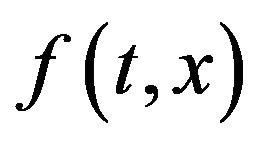 satisfies H2, and
satisfies H2, and 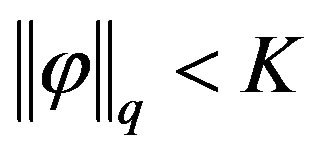 for some
for some 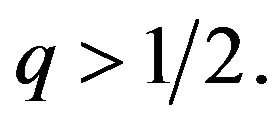 Suppose further that
Suppose further that 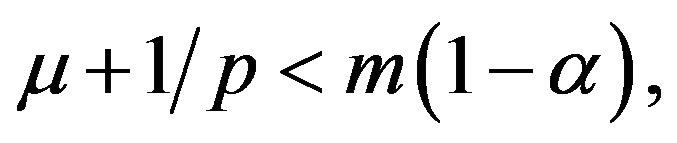 then there exists
then there exists  and
and 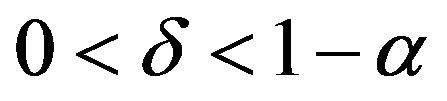 such that any solution of (6) exists globally and satisfies
such that any solution of (6) exists globally and satisfies
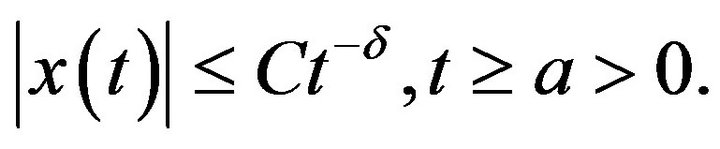 (8)
(8)
2. Main Results
Theorem 2.1 Let 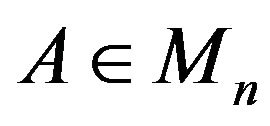 then initial problem (*) has a solution
then initial problem (*) has a solution 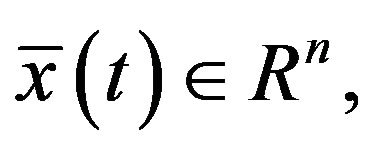 where
where
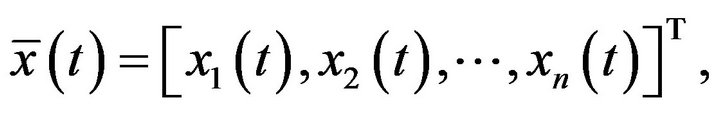

for all 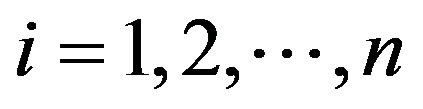 and sufficiently small
and sufficiently small 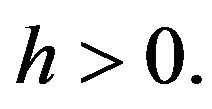
Proof. Given 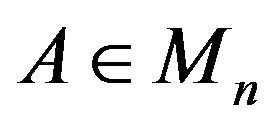 with eigenvalues
with eigenvalues 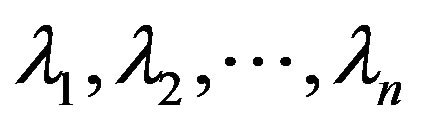 by Lemma 1.3, there is a unitary matrix
by Lemma 1.3, there is a unitary matrix 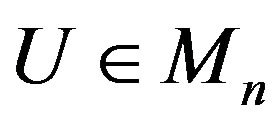 such that
such that
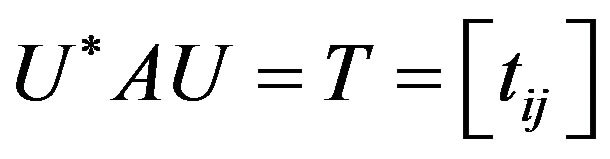
is upper triangular with diagonal entries 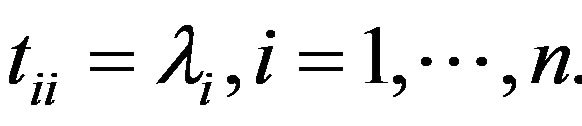
Let 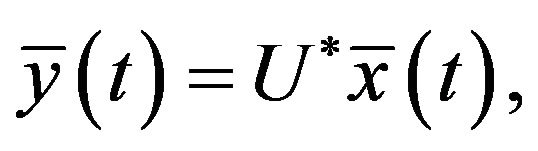 we have
we have
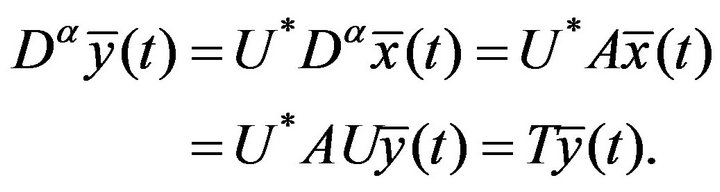
At the same time, the initial problem (*) changed into
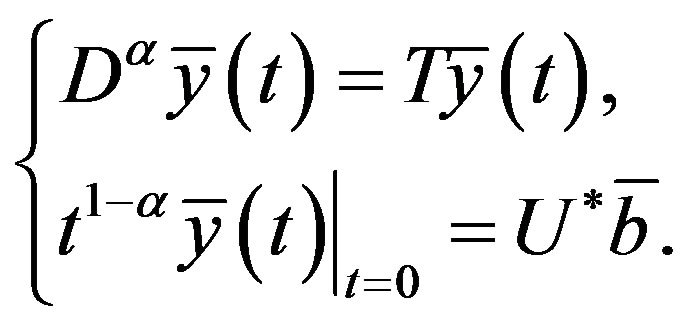 (**)
(**)
Now, let’s consider the problem (**).
Clearly, the problem (**) is equivalent to the following n problems
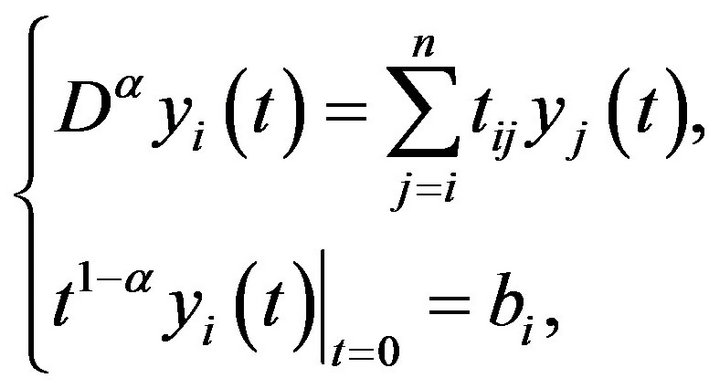
for 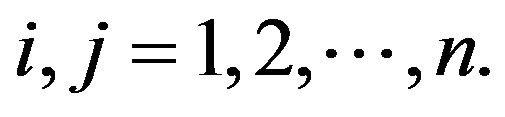 where
where 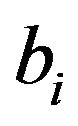 is the
is the  th entries of the vector
th entries of the vector 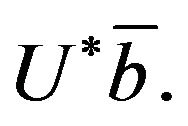
Consider the weighed Cauchy-type problem
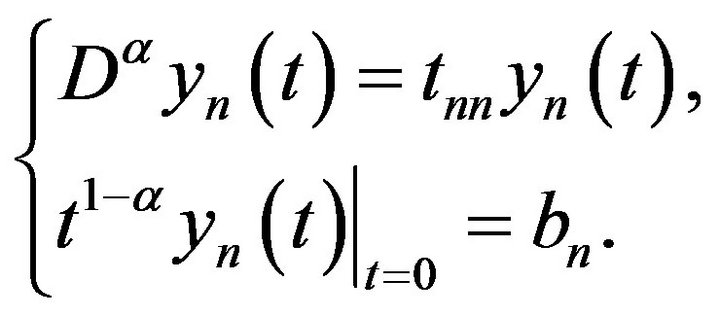
In Lemma 1.6, take 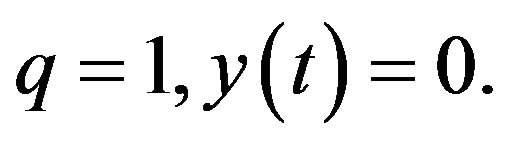 Then by lemma 1.6,
Then by lemma 1.6,  s.t. the above problem has at least a solution
s.t. the above problem has at least a solution
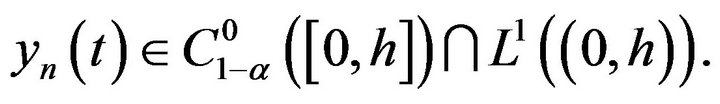
Consider the following weighed Cauchy-type problem
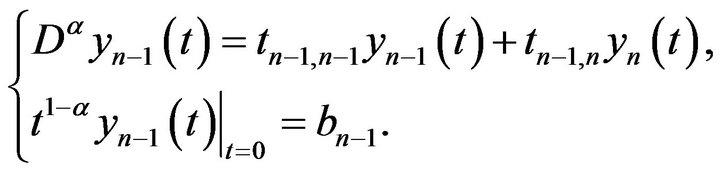
In Lemma 1.6, take 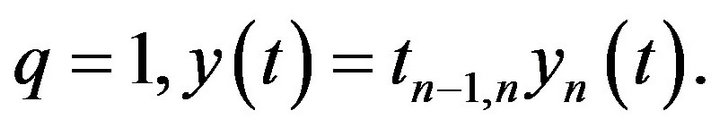 Then by Lemma 1.6,
Then by Lemma 1.6,  s.t. the above problem has at least a solution
s.t. the above problem has at least a solution 
Similarly, there has at least a solution in

for the rest n-2 initial problem in (**), denote by 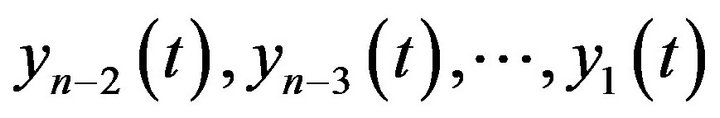 respectively. And therefore, there has at least a solution
respectively. And therefore, there has at least a solution
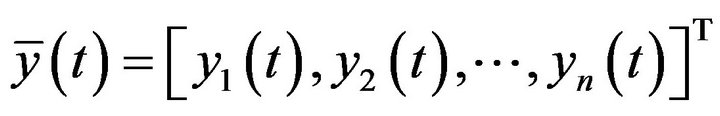
of the problem (**). Let 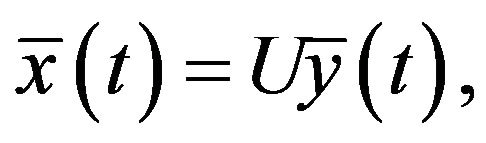 it is required for us.
it is required for us.
The proof is completed.
Since the problem (**) is equivalent to the following n problems
 (9)
(9)
for 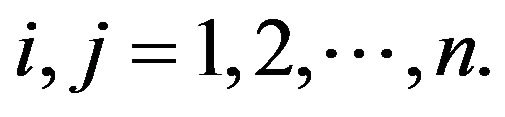 where
where 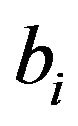 is the
is the 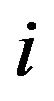 th entries of the vector
th entries of the vector 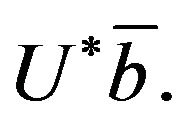 Next, we shall discuss these equations in (9).
Next, we shall discuss these equations in (9).
Theorem 2.2 Assume that the right hand of these equations in (9) satisfied H1, 
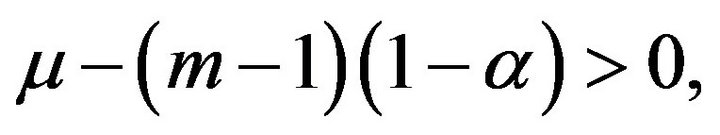 and
and 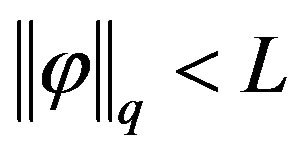 for some
for some 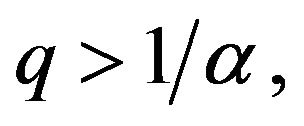 If the solution of the problems (**) denoted by
If the solution of the problems (**) denoted by
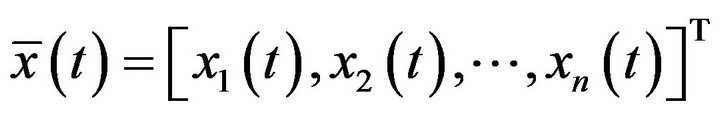 then there exists some constant
then there exists some constant 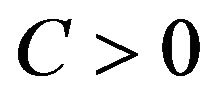 such that
such that
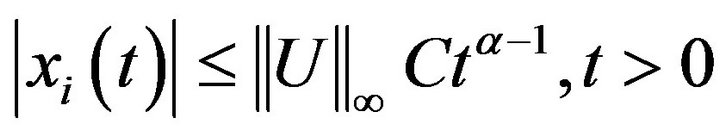 for all
for all 
Proof. Similar to the proof of Theorem 2.1, now consider the following weighted Cauchy-type problem
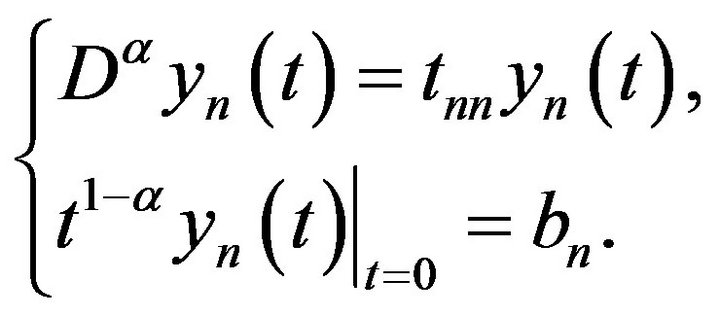
Then by Lemma 1.7, there exists some constant  such that
such that 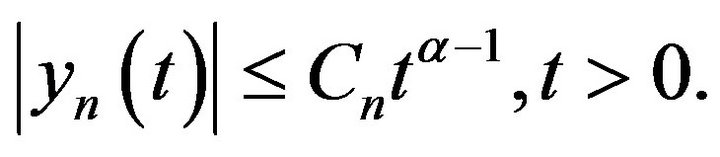
Consider the following problem
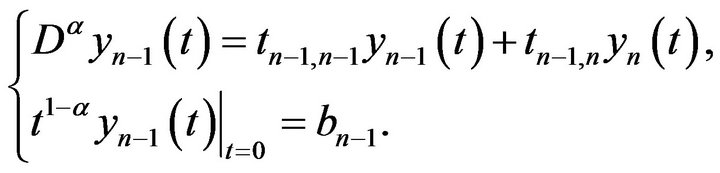
Then by Lemma 1.7, there exists some constant 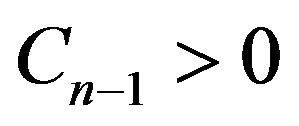 such that
such that 
Similarly, there exist some positive constants 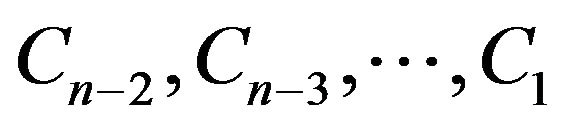 such that
such that
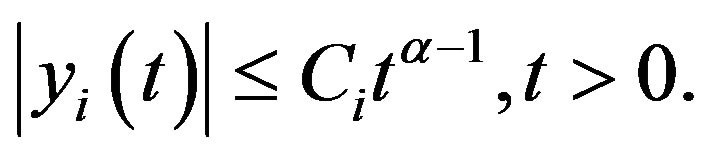
for all 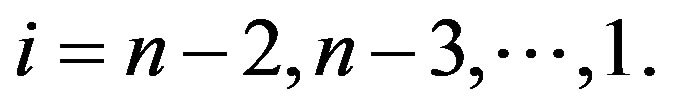
Let 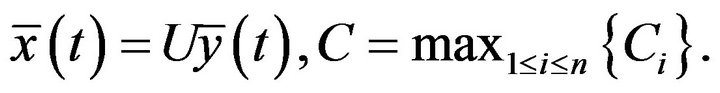 Then we have
Then we have
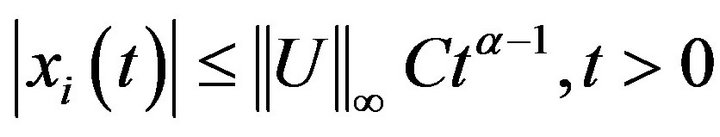 for all
for all 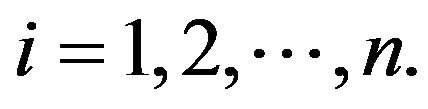
The proof is completed.
Theorem 2.3 Assume that 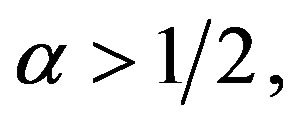 the right-hand of these equations in (9) satisfied H2, and
the right-hand of these equations in (9) satisfied H2, and 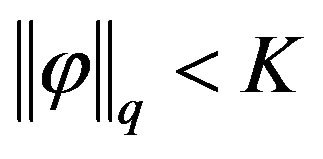
For some 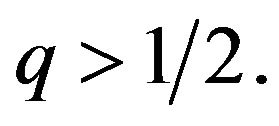 Suppose further that
Suppose further that
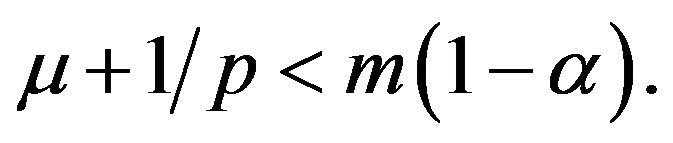
If denote solution of the problems (**)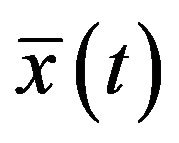 by
by
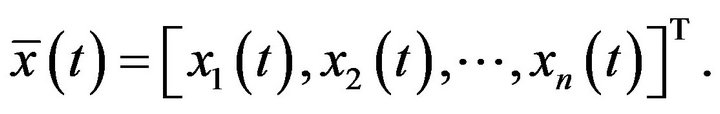
Then there exists some constant 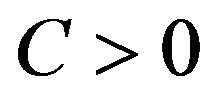 and
and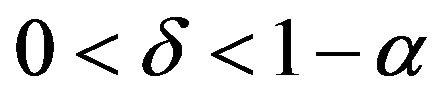 , such that
, such that
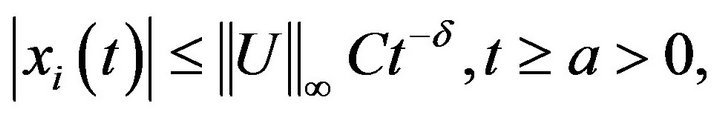
for all 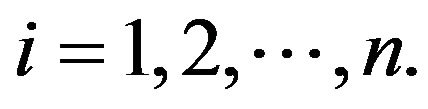
Using Lemmas 1.3 and 1.9, the proof is similar to Theorem 2.2. Therefore, it is omitted.
3. Acknowledgements
This research was supported by the NNSF of China (10961020), the Science Foundation of Qinghai Province of China (2012-Z-910) and the University Natural Science Research Develop Foundation of Shanxi Province of China (20111021).
REFERENCES
- K. M. Furati and N.-E. Tatar, “Power-Type Estmates for a Nonlear Fractional Differential Equation,” Journal of Nonlinear Analysis, Vol. 62, No. 6, 2005, pp. 1025-1036. doi:10.1016/j.na.2005.04.010
- V. Daftardar-Gejji and A. Babakhani, “Analysis of a SysTem of Fractional Differential Equations,” Journal of Mathematical Analysis and Applications, Vol. 293, No. 2, 2004, pp. 511-512. doi:10.1016/j.jmaa.2004.01.013
- D. Delbosco and L. Rodino, “Existence and Uniqueness for a Nonlinear Fractional Differential Equation,” Journal of Mathematical Analysis and Applications, Vol. 204, No. 2, 1996, pp. 511-512. doi:10.1006/jmaa.1996.0456
- I. Podlubny, “Fractional Differential Equtions,” Academic Press, New York, 1999.
- R. A. Horn and C. R. Johnson, “Matrix Analysis,” Cambridge University press, London, 1985.
NOTES
*Corresponding author.

