Applied Mathematics
Vol.4 No.6(2013), Article ID:32426,12 pages DOI:10.4236/am.2013.46119
Soret-Dufour Effects on the MHD Flow and Heat Transfer of Microrotation Fluid over a Nonlinear Stretching Plate in the Presence of Suction
1Department of Mathematics, Comilla University, Comilla, Bangladesh
2Department of Accounting and Information System, University of Chittagong, Chittagong, Bangladesh
Email: dipmahbub13@yahoo.com
Copyright © 2013 Md Abdullah Al Mahbub et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 28, 2013; revised April 29, 2013; accepted May 4, 2013
Keywords: Heat Transfer; Micropolar Fluid; Porous Media; Stretching Sheet; Soret Number; Dufour Number
ABSTRACT
In this work, the Micropolar fluid flow and heat and mass transfer past a horizontal nonlinear stretching sheet through porous medium is studied including the Soret-Dufour effect in the presence of suction. A uniform magnetic field is applied transversely to the direction of the flow. The governing differential equations of the problem have been transformed into a system of non-dimensional differential equations which are solved numerically by Nachtsheim-Swigert iteration technique along with the sixth order Runge-Kutta integration scheme. The velocity, microrotation, temperature and concentration profiles are presented for different parameters. The present problem finds significant applications in hydromagnetic control of conducting polymeric sheets, magnetic materials processing, etc.
1. Introduction
The natural convection processes involving the combined mechanism of heat and mass transfer are encountered in many natural and industrial transport processes such as hot rolling, wire drawing, spinning of filaments, metal extrusion, crystal growing, continuous casting, glass fiber production, paper production, and polymer processing, etc. Ostrach [1] the initiator of the study of convection flow, made a technical note on the similarity solution of transient free convection flow past a semi infinite vertical plate by an integral method. Goody [2] considered a neutral fluid. Sakiadis [3] analyzed the boundary layer flow over a solid surface moving with a constant velocity. This boundary layer flow situation is quite different from the classical Blasiuss problem of boundary flow over a semi-infinite flat plate due to entrainment of ambient fluid.
Micropolar fluids, distinctly non-Newtonian in nature, are referred to those that contain micro-constituents belonging to a class of complex fluids with nonsymmetrical stress tensor. These fluids respond to micro-rotational motions and spin inertia, and therefore can support couple stress and distributed body torque which are not achievable with the classical Navier-Stokes equations or the viscoelastic flow models. The Micropolar fluid models are developed to make an analysis of the flow characteristics of physiological fluids (blood containing corpuscles), colloidal suspensions, paints, liquid crystal suspensions, concentrated silica particle suspensions, oils containing very fine suspensions, industrial contaminants containing toxic chemicals, lubricants, organic/inorganic hybrid nano-composites and clay which are fabricated by melt intercalation etc. Eringen [4] first designed the study on micropolar fluid making an analysis on the theory of micropolar fluids which provided a mathematical model for non-Newtonian behavior.
Crane [5] noted that usually the sheet is assumed to be inextensible, but situations may arise in the polymer industry in which it is necessary to deal with a stretching plastic sheet. For examples, materials manufactured by aerodynamic extrusion processes and heat-treated materials traveling between a feed roll and a wind-up roll or on a conveyor belt possess the characteristics of a moving continuous stretching surface. Moreover lots of metallurgical processes occupy the system of cooling of continuous strips or filaments by drawing them through a quiescent fluid and that in the process of drawing, these strips are sometimes stretched.
An important matter is that the final product depends to a great extent on the rate of cooling. By drawing such strips in an electrically conducting fluid subjected to a magnetic field, the rate of cooling can be controlled and a final product of desired characteristics can be achieved. The study of heat and mass transfer is necessary for determining the quality of the final product. Sparrow [6] explained a parameter named Rosseland approximation to describe the radiation heat flux in the energy equation in his book.
The boundary layer models for steady or unsteady micropolar fluids in various geometries (stationary or moving surface, linear or nonlinear stretching surface etc.) with/or without heat transfer considering various flow conditions (no slip or slip, suction/injection at the surface) and thermal boundary conditions (constant/variable surface temperature or heat flux) have extensively been studied by numerous researchers [7-16].
Moreover, the thermal-diffusion (Soret) effect, for instance, has been utilized for isotope separation, and in mixtures between gases with very light molecular weight (Hz, He) and of medium molecular weight (Nz, air) the diffusion-thermo (Dufour) effect was found to be of a considerable magnitude such that it cannot be ignored, described by Eckert and Drake [17] in their book. Recently plenty of investigators [18-21] are getting interest work on Soret-Dufour effects.
From the above referenced work and the numerous possible industrial applications of the problem, it is of paramount interest in this study in order to clarify the parametric behavior of magneto-hydrodynamic flow of free convection of a micropolar fluid over a nonlinear stretching sheet in the presence of dynamic effects of suction, thermal-diffusion and diffusion-thermo.
2. Mathematical Model
We consider the isothermal, steady, laminar, hydromagnetic free convection flow of an incompressible micropolar fluid flowing past a nonlinear stretching sheet coinciding with the plane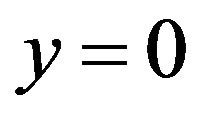 , the flow being confined in the region
, the flow being confined in the region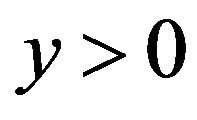 . The flow under consideration is also subjected to a strong transverse magnetic field
. The flow under consideration is also subjected to a strong transverse magnetic field 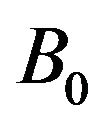 with a constant intensity along the y-axis.
with a constant intensity along the y-axis.
Two equal and opposite forces are introduced along the x-axis so that the surface is stretched keeping the origin fixed. The flow configurations and the coordinate system are shown in Figure 1. We assume that the velocity of a point on a sheet is proportional to its distance from the slit. We assume that all the fluid properties are isotropic and constant. Under the usual boundary layer and Boussinesq approximations, the governing equations for the problem under consideration can be written as follows:

Figure 1. Flow configuration and coordinate system.
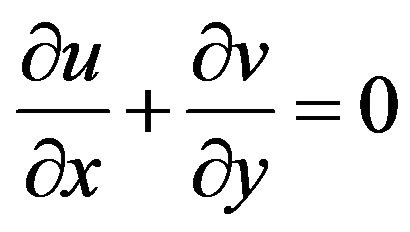 (1)
(1)
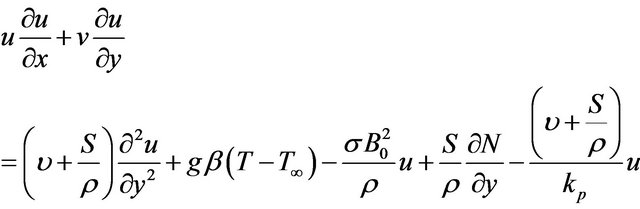 (2)
(2)
 (3)
(3)
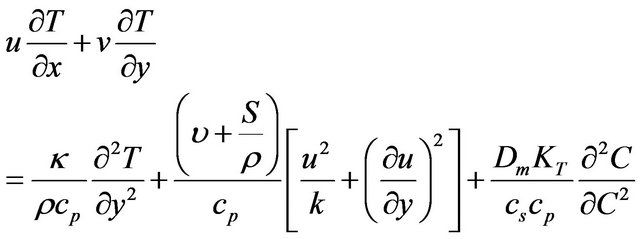 (4)
(4)
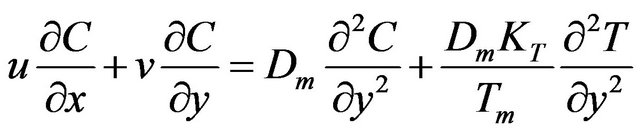 (5)
(5)
In Equation (2) the Darcian porous drag force term is defined by the term,  , which is linear in terms of the translational velocity, u. With
, which is linear in terms of the translational velocity, u. With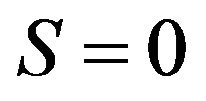 , the micropolar effects disappears and this term reduces to the conventional Newtonian Darcy drag force i.e.
, the micropolar effects disappears and this term reduces to the conventional Newtonian Darcy drag force i.e.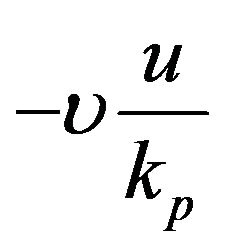 .
.
The micro-rotation component, N, is coupled to the linear momentum Equation (2) via the angular velocity gradient term,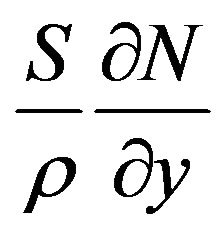 . Very strong coupling exists between the translational velocity components, u and v, in Equation
. Very strong coupling exists between the translational velocity components, u and v, in Equation
(3) via the convective acceleration terms, 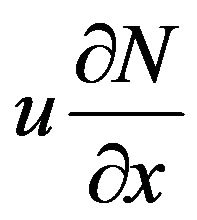 and
and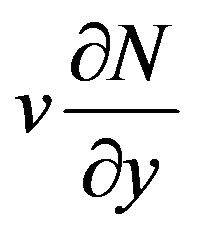 . Furthermore, there is a second coupling term linking the angular velocity with the x-direction velocity gradient, in Equation (3),
. Furthermore, there is a second coupling term linking the angular velocity with the x-direction velocity gradient, in Equation (3),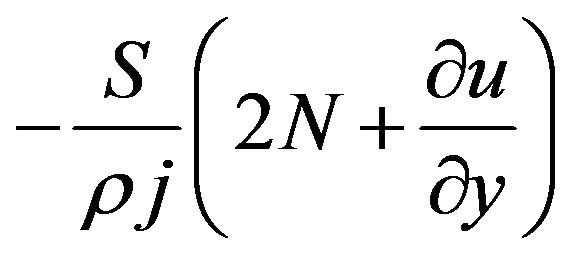 . The microrotation viscosity (or spin-gradient viscosity)
. The microrotation viscosity (or spin-gradient viscosity) 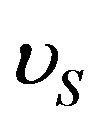 is defined by
is defined by  (Rahman [15]). We note that in the viscous shear diffusion term,
(Rahman [15]). We note that in the viscous shear diffusion term, 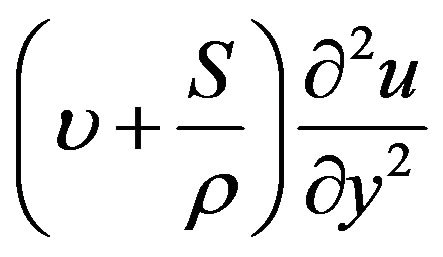 , the Newtonian kinematic viscosity is now supplemented by the Eringen micropolar vortex viscosity, S. In the present work, we assume that the micro-inertia per unit mass j is a constant. Also, positive or negative n indicate the acceleration and deceleration of the sheet from the extruded slit respectively. Here
, the Newtonian kinematic viscosity is now supplemented by the Eringen micropolar vortex viscosity, S. In the present work, we assume that the micro-inertia per unit mass j is a constant. Also, positive or negative n indicate the acceleration and deceleration of the sheet from the extruded slit respectively. Here 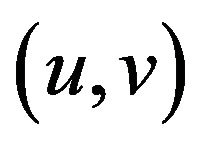 are the fluid velocity components in the x-, y-directions respectively, N is the microrotation, T is the temperature,
are the fluid velocity components in the x-, y-directions respectively, N is the microrotation, T is the temperature, ![]() is the kinematic viscosity,
is the kinematic viscosity, 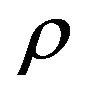 is the fluid density,
is the fluid density, ![]() is the electric conductivity, g is the acceleration due to gravity,
is the electric conductivity, g is the acceleration due to gravity,  is the volumetric coefficient of thermal expansion,
is the volumetric coefficient of thermal expansion,  is the uniform magnetic field strength,
is the uniform magnetic field strength, 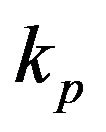 is the Darcy permeability of porous medium, j is the Microinertia per unit mass,
is the Darcy permeability of porous medium, j is the Microinertia per unit mass, ![]() is the thermal conductivity of the fluid, cp the specific heat at constant pressure,
is the thermal conductivity of the fluid, cp the specific heat at constant pressure, 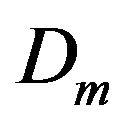 is the chemical molecular diffusivity,
is the chemical molecular diffusivity, 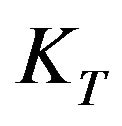 is the Thermophoretic constant,
is the Thermophoretic constant, 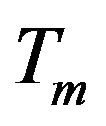 is the Mean fluid temperature and cs is the Concentration susceptibility.
is the Mean fluid temperature and cs is the Concentration susceptibility.
The appropriate boundary conditions suggested by the physical conditions are:
1) on the plate surface at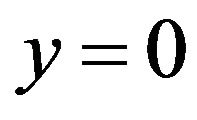 :
:
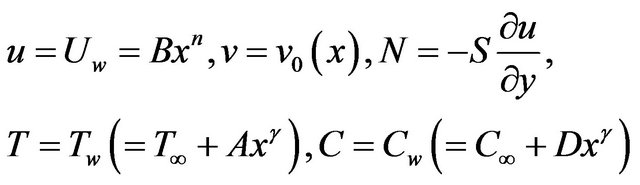 (6)
(6)
2) matching with the quiescent free stream as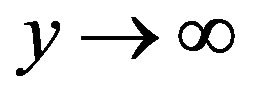 :
:
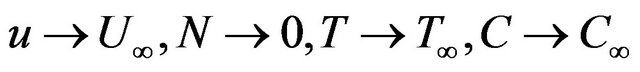 (7)
(7)
where the subscripts w and  refer to the wall and boundary layer edge, respectively. The relationship between the microrotation function N and the surface shear
refer to the wall and boundary layer edge, respectively. The relationship between the microrotation function N and the surface shear
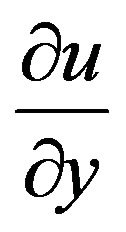 is chosen for investigating the effect of different surface conditions for the microrotation of the micropolar fluid elements. The conditions are generally of importance in micropolar boundary layer analysis. When microrotation parameter
is chosen for investigating the effect of different surface conditions for the microrotation of the micropolar fluid elements. The conditions are generally of importance in micropolar boundary layer analysis. When microrotation parameter , we obtain
, we obtain  which represents no-spin condition i.e. the microelements in a concentrated particle flow-close to the wall are not able to rotate (Rahman [15]). Finally
which represents no-spin condition i.e. the microelements in a concentrated particle flow-close to the wall are not able to rotate (Rahman [15]). Finally 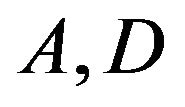 and
and 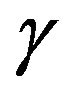 are the constants.
are the constants.
2.1. Similarity Solutions
The partial differential Equations (1) to (5) are transformed into non-dimensional form by mean of following dimensionless variables
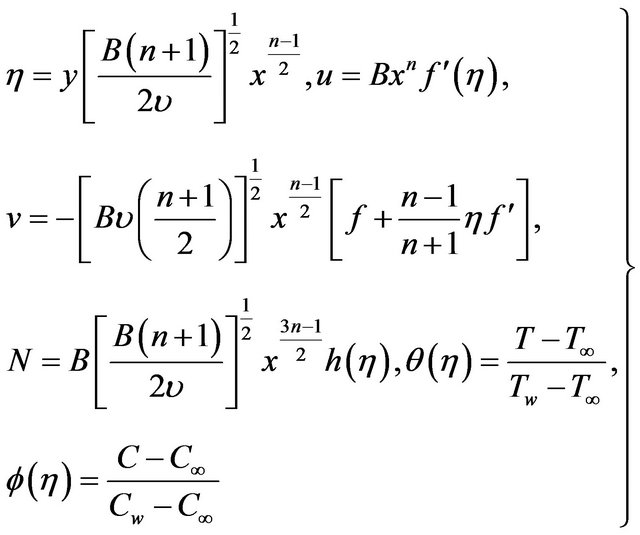 (8)
(8)
Implementing Equation (8) into Equations (1) to (5) produces the following ordinary differential equations:
 (9)
(9)
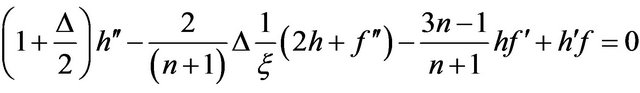 (10)
(10)
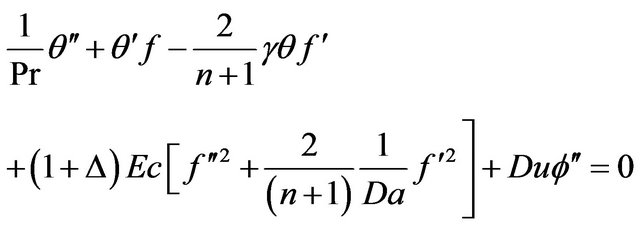 (11)
(11)
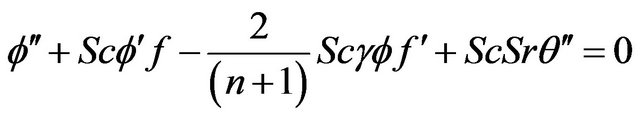 (12)
(12)
and corresponding boundary conditions are reduce to:
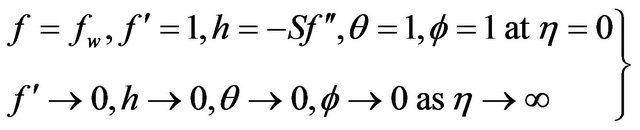 (13)
(13)
where the primes denote differentiation with respect to 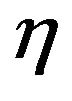
(non-dimensional y-coordinate) and 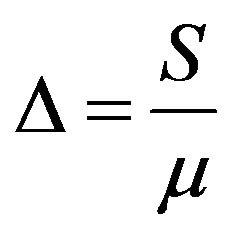 is the vortex viscosity parameter,
is the vortex viscosity parameter,  is the local Grashof number,
is the local Grashof number, 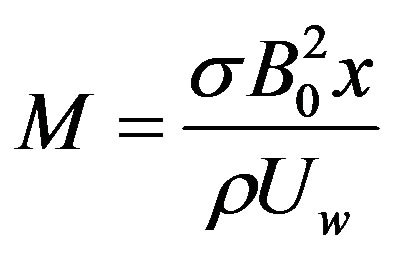 is the local magnetic parameter and
is the local magnetic parameter and  is the magnetic field,
is the magnetic field, 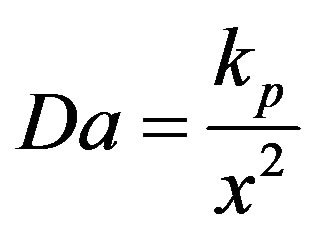 is the Darcy number,
is the Darcy number, 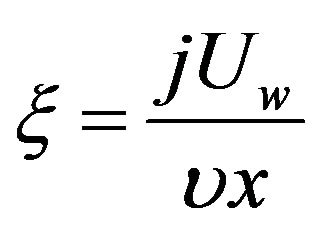 is the micro-inertia density parameter,
is the micro-inertia density parameter,  is the Prandtl number,
is the Prandtl number, 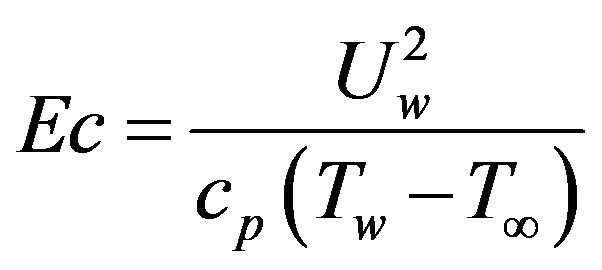 is the Eckert number,
is the Eckert number,
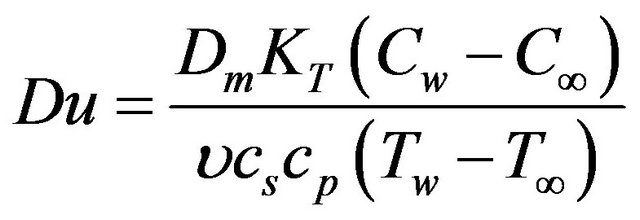 is the Dufour number,
is the Dufour number, 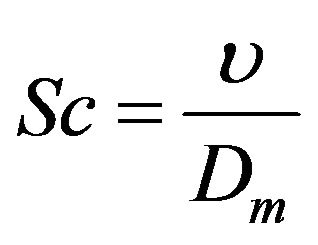 is the Schmidt number,
is the Schmidt number, 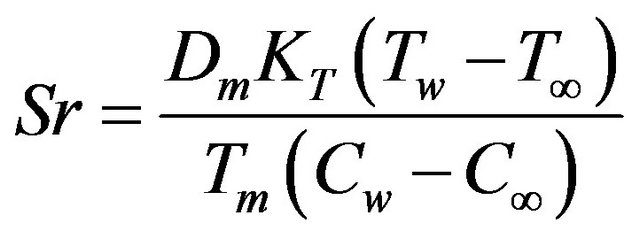 is the Soret number and
is the Soret number and 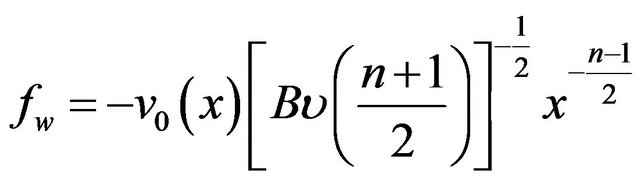
is the suction parameter.
2.2. Skin Friction, Rate of Heat and Mass Transfer
The parameters of engineering interest for the present problem are the skin friction coefficient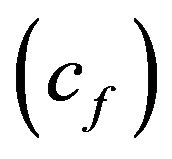 , plate couple stress
, plate couple stress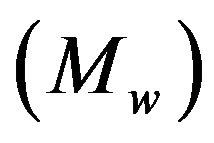 , local Nusselt number
, local Nusselt number 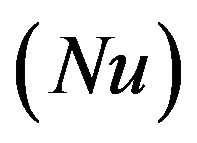 and Sherwood number
and Sherwood number 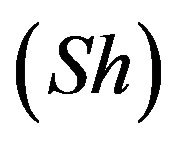 which indicate physically the wall shear stress, couple stress, the rate of heat transfer and the local surface mass flux respectively. The dimensionless skin-friction coefficient, Couple stress, Nusselt number and Sherwood number for impulsively started plate are given by
which indicate physically the wall shear stress, couple stress, the rate of heat transfer and the local surface mass flux respectively. The dimensionless skin-friction coefficient, Couple stress, Nusselt number and Sherwood number for impulsively started plate are given by
 (14)
(14)
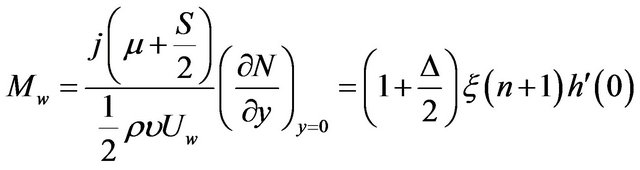 (15)
(15)
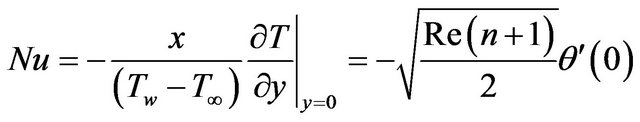 (16)
(16)
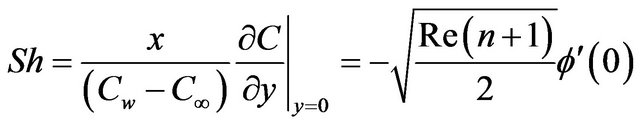 (17)
(17)
where 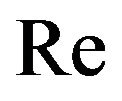 is the Reynolds number. And hence the values proportional to the skin-friction coefficient, couple stress, Nusselt number and Sherwood number are
is the Reynolds number. And hence the values proportional to the skin-friction coefficient, couple stress, Nusselt number and Sherwood number are 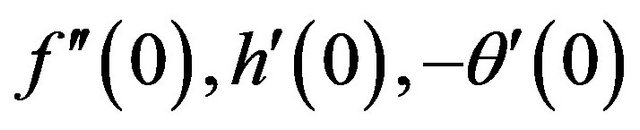 and
and  respectively.
respectively.
3. Numerical Computation
The numerical solutions of the non-linear differential Equations (9) to (12) under the boundary conditions (13) have been performed by applying a shooting method namely Nachtsheim and Swigert [22] iteration technique (guessing the missing values) along with sixth order Runge-Kutta iteration scheme. We have chosen a step size 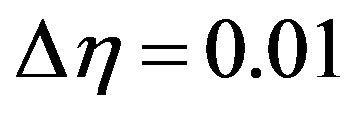 to satisfy the convergence criterion of 10−6 in all cases. The value of
to satisfy the convergence criterion of 10−6 in all cases. The value of  has been found to each iteration loop by
has been found to each iteration loop by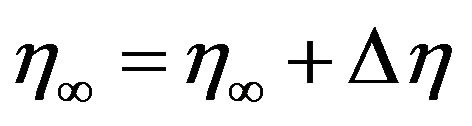 . The maximum value of
. The maximum value of  to each group of parameters
to each group of parameters 
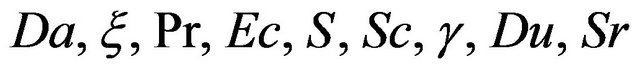 and
and 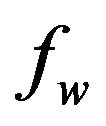 has been determined when the values of the unknown boundary conditions at
has been determined when the values of the unknown boundary conditions at 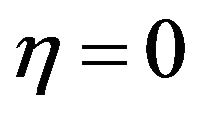 not change to successful loop with error less than 10−6. In order to verify the effects of the step size
not change to successful loop with error less than 10−6. In order to verify the effects of the step size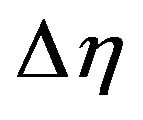 , we have run the code for our model with three different step sizes as Δη = 0.01, Δη = 0.005 and Δη = 0.001, and in each case we have found excellent agreement among them shown in Figures 2-5.
, we have run the code for our model with three different step sizes as Δη = 0.01, Δη = 0.005 and Δη = 0.001, and in each case we have found excellent agreement among them shown in Figures 2-5.
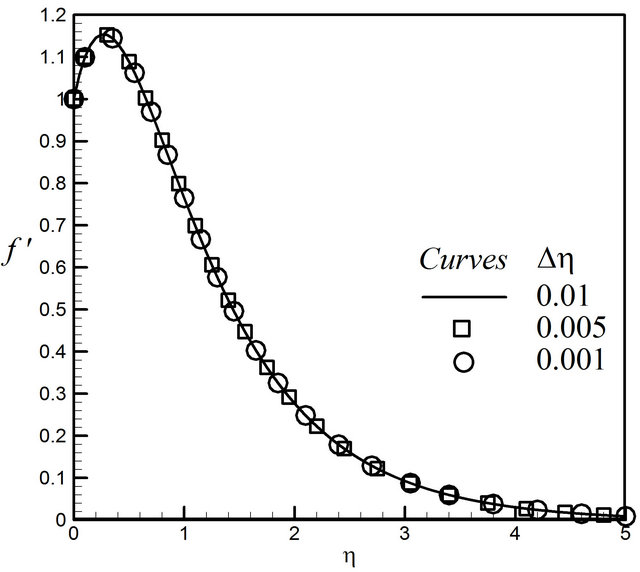
Figure 2. Distribution of velocity profiles for Δη.

Figure 3. Distribution of microrotation profiles for Δη.

Figure 4. Distribution of temperature profiles for Δη.

Figure 5. Distribution of concentration profiles for Δη.
4. Results and Discussions
For the purpose of discussing the results of the flow field represented in the Figure 1, the numerical calculations are presented in the form of non-dimensional velocity, microrotation, temperature and concentration profiles. The values of buoyancy parameter Gr is taken to be both positive to represent cooling of the plate. The parameters are chosen arbitrarily where Pr = 0.71 corresponds physically to air at 20˚C, Pr = 1.0 corresponds to the electrolyte solution such as salt water and Pr = 7.0 corresponds to water, and 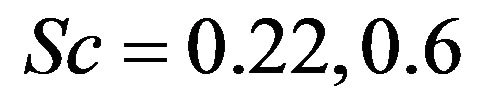 and 1.0 corresponds to hydrogen, water vapor and methanol respectively at 25˚C and 1 atmosphere. The values of Dufour and Soret numbers are chosen in such a way their production is constant provided that the meat temperature
and 1.0 corresponds to hydrogen, water vapor and methanol respectively at 25˚C and 1 atmosphere. The values of Dufour and Soret numbers are chosen in such a way their production is constant provided that the meat temperature 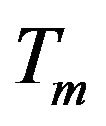 is kept constant as well.
is kept constant as well.
Due to free convection problem positive large values of  is chosen. The value of
is chosen. The value of 
 and
and . However, numerical computations have been carried out for different values of the vortex viscosity parameter
. However, numerical computations have been carried out for different values of the vortex viscosity parameter , surface nonlinearity parameter
, surface nonlinearity parameter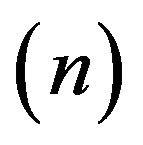 , Eckert number
, Eckert number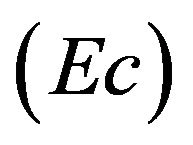 , constant parameter
, constant parameter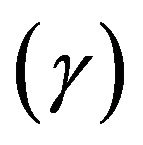 , Dufour number
, Dufour number , Soret number
, Soret number 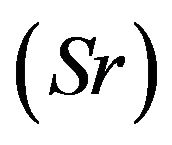 and suction parameter
and suction parameter . The numerical results for the velocity, microrotation, temperature and concentration profiles are displayed in Figures 6-33.
. The numerical results for the velocity, microrotation, temperature and concentration profiles are displayed in Figures 6-33.
Figure 6 shows the effect of vortex viscosity parameter ![]() (
(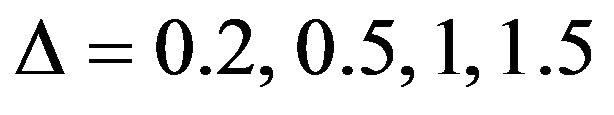 are chosen) on the velocity profiles. From here we see that velocity profiles decrease with the increase of
are chosen) on the velocity profiles. From here we see that velocity profiles decrease with the increase of![]() . Figure 7 demonstrates the effect of
. Figure 7 demonstrates the effect of ![]() on the microrotation profiles. From this figure it is seen that microrotation increases very evidently with the increase of the vortex viscosity parameter
on the microrotation profiles. From this figure it is seen that microrotation increases very evidently with the increase of the vortex viscosity parameter![]() . It is also understood that as the vortex viscosity increases the rotation of the micropolar constituents gets induced in most part of the boundary layer where kinematic viscosity dominates the flow. From Figure 8 it is found that the temperature profiles increase for the increase of
. It is also understood that as the vortex viscosity increases the rotation of the micropolar constituents gets induced in most part of the boundary layer where kinematic viscosity dominates the flow. From Figure 8 it is found that the temperature profiles increase for the increase of![]() . The effect of vortex viscosity parameter
. The effect of vortex viscosity parameter ![]() on the concentration profile is not so noteworthy displayed in Figure 9.
on the concentration profile is not so noteworthy displayed in Figure 9.
The effects of the surface nonlinearity constant n are characterized in the Figures 10-13. At the beginning the velocity profiles decrease with the increase of the value of 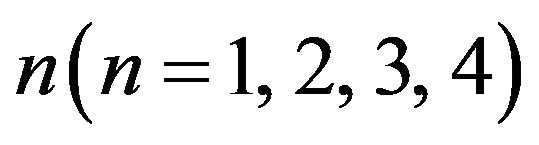 but far away from the plate they increase after
but far away from the plate they increase after 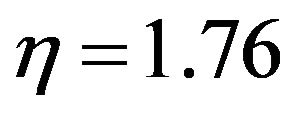 displayed in Figure 10. Figure 11 expresses that the microrotation profiles at the beginning increase extensively but at a distance from the plate they overlap and start to decrease very slowly. Figures 12 and 13 enlighten the temperature and the concentration profiles for the increasing influence of the parameter
displayed in Figure 10. Figure 11 expresses that the microrotation profiles at the beginning increase extensively but at a distance from the plate they overlap and start to decrease very slowly. Figures 12 and 13 enlighten the temperature and the concentration profiles for the increasing influence of the parameter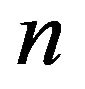 respectively.
respectively.
Figures 14-17 exhibit the velocity, microrotation, temperature and concentration profiles for the different values of the Eckert number Ec (0.03, 0.1, 0.5 and 1.0). Figure 14 demonstrates that the effect of the Ec on velocity profiles very significant. We observe that velocity increases rapidly with increasing the value of Ec. From the Figure 15 we notice that microrotation profiles decreases with the increase of the value of Ec. Figure 16 presents the increasing effect of Ec on the temperature profiles. The concentration profiles decrease with the increase of the value of Ec illustrated in Figure 17.
Figures 18-21 represent the influence of the constant parameter g for the values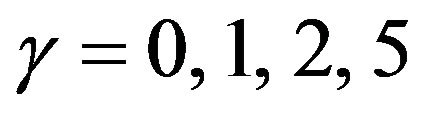 . All the profiles except microrotation profiles decrease with the increase of g. The effects of g are very significant smooth on the distributions. The microrotation profiles increase with the increase of the value of g.
. All the profiles except microrotation profiles decrease with the increase of g. The effects of g are very significant smooth on the distributions. The microrotation profiles increase with the increase of the value of g.
It is observed from the Figure 22 that with the increase
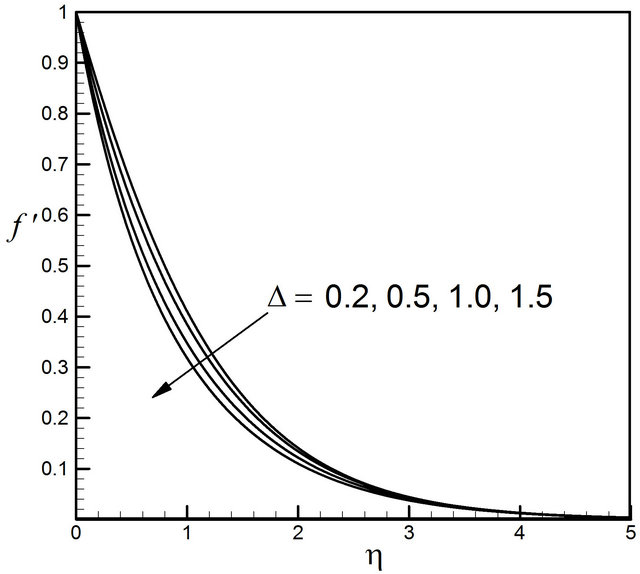
Figure 6. Distribution of velocity profiles for D.
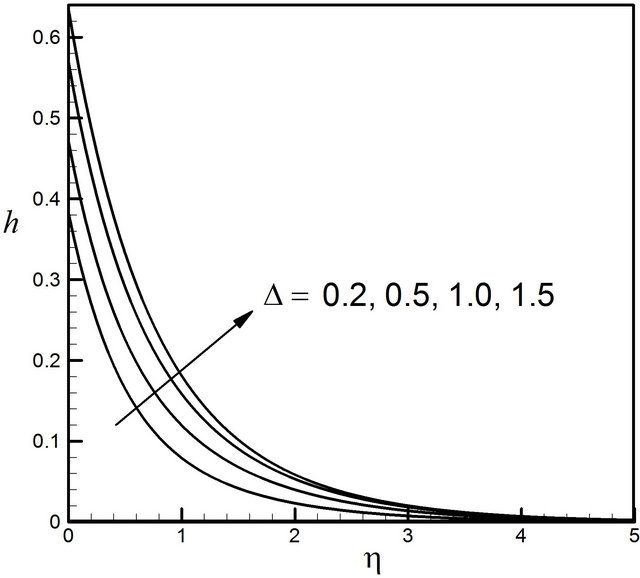
Figure 7. Distribution of microrotation profiles for D.
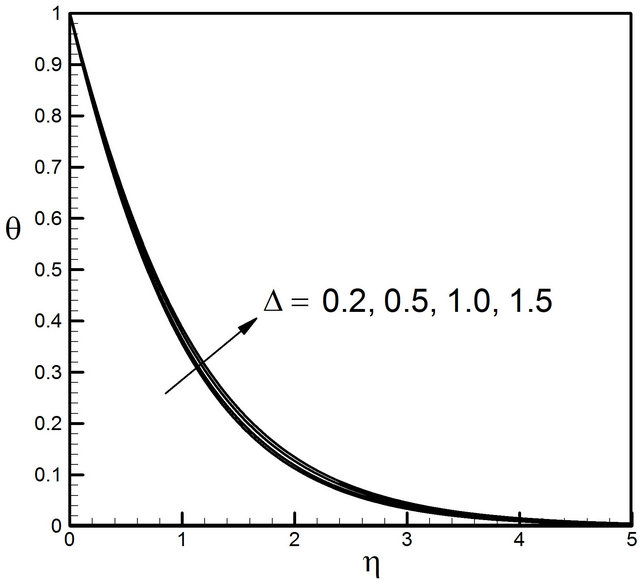
Figure 8. Distribution of temperature profiles for D.
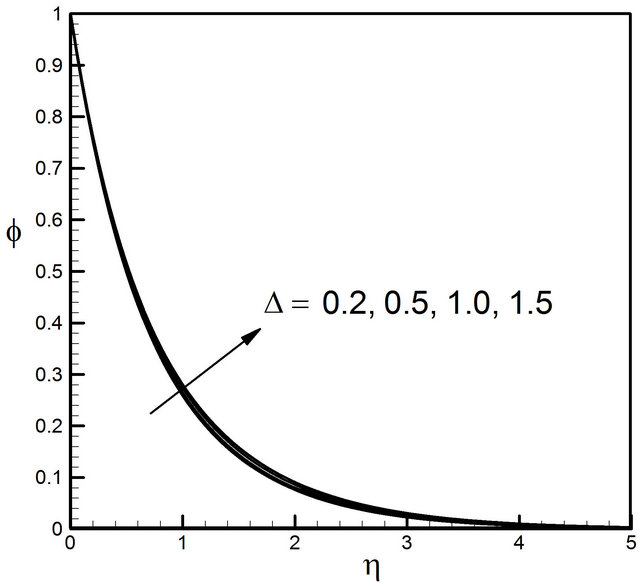
Figure 9. Distribution of concentration profiles for D.

Figure 10. Distribution of velocity profiles for n.

Figure 11. Distribution of microrotation profiles for n.
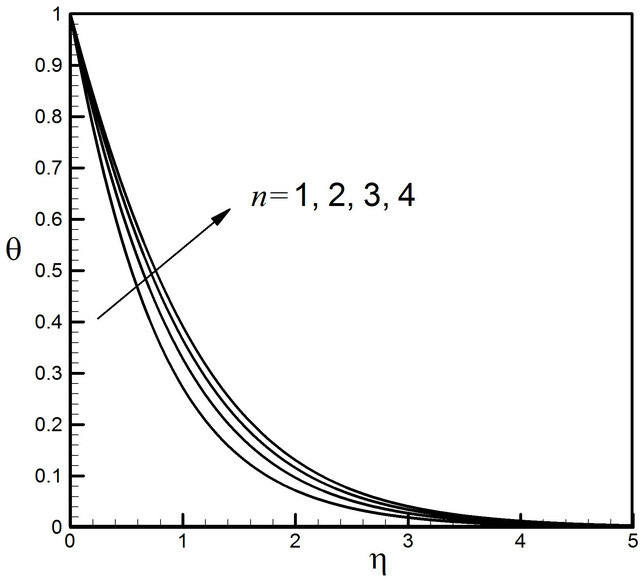
Figure 12. Distribution of temperature profiles for n.
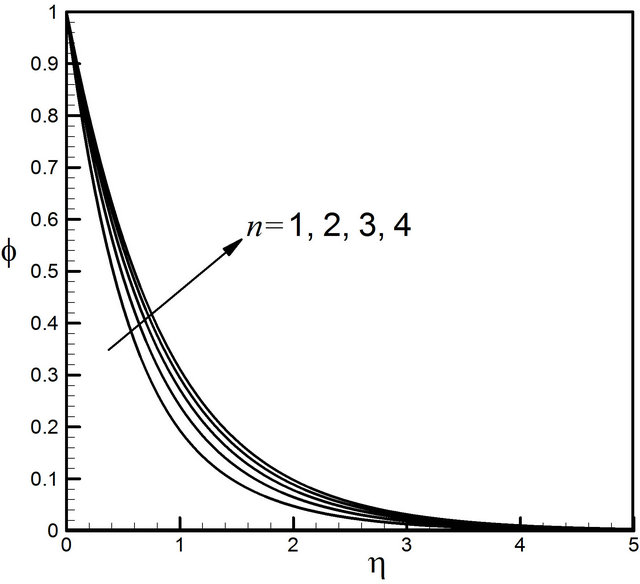
Figure 13. Distribution of concentration profiles for n.
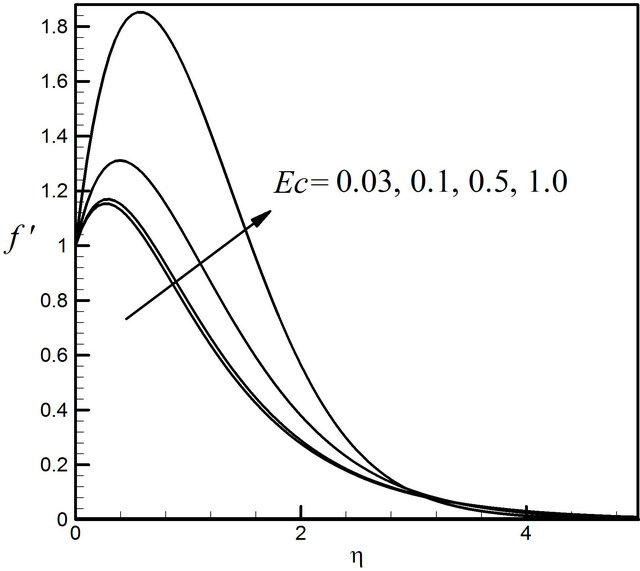
Figure 14. Distribution of velocity profiles for Ec.
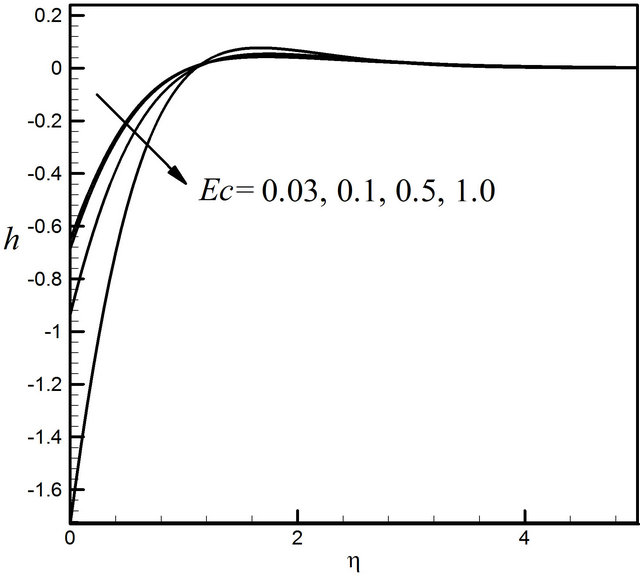
Figure 15. Distribution of microrotation profiles for Ec.
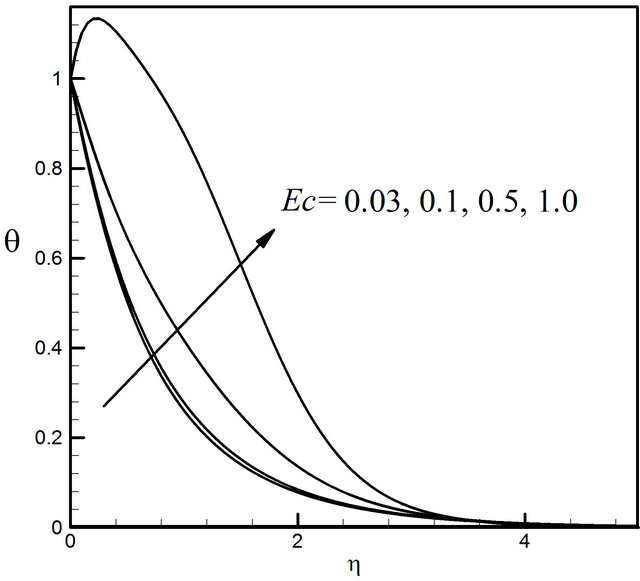
Figure 16. Distribution of temperature profiles for Ec.
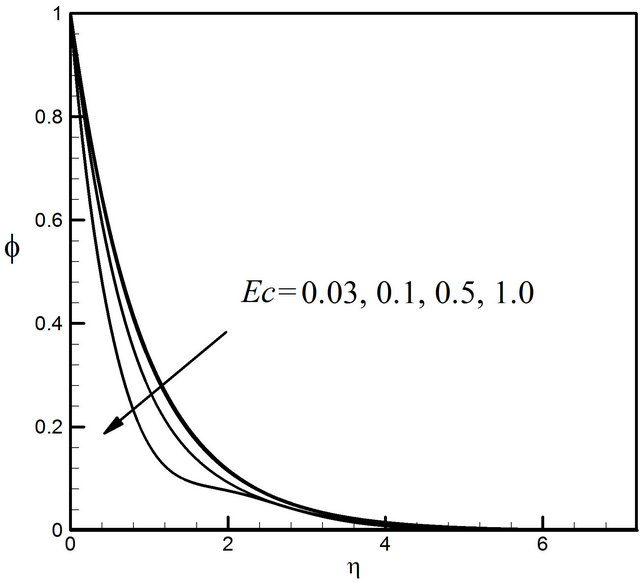
Figure 17. Distribution of concentration profiles for Ec.
Figure 18. Distribution of velocity profiles for g.
Figure 19. Distribution of microrotation profiles for g.
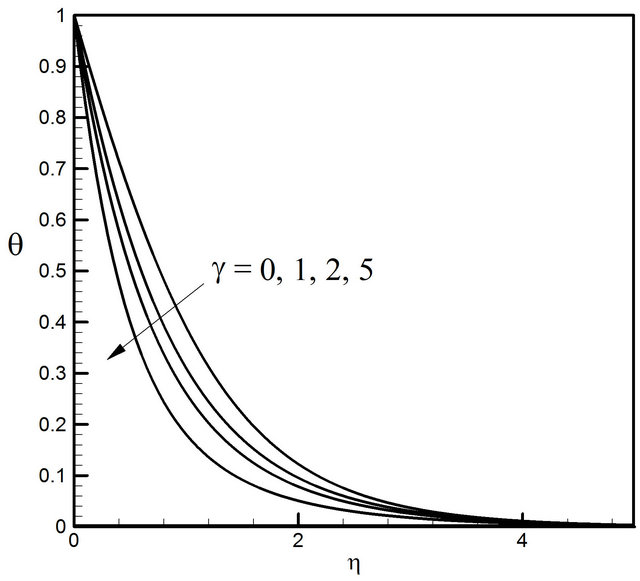
Figure 20. Distribution of temperature profiles for g.
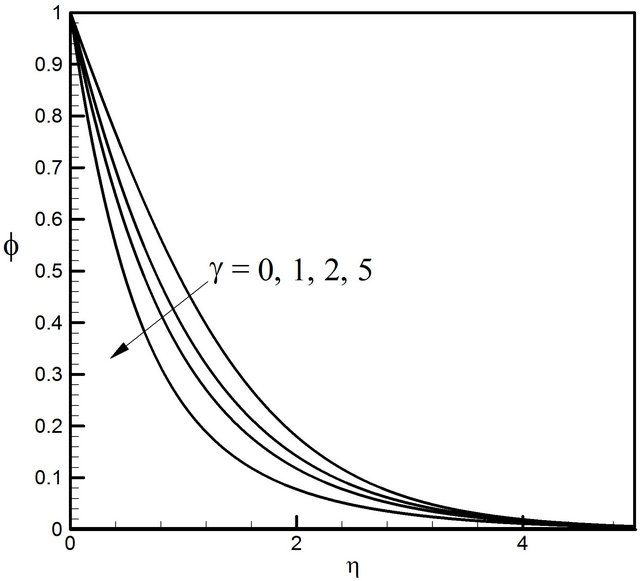
Figure 21. Distribution of concentration profiles for g.
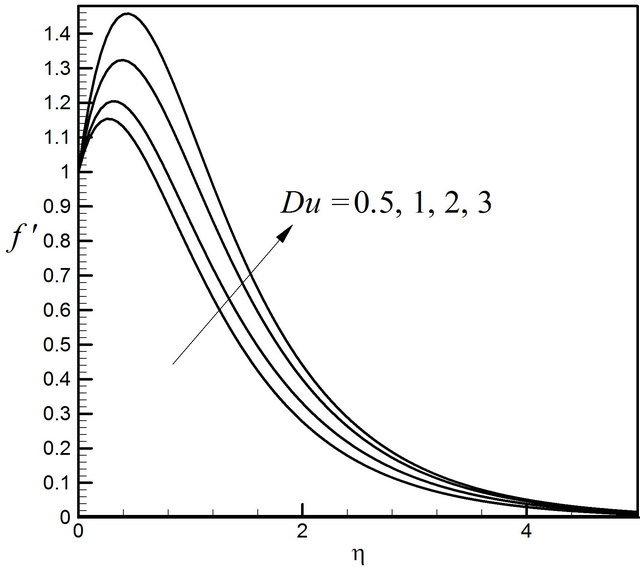
Figure 22. Distribution of velocity profiles for Du.
of the value of Du the velocity profiles occur higher. The effect of Du on the microrotation profiles is insignificant illustrated in Figure 23. From Figure 24, it is noticed that Du has remarkable effect on temperature profiles; quantitatively when 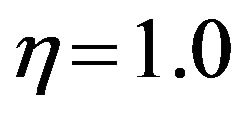 Du increases from 0.5 to 1 and there is 23.08% increase in the temperature value, whereas the corresponding increase is 19.05%, when Du increases from 2 to 3. The Dufour number has a falling effect on the concentration field shown in Figure 25. Quantitatively when
Du increases from 0.5 to 1 and there is 23.08% increase in the temperature value, whereas the corresponding increase is 19.05%, when Du increases from 2 to 3. The Dufour number has a falling effect on the concentration field shown in Figure 25. Quantitatively when  and Du increases from 0.5 to 1, there is 15.56% decrease in the concentration value, whereas the corresponding decrease is 6.67% when Du increases from 2 to 3.
and Du increases from 0.5 to 1, there is 15.56% decrease in the concentration value, whereas the corresponding decrease is 6.67% when Du increases from 2 to 3.
Figures 26-29 display the effects of the Soret number Sr on the velocity, microrotation, temperature and concentration profiles respectively. It is observed that Sr has very negligible effect on the velocity, microrotation and temperature profiles. Figure 29 reveals that the Soret
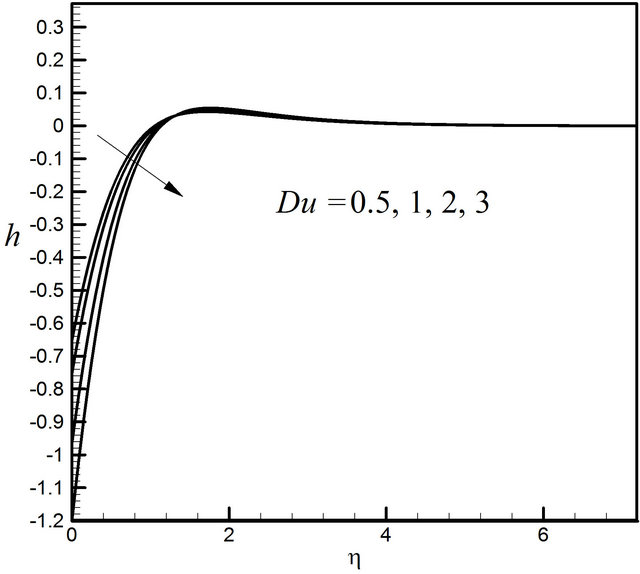
Figure 23. Distribution of microrotation profiles for Du.
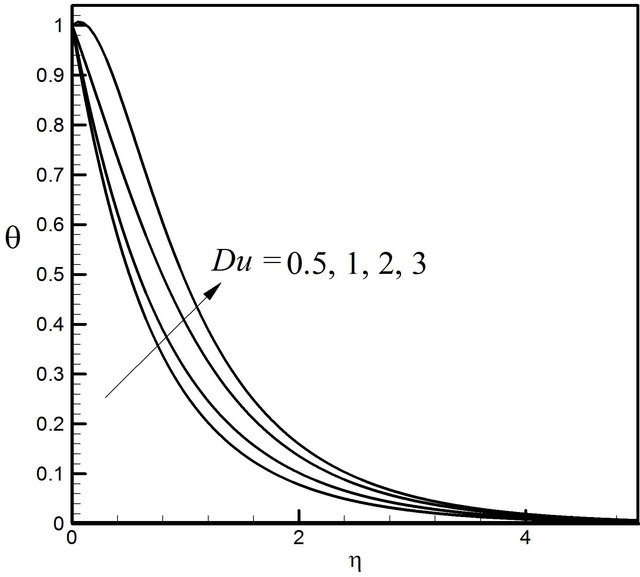
Figure 24. Distribution of temperature profiles for Du.
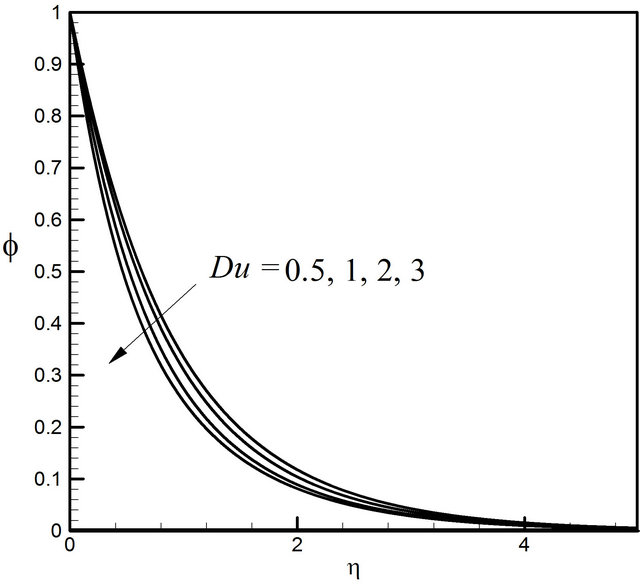
Figure 25. Distribution of concentration profiles for Du.
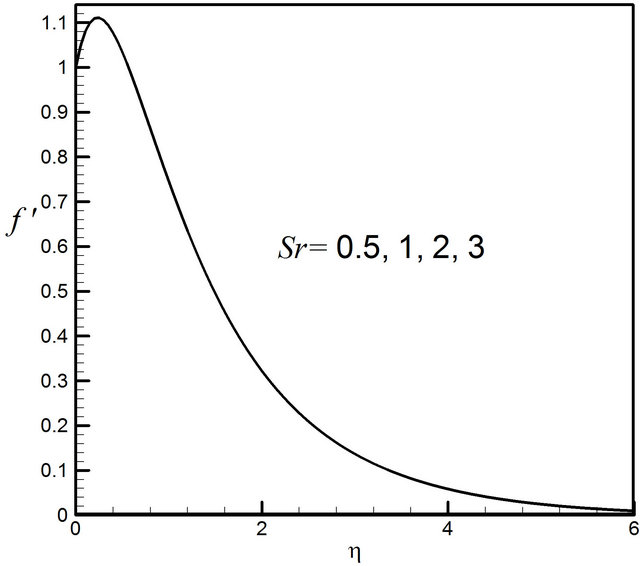
Figure 26. Distribution of velocity profiles for Sr.
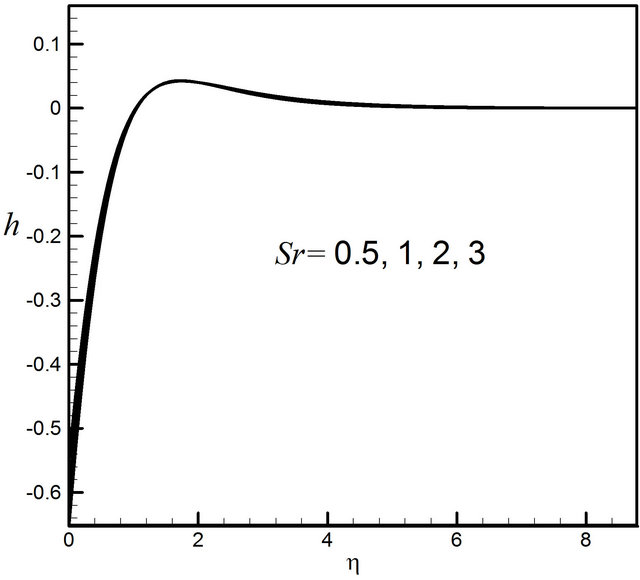
Figure 27. Distribution of microrotation profiles for Sr.
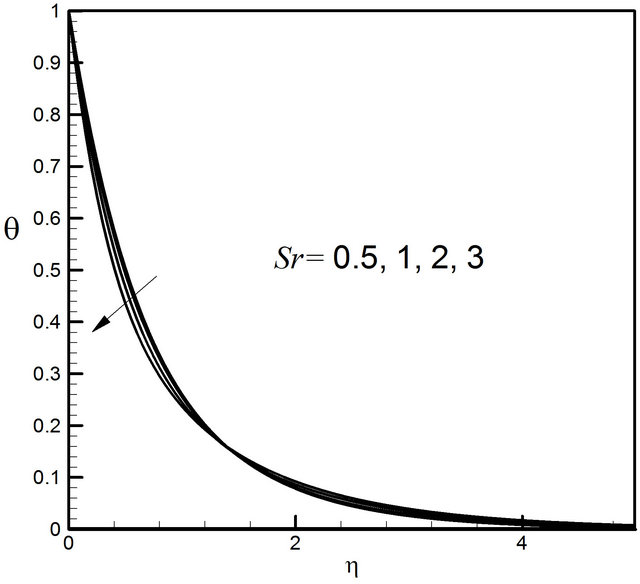
Figure 28. Distribution of temperature profiles for Sr.
number Sr influences the concentration profiles to a great extent. Quantitatively when 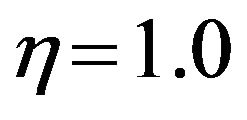 and Du increases from 0.5 to 1, there is 23.08% decrease in the concentration value, whereas the corresponding decrease is 23.07% when Du increases from 2 to 3.
and Du increases from 0.5 to 1, there is 23.08% decrease in the concentration value, whereas the corresponding decrease is 23.07% when Du increases from 2 to 3.
Figure 30 displays that the suction parameter fw has strong effect on the velocity profiles. With the increase of the value of fw the velocity profiles decrease. Elaborately when 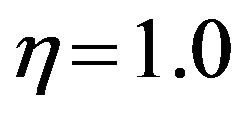 and Du decreases from 0 to 0.5, there is 176.79% decrease in the concentration value, whereas the corresponding decrease is 21.47% when Du increases from 1 to 3. It is observed that, when suction fw increases, the microrotation increase monotonically seen in Figure 31. These Figures 32 and 33 indicate that temperature as well as concentration profiles decrease with the increase of suction velocity or mass transfer parameter frequently.
and Du decreases from 0 to 0.5, there is 176.79% decrease in the concentration value, whereas the corresponding decrease is 21.47% when Du increases from 1 to 3. It is observed that, when suction fw increases, the microrotation increase monotonically seen in Figure 31. These Figures 32 and 33 indicate that temperature as well as concentration profiles decrease with the increase of suction velocity or mass transfer parameter frequently.
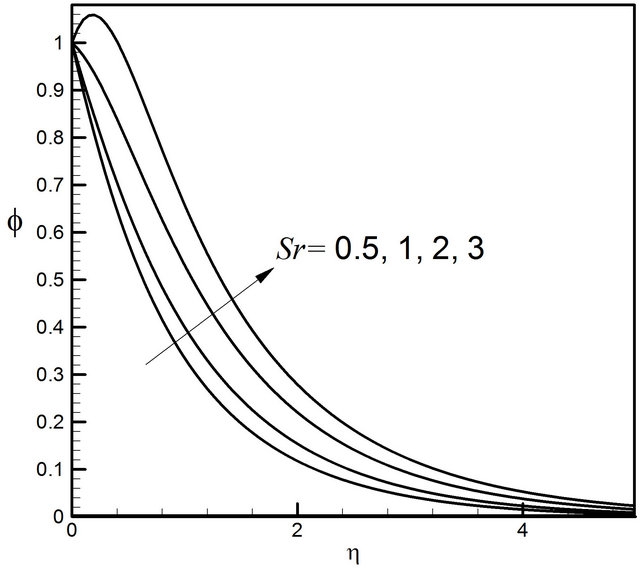
Figure 29. Distribution of concentration profiles for Sr.
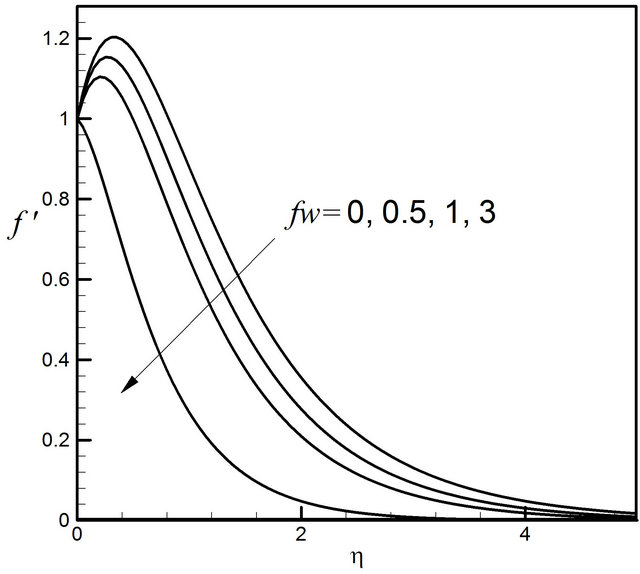
Figure 30. Distribution of velocity profiles for fw.
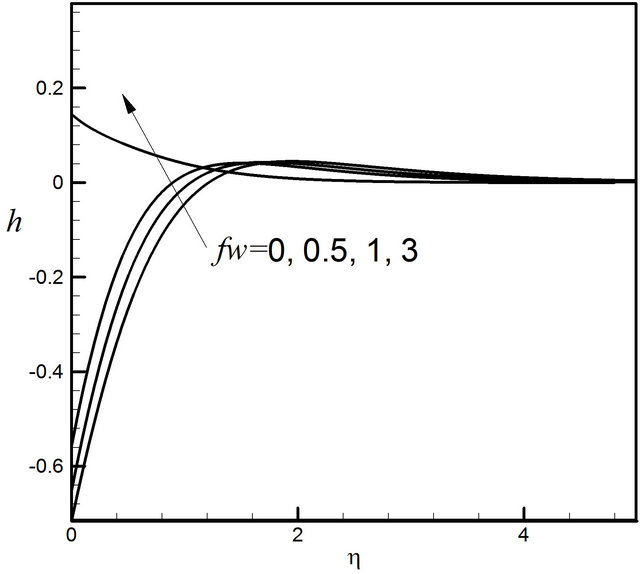
Figure 31. Distribution of microrotation profiles for fw.
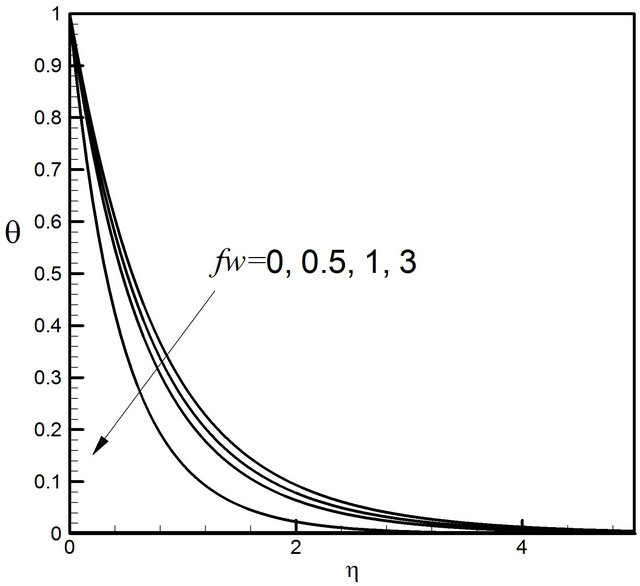
Figure 32. Distribution of temperature profiles for fw.
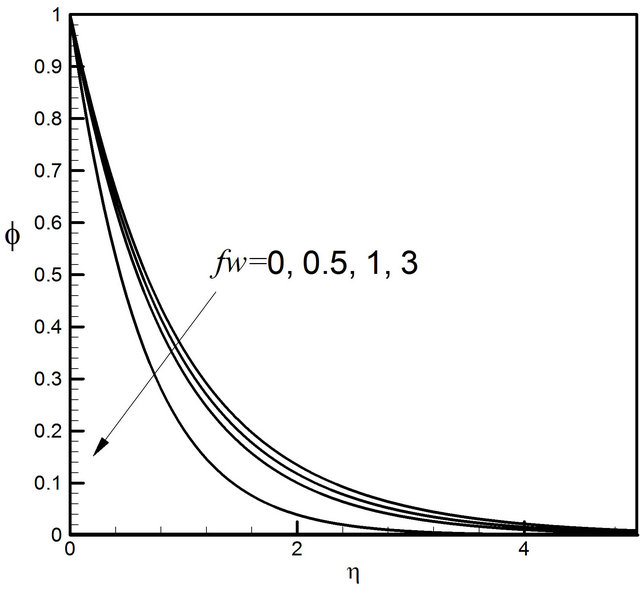
Figure 33. Distribution of concentration profiles for fw.
Finally, Finally, the effects of various parameters on the skin friction Cf, couple stress Mw, local Nusselt number Nu and local Sherwood number Sh are shown in the Tables 1-2.
5. Conclusions
In the present paper, Soret Dufour effect on the boundary layer flow and heat transfer of microrotation fluid over a nonlinear stretching plate in the presence of suction has been studied. The governing momentum and energy equations were transformed to a set of non linear ordinary differential equations by employing the appropriate similarity transformations and solve numerically for various combinations of problem parameters. The effects of the vortex viscosity parameter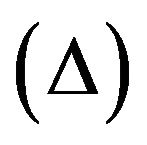 , surface nonlinearity parameter
, surface nonlinearity parameter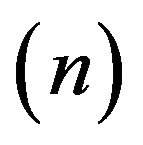 , Eckert number
, Eckert number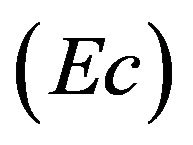 , constant parameter
, constant parameter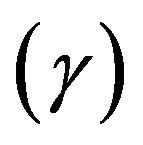 , Dufour number
, Dufour number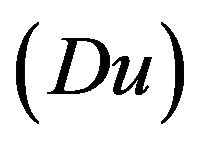 , Soret number
, Soret number 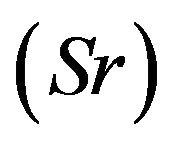 and suction parameter
and suction parameter 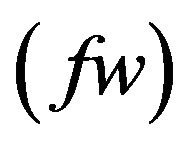 are investigated through the use of graphs.
are investigated through the use of graphs.
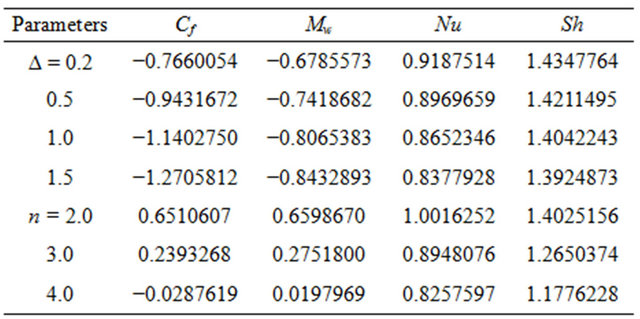
Table 1. Cf, Mw, Nu and Sh for different values of the parameters D and n.
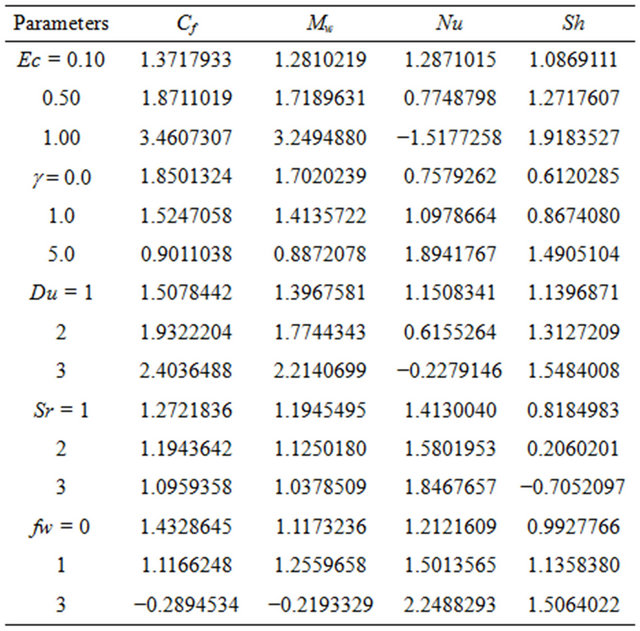
Table 2. Cf, Mw, Nu and Sh for different values of the parameter Ec, g, Du, Sr and fw.
From the present study the following conclusions are made:
1) The effect of vortex viscosity  parameter on velocity and microrotation is prominent;
parameter on velocity and microrotation is prominent;
2) Nonlinearity of the stretching surface 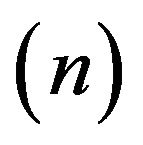 is effective on the boundary layer flow;
is effective on the boundary layer flow;
3) Effect of Eckert number  is uniform;
is uniform;
4) Boundary layer growth can be controlled by using constant parameter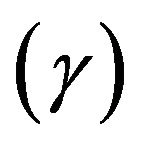 ;
;
5) The Dufour  effect is significant;
effect is significant;
6) The Soret number 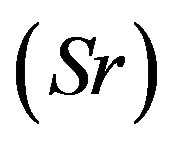 plays a role on concentration;
plays a role on concentration;
7) The effect of suction parameter 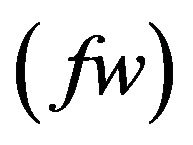 is dominating on the velocity, microrotation, temperature and concentration profiles. So, using suction boundary layer growth can be stabilized.
is dominating on the velocity, microrotation, temperature and concentration profiles. So, using suction boundary layer growth can be stabilized.
REFERENCES
- S. Ostrach, “An Analysis of Laminar Free-Convection Flow and Heat Transfer about a Flat Plate Parallel to the Direction of the Generating Body Force,” Technical Note, nACA Report, Washington DC, 1952. http://naca.central.cranfield.ac.uk/report.php?NID=5021
- R. M. Goody, “The Influence of Radiative Transfer on Cellular Convection,” Journal of Fluid Mechanics, Vol. 1, No. 4, 1956, pp. 424-435. doi:10.1017/S0022112056000263
- B. C. Sakiadis, “Boundary-Layer Behavior on Continuous Solid Surfaces: I. Boundary-Layer Equations for Two-Dimensional and Axisymmetric Flow,” AIChE Journal, Vol. 7, No. 1, 1961, pp. 26-28. doi:10.1002/aic.690070108
- A. C. Eringen, “Theory of Micropolar Fluids,” Journal of Mathematics and Mechanics, Vol. 16, No. 1, 1966, pp. 1-18.
- L. J. Crane, “Flow past a Stretching Sheet,” Zeitschrift für Angewandte Mathematik und Physik (ZAMP), Vol. 21, No. 4, 1970, pp. 645-647. doi:10.1007/BF01587695
- E. M. Sparrow, “Radiation Heat Transfer,” Augmented Edition, Hemisphere Publishing Corp., Washington DC, 1978.
- O. Aydin and I. Pop, “Natural Convection from a Discrete Heater in Enclosures Filled with a Micropolar Fluid,” International Journal of Engineering Science, Vol. 43, No. 19-20, 2005, pp. 1409-1418. doi:10.1016/j.ijengsci.2005.06.005
- M.-I. Char and C.-L. Chang, “Effect of Wall Conduction on Natural Convection Flow of Micropolar Fluids along a Flat Plate,” International Journal of Heat and Mass Transfer, Vol. 40, No. 15, 1997, pp. 3641-3652. doi:10.1016/S0017-9310(97)00006-9
- H. A. M. El-Arabawy, “Effect of Suction/Injection on the Flow of a Micropolar Fluid past a Continuously Moving Plate in the Presence of Radiation,” International Journal of Heat and Mass Transfer, Vol. 46, No. 8, 2003, pp. 1471-1477. doi:10.1016/S0017-9310(02)00320-4
- A. Ishak, R. Nazar and I. Pop, “The Schneider Problem for a Micropolar Fluid,” Fluid Dynamics Research, Vol. 38, No. 7, 2006, pp. 489-502. doi:10.1016/j.fluiddyn.2006.03.004
- M. E. Karim, M. A. Samad and M. A. Sattar, “Steady MHD Free Convection Flow with Thermal Radiation past a Vertical Porous Plate Immersed in a Porous Medium,” Research Journal of Mathematics and Statistics, Vol. 3, No. 4, 2011, pp. 141-147. http://www.maxwellsci.com/print/rjms/v3-141-147.pdf
- Y. Y. Lok, N. Amin and I. Pop, “Unsteady Boundary Layer Flow of a Micropolar Fluid near the Rear Stagnation Point of a Plane Surface,” International Journal of Thermal Sciences, Vol. 42, No. 11, 2003, pp. 995-1001. doi:10.1016/S1290-0729(03)00079-6
- R. Nazar, A. Ishak and I. Pop, “Unsteady Boundary Layer Flow over a Stretching Sheet in a Micropolar Fluid,” International Journal of Mathematical, Physical and Engineering Sciences, Vol. 2, No. 3, 2008, pp. 161-165.
- M. M. Rahman, M. A. Rahman, M. A. Samad and M. S. Alam, “Heat Transfer in a Micropolar Fluid along a NonLinear Stretching Sheet with a Temperature-Dependent Viscosity and Variable Surface Temperature,” International Journal of Thermophysics, Vol. 30, No. 5, 2009, pp. 1649-1670.
- M. M. Rahman, M. J. Uddin and A. Aziz, “Convective Flow of Micropolar Fluid in a Porous Medium with Variable Electric Conductivity, Surface Heat Flux and NonUniform Heat Source (or Sink),” International Journal of Energy & Technology, Vol. 25, No. 2, 2010, pp. 1-18.
- H. S. Takhar, R. Bhargava, R. S. Agrawal and A. V. S. Balaji, “Finite Element Solution of a Micropolar Fluid Flow and Heat Transfer between Two Porous Disks,” International Journal of Engineering Science, Vol. 38, No. 17, 2000, pp. 1907-1922. doi:10.1016/S0020-7225(00)00019-7
- E. R. G. Eckert and R. M. Drake, “Analysis of Heat and Mass Transfer,” McGraw-Hill, New York, 1972.
- T. Hayat and F. A. Hendi, “Thermal-Diffusion and Diffusion-Thermo Effects on MHD Three-Dimensional Axisymmetric Flow with Hall and Ion-Slip Currents,” Journal of American Science, Vol. 8, No. 1, 2012, pp. 284-294. http://www.jofamericanscience.org/journals/am-sci/am0801/042_7833am0801_284_294.pdf
- O. D. Makinde and P. O. Olanrewaju, “Unsteady Mixed Convection with Soret and Dufour Effects past a Porous Plate Moving through a Binary Mixture of Chemical Reacting Fluid,” Chemical Engineering Communications, Vol. 198, No. 7, 2011, pp. 920-938. doi:10.1080/00986445.2011.545296
- S. Shateyi, S. S. Motsa and P. Sibanda, “The Effects of Thermal Radiation, Hall Currents, Soret, and Dufour on MHD Flow by Mixed Convection over a Vertical Surface in Porous Media,” Mathematical Problems in Engineering, Vol. 2010, No. 1, 2010, pp. 1-20. doi:10.1155/2010/627475
- D. Srinivasacharya and K. Kaladhar, “Mixed Convection in a Couple Stress Fluid with Soret and Dufour Effects,” Internatioanl Journal of Applied Mathematics and Mechanics, Vol. 7, No. 20, 2011, pp. 59-71.
- P. R. Nachtsheim and P. Swigert, “Satisfaction of the Asymptotic Boundary Conditions in Numerical Solution of the Systems of Non-Linear Equations of Boundary Layer Type,” Ph.D. Thesis, NASA TN D-3004, Washington DC, 1965. http://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19650026350_1965026350.pdf

