Applied Mathematics
Vol. 4 No. 2 (2013) , Article ID: 27958 , 6 pages DOI:10.4236/am.2013.42042
Resonant Homoclinic Bifurcations with Orbit Flips and Inclination Flips*
College of Science, University of Shanghai for Science and Technology, Shanghai, China
Email: zhangts1209@163.com
Received December 17, 2012; revised January 17, 2013; accepted January 25, 2013
Keywords: Orbit Flip; Inclination Flip; Resonance
ABSTRACT
Homoclinic bifurcation with one orbit flip, two inclination flips and resonance in the tangent directions of homoclinic orbit is considered. By studying the associated successor functions constructed from a local active coordinate system, we prove the existence of double 1-periodic orbit, 1-homoclinic orbit, and also some coexistence conditions of 1-periodic orbit and 1-homoclinic orbit.
1. Introduction and Hypotheses
Flips homoclinic bifurcations are comprehensively investigated during the last decade (see [1-10]), which produce complicated bifurcations, such as the saddlenode bifurcations, the period-doubling bifurcations and the homoclinic-doubling bifurcations.
Recently, the flip of heterodimensional cycle or accompanied by transcritical bifurcation is discussed much (see [11-13]). The double and triple periodic orbit bifurcation are proved to exist, and also some coexistence conditions for homoclinic orbits and periodic orbits. But their research is not focused on multiple flips since it is a interesting problem and full of challenges due to the high codimension and complexity. In this paper, we develop a study of resonant homoclinic bifurcation with one orbit flip and two inclination flips, where the resonance takes place in the tangent direction of the homoclinic orbit. This is a codimension-4 problem, by using the local moving frame method established in [11,14,15], we get the existence of a double 1-periodic orbit, some 1-periodic orbits and 1-homoclinic orbits, and the coexistence conditions of 1-periodic orbits and 1-homoclinic orbits.
We consider the following two systems,
 (1.1)
(1.1)
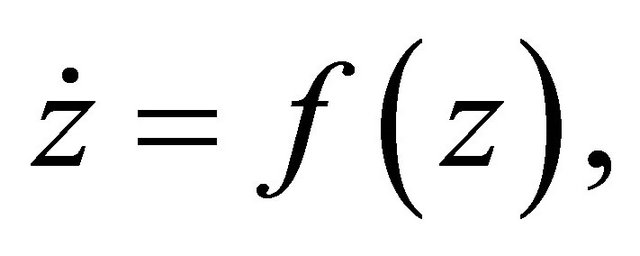 (1.2)
(1.2)
where 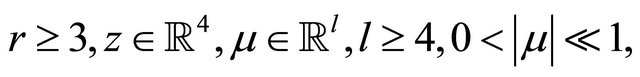
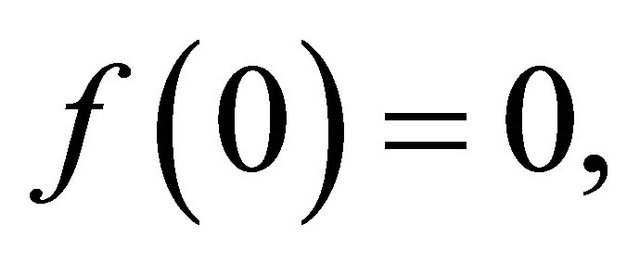
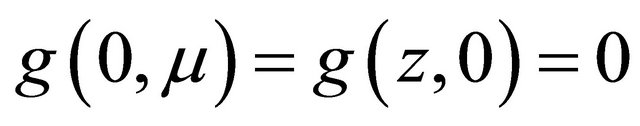 .
.
Notice that system (1.2) is an unperturbed system of (1.1) and assume it has an orbit
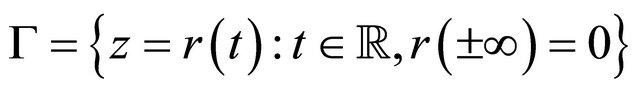
homoclinic to the hyperbolic equilibrium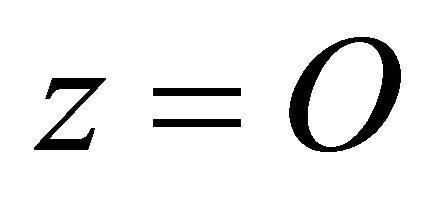 , which has two negative and two positive eigenvalues,
, which has two negative and two positive eigenvalues, 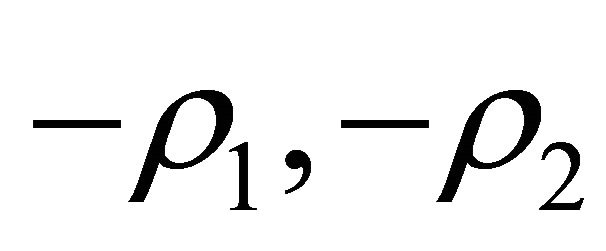
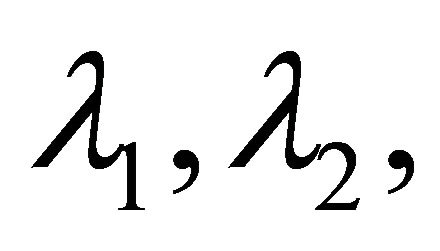 , and
, and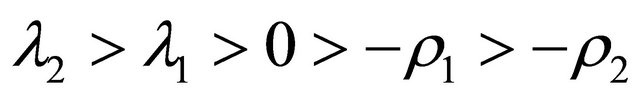 .
.
Hypotheses
Set 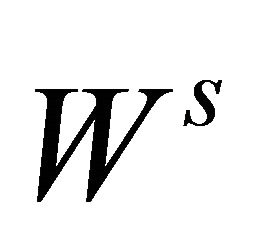 (resp.
(resp. ) and
) and 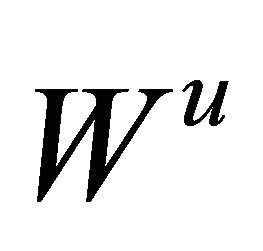 (resp.
(resp.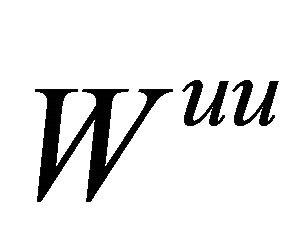 ) the stable (resp. strong stable) manifold and unstable (resp. strong unstable) manifold of the equilibrium
) the stable (resp. strong stable) manifold and unstable (resp. strong unstable) manifold of the equilibrium , respectively. We suppose that
, respectively. We suppose that
(H1) 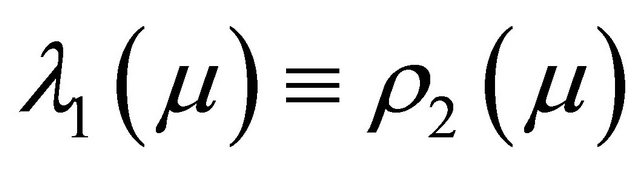 for
for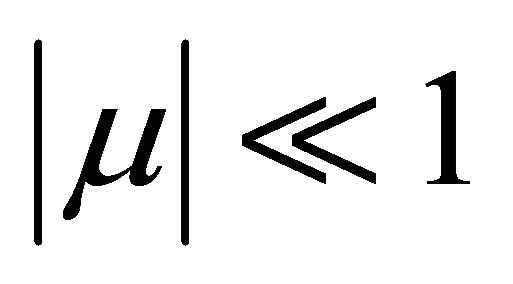 , where
, where  and
and .
.
(H2) Define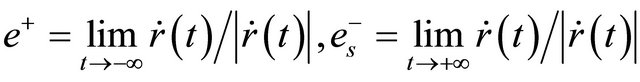 then
then 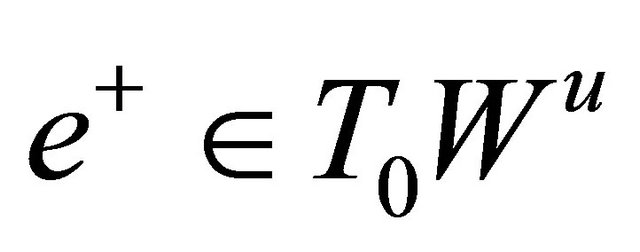 and
and  are unit eigenvectors corresponding to
are unit eigenvectors corresponding to 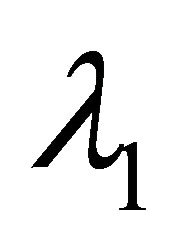 and
and 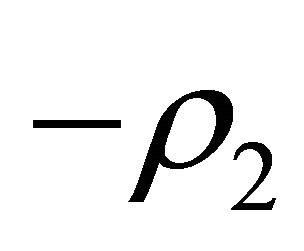 respectively, where
respectively, where 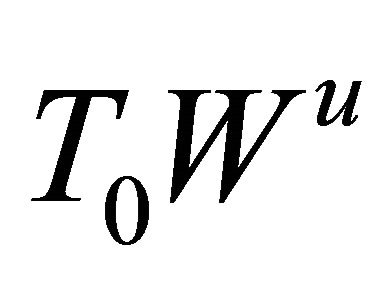 is the tangent space of the corresponding manifold
is the tangent space of the corresponding manifold 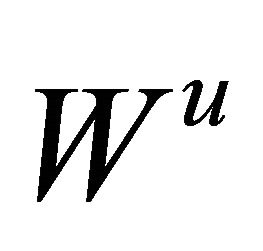 at the saddle
at the saddle , and the similar meaning for
, and the similar meaning for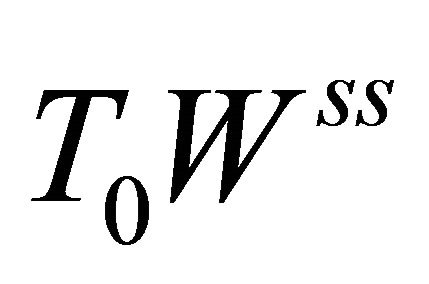 .
.
(H3) Denote by 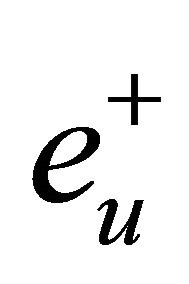 and
and 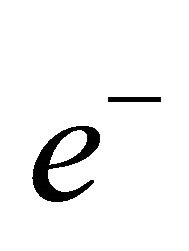 the unit eigenvectors corresponding to
the unit eigenvectors corresponding to 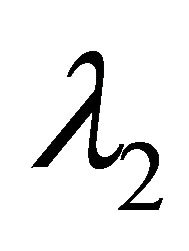 and
and 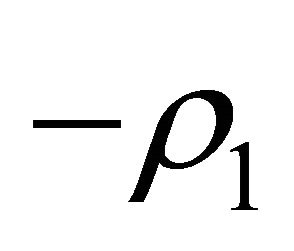 respectively, there are
respectively, there are

Remark 1.1 Hypotheses (H1) is a resonant condition, while (H2) - (H3) mean the homoclinic orbit has one orbit flip and two inclinations flips.
The paper is organized as follows. In Section 2, we first transform system (1.1) into two normal forms, then construct a regular map in some neighborhood of the homoclinic orbit and a singular map in some neighborhood of the equilibrium respectively to establish the Poincaré map. In Section 3, we develop the bifurcation study through searching for solutions of the bifurcation equation. Finally a short conclusion about the flips bifurcation is given in Section 4.
2. Local Active Coordinate Frame and Poincaré Map
We first give two normal forms of system (1.1) and then construct the Poincaré map. Firstly system (1.1) can be transformed into the following form in some neighborhood  of the origin
of the origin  due to the theory of invariance manifolds, (refer to [14,15])
due to the theory of invariance manifolds, (refer to [14,15])
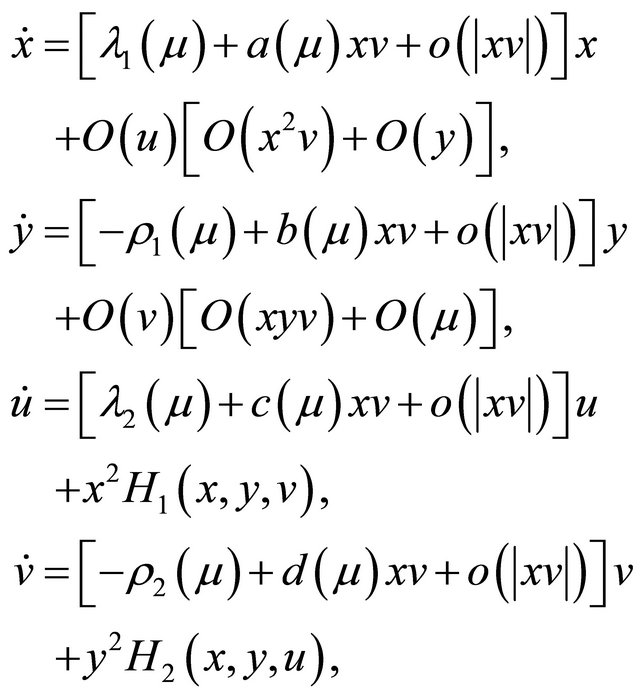 (2.1)
(2.1)
where 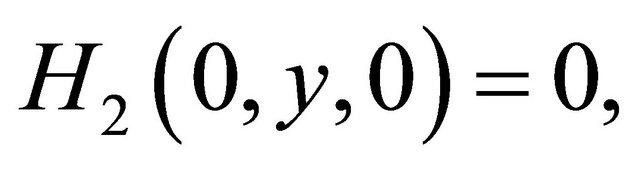
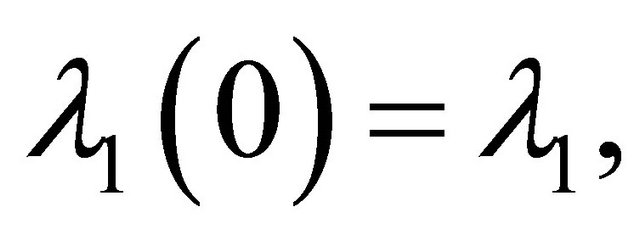
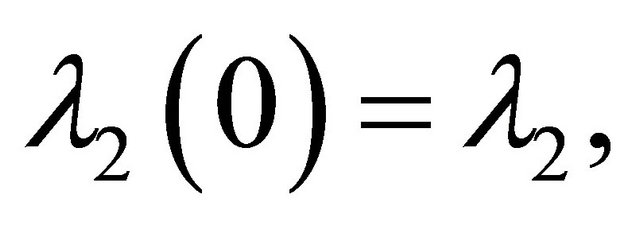
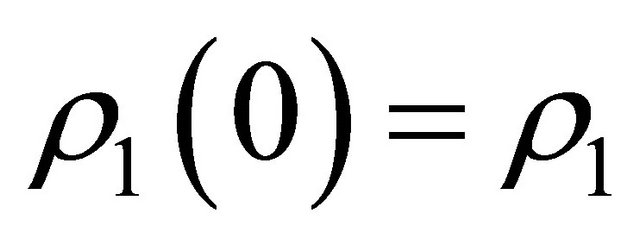 and
and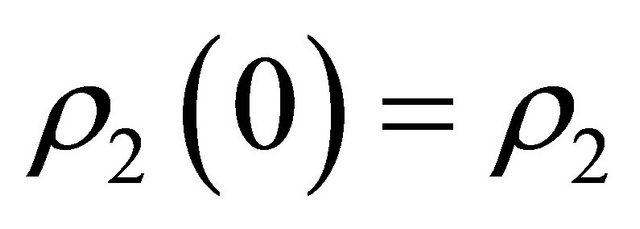 .
. 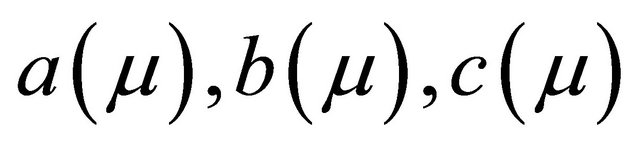 and
and 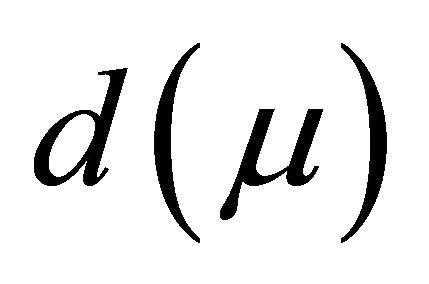 are parameters depending on
are parameters depending on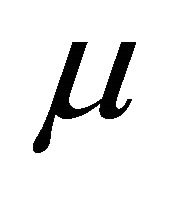 .
.
One may see that from (2.1), 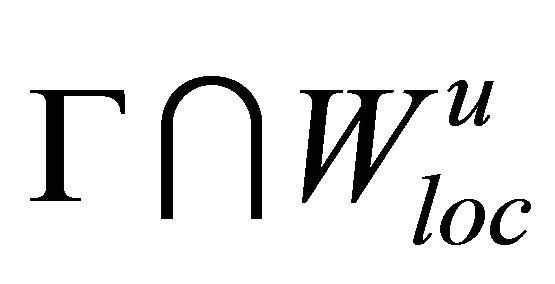 and
and 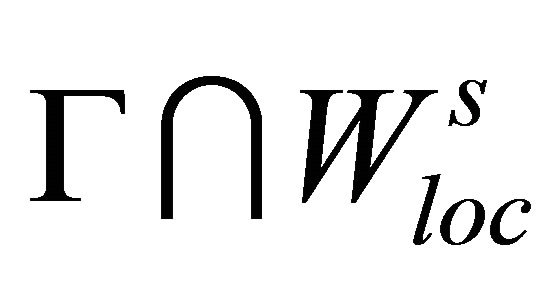 are straightened locally to be the
are straightened locally to be the 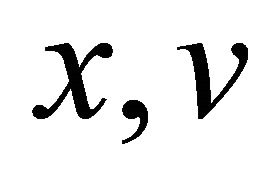 axes in neighborhood of
axes in neighborhood of , so it is possible to take some time
, so it is possible to take some time 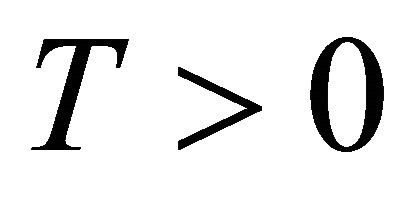 large enough, such that
large enough, such that 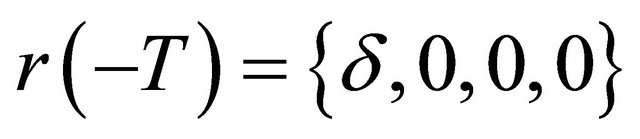 and
and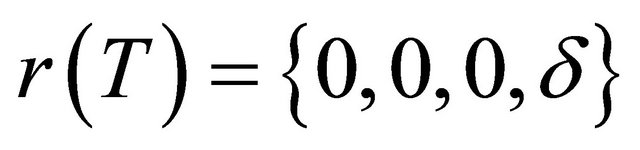 , where
, where ![]() is small and
is small and
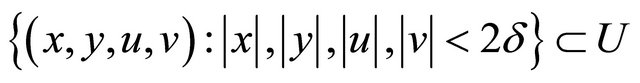 .
.
Now consider the linear variational system
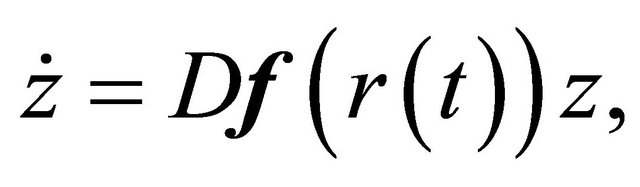 (2.2)
(2.2)
and its adjoint system
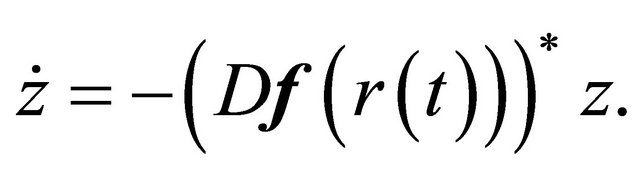 (2.3)
(2.3)
Matrix theory shows that system (2.2) has a fundamental solution matrix and furthermore it can be chosen as follows (refer to [11,14-15])
Lemma 2.1 There exists a fundamental solution matrix 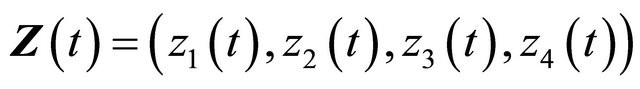 of system (2.2) satisfying
of system (2.2) satisfying
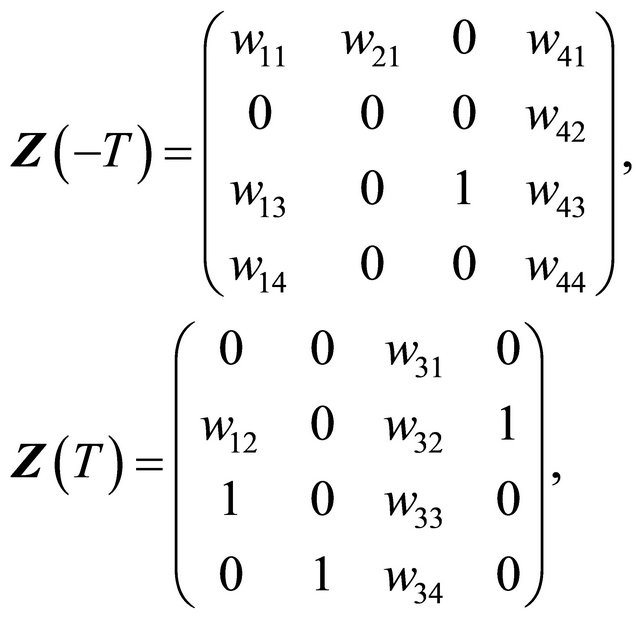
where
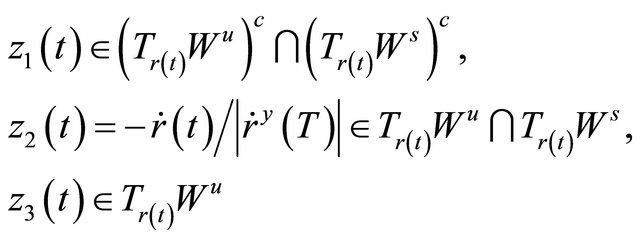
and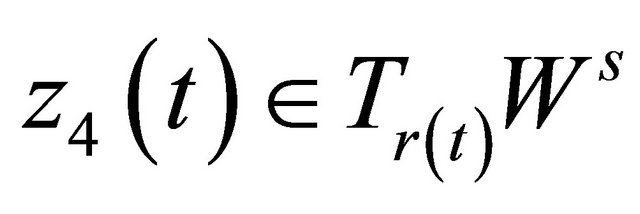 , and
, and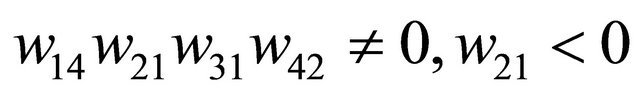 .
.
Obviously 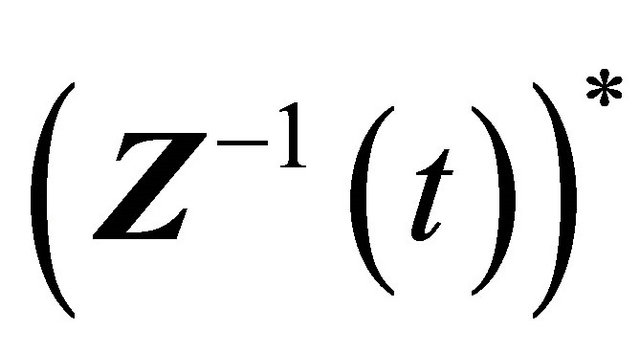 is a fundamental solution matrix of system (2.3), denote by
is a fundamental solution matrix of system (2.3), denote by
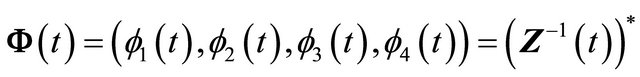 .
.
We here introduce a new coordinate  and set
and set
 (2.4)
(2.4)
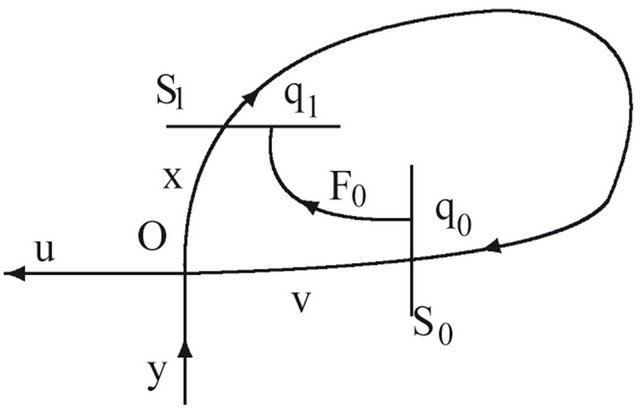
Naturally we can choose two cross sections of![]() , see Figure 1,
, see Figure 1,
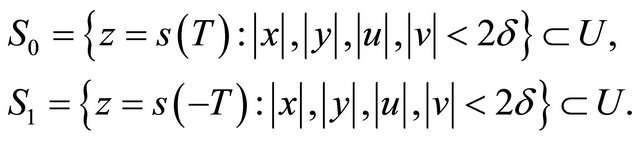
Substitute (2.4) into (1.1), there is

Integrating both sides from  to
to![]() , we further have
, we further have
 (2.5)
(2.5)
where
 .
.
Equation (2.5) defines indeed a map 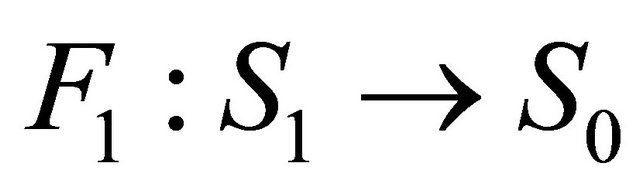 in some tube region near
in some tube region near![]() ,
,

see Figure 1(a). If set
 (a)
(a) (b)
(b)
Figure 1. Transition maps. (a) F1: S1→S0; (b) F0: S0→S1.

and
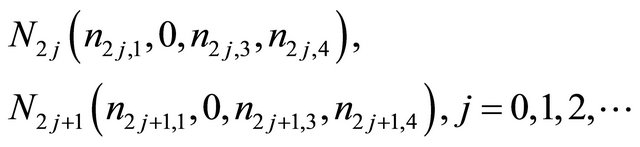
we can obtain the following expressions,
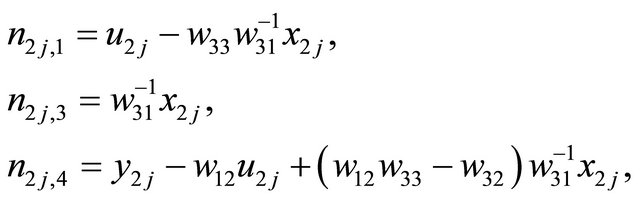 (2.6)
(2.6)
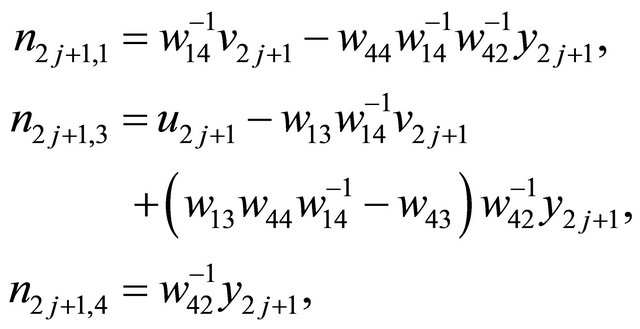 (2.7)
(2.7)
and
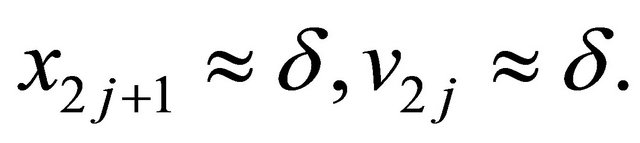 (2.8)
(2.8)
Using the flow of system (2.1) in the neighborhood , we can set up a map
, we can set up a map
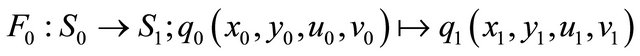
defined as (see [14,15])
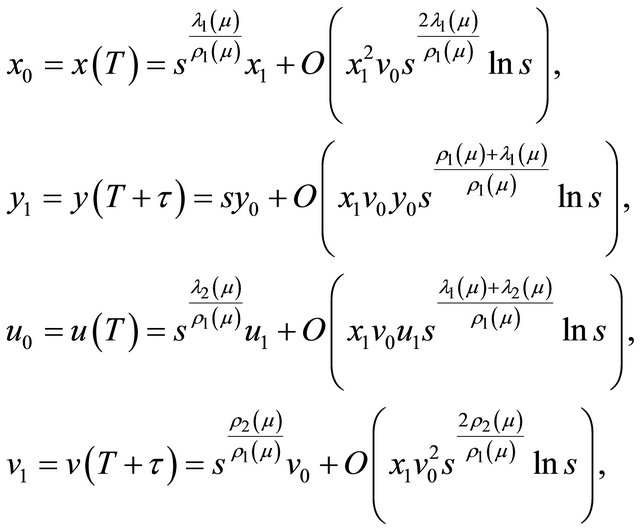 (2.9)
(2.9)
where 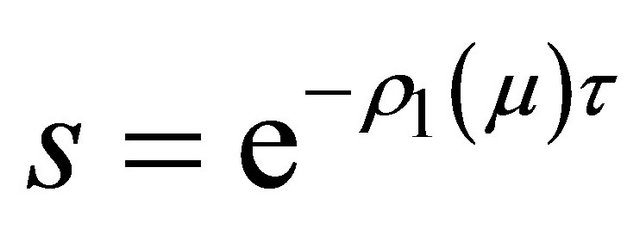 is the Silnikov time and
is the Silnikov time and ![]() is the time going from
is the time going from 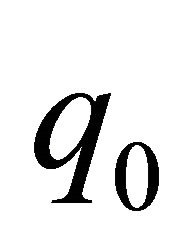 to
to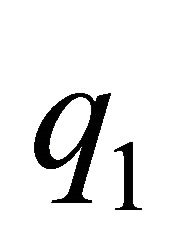 , see Figure 1(b).
, see Figure 1(b).
From the above the Poincaré map
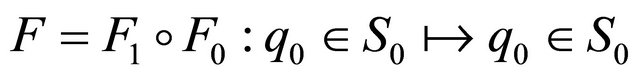
is obtained

Then the corresponding associated successor function 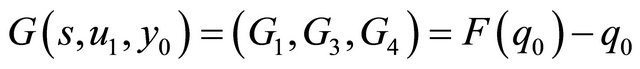 is
is
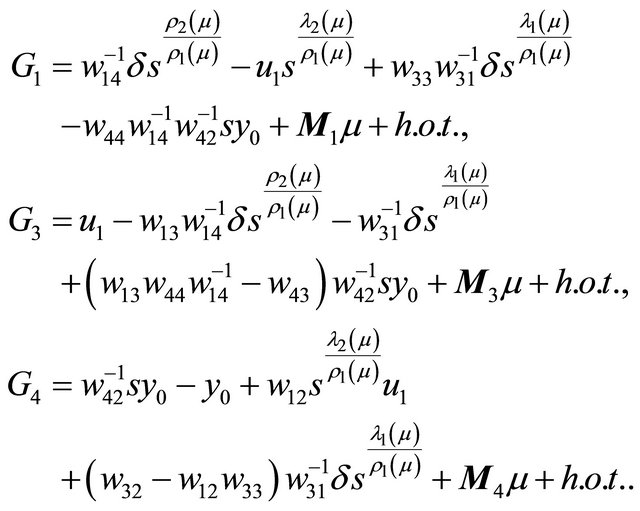 (2.10)
(2.10)
Since 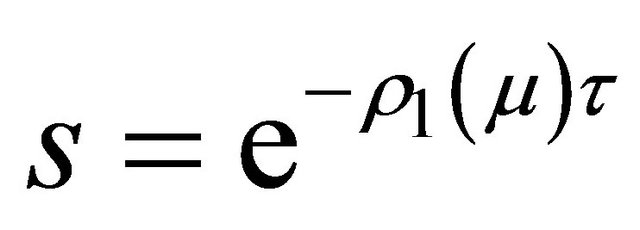 is defined by the flying time from the point in
is defined by the flying time from the point in  to
to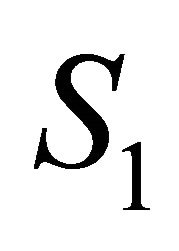 , obviously
, obviously 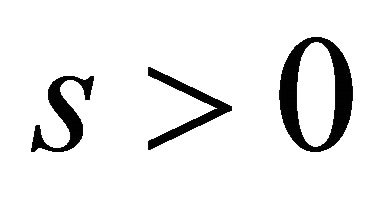 means
means ![]() is limited;
is limited; 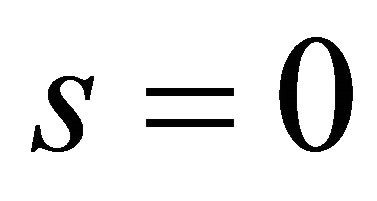 means
means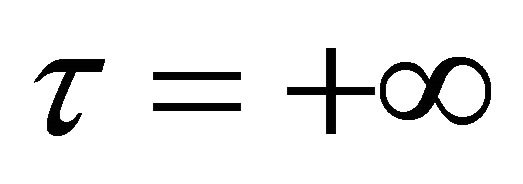 , which indicate the existence of a periodic orbit or a homoclinic orbit of system (1.1). So in the following section, we focus us on the solutions
, which indicate the existence of a periodic orbit or a homoclinic orbit of system (1.1). So in the following section, we focus us on the solutions ![]() of (2.10).
of (2.10).
3. Bifurcation Results
The last two equations in (2.10) give
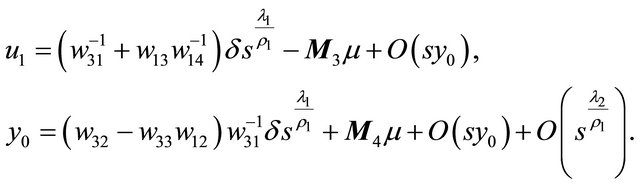
Then from 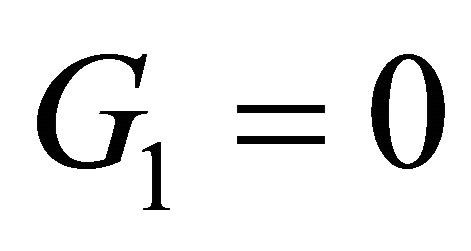 we get the bifurcation equation
we get the bifurcation equation
 (3.1)
(3.1)
Notice that we have put higher orders terms into  and omitted the parameter
and omitted the parameter  in the eigenvalues for concision.
in the eigenvalues for concision.
Define two functions as
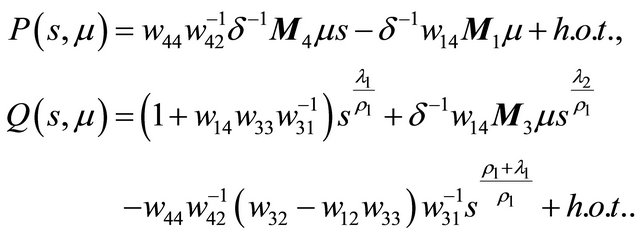
Indeed here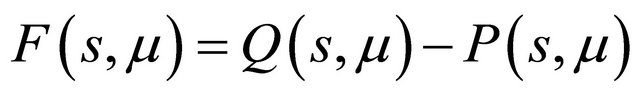 . By analysis of the curves
. By analysis of the curves 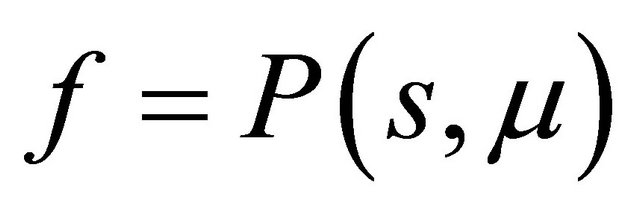 and
and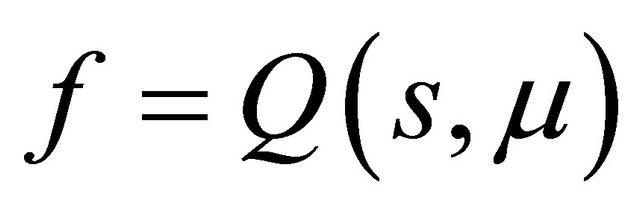 , one may immediately get the following statements.
, one may immediately get the following statements.
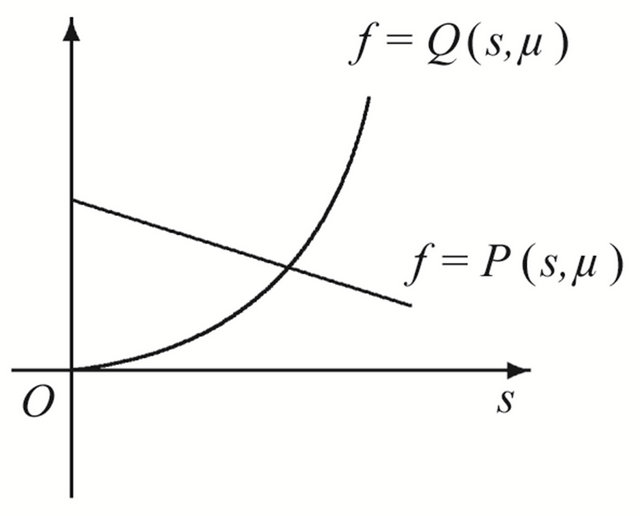
Theorem 3.1 Suppose that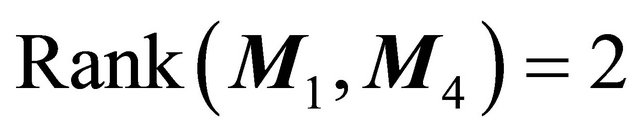 , then in the region
, then in the region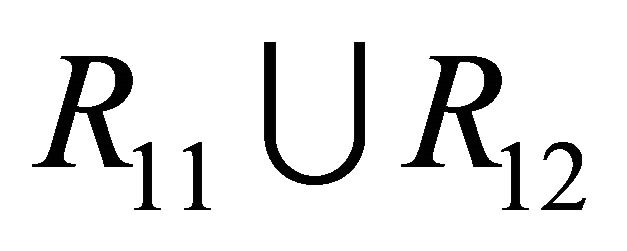 , system (1.1) has a unique 1-periodic orbit near
, system (1.1) has a unique 1-periodic orbit near![]() ; in the region
; in the region , system (1.1) has not any 1-periodic orbit.
, system (1.1) has not any 1-periodic orbit.
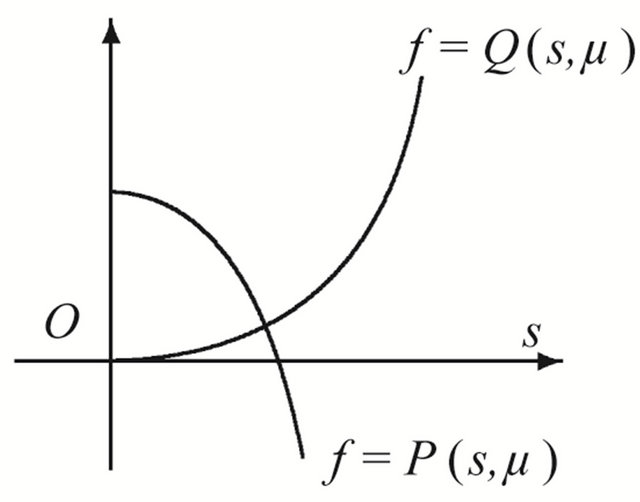
Proof Because
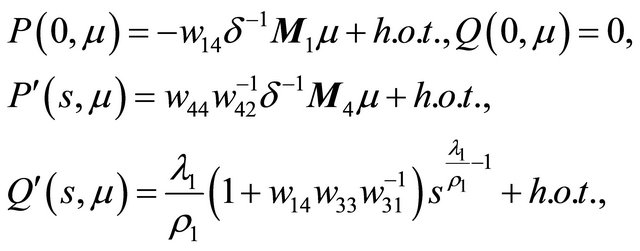
the curve 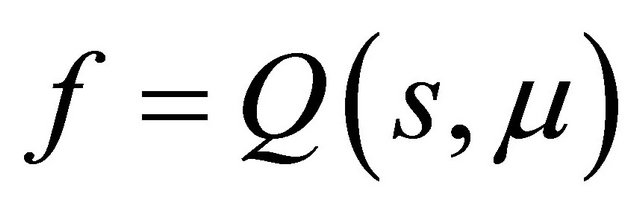 has no inflexion point, so th e line
has no inflexion point, so th e line 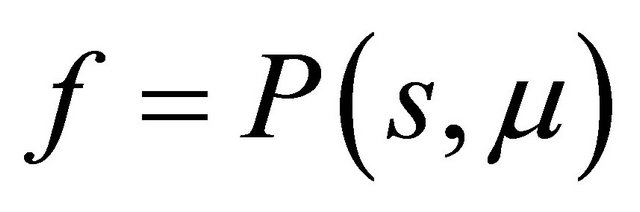 and the curve
and the curve  must intersect at a unique point in the region
must intersect at a unique point in the region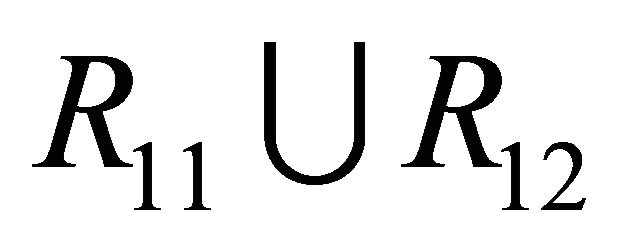 , where
, where
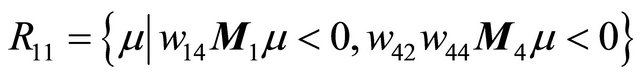
and
 see Figure 2(a). Namely there exists a point
see Figure 2(a). Namely there exists a point  such that
such that
 therefore system (1.1) has a unique 1-periodic orbit. On the contrary, there is not such a intersection point in the region
therefore system (1.1) has a unique 1-periodic orbit. On the contrary, there is not such a intersection point in the region
 see Figure 2(b).
see Figure 2(b).
Theorem 3.2 Suppose that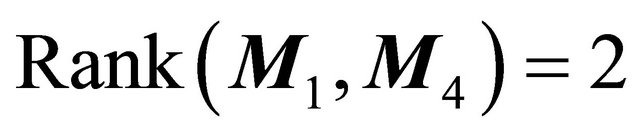 , then in the region
, then in the region , system (1.1) has a unique double 1- periodic orbit near
, system (1.1) has a unique double 1- periodic orbit near ![]() located in the bifurcation surface
located in the bifurcation surface .
.
Moreover when  lies on the side of
lies on the side of 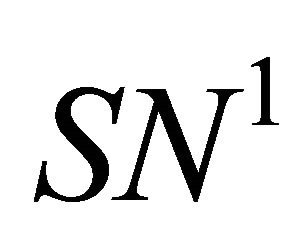 pointing to the (resp. opposite) direction
pointing to the (resp. opposite) direction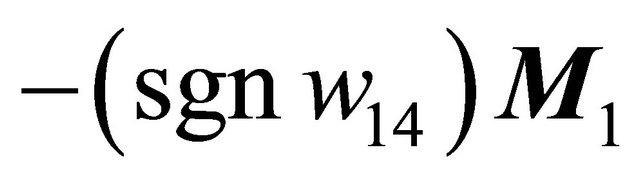 , system (1.1) has two (resp. not any) 1-periodic orbits near
, system (1.1) has two (resp. not any) 1-periodic orbits near![]() .
.
Proof We know that the existence of a double 1-periodic orbit corresponds to a double solution 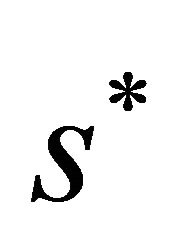 of (3.1). According to the proof of Theorem 3.1, it is enough to search the tangent point of the curves
of (3.1). According to the proof of Theorem 3.1, it is enough to search the tangent point of the curves 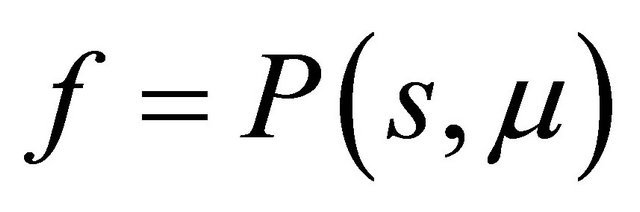 and
and
 (a)
(a)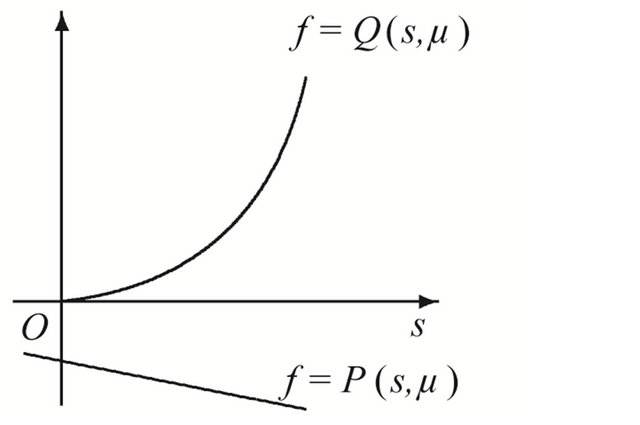 (b)
(b)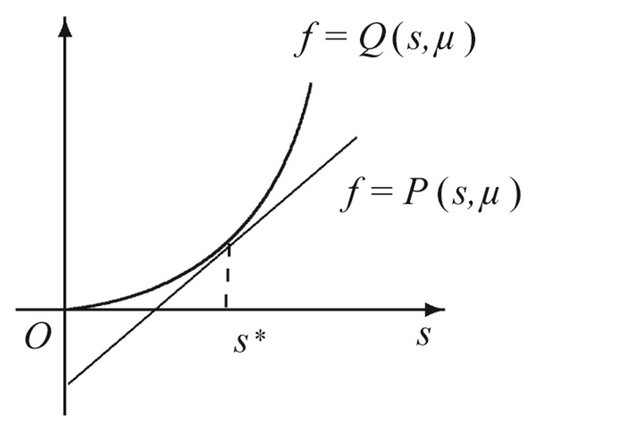 (c)
(c)
Figure 2. Location between the curves. (a) μ ∈ R11∪R12; (b) μ ∈ R21; (c) μ ∈ R22.
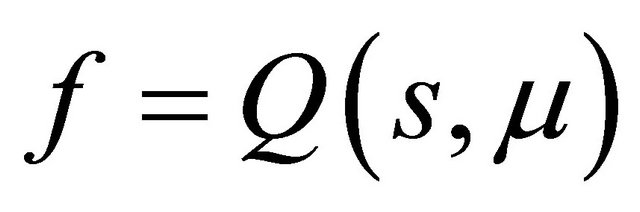 , that is to solve
, that is to solve

and , concretely,
, concretely,
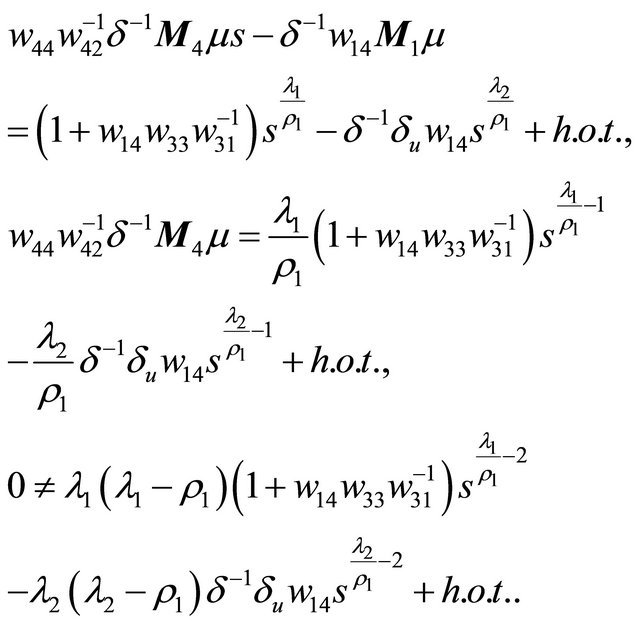 (3.2)
(3.2)
Then the tangent point

as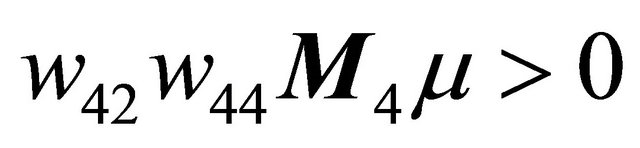 . Combining the first equation of (3.2) with the tangent point, we obtain the double periodic orbit bifurcation surface
. Combining the first equation of (3.2) with the tangent point, we obtain the double periodic orbit bifurcation surface
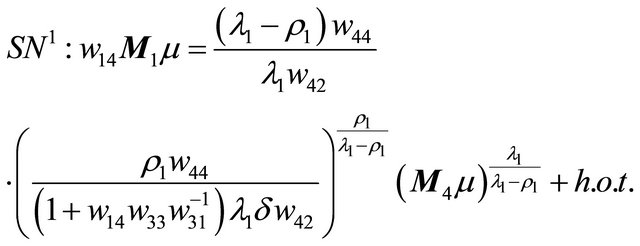
in the region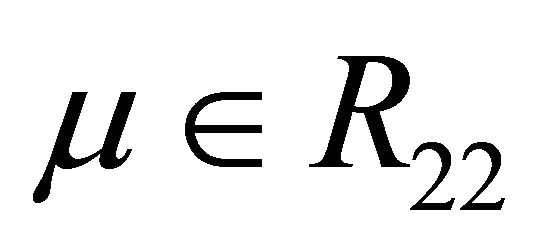 . At the same time, when
. At the same time, when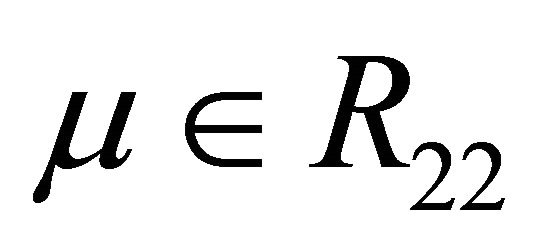 , the line
, the line 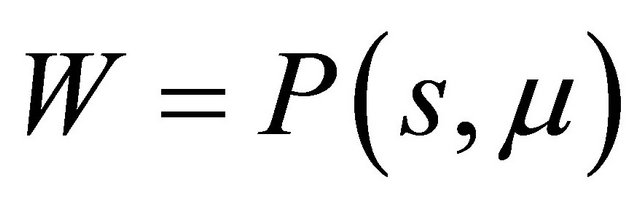 lies under the curve
lies under the curve , see Figure 2(c), so if
, see Figure 2(c), so if  increases, the line must intersects the curve at two sufficiently small positive points, therefore system (1.1) undergos two 1-periodic orbits. Then the proof is complete.
increases, the line must intersects the curve at two sufficiently small positive points, therefore system (1.1) undergos two 1-periodic orbits. Then the proof is complete.
Theorem 3.3 Suppose that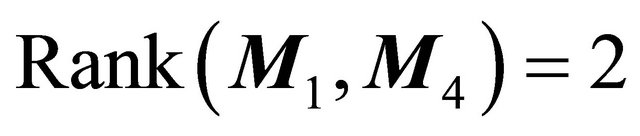 , then system (1.1) has only one 1-homoclinic orbit near
, then system (1.1) has only one 1-homoclinic orbit near ![]() in the region
in the region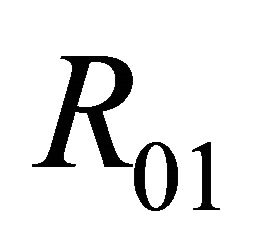 ; has only one 1-periodic orbit near
; has only one 1-periodic orbit near ![]() in the region
in the region ; has exactly one 1-homoclinic orbit and one 1-periodic orbit near
; has exactly one 1-homoclinic orbit and one 1-periodic orbit near ![]() in the region
in the region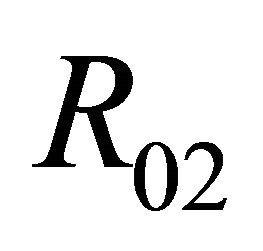 ; has not any 1-periodic orbit or 1-homoclinic orbit in the region
; has not any 1-periodic orbit or 1-homoclinic orbit in the region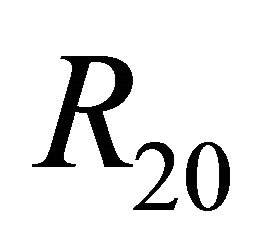 .
.
Proof When
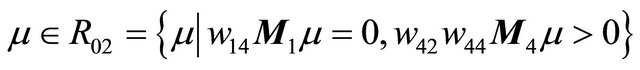 ,
,
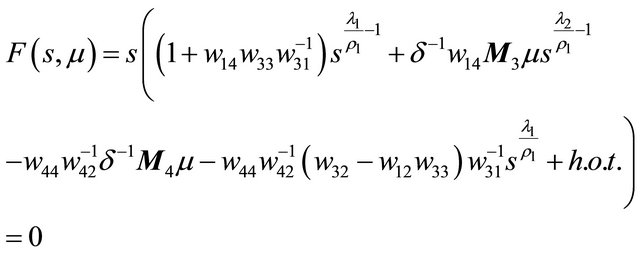
has always two solutions 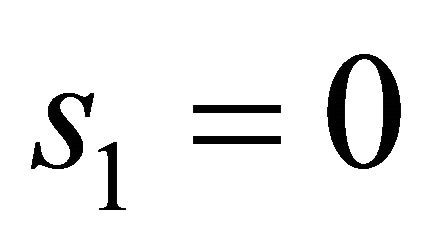 and
and

or has only a zero solution 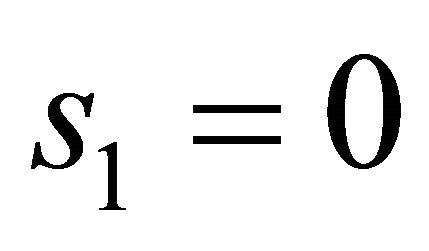 for
for
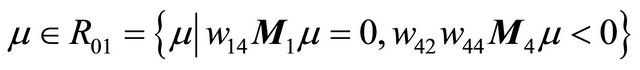 .
.
While for
 apparently the line
apparently the line  is horizontal. So
is horizontal. So  gives merely a solution
gives merely a solution
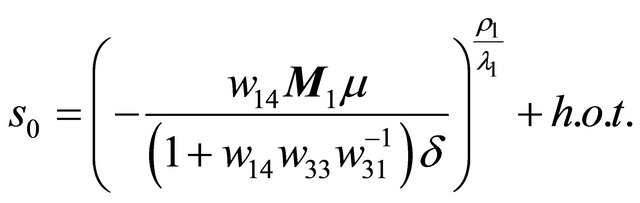 .
.
The last conclusion is obvious for
 .
.
In the following, we study the case . Then (3.1) is
. Then (3.1) is
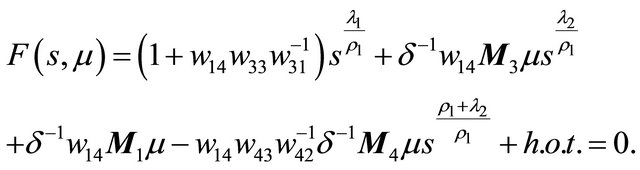
Similar to the proof of Theorem 3.1 and 3.3, we have Theorem 3.4 Suppose that , then in the region
, then in the region , system (1.1) has a unique 1-periodic orbit near
, system (1.1) has a unique 1-periodic orbit near![]() ; in the region
; in the region , system (1.1) has not any 1-periodic orbit.
, system (1.1) has not any 1-periodic orbit.
Proof Redefine
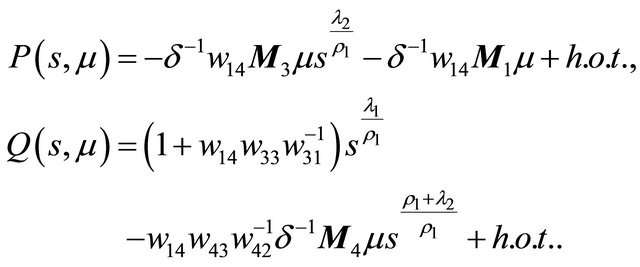
By studying the relationship between the curves 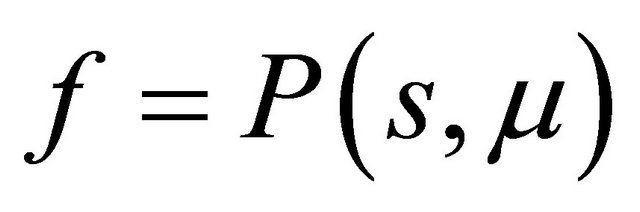 and
and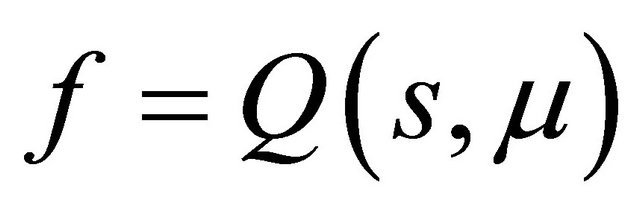 , it is easy to get the main ideas, see Figure 3. Here
, it is easy to get the main ideas, see Figure 3. Here
 (a)
(a)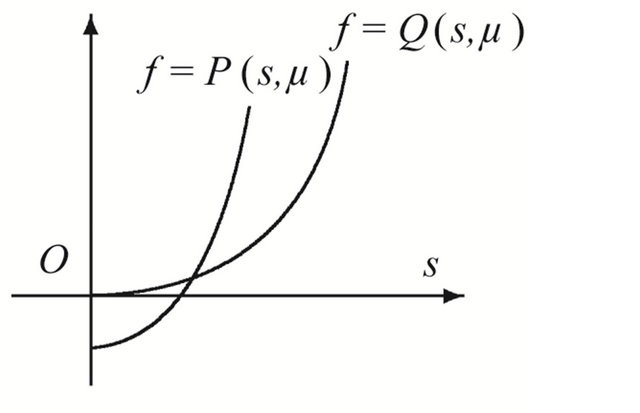 (b)
(b)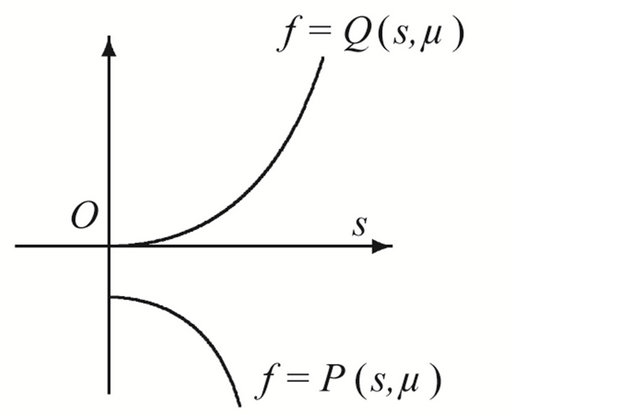 (c)
(c)
Figure 3. Location between the curves. (a) μ ∈ D12; (b) μ ∈ D21; (c) μ ∈ D22.
and
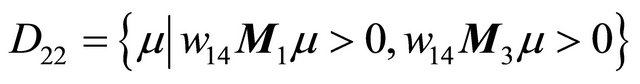 .
.
Remark 3.1 For the case , system (1.1) has no longer double 1-periodic orbits and the double 1-periodic orbit bifurcation surfaces.
, system (1.1) has no longer double 1-periodic orbits and the double 1-periodic orbit bifurcation surfaces.
Theorem 3.5 Suppose that , then system (1.1) has only one 1-homoclinic orbit near
, then system (1.1) has only one 1-homoclinic orbit near ![]() in the region
in the region ; has only one 1-periodic orbit near
; has only one 1-periodic orbit near ![]() in the region
in the region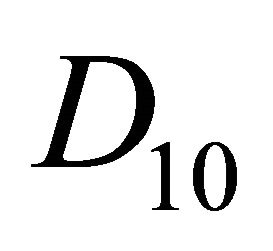 ; has not any 1-periodic orbit or 1-homoclinic orbit in the region
; has not any 1-periodic orbit or 1-homoclinic orbit in the region .
.
Proof Notice that
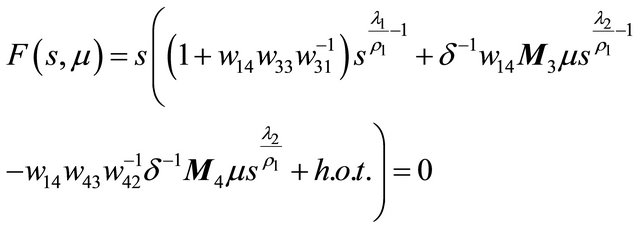
has only a zero solution 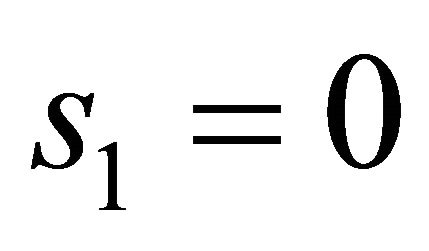 for
for
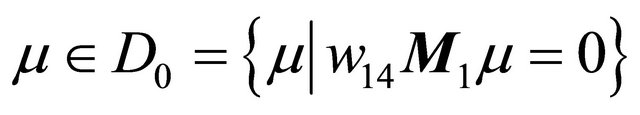 .
.
And the line 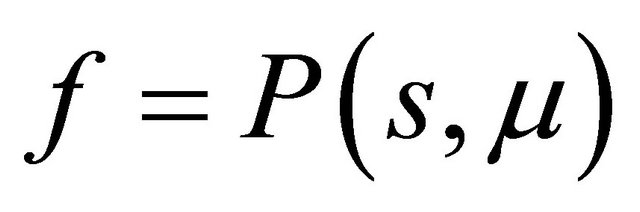 is horizontal for
is horizontal for
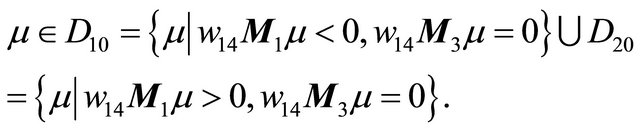
Thereby the conclusion is clear. We omit the details here.
4. Conclusion
The theoretical development of flip bifurcations indeed advanced much in recent years. More and more complicated cases with several flips or accompanied by transcritical bifurcation nowadays are discussed. This paper focuses on a kind of three flips homoclinic case with resonance and introduces an effective method to extend the study. By the analysis of the bifurcation equation, the existence of a double 1-periodic orbit, some 1-periodic orbits and 1-homoclinic orbits, and the coexistence conditions of 1-periodic orbits and 1-homoclinic orbits are given. From the study, one notice that different leading terms of the bifurcation equation may cause different bifurcation phenomena, so we can go further in the future work.
REFERENCES
- A. J. Homburg and B. Krauskopf, “Resonant Homoclinic Flip Bifurcations,” Journal of Dynamics and Differential Equations, Vol. 12, No. 4, 2000, pp. 807-850. doi:10.1023/A:1009046621861
- A. J. Homburg, H. Kokubu and M. Krupa, “The Cusp Horseshoe and Its Bifurcations in the Unfolding of an Inclinication-Flip Homoclinic Orbit,” Ergodic Theory and Dynamical Systems, Vol. 14, No. 4, 1994, pp. 667-693. doi:10.1017/S0143385700008117
- B. E. Oldeman, B. Krauskopf and A. R. Champneys, “Numerical Unfoldings of Codimension-Three Resonant Homoclinic Flip Bifurcations,” Nonlinearity, Vol. 14, No. 3, 2001, pp. 597-621. doi:10.1088/0951-7715/14/3/309
- C. A. Morales and M. J. Pacifico, “Inclination-Flip Homoclinic Orbits Arising from Orbit-Flip,” Nonlinearity, Vol. 14, No. 2, 2001, pp. 379-393. doi:10.1088/0951-7715/14/2/311
- E. Catsigeras and H. Enrich, “Homoclinic Tangencies Near Cascades of Period Doubling Bifurcations,” Annales de l'Institut Henri Poincare (C) Non Linear Analysis, Vol. 15, No. 3, 1998, pp. 255-299. doi:10.1016/S0294-1449(98)80119-4
- H. Kokubu, M. Komuru and H. Oka, “Multiple Homoclinic Bifurcations from Orbit Flip I. Sucessive Homoclinic Doublings,” International Journal of Bifurcation and Chaos, Vol. 6, No. 5, 1996, pp. 833-850. doi:10.1142/S0218127496000461
- J. A. Yorke and K. T. Alligood, “Cascades of Period Doubling Bifurcations: A Prerequisite for Horseshoes,” Bulletin of the American Mathematical Society, Vol. 9, 1983, pp. 319-322. doi:10.1090/S0273-0979-1983-15191-1
- M. V. Shashkov and D. V. Turaev, “An Existence Theorem of Smooth Nonlocal Center Manifolds for Systems Close to a System with a Homoclinic Loop,” Journal of Nonlinear Science, Vol. 9, No. 5, 1999, pp. 525-573. doi:10.1007/s003329900078
- M. Kisaka, H. Kokubu and H. Oka, “Supplement to Homoclinic-Doubling Bifurcation in Vector Fields,” Dynamical Systems, Longman, London, 1993, pp. 92-116.
- M. Kisaka, H. Kokubu and H. Oka, “Bifurcations to NHomoclinic Orbits and N-Periodic Orbits in Vector Fields,” Journal of Dynamics and Differential Equations, Vol. 5, No. 2, 1993, pp. 305-357. doi:10.1007/BF01053164
- F. Geng and D. Zhu, “Bifurcations of Generic Heteroclinic Loop Accompanied by Transcritical Bifurcation,” International Journal of Bifurcation and Chaos, Vol. 18, No. 4, 2008, pp. 1069-1083. doi:10.1142/S0218127408020847
- Q. Lu, Z. Qiao, T. Zhang and D. Zhu, “Heterodimensional Cycle Bifurcation with Orbit-Filp,” International Journal of Bifurcation and Chaos, Vol. 20, No. 2, 2010, pp. 491-508. doi:10.1142/S0218127410025569
- X. Liu, “Homoclinic Flip Bifurcations Accompanied by Transcritical Bifurcation,” Chinese Annals of Mathematics, Series B, Vol. 32, No. 6, 2011, pp. 905-916. doi:10.1007/s11401-011-0675-y
- T. Zhang and D. Zhu, “Homoclinic Bifurcation of Orbit Flip with Resonant Principal Eigenvalues,” Acta Mathematica Sinica, Vol. 22, No. 3, 2006, pp. 855-864.
- T. Zhang and D. Zhu, “Bifurcations of Homoclinic Orbit Connecting Two Nonleading Eigendirections,” Interna- tional Journal of Bifurcation and Chaos, Vol. 17, No. 3, 2007, pp. 823-836. doi:10.1142/S0218127407017574
[16] NOTES
[17] *Project supported by National Natural Science Foundation of China (Grant: 11126097) and by Scientific Research Foundation for the Returned Overseas Chinese Scholars, State Education Ministry.

