Applied Mathematics
Vol.4 No.5(2013), Article ID:31224,7 pages DOI:10.4236/am.2013.45103
On the Geometry of Curves in Minkowski 3-Space and Its Foldings
1Mathematics Department, Faculty of Science, Taibah University, Madinah, KSA
2Mathematics Department, Faculty of Science, Tanta University, Tanta, Egypt
Email: a_elahmady@hotmail.com, e-1.e-1@hotmail.com
Copyright © 2013 A. E. El-Ahmady, E. Al-Hesiny. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received November 13, 2012; revised April 4, 2013; accepted April 12, 2013
Keywords: Retractions; Deformation Retracts; Folding; Contraction; Minkowski 3-Space
ABSTRACT
We will introduce a new connection between some transformations and some aspects of differential geometry of some curves in Minkowski space. The concept of folding, retractions and contraction on some curves in Minkowski space will be characterized by using some aspects of differential geometry. Types of the deformation retracts of some curves in Minkowski 3-space are obtained. The relations between the foldings and the deformation retracts of some curves are deduced. The connections between some transformations and time like, space like, light like of some curves in Minkowski 3-space are also presented.
1. Introduction and Definitions
As is well known, the theory of deformation retract is always one of the interesting topics in Euclidian and Non-Euclidian space and it has been investigated from the various viewpoints by many branches of topology and differential geometry El-Ahmady [1-3].
Minkowski space is originally from the relativity in physics. In fact, a time like curve corresponds to the path of an observer moving at less than the speed of light, a light like curve corresponds to moving at the speed of light and a space like curve moving faster than light El-Ahmady [4,5].
The Minkowski 3-space  is the Euclidean 3-space
is the Euclidean 3-space  provided with the standard flat metric given by
provided with the standard flat metric given by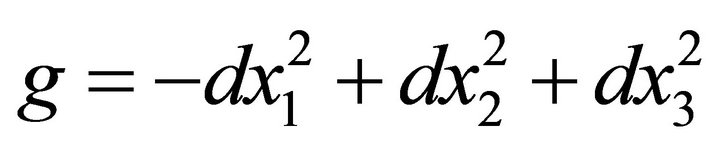 , where (x1, x2, x3) is a rectangular coordinate system of
, where (x1, x2, x3) is a rectangular coordinate system of . Since g is an indefinite metric, recall that a vector
. Since g is an indefinite metric, recall that a vector 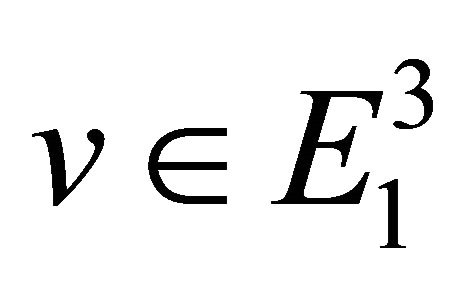 can have one of three Lorentzian causal characters, it can be space like if
can have one of three Lorentzian causal characters, it can be space like if 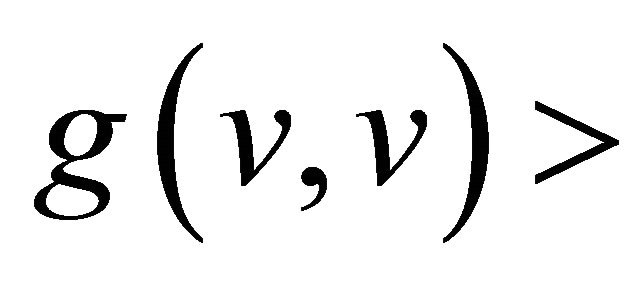 0 or
0 or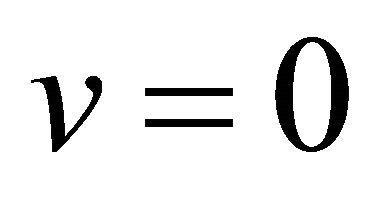 , time like if
, time like if 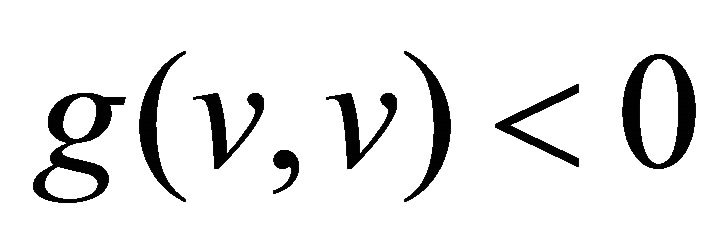 and light like if
and light like if 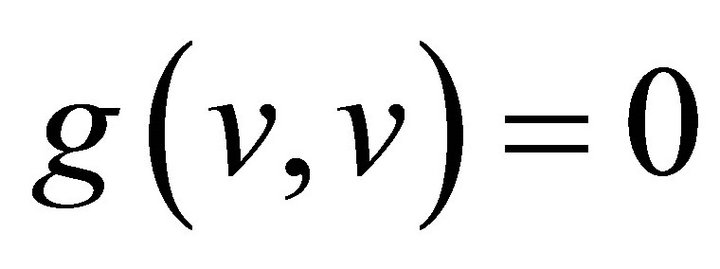 and
and . Similarly, an arbitrary curve
. Similarly, an arbitrary curve 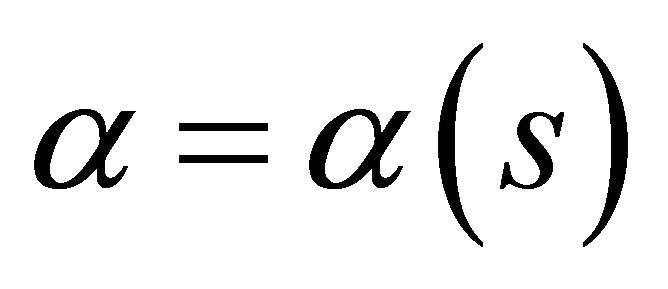 in
in  can locally be space like, time like or light like, if all of its velocity vectors
can locally be space like, time like or light like, if all of its velocity vectors  are respectively, space like, time like or light like respectively. A curve in Lorentzian space Ln is a smooth map
are respectively, space like, time like or light like respectively. A curve in Lorentzian space Ln is a smooth map 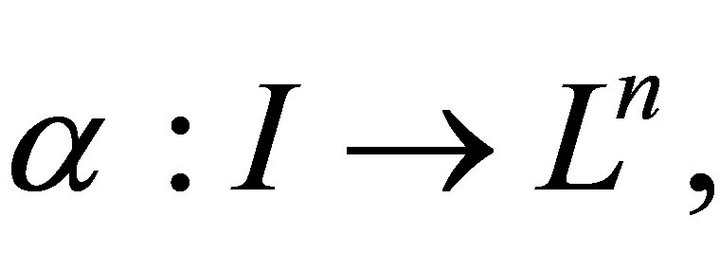 where I is the open interval in the real line
where I is the open interval in the real line . The interval has a coordinate system consisting of the identity map u of I. The velocity of
. The interval has a coordinate system consisting of the identity map u of I. The velocity of  at
at 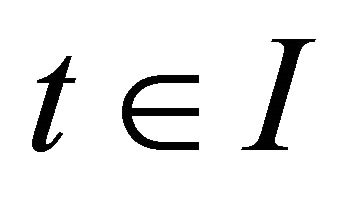 is
is .
.
A curve  is said to be regular if
is said to be regular if 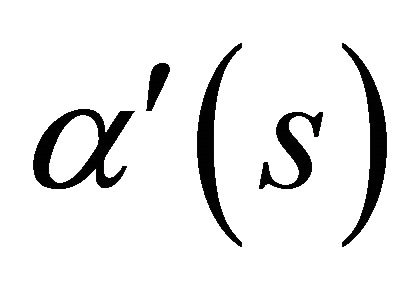 does not vanish for all
does not vanish for all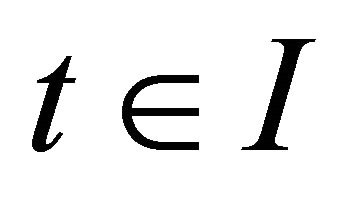 .
.  is space like if its velocity vectors
is space like if its velocity vectors 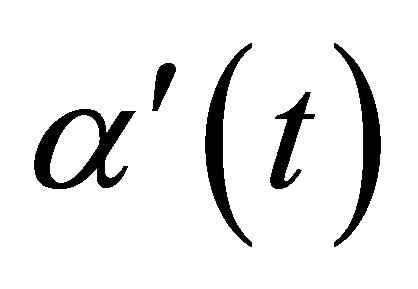 are space like for all
are space like for all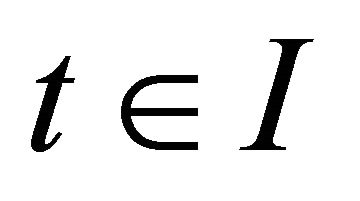 , similarly for timelike and null. If
, similarly for timelike and null. If  is a null curve, we can reparametrize it such that
is a null curve, we can reparametrize it such that 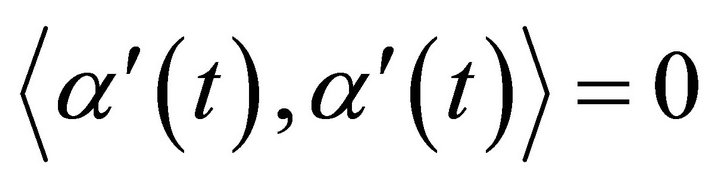 and
and 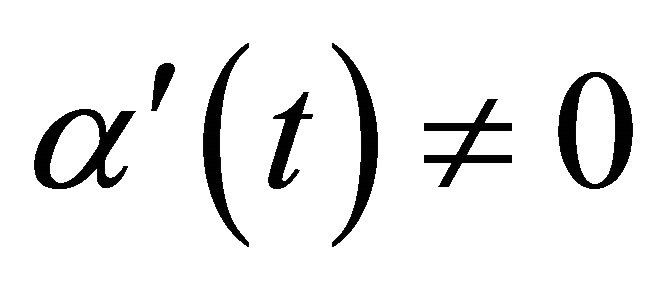 El-Ahmady [5].
El-Ahmady [5].
Most folding problems are attractive from a pure mathematical standpoint, for the beauty of the problems themselves. The folding problems have close connections to important industrial applications. Linkage folding has applications in robotics and hydraulic tube bending. Paper folding has application in sheet-metal bending, packaging, and air-bag folding El-Ahmady [6]. Following the great Soviet geometer El-Ahmady [5], also, used folding to solve difficult problems related to shell structures in civil engineering and aero space design, namely buckling instability El-Ahmady [7]. Isometric folding between two Riemannian manifold may be characterized as maps that send piecewise geodesic segments to a piecewise geodesic segments of the same length [8,9]. For a topological folding the maps do not preserves lengths El-Ahmady [8-10] i.e. A map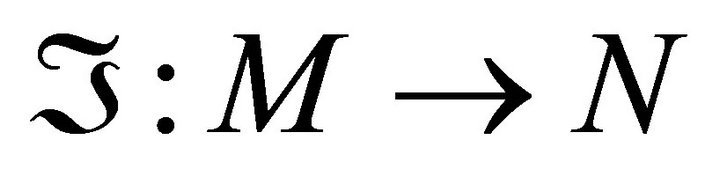 , where M and N are
, where M and N are  -Riemannian manifolds of dimension m, n respectively is said to be an isometric folding of M into N, iff for any piecewise geodesic path
-Riemannian manifolds of dimension m, n respectively is said to be an isometric folding of M into N, iff for any piecewise geodesic path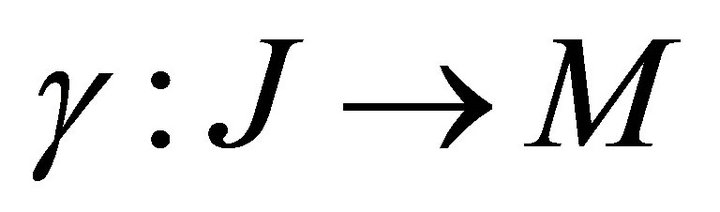 , the induced path
, the induced path 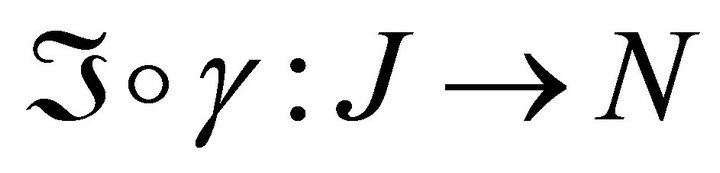 is a piecewise geodesic and of the same length as
is a piecewise geodesic and of the same length as . If
. If  does not preserve length, then
does not preserve length, then  is a topological folding El-Ahmady [10-12].
is a topological folding El-Ahmady [10-12].
A subset A of a topological space X is called a retract of X if there exists a continuous map 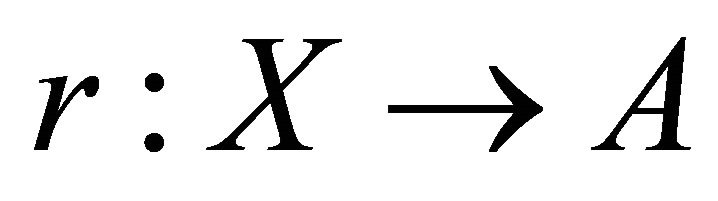 such that
such that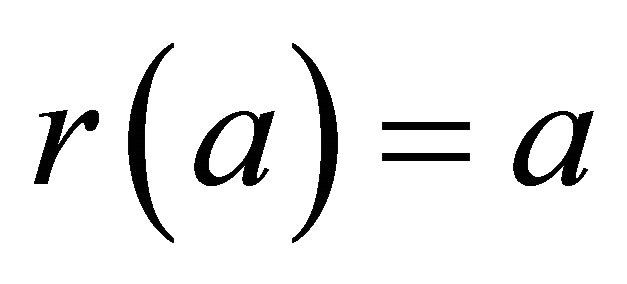 ,
,  , where A is closed and X is open. El-Ahmady [7-12] and Gregory [13]. This can be restated as follows. If
, where A is closed and X is open. El-Ahmady [7-12] and Gregory [13]. This can be restated as follows. If 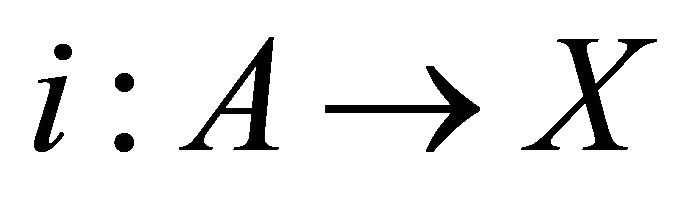 is the inclusion map, then
is the inclusion map, then 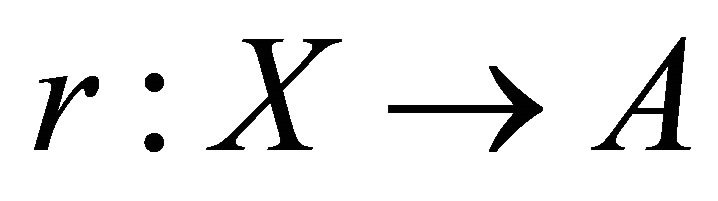 is a map such that
is a map such that 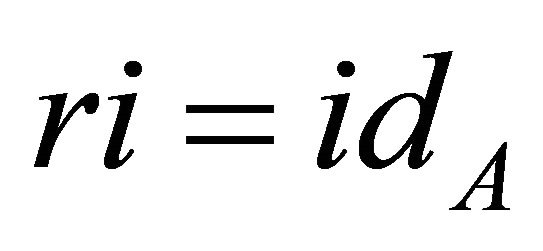 Miles [14] and Martin [15]. If, in addition
Miles [14] and Martin [15]. If, in addition , we call r a deformation retract and A a deformation retract of X Jeffrey [16] and John [17].
, we call r a deformation retract and A a deformation retract of X Jeffrey [16] and John [17].
2. Main Result
Let 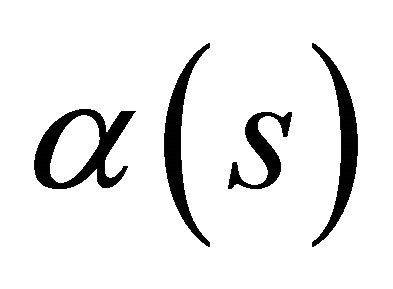 be a curve in the space-time
be a curve in the space-time , parameterized by arc length function
, parameterized by arc length function  Lopez [18] and Formiga [19]. Then for the unit speed curve
Lopez [18] and Formiga [19]. Then for the unit speed curve 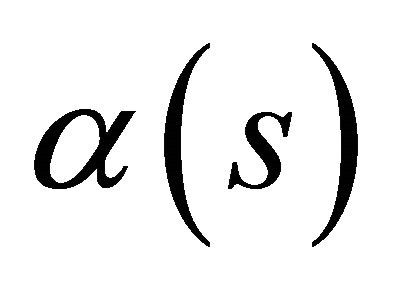 with non-null frame vectors the following Frenet equations are given in
with non-null frame vectors the following Frenet equations are given in
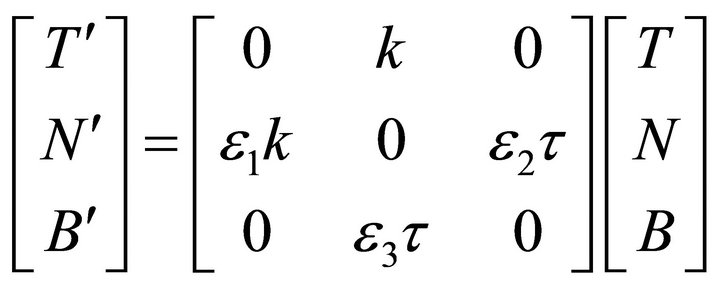 (1)
(1)
We write following subcases.
1) If  is space-like curve in
is space-like curve in , then T is a space-like vector. Thus, we distinguish according to N.
, then T is a space-like vector. Thus, we distinguish according to N.
Case 1: If N is space-like vector, then B is time-like vector, then 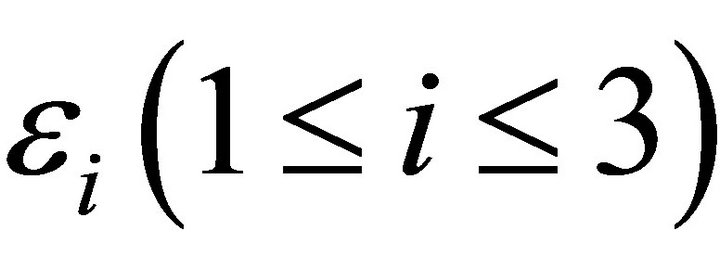 read
read ,
,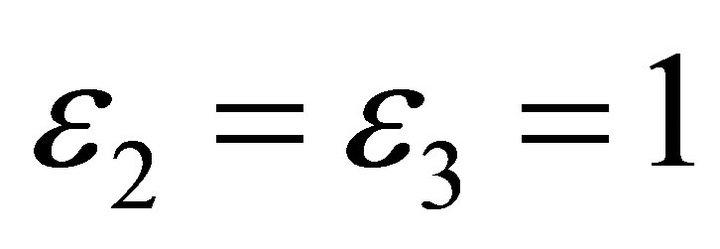 . And T, N and B are mutually orthogonal vectors satisfying equations,
. And T, N and B are mutually orthogonal vectors satisfying equations, 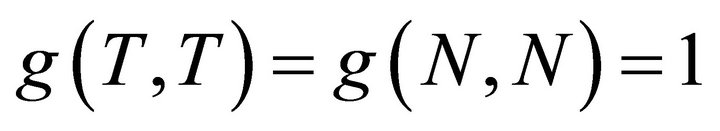 ,
,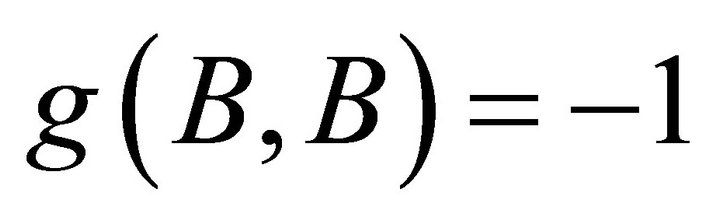 .
.
Case 2: 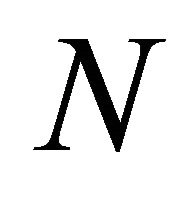 is time-like vector, then
is time-like vector, then 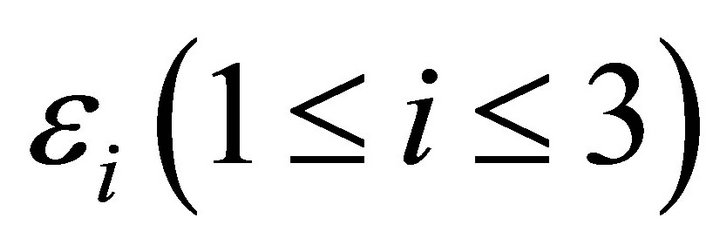 read
read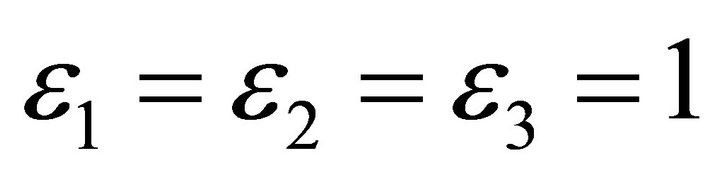 .
.
And T, N and B are mutually orthogonal vectors satisfying equations
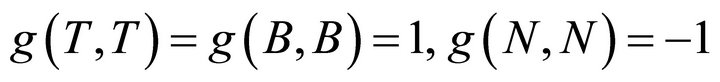 .
.
2) If 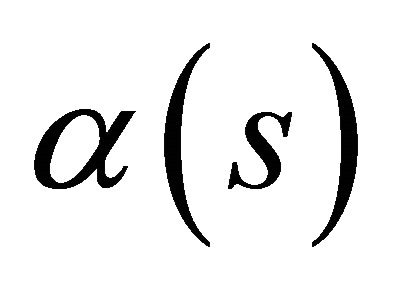 is time-like curve in
is time-like curve in , then T is timelike vector. Then
, then T is timelike vector. Then 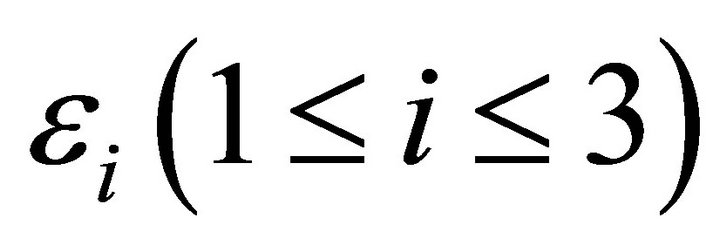 read
read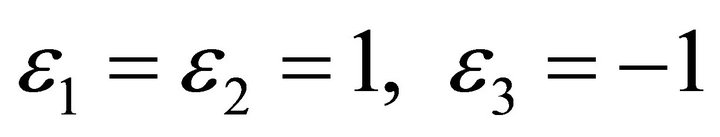 . And T, N and B are mutually orthogonal vectors satisfying equations,
. And T, N and B are mutually orthogonal vectors satisfying equations,
 .
.
3) If 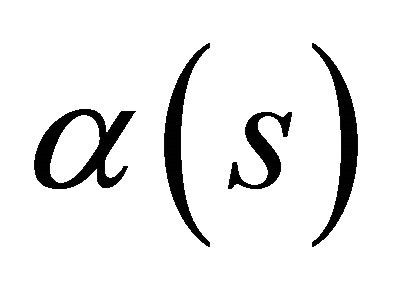 is light-like curve in
is light-like curve in 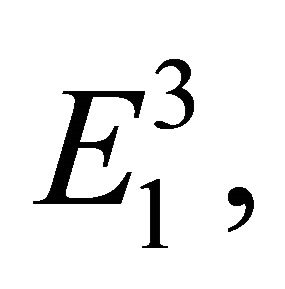 then the following Frenet equations are given in
then the following Frenet equations are given in
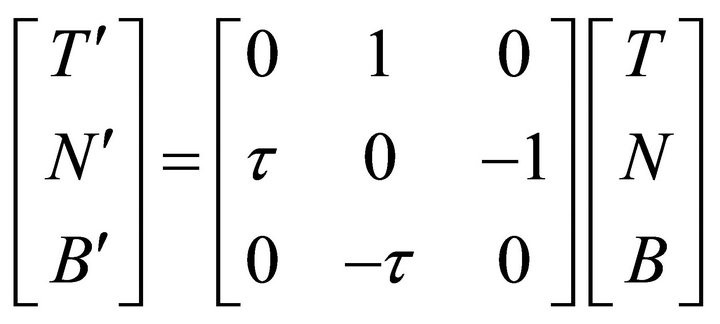 (2)
(2)
Also, if 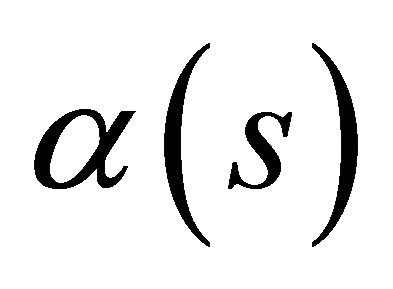 be a curve in the space-time
be a curve in the space-time , parameterized by arc length function
, parameterized by arc length function 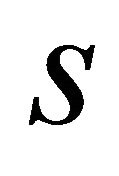 . Then for the unit speed curve
. Then for the unit speed curve 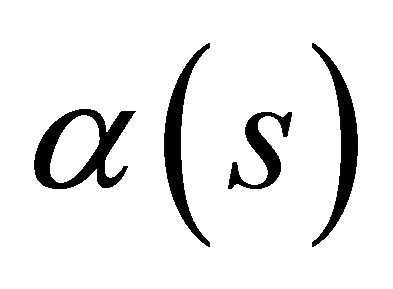 with non-null frame vectors the following Frenet equations are given in
with non-null frame vectors the following Frenet equations are given in
 (3)
(3)
Due to character of , we write following subcases.
, we write following subcases.
1) If 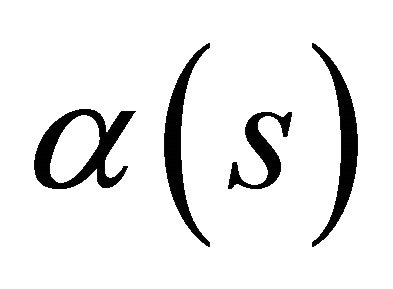 is space-like curve in
is space-like curve in , then T is a space-like vector. Thus, we distinguish according to N.
, then T is a space-like vector. Thus, we distinguish according to N.
Case 1: If N is space-like vector, then  can have two causal characters.
can have two causal characters.
Case 1.1:  is space-like vector, then
is space-like vector, then  read,
read, . And
. And 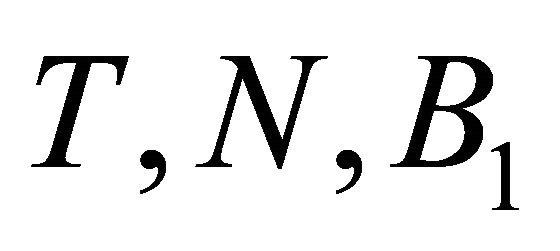 and
and 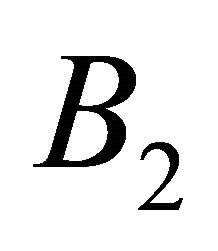 are mutually orthogonal vectors satisfying equations
are mutually orthogonal vectors satisfying equations

Case 1.2:  is time-like vector, then
is time-like vector, then 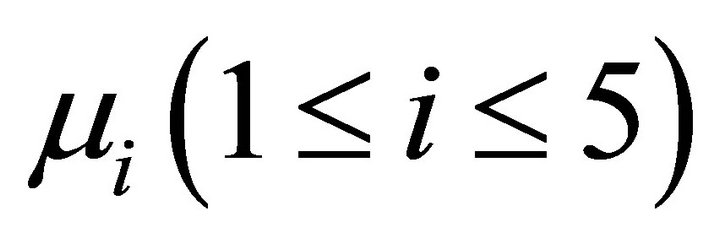 read
read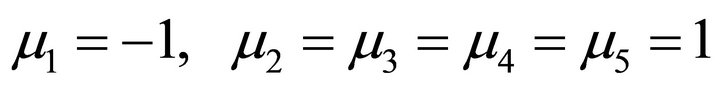 . And
. And 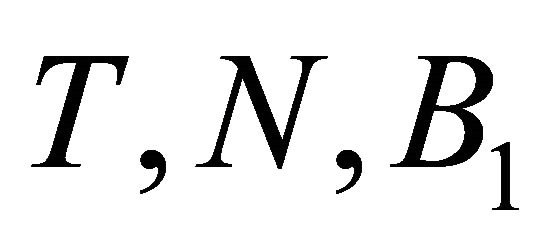 and
and 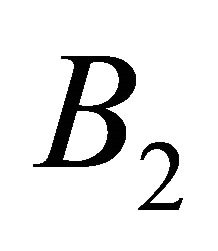 are mutually orthogonal vectors satisfying equations
are mutually orthogonal vectors satisfying equations
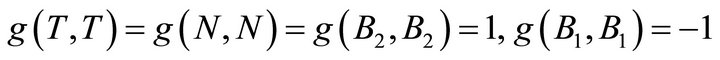
Case 2: N is time-like vector, then 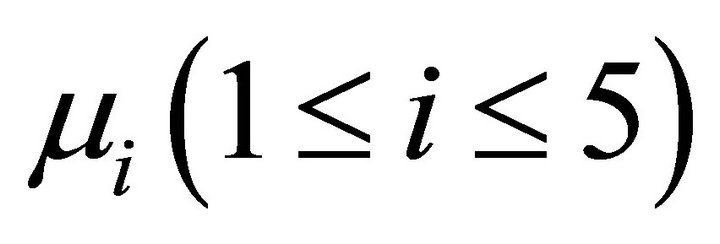 read
read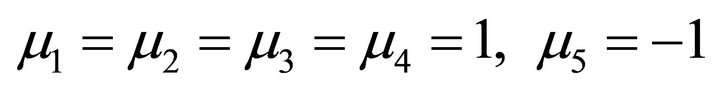 . And
. And 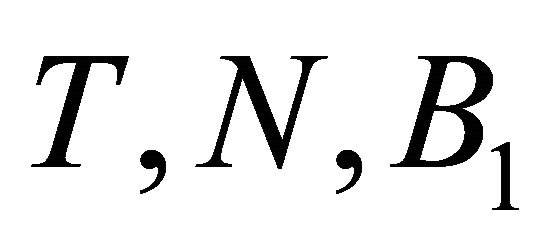 and
and 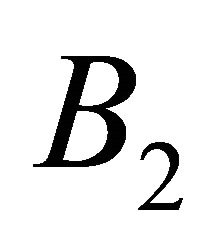 are mutually orthogonal vectors satisfying equations
are mutually orthogonal vectors satisfying equations
 .
.
2) If  is time-like curve in
is time-like curve in , then T is timelike vector. Then
, then T is timelike vector. Then  read
read ,
,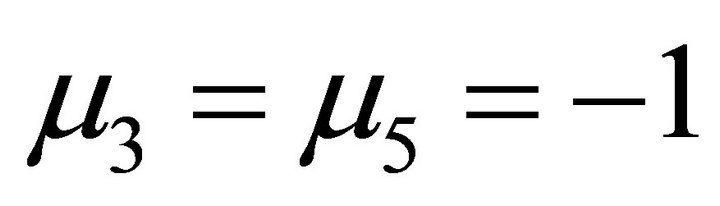 . And
. And  and
and  are mutually orthogonal vectors satisfying equations
are mutually orthogonal vectors satisfying equations

Hence, we can formulate the following theorems.
Theorem 1. Under the retraction, a spacelike curve and a timelike curve 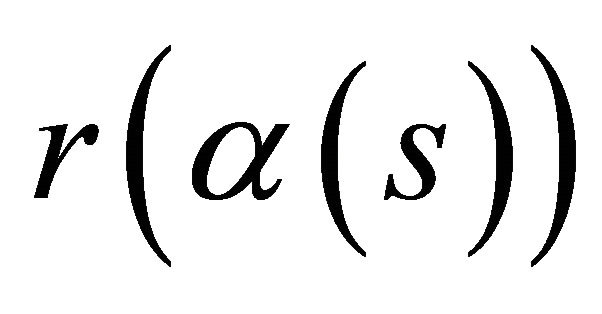 in the space-time
in the space-time  parameterized by arc length function s, where
parameterized by arc length function s, where  and with non-vanishing curvature, lies in ahyperplane if and only if the torsion vanishes identically.
and with non-vanishing curvature, lies in ahyperplane if and only if the torsion vanishes identically.
Proof. Suppose the curve 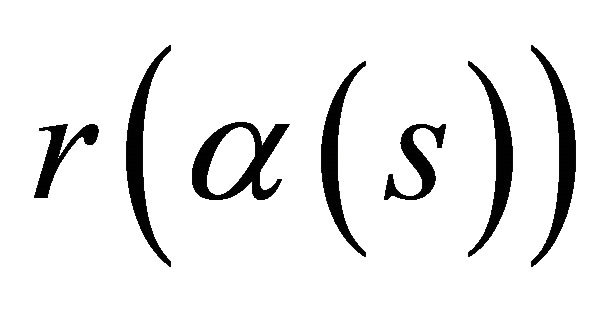 lies in a hyperplane. Let us assume that we can bring
lies in a hyperplane. Let us assume that we can bring 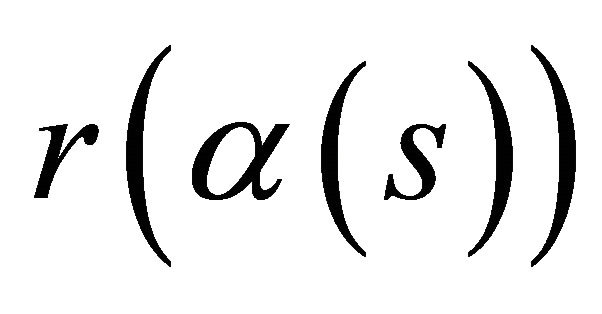 to lie in the
to lie in the 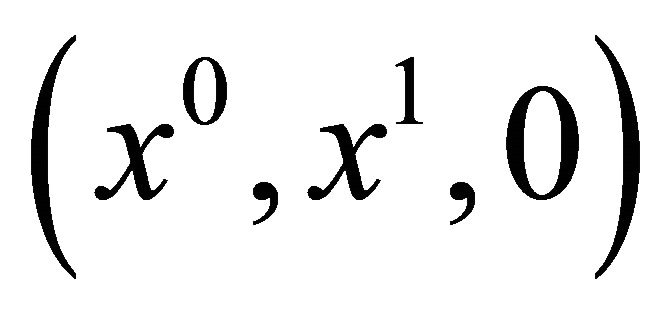 -hyperplane. Then the parametric equations of
-hyperplane. Then the parametric equations of 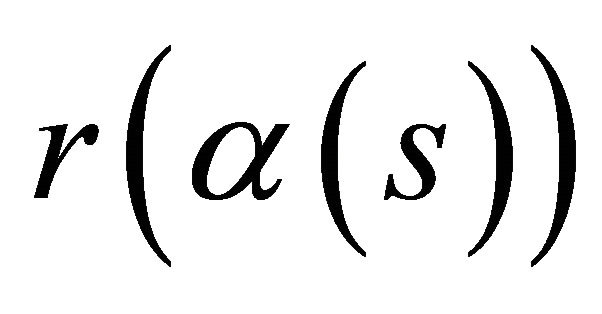 are of the form
are of the form
 . Let
. Let  denote the vectors of the canonical coordinate basis. Thus, in these coordinates,
denote the vectors of the canonical coordinate basis. Thus, in these coordinates,
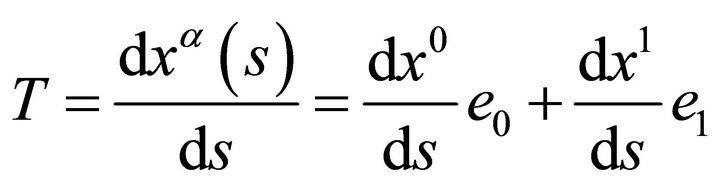
and
 .
.
From (1) we have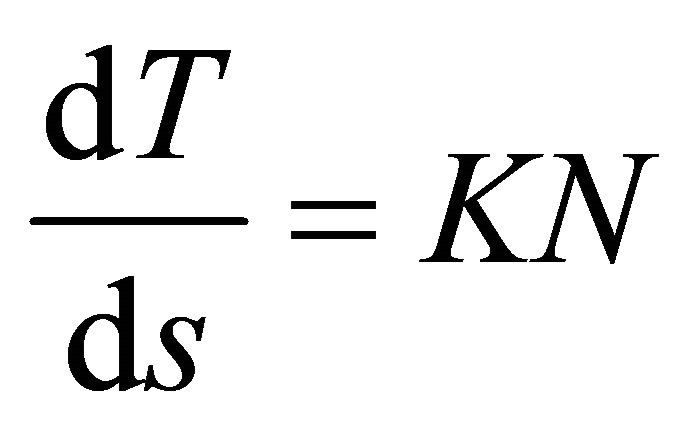 . Since
. Since 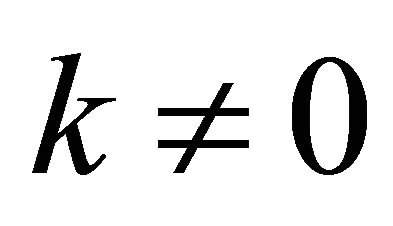 then
then 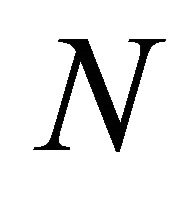 has no components in the
has no components in the 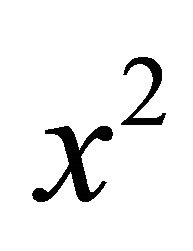 -direction, i.e.
-direction, i.e.
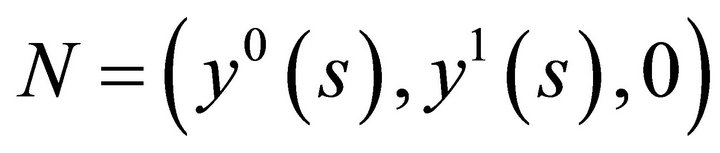 .
.
Thus, 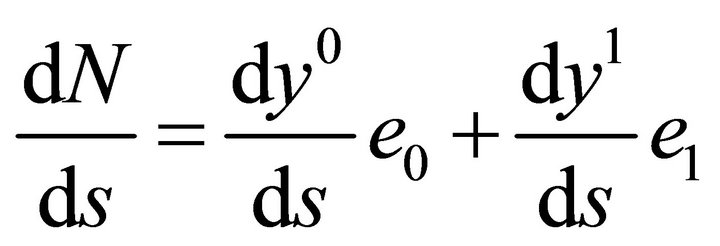 hence from the equation
hence from the equation 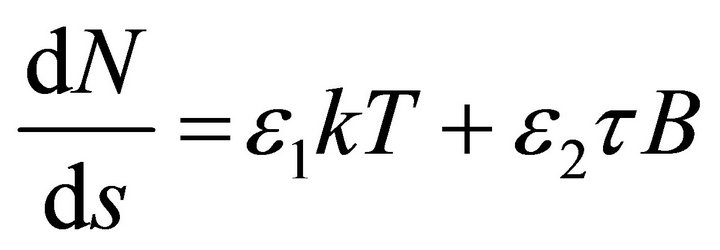 we conclude that
we conclude that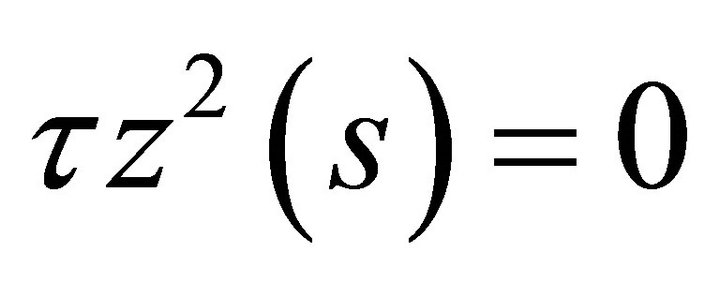 , where
, where
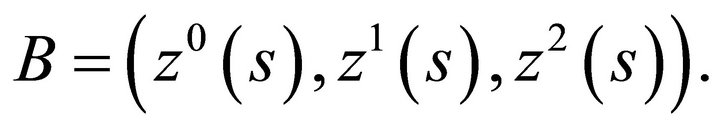 However,
However,  cannot be zero. Otherwise the set of vectors
cannot be zero. Otherwise the set of vectors 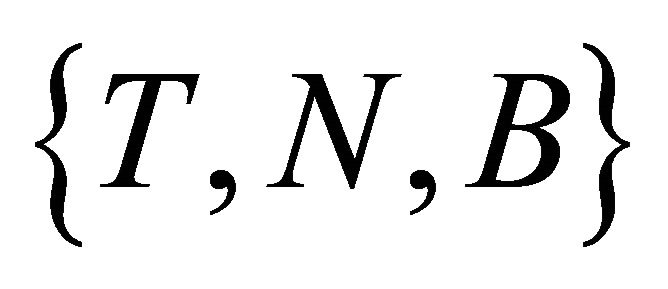 would not be linearly independent. Then
would not be linearly independent. Then ![]() must vanish.
must vanish.
Suppose that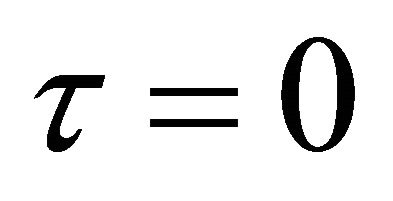 . Since
. Since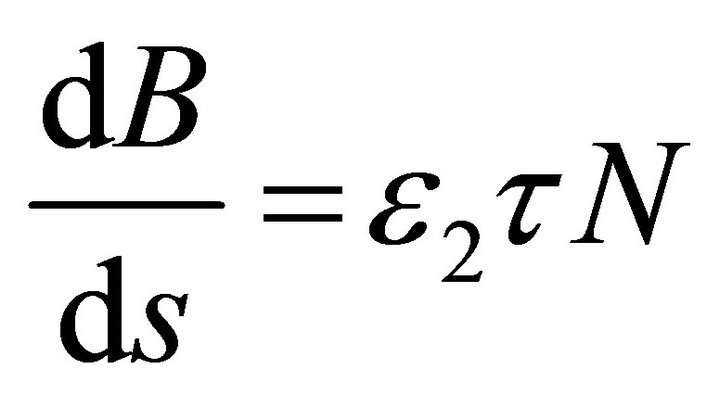 , then B is a constant vector. Let us conveniently choose our coordinate system in such a way that
, then B is a constant vector. Let us conveniently choose our coordinate system in such a way that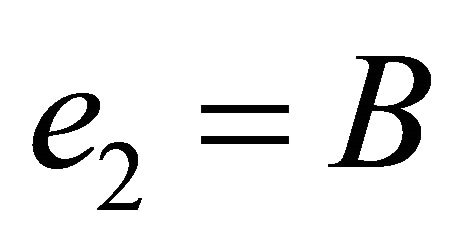 . Now, since T is orthogonal to B we must have
. Now, since T is orthogonal to B we must have , which means that
, which means that 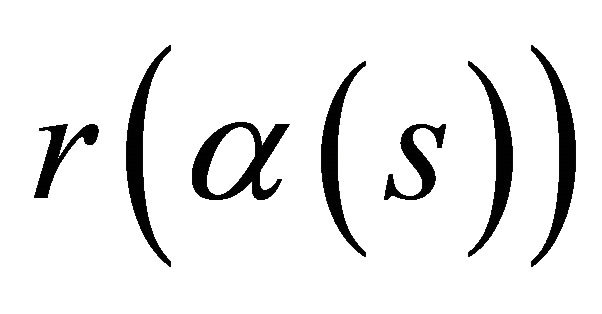 lies in the hyperplane
lies in the hyperplane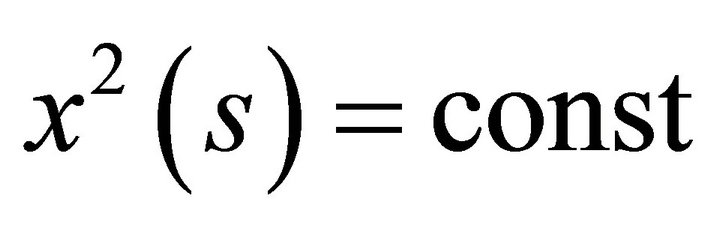 .
.
Corollary 1. Under the folding,  , a spacelike curve and a timelike curve
, a spacelike curve and a timelike curve 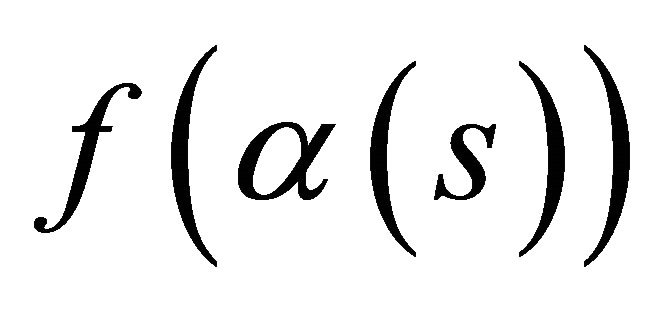 in the space-time
in the space-time  parametrized by arc length function s, with non-vanishing curvature, lies in a hyperplane if and only if the torsion vanishes identically.
parametrized by arc length function s, with non-vanishing curvature, lies in a hyperplane if and only if the torsion vanishes identically.
Theorem 2. Under the retraction, if the curve is a lightlike curve 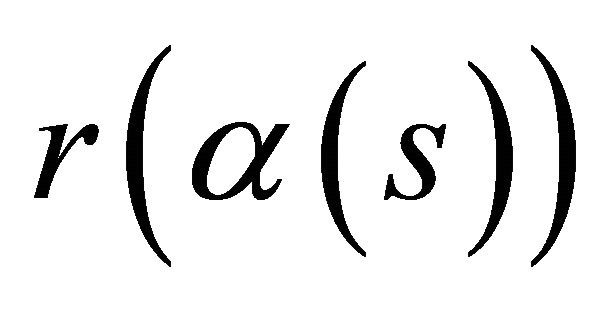 in the space-time
in the space-time  parameterized by arc length function s, where
parameterized by arc length function s, where 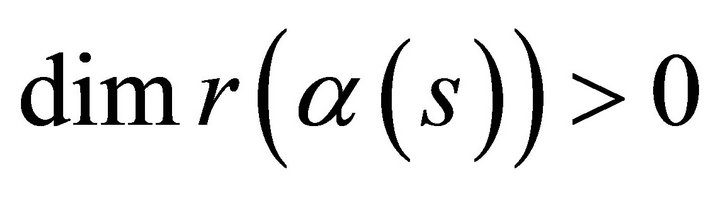 then the curve is not lies in a hyperplane.
then the curve is not lies in a hyperplane.
Proof. Suppose the curve 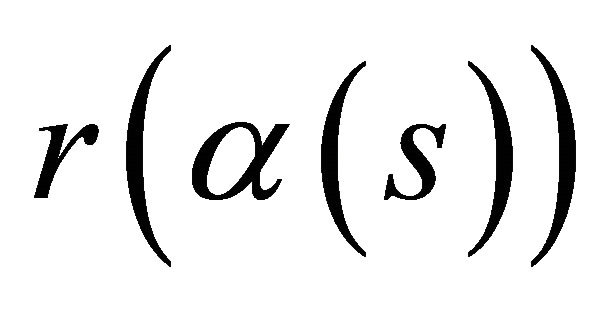 lies in a hyperplane. Let us assume that we can bring
lies in a hyperplane. Let us assume that we can bring  to lie in the
to lie in the  -hyperplane. Then the parametric equations of
-hyperplane. Then the parametric equations of 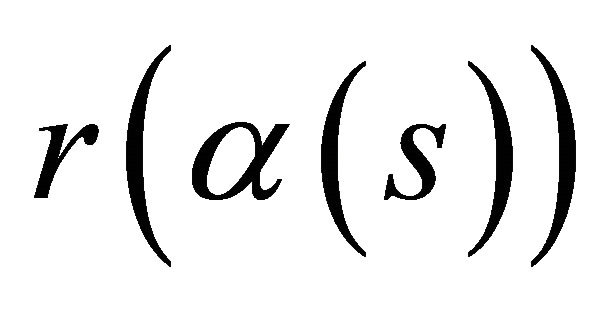 are of the form
are of the form
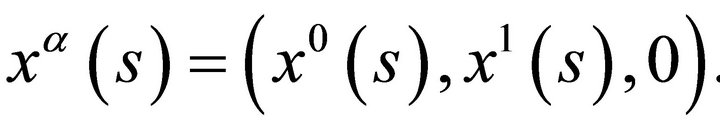 Let
Let 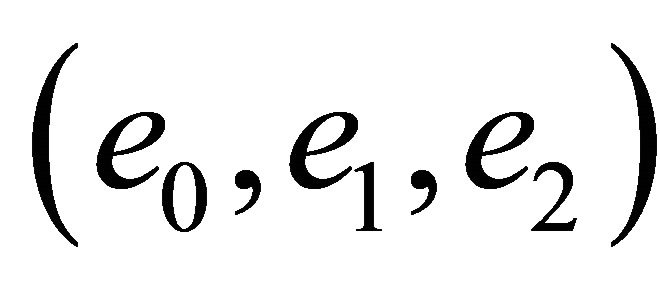 denote the vectors of the canonical coordinate basis. Thus, in these coordinates,
denote the vectors of the canonical coordinate basis. Thus, in these coordinates,
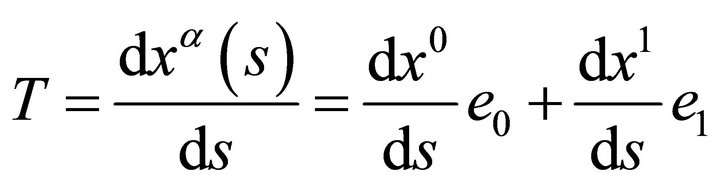
and
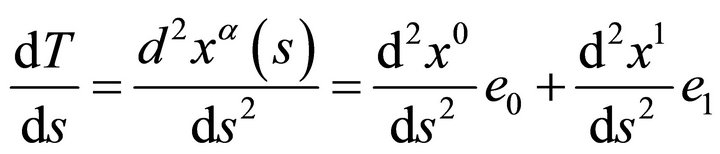 .
.
From (2) we have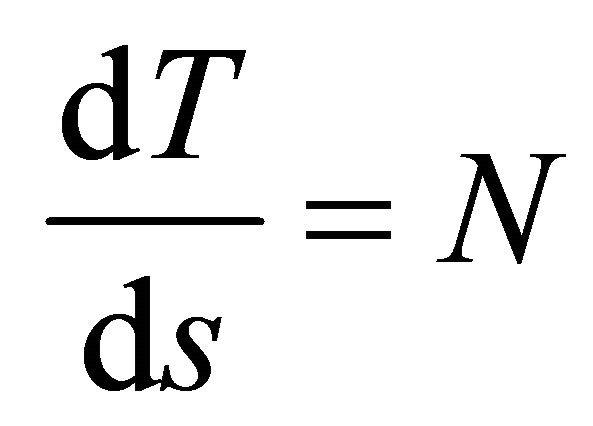 . Then
. Then  has no components in the
has no components in the 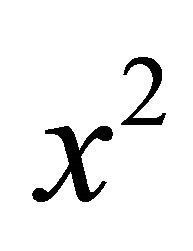 -direction, i.e.
-direction, i.e. 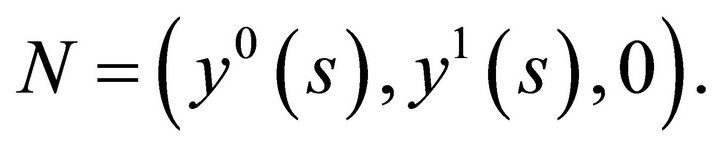 Thus,
Thus, 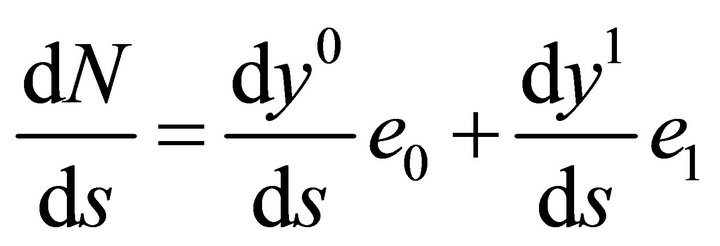 , hence from the equation
, hence from the equation , we conclude
, we conclude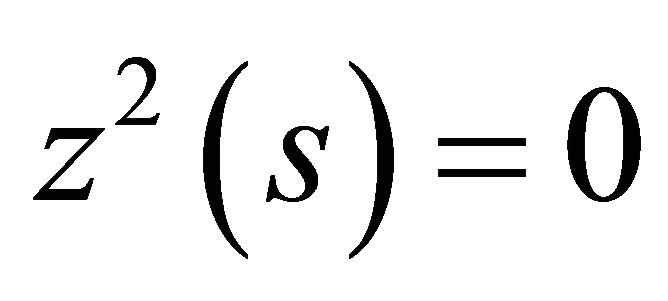 , where
, where
 . But
. But 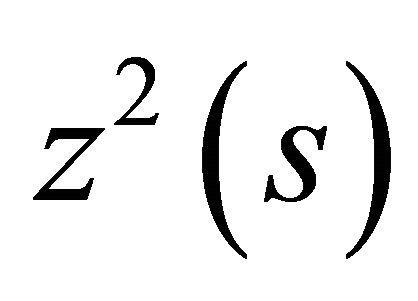 cannot be zero because the set of vectors
cannot be zero because the set of vectors 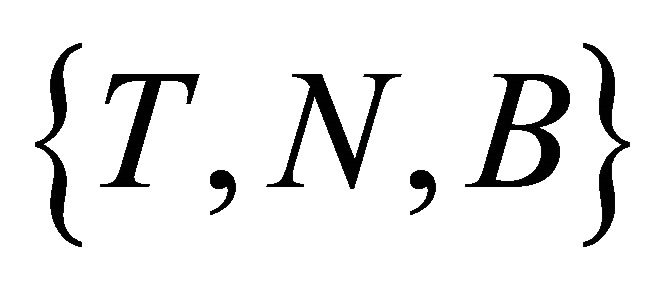 would not be linearly independent, then the curve is not lies in a hyperplane.
would not be linearly independent, then the curve is not lies in a hyperplane.
Corollary 2. Under the folding, 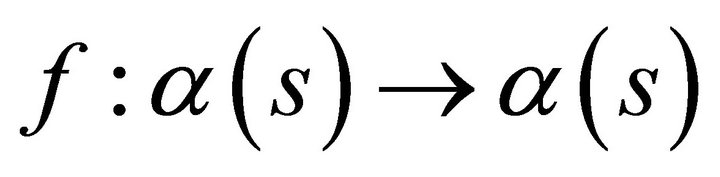 if the curve is a lightlike curve
if the curve is a lightlike curve 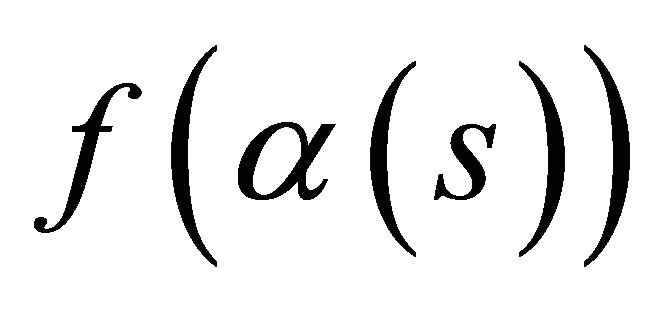 in the spacetime
in the spacetime  parameterized by arc length function s, then the curve is not lies in a hyperplane.
parameterized by arc length function s, then the curve is not lies in a hyperplane.
Theorem 3. Under the retraction, a spacelike curve and a timelike curve 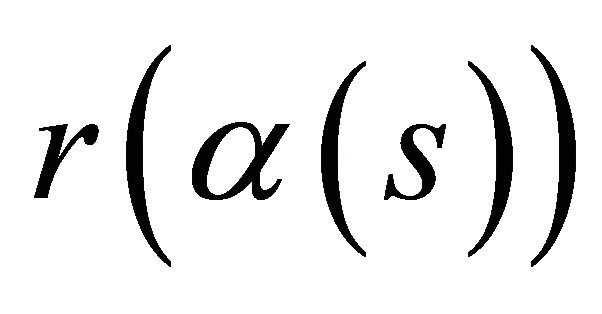 in the space-time
in the space-time  parameterized by arc length function s, where
parameterized by arc length function s, where 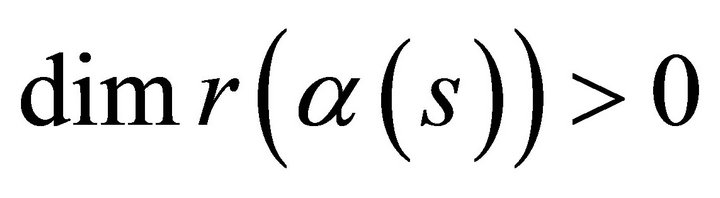 and with non-vanishing curvature, lies in ahyperplane if and only if the second torsion vanishes identically.
and with non-vanishing curvature, lies in ahyperplane if and only if the second torsion vanishes identically.
Proof. Let us start with the necessary condition. Suppose the curve 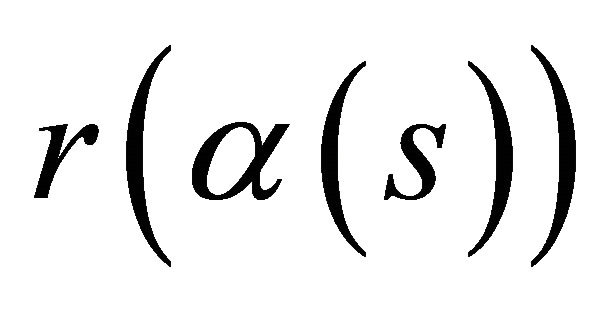 lies in a hyperplane. Let us assume that we can bring
lies in a hyperplane. Let us assume that we can bring 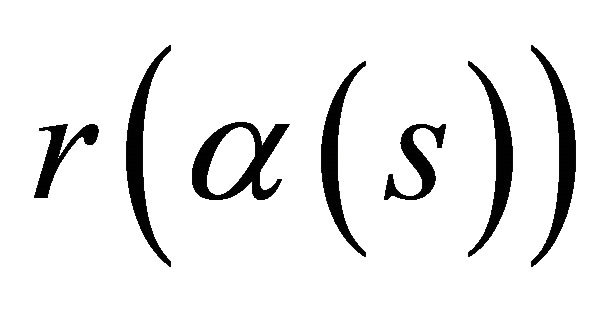 to lie in the
to lie in the
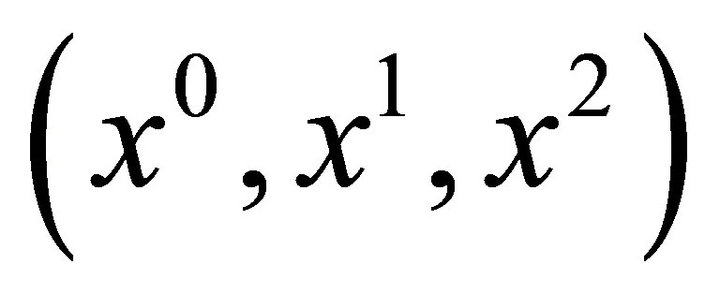 -hyperplane. Then the parametric equations of
-hyperplane. Then the parametric equations of 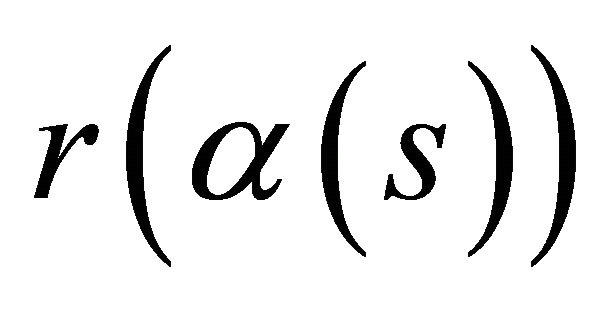 are of the form
are of the form
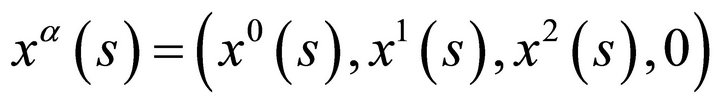 . Let
. Let 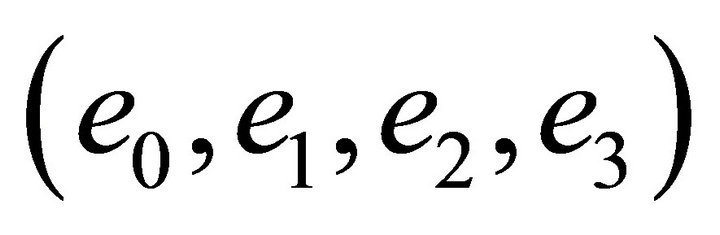 denote the vectors of the canonical coordinate basis. Thus, in these coordinates,
denote the vectors of the canonical coordinate basis. Thus, in these coordinates,
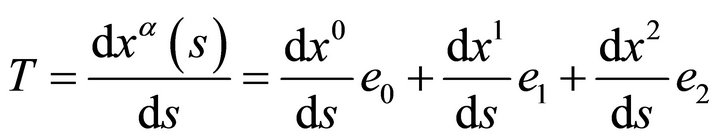
and
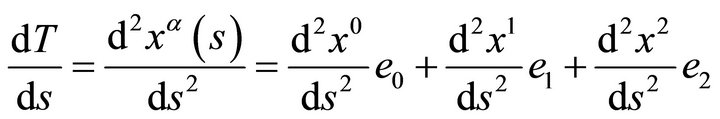 .
.
From (3) we have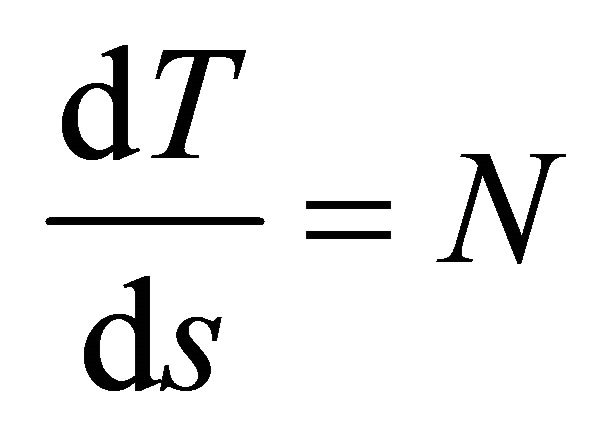 . Since
. Since 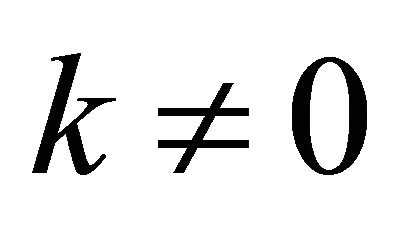 then N has no components in the
then N has no components in the  -direction, i.e.
-direction, i.e.
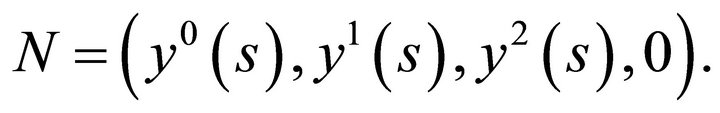
Thus,  , hence from the equation
, hence from the equation 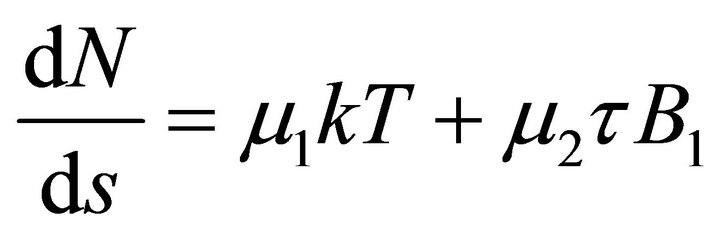 and we conclude that
and we conclude that
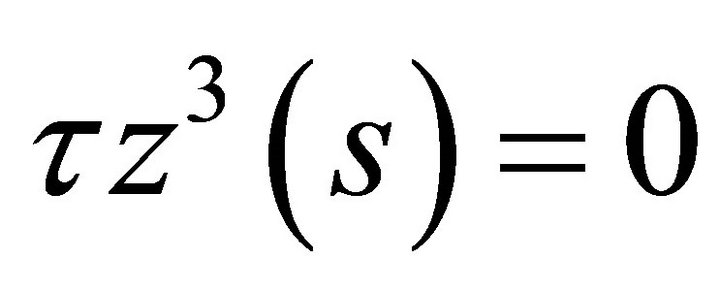 , where
, where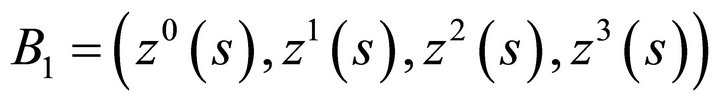 . If
. If , then
, then  also must vanish, for in this case
also must vanish, for in this case  is chosen to be constant. If
is chosen to be constant. If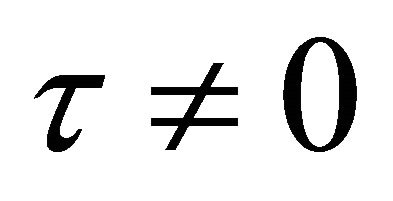 , then
, then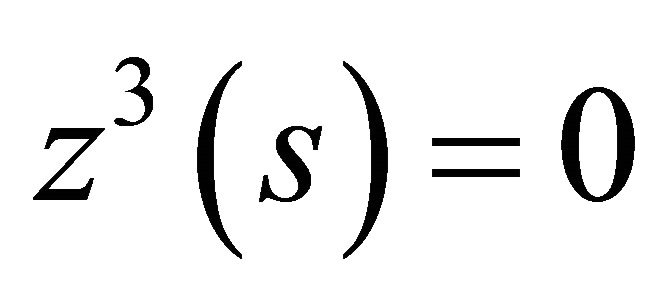 , hence
, hence 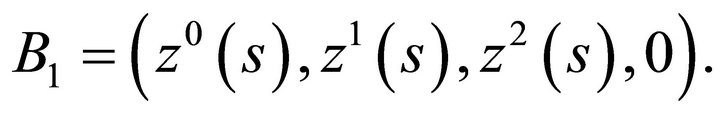 Also,
Also,
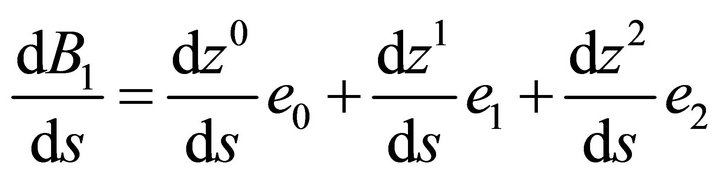 and the third Serret-Frenet equation
and the third Serret-Frenet equation 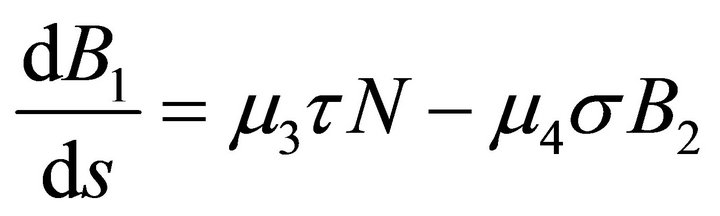 we are led to conclude that
we are led to conclude that , where
, where
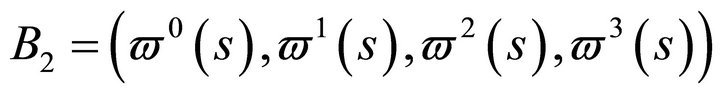 .
.
However, 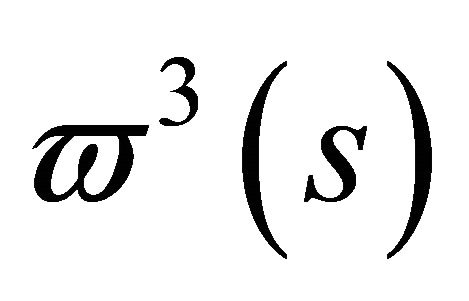 cannot be zero. Otherwise the set of vectors
cannot be zero. Otherwise the set of vectors 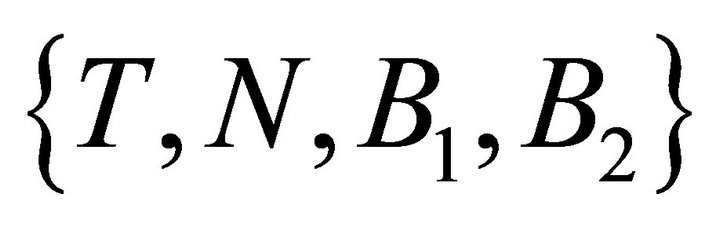 would not be linearly independent. Then
would not be linearly independent. Then  must vanish.
must vanish.
Suppose that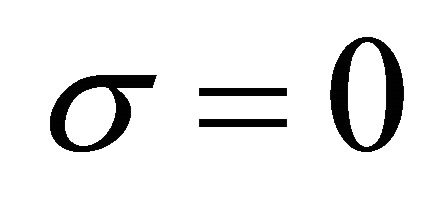 . Since
. Since , then
, then 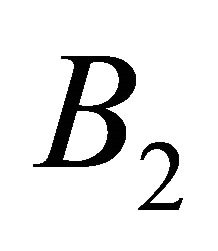
is a constant vector. Let us conveniently choose our coordinate system in such a way that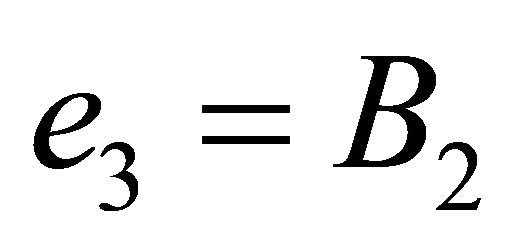 . Now, since
. Now, since 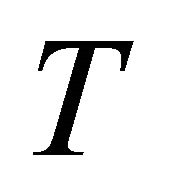 is orthogonal to
is orthogonal to 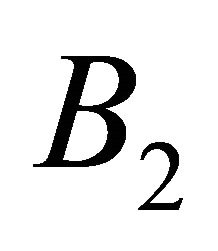 we must have
we must have , which means that
, which means that 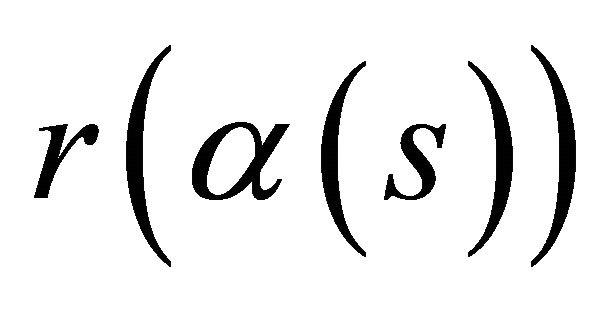 lies in the hyperplane
lies in the hyperplane .
.
Corollary 3. Under the contraction, a spacelike curve and a timelike curve 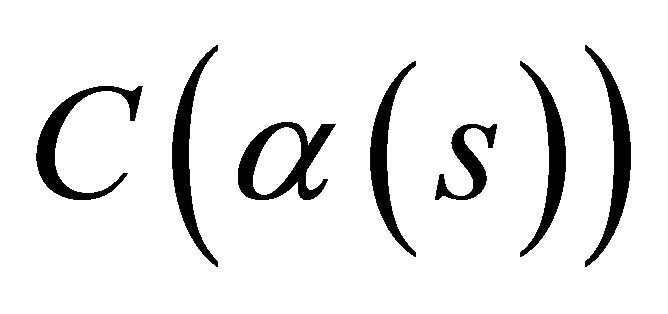 in the space-time
in the space-time  parameterized by arc length function s, where
parameterized by arc length function s, where  and with non-vanishing curvature, is lies in a hyperplane if the first and second torsions vanishes identically.
and with non-vanishing curvature, is lies in a hyperplane if the first and second torsions vanishes identically.
Corollary 4. Under the folding, a spacelike curve and a timelike curve 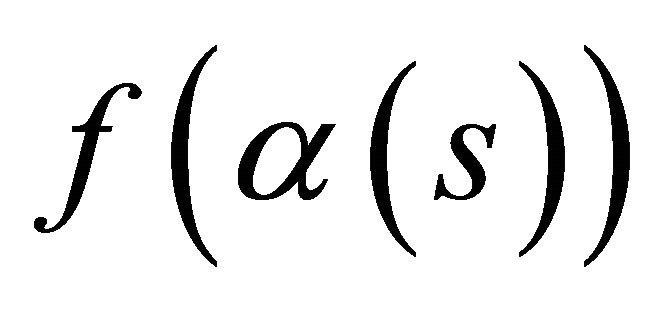 in the space-time
in the space-time  parameterized by arc length function s, with non-vanishing curvature, lies in a hyperplane if and only if the second torsion vanishes identically.
parameterized by arc length function s, with non-vanishing curvature, lies in a hyperplane if and only if the second torsion vanishes identically.
Corollary 5. Under the folding, 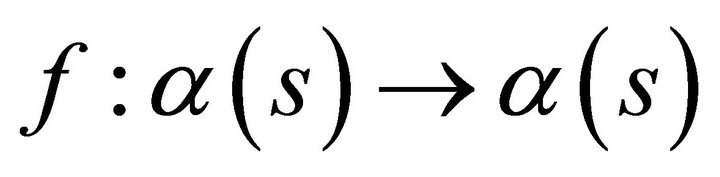 , a spacelike curve and a timelike curve
, a spacelike curve and a timelike curve 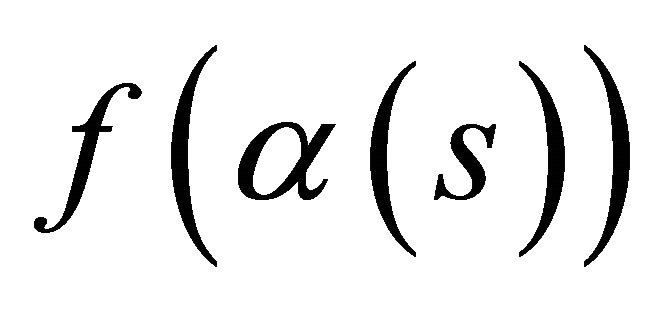 in the space-time
in the space-time  parameterized by arclength function s, with non-vanishing curvature, is lies in a hyperplane if the first and second torsions vanishes identically.
parameterized by arclength function s, with non-vanishing curvature, is lies in a hyperplane if the first and second torsions vanishes identically.
Theorem 4. Given differentiable functions 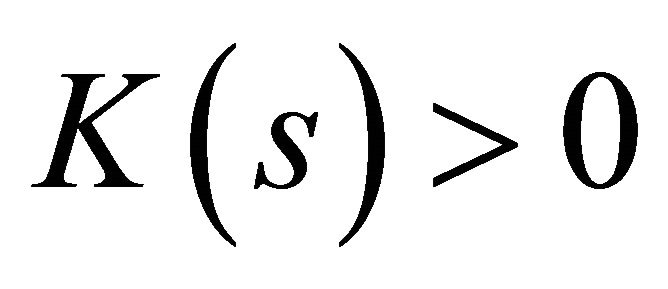 and
and 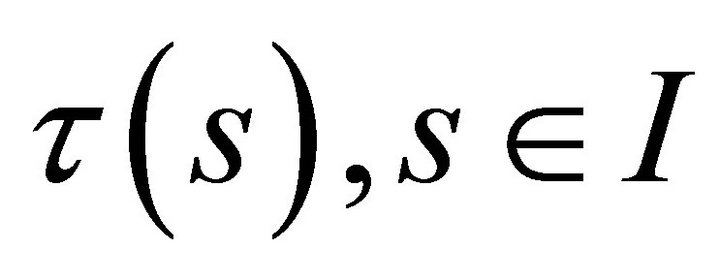 such that s is the arc length, there exists a regular parameterized spacelike curve under the folding with the spacelike vector N,
such that s is the arc length, there exists a regular parameterized spacelike curve under the folding with the spacelike vector N, 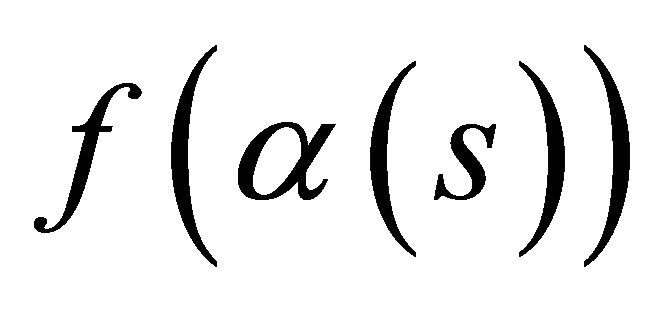 , in the space-time
, in the space-time . Also,
. Also, 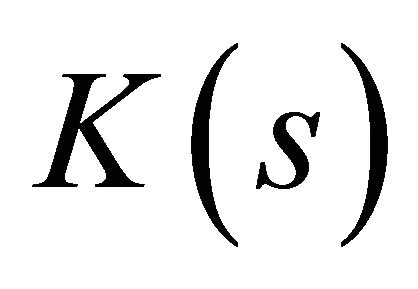 is the curvature and
is the curvature and 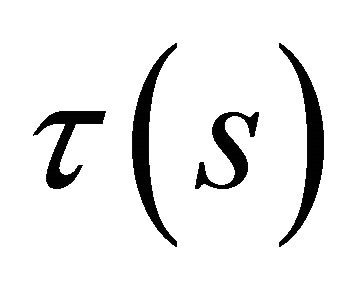 is the torsion of
is the torsion of . Moreover, any other spacelike curve
. Moreover, any other spacelike curve  with the spacelike vector
with the spacelike vector  satisfying the same conditions and
satisfying the same conditions and 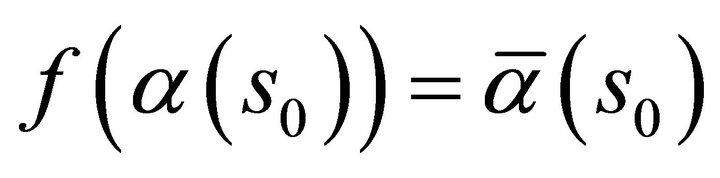 at
at  then
then
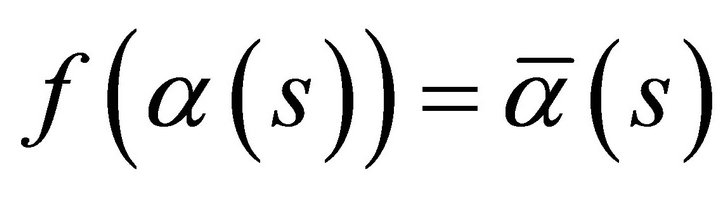 and the Frenet trihedrons of
and the Frenet trihedrons of  and
and 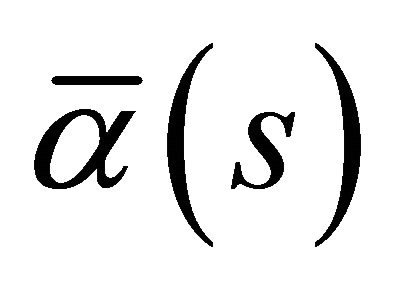 is identically.
is identically.
Proof. Now, assume that two curves 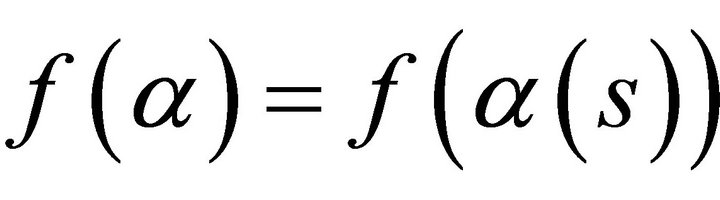 and
and 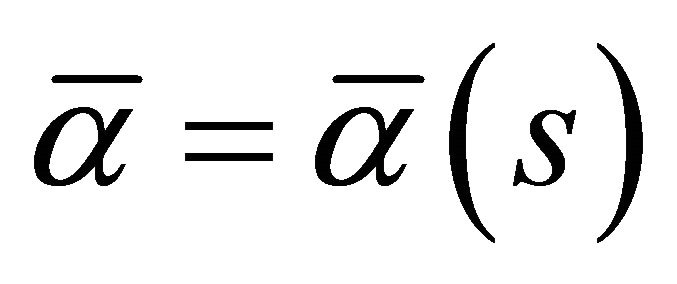 satisfy the conditions
satisfy the conditions 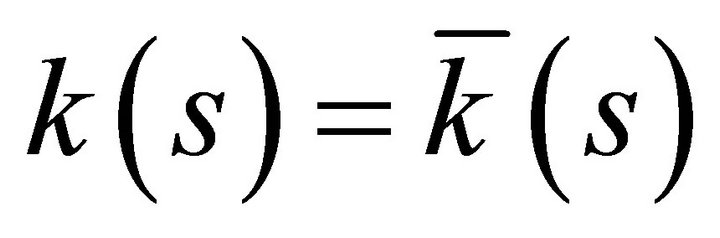 and
and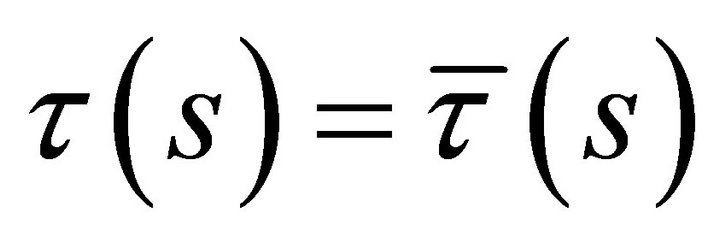 ,
,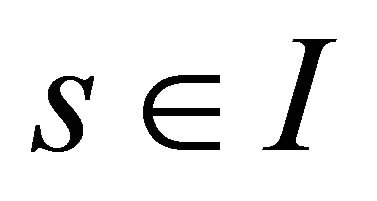 . Let T0, N0, B0 and
. Let T0, N0, B0 and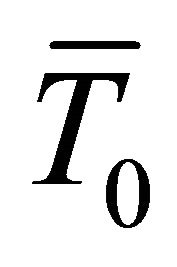 ,
, 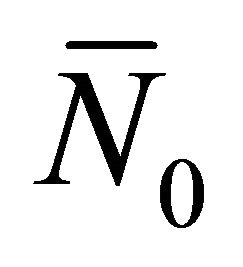 ,
, 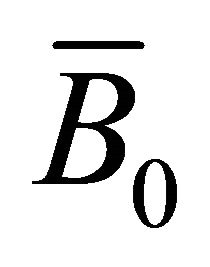 be the Frenet trihedrons of
be the Frenet trihedrons of  and
and 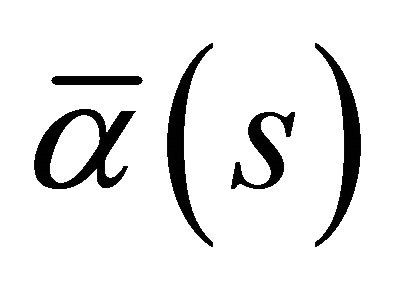 at
at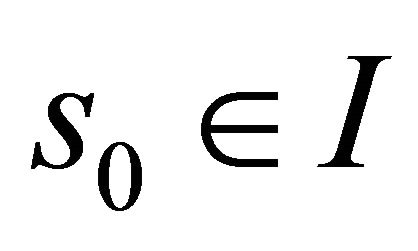 , respectively. Since
, respectively. Since 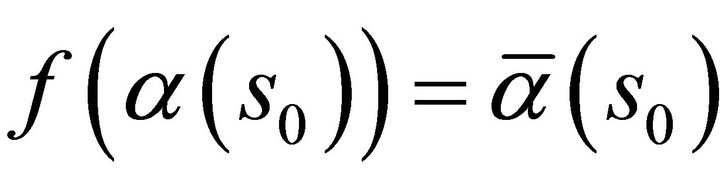 then
then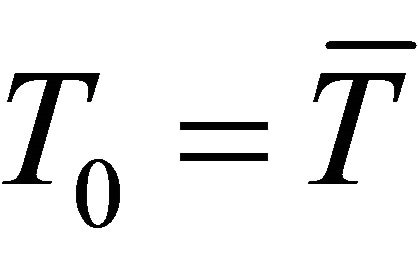 ,
, 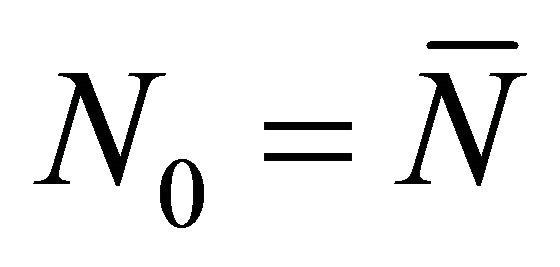 and
and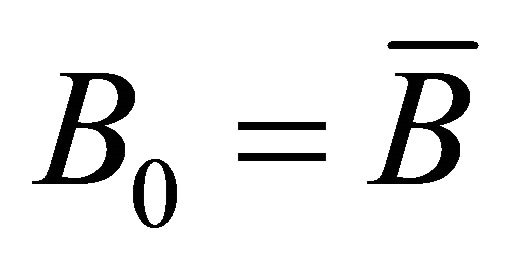 , where
, where ,
, 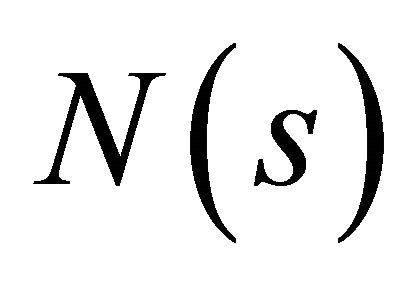 ,
,  and
and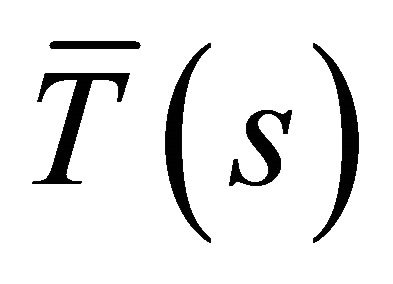 ,
, 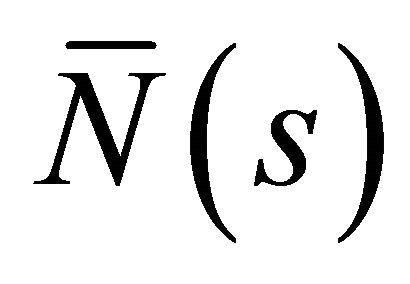 ,
, 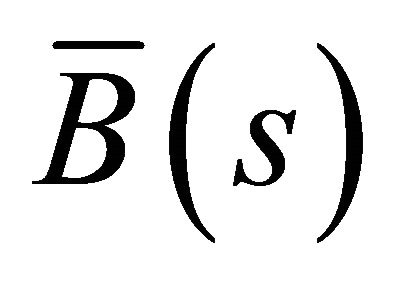 are the Frenet trihedrons of
are the Frenet trihedrons of 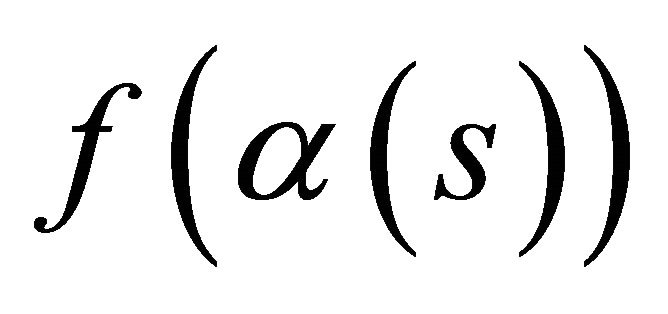 and
and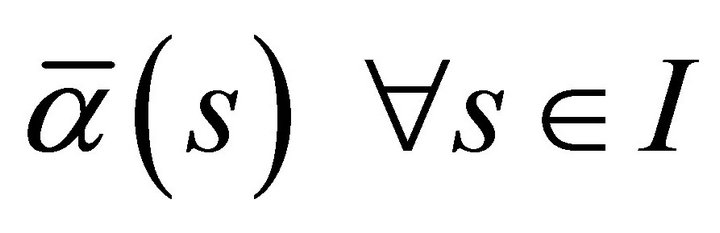 , respectively. We now observe, by using the Frenet equations at (1), that
, respectively. We now observe, by using the Frenet equations at (1), that

for all . Thus, the above expression is constant, and, since it is zero for
. Thus, the above expression is constant, and, since it is zero for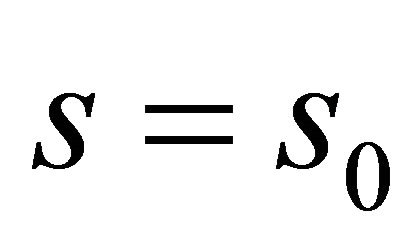 , it is identically zero. It follows that
, it is identically zero. It follows that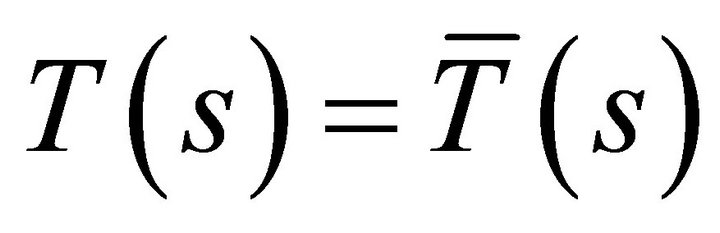 ,
, 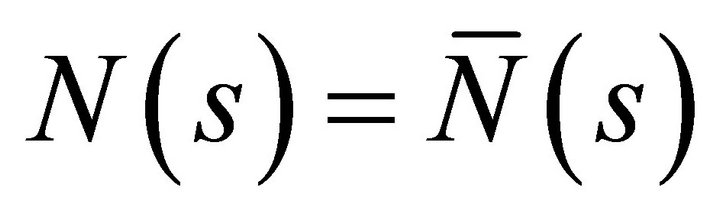 ,
, 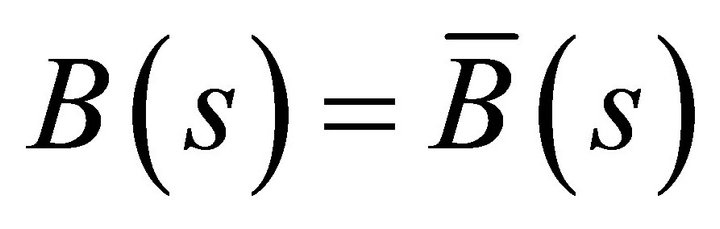 for all
for all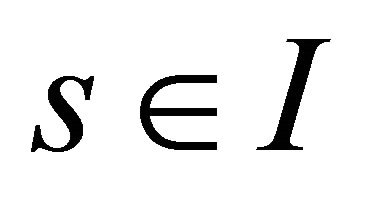 .
.
Since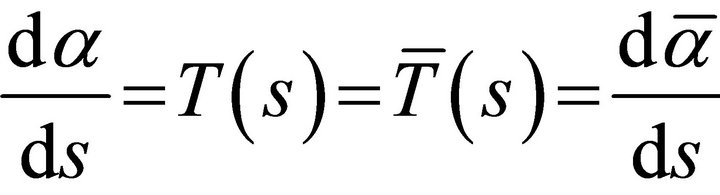 , we obtain
, we obtain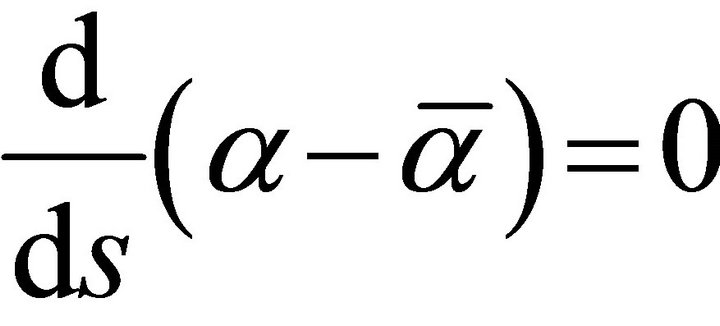 .
.
Thus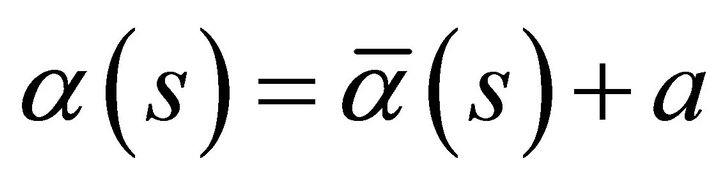 , where a is a constant vector. Since
, where a is a constant vector. Since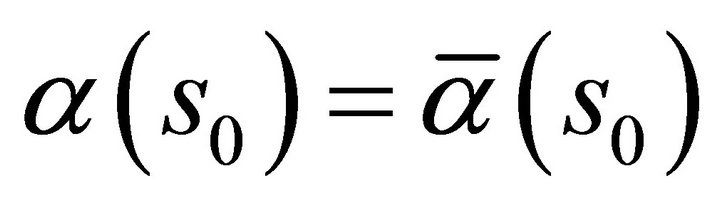 , we have
, we have ; hence,
; hence, 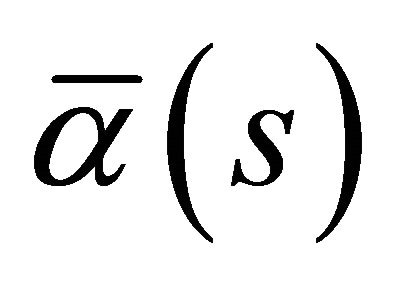
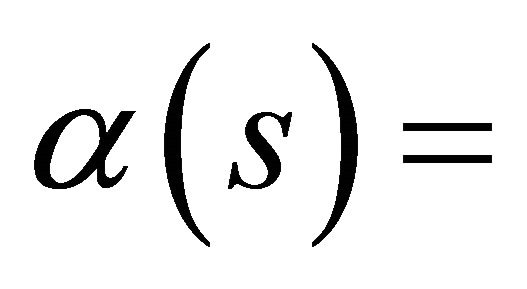 for all
for all .
.
Corollary 6. Given differentiable functions  and
and ,
, 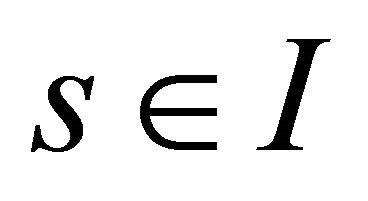 such that s is the arc length, there exists a regular parameterized spacelike curve under the contraction with the spacelike vector
such that s is the arc length, there exists a regular parameterized spacelike curve under the contraction with the spacelike vector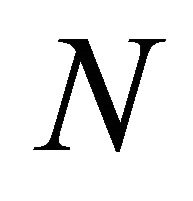 ,
, 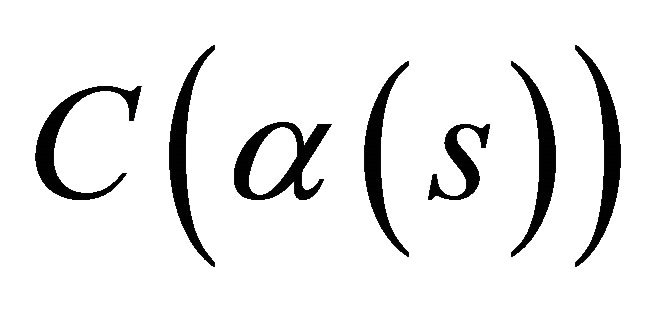 , in the space-time
, in the space-time . Also,
. Also, 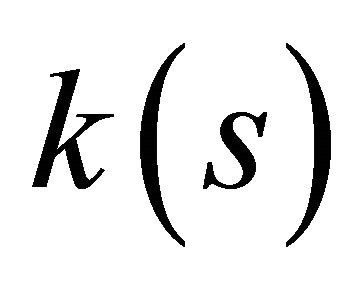 is the curvature and
is the curvature and 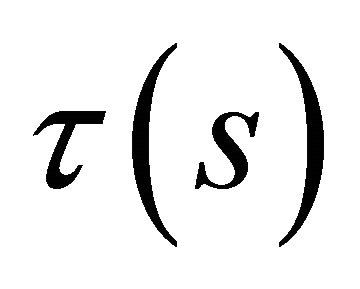 is the torsion of
is the torsion of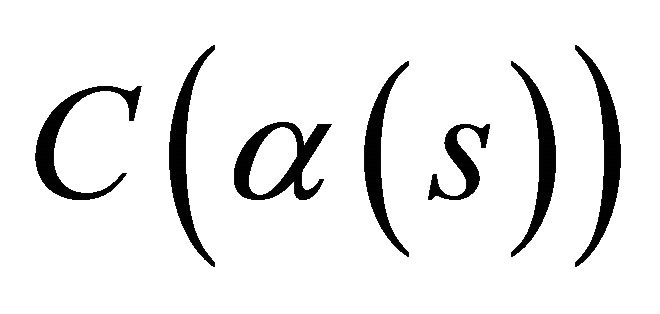 . Moreover, any other spacelike curve
. Moreover, any other spacelike curve 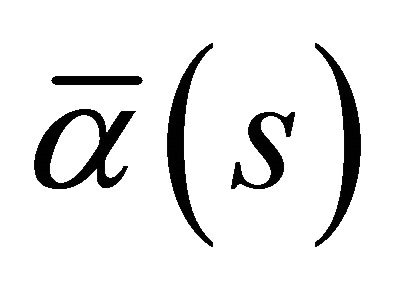 with the spacelike vector
with the spacelike vector 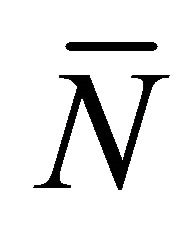 satisfying the same conditions and
satisfying the same conditions and 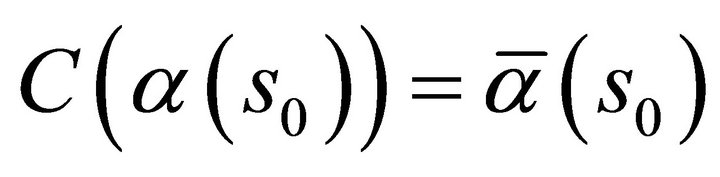 at
at 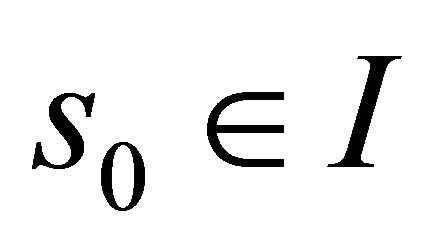 then
then  and the Frenet trihedrons of
and the Frenet trihedrons of 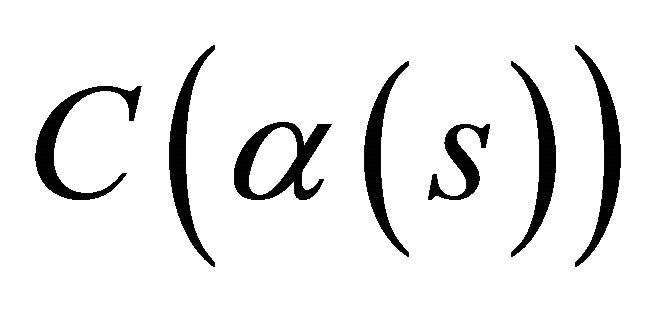 and
and 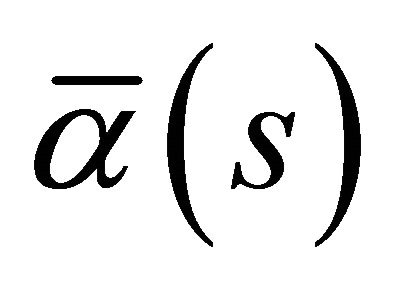 is identically.
is identically.
Theorem 5. Given differentiable functions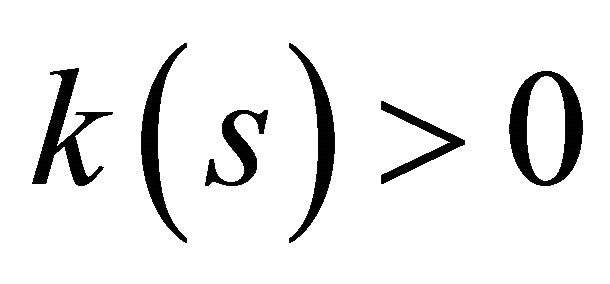 ,
,  and
and  such that s is the arc length, there exists a regular parameterized spacelike curve under the folding with the spacelike vectors
such that s is the arc length, there exists a regular parameterized spacelike curve under the folding with the spacelike vectors 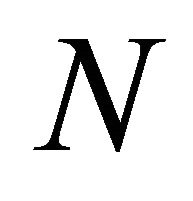 and
and ,
,  in the space-time
in the space-time . Also,
. Also, 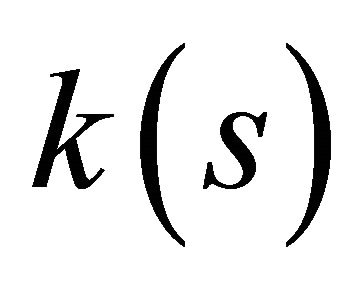 is the curvature,
is the curvature, 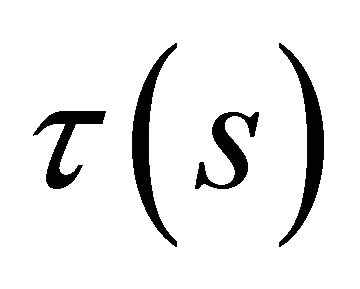 is the first torsion, and
is the first torsion, and 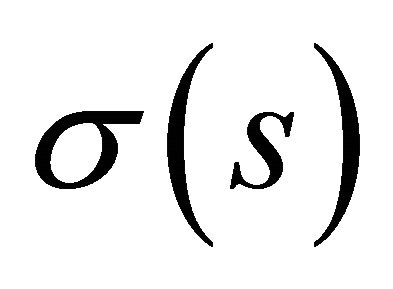 is the second torsion of
is the second torsion of . Moreover, any other spacelike curve
. Moreover, any other spacelike curve 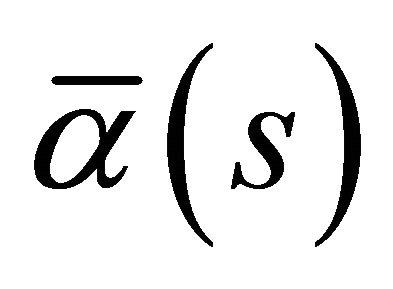 with the spacelike vectors
with the spacelike vectors  and
and  satisfying the same conditions and
satisfying the same conditions and 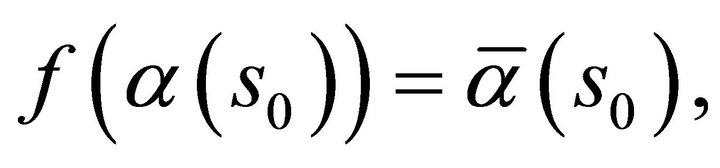 where
where 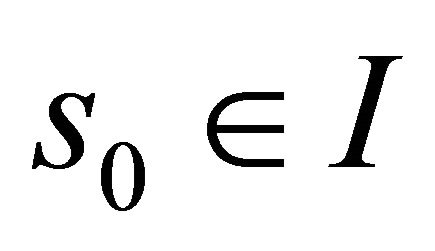 then
then 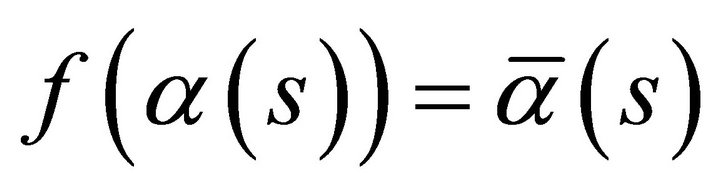 and the FrenetSerret formulas of
and the FrenetSerret formulas of  and
and  is identically.
is identically.
Proof. Now assume that two curves 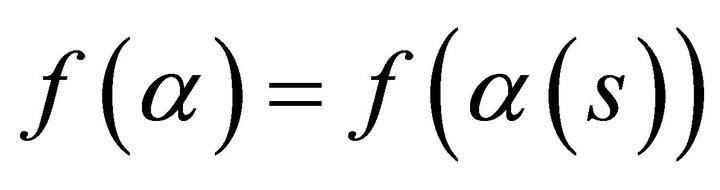 and
and 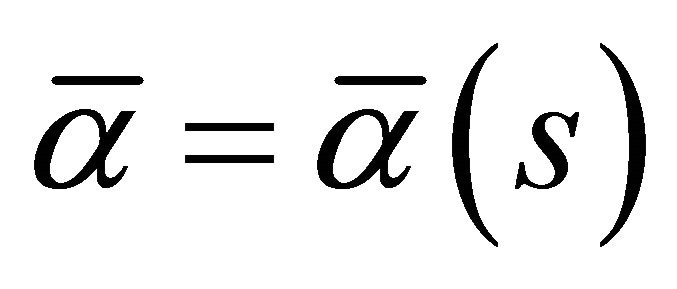 satisfy the conditions
satisfy the conditions ,
,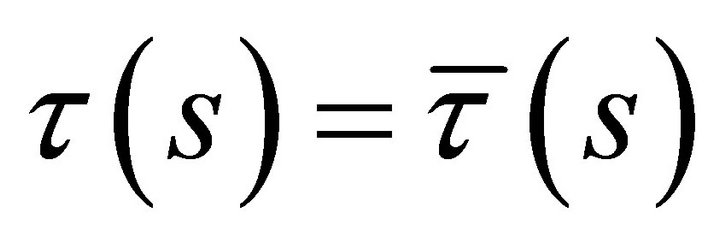 and
and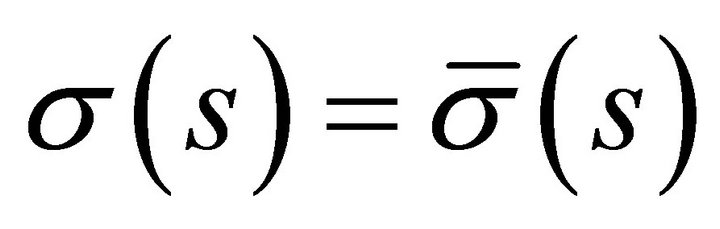 ,
,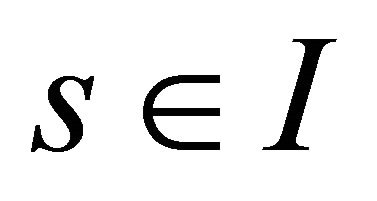 . Let
. Let ,
, 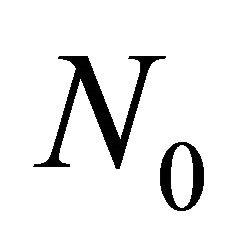 ,
, 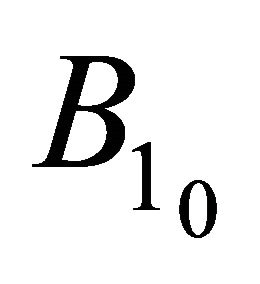 ,
, 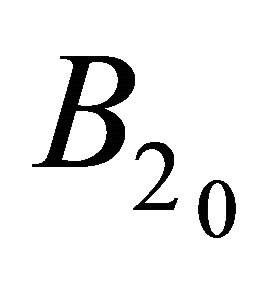 and
and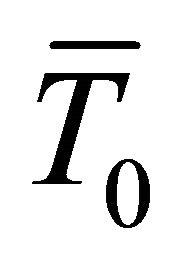 ,
, 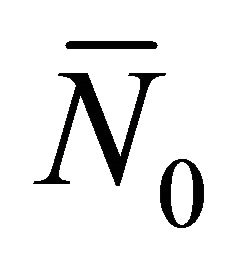 ,
, 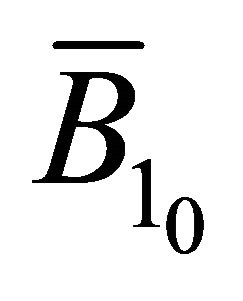 ,
, 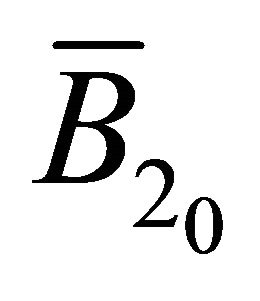 be the Frenet-Serret formulas of
be the Frenet-Serret formulas of 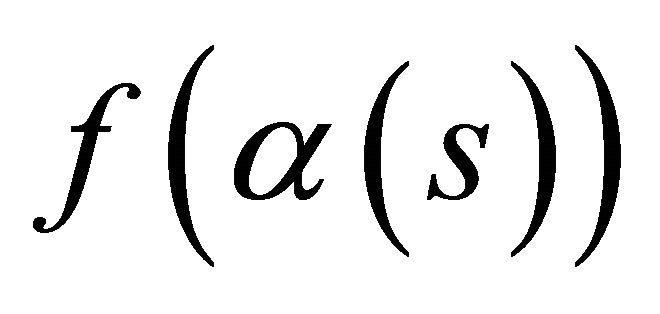 and
and 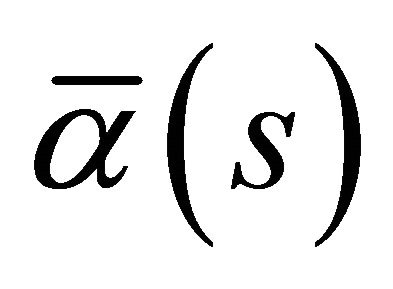 at
at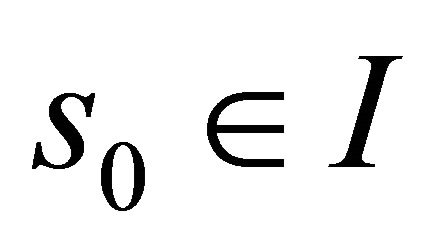 , respectively. Since
, respectively. Since 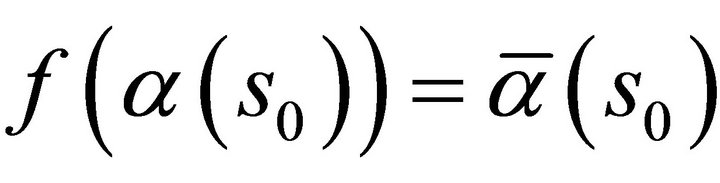 then
then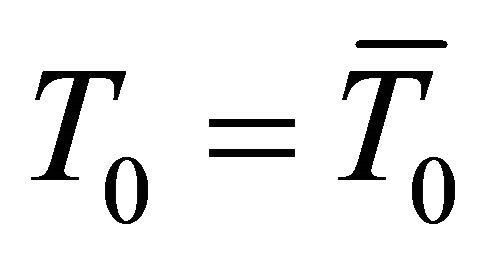 ,
, 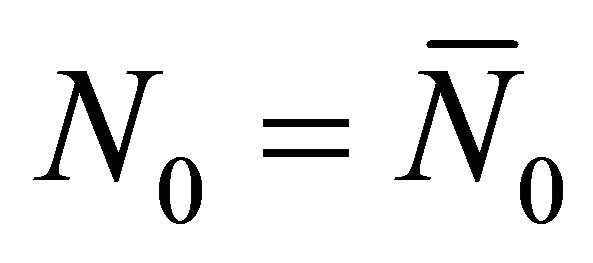 ,
, 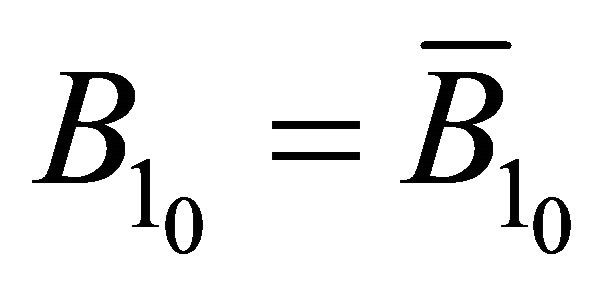 , and
, and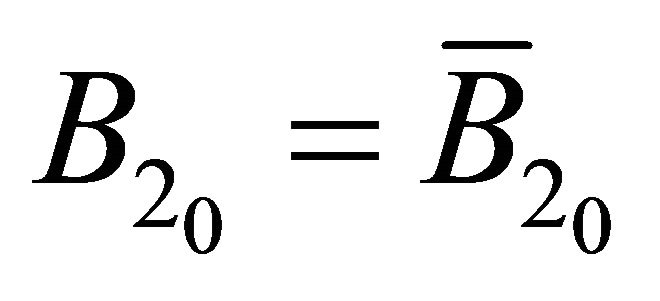 . And
. And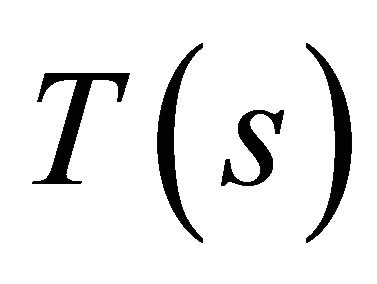 ,
, 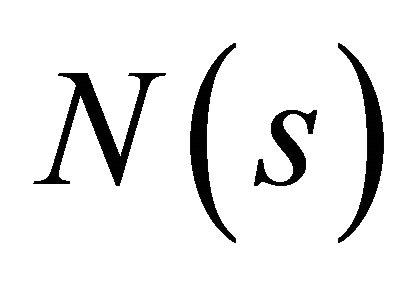 ,
, 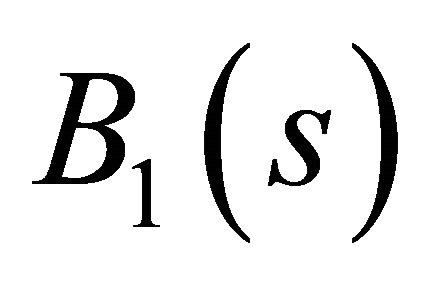 ,
,
 and
and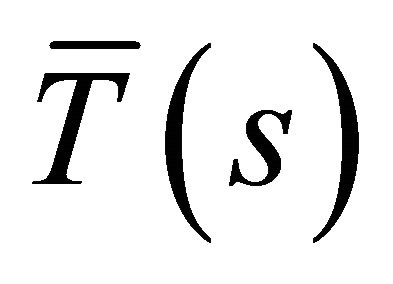 ,
, 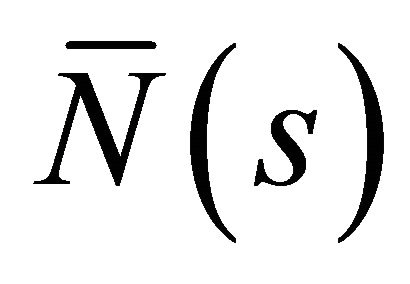 ,
, 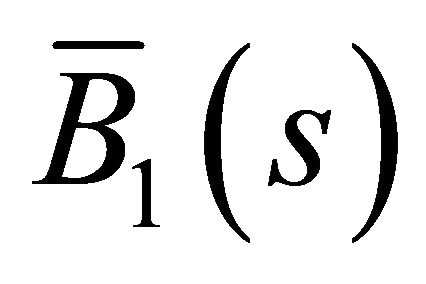 ,
, 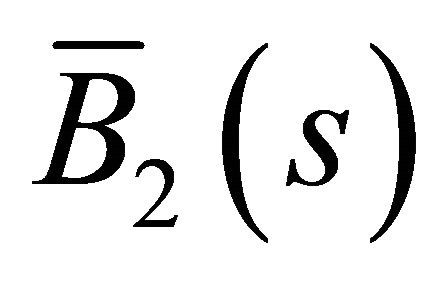 are the Frenet-Serret formulas of
are the Frenet-Serret formulas of  and
and 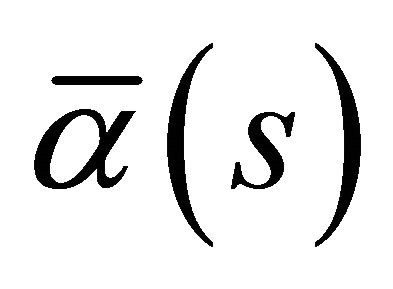
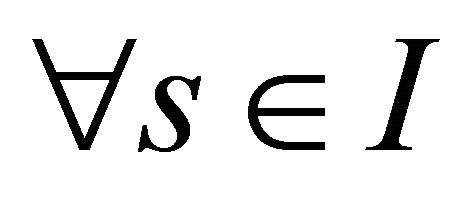 , respectively. We now observe, by using the Frenet equations at (3), that
, respectively. We now observe, by using the Frenet equations at (3), that
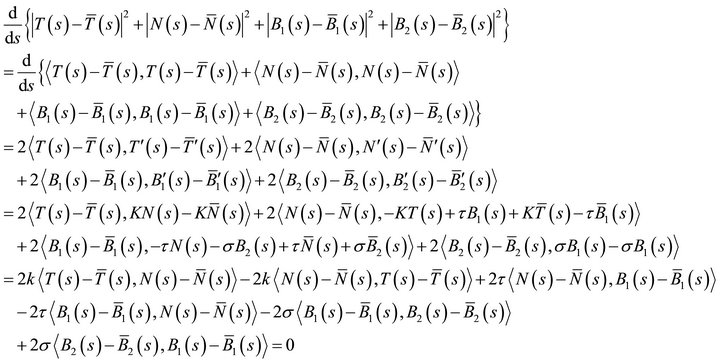
for all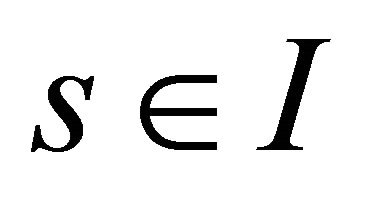 . Thus, the above expression is constant and, since it is zero for
. Thus, the above expression is constant and, since it is zero for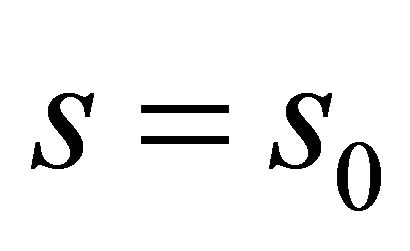 , it is identically zero. It follows that
, it is identically zero. It follows that

for all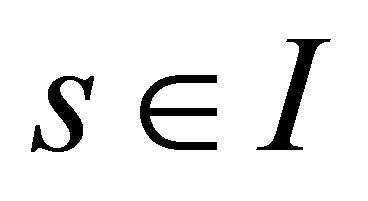 . Since
. Since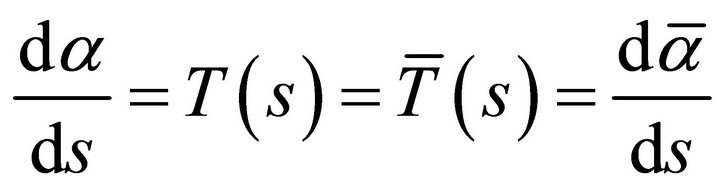 . We obtain
. We obtain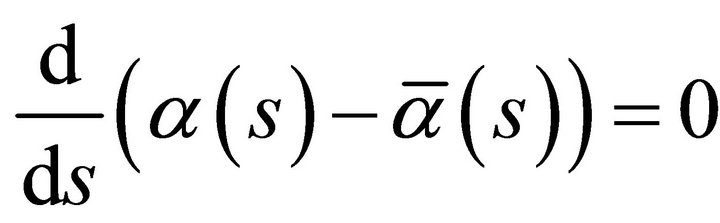 . Thus
. Thus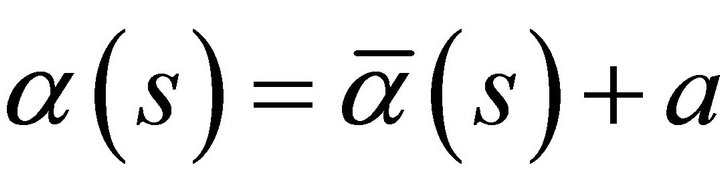 , where
, where
![]() is a constant vector. Since
is a constant vector. Since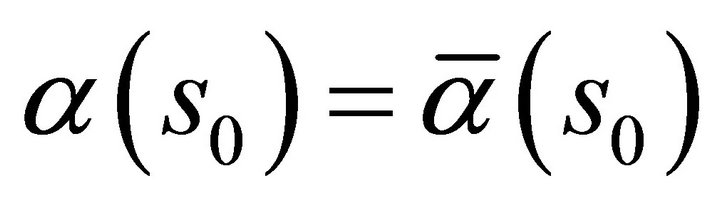 , we have
, we have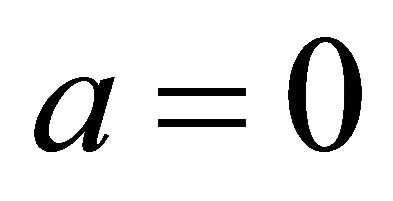 ; hence,
; hence,  for all
for all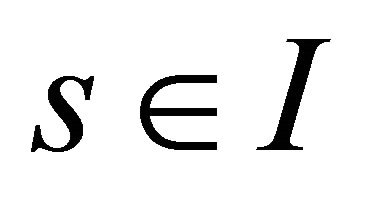 .
.
Theorem 6. Given differentiable functions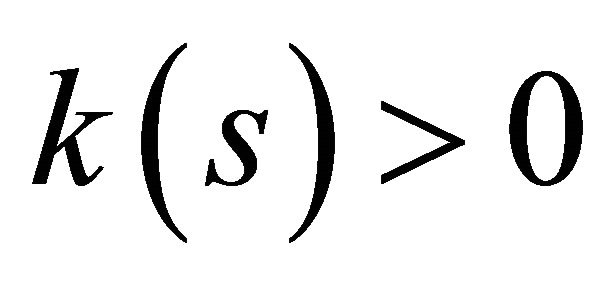 ,
, 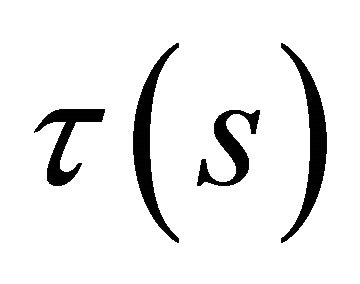 and
and 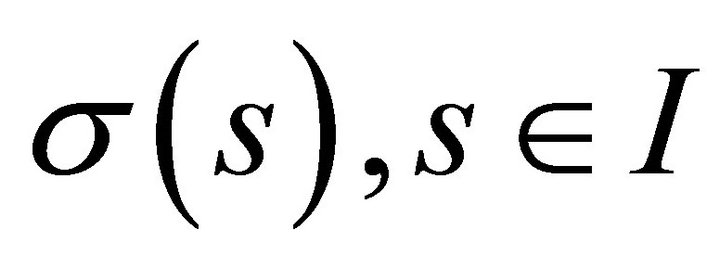 such that s is the arc length, there exists a regular parameterized spacelike curve under the deformation retract with the spacelike vectors
such that s is the arc length, there exists a regular parameterized spacelike curve under the deformation retract with the spacelike vectors  and
and ,
,  , in the space-time
, in the space-time . Also,
. Also, 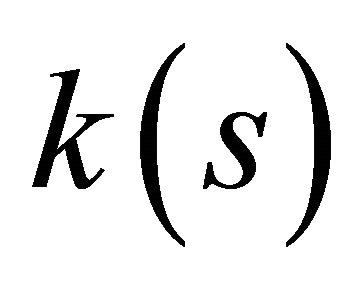 is the curvature,
is the curvature, 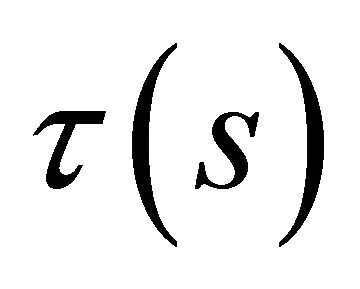 is the first torsion, and
is the first torsion, and 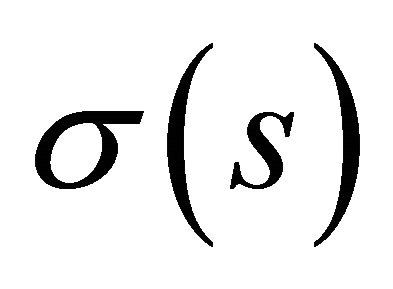 is the second torsion of
is the second torsion of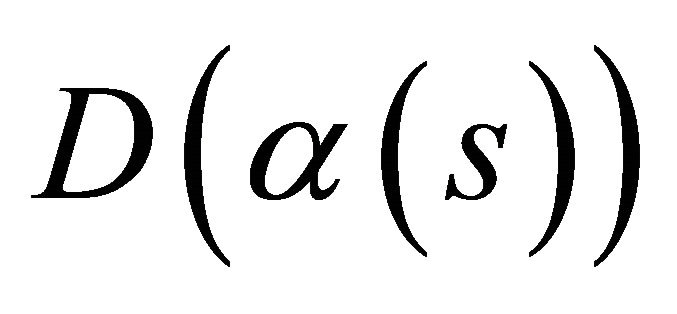 . Moreover, any other spacelike curve
. Moreover, any other spacelike curve 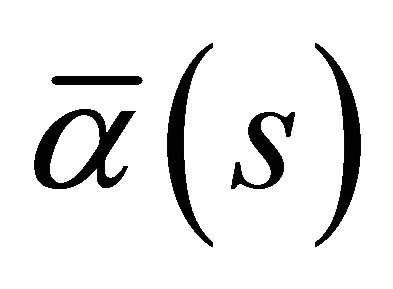 with the spacelike vectors
with the spacelike vectors 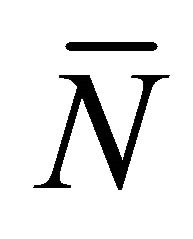 and
and  satisfying the same conditions and
satisfying the same conditions and
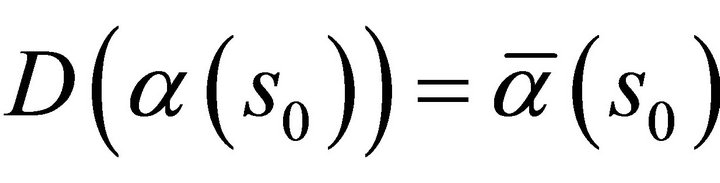 where
where 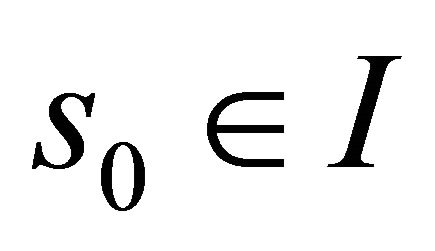 then
then 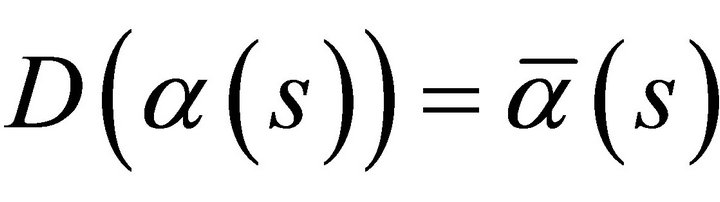 and the Frenet-Serret formulas of
and the Frenet-Serret formulas of 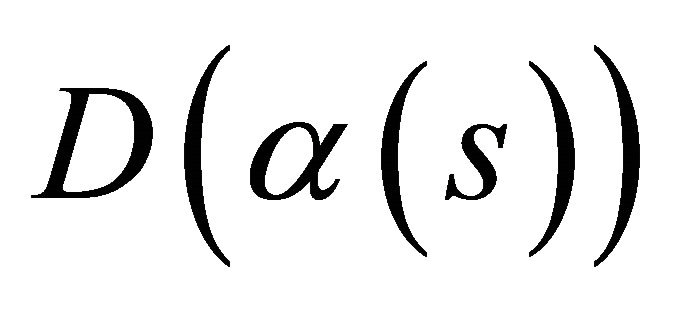 and
and 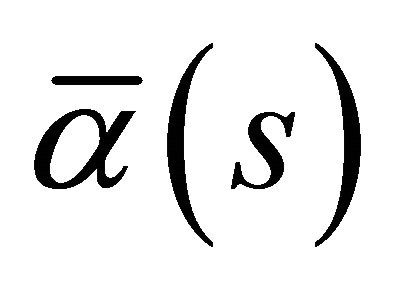 is identically.
is identically.
Theorem 7. Let 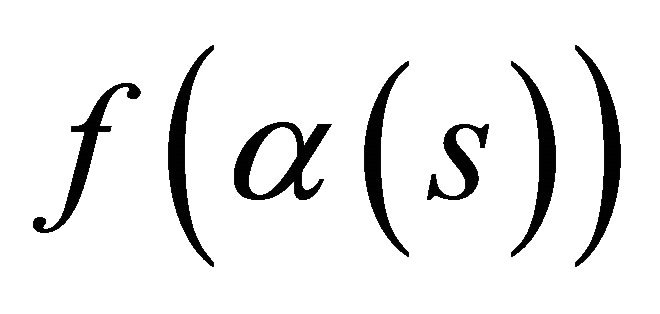 be a simple closed hyperplane curve under the folding in
be a simple closed hyperplane curve under the folding in  with length
with length , and let A be the area of the region bounded by
, and let A be the area of the region bounded by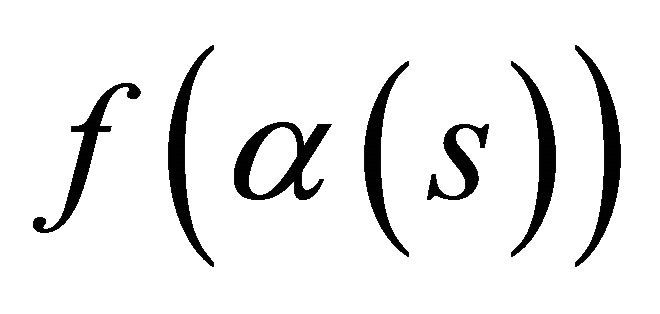 . Then
. Then
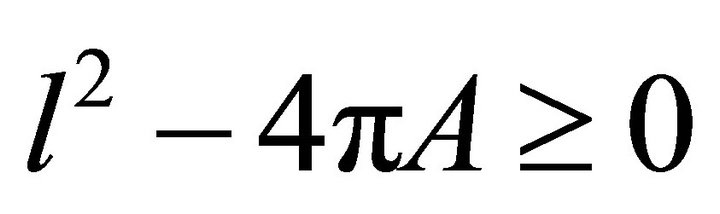 (4)
(4)
and equality holds if and only if 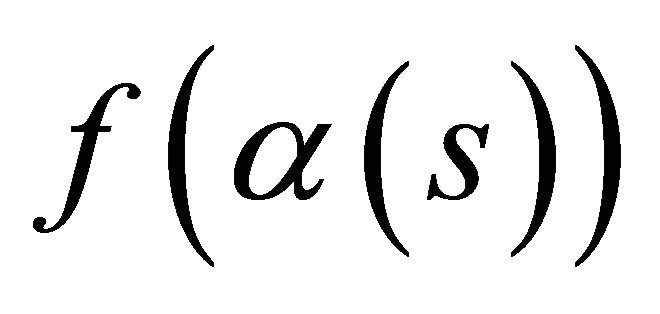 is a circle.
is a circle.
Proof. Let E and 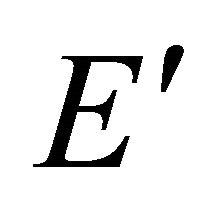 be two parallel lines which do not meet the closed curve
be two parallel lines which do not meet the closed curve 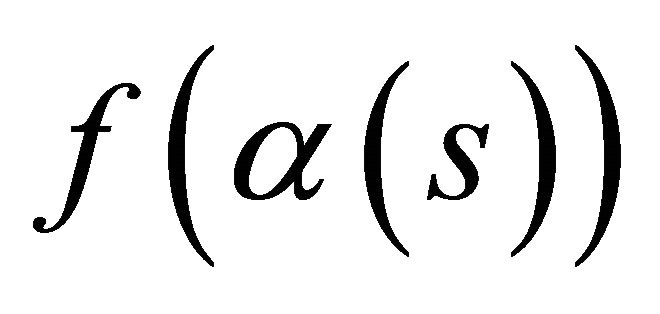 and moves them together until they first meet
and moves them together until they first meet 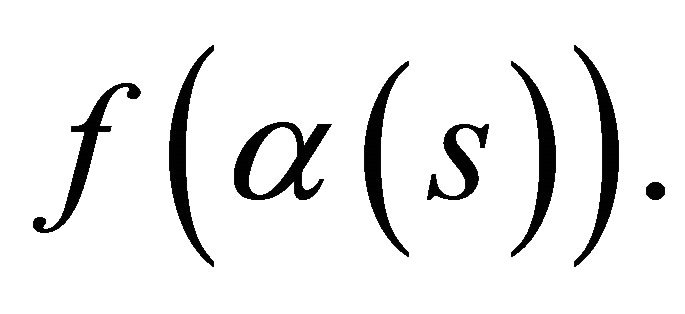 We thus obtain two parallel tangent lines to
We thus obtain two parallel tangent lines to , L and
, L and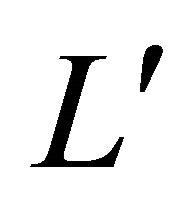 , so that the curve is entirely contained in the strip bounded by L and
, so that the curve is entirely contained in the strip bounded by L and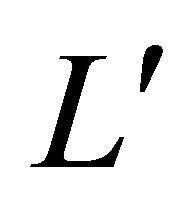 . Consider a circle
. Consider a circle 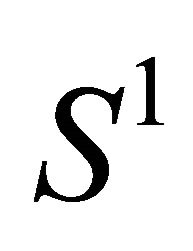 which is tangent to both L and
which is tangent to both L and 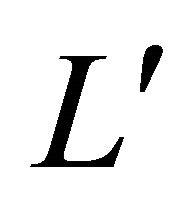 and does not meet
and does not meet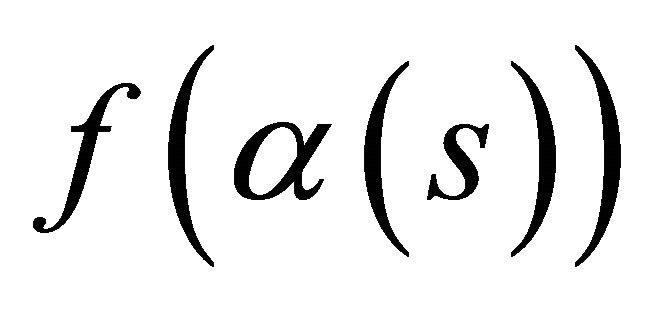 . Let O be the center of
. Let O be the center of 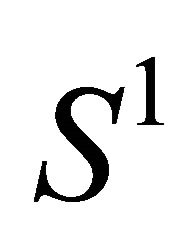 and take a coordinate system with origin at O and the
and take a coordinate system with origin at O and the ![]() axis perpendicular to L and
axis perpendicular to L and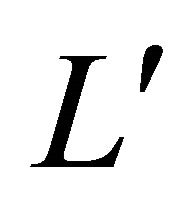 . Parameterize
. Parameterize  by arc length, since
by arc length, since 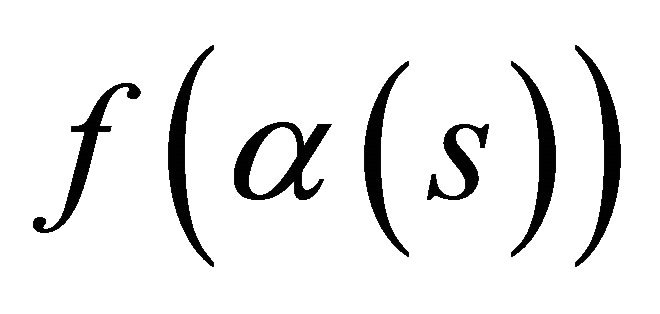 simple closed a hyperplane curve, then
simple closed a hyperplane curve, then 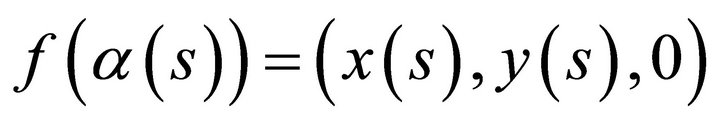 , so that it is positively oriented and the tangency points of L and
, so that it is positively oriented and the tangency points of L and 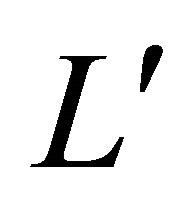 are
are  and
and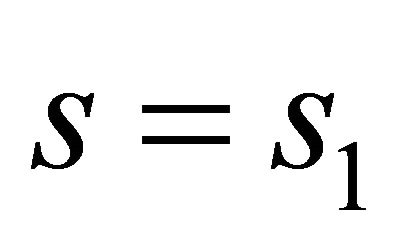 , respectively. We can assume that the equation of
, respectively. We can assume that the equation of 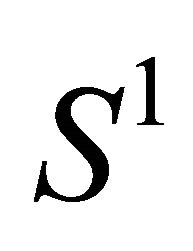 is
is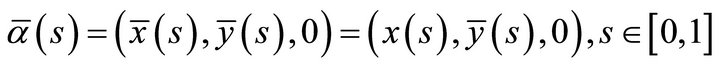 , where 2r is the distance between L and
, where 2r is the distance between L and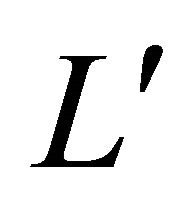 . Denoting by
. Denoting by  the area bounded by
the area bounded by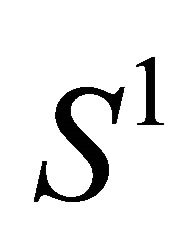 , we have
, we have
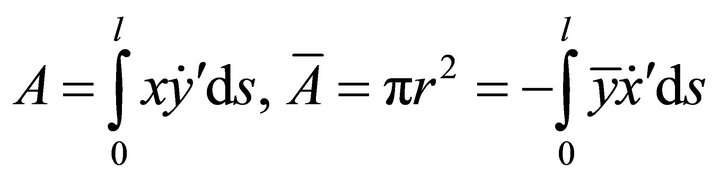
thus
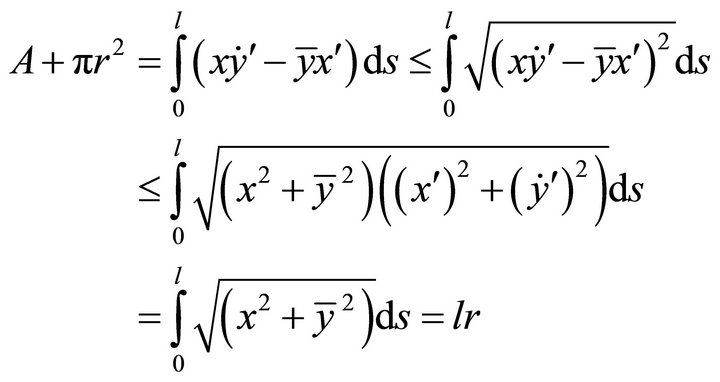 (5)
(5)
We now notice the fact that the geometric mean of two positive numbers is smaller than or equal to their arithmetic mean, and equality holds if and only if they are equal. It follows that
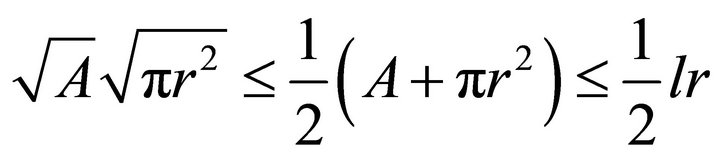 (6)
(6)
Therefore, 
Now, assume that equality holds in Equation (4). Then equality must hold everywhere in Equations (5) and (6). From the equality in Equation (6) it follows that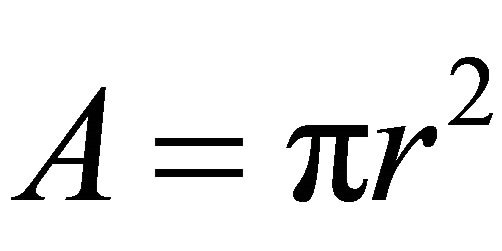 . Thus,
. Thus, 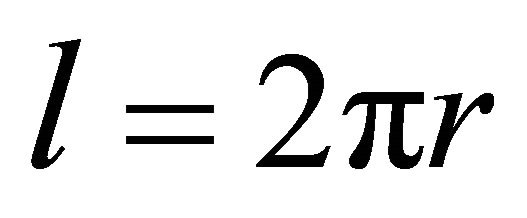 and
and 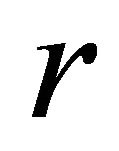 does not depend on the choice of the direction of
does not depend on the choice of the direction of![]() . Furthermore, equality in Equation (5) implies that
. Furthermore, equality in Equation (5) implies that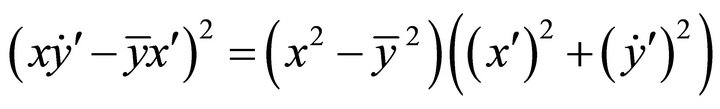 , or
, or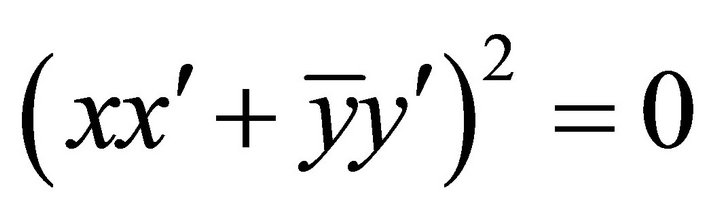 ; that is,
; that is,
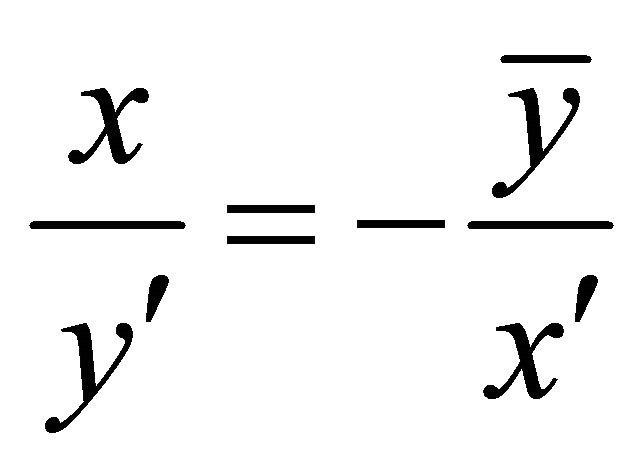

Since  does not depend on the choice of the direction of
does not depend on the choice of the direction of![]() , we can interchange
, we can interchange ![]() and
and ![]() in the last relation and obtain
in the last relation and obtain . Thus,
. Thus,
 and
and  is a circle.
is a circle.
Theorem 8. Let 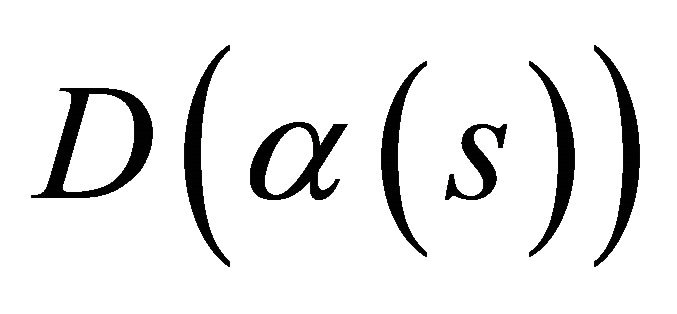 be a simple closed a hyperplane curve under the deformation retract in
be a simple closed a hyperplane curve under the deformation retract in  with length
with length , and let
, and let  be the area of the region bounded by
be the area of the region bounded by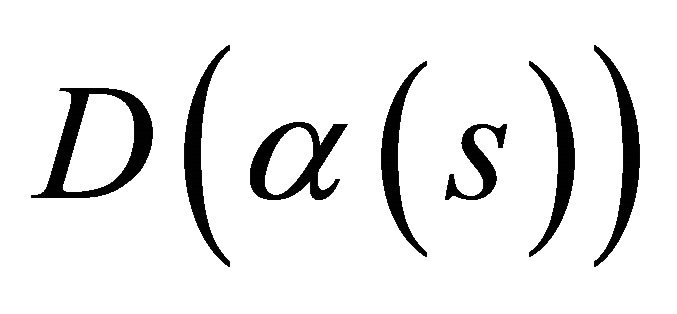 . Then
. Then 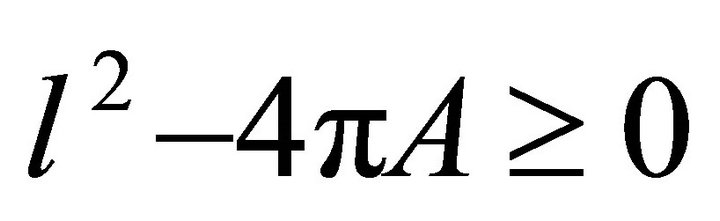 , and equality holds if and only if
, and equality holds if and only if 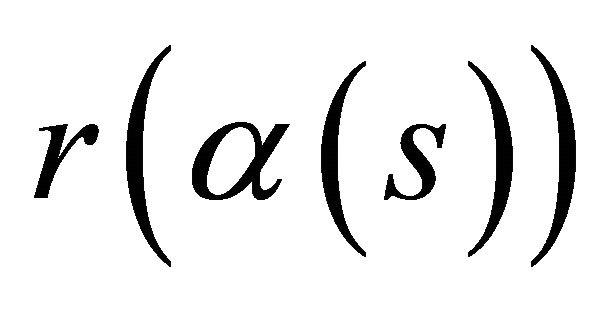 is a circle.
is a circle.
Corollary 7. Let  be a simple closed a hyperplane curve under the contraction in
be a simple closed a hyperplane curve under the contraction in  with length
with length , and let
, and let  be the area of the region bounded by
be the area of the region bounded by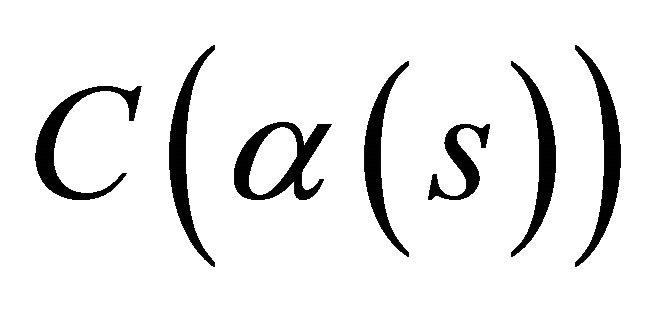 . Then
. Then , and equality holds if and only if
, and equality holds if and only if 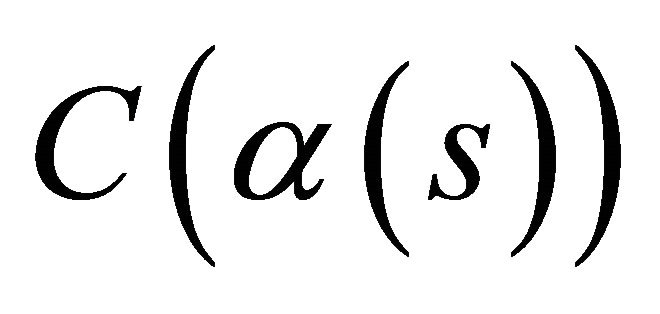 is a circle.
is a circle.
Any n vectors forming a basis for 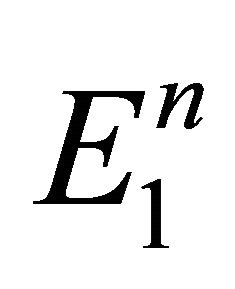 will be written
will be written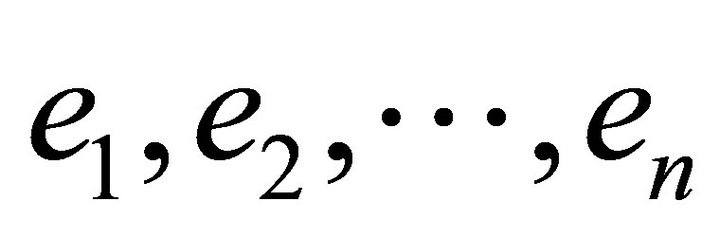 , i.e. the basis will be written
, i.e. the basis will be written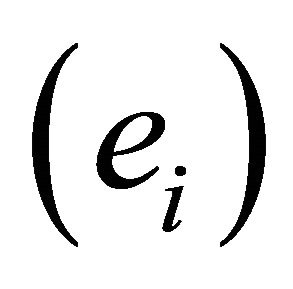 . Relative to a basis
. Relative to a basis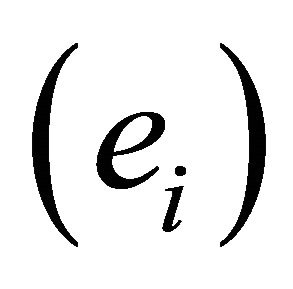 , any vector
, any vector ![]() in
in 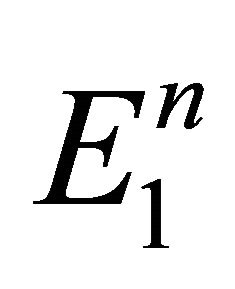 is uniquely expressible in the form
is uniquely expressible in the form
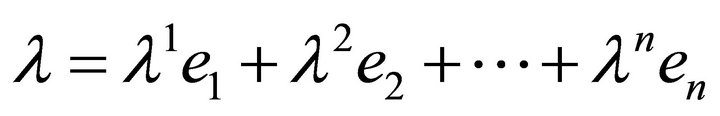
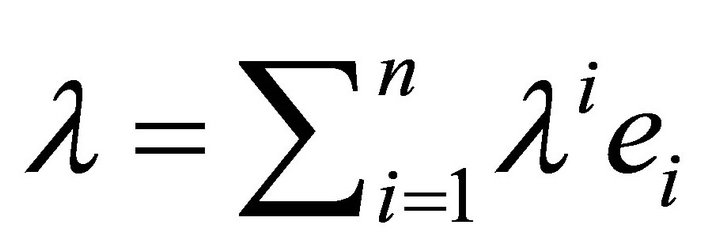
The numbers , where
, where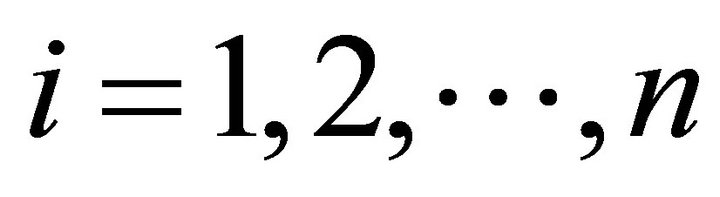 , are called the components of
, are called the components of ![]() relative to the basis
relative to the basis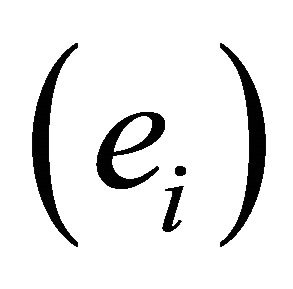 . If
. If 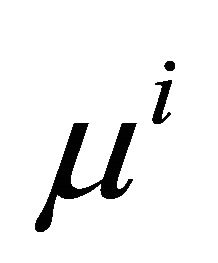 are the components of another vector
are the components of another vector 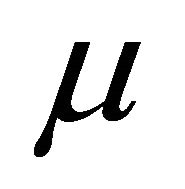 relative to the same basis
relative to the same basis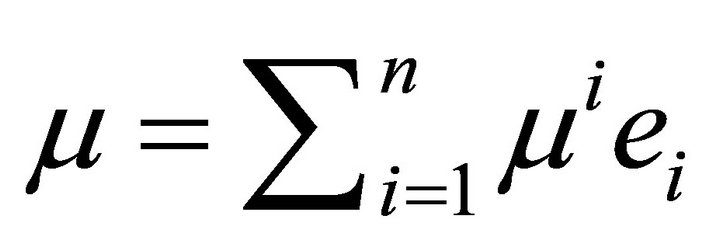 . Let the vectors
. Let the vectors 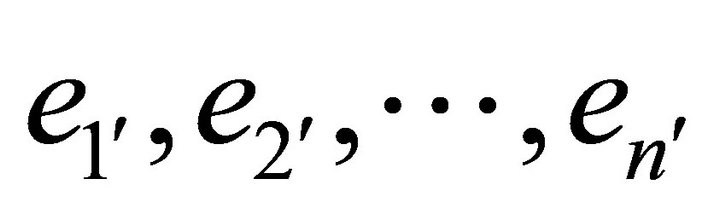 form another basis of
form another basis of . Since each vector
. Since each vector 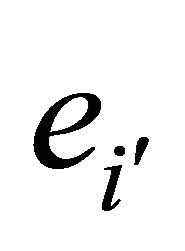 is uniquely expressible as a linear combination of the vectors
is uniquely expressible as a linear combination of the vectors , we have
, we have
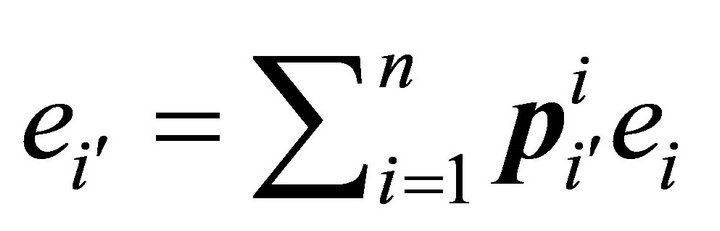 (7)
(7)
where 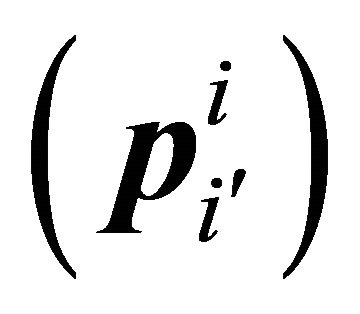 is an
is an ![]() matrix, non-singular because the vectors
matrix, non-singular because the vectors![]() , are linearly independent. Similarly, the vector
, are linearly independent. Similarly, the vector 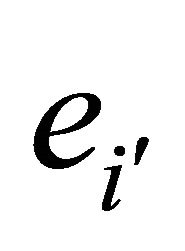 is uniquely expressible in the form
is uniquely expressible in the form
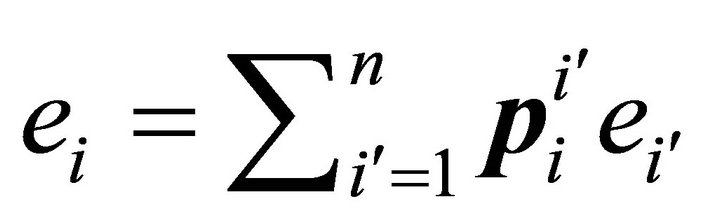 (8)
(8)
where 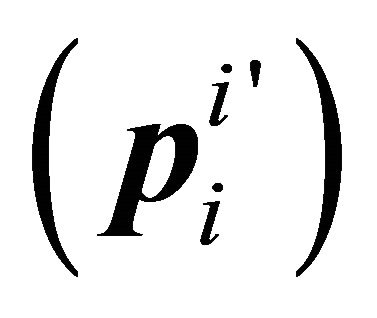 is a non-singular
is a non-singular ![]() matrix. Then
matrix. Then
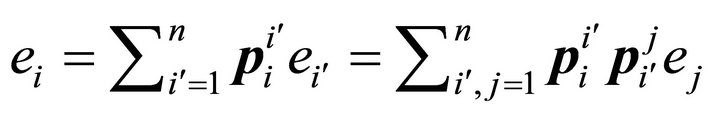
The linear independence of the basis vectors implies that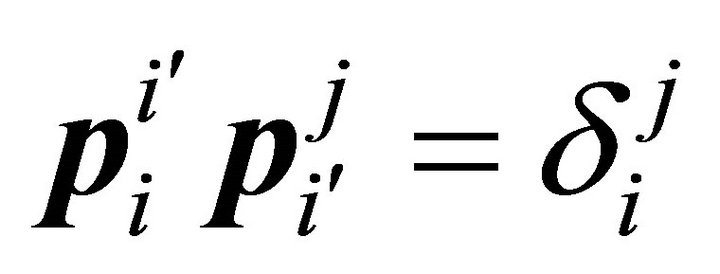 , where
, where 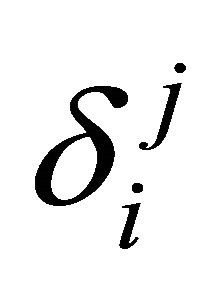 called the kroneckel delta, takes the value 1 if
called the kroneckel delta, takes the value 1 if 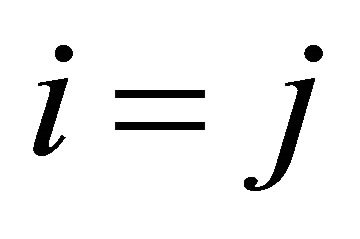 and is otherwise zero.
and is otherwise zero.
Theorem 9. The components of a vector ![]() in
in  where defined relative to the basis
where defined relative to the basis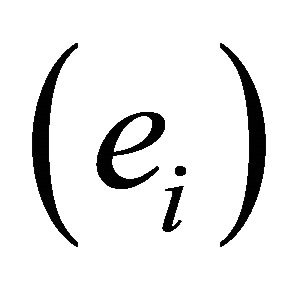 , and a change of basis will induce a change of components.
, and a change of basis will induce a change of components.
Proof. The law of transformation for the components of the vector ![]() will now be found when the basis is change from
will now be found when the basis is change from 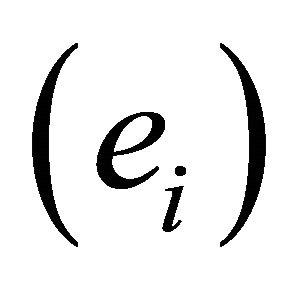 to
to 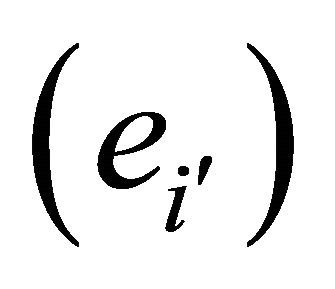 according the Equation (7). If the vector
according the Equation (7). If the vector ![]() has components
has components 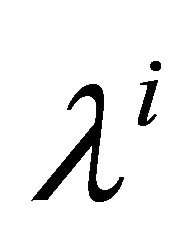 relative to the basis
relative to the basis , it is convenient to write
, it is convenient to write 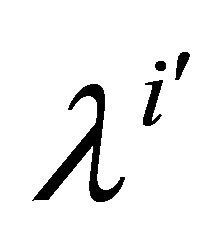 for it’s components relative to the new basis
for it’s components relative to the new basis , related to the former by (7). Then
, related to the former by (7). Then
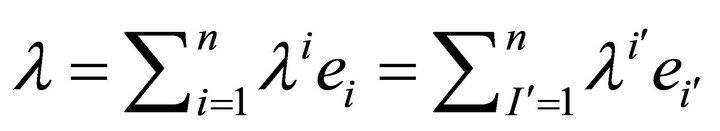 (9)
(9)
Equations (7), (9) give
![]()
From which, since the basis vectors 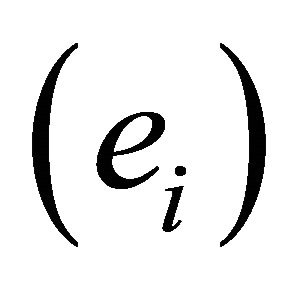 are linearly independent, it follows that
are linearly independent, it follows that
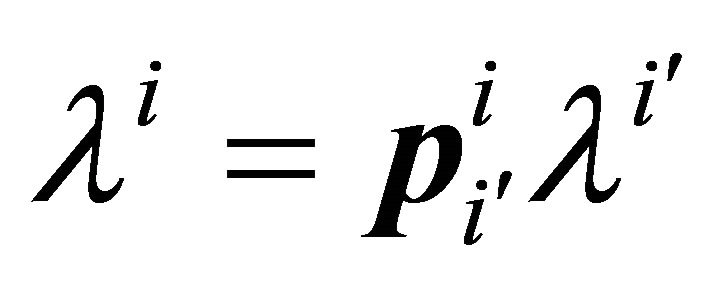 (10)
(10)
Similarly, substitute in (9) for ![]() from (8) to get
from (8) to get
![]()
From which, since the basis vectors 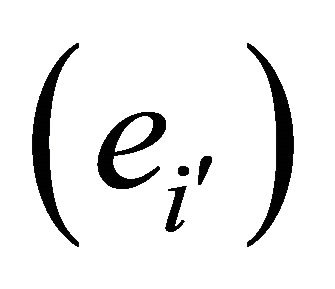 are linearly independent
are linearly independent
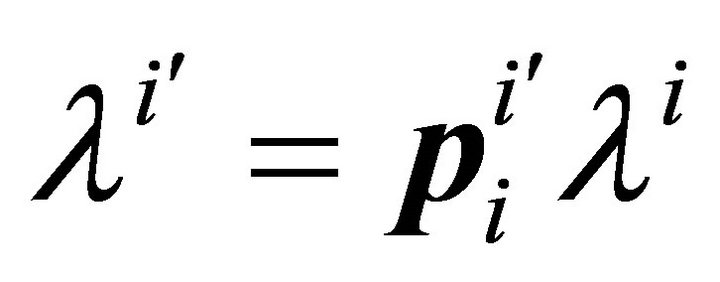 (11)
(11)
The Equation (11) expresses the new components in terms of the old component, while Equation (10) expresses the old components in terms of the new component.
Theorem 10. Under the retraction, given differentiable functions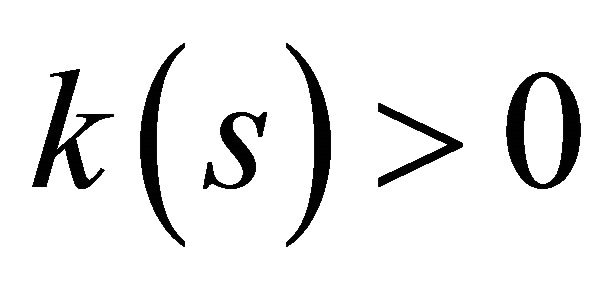 ,
, 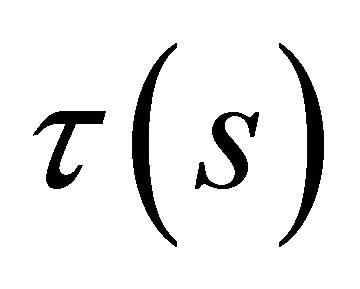 and
and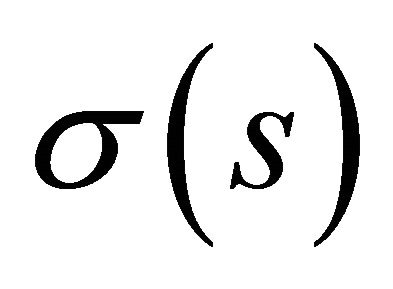 , there exists a retraction of regular parameterized timelike curve
, there exists a retraction of regular parameterized timelike curve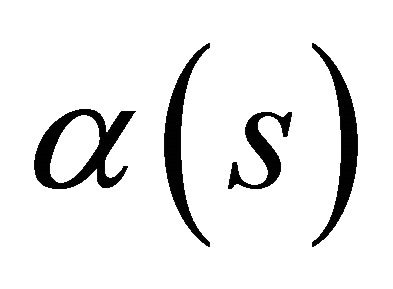 ,
, 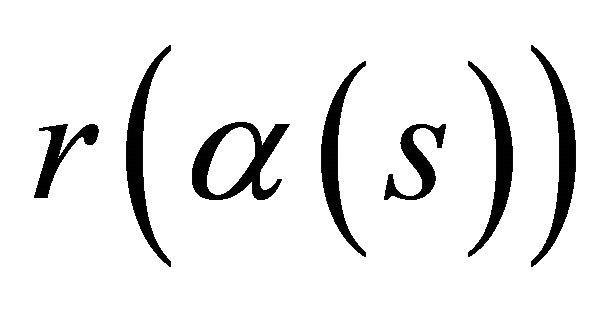 , such that
, such that  is the curvature,
is the curvature, 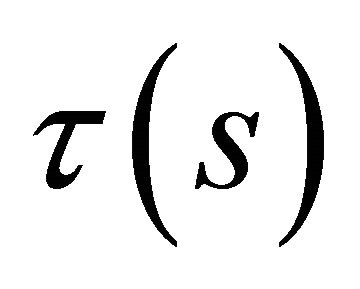 and
and  are, respectively, the first and second torsion of
are, respectively, the first and second torsion of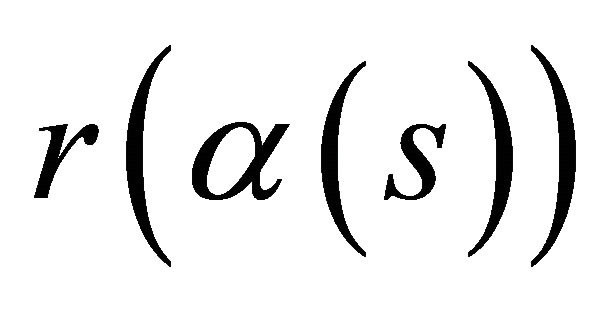 . Any other curve
. Any other curve 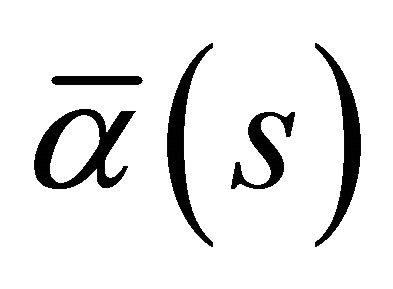 satisfying the same conditions, different from
satisfying the same conditions, different from  By a Poincaré transformation.
By a Poincaré transformation.
Proof. Let us assume that two timelike curves 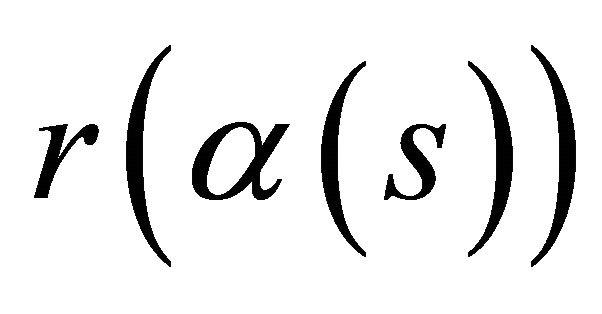 and
and  satisfy the conditions
satisfy the conditions ,
, 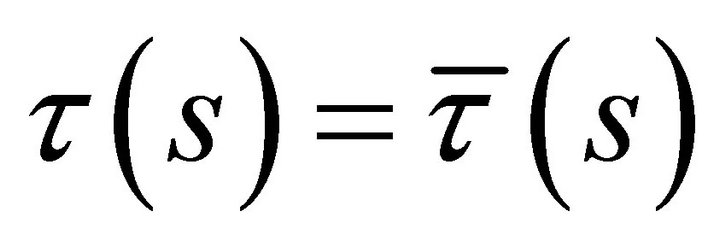 and
and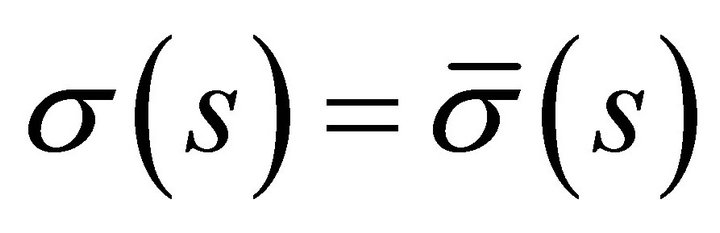 , with
, with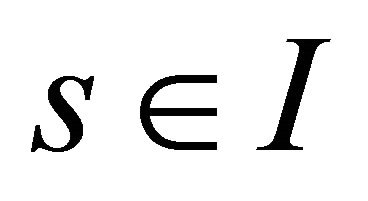 , where
, where  is an open interval of
is an open interval of , and
, and 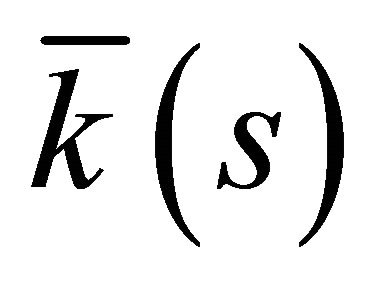 ,
,  and
and 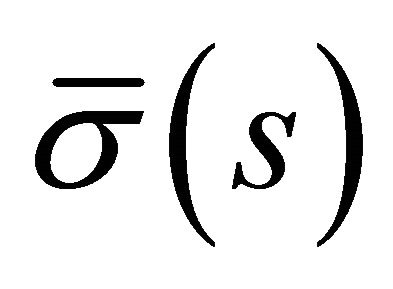 are, respectively, the curvature, first and second torsion of
are, respectively, the curvature, first and second torsion of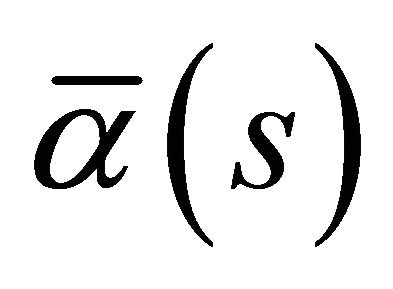 . Let
. Let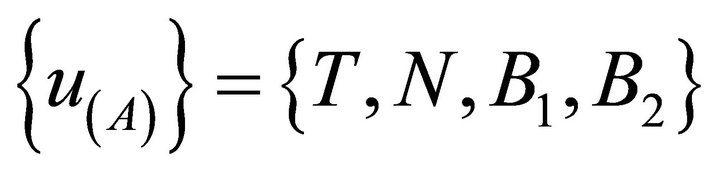 and
and
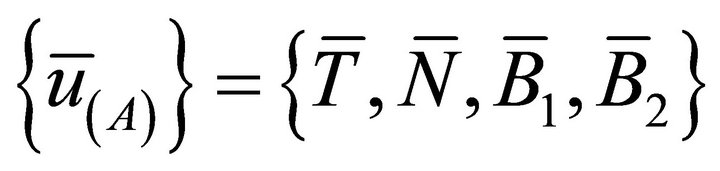 , where
, where 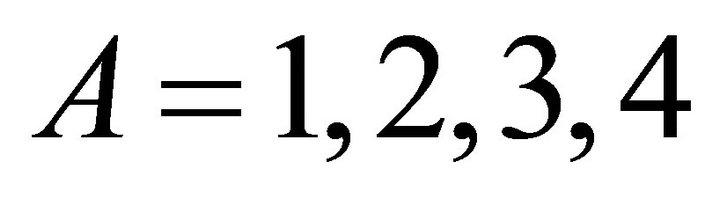 be the Serret-Frenet tetrads at
be the Serret-Frenet tetrads at  of
of 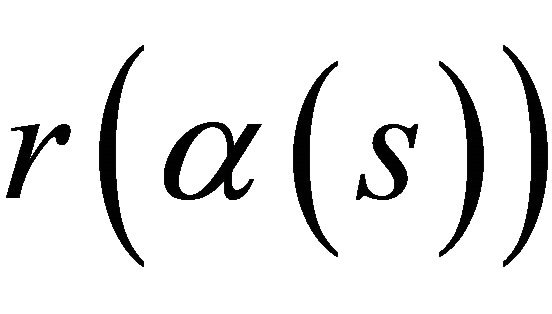 and
and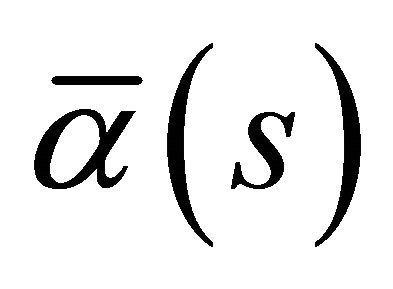 , respectively. Now, the two Serret-Frenet tetrads of
, respectively. Now, the two Serret-Frenet tetrads of 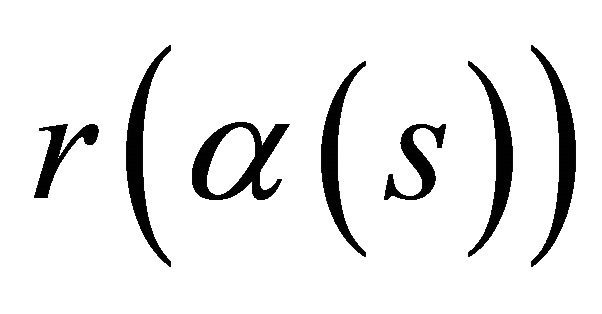 and
and  satisfy the equations
satisfy the equations
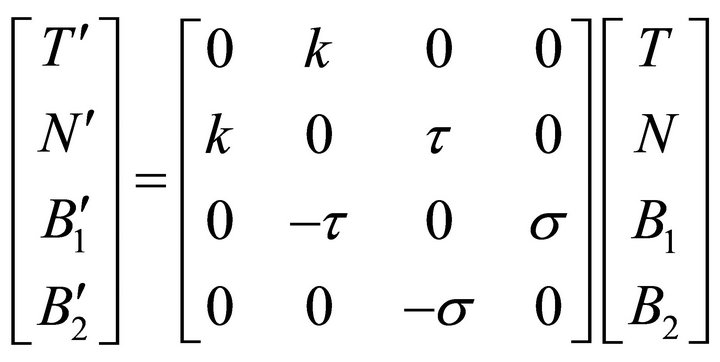
and
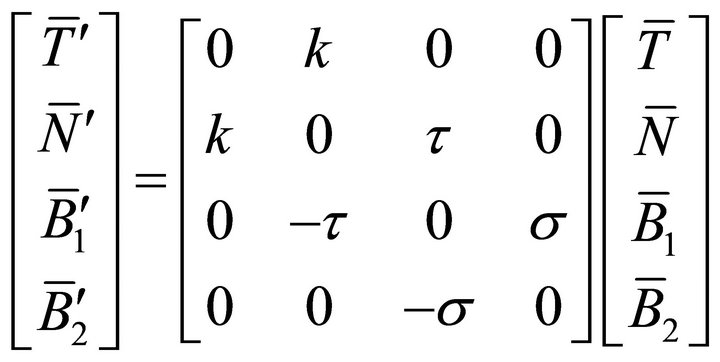
This can be written in a more compact form as
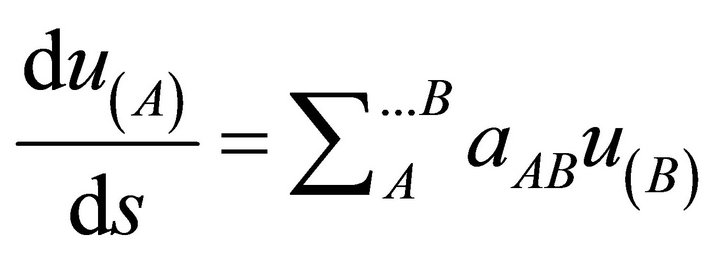 (12)
(12)

where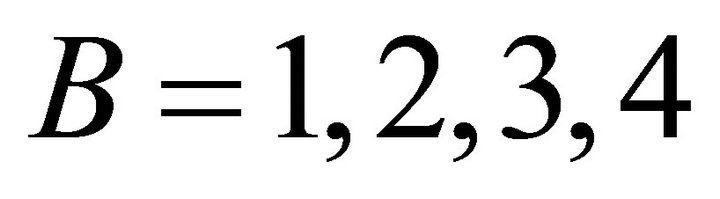 , with
, with 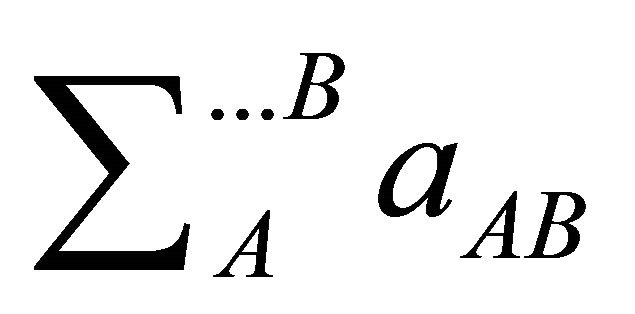 and
and 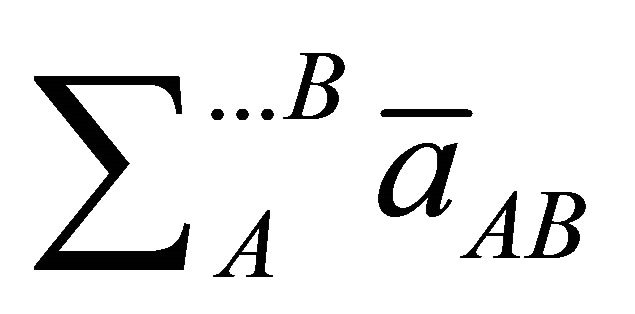 denoting the elements of the Serret-Frenet matrix. Clearly, the two tetrads
denoting the elements of the Serret-Frenet matrix. Clearly, the two tetrads ,
, 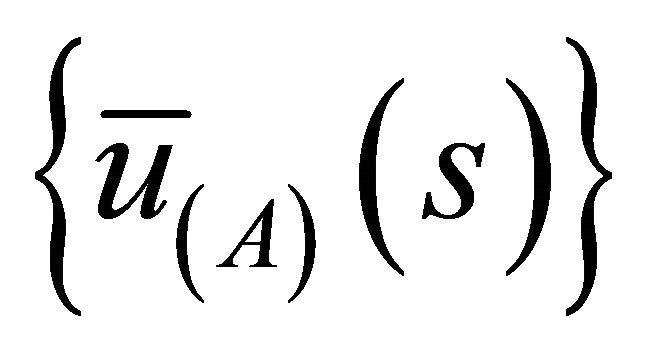 are related by an equation of the type
are related by an equation of the type
![]() (13)
(13)
with the elements of the matrix 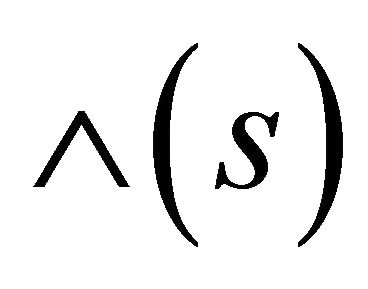 satisfying the condition
satisfying the condition
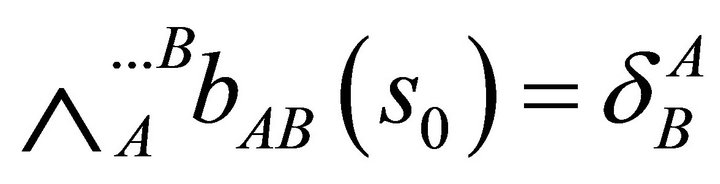
Since we are assuming that 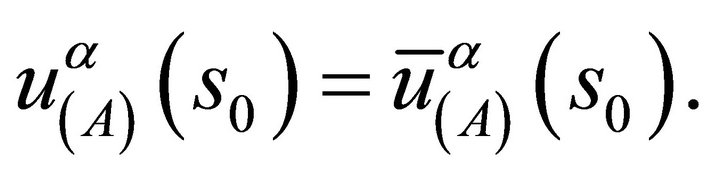
From (12) and (13) we obtain a system of first-order differential equations for the elements of 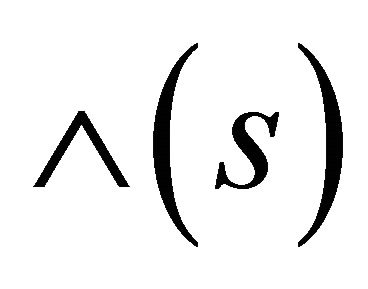 given by
given by
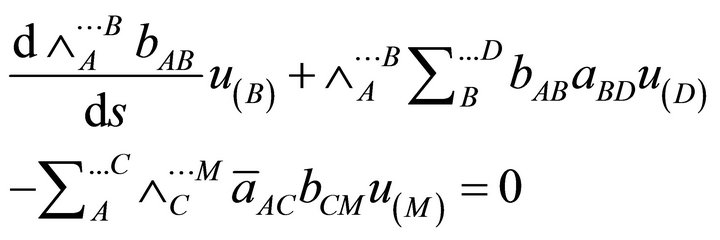 (14)
(14)
By assumption,  are differentiable functions of the proper parameter s. From the theory of ordinary differential equations, we know that if we are given a set of initial conditions
are differentiable functions of the proper parameter s. From the theory of ordinary differential equations, we know that if we are given a set of initial conditions  then the above system admits a unique solution
then the above system admits a unique solution
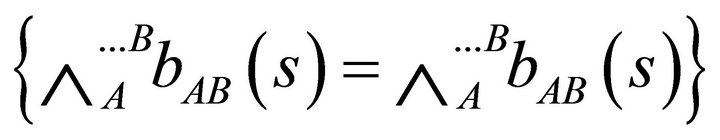
defined in an open interval 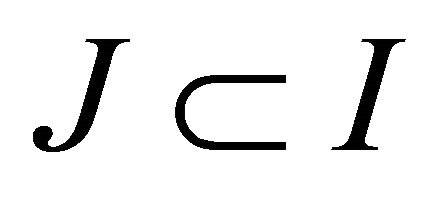 containing
containing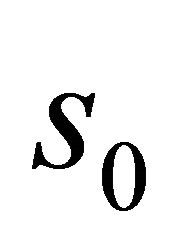 . On the other hand, it is easily seen that
. On the other hand, it is easily seen that  is a solution of (14). Therefore, we conclude that
is a solution of (14). Therefore, we conclude that
 .
.
REFERENCES
- A. E. El-Ahmady and E. Al-Hesiny, “Conditional Retraction of Some Curves in Minkowski 3-Space,” International Journal of Applied Mathematics and Statistics, Vol. 32, No. 2, 2012, pp. 39-47.
- A. E. El-Ahmady, “The Variation of the Density on Chaotic Spheres in Chaotic Space-Like Minkowski Space Time,” Chaos, Solitons and Fractals, Vol. 31, No. 5, 2007, pp. 1272-1278. doi:10.1016/j.chaos.2005.10.112
- A. E. El-Ahmady and E. Al-Hesiny, “The Topological Folding of the Hyperbola in Minkowski 3-Space,” The International Journal of Nonlinear Science, Vol. 11, No. 4, 2011, pp. 451-458.
- A. E. El-Ahmady and E. Al-Hesiny, “Folding and Differential Equations of Some Curves in Minkowski Space,” Life Science Journal, Vol. 9, No. 2, 2012, pp. 579-584.
- A. E. El-Ahmady and E. Al-Hesiny, “Folding and Deformation Retract of Hyperhelix,” Journal of Mathematics and Statistics, Vol. 8, No. 2, 2012, pp. 241-247. doi:10.3844/jmssp.2012.241.247
- A. E. El-Ahmady, “Retraction of Chaotic Black Hole,” The Journal of Fuzzy Mathematics, Vol. 19, No. 4, 2011, pp. 833-838.
- A. E. El-Ahmady, “Limits of Fuzzy Retractions of Fuzzy Hyperspheres and Their Foldings,” Tamkang Journal of Mathematics, Vol. 37, No. 1, 2006, pp. 47-55.
- A. E. El-Ahmady, “The Deformation Retract and Topo Logical Folding of Buchdahi Space,” Periodica Mathematica Hungarica, Vol. 28, No. 1, 1994, pp. 19-30. doi:10.1007/BF01876366
- A. E. El-Ahmady, “Folding and Fundamential Group of Buchdahi Space,” Indian Journal of Science and Technology, Vol. 6, No. 1, 2013, pp. 3940-3945.
- A. E. El-Ahmady, “On the Fundamental Group and Folding of Klein Bottle,” International Journal of Applied Mathematics and Statistics, Vol. 37, No. 6, 2013, pp. 56-64.
- A. E. El-Ahmady, “The Geodesic Deformation Retract of Klein Bottle and Its Folding,” The International Journal of Nonlinear Science, Vol. 12, No. 3, 2011, pp. 323-330.
- A. E. El-Ahmady and E. Al-Hesiny, “On Some Curves in Minkowski 3-Space and Its Deformation Retract,” International Journal of Applied Mathematics and Statistics, Vol. 36, No. 6, 2013, pp. 42-53.
- G. L. Naber, “Topology, Geometry and Gauge Fields, Foundations,” Springer-Verlage, New York, Berlin, 2011.
- M. Reid and B. Szendroi, “Geometry and Topology,” Cambridge University Press, Cambridge, New York, 2005. doi:10.1017/CBO9780511807510
- M. Reid and B. Szendroi, “Topology and Geometry,” Cambridge University Press, New York, 2005. doi:10.1017/CBO9780511807510
- M. Arkowitz, “Introduction to Homotopy Theory,” Springer-Village, New York, 2011.
- J. Strom, “Modern Classical Homotopy Theory,” American Mathematical Society, 2011.
- J. M. Lee, “Introduction to Topological Manifolds,” Springer-Verlage, New York, 2011. doi:10.1007/978-1-4419-7940-7
- R. Lopez, “Differential Geometry of Curves and Surfaces in Lorentz-Minkowski Space,” Instituto de Matematica e Estatistica, University of Sao Paulo, Sao Paulo, 2008.

