Applied Mathematics
Vol. 3 No. 11 (2012) , Article ID: 24329 , 4 pages DOI:10.4236/am.2012.311219
Computing Reachable Sets as Capture-Viability Kernels in Reverse Time
1National Institute of Demographic Studies, Paris, France
2Advanced Studies in Social Sciences, Paris, France
Email: bonneuil@ined.fr
Received August 3, 2012; revised September 14, 2012; accepted September 21, 2012
Keywords: Set-Valued Analysis; Reachable Set
ABSTRACT
The set 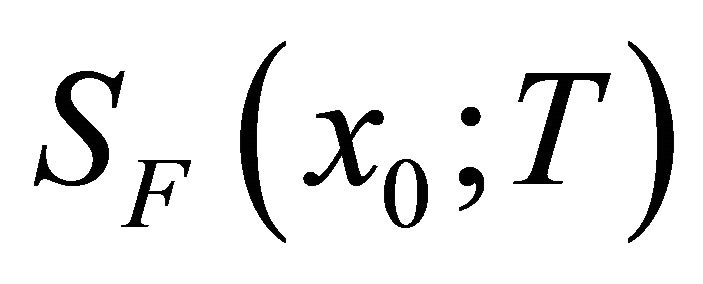 of states y reachable from a given state
of states y reachable from a given state 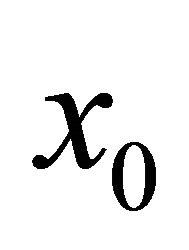 at time
at time  under a set-valued dynamic
under a set-valued dynamic 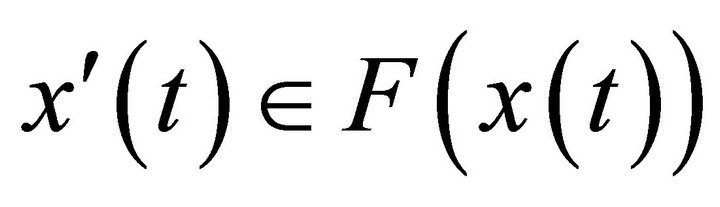 and under constraints
and under constraints 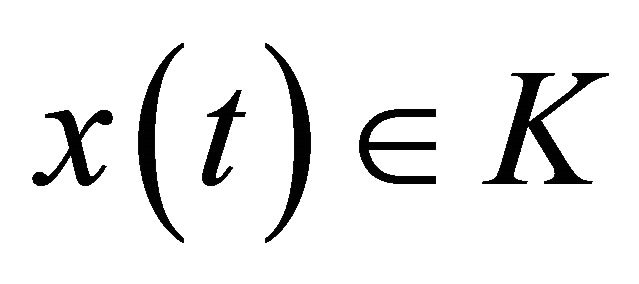 where
where 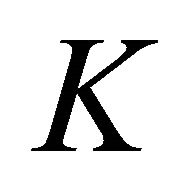 is a closed set, is also the capture-viability kernel
is a closed set, is also the capture-viability kernel 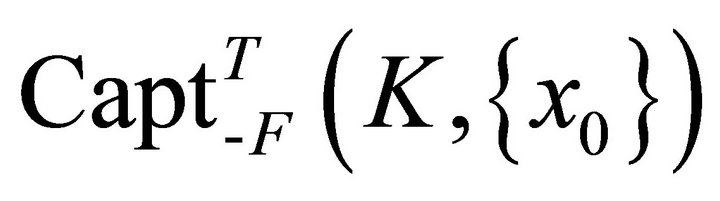 of
of 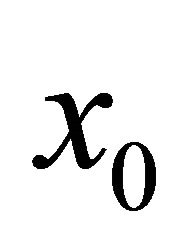 at
at  in reverse time of the target
in reverse time of the target 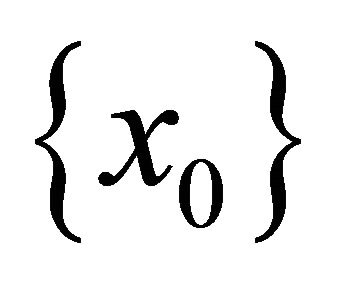 while remaining in
while remaining in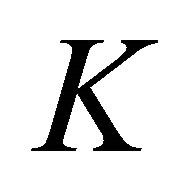 . In dimension up to three, Saint-Pierre’s viability algorithm is well-adapted; for higher dimensions, Bonneuil’s viability algorithm is better suited. It is used on a large-dimensional example.
. In dimension up to three, Saint-Pierre’s viability algorithm is well-adapted; for higher dimensions, Bonneuil’s viability algorithm is better suited. It is used on a large-dimensional example.
1. Introduction
Reachable sets gather the possible future states that a controlled set-valued system can take. The usual method for computing relies on solving HJB. For example, “project grid points from an equidistant grid onto the reachable set;” and “each projection requires to solve an optimal control problem” [1]. This method requires a huge computation, and is often limited to three dimensions. References of other clever methods are in [2,3].
I shall compute reachable sets in identifying them to capture basins. As such, they can be computed by viability algorithms, which do not need to solve HJB. Beside this advantage of avoiding the roundabout of HJB, the viability approach to reachable sets, from the very start, deals with non linear dynamics. Reachable sets appear as a straightforward consequence of set-valued analysis. At last, reachable sets can have a large state dimension.
Viability algorithms are normally used to compute the viability kernel of a closed set 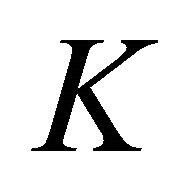 under a dynamic F. The viability kernel is the largest set of initial states x, from which at least one solution to the dynamic F remains in a closed set
under a dynamic F. The viability kernel is the largest set of initial states x, from which at least one solution to the dynamic F remains in a closed set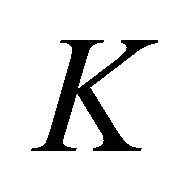 . Moreover, the computation of reachable sets impinges on the dimension of the dynamical system: after the dimension three, the computation becomes rapidly intractable. I shall show that Bonneuil’s viability algorithm [4], which neither requires solving HJB nor relies on a grid, but uses stochastic optimization, overcomes the curse of dimensionality and provides sets of reachable states. To do this, I shall highlight the fact that reachable sets are also capture basins of a convenient augmented dynamic. After defining reachable sets and capture-viability kernels, I shall identify reachable sets to capture-viability kernels under the dynamic in reverse time. Then, after presenting viability algorithms, I shall compute the reachable sets to the three noteworthy non-linear cases of [1] and to a 10-dimensional case.
. Moreover, the computation of reachable sets impinges on the dimension of the dynamical system: after the dimension three, the computation becomes rapidly intractable. I shall show that Bonneuil’s viability algorithm [4], which neither requires solving HJB nor relies on a grid, but uses stochastic optimization, overcomes the curse of dimensionality and provides sets of reachable states. To do this, I shall highlight the fact that reachable sets are also capture basins of a convenient augmented dynamic. After defining reachable sets and capture-viability kernels, I shall identify reachable sets to capture-viability kernels under the dynamic in reverse time. Then, after presenting viability algorithms, I shall compute the reachable sets to the three noteworthy non-linear cases of [1] and to a 10-dimensional case.
2. The Reachable Set as a Capture Basin
Consider a finite-dimensional vector space 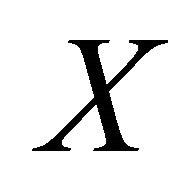 and the dynamic:
and the dynamic:
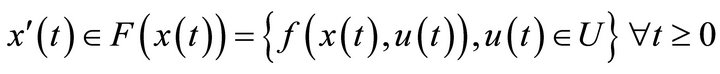 , (1)
, (1)
where  is a Marchaud map. A map
is a Marchaud map. A map 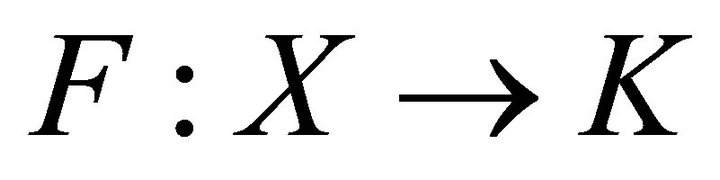 is Marchaud if and only if:
is Marchaud if and only if:
Assumption 2.1 (i) the graph and the domain of  are closed and not empty(ii) the values
are closed and not empty(ii) the values 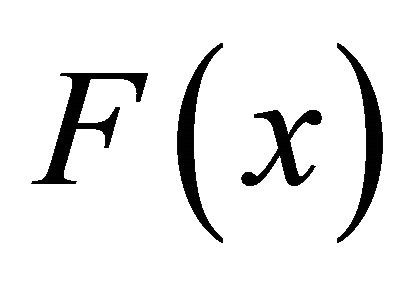 are convex(iii)
are convex(iii) 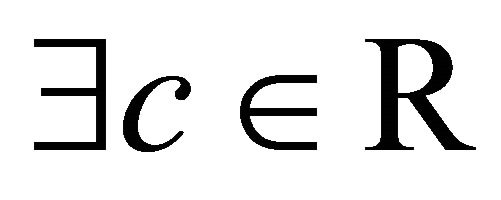 such that
such that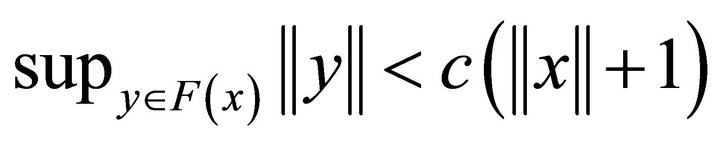 Assumptions (i) and (ii) hold true if the continuoustime control set
Assumptions (i) and (ii) hold true if the continuoustime control set 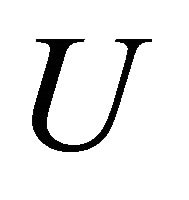 is a nonempty convex compact subset of a metric space and the function
is a nonempty convex compact subset of a metric space and the function 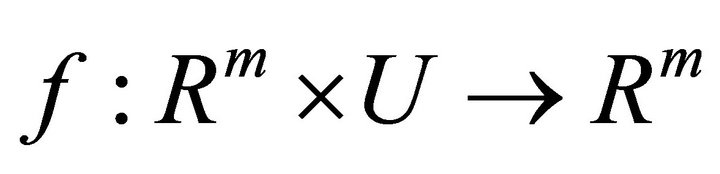 is Lipschitz with respect to each variable, and affine with respect to u.
is Lipschitz with respect to each variable, and affine with respect to u.
The state space is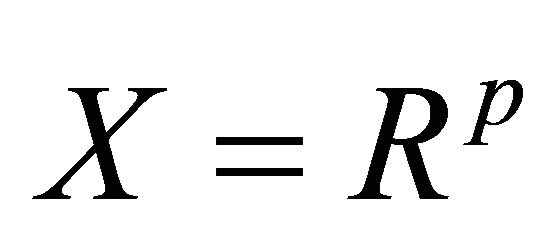 , the control space
, the control space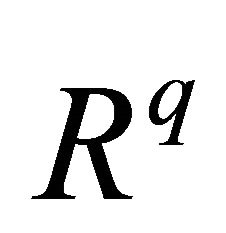 , and
, and 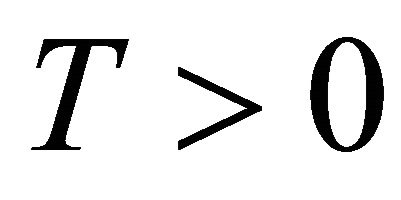 the time horizon. I denote S(x) the set of all solutions to Equation (1) starting from a given state x.
the time horizon. I denote S(x) the set of all solutions to Equation (1) starting from a given state x.
Definition 2.1 A reachable set from a set D at date T under the dynamic F within a closed set K is the set of the states 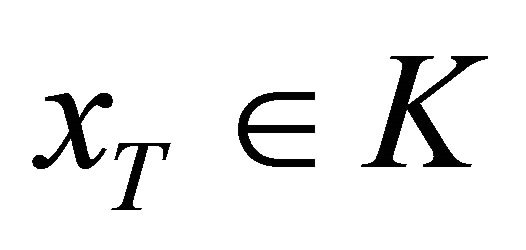 for which there exists an initial state
for which there exists an initial state 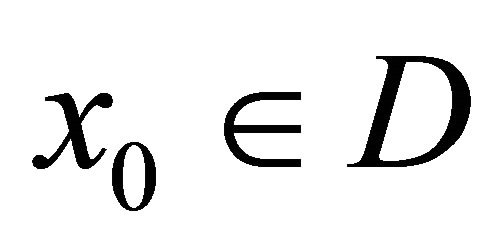 and a solution
and a solution 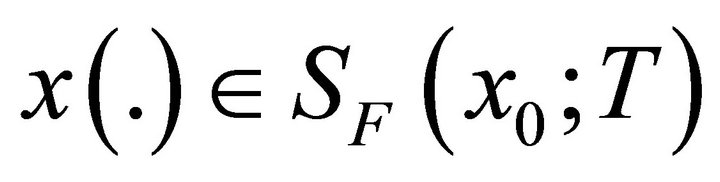 such that
such that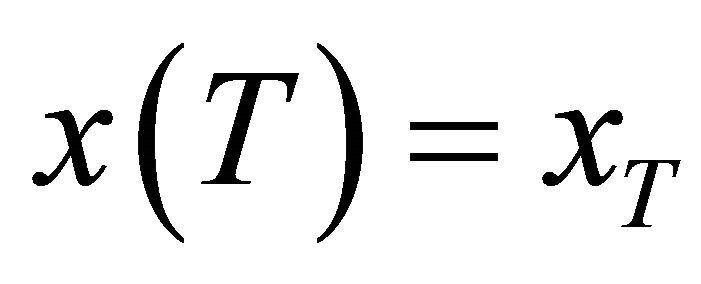 . It is denoted
. It is denoted
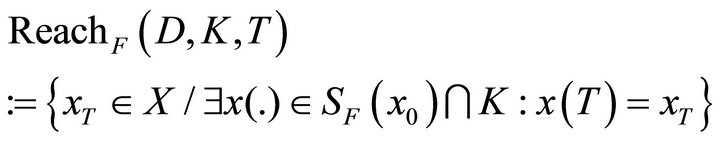 (2)
(2)
The reachable set in the interval [0; T] is defined as:
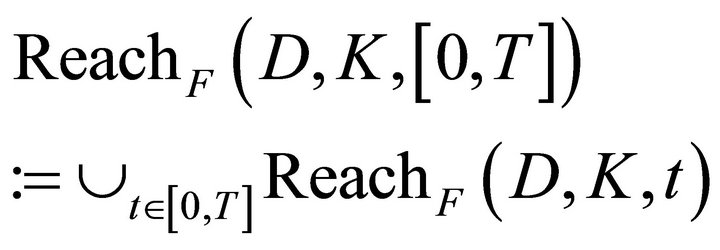 (3)
(3)
A state 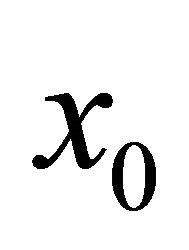 is said to be viable in K under F if there exists at least one solution
is said to be viable in K under F if there exists at least one solution 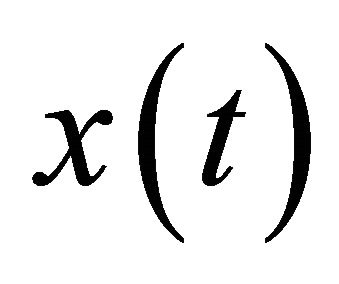 of Equation (1) starting from
of Equation (1) starting from 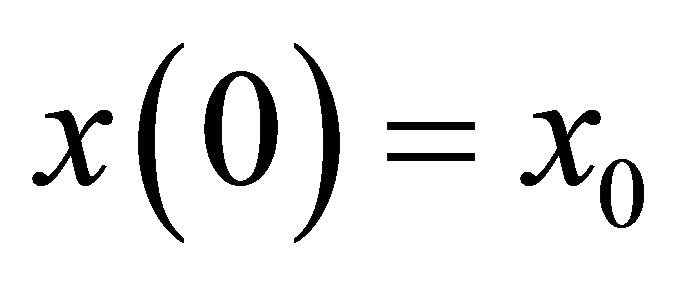 and remaining in K until T. A set of viable states is called a viability domain, and [5] showed that there exists a maximal viability domain including all others. This set is the viability kernel denoted
and remaining in K until T. A set of viable states is called a viability domain, and [5] showed that there exists a maximal viability domain including all others. This set is the viability kernel denoted 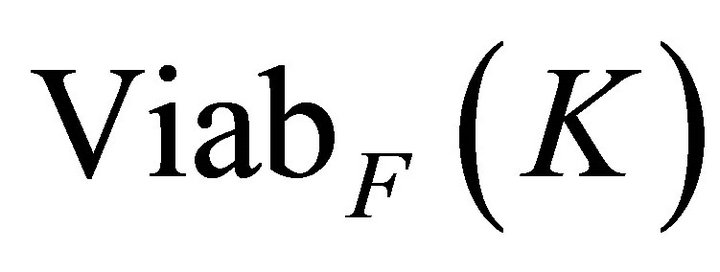 (which is then a set of initial conditions):
(which is then a set of initial conditions):
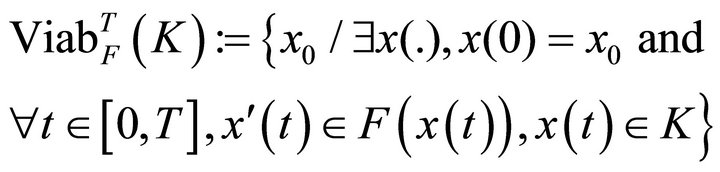 . (4)
. (4)
Definition 2.2 A capture-viability domain of a set C viable in the set K under the dynamic F is a subset of initial states 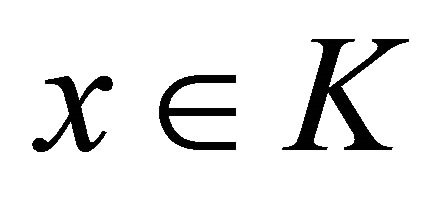 from which at least one solution viable in K starts until it reaches the target C at time T.
from which at least one solution viable in K starts until it reaches the target C at time T.
When F is Marchaud, there exists one largest captureviability domain with target C including all others [5]. It is denoted:
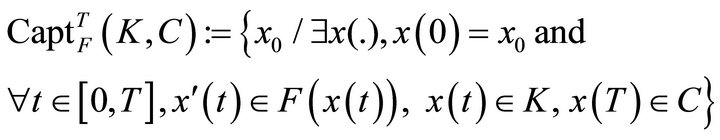 (5)
(5)
and called capture-viability kernel of the target C in K under F for time horizon T.
From definitions 2.1 and 2.2, it follows Theorem 2.3 The reachable set at time T from a subset C in the closed set K under the Marchaud dynamic F is also the capture-viability kernel of C in reverse time:
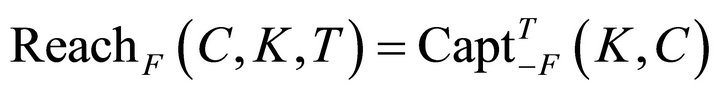 . (6)
. (6)
The proof is a consequence of articulating Definitions 2.1 and 2.2. The consequence of Theorem 2.3 is that the reachable set can be computed by a viability algorithm.
3. Algorithms
Saint-Pierre [6] devised an algorithm to compute captureviability kernels when F is Marchaud and Lipschitz. First, he showed that the capture-viability kernel of C under F in a closed set K is another set, the viability kernel of K under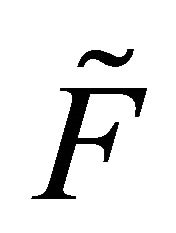 , defined as:
, defined as:
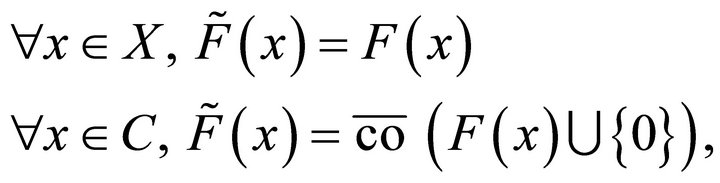 (7)
(7)
where 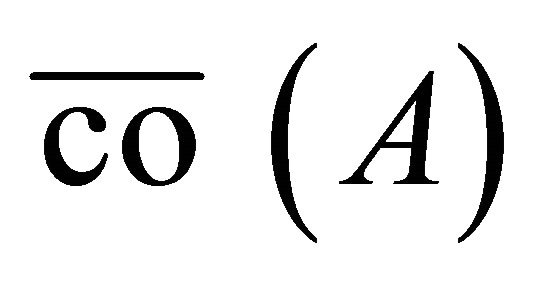 is the adherence of the convexified of a set A.
is the adherence of the convexified of a set A.
Second, he applied his viability algorithm to 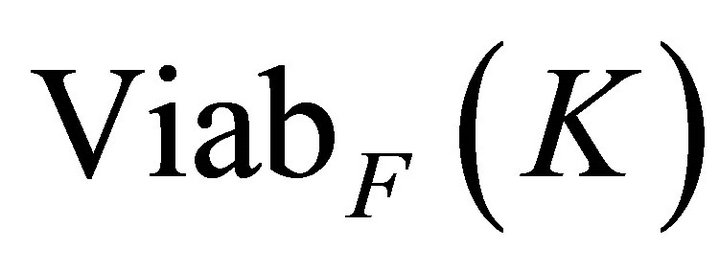 . The principle of this algorithm is to discretize Equation (1) so that the sequence of subsets
. The principle of this algorithm is to discretize Equation (1) so that the sequence of subsets 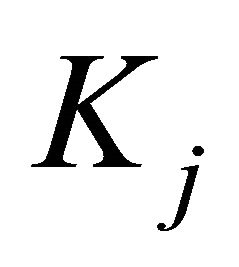 starting at
starting at 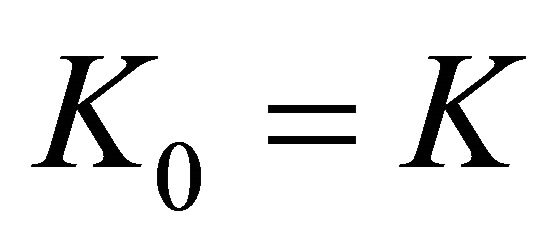 and defined recursively by
and defined recursively by
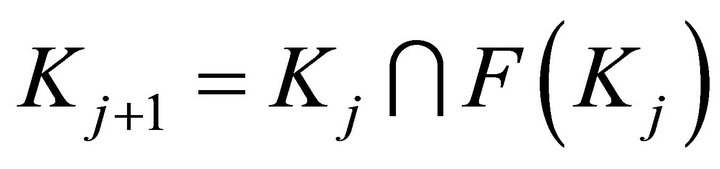 (8)
(8)
converges to a subset contained in the viability kernel of K under F. Saint-Pierre [6] showed that this sequence converges to the viability kernel if F is also Lipschitz:
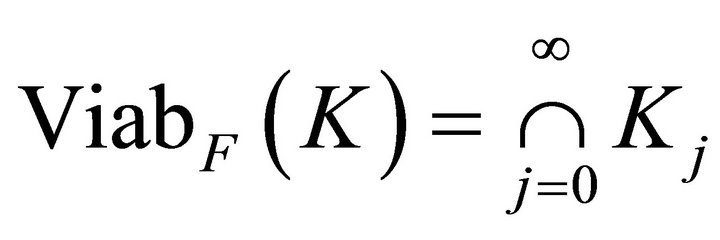 (9)
(9)
Although this algorithm is theoretically valid in any dimension, in practice, as K is reduced to a discrete grid, the algorithm must be able to update every cell of the grid at any time, which is a formidable task. The algorithm is then limited to three state dimensions.
Bonneuil [4] addressed the computation of viable states and of the viability kernel in large state dimension, using a different procedure, based on stochastic optimization. The idea is to minimize the distance to the set of constraints of solutions starting from a given state, and to assess the viability status of this state whether or not the distance minimization leads to at least one trajectory remaining in the set of constraints.
The set of constraints K is represented by a constraint on state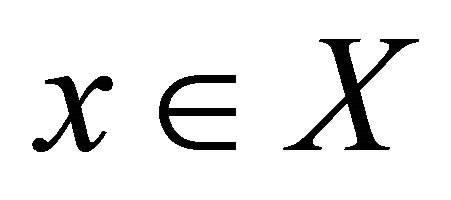 :
:
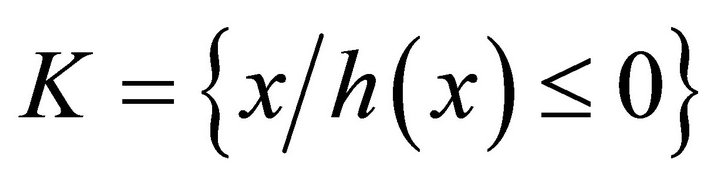 . (10)
. (10)
This constraint on h(x) can be either explicit, such as:
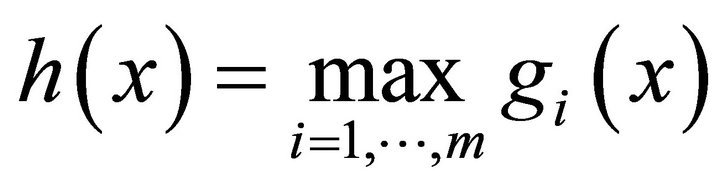 (11)
(11)
where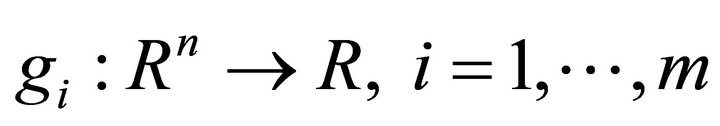 ; or implicit:
; or implicit:
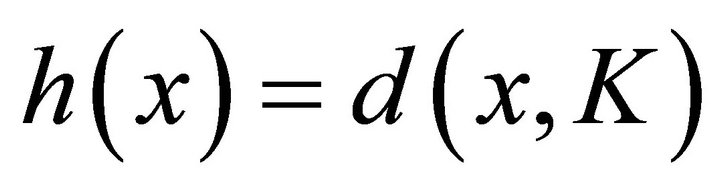 . (12)
. (12)
Define a cost c(T; x) at state x for a given time horizon T as:
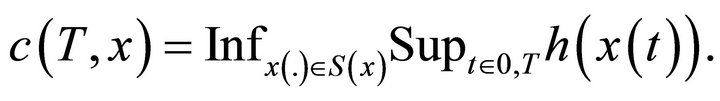 (13)
(13)
Bonneuil [4] showed the theorem:
 . (14)
. (14)
The implementation of Equation (13) in T dimensions requires a minimization routine in large dimension, such as stochastic optimization. I found exact consistency with the results obtained from Saint-Pierre’s algorithm for the three examples of [1]. For the cases involving a higher state dimension, I checked that the same result is obtained with Saint-Pierre’s algorithm when fixing all but three of the variables. To summarize the presentation of the large state dimension procedure:
• If x belongs to the interior of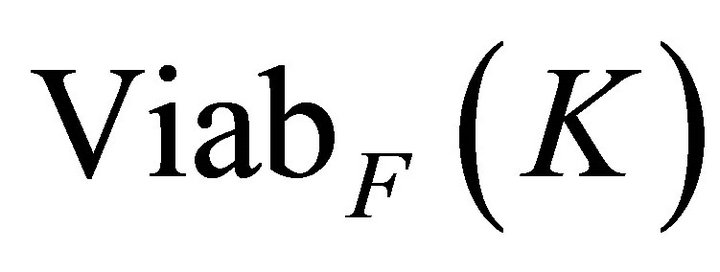 , then there is no need to go as far as the minimum of
, then there is no need to go as far as the minimum of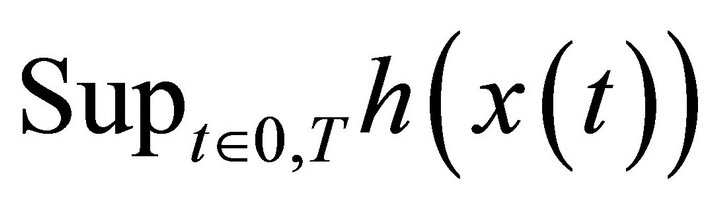 : the optimization stops as soon as one solution remaining in K is found.
: the optimization stops as soon as one solution remaining in K is found.
• If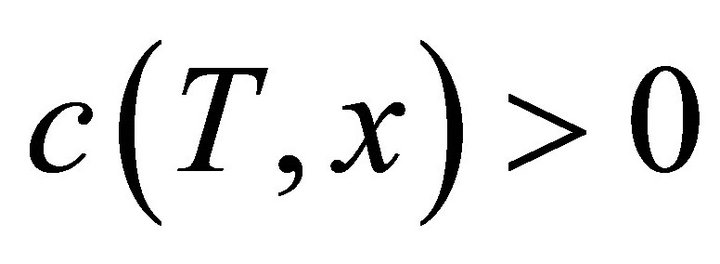 , the solution starting from x leaves K, and simulated annealing runs its course. The search for viable states is also achieved by the minimization of a distance to the set of constraints, so that the procedure relies on a double stochastic optimization: one where the initial state under examination is fixed, so as to decide whether it is viable or not, and one where this initial state is varied. There is no longer a need to memorize the state of every cell in a grid.
, the solution starting from x leaves K, and simulated annealing runs its course. The search for viable states is also achieved by the minimization of a distance to the set of constraints, so that the procedure relies on a double stochastic optimization: one where the initial state under examination is fixed, so as to decide whether it is viable or not, and one where this initial state is varied. There is no longer a need to memorize the state of every cell in a grid.
In order to compute reachable sets, I apply one of these two algorithms to the viability-capture basins identified with the reachable sets through Theorem 2.3. In the section below, I treat three noteworthy examples, moreover with time t varying.
4. Computation of Sets of Reachable States
I suggest to compute the three nonconvex reachable sets taken as examples by [1]. The image F(x) is convex in the assumption of Marchaud, but the reachable set can be nonconvex.
The results by Saint-Pierre’s [6] algorithm, as I explained, are obtained by up-dating a 3-dimensional grid, so that the display can be given with shaded facets. Bonneuil’s algorithm [4] works with points, so that, unless applying a vizualization software, the display is made of points. Baier and Gerdts [1] study the reachable set at fixed T, and in their conclusion, they call for the computation of the reachable set on an interval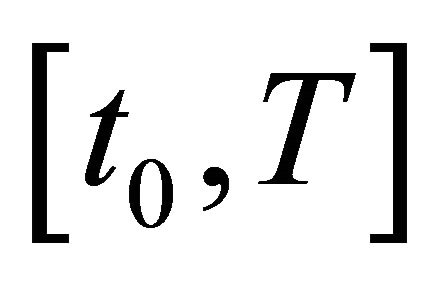 . I consider T as an additional dimension, so that I compute the capture-viability kernel of target C within K under the augmented dynamics:
. I consider T as an additional dimension, so that I compute the capture-viability kernel of target C within K under the augmented dynamics:
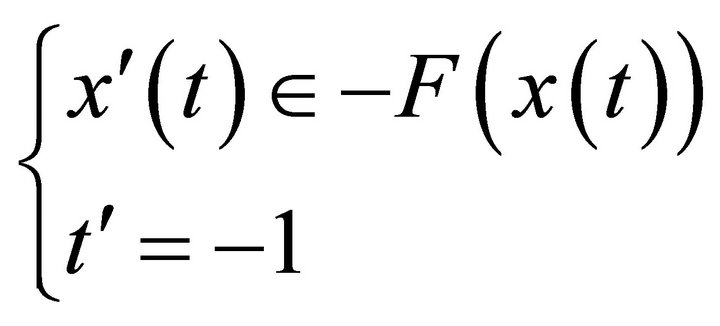 (16)
(16)
and search for the initial states 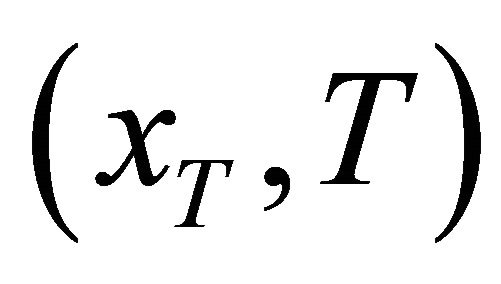 for which there exists a solution x(.) remaining in K and such that:
for which there exists a solution x(.) remaining in K and such that:
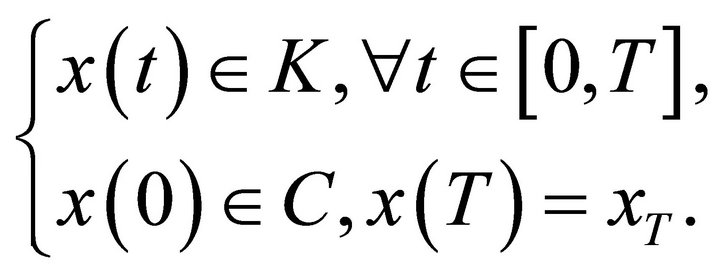 (17)
(17)
The representation is then done in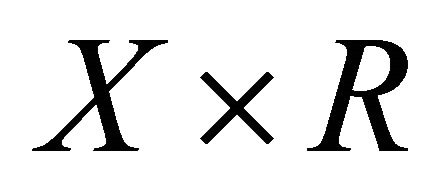 .
.
Example 1: the brachistochrone corresponds to the control problem:
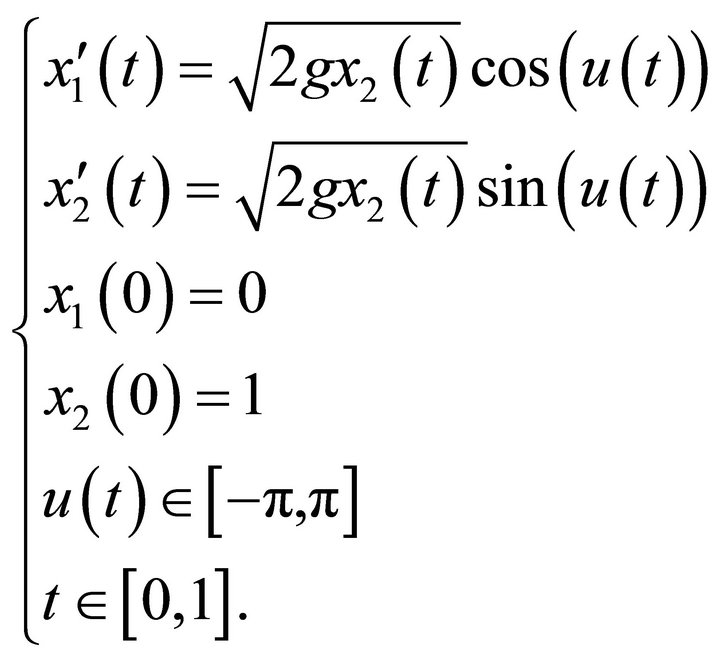 (18)
(18)
I rewrite this problem as a target problem in reverse time, for 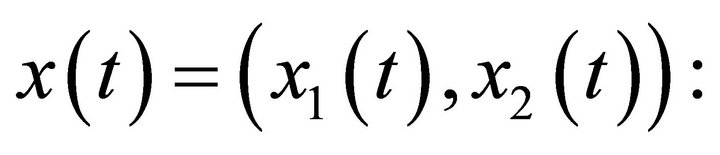
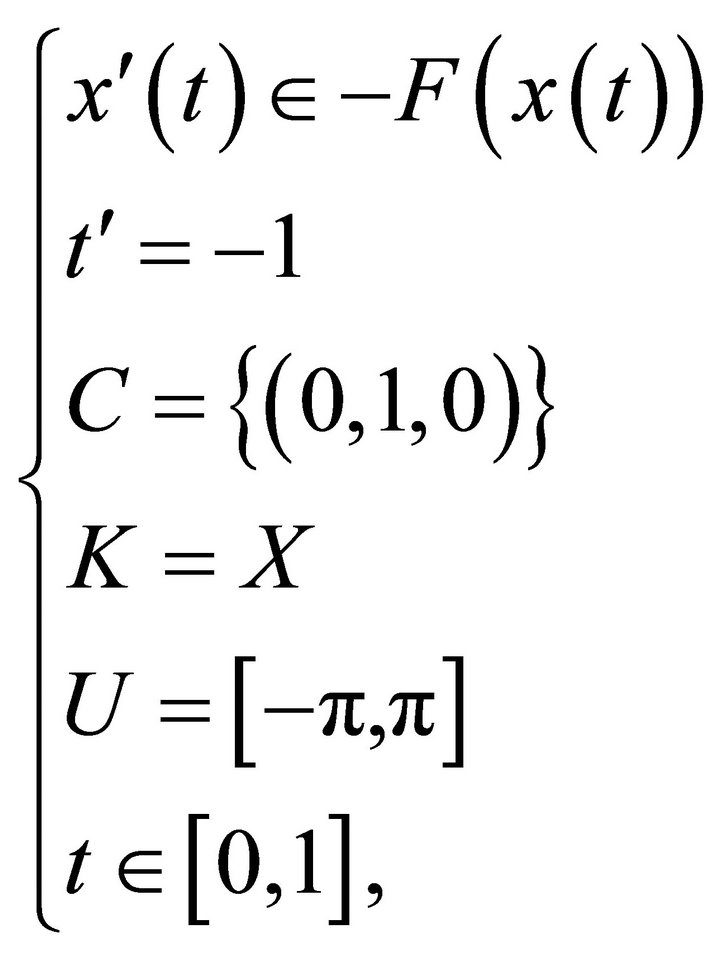 (19)
(19)
with
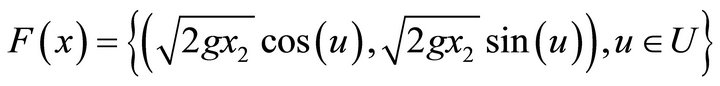 . (20)
. (20)
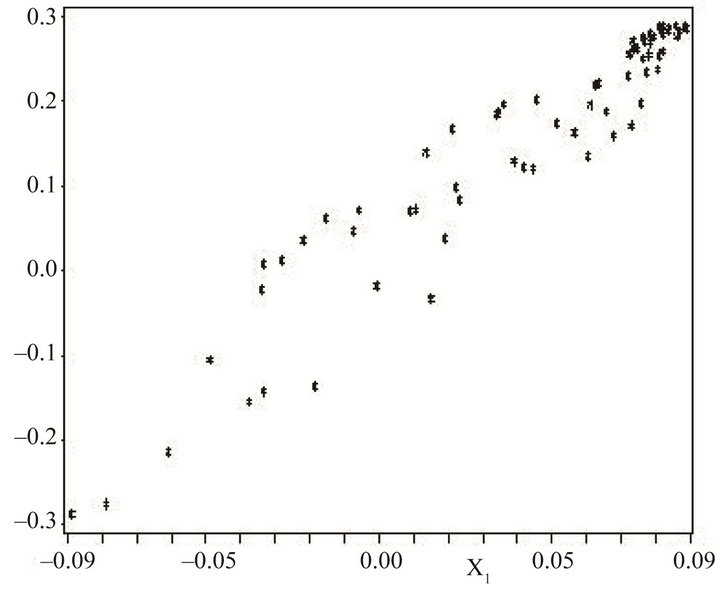
Figure 1 represents the capture-viability kernel in , with X equal to R. To get the reachable set at a given time T, one has to take a section of this set at T constant; to get the reachable set in
, with X equal to R. To get the reachable set at a given time T, one has to take a section of this set at T constant; to get the reachable set in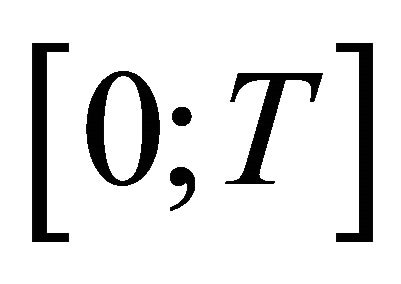 , one has to take the projection of the capture-viability up to T onto the T = 0 plane. In viability algorithms, the time horizon T is taken as an additional variable, so that the reachable sets for all T are computed at once, contrary to other procedures.
, one has to take the projection of the capture-viability up to T onto the T = 0 plane. In viability algorithms, the time horizon T is taken as an additional variable, so that the reachable sets for all T are computed at once, contrary to other procedures.
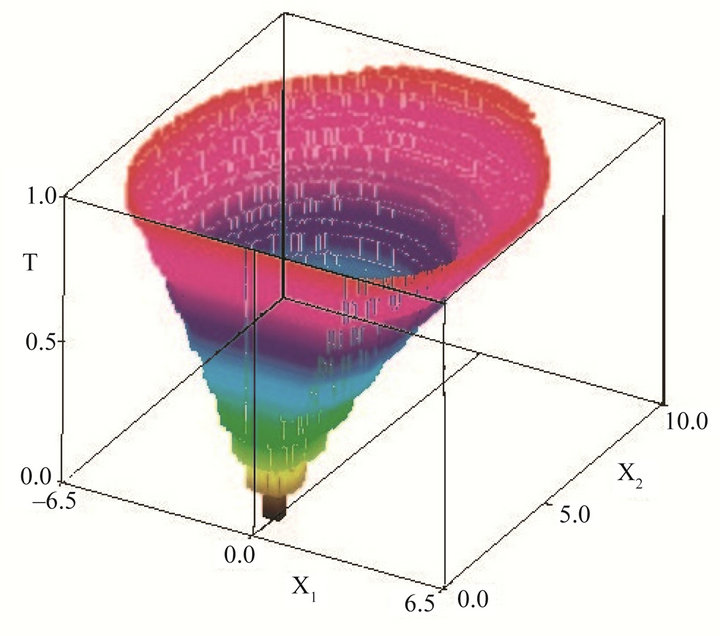
Figure 1. Reachable sets at time T varying: brachistochrone.
Example 2: Rayleigh problem The control problem [1] is:
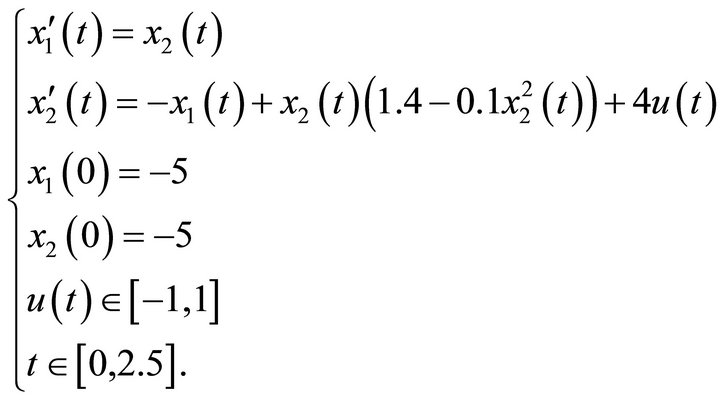 (21)
(21)
I rewrite this problem as a target problem in reverse time, for 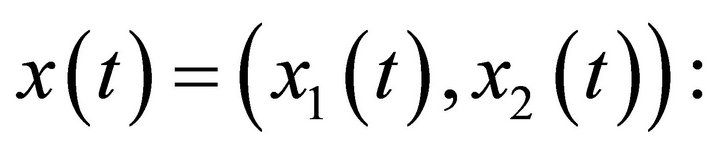
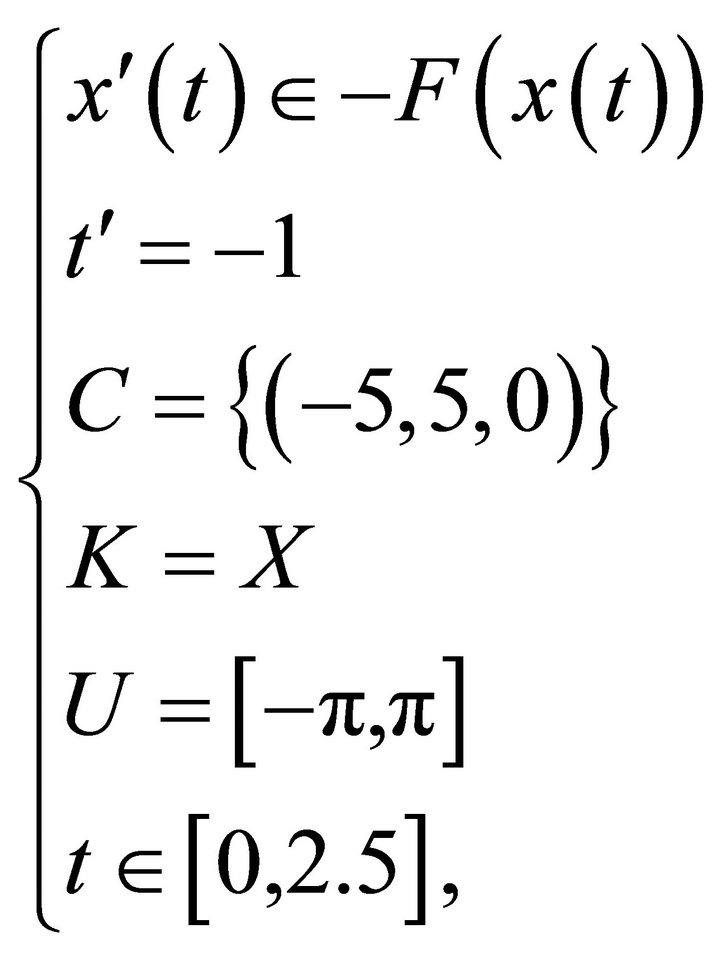 (22)
(22)
with
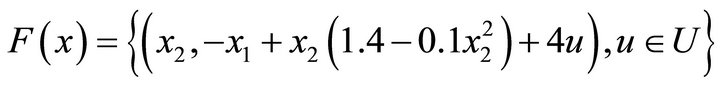 (23)
(23)
The reachable sets at T varying are represented on Figure 2.
Example 3: Kenderov The control problem [1] is:
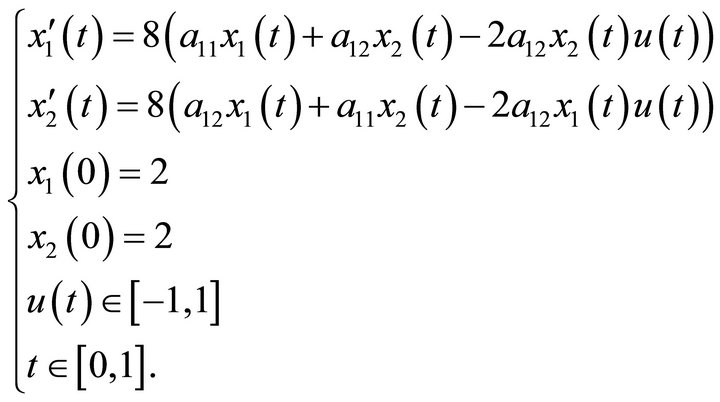 (24)
(24)
Baier and Gerdts [1] consider 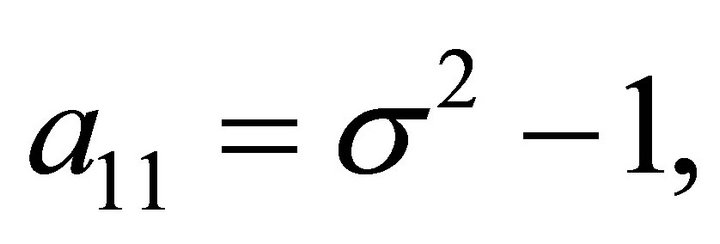
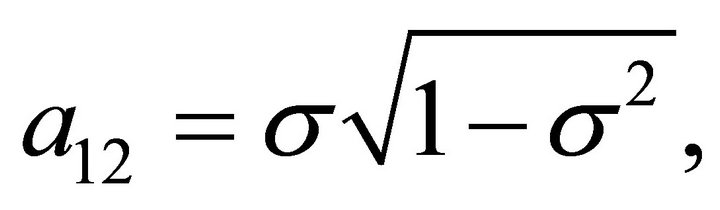 and
and 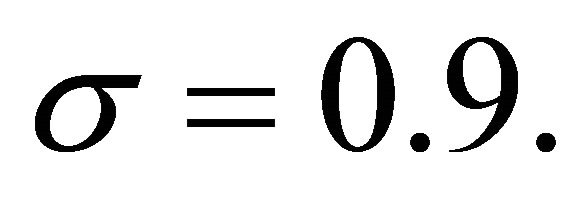 I rewrite this problem as a target problem in reverse time, for
I rewrite this problem as a target problem in reverse time, for
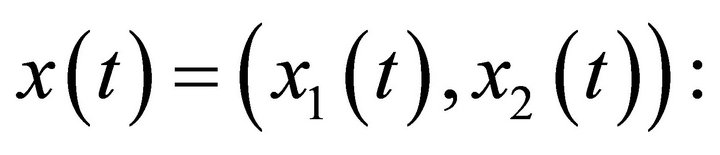
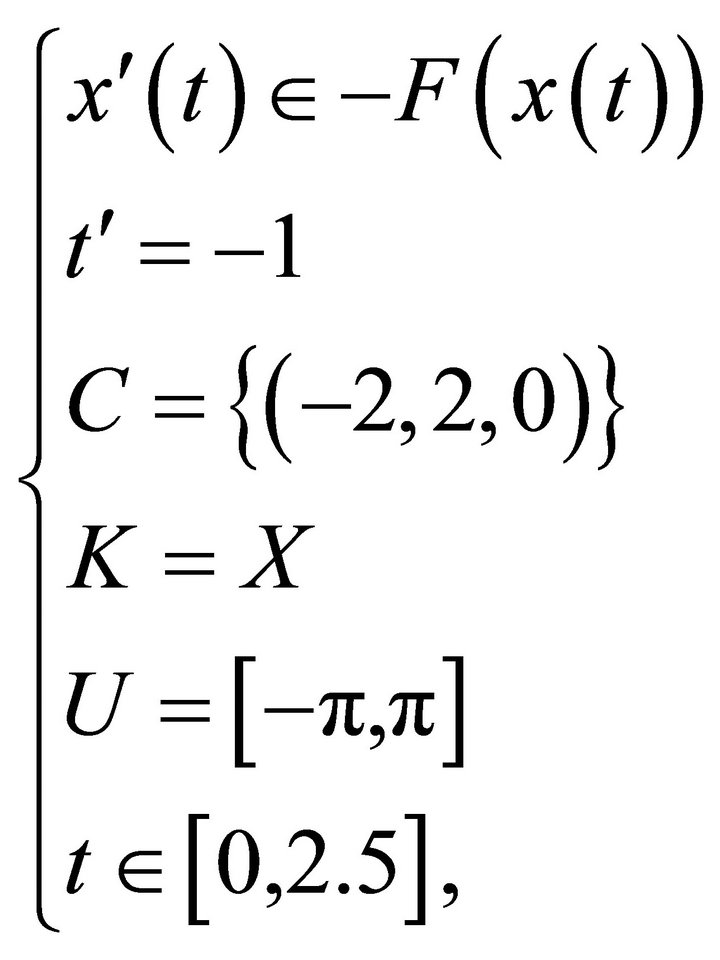 (25)
(25)
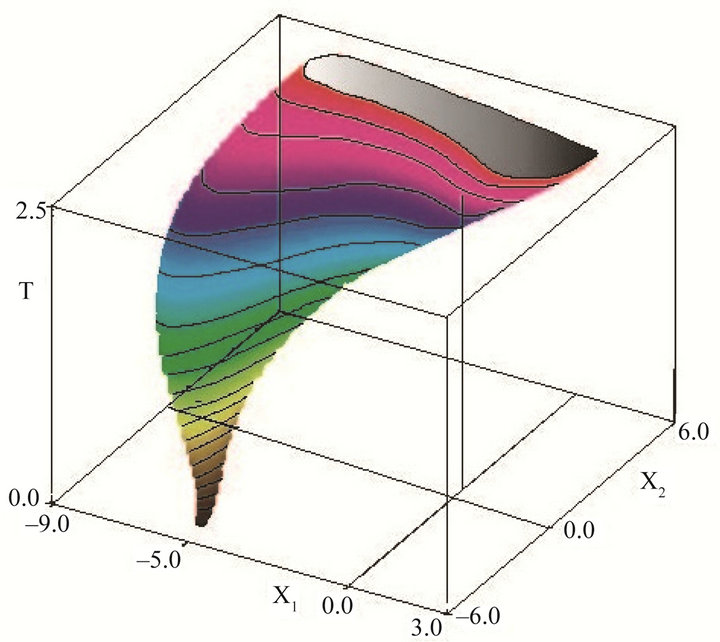
Figure 2. Reachable sets at time T varying: Rayleigh.
with
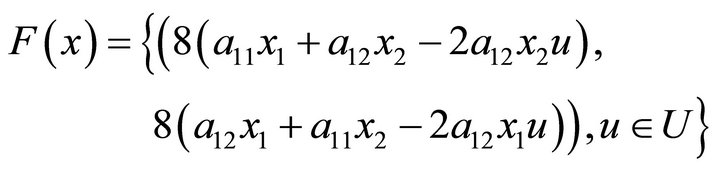 (26)
(26)
The reachable sets at T varying are represented on Figure 3.
Example 4: in dimension p + 1 I suggest the control problem:
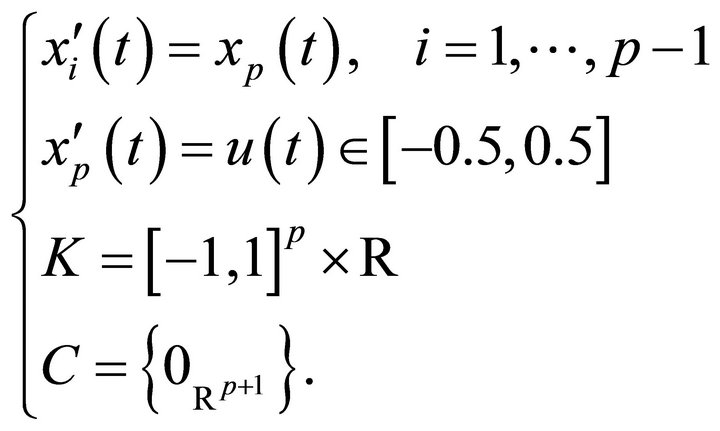
The projection of the reachable sets at T varying in [0;
0.6] onto the plane 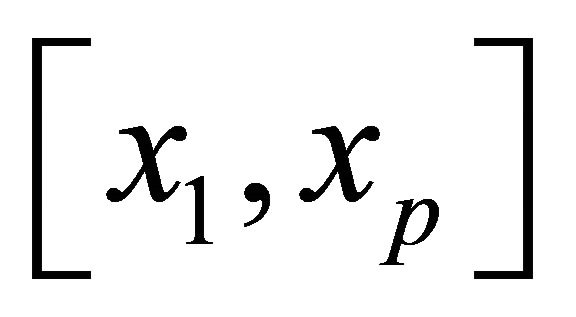 for p = 10 is represented on
for p = 10 is represented on
Figure 4, and the same projection at T = 0.6 on Figure 5. The representation of sets in dimension above three is problematic, but the result is that, in large state dimension, a data set of points can be produced to encompass the reachable set. Then it becomes a problem of delineating a set through knowing a cloud of points.
5. Conclusion
Reachable sets expressed as capture-viability kernels in reverse time allow the use of viability algorithms, either in 2 + 1 dimensions with Saint-Pierre’s [6] or in any finite state dimension p + 1 with Bonneuil’s [4]. This procedure firstly allows avoiding the difficult solving of HJB, and secondly allows the computation of reachable sets in large dimensions. This reasoning in terms of viability
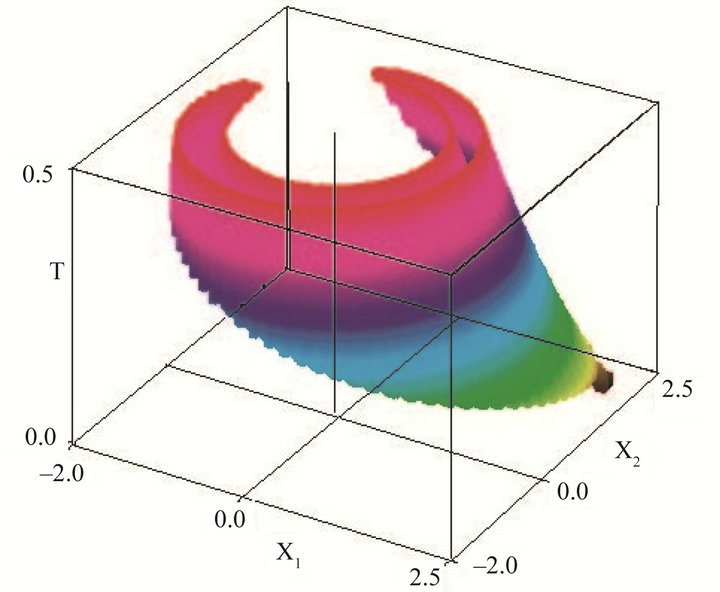
Figure 3. Reachable sets at time T varying: Kenderov.
is flexible and proved useful in the computation of maxima under viability constraints [7].
REFERENCES
- R. Baier and M. Gerdts, “A Computational Method for Non-Convex Reachable Sets Using Optimal Controls,” Proceedings of the European Control Conference 2009, Budapest, 23-26 August 2009, pp. 97-101.
- R. Baier, “Set-Valued Integration and Discrete Approximation. Reachable Sets,” Bayreuth Mathematical Reports 50, University of Bayreuth, Bayreuth, 1995.
- R. Baier, M. Gerdts and I. Xausa, “Approximation of Reachable Sets Using Optimal Control Algorithms,” 2011. http://num.math.uni-bayreuth.de/en/publications/2012/baier_gerdts_xausa_approx_reach_sets_2011/index.html
- N. Bonneuil, “Computing the Viability Kernel in Large State Dimension,” Journal of Mathematical Analysis and Applications, Vol. 323, No. 2, 2006, pp. 1444-1454. doi:10.1016/j.jmaa.2005.11.076
- J.-P. Aubin, “A concise introduction to Viability Theory, Optimal Control and Robotics,” École Normale Supérieure de Cachan, Cachan, 2003.
- P. Saint-Pierre, “Approximation of the Viability Kernel,” Applied Mathematics and Optimization, Vol. 29, No. 2, 1994, pp. 187-209. doi:10.1007/BF01204182
- N. Bonneuil, “Maximum under Continuous-Discrete-Time Dynamic with Target and Viability Constraints,” Optimization, Vol. 61, No. 8, 2012, pp. 901-913. doi:10.1080/02331934.2011.605127


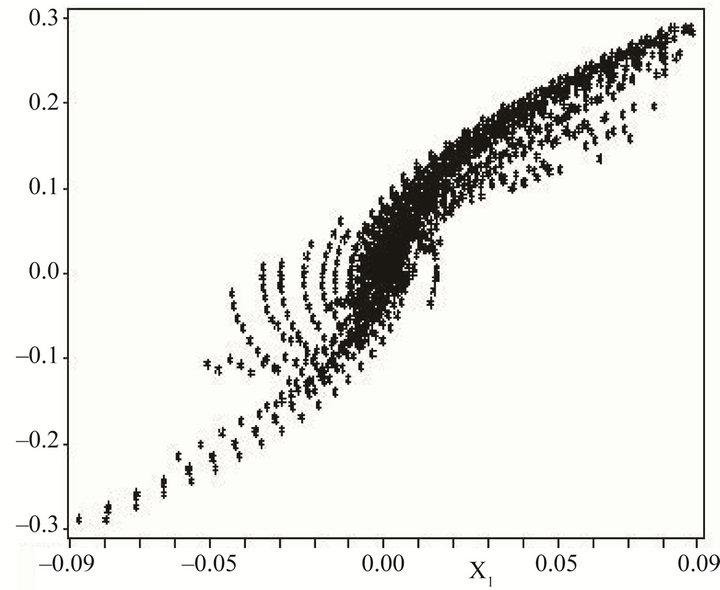
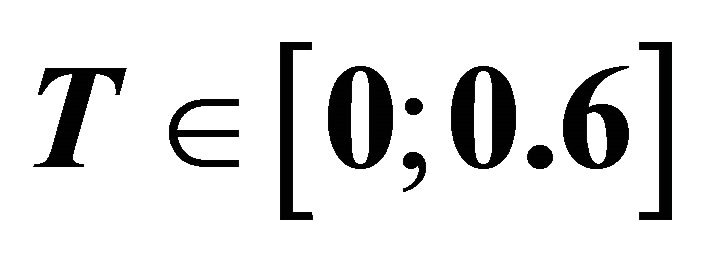 for the 10 + 1 dimension example.
for the 10 + 1 dimension example.