Applied Mathematics
Vol.3 No.8(2012), Article ID:21485,14 pages DOI:10.4236/am.2012.38123
The Mathematical Modelling for Studying the Influence of the Initial Stresses and Relaxation Times on Reflection and Refraction Waves in Piezothermoelastic Half-Space
Department of Mathematics, Science College, Jazan University, Jazan, KSA
Email: dr.math999@hotmail.com
Received June 4, 2012; revised July 4, 2012; accepted July 11, 2012
Keywords: Piezo-Thermoelasticity; Quasi Plane Longitudinal Waves; Reflection and Refraction Coefficients; Initial Stresses; Green and Lindsay Theory; Relaxation Time
ABSTRACT
The present paper concentrates on the study of reflection and refraction phenomena of waves in pyroelectric and piezoelectric media under initial stresses and two relaxation times influence by apply suitable conditions. The generalized theories of linear piezo-thermoelasticity have been employed to investigate the problem. In two-dimensional model of transversely isotropic piezothermoelastic medium, there are four types of plane waves quasi-longitudinal (qP), quasitransverse (qSV), thermal wave (T-mode), and potential electric waves (φ-mode) The amplitude ratios of reflection and refraction waves have been obtained. Finally, the results in each case are presented graphically.
1. Introduction
Piezoelectricity is the phenomenon of electricity produced by the squeezing or stretching of certain materials. The propagation of waves in piezoelectric materials is one of the richest fields for scientists because it has many applications in piezoelectric: filters, resonators, transducers, sensors and other devices. This kind of devices represent a great challenge in the industry, and as a result it has been an object of different investigations in the last decades, because these devices are to operate under various piezoelectric-thermo-mechanical conditions over a broad spectrum, in view of its importance to industry applications. The theory of thermo-piezoelectricity was first proposed by Mindlin [1]. The physical laws for the thermo-piezoelectric materials have been explored by Nowacki [2,3]. Chandrasekharaiah [4] developed the generalized theory of thermo-piezoelectricity by taking in account the finite speed of propagation of thermal disturbances. Sharma and Kumar [5] studied plane harmonic waves in piezothermoelastic materials. The propagation of Rayleigh waves in generalized piezothermoelastic half space is investigated by Sharma and Walia [6].
Deresiewicz [7] studied the reflection of plane waves from a plane stress free boundary in coupled theory of thermoelasticity and investigated the effect of boundaries on the waves. Generalized theories of thermoelasticity were introduced in order to eliminate the shortcomings of the classical dynamic thermoelasticity. A flux rate term into Fourier law of heat conduction is incorporated by Lord and Shulman [8], which includes a hyperbolic heat transport equation admitting finite speed, though large for thermal signals. Green and Lindsay [9], by including temperature-rate among the constitutive variables, developed a temperature-rate-dependent thermo-elasticity that does not violate the classical Fourier law of heat conduction for bodies having center of symmetry. Many authors concentrate in studying the reflection and refraction waves in thermoelastic media, like Sinha and Sinha [10], Sharma [11], Sinha and Elsibai [12,13], Abd-Alla and Al-Dawy [14], Sharma et al. [15]. The reflection of piezothermoelastic waves from the stress free, thermally insulated or isothermal, open circuit boundary of transversely isotropic piezothermo-elastic half space under the influence of thermal relaxation have been discussed by Sharma et al. [16], they proved that the amplitude coefficients of waves are related to the positions on the interface. Kuang and Yuan [17] studied the reflection and transmission theories of homogeneous and inhomogeneous waves in pyroelectric and piezoelectric medium. Abd-alla et al. [18,19] studied the reflection and refraction phenomena in piezoelectric media under initial stresses. In this paper, the reflection and refraction problem from the interface of the piezothermoelastic materials under initial stresses influence in the context of Green and Lindsay theory are studied in details and numerical results are given. In two dimensional reflection and refraction problem there is only one incident quasi-Longitudinal wave, so there are four modes of thermo elastic and potential waves.
2. Governing Equations of Generalized Piezothermoelastic of Hexagonal Type
Consider a homogeneous, anisotropic, generalized piezothermoelastic medium of hexagonal type. The origin is taken on the thermoelasticity and stress-free plane surface and z-axis is directed normally into the half-space which is represented by . Let the wave motion in this medium be characterized by: the displacement vector
. Let the wave motion in this medium be characterized by: the displacement vector 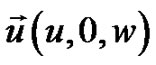 , the electric potential function
, the electric potential function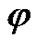 , all these quantities being dependent only on the variables x, z, t. (see Figure 1).
, all these quantities being dependent only on the variables x, z, t. (see Figure 1).
The governing field equations of generalized hexagonal piezothermoelastic for two dimensional motion in the 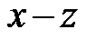 plane are [5]:
plane are [5]:
• The coupled constitutive relations can be written in the forms:
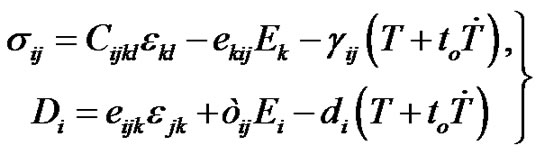 (1)
(1)
• The strain-displacement relation and the electric field according to the quasi-static approximation have the forms as:

 (2)
(2)
• The equations of motion under initial stress, Gauss’s divergence equation, and heat conduction can be written as (3).
where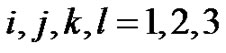 ;
;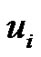 ,
, 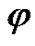 , and
, and 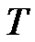 are the mechanical displacement, electric potential and absolute temperature, respectively;
are the mechanical displacement, electric potential and absolute temperature, respectively; ,
, 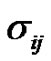 and
and 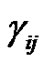 are the strain, stress and thermal elastic coupling tensors, respectively;
are the strain, stress and thermal elastic coupling tensors, respectively;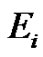 ,
, 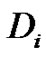 are the electric field and electric displacement, respectively;
are the electric field and electric displacement, respectively;  is the elastic parameters tensor;
is the elastic parameters tensor;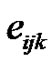 ,
,  and
and 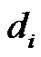 are the piezoelectric, dielectricpyroelectric moduli, respectively;
are the piezoelectric, dielectricpyroelectric moduli, respectively; 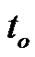 is the relaxation time;
is the relaxation time;  and
and 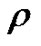 are the initial stress tensor and mass density, respectively;
are the initial stress tensor and mass density, respectively; 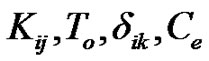 are the heat conduction tensor, reference temperature, Kronecker delta, specific heat at constant strain, respectively. The constitutive relations (1) of the hexagonal (6 mm) crystals symmetry given by
are the heat conduction tensor, reference temperature, Kronecker delta, specific heat at constant strain, respectively. The constitutive relations (1) of the hexagonal (6 mm) crystals symmetry given by
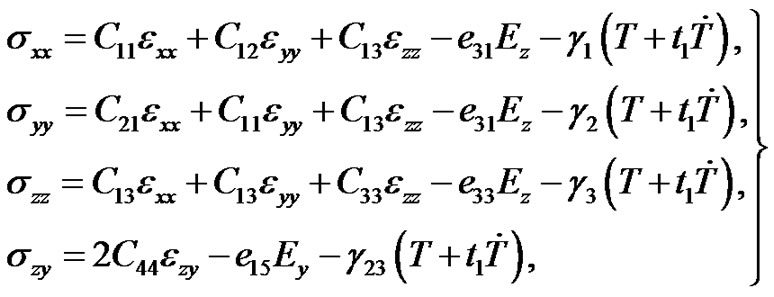
 (4)
(4)
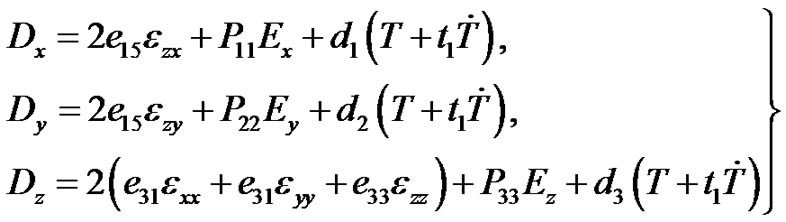 (5)
(5)
Substituting Equations (4)-(5) into Equation (3), we get (6).
3. Solution of the Problem for Incident qP-Wave
We will consider a transversely isotropic piezoelectric half space (see Figure 1). The lower medium and upper medium occupy the spaces 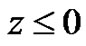 and
and  respectively. The x-axis is taken along the interface and the z-axis is directed vertically downwards. For the oblique incidence of the lower plane quasi-longitudinal (qP) wave from the piezothermoelastic medium at the interface z = 0, all kinds of scattered waves are depicted in Figure 1. The reflection and refraction wave fields consist of the reflected quasi-longitudinal (qP), quasi-transverse (qSV) waves and refracted (qP) and (qSV) waves, electric potential (
respectively. The x-axis is taken along the interface and the z-axis is directed vertically downwards. For the oblique incidence of the lower plane quasi-longitudinal (qP) wave from the piezothermoelastic medium at the interface z = 0, all kinds of scattered waves are depicted in Figure 1. The reflection and refraction wave fields consist of the reflected quasi-longitudinal (qP), quasi-transverse (qSV) waves and refracted (qP) and (qSV) waves, electric potential (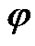 ), and heat (T) waves. For the pre-
), and heat (T) waves. For the pre-
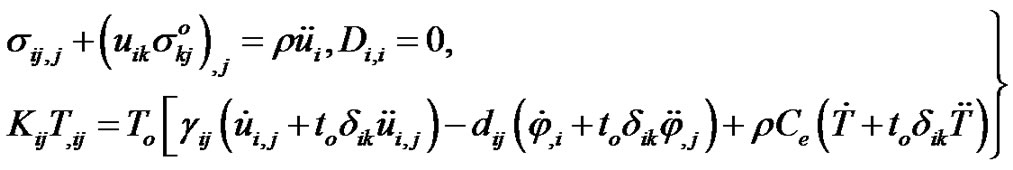 (3)
(3)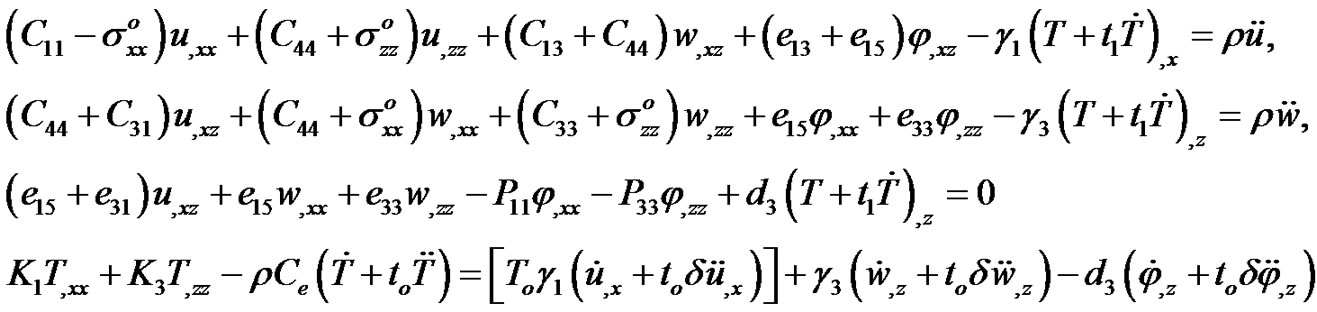 (6)
(6)

Figure 1. Incidence, reflected and refracted qP waves.
sent hexagonal crystals (transversely isotropic materials), we will consider the motion in the plane ( plane). According to Achenbach [20] the solution of Equations (6) written as
plane). According to Achenbach [20] the solution of Equations (6) written as
 (7)
(7)
where 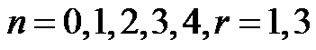
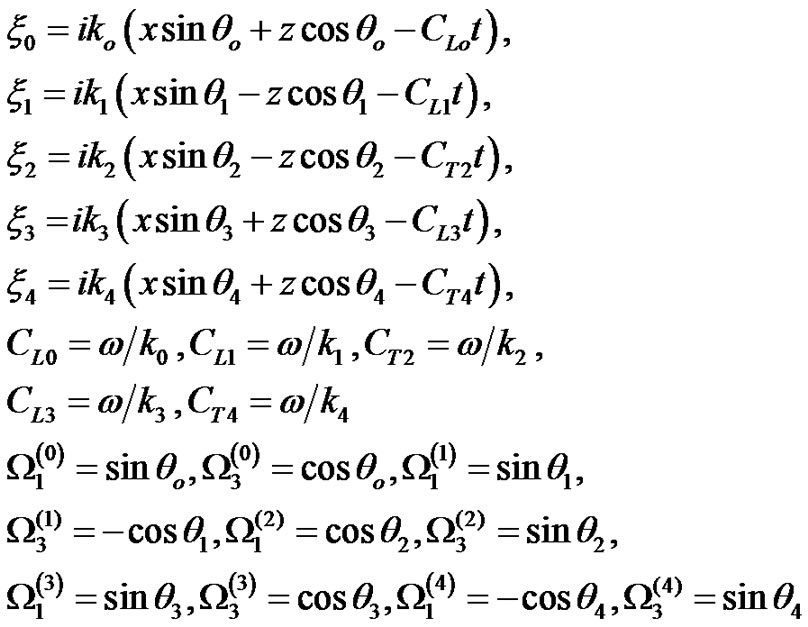
where n = 0 represent the incidence of qP wave, n = 1, 2, represent the reflected waves, n = 3, 4 represent the refracted waves.
4. Continuous Conditions on the Interface of Piezothermoelastic Materials
Consider the problem of two bounded semi-infinite pie-- zothermoelastic materials with the interface z = 0 subjected to a harmonic incident wave of frequency ω with an incident angle  as shown in Figure 1. The continuous conditions on the interface are:
as shown in Figure 1. The continuous conditions on the interface are:
1) The free mechanical boundary conditions:
 (8)
(8)
2) The electrical condition:
 (9)
(9)
3) The thermal condition:
 (10)
(10)
Substituting Equations (2), (4), and (7) into Equations (8)-(10), we obtain the following set of equations:
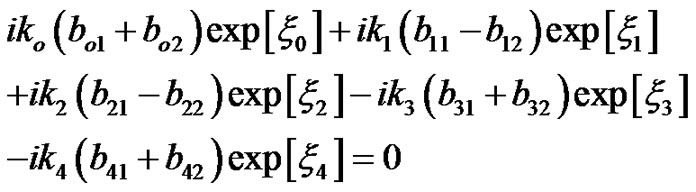 (11)
(11)
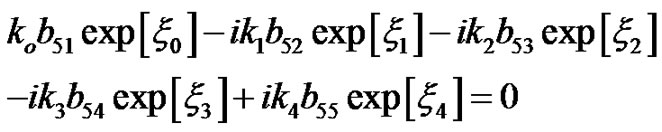 (12)
(12)
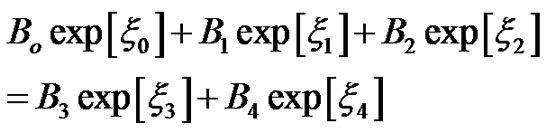 (13)
(13)
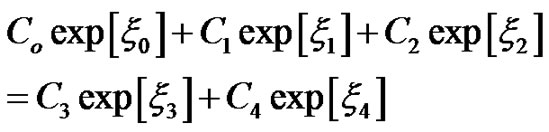 (14)
(14)
where
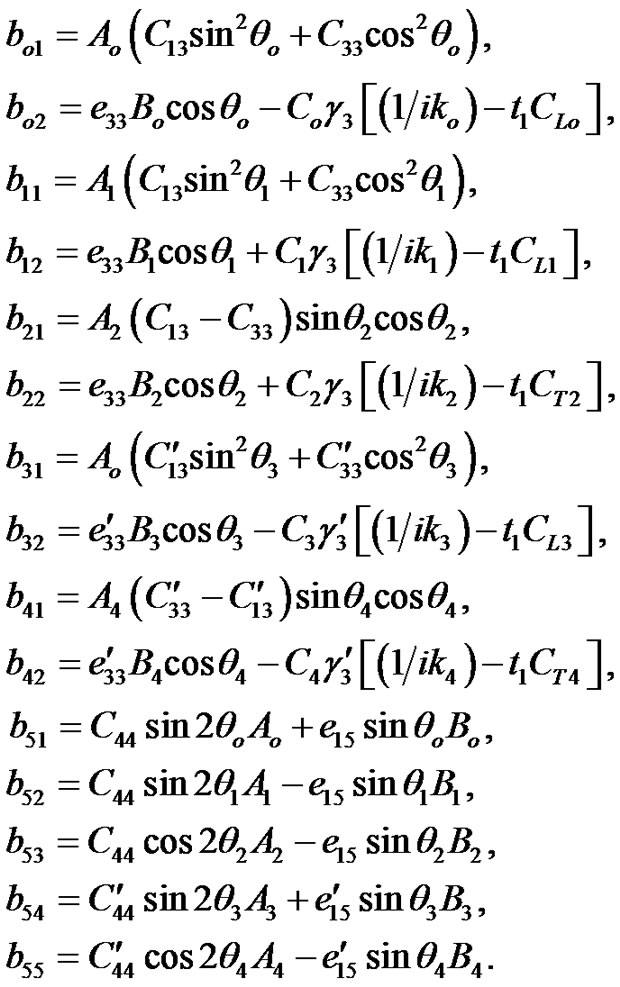
Equations (11)-(14) must be valid for all values of t and x, hence
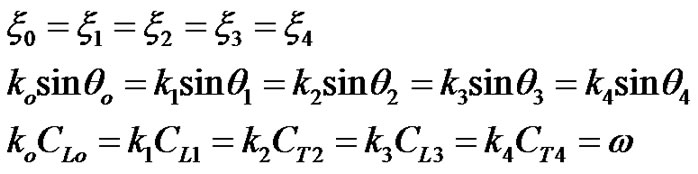 (15)
(15)
From the above relations, we get
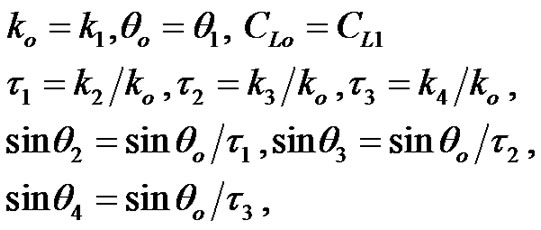 (16)
(16)
Furthermore, we should now use the equations of motion of the media, i.e., Equation 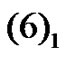 which will give us additional relations between amplitudes.
which will give us additional relations between amplitudes.
 (17)
(17)
where .
.
So, substituting from Equation (7) (when z = 0) into Equation (17) for the incident (qP) wave, the reflected and refracted waves, we get
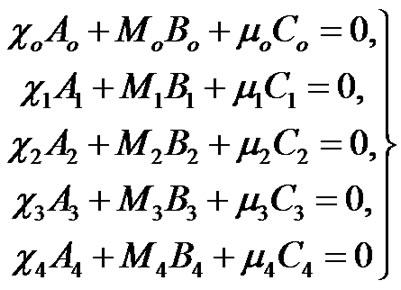 (18)
(18)
where
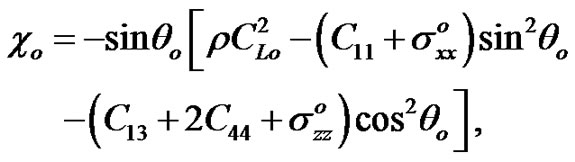
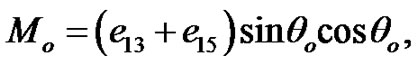

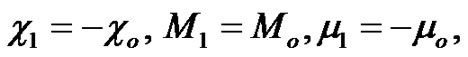
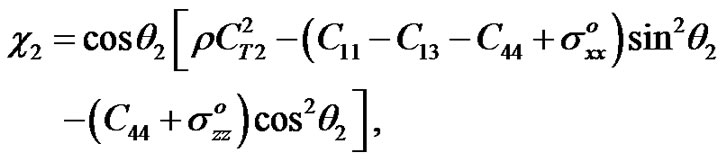
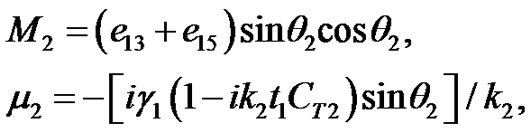
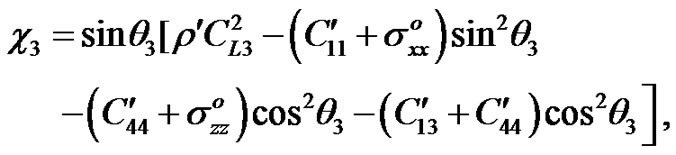
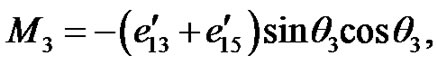
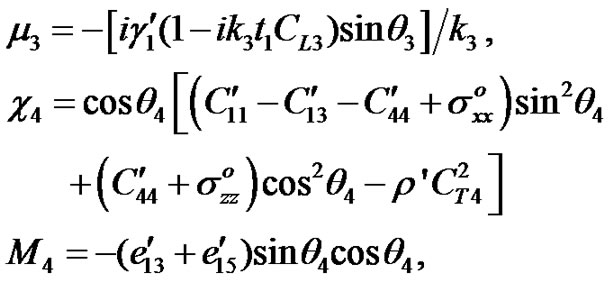

By using Equation (7) into Equation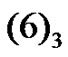 , we get
, we get
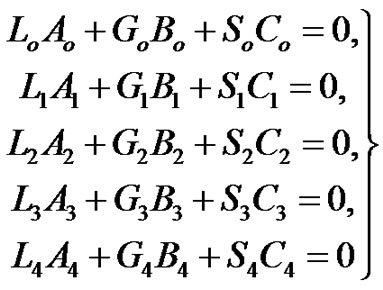 (19)
(19)
where

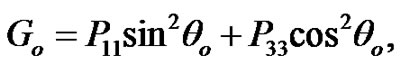

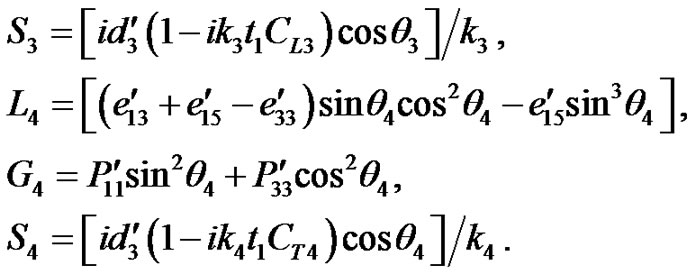
By using Equation (7) into Equation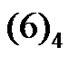 , we get
, we get
 (20)
(20)
where
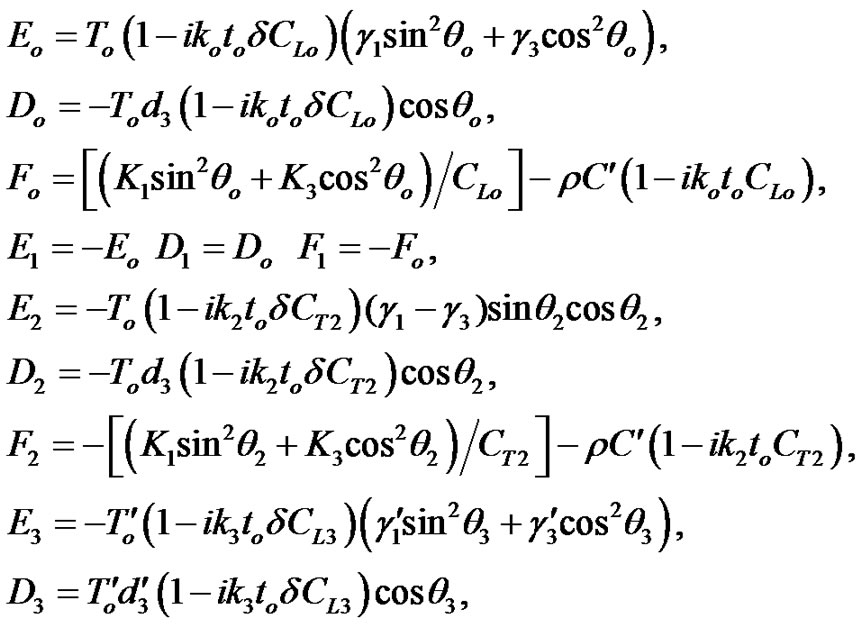
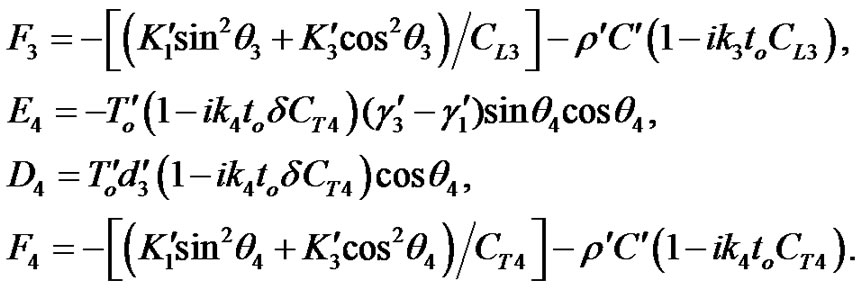
From Equations (11)-(14), it is easy to see that
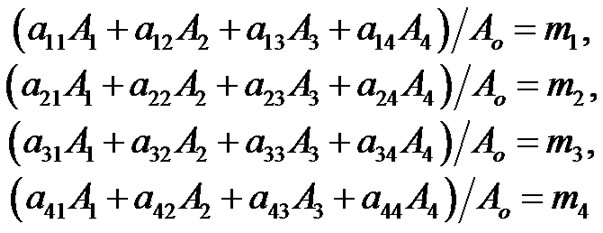 (21)
(21)
where


Solving Equation (21), we can determine the reflection and refraction coefficients as:
 (22)
(22)
where

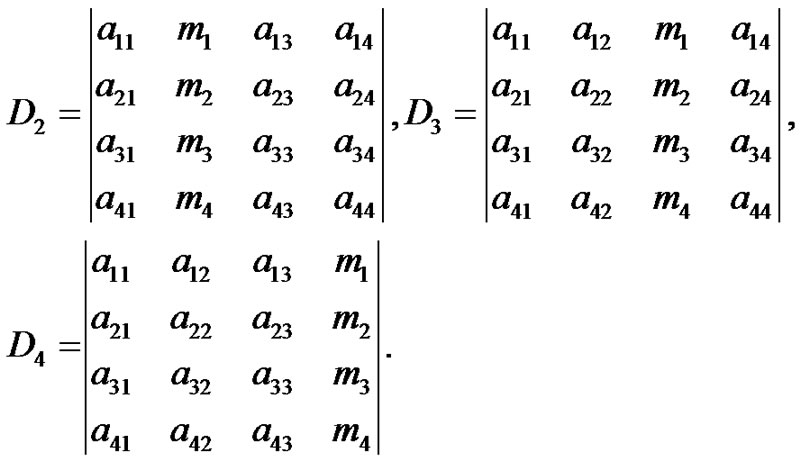
By using Equations (18)-(20) we get:
 (23)
(23)
5. Numerical Results and Discussion
The material chosen for the purpose of numerical calculations is (6 mm class) Cadmium Selenide (CdSe) for upper medium and Lead Zirconate Titanate ceramics (PZT-5A) for lower medium, which are transversely isotropic materials. The physical data for a single crystal of CdSe material and PZT-5A ceramics are given as [6,21]:
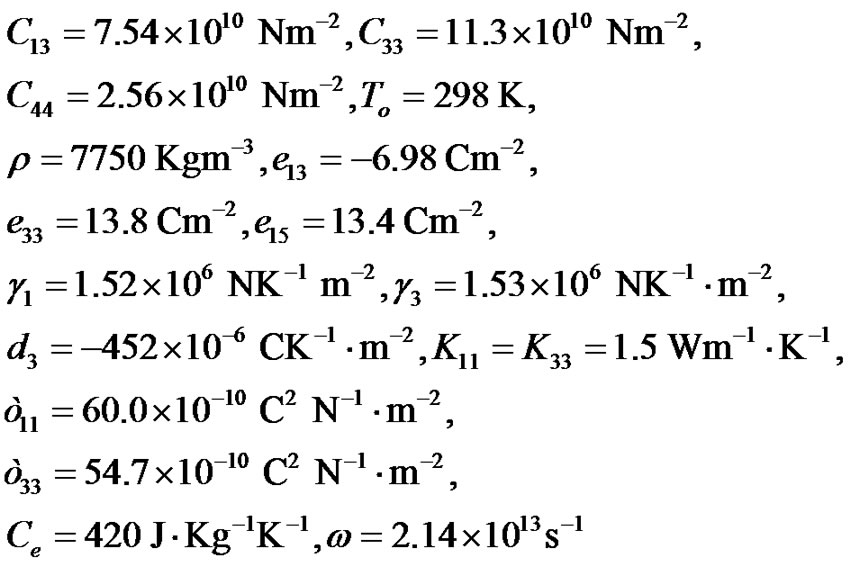
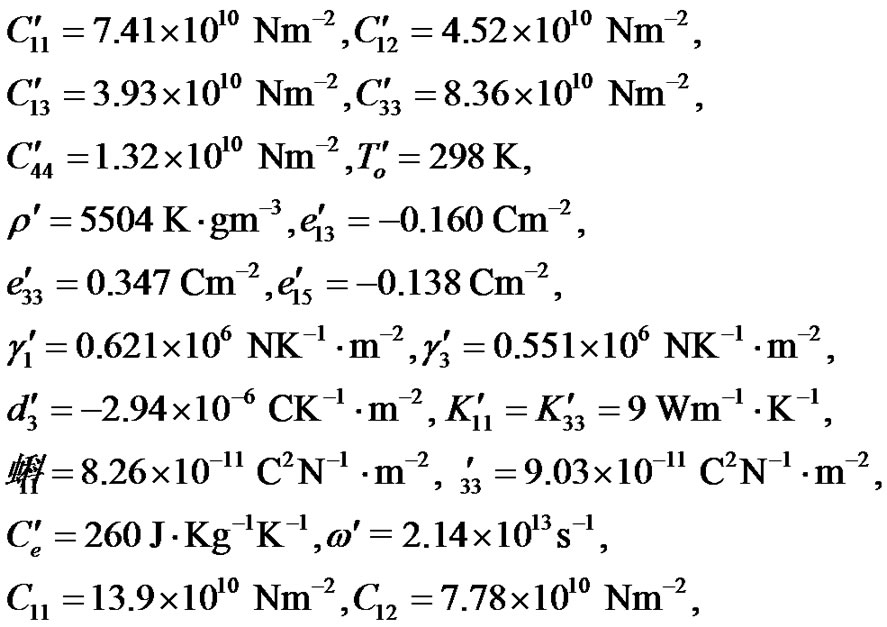
Here the thermal relaxation time  is estimated its value about
is estimated its value about 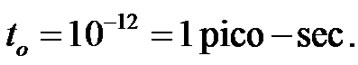 and
and  is taken proportional to
is taken proportional to . The variations of phase velocities computed from
. The variations of phase velocities computed from
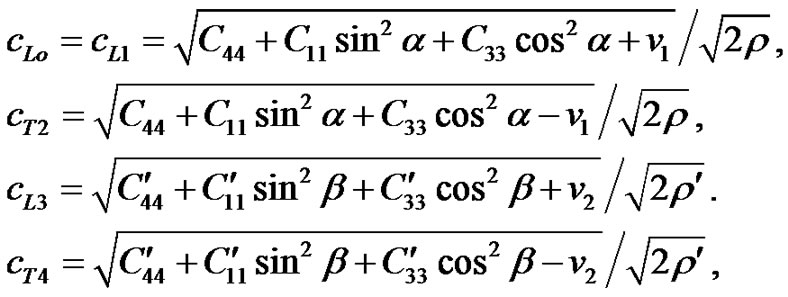
where 

The real and imaginary values of the amplitude ratios 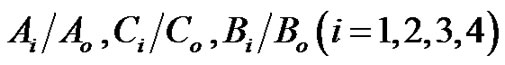 corresponds to qP, qSV, T,
corresponds to qP, qSV, T,  -mode for incident qP wave are computed for various angle of incidence (in degrees) under various of initial stresses
-mode for incident qP wave are computed for various angle of incidence (in degrees) under various of initial stresses , in the context of Green and Lindsay theory (G-L) of generalized thermoelasticity [9] where
, in the context of Green and Lindsay theory (G-L) of generalized thermoelasticity [9] where
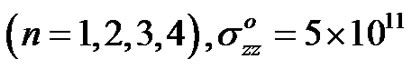
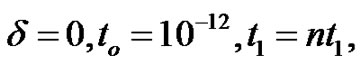 .
.
The reflection and refraction coefficients have been presented on curves in Figures 2-21 which have the following observations:
• Figure 2 represents the relation between the imaginary and real parts of reflection coefficient 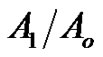 and angle of incidence
and angle of incidence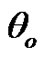 , we also observe that the relaxation time
, we also observe that the relaxation time 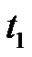 effect appears only in the range
effect appears only in the range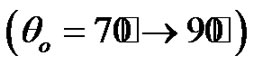 .
.
• Figure 3 represents the relation between the imaginary and real part of the reflection coefficient 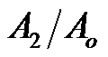 with the angle of incidence
with the angle of incidence , as well as the relaxation time
, as well as the relaxation time 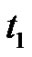 effect.
effect.
• Figure 4 represents the relation between the imaginary and real of refraction coefficient  with the angle of incidence
with the angle of incidence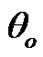 , as well as the relaxation time
, as well as the relaxation time 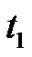 effect, in those Figures we noted the
effect, in those Figures we noted the  values decreases with
values decreases with 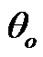 increase gradually until it reaches the minimum value when
increase gradually until it reaches the minimum value when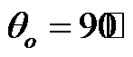 , also the relaxation time
, also the relaxation time 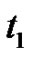 related by inverse relation with , and the positive relation with
related by inverse relation with , and the positive relation with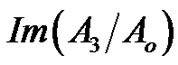 .
.
• Figure 5 represents the relation between the imaginary and real of refraction coefficient 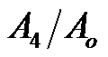 with
with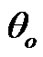 , as well as the relaxation time
, as well as the relaxation time 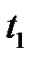 effect, in those figures we noted
effect, in those figures we noted 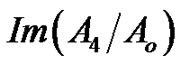 increases with the value of
increases with the value of 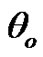 increase gradually until it reaches the maximum value when
increase gradually until it reaches the maximum value when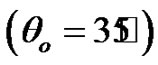 , and then decreasing Its value in the following period, while decreasing Its value in
, and then decreasing Its value in the following period, while decreasing Its value in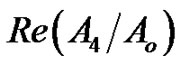 , with increasing
, with increasing  until it reaches the minimum value when
until it reaches the minimum value when  It is clear
It is clear

Figure 2. Imaginary and real parts of reflection coefficient A1/Ao as a function of incidence angle θo for different values of the relaxation times for (G-L) model.
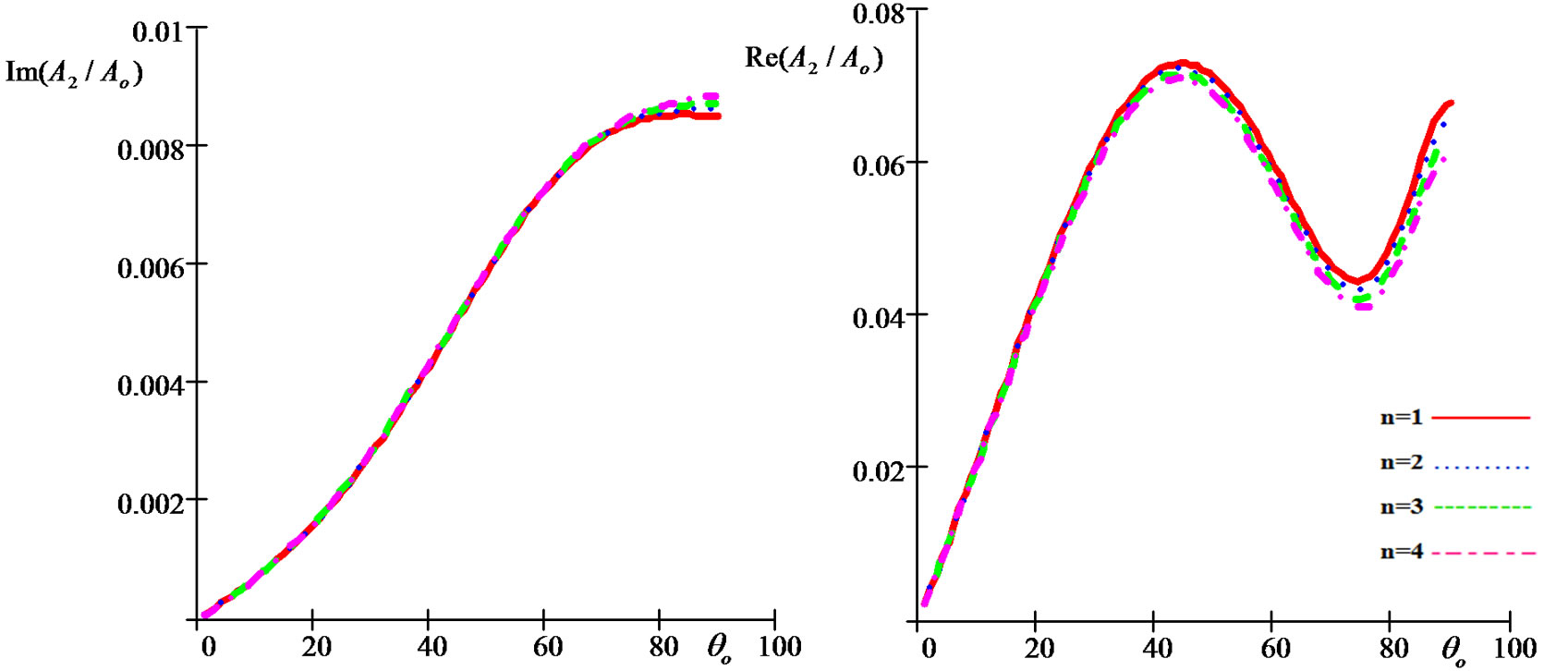
Figure 3. Imaginary and real parts of reflection coefficient A2/Ao as a function of incidence angle θo for different values of the relaxation times for (G-L) model.
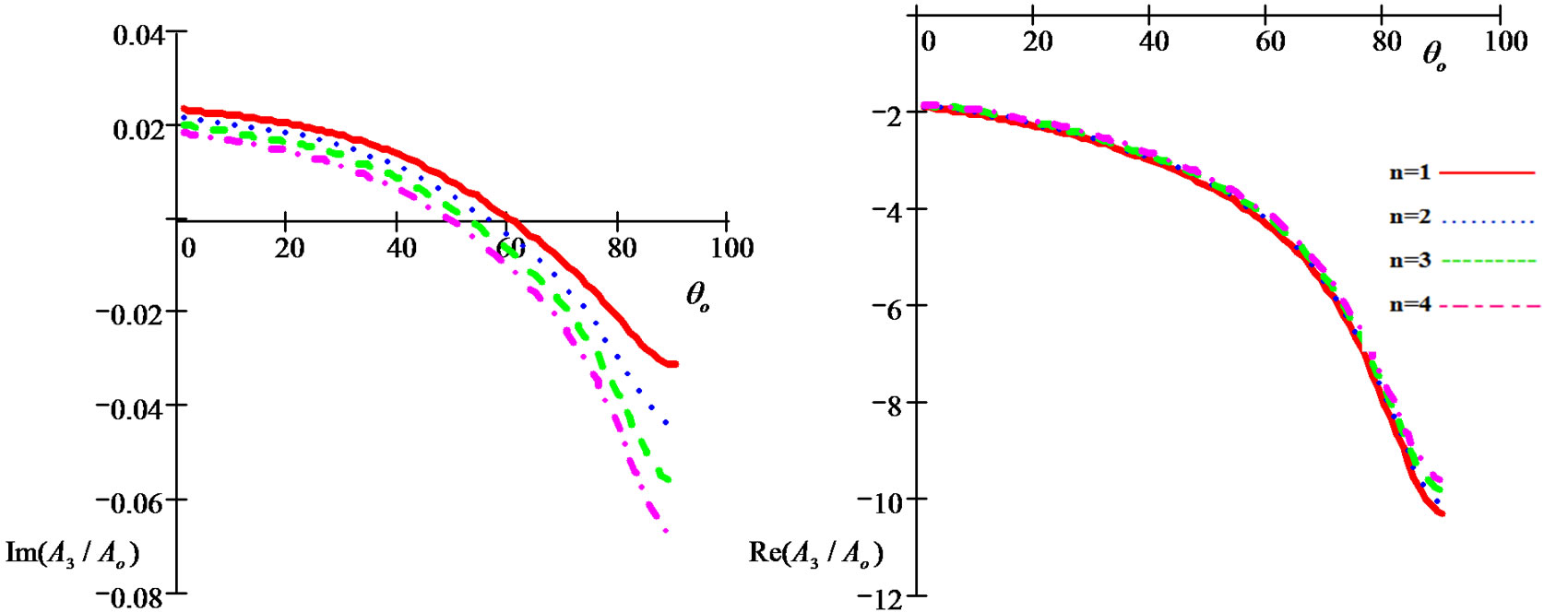
Figure 4. Imaginary and real parts of refraction coefficient A3/Ao as a function of incidence angle θo for different values of the relaxation times for (G-L) model.
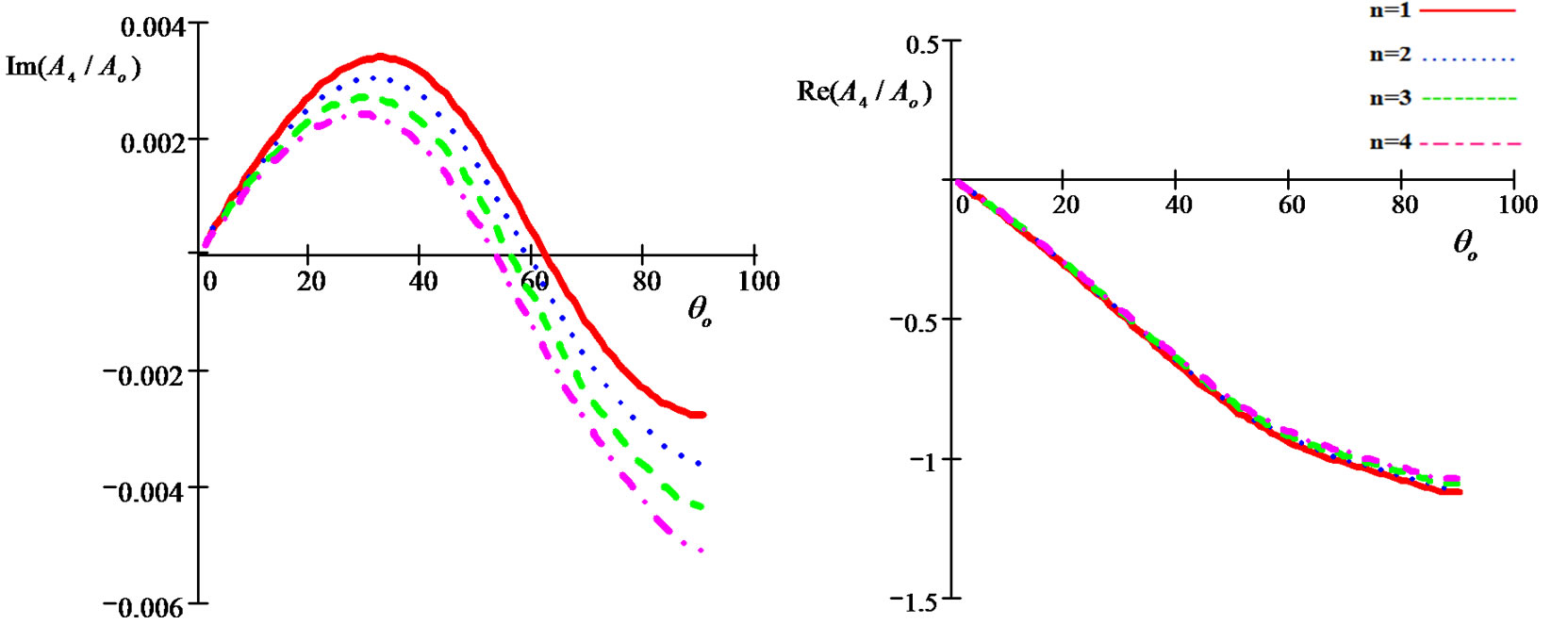
Figure 5. Imaginary and real parts of refraction coefficient A4/Ao as a function of incidence angle θo for different values of the relaxation times for (G-L) model.
from the figures that the effect caused by the relaxation time 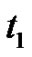 on
on 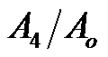 is very slight.
is very slight.
• Figures 6-8 represent the relation between the electric potential coefficients 
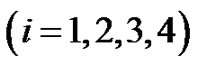 with the angle of incidence
with the angle of incidence , as well as the relaxation time
, as well as the relaxation time  effect.
effect.
• Figures 9-11 represent the relation between the thermal coefficients 
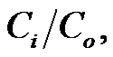 with the angle of incidence
with the angle of incidence 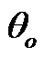 , as well as the relaxation time
, as well as the relaxation time 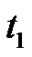 effect.
effect.
• Figures 12-21 show the initial stress effect 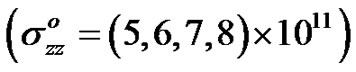 on relative reflection and refraction, thermal, and electric potential coefficients when
on relative reflection and refraction, thermal, and electric potential coefficients when 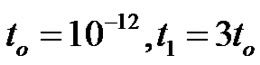 , In the period that shows the initial stress effect, we note that inverse relationship between the initial stress and reflection coefficients (
, In the period that shows the initial stress effect, we note that inverse relationship between the initial stress and reflection coefficients (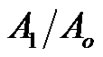 and
and 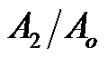 ) and the opposite what happens with the relative refraction coefficients (
) and the opposite what happens with the relative refraction coefficients (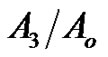 and
and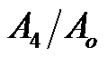 ).
).
• Equations (22)-(23) show the existence proportionality relations between the reflection coefficients of the quasi-longitudinal wave falling and reflection coefficients at the fall of the other two types of waves (T-mode), (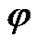 -mode). The constants of proportionality for these relations are functions of angle of incidence, relaxation times, and piezoelectric.
-mode). The constants of proportionality for these relations are functions of angle of incidence, relaxation times, and piezoelectric.
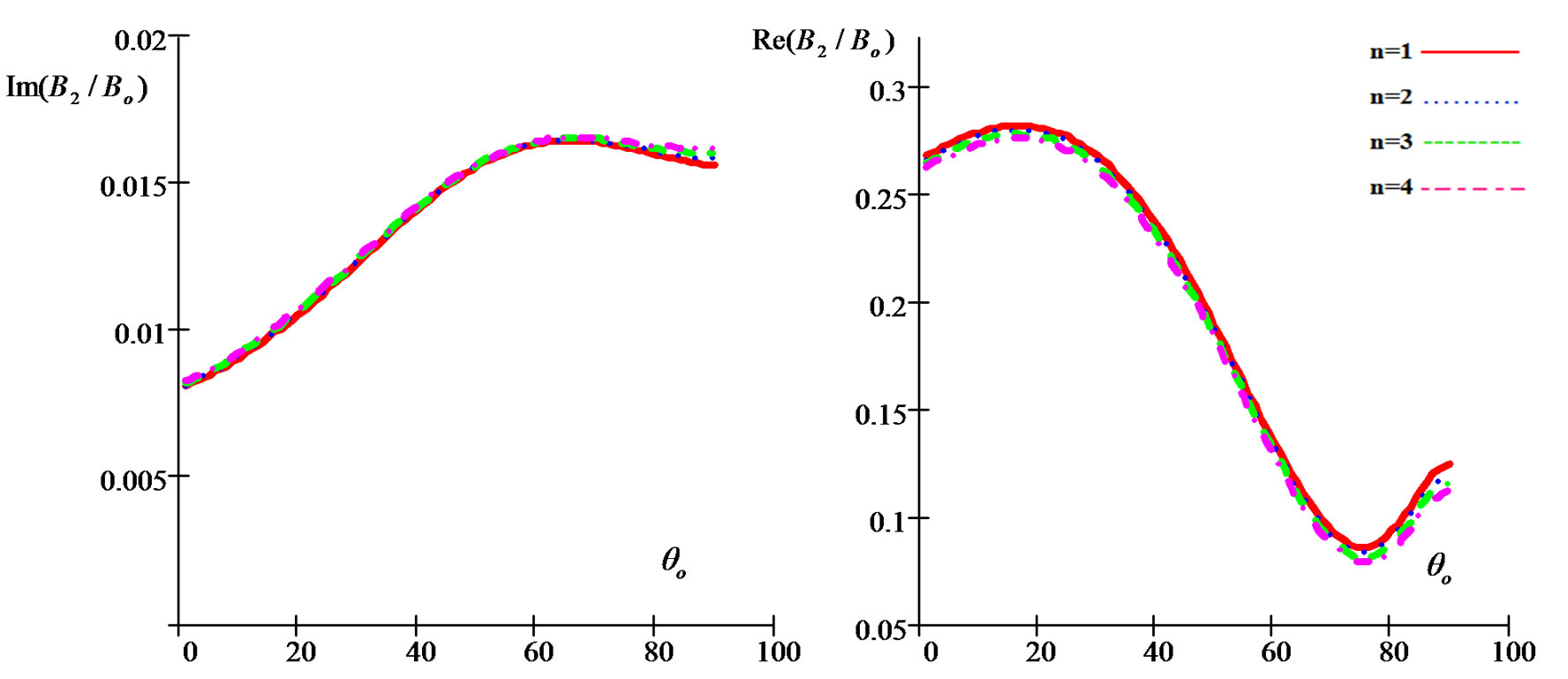
Figure 6. Imaginary and real parts of reflection coefficient B2/Bo as a function of incidence angle θo for different values of the relaxation times for (G-L) model.

Figure 7. Imaginary and real parts of refraction coefficient B3/Bo as a function of incidence angle θo for different values of the relaxation times for (G-L) model.

Figure 8. Imaginary and real parts of refraction coefficient B4/Bo as a function of incidence angle θo for different values of the relaxation times for (G-L) model.
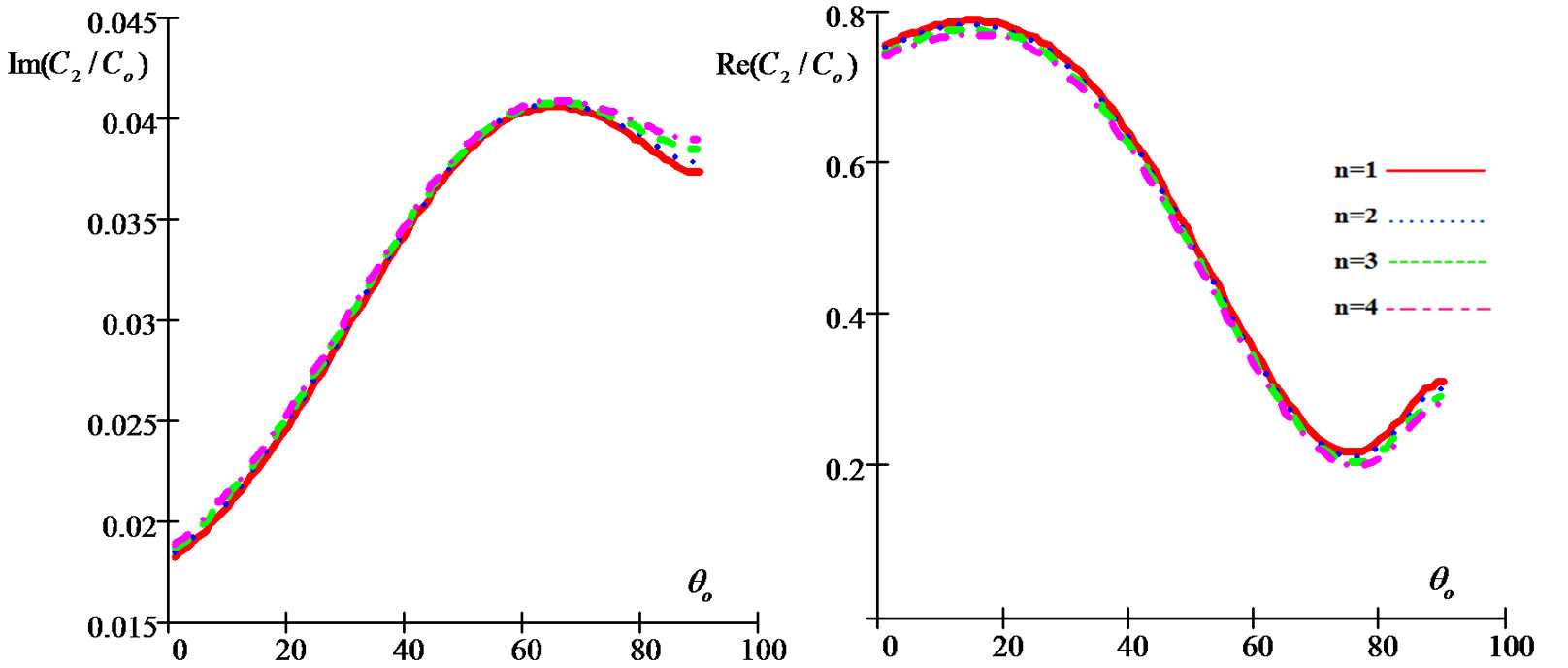
Figure 9. Imaginary and real parts of reflection coefficient C2/Co as a function of incidence angle θo for different values of the relaxation times for (G-L) model.
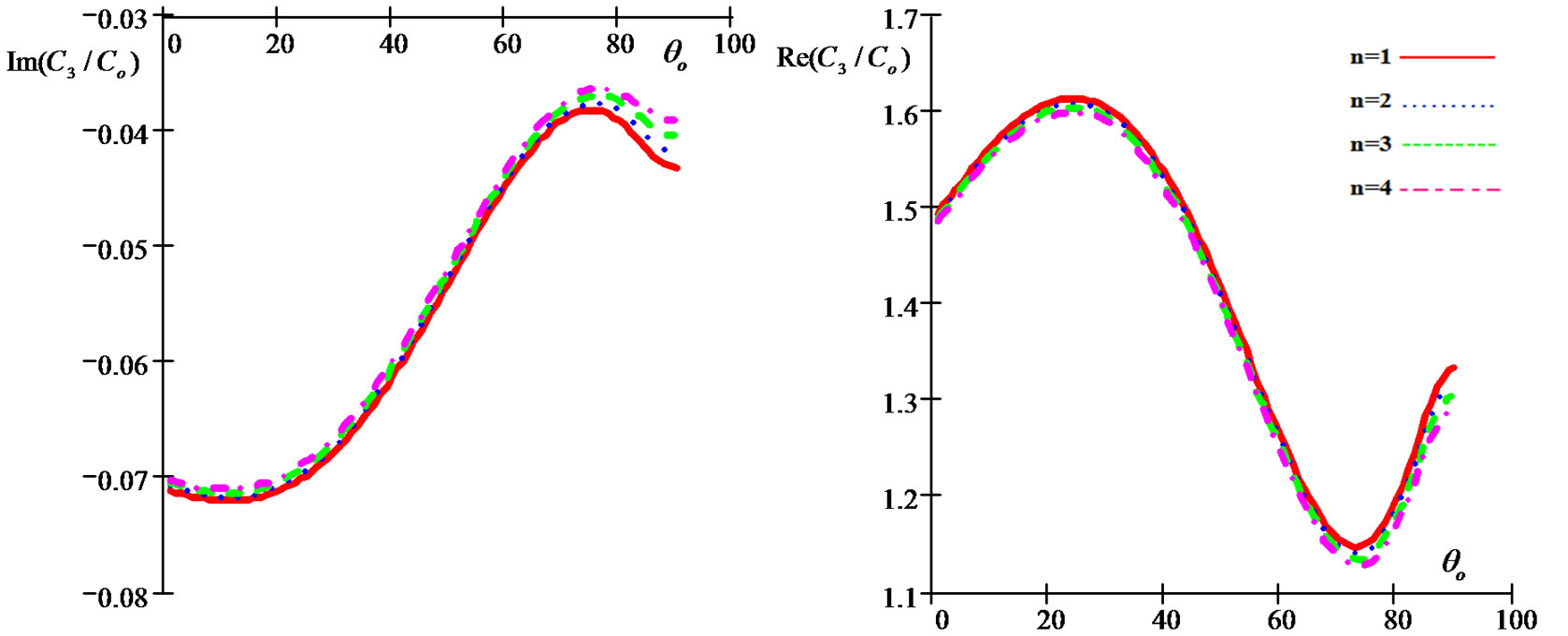
Figure 10. Imaginary and real parts of refraction coefficient C3/Co as a function of incidence angle θo for different values of the relaxation times for (G-L) model.
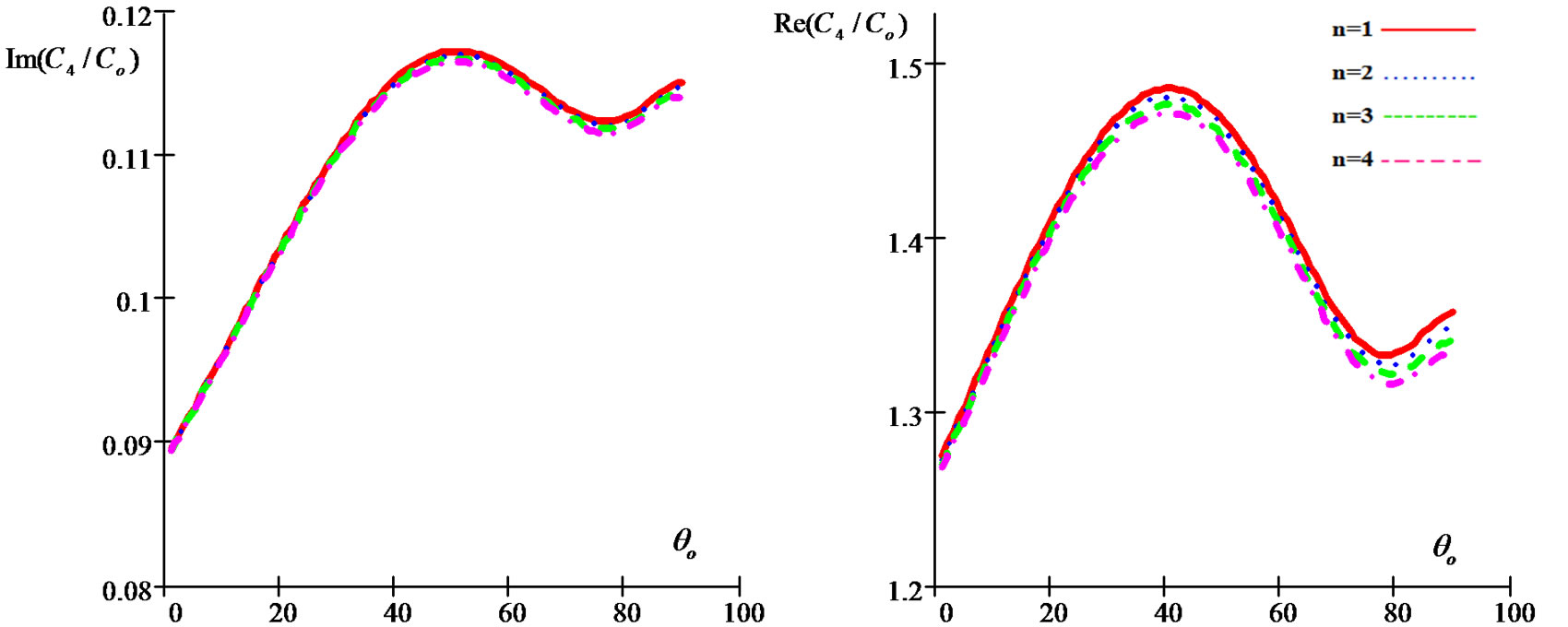
Figure 11. Imaginary and real parts of refraction coefficient C4/Co as a function of incidence angle θo for different values of the relaxation times for (G-L) model.
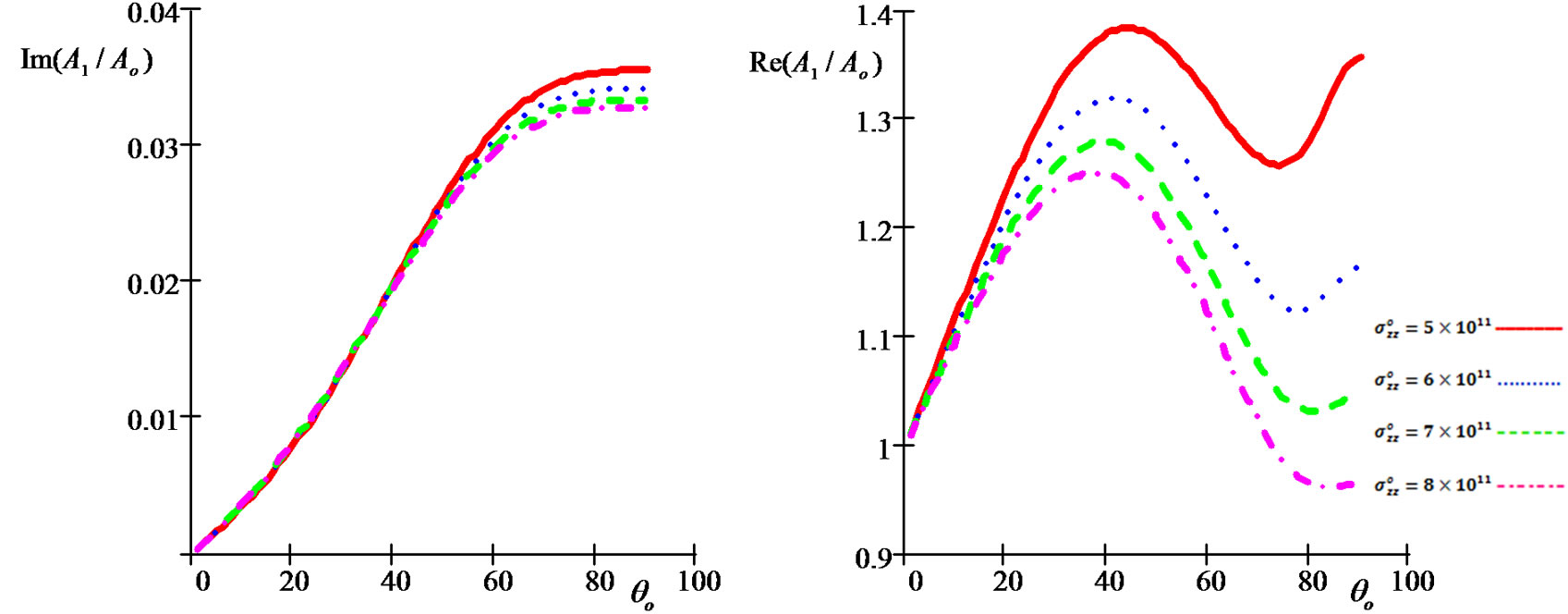
Figure 12. Imaginary and real parts of reflection coefficient A1/Ao as a function of incidence angle θo under influence of different values of the initial stress for (G-L) model.

Figure 13. Imaginary and real parts of reflection coefficient A2/Ao as a function of incidence angle θo under influence of different values of the initial stress for (G-L) model.

Figure 14. Imaginary and real parts of refraction coefficient A3/Ao as a function of incidence angle θo under influence of different values of the initial stress for (G-L) model.

Figure 15. Imaginary and real parts of refraction coefficient A4/Ao as a function of incidence angle θo under influence of different values of the initial stress for (G-L) model.
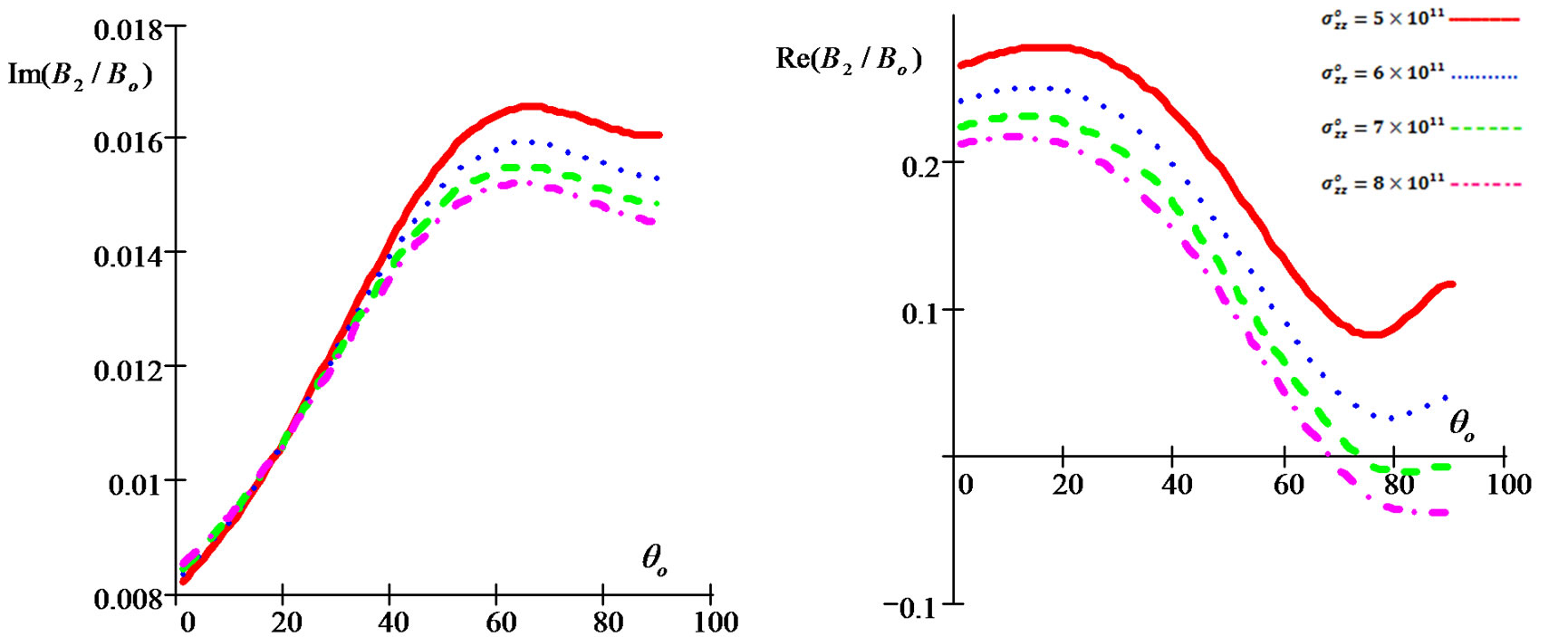
Figure 16. Imaginary and real parts of reflection coefficient B2/Bo as a function of incidence angle θo under influence of different values of the initial stress for (G-L) model.
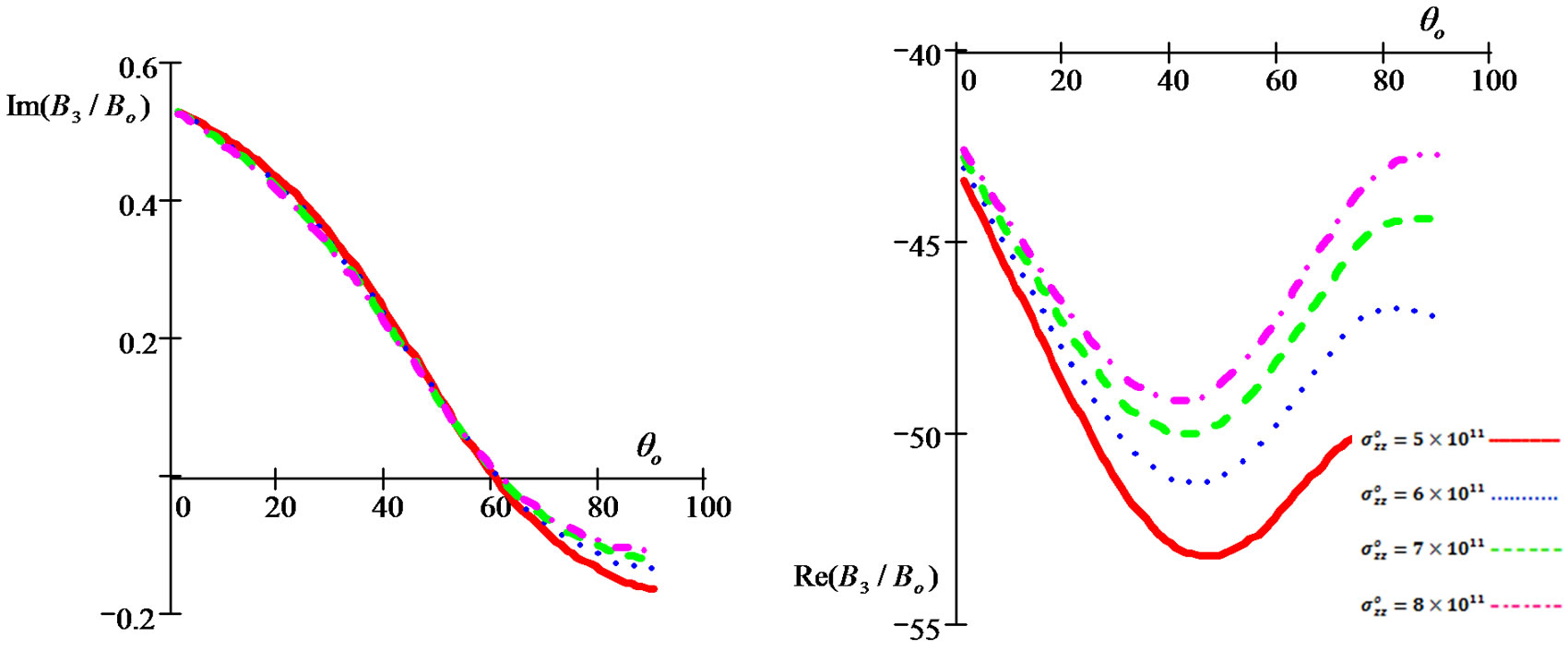
Figure 17. Imaginary and real parts of refraction coefficient B3/Bo as a function of incidence angle θo under influence of different values of the initial stress for (G-L) model.
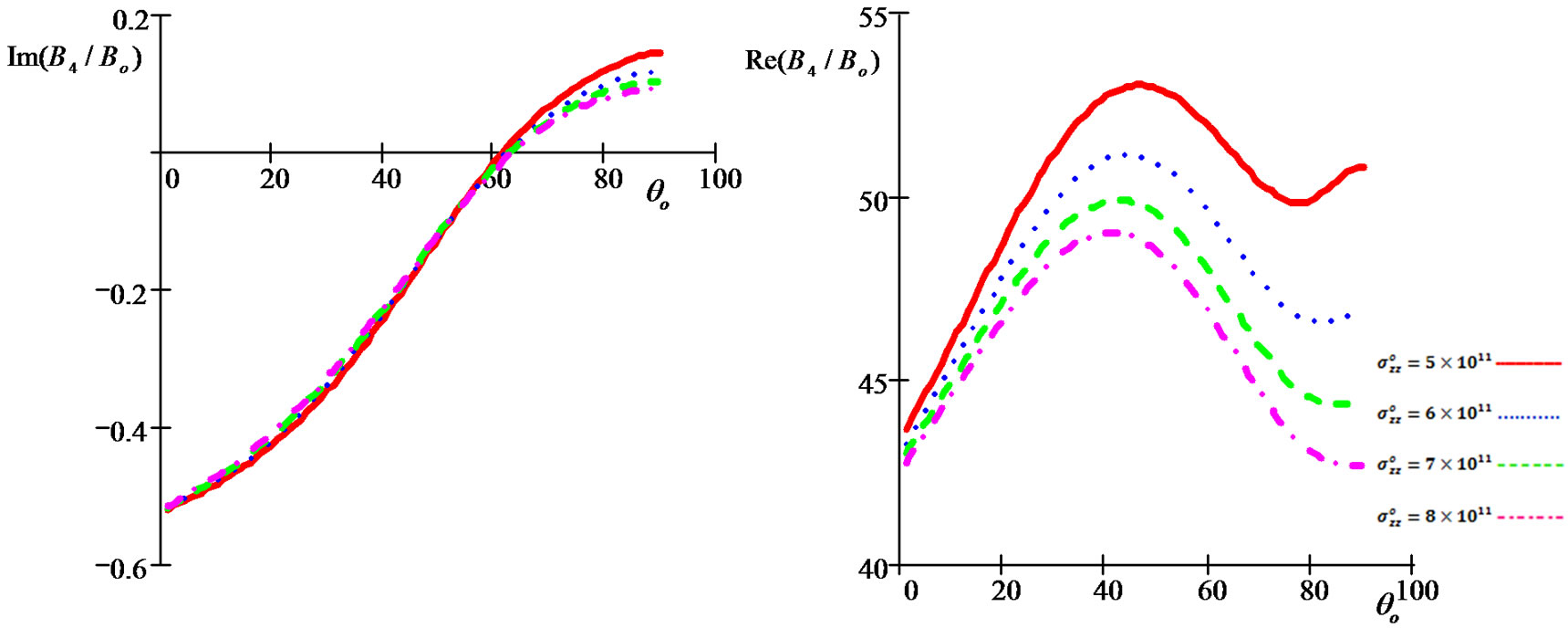
Figure 18. Imaginary and real parts of refraction coefficient B4/Bo as a function of incidence angle θo under influence of different values of the initial stress for (G-L) model.
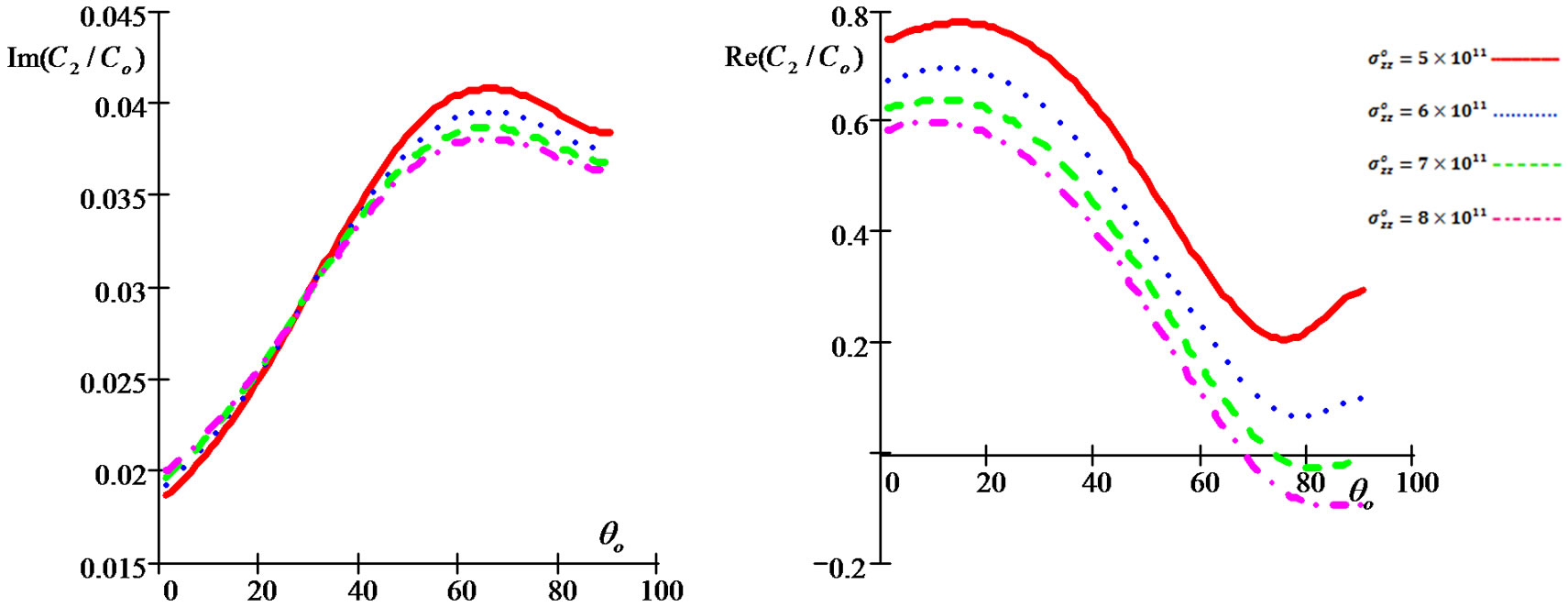
Figure 19. Imaginary and real parts of reflection coefficient C2/Co as a function of incidence angle θo under influence of different values of the initial stress for (G-L) model.
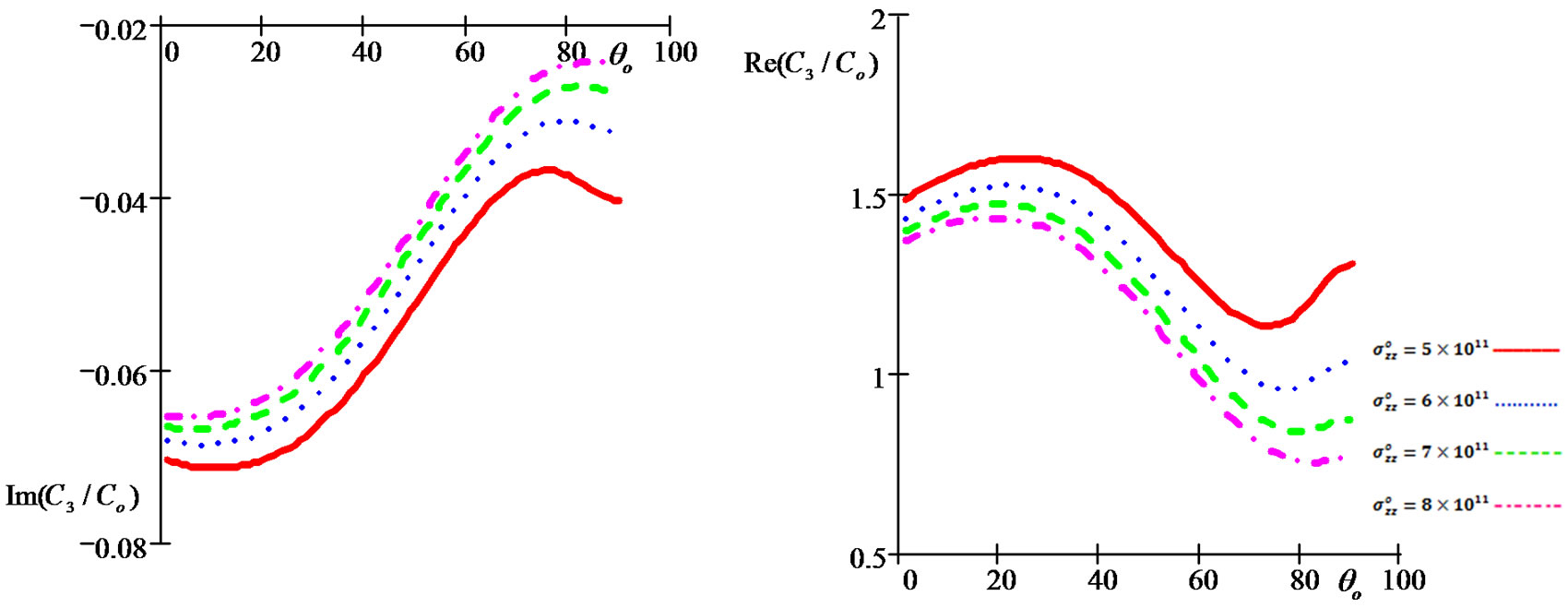
Figure 20. Imaginary and real parts of refraction coefficient C3/Co as a function of incidence angle θo under influence of different values of the initial stress for (G-L) model.

Figure 21. Imaginary and real parts of refraction coefficient C4/Co as a function of incidence angle θo under influence of different values of the initial stress for (G-L) model.
• It can get some previous studies as a special case through neglect the thermal effects and the relaxation times as [18].
REFERENCES
- R. D. Mindlin, “On the Equations of Motion of Piezoelectric Crystals,” In: N. I. Muskilishivili, Ed., Problems of Continuum Mechanics, 70th Birthday Volume, SIAM, Philadelphia, 1961, pp. 282-290.
- W. Nowacki, “Some General Theorems of Thermo-Piezoelectricity,” Journal of Thermal Stresses, Vol. 1, No. 2, 1978, pp. 171-182.doi:10.1080/01495737808926940
- W. Nowacki, “Foundation of Linear Piezoelectricity,” In: H. Parkus, Ed., Interactions in Elastic Solids, Springer, Wein, 1979.
- D. S. Chandrasekharaiah, “A Generalized Thermoelastic Wave Propagation in a Semi-Infinite Piezoelectric Rod,” Acta Mechanica, Vol. 71, No. 1-4, 1988, pp. 39-49.doi:10.1007/BF01173936
- J. N. Sharma and M. Kumar, “Plane Harmonic Waves in Piezo-Thermoelastic Materials,” Indian Journal of Engineering and Material Science, Vol. 7, 2000, pp. 434-442.
- J. N. Sharma and V. Walia, “Further Investigations on Rayleigh Waves in Piezothermoelastic Materials,” Journal of Sound and Vibration, Vol. 301, No. 1-2, 2007, pp. 189-206. doi:10.1016/j.jsv.2006.09.018
- H. Deresiewicz, “Effect of Boundaries on Waves in a Thermoelastic Solid: Reflexion of Plane Waves from Plane Boundary,” Journal of the Mechanics Physics of Solids, Vol. 8, No. 3, 1960, pp. 164-172. doi:10.1016/0022-5096(60)90035-1
- H. Lord and Y. Shulman, “A Generalized Dynamical Theory of Thermoelasticity,” Journal of the Mechanics and Physics of Solid, Vol. 15, No. 5, 1967, pp. 299-309. doi:10.1016/0022-5096(67)90024-5
- A. E. Green and K. A. Lindsay, “Thermoelasticity,” Journal of Elasticity, Vol. 2, No. 1, 1972, pp. 1-7. doi:10.1007/BF00045689
- A. N. Sinha and S. B. Sinha, “Reflection of Thermoelastic Waves at a Solid Half-Space with Thermal Relaxation,” Journal of Physics of the Earth, Vol. 22, No. 2, 1974, pp. 237-244. doi:10.4294/jpe1952.22.237
- J. N. Sharma, “Reflection of Thermoelastic Waves from the Stress-Free Insulated Boundary of an Anisotropic Half-Space,” Indian Journal of Pure and Applied Mathematics, Vol. 19, 1988, pp. 294-304.
- S. B. Sinha and K. A. Elsibai, “Reflection of Thermoelastic Waves at a Solid Half-Space with Two Thermal Relaxation Times,” Journal of Thermal Stresses, Vol. 19, 1996, pp. 763-777. doi:10.1080/01495739608946205
- S. B. Sinha and K. A. Elsibai, “Reflection and Refraction of Thermoelastic Waves at an Interface of Two Semi-Infinite Media with Two Thermal Relaxation Times,” Journal of Thermal Stresses, Vol. 20, No. 2, 1997, pp. 129- 146. doi:10.1080/01495739708956095
- A. N. Abd-Alla and A. A. S. Al-Dawy, “The Reflection Phenomena of SV Waves in a Generalized Thermoelastic Medium,” International Journal of Mathematics and Mathematical Sciences, Vol. 23, No. 8, 2000, pp. 529- 546. doi:10.1155/S0161171200004221
- J. N. Sharma, V. Kumar and D. Chand, “Reflection of Generalized Thermoelastic Waves from the Boundary of a Half-Space,” Journal of Thermal Stresses, Vol. 26, No. 10, 2003, pp. 925-942. doi:10.1080/01495730306342
- J. N. Sharma, V. Walia and S. K. Gupta, “Reflection of Piezo-Thermoellastic Waves from the Charge and Stress Free Boundary of a Transversely Isotropic Half Space,” International Journal of Engineering Science, Vol. 46, No. 2, 2008, pp. 131-146. doi:10.1016/j.ijengsci.2007.10.003
- Z.-B. Kuang and X.-G. Yuan, “Reflection and Transmission of Waves in Pyroelectric and Piezoelectric Materials,” Journal of Sound and Vibration, Vol. 330, No. 6, 2011, pp. 1111-1120. doi:10.1016/j.jsv.2010.09.026
- A. N. Abd-Alla and F. A. Alsheikh,” Reflection and Refraction of Plane Quasi-Longitudinal Waves at an Interface of Two Piezoelectric Media under Initial Stresses,” Archive of Applied Mechanics, Vol. 79, No. 9, 2009, pp. 843-857. doi:10.1007/s00419-008-0257-y
- A. N. Abd-Alla, F. A. Alsheikh and A. Y. Al-Hossain, “The Reflection Phenomena of Quasi-Vertical Transverse Waves in Piezoelectric Medium under Initial Stresses,” Meccanica, Vol. 47, No. 3, 2012, pp. 731-744.doi:10.1007/s11012-011-9485-2
- J. D. Achenbach, “Wave Propagation in Elastic Solids,” North-Holland Publishing Company, Amsterdam, 1973.
- J. N. Sharma, M. Pal and D. Chand, “Three-Dimensional Vibration Analysis of a Piezothermoelastic Cylindrical Panel,” International Journal of Engineering Science, Vol. 42, No. 15-16, 2005, pp. 1655-1673.doi:10.1016/j.ijengsci.2004.01.006

