Applied Mathematics
Vol.3 No.10A(2012), Article ID:24088,16 pages DOI:10.4236/am.2012.330178
A Genetic Algorithm with Weighted Average Normally-Distributed Arithmetic Crossover and Twinkling
Department of Mechanical Engineering,University of Nevada, Las Vegas, USA
Email: *Mohamed.Trabia@unlv.edu
Received May 24, 2012; revised June 24, 2012; accepted July 2, 2012
Keywords: Genetic Algorithms; Crossover Techniques; Twinkling; Engineering Design; Global Optimization
ABSTRACT
Genetic algorithms have been extensively used as a global optimization tool. These algorithms, however, suffer from their generally slow convergence rates. This paper proposes two approaches to address this limitation. First, a new crossover technique, the weighted average normally-distributed arithmetic crossover (NADX), is introduced to enhance the rate of convergence. Second, twinkling is incorporated within the crossover phase of the genetic algorithms. Twinkling is a controlled random deviation that allows only a subset of the design variables to undergo the decisions of an optimization algorithm while maintaining the remaining variable values. Two twinkling genetic algorithms are proposed. The proposed algorithmsare compared to simple genetic algorithms by using various mathematical and engineering design test problems. The results show that twinkling genetic algorithms have the ability to consistently reach known global minima, rather than nearby sub-optimal points, and are able to do this with competitive rates of convergence.
1. Introduction
Genetic algorithms [1] are global optimization algorithms based on observing the rules of biological evolution. A simple genetic algorithm (SGA) employs two main operations for a sequence of generations: crossover and mutation. The objective of an SGA is to improve the overall fitness of the population while avoiding being trapped ata local extremum. In general, SGAssuffer from their inability to guide the search in a well-controlled fashion. Thus, they often need to perform a very large number of function evaluationsin order to achieve the objective of the search. They also have the tendency to stagnate at sub-optimal solutions, including but not limited to localminima.
To address these limitations, many researchers have observed that using a combination of uniformly distributed random numbers in the crossover process limits the potential “genetic diversity” of the population, which either slows the pace of progression toward the solution or else causes the search to stagnate. To address this issue, a number of alternatives were proposed. For example, a specialized weighted average crossover was proposed [2]. This technique, which was labeled the Simulated Binary Crossover (SBX), is a variation of the affine hull, which combines a random number multiplier with a normal distribution. Aunimodal normal distribution crossover that generates two “children” from a region of a normal distribution defined by three “parents” was introduced [3]. To avoid premature convergence due to lack of diversity, a new crossover operator was presented [4], based on fuzzy connectives for real-coded genetic algorithms. Additionally, a comprehensive survey of the crossover operators was presented [5].
Hybrid genetic algorithms that can incorporate local search techniques in conjunction with the genetic algorithms were created in order to improve the performance of genetic algorithms. For example, a solution was proposed for the problem of flowshop scheduling with fuzzy due dates, using a hybrid genetic algorithm that combineda genetic algorithm with a neighborhood search composed of multi-start descent, taboo search, and simulated annealing [6]. A hybrid interval algorithm was introduced that starts by using interval arithmetic to determine a possible range for the minimum [7]. A hybrid method was proposed that combined a genetic algorithm with the simplex method [8]; this algorithm reflected W points out of N + W simplex points instead of reflecting one point only, as in the classical simplex algorithm. A genetic algorithm was used at the second stage of the search, and this process occurred concurrently along with an elitist genetic algorithm. In order to avoid being trapped in a local minimum, another method incorporated a genetic algorithminto a modified form of the Powell method [8]. The output of a genetic algorithm was used as an input to a Quasi-Newton algorithm [10] wherethe difference between Darwin-inspired and Lamarck-inspired strategies was discussed. A solution was proposed for the minimum cost expansion pattern of new reactive power sources to be installed in power systems [11], where each iterationof the algorithm started with a simulated annealing followed by a genetic algorithm. Simplex and genetic algorithms were combined [12]. Thisalgorithm started by choosing N + 1 random pairs from the population. After applying the crossover and mutation operations, the simplex algorithm was used on these points for k iterations. The points with the lowest function values replaced those with the highest function values in the original population. A hybrid Nelder and Mead simplex genetic algorithm for the shape optimization of a solid C-frame cross-section was suggested by [13]. A hybrid genetic algorithm/sequential linear programming (SLP) algorithm was presented [14]. This algorithm used two metrics for evaluating the modality of the design space: the variance in the fitness of the population and the error associated with fitting a response surface to the designs. These two metrics were used to switch between the genetic and the SLP algorithms. A hybrid fuzzy simplex genetic algorithm that used a fuzzy simplex search was developed to improve the fitness of the individuals before they are reintroduced for the crossover and the mutation operations [15].
Global optimization presents many challenges. For example, an evolutionary algorithm for efficient global minimization of an expensive black-box function was developedthat utilizes information from local-searches to efficiently bias its domain exploration [16]; analysis of the population density clusters was incorporated in the algorithm. Otherresearchers approach the problem of global optimization through stochastic strategies, manyadopting a global stochastic strategy consisting of global and local search phases [17]. During the global phase, random points are drawn from the domain of search according to a uniform distribution. During the local phase, a set of drawn points is transformed by means of local optimization methods to obtain approximatesof the global and local extremes.
Twinkling strategy presents an alternative philosophy to approach optimization problems. The concept of twinkling, introduced to improve the optimization search moves [18], canreduce the evaluation effort needed to reach a pseudo-optimal solution of the Traveling Salesman Problem. The application of twinkling to gradient search techniques (steepest descent and conjugate gradient) has been presented with an application to the problem of numerical identification of two dimensional shapes by non-uniform rational B-Splines [19]. Several aspects of the simplex search also use the twinkling technique [20]. Additionally, twinkling was incorporated in a naive random search algorithm [21]. This approach demonstrated certain advantages in terms of number of function evaluations, when compared to several techniques including, genetic algorithm, simulated annealing, particle swarm, and random search algorithms.
The objective of this paper is to explore the possibilities of incorporating twinkling within genetic algorithms. Thiswork is divided as follows. Section 2 explains the twinkling paradigm, anda brief overview of the simple genetic algorithm is presented in Section 3. The weighted average normally-distributed arithmetic crossover (NADX) is introduced in Section 4. Section 5 describes the process of incorporating twinkling in the SGA crossover operation. The steps of the algorithms proposed in this paper are presented in Section 6. A detailed assessment of the influence of the various components of the proposed algorithms on the search progression is discussed in Section 7. Evaluation of the proposed algorithms using various benchmark test functions and engineering design problems is included in Section 8. Finally, conclusions and recommendations for future work are provided in Section 9.
2. The Twinkling Paradigm
In principle, twinkling introduces a deviation from the standard practice of any algorithm by allowing only a random subset of the variables to undergo the heuristic decisions of an optimization algorithm. The remaining variables maintain their values as in the previous iteration or generation.In describing the twinkling operation, consider a point g under consideration within an optimization algorithm,
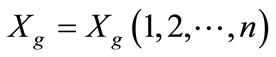
The twinkling operation starts by introducing a “twinkling dimension,” t1, which is a randomly chosen integer between 1 and n. Twinkling dimensions are used to determine the number of variables that undergoes the change. A “twinkling array,” t2, is then created. The size of this array is equal to t1. Each element in this array is randomly chosen to be a number between 1 and n. The values of the twinkling array, t2, are unique and nonrepeating numbers. The elements in t2 represent the random subset of variables that will be subject to twinkling. The two operations described here can be represented as follows:
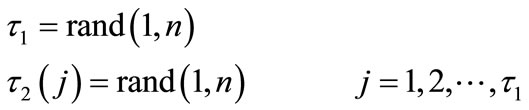 (1)
(1)
Thus, twinkling can be applied to any standard optimization algorithm to update Xg as follows:
 (2)
(2)
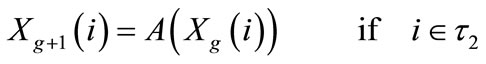 (3)
(3)
where, A(X) is the optimization algorithm of choice.
3. Simple Genetic Algorithm
Simple genetic algorithms have several variations that differ slightly. The algorithm described in this section follows that of [22]. The following discussion assumes that the algorithm is used to find the minimum of a problem.
A simple genetic algorithm begins by randomly generating an initial population of m individuals, or “chromosomes”. Each individual is a string composed of n variables using real values. The algorithm selects a percentage of the population p with the best fitness, lowest function value, as “parents”, as well as members of the next generation. The “children”, which are the remainder of the population, are generated by crossing over two randomly chosen parents (P1 and P2) from the selected population by using a weighted average operator to create two children (C1 and C2) as follows:
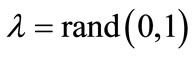 (4)
(4)
 (5)
(5)
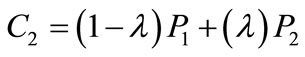 (6)
(6)
The above formulation is known as a convex combination in the presence of the non-negative conditions [23].
A random number of variable values are mutated in each generation:
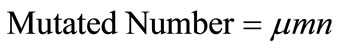 (7)
(7)
where, m is the mutation rate from [0,1]. The positions of the mutated variables are chosen randomly from a unique array of random integer numbers [1, 2, ···, mn]. In the remainder of this work,this algorithm is labeled SGAU (simple genetic algorithm with theconvex combination).
4. The Weighted Average Normally-Distributed Arithmetic Crossover (NADX)
The blending of genes, which is typically used to mathematically approximate the occurrence within the crossover operation, is not an accurate biological analogy as this process does not provide for the equivalent to the recessive genes that parents can pass on their children. This work proposes a method that is closer to the true biological analogy by allowing a specific “gene value” from a crossover to be outside the limited physical bounds of the two parents, therefore mimicking the diversity of the genes that a parent could pass on. This method is labeled as the weighted average normallydistributed arithmetic crossover (NADX).
The proposed crossover creates individuals based on a normal distribution defined by the two parents.A standard normal distribution is centered upon each of the two parents, which is used as the basis for the weighted average parameter. Arandom number multiplier,l,which hasa mean of 0, a varianceof σ2 = 1, and a standard deviation of σ = 1 is introduced. l is restricted to an affine combination, where the sum of the multipliers is equal to one. The resulting crossover is governed by:
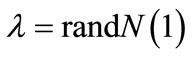 (8)
(8)
where, 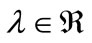 and randN is a normally distributed random number that is restricted to be a real number with mean, variance, and standard deviation, as described above.
and randN is a normally distributed random number that is restricted to be a real number with mean, variance, and standard deviation, as described above.
The two children (C1 and C2) are generated by crossing over two randomly-chosen parents (P1 and P2) from the selected population as follows:
 (9)
(9)
 (10)
(10)
NADX genetic distributions can be compared to common techniques that use a uniformly distributed parameter, such as convex combination (see Section 3) and SBX crossover [2]. SBX crossover is designed to produce children that are evenly distributed around the parentsby using a transformed uniform distribution:
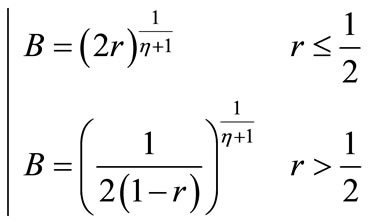 (11)
(11)
where, r is a uniformly distributed random number {0, 1} andhis a constant that is equal to .
.
When the SBX is used, the children (C1 and C2), are generated by crossing over two randomly-chosen parents (P1 and P2) from the selected population as follows:
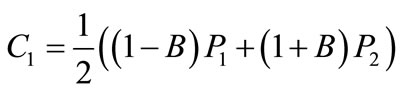 (12)
(12)
 (13)
(13)
When comparing the behavior and distribution of offspring of these three crossover algorithms, aunivariate exampleis where two parents with values of {−100, 100} are chosen. The three crossover techniques are performed 10,000 times with these parents to produce 20,000 children. Figure 1 compares the results of using these three
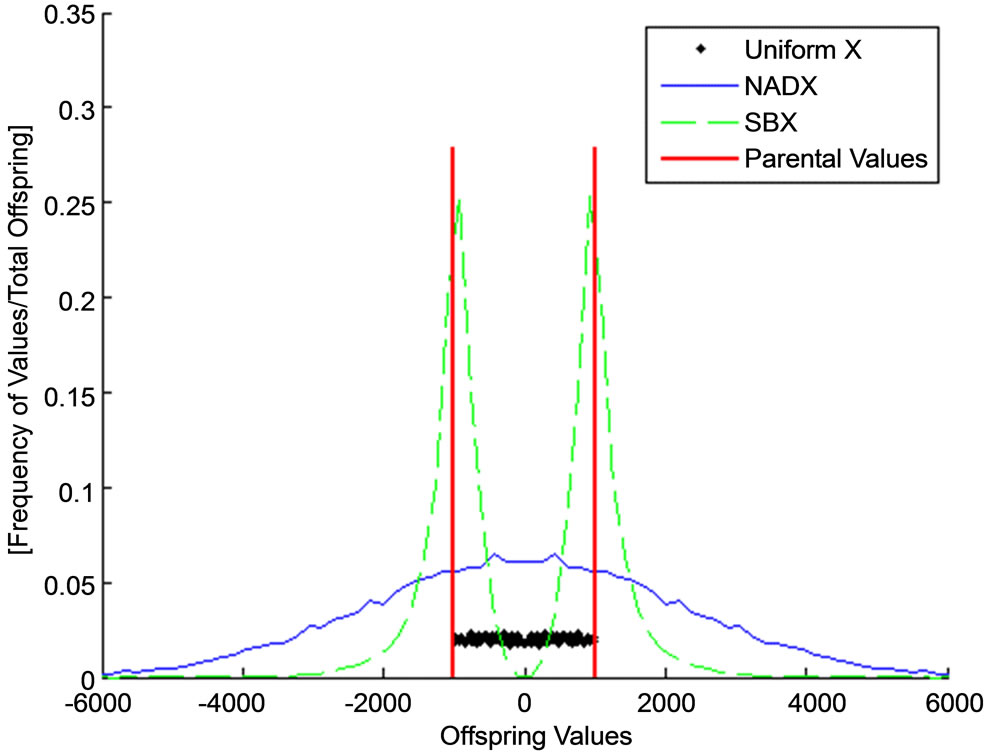
Figure 1. Histogram of offspring values based on percentage of total population.
algorithms. The results show that the NADX produces a distribution of children with the highest percentage of children located at the average value of the two parents. However, NADX generates a higher percentage of individuals in the regions outside the one that is between the parental values. On the other hand, the convex combination crossover produces children with values only between −100 and 100. SBX has a more distributed population; however, SBX also creates a large percentage of population with values that are close to those of the parents. Therefore, NADX creates a greater variety of individuals by increasing the “genetic diversity” of the population while still maintaining adequate coverage of the ranges near and between the parents.
5. Twinkling Crossover Operation
The objective of this section is to explore ways for incorporating twinkling within a genetic algorithm. While twinkling can be added in any of the stages of a genetic algorithm,this paper proposes applying twinkling during the crossover phase. Twinkling is used to choose the variables, within each of the generated children that the crossover is applied to. This section shows that the twinkling operator behaves in a manner that exploits the search space of the two parents by allowing certain gene values of a parent to pass to the offspring, which increases the likelihood that a “good” gene survives. Two variations of this approach are presented.
5.1. Crossover Operation Using the Twinkling Dimension
Crossover starts by introducing a “twinkling dimension” after all pairs of parents are chosen. This twinkling dimension is used to determine the number of variables that are crossed over:
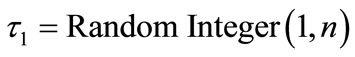 (14)
(14)
Next, a unique random array is chosen of integers, t, of length nwith values between [1, 2, ···, n]. A twinkling array whose length is t1 is created as follows:
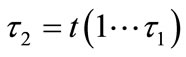 (15)
(15)
In order to avoid stagnation of the population around a local minimum, both twinkling dimensions are randomly generated for every pair of parents, rather than having a single set of twinkling dimensions at the onset of every generation. The reason for this decision is to prevent the children of a particular generation from being biased towards the selected twinkling genes, which can affect the overall direction of search. The kth variable of either child (C1 or C2) is generated by crossing over two randomly chosen parents (P1 and P2) as follows:
 (16)
(16)
 (17)
(17)
If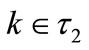 , use a crossover technique to generate the variables of the children.
, use a crossover technique to generate the variables of the children.
5.2. Crossover Operation Using the Twinkling Dimension and the Choice Operator
The genetic diversity of children can be further enhanced by adding a choice operator to the procedure of the previous section. Thischoice operator can be usedto determine the number of children who will be bred from a parental pairing. Therefore, the genetic diversity of the resulting population can be enhanced by potentially increasing the number of parental pairings. At each crossover operation, a choice operator, S, is randomly generated as follows:
 (18)
(18)
Thus, one of the following three breeding scenarios is chosen randomly to generate children based on the value of S. Either child, with a preference to one of the two parents, is created. Alternatively, two children are created according to Section 5.1. The process is repeated for every parental pairing until the new population is completed. In each of the three cases, twinkling is used to generate the kth variable of a child (C) if k is of the set t2; otherwise the crossover is performed:
Case 1 (S = 1): A single child with preference to P1
 (19)
(19)
If , use a crossover technique to generate the variables of the children.
, use a crossover technique to generate the variables of the children.
Case 2 (S = 2): A single child with preference to P2
 (20)
(20)
If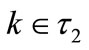 , use a crossover technique to generate the variables of the children.
, use a crossover technique to generate the variables of the children.
Case 3 (S = 3): Two children with no preference to either parent.Children are generated as in Section 5.2.
It may be of interest to contrast this approach with the macro-mutation approach of [24]. Macro-mutation is a mutation of many bits instead of limited number, where a contiguous sequence of positions is taken and then replaced with a random string. The objective of twinkling is to maintain good genes within the search. Therefore, some variables of the children are randomly selected in the twinkling crossover. Using the proposed twinkling approach, children will either be copies of their parents or will be the result of crossover.
6. Outline of the Twinkling Genetic Algorithm
This section presents the outline of the proposed approach as follows:
1. Input the number of strings (variables), n.
2. Input the population number, m.
3. Input the maximum number of generations, G.
4. Input the bounds for each string, ximin and ximax (i = 1, ···, n).
5. Input the fraction of the population that will be the parents in the crossover operation, p.
6. Input the mutation rate, m.
7. Randomly the initialize population within the ranges of the variables.
8. For g = 1 to G
8.1. Evaluate the fitness (function value) of the population.
8.2. Select pm of the population with best fitness.
8.3. Perform the crossover operation using parents randomly selected from the pm parents selected in Step 8.2 to generate new members of the population. For each pairing of parents, carry out the choice of crossover and twinkling operations.
8.4. Perform mutation operation on the population using Equation (7).
8.5. Replace old population by the new one.
8.6. Go back to Step 8.
Fifty percent crossover and one percent mutation ratio are used for all examples in the remainder of this work.
Various versions of the algorithm are considered:
• SGA (Simple genetic algorithm with the NADX crossover)
• TGA (Genetic algorithm with the NADX crossover and the twinkling dimension)
• TGASO (Genetic Algorithm with the NADX crossover and the twinkling dimension and the choice operator)
• SGAU (Simple genetic algorithm with the convex combination crossover)
• TGAU (Genetic algorithm with the convex combination crossover and the twinkling dimension)
• TGASOU (Genetic algorithm with the convex combination crossover and the twinkling dimension and the choice operator)
7. Assessment of the Influence of the Various Components of the Proposed Algorithms
The Multi-Peak Problem [25], (Figure 2), is used to assess the contribution of the crossover method and of twinkling operators to the proposed algorithm. This problem can be stated as follows:
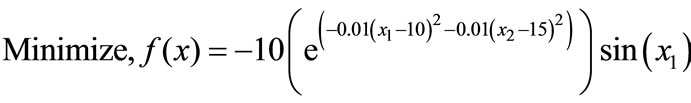 (21)
(21)
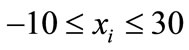
The minimum of the function within these bounds is −9.5585 at [7.896 15]T. The function has a sequence of four narrow valleys with extremely steep slopes that are surrounded by flat regions as Figure 2 shows. These valleys are located at: 0 < x1 < 3, 6 < x1 < 10, and 12.5 < x1 < 15.5, and 19 < x1 < 22. The Multi-Peak Problem is used to test the SGAU, SGA, TGAU, and TGA algorithms using a population of 20n. The same initial population, Figure 3 is used in all four cases.
While all algorithms are able to reach within 10−4 of the known minimum, the average number of function evaluations needed to reach this minimum varies
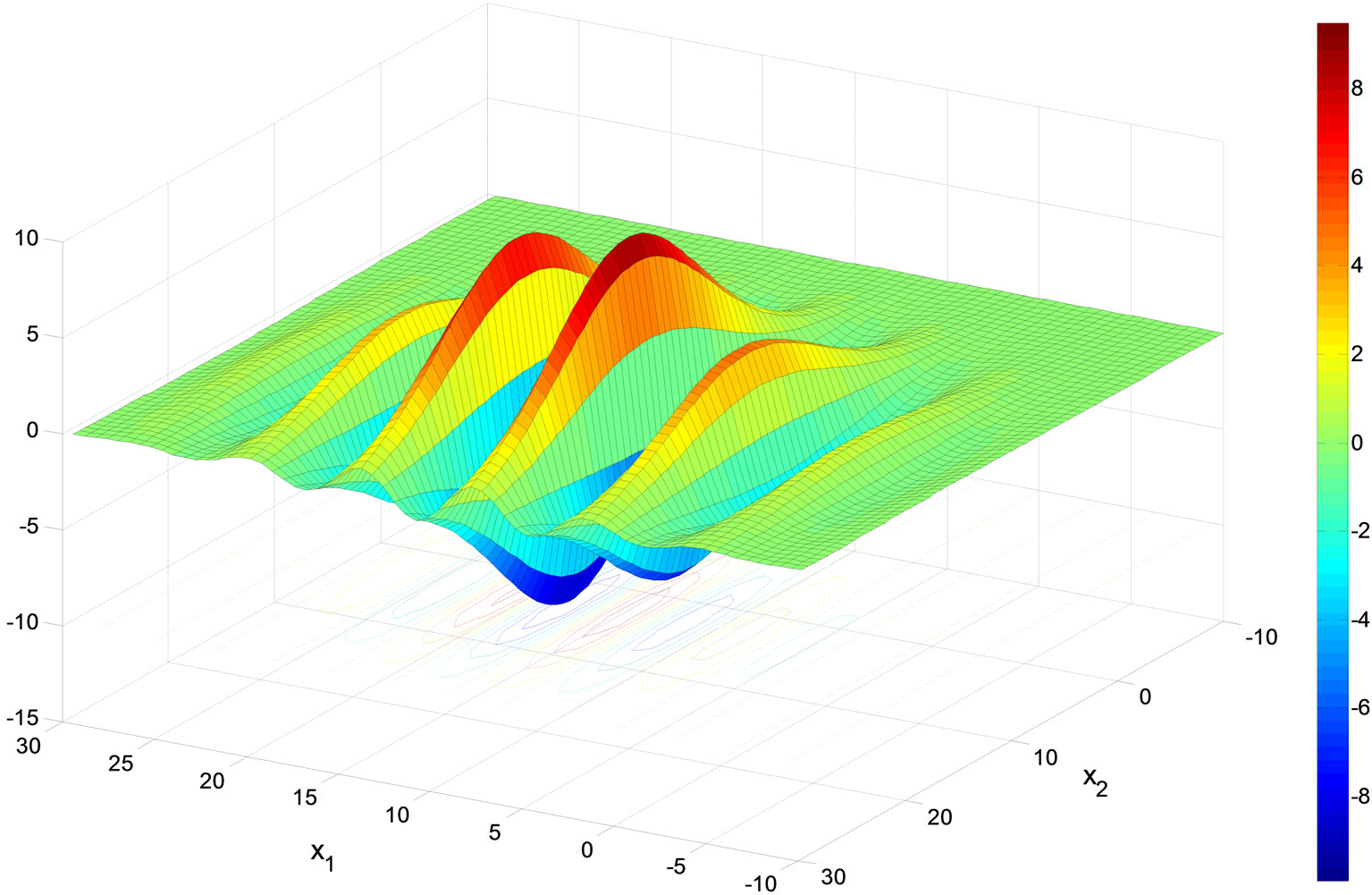
Figure 2. Multi-Peak Problem.

Figure 3. Population of a typical run for the Multi-Peak Problem (this population is used for the SGAU, SGA, TGAU, and TGA algorithms).
significantly. The results of Figure 4 indicate that, after a brief movement away from the minimum,the TGA reaches the minimum after less than 334 function evaluations. The TGA is followed by the TGAU after 355 function evaluations. The SGAis able to reach the minimum after 565 function evaluations. The SGAU stagnates for several generations. However, it is able to reach the minimum after 3610 function evaluations.The increase in genetic diversity of the twinkling genetic algorithms, described in Section 4, is due to their ability to explore the search space more quickly.
The above results can be confirmed by observing thepopulation number at each of the four narrow valleys of the Multi-Peak problem. In the case of the SGA, as Figure 5 shows, most of the population is equally distributed among the fourcritical regions for the first three generations. After that,the population becomes concentrated in the 6 < x1 < 10 region, which has the global minimum. However,the SGA is not able to reach the minimum for many generations, as can be seen in Figure 6. These results may be attributed to the use of the convex combination and the lack of twinkling operators. Both factors limit the diversity of the population.
Figure 7 shows that the SGA produced more diversity as the population is almost equally distributed among the first three valleys for the first eight generations. After that, most of the population becomes concentrated in the 6 < x1 < 10 region, as can be seen in Figure 8. This indicates that theNADX crossover produces a more diverse population.
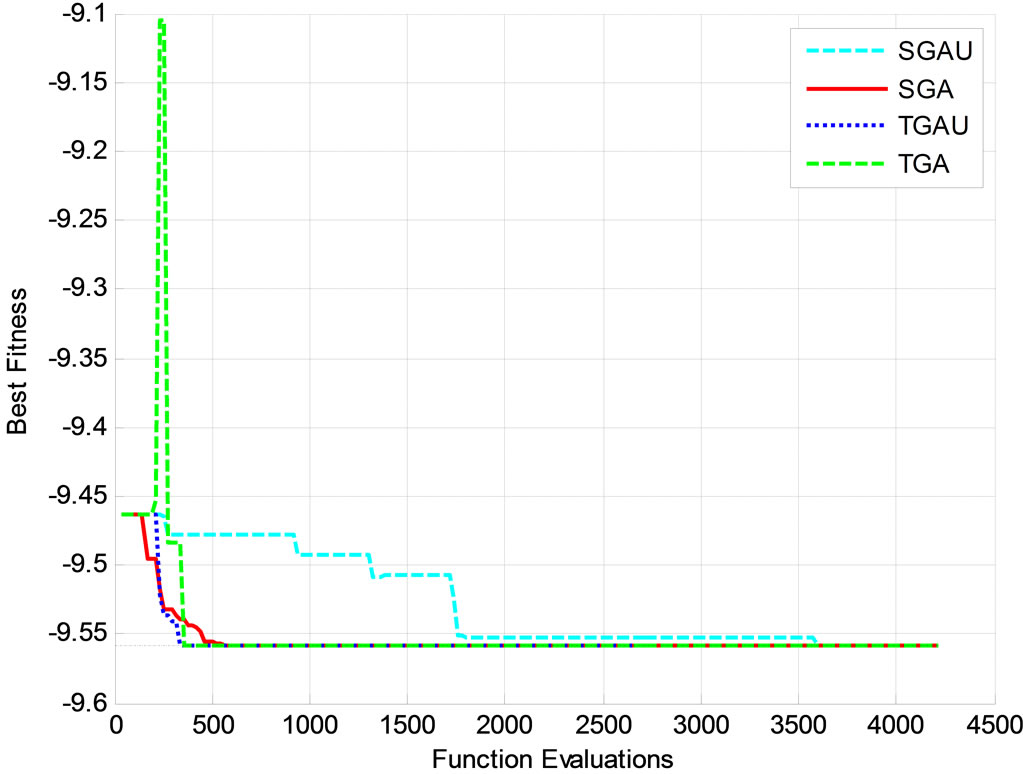
Figure 4. Results of using the initial population of Figure 3 on the proposed algorithms for the Multi-Peak Problem.

Figure 5. Progression of population number at each of the critical regions when using the SGAU to solve the Multi-Peak Problem.
The results of Figure 9 indicate that the TGAU concentrates the majority of the population in the 6 < x1 < 10 region after the tenth generation. Similar behavior is observed in Figure 10. The results of Figure 11 show the population at the 20th generation when using the TGA algorithm. The results point to the combined effectiveness of using the twinkling and the NADX crossover.
To further verify the above observations, all six algorithms are tested two hundred times by using the same initial population in each case. The above conditions are maintained except when using a population size of 40n. Table 1 lists the results of testing the six algorithms hundred times, using the same initial population in each case. While all algorithms are able to reach values that are very close to the minimum (−9.5585), the final function values and standard deviations are significantly lower when using the NADX crossover. It is also noted that SGAU has the highest standard deviation value. Comparing the averagesand standard deviations in Table 1 can lead to the following observations:
Figure 6. Population of the Multi-Peak Problem when the SGAU algorithm is used (20th generation).

Figure 7. Progression of population number at each of the critical regions when using the SGA to solve the Multi-Peak Problem.
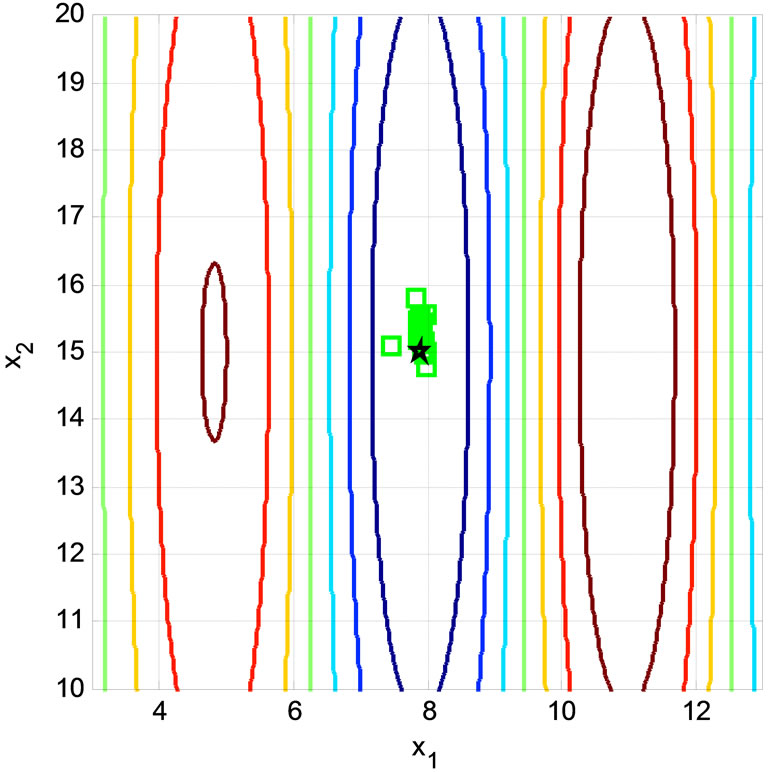
Figure 8. Population of the Multi-Peak Problem when the SGA algorithm is used (20th generation).
• The algorithms that use the NADX crossover consistently outperform those that use the uniformly distributed crossover.
• In the case of the uniformly distributed crossover, the twinkling algorithms consistently produce better results than the simple genetic algorithm.
• The two variations of twinkling presented in this work have about the same level of effectiveness, regardless of which crossover operator is used.
8. Evaluation and Design Examples
To further evaluate the performance of the proposed algorithm, several mathematical test functions and engineering design examples are explored in this section. Mathematical test functions often have simple bounds on the variables as well as a large number of local minima. On the other hand, engineering design problems typically have many nonlinear constraints and hyper-planes, where

Figure 9. Progression of population number at each of the critical regions when using the TGAU to solve the Multi-Peak Problem.
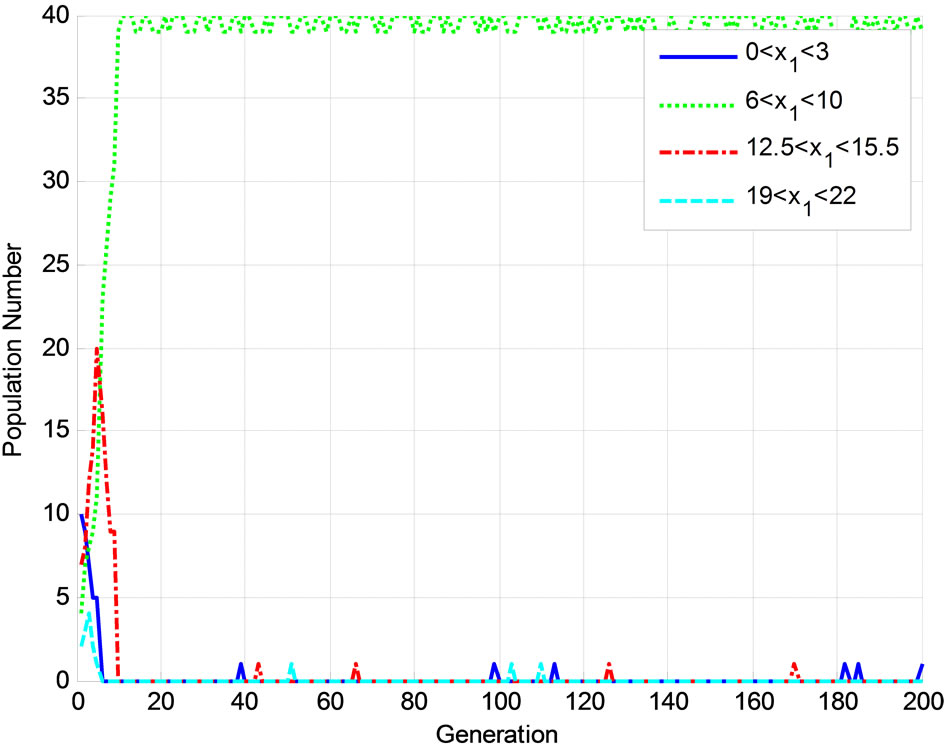
Figure 10. Progression of population number at each of the critical neighborhoods when using the TGA to solve the Multi-Peak Problem.
the value of the objective function changes slowly before reaching the minimum. This section compares the performance of the six genetic algorithms introduced in Section 6. At each run, the same initial population is used for all algorithms in order to allow objective comparison. The reported results represent one hundred runs for all algorithms.
8.1. The Sine Function
The Sine function [8], can be expressed as:
 (22)
(22)
When m is equal to 100, this problem becomes notoriously difficult because of its large number of local minima, which are equal to 100!. In this case, the known global minimum is equal to −9.655.Some of the best results for this Sine function uses the 57% Simplex-GA hybrid algorithm, which reaches the global minima in
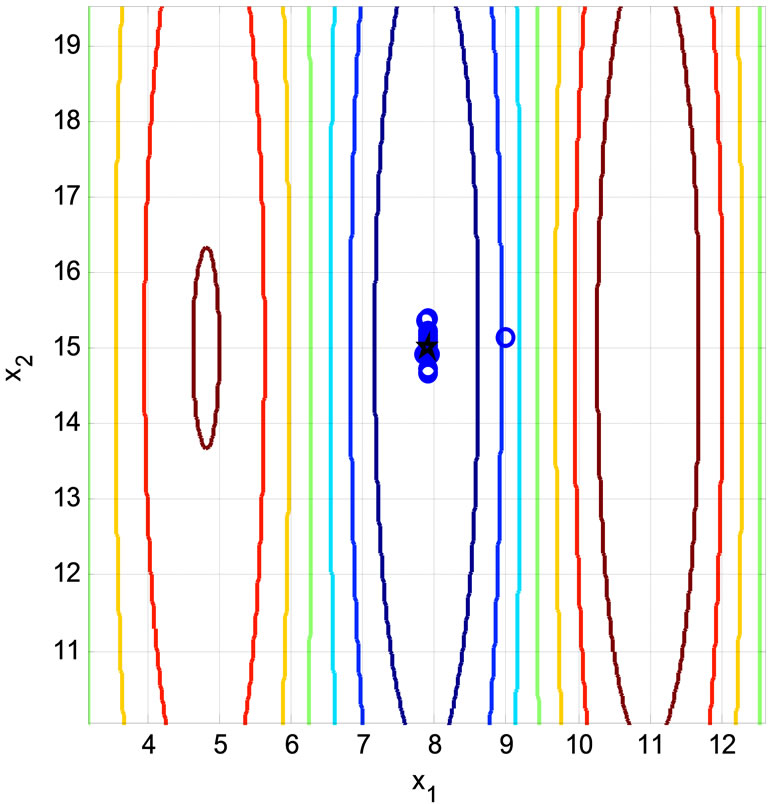
Figure 11. Population of the Multi-Peak Problem when the TGA algorithm is used (20th generation).
1.32e+5 function evaluations.
A population size of 40n is used, and allalgorithmsare run for 50n generations. Figure 12 shows typical runs of the proposed algorithms. In this case, all algorithms follow the same trend toward the minimum. However,the SGA and the SGAU fails to reach the minimum. The TGAis able to reach the minimum after 105 function evaluations.TGASO, TGAU, and TGASOU stopped at −9.642 (0.13% from the minimum) after 9.30e+4, 8.13e +4, and 1.10e+5 function evaluations,respectively.
Generally, these results are consistent with those of testing by conducting 100 runs of each algorithm, listed in Table 2. While all algorithms are able to reach the neighborhood of the minimum, the results indicate that the twinkling consistently produces better solutions than the simple genetic algorithms irrespective of the crossover method, which has a limited effect for this case. The standard deviation values of these algorithms lead to the same conclusion. These results may be explained by the fact that the function contains a large number of local minima, which may limit the contribution of the crossover method while emphasizing the importance of twinkling as it helps free the search from local minima.

Table 1. Results of testing the Multi-Peak function.
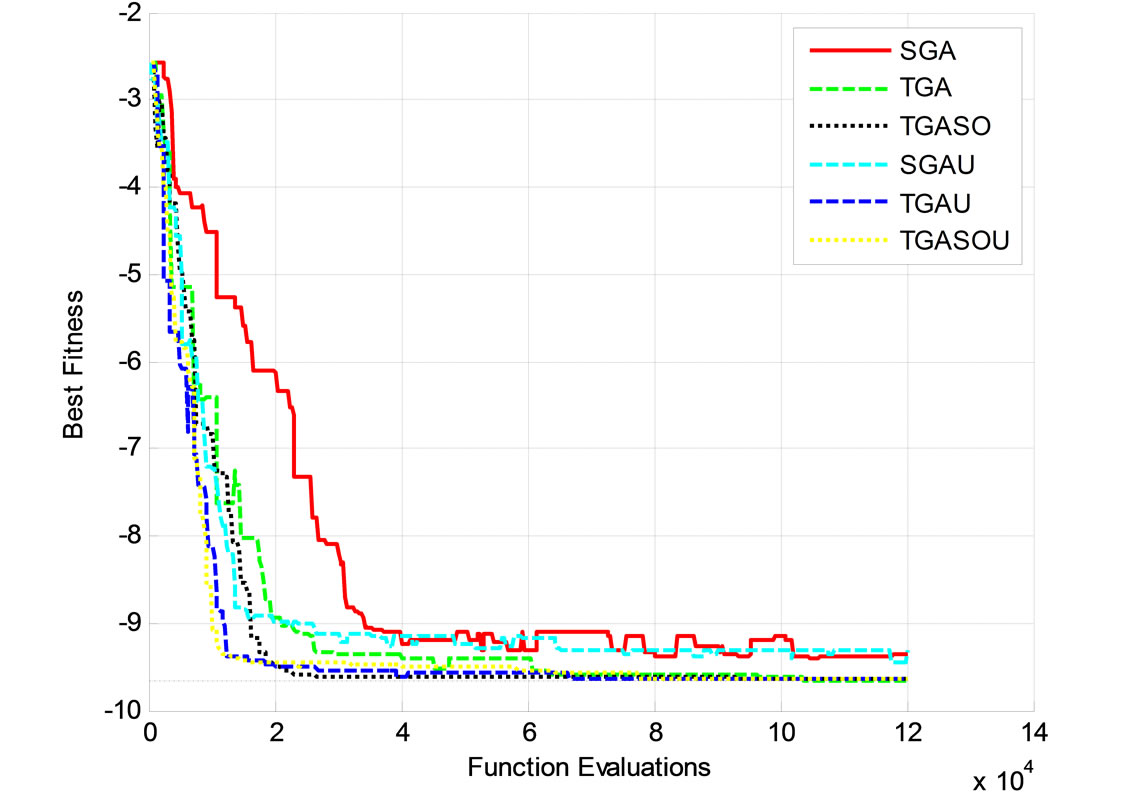
Figure 12. A typical run of the proposed algorithms for the Sine function (m = 100).
8.2. Nonlinear Quadratic Test Function
The Nonlinear Quadratic Test Functionproblem has been solved by various techniques to handle the effect of nonlinear constraints [26]. This problem has ten variables and eight nonlinear constraints. Genetic algorithms can be adapted for constrained minimization problems in the form of:
 (23)
(23)
The problem can be transformed into an unconstrained one by including the constraints in the objective function as penalty terms [27]. Constraints can be incorporated in the objective function using the bracket function. The modified function is:
 (24)
(24)
R is equal 10e+8 for all constrained problems considered in this work unless otherwise specified. The known minimum of the nonlinear quadratic functionis 24.3062. Two out of five algorithms used in [26] yielded best results of 25.486 and 25.653, using a population of 70 over 5000 generations.
A population size of 100n is used. All algorithms are run for 50n generations. Figure 13 show typical runs of the proposed algorithms. The results of this case show that the algorithms that use the convex combination stopped around a function value of 30. On the other hand, the algorithms using the NADX crossover showed steadier progression towardsthe minimum. Out of these three algorithms, the TGA andthe TGASO converged toward the minimum at a significantly faster rate.
The average numbers of function evaluations needed to reach the minimum after 100 runs of the six algorithms are listed in Table 3. The results of this table confirm the conclusions reached for the multi-peak problem considered in Section 7.
8.3. Minimum Cost of a Welded Beam
The second design example involves the minimum cost

Table 2. Results of testing the Sine function (m = 100).
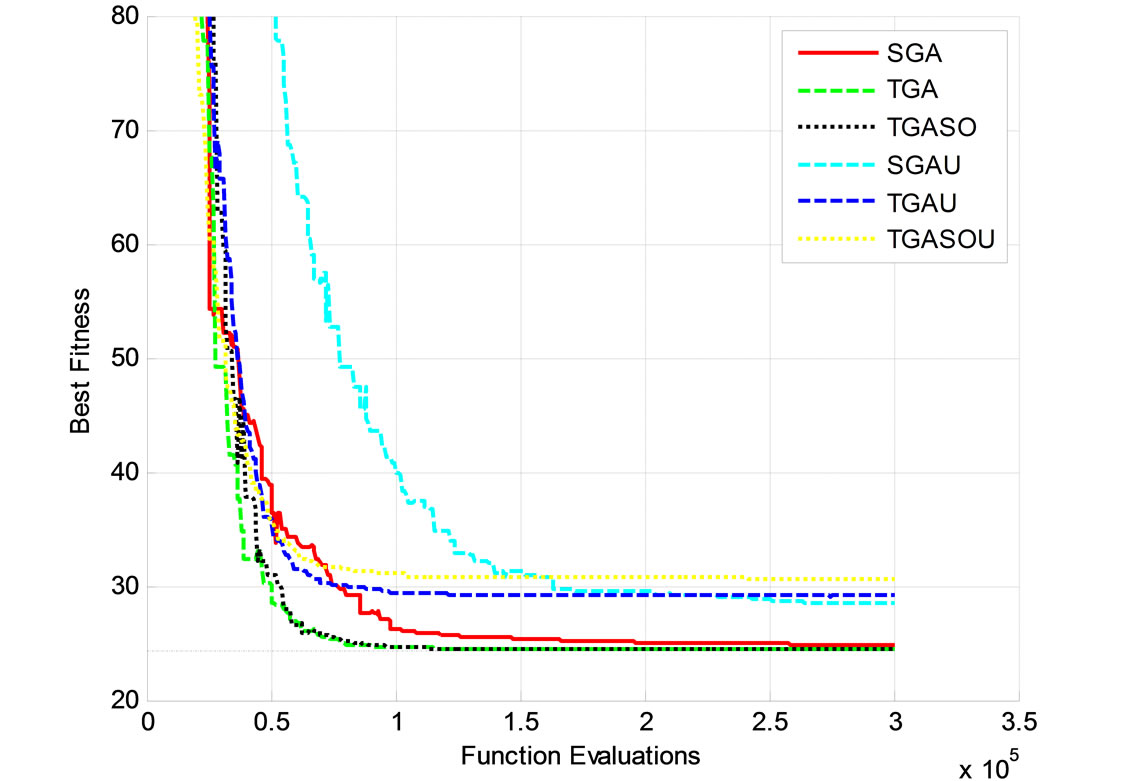
Figure 13. A typical run of the proposed algorithms for the nonlinear quadratic test function.
of a welded cantilever beam [28] (Chapter 1). It has four variables and five nonlinear constraints. The minimum value is 2.3403 at [0.2536, 7.1405, 7.1052, 0.2536]T.
A population size of 50n is used in this example. All algorithms are run for 50n generations. Figure 14 shows typical runs of the proposed algorithms. The behavior of the algorithms closely follows those at the Nonlinear Quadratic test function of the previous section. In this case, the TGASO was able to reach minimum after 15,000 function evaluations. Both the SGA and the TGA progressed more slowly toward the minimum and stopped at 2.3470 function value at the end of last generation.
Table 4 shows the results of 100 runs, which indicate the consistency of the observations in Section 7 regarding the choice of crossover and twinkling. The TGA and the TGASO were able to reach a value of 2.3403. Standard deviations for the cases of the NADX crossover are significantly less than those using the convex combination.
This problem was solved by using an improved particle swarm optimizer that handles constraints to maintain feasible solution [29]. The same problem was solved using the ranking selection-based particle swarm

Table 3. Results of testing the nonlinear quadratic test function.
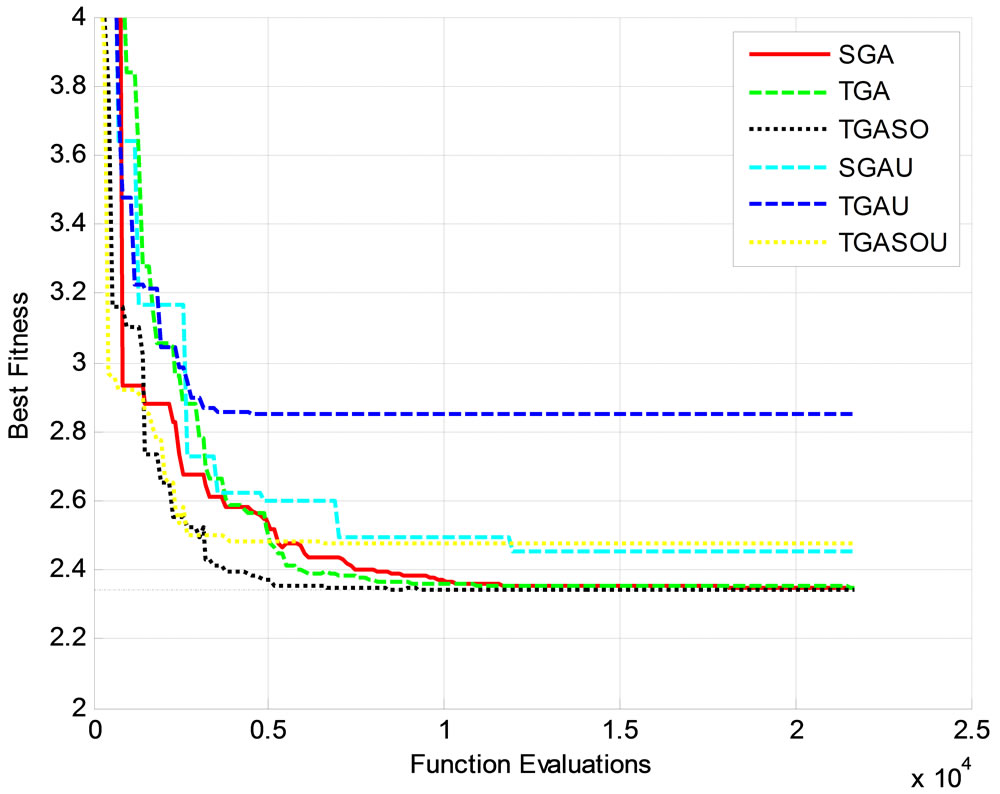
Figure 14. A typical run of the proposed algorithms for the minimum cost of a welded beam problem.

Table 4. Results of testing the minimum cost of a welded beam problem.
algorithm [30]. The results of Table 5 indicate the ability of the proposed algorithms to reach the minimum with a significantly lower number of function evaluations.
8.4. Minimum Cost of a Pressure Vessel
The minimum cost problem of a pressure vessel was used by many researchers to test various optimization algorithms. For example, in order to adapt the penalty factors of a fitness function, it was used to test a genetic algorithm with co-evolution [31]. An improved particle swarm optimizer for solving mechanical design problems was used to solve this problem [29]. The characteristics of particle swarm optimization for global optimization and its application to the mixed discrete nonlinear problems (MDNLP) is suggested as a method to solve this problem [32]. This problem was solved using a hybrid particle swarm optimization with a feasibility-based rule for constrained optimization [33]. Alternatively, a ranking selection-based particle swarm algorithm was applied to solve the same problem [30].
This problem has four variables and eleven constraints. Two of the four variables are discrete. A population size of 100n is used in this example. All algorithms are run for 25n generations. Figure 15 presents typical runs of the proposed algorithms using the same initial population. In this case, the SGA is able to reach the minimum within 18,000 function evaluations. This algorithm is followed by the TGASO and the TGASOU, which that stagnate close to the known minimum of 6059. The TGA and the TGAU stopped in the neighborhood of 6400.
Table 6 lists the results obtained running the six algorithms for a hundred times. These results indicate that the algorithms that use the NADX crossover out perform those using the convex combination. This represents the only case where the result of using the SGA is slightly better than the two twinkling algorithms (TGA and TGASO) whenusing the NADX crossover. However, when using theconvex combination, twinkling algorithms perform better than the simple genetic algorithm.

Table 5. Comparison between the results of testing the minimum cost of a welded beam problem using the twinkling genetic algorithms with two particle swarm algorithms.
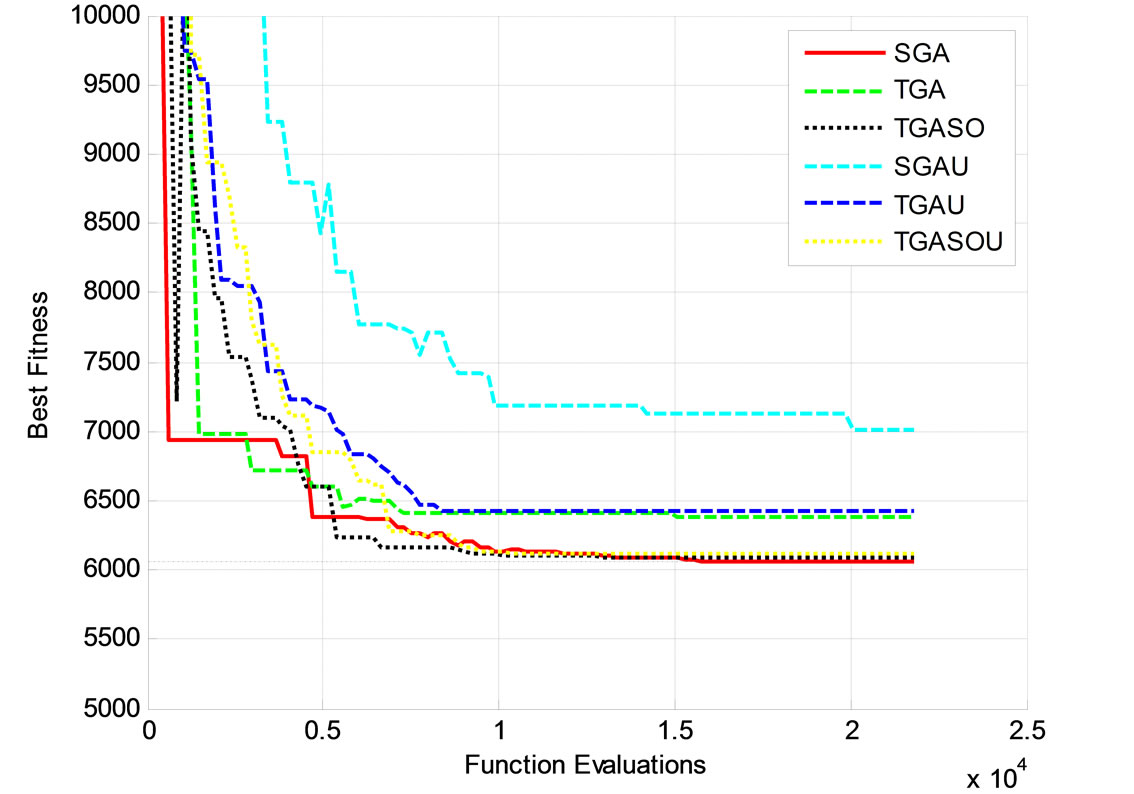
Figure 15. A typical run of the proposed algorithms for the minimum cost of a pressure vessel problem.
Table 7 lists the results of these researchers along with the results of the SGA, TGA, and TGASO of Table 6. The results indicate that the proposed algorithms were able to converge to the same neighborhood of the minimum as other researchers. The proposed algorithms produced a lower number of function evaluations.
9. Conclusions
Genetic algorithms provide the means for global optimization. The simplest form of a genetic algorithm shares some resemblance to these two biological operations: crossover and mutation. Combining these two operations over multiple generations helps reach the optimal point. However, asimplegenetic algorithm suffers from slow convergence. Also, itmay stagnate at a local extremum, especially in the case of a problem with nonlinear constraints. The objective of this paper is to address the limitations of typical genetic algorithms: a slow rate of convergence and the final accuracy. This is accomplished by introducing bio-mimetic behavior in the form of a NADX crossover, which increase the genetic diversity, and twinkling operators, which allow the retention of desirable solutions between generations.
Thispaperintroduces two modifications to the simple genetic algorithm. The first change involvesusing the normally distributed arithmetic crossover (NADX). This crossover techniquemimics the greater diversity of the genes that parents can pass on to their children. NADX is closer to a true biological analogy because it allows a specific “gene value” from a crossover to be outside the limited bounds of the two parents. The second changeis to incorporate twinkling operatorsinto the genetic algorithm. Twinkling introduces a deviation from the standard practice of any optimization algorithm by only allowing a random subset of the variables to undergo the heuristic decisions of the optimization algorithm. The remaining variables carry identical information to the previous iteration or generation. This process has been shown to increase the likelihood of finding the global minimum by maintainingthe “good genes” within a population. Another variation on incorporating the twinkling is introduced using a choice operator, which randomly determines the number of children that are bred from a parental pairing.
To assess the proposed ideas, NADX and twinkling are incorporated into the simple genetic algorithm to produce the following algorithms:
• SGA (Simple genetic algorithm with the NADX crossover)
• TGA (Genetic algorithm with the NADX crossover and the twinkling dimension)
• TGASO (Genetic Algorithm with the NADX crossover and the twinkling dimension and the choice operator)
• SGAU (Simple genetic algorithm with the convex

Table 6. Results of testing theminimum cost of a pressure vessel problem.
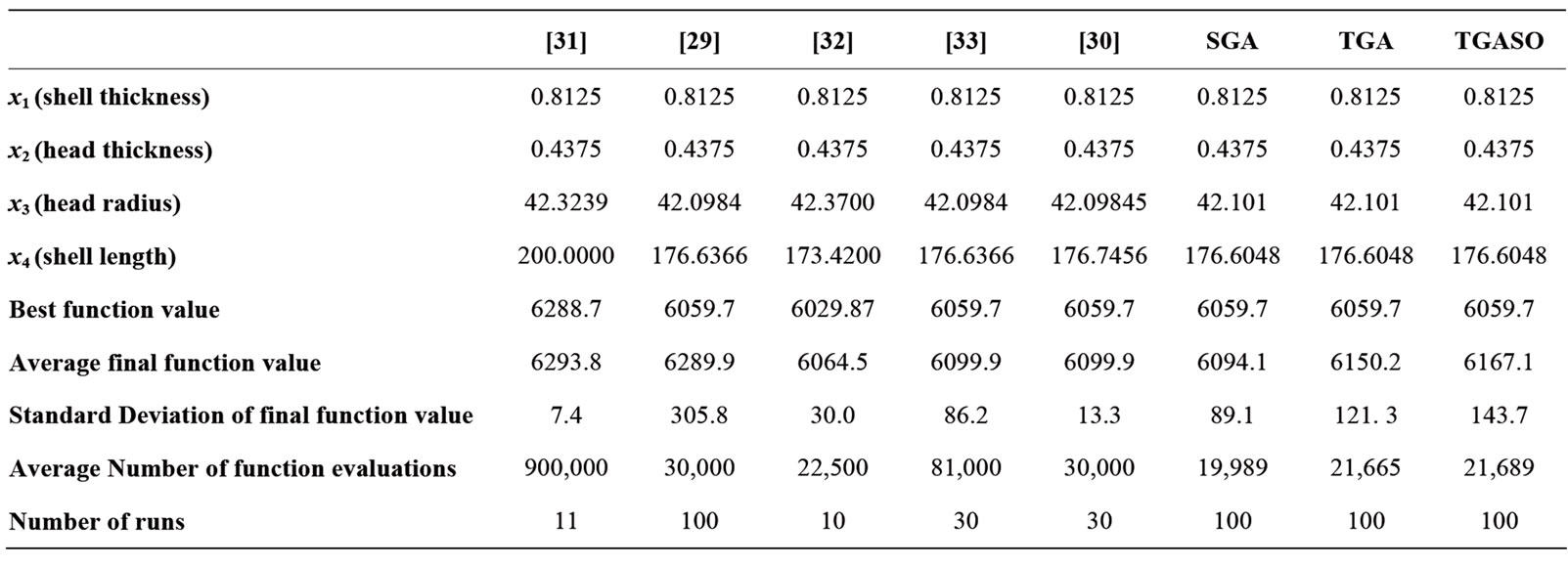
Table 7. Comparison between the results of testing the minimum cost of a pressure vessel problem using the NADX simple and twinkling genetic algorithms with those of other algorithms.
combination crossover)
• TGAU (Genetic algorithm with the convex combination crossover and the twinkling dimension)
• TGASOU (Genetic algorithm with the convex combination crossover and the twinkling dimension and the choice operator)
By using a typical test problem, the effects are compared of the weighted average of the normally distributed arithmetic crossover as well as the twinkling on simple genetic algorithms. In addition, the distribution of population in various critical regions of the search space of this problem is explored. The results indicate the combined effectiveness of using both the NADX crossover and the twinkling; the combined use of these two techniques rapidly concentrates the population closer to the global minimum.
Extensive evaluation of a variety of mathematical and engineering design problems is presented along with the results of earlier researchers. Statistical results show that the proposed algorithms are consistently able to reach the neighborhood of the global minima with competitive speeds of convergence. The following general observation can be presented:
• Algorithms that use the NADX crossover consistently outperform those using the uniformly distributed crossover.
• The twinkling algorithms consistently produce better results than the non-twinkling algorithms. The only exception is the compressed air storage tankproblem, where the SGA producesa slightly better average final function value and average number of function evaluations than the two twinkling algorithms (TGA and TGASO). The advantage of using twinkling becomes apparent in multimodal problems that havea large number of local minima, for example, the Sine Function (Section 8.1).
• The two variations of twinkling presented in this work have about the same level of effectiveness, regardless of which crossover operator is used.
It may be of interest to contrast the proposed algorithm with the hybrid genetic algorithms, where a genetic algorithm is combined with some form of optimization search algorithm. The proposed twinkling genetic algorithms differ from typical hybrid algorithms in the sense that it is still a global optimization problem, and unlike hybrid algorithms, no local searches take place. Thus,the goalof the proposed algorithms is to find the global minimum of the problem under consideration.
There is a significant potential for future work on this area. For example, the effect of the size of the twinkling dimension on the performance of the proposed algorithms should be considered. The incorporation of twinkling into hybrid genetic algorithms can result incomebining the advantages of the local search with the ability of twinkling to accelerate the search globally. Lastly, in order to vary the total and the parental population sizes at each generation, it is desirable to study the use of twinkling in a semi-adaptive fashion within a genetic algorithm. By using NADX crossover, increased emphasis on exploration may result. Assuredly, by combining these two techniques, the success and efficiency of the global search will increase.
REFERENCES
- D. Goldberg, “Genetic Algorithms in Search, Optimization, and Machine Learning,” Addison-Wesley Reading, Boston, 1989.
- K. Deb and R. Agrawal, “Simulated Binary Crossover for Continuous Search Space,” Complex Systems, Vol. 9, 1995, pp. 115-148.
- I. Ono and S. Kobayashi, “A Real Coded Genetic Algorithm for Function Optimization Using Unimodal Normal Distribution Crossover,” Proceedings of the 7th International Conference on Genetic Algorithms, Vol. 14, No. 6, 1997, pp. 246-253.
- F. Herrera, M. Lozano and J. Verdegay, “Fuzzy Connectives Based Crossover Operators to Model Genetic Algorithms Population Diversity,” Fuzzy Sets and Systems, Vol. 92, No. 1, 1997, pp. 21-30. doi:10.1016/S0165-0114(96)00179-0
- F. Herrera, M. Lozano and A. Sanchez, “Taxonomy for the Crossover Operator for Real-Coded Genetic Algorithms: an Experimental Study,” International Journal of Intelligent Systems, Vol. 18, No. 3, 2003, pp. 309-338. doi:10.1002/int.10091
- H. Ishibuchi, N. Yamamoto, T. Murata and H. Tanaka, “Genetic Algorithms and Neighborhood Search Algorithms for Fuzzy Flowshop Problems,” Fuzzy Sets and Systems, Vol. 67, No. 1, 1994, pp. 81-100. doi:10.1016/0165-0114(94)90210-0
- D. Sotiropoulos, E. Stavropoulos and M. Vrahatis, “A New Hybrid Genetic Algorithm for Global Optimization,” Nonlinear Analysis, Vol. 30, No. 7, 1997. pp. 4529-4538. doi:10.1016/S0362-546X(96)00367-7
- J. Yen, J. Liao and D. Randolph, “A Hybrid Approach to Modeling Metabolic Systems Using a Genetic Algorithm and Simplex Method,” IEEE Transactions on Systems, Man, and Cybernetics, Vol. 28, No. 2, 1998, pp. 173-191. doi:10.1109/3477.662758
- M. Okamoto, T., Nonaka, S. Ochiai and D. Tominaga, “Nonlinear Numerical Optimization with Use of a Hybrid Genetic Algorithm Incorporating the Modified Powell Method,” Applied Mathematics and Computation, Vol. 91, No. 1, 1998, pp. 63-72. doi:10.1016/S0096-3003(97)10007-8
- J. Renders and S. Flasse, “Hybrid Methods Using Genetic Algorithms for Global Optimization,” IEEE Transactions on Systems, Man and Cybernetic, Vol. 26, No. 2, 1999, pp. 243-258.
- W. Jwo, C. Liu and C. Liu, “Large-Scale Optimal VAR Planning by Hybrid Simulated Annealing/Genetic Algorithm,” International Journal of Electrical Power & Energy Systems, Vol. 21, No. 1, 1999, pp. 39-44. doi:10.1016/S0142-0615(98)00020-9
- M. Musil, M. Wilmut and N. Chapman, “A Hybrid Simplex Genetic Algorithm for Estimating Geoacoustic Parameters Using Matched-Field Inversion,” IEEE Journal of Oceanic Engineering, Vol. 24, No. 3, 1999, pp. 358- 369. doi:10.1109/48.775297
- A. Nassef, H. Hegazi and S. Metwalli, “A Hybrid Genetic Direct Search Algorithm for Global Optimization of Solid C-Frame Cross Sections,” Proceedings of the 26th Design Automation Conference, Baltimore, 11-13 September 2000.
- K. Hacker, J. Eddy and K. Lewis, “Tuning a Hybrid Optimization Algorithm by Determining the Modality of the Design Space,” Proceedings of the 27th Design Automation Conference, Pittsburgh, 9-12 September 2001, pp. 773-782.
- M. Trabia, “A Hybrid Fuzzy Simplex Genetic Algorithm,” Journal of Mechanical Design, Vol. 126, No. 6, 2004, pp. 969-974. doi:10.1115/1.1803852
- Y. Tenne and S. Armfield, “A Novel Evolutionary Algorithm for Efficient Minimization of Expensive Black-Box Functions with Assisted-Modelling,” IEEE Congress on Evolutionary Computation, Vancouver, 11 September 2006, pp. 3220-3226.
- H. Telega, “Two-Phase Stochastic Global Optimization Strategies,” Studies in Computational Intelligence, Vol. 74, 2007, pp. 153-197. doi:10.1007/978-3-540-73192-4_6
- M. Mekhilef, “A Twinkling Technique for Brownian Moves in Optimization,” Proceedings of the 25th Design Automation Conference, Las Vegas, 12-16 September 1999.
- M. Mekhilef, “Introducing the Twinkling Technique in Non-Linear Optimization,” Proceedings of the 26th Design Automation Conference, Baltimore, 10-13 September 2000.
- M. Mekhilef and M. Trabia, “Successive Twinkling Simplex Search Optimization Algorithms,” Proceedings of the ASME 27th Design Automation Conference, Pittsburgh, 9-12 September 2001.
- M. Mekhilef, “Twinkling a Random Search Algorithm for Design Optimization,” ASME 31st Design Automation Conference, Long Beach, 24-28 September 2005, pp. 321-330.
- Z. Michalewicz, “Genetic Algorithms/Data Structure = Evolutionary Programs,” Springer-Verlag, New York, 1994.
- M. Gen and R. Cheng, “Genetic Algorithms & Engineering Optimization,” Wiley Interscience, New York, 2000.
- R. Kasat and K. Gupta, “Multi-Objective Optimization of an Industrial Fluidized-Bed Catalytic Cracking Unit (FCCU) Using Genetic Algorithm (GA) with the Jumping Genes Operator,” Computers and Chemical Engineering, Vol. 27, No. 12, 2003, pp. 1785-1800. doi:10.1016/S0098-1354(03)00153-4
- M. Arakawa, T. Mayashita and H. Ishikawa, “Genetic Range Genetic Algorithms to Obtain Quasi-Optimum Solutions,” ASME 29th Design Automation Conference, Chicago, 2-6 September 2003, pp. 927-934.
- Z. Michalewicz, “Genetic Algorithms, Numerical Optimization, and Constraints,” Proceedings of the 6th International Conference on Genetic Algorithms, Pittsburgh, 15-19 July 1995, pp. 151-158.
- S. Rao, “Engineering Optimization: Theory and Practice,” Wiley-Interscience, New York, 1996.
- V. Rekalitis, A. Ravindaran and K. Ragsdell, “Engineering Optimization: Methods and Applications,” Wiley Interscience, New York, 2006.
- S. He, E. Prempain and Q. Wu, “An Improved Particle Swarm Optimizer for Mechanical Design Optimization Problems,” Engineering Optimization, Vol. 36, No. 5, 2004, pp. 585-605. doi:10.1080/03052150410001704854
- J. Wang and Z. Yin, “A Ranking Selection-Based Particle Swarm Optimizer for Engineering Design Optimization Problems,” Structural Multidisclinary Optimization, Vol. 37, No. 2, 2008, pp. 131-147. doi:10.1007/s00158-007-0222-3
- C. Coello, “Use of a Self-Adaptive Penalty Approach for Engineering Optimization Problems,” Computers in Industry, Vol. 41, No. 2, 2000, pp. 113-127.
- S. Kitayama, M. Arakawa and K. Yamazaki, “Penalty Function Approach for the Mixed Discrete Nonlinear Problems by Particle Swarm Optimization,” Structural Multidisclinary Optimization, Vol. 32, No. 3, 2006, pp. 191-202. doi:10.1007/s00158-006-0021-2
- Q. He and L. Wang, “A Hybrid Particle Swarm Optimization with a Feasibility-Based Rule for Constrained Optimization,” Applied Mathematics and Computation, Vol. 86, No. 2, 2007, pp. 1407-1422. doi:10.1016/j.amc.2006.07.134
NOTES
*Corresponding author.

