Applied Mathematics
Vol. 3 No. 4 (2012) , Article ID: 18875 , 7 pages DOI:10.4236/am.2012.34047
A Similarity Technique for Solving Two-Layer Shallow-Water Equations
Department of Engineering Physics and Mathematics, Faculty of Engineering, Zagazig University, Zagazig, Egypt
Email: emadabdelhafiez@yahoo.com
Received December 28, 2011; revised February 10, 2012; accepted February 17, 2012
Keywords: The Characteristic Function Method; The Two-Layer Shallow-Water Equations; Gravity Currents
ABSTRACT
This paper is devoted to the analysis of the two-layer shallow-water equations representing gravity currents. A similarity technique which is the characteristic function method is applied for this study. The application of the characteristic function method makes it possible to obtain the similarity forms depending on a group of infinitesimal transformations. Thus, the number of independent variables is reduced by one and the governing partial differential equations with the auxiliary conditions reduce to a system of ordinary differential equations with the appropriate auxiliary conditions. Numeric solutions are presented and discussed.
1. Introduction
The present study focuses on a two-layer shallow-water system of incompressible, immiscible and inviscid fluids with a free surface. When two fluids of differing densities interact in such a way that a vertical interface exists between the fluids, the resulting motion consists of the heavier fluid flowing horizontally beneath the lighter fluid. Such a flow is said to form gravity current, an overall view of many of the phenomena associated with the gravity currents is presented by Simpson [1]. Various numerical methods have been employed to solve these model equations such as finite difference, finite element and spectral methods [2]. Leveque use MacCromick’s method [3] and Godunov’s method used by Godlewski et al. [4] which gives numerical standard schemes to solve the systems of conservation laws. Jin et al. [5] have presented finite difference methods, called relaxation schemes. Thereby, Montogomery et al. [6] have used these relaxation schemes for systems of conservation laws associated with the gravity currents for a two-layer model. D’Alesio et al. [7]. Gravity currents considering Lie symmetry groups has been investigated by Glaister [8]. He did apply Lie symmetry groups of two-dimensional shallow-water equations with cylindrical symmetry numerically in conjunction with the Rankine_Hugoniot shock relations. Velan et al. [9] studied Lie symmetries and found the invariant solutions of the dispersive shallow-water equation which is in the single equation form. Özer [10,11]. Also there are several solution techniques to deal with the determining equations in the Lie group analysis of differential equations [12,13]. The main purpose of this paper is to find similarity solutions of twolayer shallow-water equations representing gravity currents by using the characteristic function method. As the characteristic function method is not based on linear operators, it is applicable to both linear and nonlinear differential models [14-16].
2. Mathematical Formulation of the Problem
In this study, we consider a two-layer shallow water resting on a horizontal surface with respective densities ρ1, ρ2. We neglect the friction between the fluids and the bottom and we also assume that the effect of viscosity is negligible. According to the shallow-water theory, we shall assume that the length of the current is much larger than its depth. By using this assumption we neglect the vertical accelerations and we can say that the pressure is hydrostatic. Assuming that the depth of an ambient fluid is much larger than the thickness of the current. The horizontal velocities u1 in the upper layer and u2 in the lower layer are independent of height and pressure field by using the assumption that the pressure is hydrostatic [17]. We also assume that Reynolds number of the flow is sufficiently high so that viscous forces are negligible, as well as the surface tension. We also assume that there is no mixing between layers. By employing these assumptions and using the kinematics and dynamic boundary conditions at the interface, the two-layer shallowwater equations are modeled as follows [18].
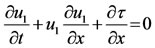 (1)
(1)
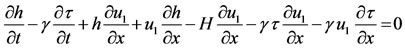 (2)
(2)
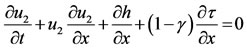 (3)
(3)
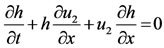 (4)
(4)
This model is illustrated in Figure 1, where 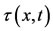 represents the displacement of the upper layer,
represents the displacement of the upper layer, 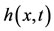 is the thickness of the lower layer, H is the mean total depth, x is an coordinate system with the x-axis along the bottom.
is the thickness of the lower layer, H is the mean total depth, x is an coordinate system with the x-axis along the bottom.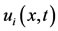 , (i = 1, 2), denotes the horizontal velocity components for the upper and the lower layer, t is the time and
, (i = 1, 2), denotes the horizontal velocity components for the upper and the lower layer, t is the time and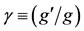 ,
, 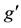 is the combined gravity defined by
is the combined gravity defined by , g is the gravity.
, g is the gravity.
We study the system under the following conditions;
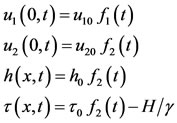 (5)
(5)
2.1. Invariance Analysis
The infinitesimal transformation of the system variables (t, x; u1, u2, h, τ) is defined as follows;
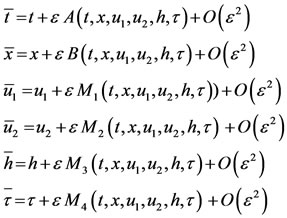 (6)
(6)

Figure 1. Two-layer shallow-water representation.
The transformation of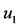 ,
, 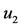 , h and τ derivatives p’s, q’s, r’s and s’s are defined as;
, h and τ derivatives p’s, q’s, r’s and s’s are defined as;
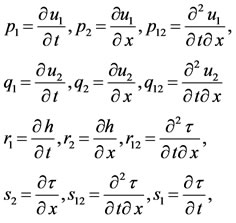 (7)
(7)
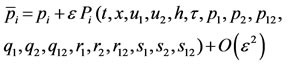
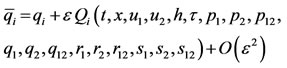

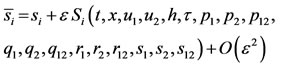

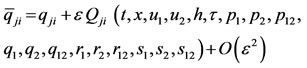
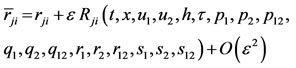
 (8)
(8)
where the subscript i and j stand for derivative with respect to t, x.
A, B, M’s, P’s, Q’s, S’s and S’s are the infinitesimal prolongations. According to these Definitions (1)-(4) reduce to;
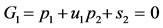 (9)
(9)
 (10)
(10)
 (11)
(11)
 (12)
(12)
the system of differential Equations (1)-(4) of the form Gi = 0, (i = 1 - 4), will be invariant if DGi = 0, Where the total operator D is written as:
 (13)
(13)
The applications of the total operator D to Equations (7)-(10) gives:
 (14)
(14)
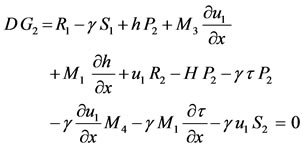 (15)
(15)
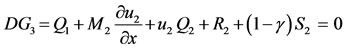 (16)
(16)
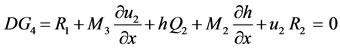 (17)
(17)
2.2. Evaluation of Infinitesimals
Here we will find the explicit solutions of the infinitesimal functions A, B and M’s, by solving the Equations (14)-(17). “The power-series solution form” is one of the most effective techniques for finding the solutions of determining equations in the symmetry group analysis of differential equations [14,19]. So we consider the following power-series forms for the infinitesimal functions:
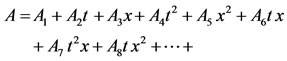 (18)
(18)
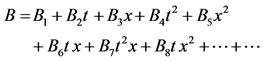 (19)
(19)
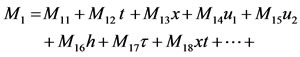 (20)
(20)
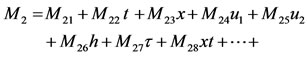 (21)
(21)
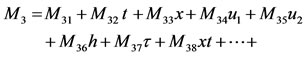 (22)
(22)
 (23)
(23)
where Aij, Bij and Mij i, j = 1, 2 are constant coefficients. Then substituting the power-series forms (18)-(23) into the determining Equations (14)-(17) we equate powers of the variables x, t, u1, u2, h and τ and calculate the constant coefficients of the power-series forms by equating each coefficient of various powers to zero, which gives the general characteristic function of two-layer shallow-water equations. After the straightforward calculations for any finite integer order of power-series forms, we find that:
 (24)
(24)
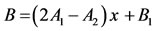 (25)
(25)
 (26)
(26)
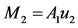 (27)
(27)
 (28)
(28)
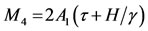 (29)
(29)
2.3. Reduction to Ordinary Differential Equations
In this section, we will obtain the reduced forms of the two-layer shallow-water equations by using infinitesimal group transformations obtained in the previous section. Here we will try to reduce for each sub algebra in the optimal system to obtain the reduced forms of the system (1)-(4). For this purpose, we need to write the characteristic equation in the following form:
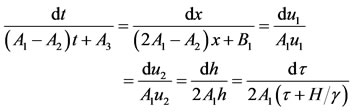 (30)
(30)
Case (1).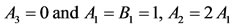 . The characteristic equation can be rewritten as
. The characteristic equation can be rewritten as
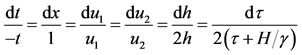 (31)
(31)
Solving Equation (31) yields the similarity variable,
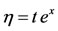 (32)
(32)
And the similarity forms are obtained by the integration of equations in the characteristic Equation (31) giving
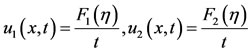 (33)
(33)
 (34)
(34)
with the corresponding boundary conditions
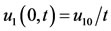 ,
, (35)
(35)
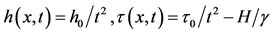 (36)
(36)
Now, we have the reduced system of ordinary differential equations
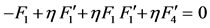 (37)
(37)

(38)
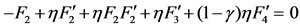 (39)
(39)
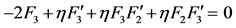 (40)
(40)
with the reduced associated boundary conditions
 (41)
(41)
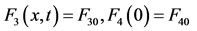 (42)
(42)
Case (2). 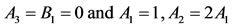
We can rewrite the characteristic equation in the following form as:
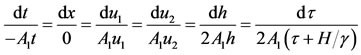 (43)
(43)
Giving the similarity variable,
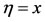 (44)
(44)
Integrating equation (43), the similarity forms are obtained as
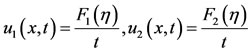 (45)
(45)
 (46)
(46)
with the corresponding boundary conditions
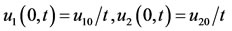 (47)
(47)
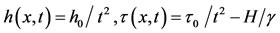 (48)
(48)
and the reduced system of ordinary differential equations is
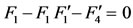 (49)
(49)
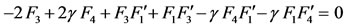 (50)
(50)
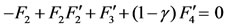 (51)
(51)
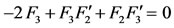 (52)
(52)
with the reduced boundary conditions
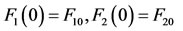 (53)
(53)
 (54)
(54)
Case (3). 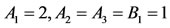
The characteristic equation is
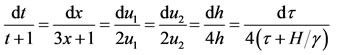 (55)
(55)
Giving the similarity variable
 (56)
(56)
and the similarity forms
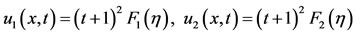 (57)
(57)
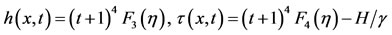 (58)
(58)
with the boundary conditions
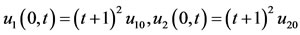 (59)
(59)
 (60)
(60)
The reduced system of ordinary differential equations is
 (61)
(61)
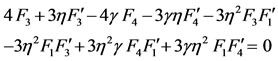 (62)
(62)
 (63)
(63)
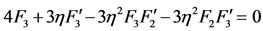 (64)
(64)
with the reduced boundary conditions
 (65)
(65)
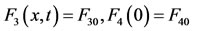 (66)
(66)
3. Numerical Results and Discussion
As the analytic solution of systems of ordinary differential Equations (37)-(40), (49)-(52) and (61)-(64), we solve these systems of ordinary differential equations numerically by using fourth order-Runge-Kutta method coupled with the shooting method by employing the corresponding boundary conditions in terms of the similarity variables given above, the results are illustrated in the following figures.
Figure 2 shows the behavior of the dimensionless velocities of the two layers 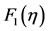 and
and , where
, where  increases with respect to the similarity variable similar to log-shape, at the same time
increases with respect to the similarity variable similar to log-shape, at the same time  increases up to
increases up to 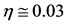 after that the velocity is nearly constant. On the other hand Figure 3 shows the behavior of the height of the lower layer
after that the velocity is nearly constant. On the other hand Figure 3 shows the behavior of the height of the lower layer 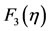 and the free surface of
and the free surface of

Figure 2. Singular wave solutions for the flow velocities F1(η), F2(η) corresponding to Case (1) for large value of η and γ = 1.0, where F1(η) refer to u1(x,t) and F2(η) refer to u2(x,t).

Figure 3. Singular wave solutions of the height of the lower layer F3(η) and the free surface of the upper layer F4(η) of Case (I) for large value of η and γ = 1.0, where F3(η) refer to h(x,t) and F4(η) refer to τ(x,t).
the upper layer 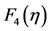 they increase until
they increase until 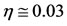 after that
after that 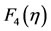 decrease with low rate, at the same time
decrease with low rate, at the same time 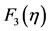 decrease with high rate similar to exponentialshape.
decrease with high rate similar to exponentialshape.
In Figures 4-7, there is a similarity in the shape between the two velocities  and
and 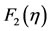 from one hand, and between the profile depth of the lower layer
from one hand, and between the profile depth of the lower layer 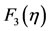 against the free displacement of the upper layer
against the free displacement of the upper layer 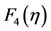 from another hand, because we have paid the two fluids in the same direction and velocities close to each other. These velocities and the profile depth of the lower layer and the free displacement of the upper layer increase abruptly up to
from another hand, because we have paid the two fluids in the same direction and velocities close to each other. These velocities and the profile depth of the lower layer and the free displacement of the upper layer increase abruptly up to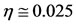 , after this value, the velocities
, after this value, the velocities  and
and  and the profile depth of the lower layer
and the profile depth of the lower layer  and the free displacement of the upper layer
and the free displacement of the upper layer  linearly increase in a low rate with respect to the value of η.
linearly increase in a low rate with respect to the value of η.
According to Figures 8 and 9, under a specific condition there are disturbances on the dimensionless veloci-
Figure 4. Plot of similarity solutions for the flow velocities F1(η), F2(η) Corresponding to Case (2) for constants: F10 = –15, F20 = –10, F30 = 25, F40 = 10, and γ = 1.0, where F1(η) refer to u1(x,t) and F2(η) refer to u2(x,t).

Figure 5. Plot of similarity solutions for the height and the free surface F3(η), F4(η) respectively corresponding to Case (2) for constants: F10 = –15, F20 = –10, F30 = 25, F40 = 10, and γ = 1.0, where F3(η) refer to h(x,t) and F4(η) refer to τ(x,t).
Figure 6. Plot of similarity solutions for the flow velocities F1(η), F2(η) corresponding to Case (2) for constants: F10 = 5, F20 = –5, F30 = 5, F40 = –5, and γ = 1.0, where F1(η), refer to u1(x,t) and F2(η) refer to u2(x,t).
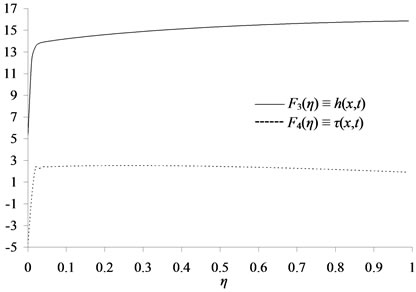
Figure 7. Plot of similarity solutions for the height and the free surface, F3(η), F4(η) respectively corresponding to Case (2) for constants: F10 = 5, F20 = –5, F30 = 5, F40 = –5, and γ = 1.0, where F3(η) refer to h(x,t) and F4(η) refer to τ(x,t).
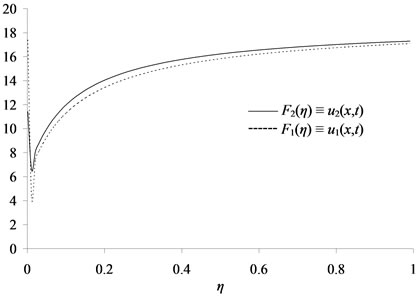
Figure 8. Singular wave solutions for the flow velocities F1(η), F2(η) corresponding to Case (3) for large value of η and γ = 1.0, where F1(η) refer to u1(x,t) and F2(η) refer to u2(x,t).
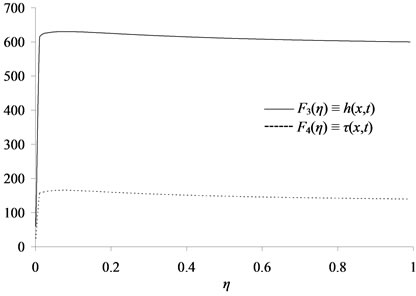
Figure 9. Singular wave solutions of the height of the lower layer F3(η) and the free surface of the upper layer F4(η) of Case (3) for large value of η and γ = 1.0, where F3(η) refer to h(x,t) and F4(η) refer to τ(x,t).
ties profiles of the two layers up to , these disturbances occurring at the same time which hydraulic jump occurs in the dimensionless depth of the lower layer and the displacement of the upper layer, after this value the two layers velocities profiles increase with respect to the similarity variable η similar to log-shape, at the same time
, these disturbances occurring at the same time which hydraulic jump occurs in the dimensionless depth of the lower layer and the displacement of the upper layer, after this value the two layers velocities profiles increase with respect to the similarity variable η similar to log-shape, at the same time 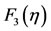 and
and  decreases with low rate.
decreases with low rate.
4. Conclusion
The present analysis employed the characteristic function method to solve the equations representing the two-layer shallow-water equations. Different reduction forms were obtained, illustrated and discussed. Although the analytic solutions of the reduced forms were not available, the obtained numeric solution well presented the behavior of the two layers of the problems. For specific values of the group parameters, the solutions were obtained and presented and it’s also available to obtain and present the solutions for other cases. In our analysis a new similarity variable was obtained in Case (2), also other new similarity variables were obtained in Cases (1) and (3) giving critical singular wave solutions which have not been reported in [12].
REFERENCES
- J. E. Simpson, “Gravity Currents: In the Environment and Laboratory,” Cambridge University Press, Cambridge, 1997.
- C. B. Vreugdenhil, “Numerical Methods for ShallowWater Flow,” Kluwer, Dordrecht, 1994.
- R. Leveque, “Numerical Methods for Conservation Laws,” Birkhauser, Basel, 1992. doi:10.1007/978-3-0348-8629-1
- E. Godlewski and P. A. Raviart, “Numerical Approximation of Hyperbolic Systems of Conservation Laws,” Springer, New York, 1996.
- S. Xin and Z. Xin, “The Relaxation Schemes for Systems of Conservation Laws in Arbitrary Space Dimensions,” Communications on Pure and Applied Mathematics, Vol. 48, No. 3, 1955, pp. 235-276.
- P. J. Montgomery and T. B. Moodie, “Generalization of a Relaxation Scheme for Systems of Forced Nonlinear Hyperbolic Conservation Laws with Spatially Dependent Flux Functions,” Studies in Applied Mathematics, Vol. 110, No. 1, 2003, pp. 1-19. doi:10.1111/1467-9590.00228
- S. J. D’Alessio, T. B. Moodie, J. P. Pascal and G. E. Swaters, “Gravity Currents Produced by Sudden Releases of a Fixed Volume of Heavy Fluid,” Studies in Applied Mathematics, Vol. 96, No. 4, 1996, pp. 359-385.
- P. Glaister, “Similarity Solutions of the Shallow-Water Equations,” Journal of Hydraulic Research, Vol. 29, No. 1, 1991, pp. 107-116. doi:10.1080/00221689109498995
- M. S. Velan and M. Lakshmanan, “Lie Symmetries and Invariant Solutions of the Shallow-Water Equation,” International Journal of Non-Linear Mechanics, Vol. 31, No. 3, 1996, pp. 339-344. doi:10.1016/0020-7462(95)00063-1
- T. Özer, “Symmetry Group Analysis of Benney System and Application for the Shallow-Water Equations,” Mechanics Research Communications, Vol. 32, No. 3, 2005, pp. 241-254. doi:10.1016/j.mechrescom.2004.10.002
- T. Özer, “On Symmetry Group Properties and General Similarity Forms of the Benney Equations in the Lagrangian Variables,” Journal of Computational and Applied Mathematics, Vol. 169, No. 2, 2004, pp. 297-313. doi:10.1016/j.cam.2003.12.027
- T. Özer and N. Antar, “The Similarity Forms and Invariant Solutions of the Two-Layer Shallow-Water Equations,” Nonlinear Analysis: Real World Applications, Vol. 9, No. 3, 2008, pp. 791-810. doi:10.1016/j.nonrwa.2006.12.010
- B. J. Cantwell, “An Introduction to Symmetry Analysis,” Cambridge University Press, Cambridge, 2002.
- R. Seshadri and T. Y. Na, “Group Invariance in Engineering Boundary Value Problems,” Springer-Verlag, New York, 1985. doi:10.1007/978-1-4612-5102-6
- M. B. Abd-el-Malek and M. M. Helal, “Characteristic Function Method for Classification of Equations of Hydrodynamics of a Perfect Fluid,” Journal of Computational and Applied Mathematics, Vol. 182, No. 1, 2005, pp. 105-116. doi:10.1016/j.cam.2004.11.042
- M. B. Abd-el-Malek and M. M. Helal, “The Characteristic Function Method and Exact Solutions of Nonlinear Sheared Flows with Free Surface under Gravity,” Journal of Computational and Applied Mathematics, Vol. 189, No. 1-2, 2006, pp. 2-21. doi:10.1016/j.cam.2005.04.038
- J. W. Rottman and R. E. Grundy, “Self-Similar Solutions of the Shallow-Water Equations Representing Gravity Currents with Variable Inflow,” Journal of Fluid Mechanics, Vol. 169, 1986, pp. 337-351. doi:10.1017/S0022112086000678
- S. J. D. D’Alessio, T. B. Moodie, J. P. Pascal and G. E. Swaters, “Gravity Currents Produced by Sudden Release of a Fixed Volume of Heavy Fluid,” Studies in Applied Mathematics, Vol. 96, No. 4, 1996, pp. 359-385.
- B. J. Cantwell, “Introduction to Symmetry Analysis,” Cambridge University Press, Cambridge, 2002.

