Applied Mathematics
Vol. 3 No. 3 (2012) , Article ID: 18087 , 5 pages DOI:10.4236/am.2012.33032
Boundary Layer Flow past a Stretching Cylinder and Heat Transfer with Variable Thermal Conductivity
Department of Mathematics, Jamia Millia Islamia, New Delhi, India
Email: rdrekhadahiya@gmail.com
Received October 28, 2011; revised December 24, 2011; accepted January 2, 2012
Keywords: Boundary Layer Equation; Keller-Box Method; Energy Equation; Variable Thermal Conductivity; Prandtl Number
ABSTRACT
The boundary layer flow of viscous incompressible fluid over a stretching cylinder has been considered to study flow field and temperature field. Due to non-linearity, a numerical approach called Keller-box technique has been used to compute the values of velocity function f and temperature field at different points of dynamic region. The expressions for skin friction and Nusselt number have also been obtained. The dependence of velocity profile and temperature profile on the dimensionless parameter of practical interest has been analyzed in detail by graphs. The dependence of Skin friction and Nusselt number has been seen through tables.
1. Introduction
The boundary layer flow and heat transfer due to stretching flat plates or cylinders are of practical importance in fiber technology and extrusion processes, and of theoretical interest as well. The production of polymer sheets and plastic films is based on this technology. There are number of examples which include the cooling of an infinite metallic plate in a cooling bath, the boundary layer along material handling conveyers, the aerodynamic extrusion of plastic sheets, the boundary layer along a liquid film in condensation processes, paper production, glass blowing, metal spinning and drawing plastic films, and polymer extrusion. The quality of the final product depends on the rate of heat transfer at the stretching surface. Sakiadis [1] was the first to consider the boundary layer flow on a moving continuous solid surface. Crane [2] extended this concept to a stretching sheet with linearly varying surface speed and presented an exact solution for the steady two-dimensional flow over stretching surface in a quiescent fluid. Since then, many authors have considered various aspects of this problem and obtained similarity solutions. A similarity solution is one in which the number of independent variables is reduced by at least one, usually by a coordinate transformation. The idea is analogous to dimensional analysis, but instead of parameters, like the Reynolds number, the coordinates themselves are collapsed into dimensionless groups that scale the velocities [3].
The boundary layer flow due to a stretching vertical surface in a quiescent viscous and incompressible fluid when the buoyancy forces are taken into consideration have been considered in the papers [4-11]. Lin and Shih [12,13] considered the laminar boundary layer and heat transfer along horizontally and vertically moving cylinders with constant velocity and found that the similarity solutions could not be obtained due to the curvature effect of the cylinder. In the present paper, we find velocity and temperature field for boundary layer flow past a stretching cylinder where cylinder is continuously moving with  velocity. Due to nonlinearity of the problem, we use the numerical approach called Keller-box technique [14]. Since the lateral surface of cylinder changes according to curvature parameter γ = 0.0, 0.25, 0.5, 0.75, 1, so we have studied the influence of γ on velocity and temperature fields. The expressions of skin friction
velocity. Due to nonlinearity of the problem, we use the numerical approach called Keller-box technique [14]. Since the lateral surface of cylinder changes according to curvature parameter γ = 0.0, 0.25, 0.5, 0.75, 1, so we have studied the influence of γ on velocity and temperature fields. The expressions of skin friction 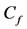 and Nusselt number
and Nusselt number 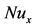 have been obtained. They have been discussed in respect to pertinent parameters like prandtl number Pr, curvature parameter γ and thermal variable parameter ε.
have been obtained. They have been discussed in respect to pertinent parameters like prandtl number Pr, curvature parameter γ and thermal variable parameter ε.
2. Mathematical Formulation of the Problem
Consider a steady, axisymmetric boundary layer flow of a viscous incompressible fluid along a continuously stretching cylinder as shown in Figure 1. It is assumed that the stretching velocity 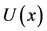 is of the form
is of the form  where
where 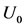 is positive constant and l is characteristic length. Under these assumptions along with the boundary layer approximations, the equations which
is positive constant and l is characteristic length. Under these assumptions along with the boundary layer approximations, the equations which
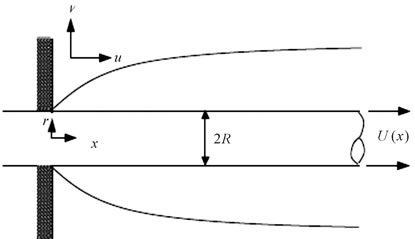
Figure 1. Physical model and coordinate system.
model the problem under consideration are
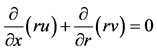 (2.1)
(2.1)
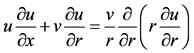 (2.2)
(2.2)
together with boundary conditions
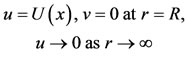 (2.3)
(2.3)
where u and v are the velocity components in the xand r-directions, respectively. The continuity Equation (2.1) can be satisfied by introducing a stream function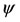 such that
such that 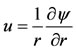 and
and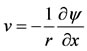 . Following [15,16], we define
. Following [15,16], we define  and
and 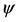 as
as
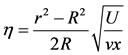 ,
, (2.4)
(2.4)
so that the momentum equation becomes
 (2.5)
(2.5)
together with boundary conditions
 (2.6)
(2.6)
The Equations (2.5) and (2.6) constitute a non-linear boundary-value problem in infinite domain . Since no prescribed methods are available to deal with nonlinear boundary equations that to be in infinite domain, so we solve it by numerical method called Keller-box method for different curvature parameter γ.
. Since no prescribed methods are available to deal with nonlinear boundary equations that to be in infinite domain, so we solve it by numerical method called Keller-box method for different curvature parameter γ.
3. Skin Friction Coefficient
Surface shear stress is calculated by 
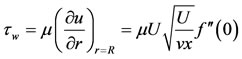 (3.1)
(3.1)
Therefore, the skin friction coefficient is given by
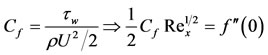 (3.2)
(3.2)
4. Heat Transfer Problem
The heat flow problem for the stretching cylinder to the fluid in the absence of energy dissipation, is governed by
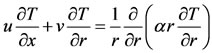 (4.1)
(4.1)
with boundary conditions
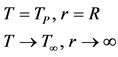 (4.2)
(4.2)
Defining the dimensionless temperature by
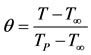
It has been observed that for liquid metals the thermal conductivity 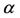 varies with temperature in an approximately linear manner in the range from
varies with temperature in an approximately linear manner in the range from 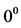 F to
F to 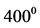 F. Therefore, we assume
F. Therefore, we assume  as
as 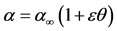
Now, the Equation (4.1) reduces to
 (4.3)
(4.3)
Equation (4.3) again constitutes a non-linear boundary value problem involving velocity function f. We again use Keller-box method for different values of flow parameter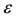 , γ and Pr .
, γ and Pr .
5. Local Nusselt Number
The energy is transit by virtue of temperature gradient is given by
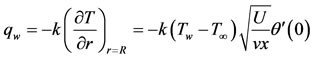 (5.1)
(5.1)
Hence, nusselt number is calculated as
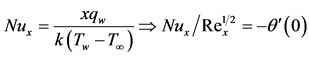 (5.2)
(5.2)
where  is the local Reynolds number.
is the local Reynolds number.
6. Discussions and Results
In the course of analysis of the problem of boundary layer flow past a stretching cylinder and heat transfer with variable thermal conductivity, we come across the following results:
The Equation (2.5) together with boundary conditions (2.6) constitutes a non-linear boundary value problem of order three. We use Keller-box [16] technique of implicit finite difference to find 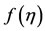 and
and 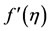 so that the velocity components of viscous incompressible fluid over stretching cylinder may be obtained. Referring Figure 2, we see that the transverse velocity component has not been influenced by curvature parameter γ within the dynamic region [0, 1.25], thereafter, as curvature of stretching cylinder decreases, this velocity component decreases. Physically, as
so that the velocity components of viscous incompressible fluid over stretching cylinder may be obtained. Referring Figure 2, we see that the transverse velocity component has not been influenced by curvature parameter γ within the dynamic region [0, 1.25], thereafter, as curvature of stretching cylinder decreases, this velocity component decreases. Physically, as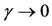 , the outer surface of cylinder behaves like a flat surface. It means as
, the outer surface of cylinder behaves like a flat surface. It means as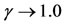 , the viscosity effect reduces due to contact area of surface with fluid tends to the tangential position.
, the viscosity effect reduces due to contact area of surface with fluid tends to the tangential position.
Looking at the Figure 3, we see that the effect of curvature parameter on horizontal component of velocity field is almost nil within the dynamic region [0, 0.75]. This velocity component approaches to zero asymptotically within the region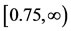 . In this case, the velocity within
. In this case, the velocity within  is free stream velocity and in this region, as γ increases, the velocity component increases.
is free stream velocity and in this region, as γ increases, the velocity component increases.
Reading the Table 1, we see that . Thus, as Reynolds number increases
. Thus, as Reynolds number increases 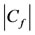 decreases. It is well known fact that as
decreases. It is well known fact that as 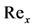 increases, the viscous forces decreases, in turn
increases, the viscous forces decreases, in turn 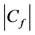 decreases. In the present case,
decreases. In the present case,  depends on curvature parameter γ. We see that as γ
depends on curvature parameter γ. We see that as γ
increases  increases which means as γ increases, the viscous forces start reducing.
increases which means as γ increases, the viscous forces start reducing.
Reading the Figures 4 and 5, we see the trend of the behavior of temperature profile. According to Figure 4, where Pr = 1.0, we note the following:
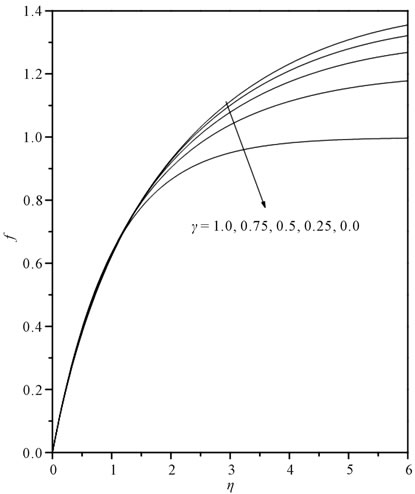
Figure 2. Transverse velocity profiles for different values of γ.
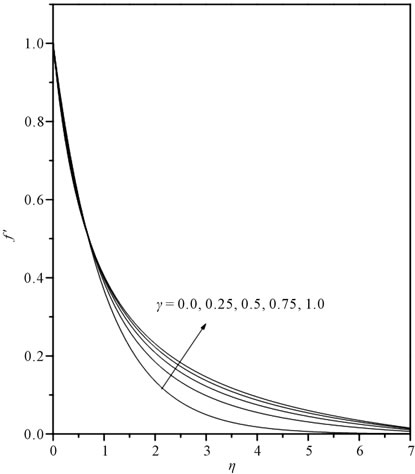
Figure 3. Horizontal velocity profiles for different values of γ.

Table 1. The variation of 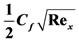 with respect to curvature parameter γ.
with respect to curvature parameter γ.
1) In case constant thermal conductivity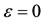 , curvature parameter γ has no effects on temperature field within dynamic region [0, 0.7]. As the flow boundary layer is thinner than the thermal boundary layer, therefore, this dynamic region is sub interval of flow dynamic region. In free stream, as curvature increases, the heat transfer from surface to fluid enhances.
, curvature parameter γ has no effects on temperature field within dynamic region [0, 0.7]. As the flow boundary layer is thinner than the thermal boundary layer, therefore, this dynamic region is sub interval of flow dynamic region. In free stream, as curvature increases, the heat transfer from surface to fluid enhances.
2) When thermal conductivity is variable, that is , we see that there is no region which has not been affected by curvature parameter γ. In this case, as γ increases, the heat transfers becomes fast from surface to fluid too.
, we see that there is no region which has not been affected by curvature parameter γ. In this case, as γ increases, the heat transfers becomes fast from surface to fluid too.
3) If further , transfer of heat is in better position than the case where
, transfer of heat is in better position than the case where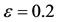 .
.
The Figure 5 shows the pattern of temperature field variation when the thermal conductivity parameter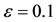 . We see that in the case Pr = 1.0, we see that curvature parameter γ does not having any effect on heat transfer within dynamic region [0, 0.75] while for Pr = 2.0 and Pr = 3.0, the curvature parameter influences the heat transfer everywhere. The enhancement in γ accelerates the heat transfer in both the cases Pr = 0.2 and Pr = 0.4.
. We see that in the case Pr = 1.0, we see that curvature parameter γ does not having any effect on heat transfer within dynamic region [0, 0.75] while for Pr = 2.0 and Pr = 3.0, the curvature parameter influences the heat transfer everywhere. The enhancement in γ accelerates the heat transfer in both the cases Pr = 0.2 and Pr = 0.4.

Figure 4. Temperature profiles for different values of γ and ε with Pr = 1.0.
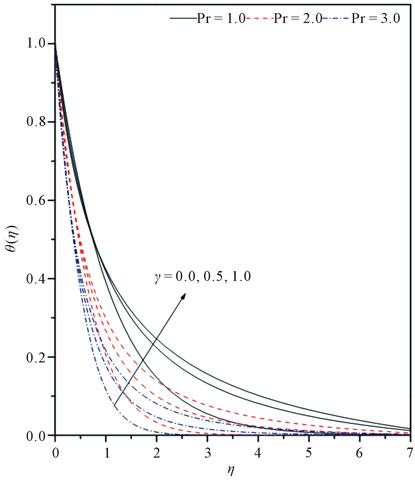
Figure 5. Temperature profiles for different values of γ and Pr with ε = 0.1.
The Equation (5.2) establishes the relation between the coefficient of convectional heat transfer, i.e. Nusselt number Nux and Reynolds number. We see that . Further, we conclude that as Reynolds number increases,
. Further, we conclude that as Reynolds number increases,
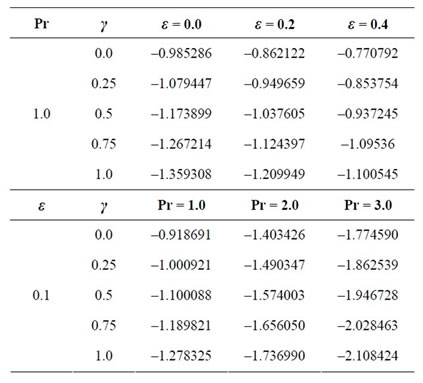
Table 2. Temperature gradient –θ'(0) at the outer surface of cylinder for different values of pertinent parameters.
i.e. 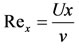 increases when viscosity decreases, so the decrease in viscosity enhances the magnitude of rate of convectional heat transfer in case of stretching cylinder. Also, the coefficient of convectional heat depends on Prandtl number Pr, curvature parameter γ and thermal variable parameter ε. The behavior of the coefficient of convectional heat transfer may be studied from Table 2 with respect to pertinent parameters.
increases when viscosity decreases, so the decrease in viscosity enhances the magnitude of rate of convectional heat transfer in case of stretching cylinder. Also, the coefficient of convectional heat depends on Prandtl number Pr, curvature parameter γ and thermal variable parameter ε. The behavior of the coefficient of convectional heat transfer may be studied from Table 2 with respect to pertinent parameters.
7. Conclusion
The curvature of stretching cylinder is very vital parameter affecting flow and temperature field both. In case of thermal conductivity, curvature helps to enhance the heat transfer. The reduction in fluid viscosity accelerates the rate of convectional heat transfer.
8. Acknowledgements
The authors of this paper are thankful to Dr. K. V. Prasad, Department of Mathematics, Bangalore University, Bangalore, Karnataka for the help extended to produce the investigation in this article.
REFERENCES
- B. C. Sakiadis, “Boundary-Layer Behaviour on Continuous Solid Surfaces: I. Boundary-Layer Equations for Two-Dimensional and Axisymmetric Flow,” AIChE Journal, Vol. 7, 1961, pp. 26-28. doi:10.1002/aic.690070108
- L. J. Crane, “Flow past a Stretching Plate,” Zeitschrift für Angewandte Mathematik und Physik, Vol. 21, No. 4, 1970, pp. 645-647. doi:10.1007/BF01587695
- F. M. White, “Viscous Fluid Flow,” Mc Graw Hill, New York, 2006.
- J. E. Daskalakis, “Free Convection Effects in the Boundary Layer along a Vertically Stretching Flat Surface,” Canadian Journal of Physics, Vol. 70, 1993, pp. 1253- 1260. doi:10.1139/p92-204
- C. H. Chen, “Laminar Mixed Convection Adjacent to Vertical, Continuously Stretching Sheets,” Heat Mass Transfer, Vol. 33, No. 5-6, 1998, pp. 471-476. doi:10.1007/s002310050217
- C. H. Chen, “Mixed Convection Cooling of a Heated, Continuously Stretching Surface,” Heat Mass Transfer, Vol. 36, No. 1, 2000, pp. 79-86. doi:10.1007/s002310050367
- C. R. Lin and C. K. Chen, “Exact Solution of Heat Transfer from a Stretching Surface with Variable Heat Flux,” Heat Mass Transfer, Vol. 33, 1998, pp. 477-480. doi:10.1007/s002310050218
- M. E. Ali, “The Buoyancy Effect on the Boundary Layers Induced by Continuous Surfaces Stretched with Rapidly Decreasing Velocities,” Heat Mass Transfer, Vol. 40, No. 3-4, 2004, pp. 285-291. doi:10.1007/s00231-002-0405-9
- M. K. Partha, P. V. S. N. Murthy and G. P. Rajasekhar, “Effect of Viscous Dissipation on the Mixed Convection Heat Transfer from an Exponentially Stretching Surface,” Heat Mass Transfer, Vol. 41, No. 4, 2005, pp. 360-366. doi:10.1007/s00231-004-0552-2
- A. Ishak, R. Nazar and I. Pop, “Mixed Convection on a Stagnation Point Flow toward a Vertical, Continuously Stretching Sheet,” Journal of Heat Transfer, Vol. 129, No. 9, 2007, pp. 1087-1090. doi:10.1115/1.2737482
- A. Ishak, R. Nazar and I. pop, “Hydromagnetic Flow and Heat Transfer Adjacent to a Stretching Vertical Sheet,” Heat Mass Transfer, Vol. 44, No. 8, 2008, pp. 921-927. doi:10.1007/s00231-007-0322-z
- H. T. Lin and Y. P. Shih, “Laminar Boundary Layer Heat Transfer along Static and Moving Cylinder,” Journal of the Chinese Institute of Engineers, Vol. 3, No. 1, 1980, pp. 73-79. doi:10.1080/02533839.1980.9676650
- H. T. Lin and Y. P. Shih, “Buoyancy Effects on the Laminar Boundary Layer Heat Transfer along Vertically Moving Cylinders,” Journal of the Chinese Institute of Engineers, Vol. 4, No. 1, 1981, pp. 47-51. doi:10.1080/02533839.1981.9676667
- T. Cebeci and P. Bradshaw, “Physical and Computational Aspects of Convective Heat Transfer,” Springer-Verlag, New-York, 1984.
- T. Mahmood and J. H. Merkin, “Similarity Solutions in Axisymmetric Mixed-Convection Boundary-Layer Flow,” Journal of Engineering Mathematics, Vol. 22, No. 1, 1988, pp. 73-92. doi:10.1007/BF00044366
- A. Ishak, “Mixed Convection Boundary Layer Flow over a Vertical Cylinder with Prescribed Surface Heat Flux,” Journal of Physics A: Mathematical and Theoretical, Vol. 42, No. 19, 2009, pp. 1-8. doi:10.1088/1751-8113/42/19/195501

