Applied Mathematics
Vol. 3 No. 2 (2012) , Article ID: 17382 , 6 pages DOI:10.4236/am.2012.32019
Forced Convection Flow of Nanofluids Past Power Law Stretching Horizontal Plates
1Department of Mathematics, Faculty of Science, Assiut University, Assiut, Egypt
2Department of Mathematics, University College in Jamoum, Umm-Alqurah University, Makkah, Saudi Arabia
Email: fekrymh@hotmail.com, fibrahim@aun.edu.eg, ahscience2007@yahoo.com
Received October 27, 2011; revised December 13, 2011; accepted December 21, 2011
Keywords: Forced Convection; Nanofluid; Nonsimilar Solution; Heat Transfer Component
ABSTRACT
In the present work, we studied a nonsimilar solution of steady forced convection boundary layer flow and heat transfer of a nanofluid past a stretching horizontal plate. One-phase model has been used for this study. The nonsimilarity equations are solved numerically. We considered a nanofluid consists of 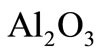 as a nanoparticles and water as a base fluid. The volume fraction of nanoparticles is considered in the range
as a nanoparticles and water as a base fluid. The volume fraction of nanoparticles is considered in the range . with prandtl number
. with prandtl number  for the water working as a regular fluid. The parameters which governing the solution are volume fraction of nanoparticles
for the water working as a regular fluid. The parameters which governing the solution are volume fraction of nanoparticles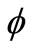 , stretching plate parameter
, stretching plate parameter  and power law index N. We investigated the effect of these parameters on the skin friction coefficient, Nusselt number, velocity and temperature profiles. We found that heat transfer rate and skin fraction increased when
and power law index N. We investigated the effect of these parameters on the skin friction coefficient, Nusselt number, velocity and temperature profiles. We found that heat transfer rate and skin fraction increased when 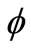 increased. On the other hand, we concluded that the increase in
increased. On the other hand, we concluded that the increase in  and N made heat transfer rate increases and skin fraction decreases.
and N made heat transfer rate increases and skin fraction decreases.
1. Introduction
Various industries such as power, manufacturing, transportation, and electronics demand an efficient heat exchanger devices. Classical heat transfer fluids such as water, ethylene glycol, and engine oil have a serious limitation in heat transfer efficiency. In contrast, metals are a very good conductivities. To overcome this disadvantage of fluids, it would be desired to combine metals and fluids to produce a heat transfer medium that behaves like a fluid, but has the thermal conductivity of a metal. The idea of putting small metal particles in fluid to enhance the fluid’s heat transfer properties is nothing new, as it was documented by Maxwell in 1904 [1].
Nanofluids are a new class of advanced heat-transfer fluids, which are liquids containing a dispersion of submicronic solid particles (nanoparticles). Typical dimension of the nanoparticles is in the range of a few to about 100 nm. Various types of powders such as metal or metal oxide nanoparticles, can be combined with a conductive base fluid, such as water or ethylene glycol to produce a nanofluid. Thermal conductivity of nanofluid has been measured with several nanoparticles volume fraction, material and dimension in several base fluids and all findings show that thermal conductivity of nanofluid is higher than the base fluids. Nanofluids commonly contain up to a 5% volume fraction of nanoparticles to see effective heat transfer enhancements. Lee et al. [2] have demonstrated that oxide ceramic nanofluids consisting of 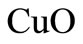 or
or  nanoparticles in water or ethylene glycol exhibit enhanced thermal conductivity. Estman et al. [3] observed that the effective thermal conductivity of metallic nanofluid increase by up to 40% for the nanofluid consisting of ethylene glycol containing approximately 0.3% volume
nanoparticles in water or ethylene glycol exhibit enhanced thermal conductivity. Estman et al. [3] observed that the effective thermal conductivity of metallic nanofluid increase by up to 40% for the nanofluid consisting of ethylene glycol containing approximately 0.3% volume 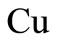 nanoparticles of mean diameter less than 10 nm. This capabilities suggests the possibility of using nanofluids in air conditioning systems [4]. Buongiorno [5] made a comprehensive survey of convective transport in nanofluids. Who says that a satisfactory explanation for the abnormal increase of the thermal conductivity and viscosity is yet to be found. He has shown that in the absence of turbulent effects, it is the Brownian diffusion and the thermophoresis that are important and he has written down conservation equations based on these two effects. Mahdy and Hady [6] studied the effect of thermophoresis and Brownian diffusion in non-Newtonian free convection flow over a vertical plate with magnetic field effect. Nield and Kuznetsov [7] studied the Cheng-Minkowycz problem for natural convective boundary-layer flow in a porous medium saturated by a nanofluid. Kuznetsov and Nield [8] studied the natural convective boundary-layer flow of a nanofluid past a vertical plate. They made a correlation for the reduced Nusselt number and investigated the effect of buoyancy ratio, Brownian motion parameter and thermophoresis parameter. They used a model for the nanofluid incorporates the effects of Brownian motion and thermophoresis as proposed by Buongiorno [5]. Very recently, Syakila et al. [9] studied Blasius and Sakiadis problems in nanofluids for various values of volume fraction.
nanoparticles of mean diameter less than 10 nm. This capabilities suggests the possibility of using nanofluids in air conditioning systems [4]. Buongiorno [5] made a comprehensive survey of convective transport in nanofluids. Who says that a satisfactory explanation for the abnormal increase of the thermal conductivity and viscosity is yet to be found. He has shown that in the absence of turbulent effects, it is the Brownian diffusion and the thermophoresis that are important and he has written down conservation equations based on these two effects. Mahdy and Hady [6] studied the effect of thermophoresis and Brownian diffusion in non-Newtonian free convection flow over a vertical plate with magnetic field effect. Nield and Kuznetsov [7] studied the Cheng-Minkowycz problem for natural convective boundary-layer flow in a porous medium saturated by a nanofluid. Kuznetsov and Nield [8] studied the natural convective boundary-layer flow of a nanofluid past a vertical plate. They made a correlation for the reduced Nusselt number and investigated the effect of buoyancy ratio, Brownian motion parameter and thermophoresis parameter. They used a model for the nanofluid incorporates the effects of Brownian motion and thermophoresis as proposed by Buongiorno [5]. Very recently, Syakila et al. [9] studied Blasius and Sakiadis problems in nanofluids for various values of volume fraction.
The aim of present work is therefore, to study the physical properties of a nanofluid ( -water) flow past a power law stretching horizontal plate. We presented a nonsimilarity solution for the problem. We used two numerical methods to solve the resulting ordinary differential equations and compared their results. The parameters of this problem are volume-fraction of nanoparticles
-water) flow past a power law stretching horizontal plate. We presented a nonsimilarity solution for the problem. We used two numerical methods to solve the resulting ordinary differential equations and compared their results. The parameters of this problem are volume-fraction of nanoparticles 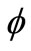 and stretching plate parameter
and stretching plate parameter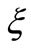 . We presented the non-dimensional form of reduced Nusselt number
. We presented the non-dimensional form of reduced Nusselt number 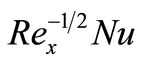 and reduced skin fraction
and reduced skin fraction 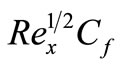 which are discussed for various values of the proceeding parameters. The variables of motion are investigated and presented in graphical forms.
which are discussed for various values of the proceeding parameters. The variables of motion are investigated and presented in graphical forms.
2. Analysis
We consider the steady two-dimensional boundary layer flow past a stretching horizontal flat plate in a waterbased nanofluid and 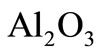 as a nanoparticles. The nanofluid is assumed incompressible, the flow is assumed to be laminar, and the viscous dissipation and radiation effects are neglected. It is also assumed that the base fluid and the nanoparticles are in thermal equilibrium and no slip occurs between them. The thermophysical properties of the nanofluids are given in Table 1 (see [10]). Under these assumptions and following the model equations of a nanofluid proposed by Ref. [11], the basic continuity, momentum, and energy equations in the vectorial form for the steady-state flow are
as a nanoparticles. The nanofluid is assumed incompressible, the flow is assumed to be laminar, and the viscous dissipation and radiation effects are neglected. It is also assumed that the base fluid and the nanoparticles are in thermal equilibrium and no slip occurs between them. The thermophysical properties of the nanofluids are given in Table 1 (see [10]). Under these assumptions and following the model equations of a nanofluid proposed by Ref. [11], the basic continuity, momentum, and energy equations in the vectorial form for the steady-state flow are
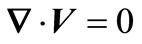 (1)
(1)
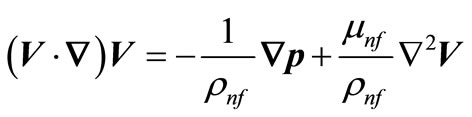 (2)
(2)
 (3)
(3)
The boundary conditions are taken to be
 (4)
(4)
 (5)
(5)
where  is the velocity vector,
is the velocity vector, 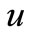 and
and 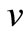 are the velocity components along the axes x and y, U is the constant velocity of the free stream,
are the velocity components along the axes x and y, U is the constant velocity of the free stream,  is a constant and
is a constant and 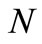 is a power law index. Further,
is a power law index. Further, 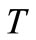 is the temperature of the nanofluid,
is the temperature of the nanofluid, 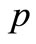 is the pressure of the nanofluid,
is the pressure of the nanofluid, 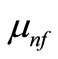 is the dynamic viscosity of the nanofluid,
is the dynamic viscosity of the nanofluid, 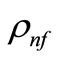 is the density of the nanofluid, and
is the density of the nanofluid, and 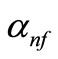 is the thermal
is the thermal
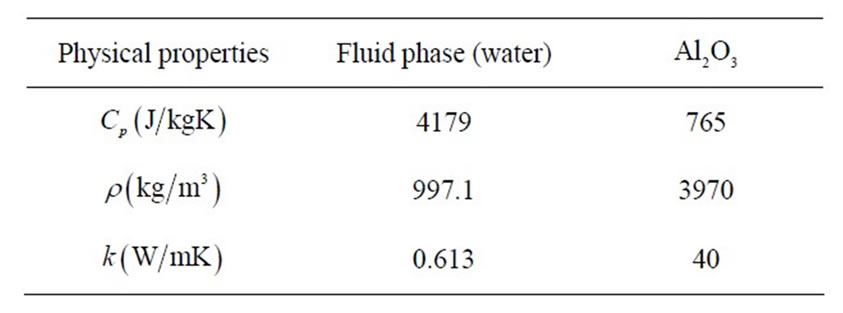
Table 1. Thermophysical properties of the fluid phase (water) and nanoparticles [10].
diffusivity of the nanofluid, which are given by
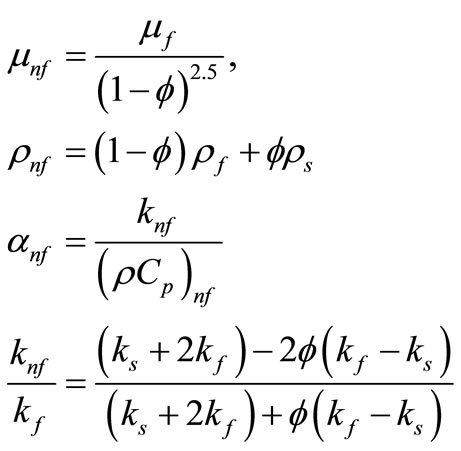 (6)
(6)
here,  is the thermal conductivity of the nanofluid,
is the thermal conductivity of the nanofluid,  is the solid volume fraction parameter of the nanofluid,
is the solid volume fraction parameter of the nanofluid,  is the reference density of the fluid fraction,
is the reference density of the fluid fraction,  is the reference density of the solid fraction,
is the reference density of the solid fraction, 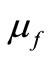 isthe viscosity of the fluid fraction,
isthe viscosity of the fluid fraction, 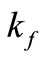 is the thermal conductivity of the fluid fraction, and
is the thermal conductivity of the fluid fraction, and 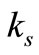 is the thermal conductivity of the solid volume fraction. Further,
is the thermal conductivity of the solid volume fraction. Further,  is the heat capacitance of the nanofluid, where
is the heat capacitance of the nanofluid, where 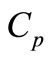 is the specific heat at constant pressure.
is the specific heat at constant pressure.
It is worth mentioning that the viscosity  of the nanofluid can be approximated as viscosity of the base fluid
of the nanofluid can be approximated as viscosity of the base fluid 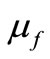 containing dilute suspension of fine spherical particles and is given by Brinkman [12]. The effective thermal conductivity of the nanofluid
containing dilute suspension of fine spherical particles and is given by Brinkman [12]. The effective thermal conductivity of the nanofluid  is approximated by the Maxwell-Garnetts model, which is found to be appropriatefor studying heat transfer enhancement using nanofluids (Maiga et al. [13] and Abu-Nada [14]).
is approximated by the Maxwell-Garnetts model, which is found to be appropriatefor studying heat transfer enhancement using nanofluids (Maiga et al. [13] and Abu-Nada [14]).
We consider a Cartesian coordinate system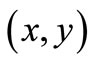 , where
, where 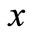 and
and  are the coordinates measured along the plate and normal to it, respectively, and assume that the flow takes place at
are the coordinates measured along the plate and normal to it, respectively, and assume that the flow takes place at . It is also assumed that the constant temperature of the flat plate is
. It is also assumed that the constant temperature of the flat plate is 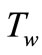 and that of the ambient nanofluid is
and that of the ambient nanofluid is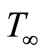 . Under the boundary layer approximations and the fact that this flow is one of zero pressure gradient, the basic Equations (1)-(3) can be written in the Cartesian coordinates x and y as follows:
. Under the boundary layer approximations and the fact that this flow is one of zero pressure gradient, the basic Equations (1)-(3) can be written in the Cartesian coordinates x and y as follows:
 (7)
(7)
 (8)
(8)
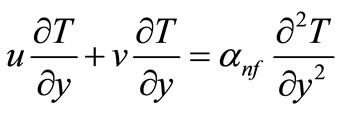 (9)
(9)
The boundary conditions becomes
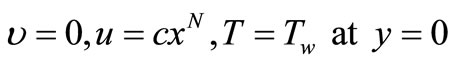 (10)
(10)
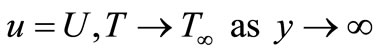 (11)
(11)
We introduce a stream function  defined by
defined by
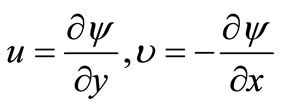 (12)
(12)
so that Equation (7) is satisfied identically. We are then left with the following two equations
 (13)
(13)
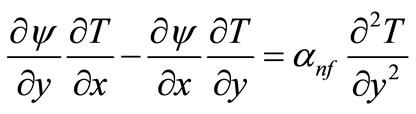 (14)
(14)
We look for a nonsimilar solution of Equations (8) and (9) with the boundary conditions (10) and (11) of the following form
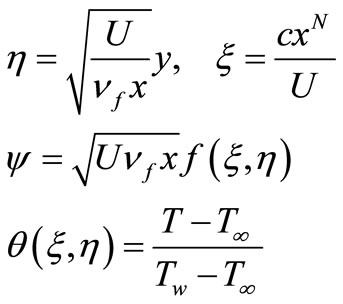 (15)
(15)
where 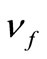 is the kinematic viscosity of the fluid fraction and
is the kinematic viscosity of the fluid fraction and 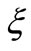 is the stretching plate parameter.
is the stretching plate parameter.
On substituting Equation (15) into Equations (8) and (9), we obtain the following uncoupled ordinary differential equations:
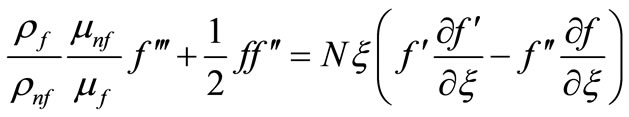 (16)
(16)
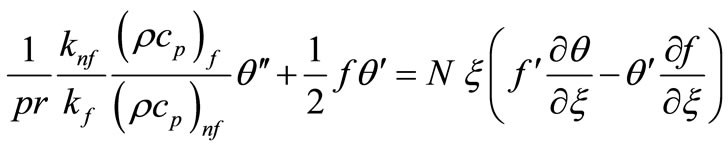 (17)
(17)
the boundary conditions (10) and (11) becomes
 (18)
(18)
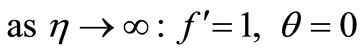 (19)
(19)
where primes denote differentiation with respect to the variable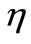 , and
, and 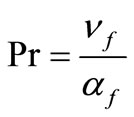 is the Prandtl number. It is worth mentioning that Equation (16) reduces to that derived by Blasius [15] when
is the Prandtl number. It is worth mentioning that Equation (16) reduces to that derived by Blasius [15] when  (regular fluid flowing over a non-stretching stationary plate).
(regular fluid flowing over a non-stretching stationary plate).
Quantities of practical interest in this study are the skin friction coefficient 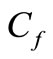 and the local Nusselt number
and the local Nusselt number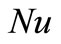 , which are defined as
, which are defined as
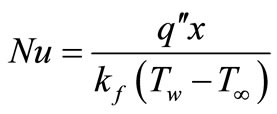 (20)
(20)
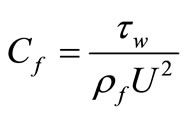 (21)
(21)
where  is the skin friction or the shear stress and
is the skin friction or the shear stress and 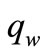 is the heat flux from the plate which are given by
is the heat flux from the plate which are given by
 (22)
(22)
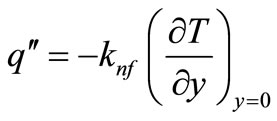 (23)
(23)
Substituting Equations (15) into (20) and (21), we obtain
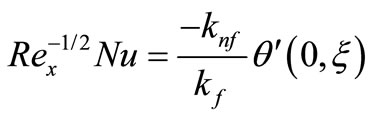 (24)
(24)
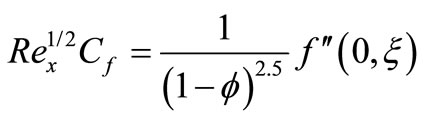 (25)
(25)
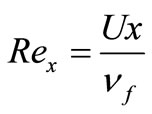 (26)
(26)
where 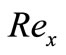 is the local Reynolds number.
is the local Reynolds number.
3. Numerical Methods
To solve the Equations (16) and (17) with the boundary conditions (18) and (19), the first step is to write the ODEs as a system of first order ODEs. The basic idea is to introduce new variables, one for each variable in the original problem plus one for each of its derivatives up to one less than the highest derivative appearing.
We implemented a collocation method for the solution of boundary value problem of the form
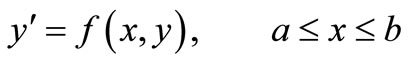 (27)
(27)
subject to general nonlinear, two-point boundary conditions
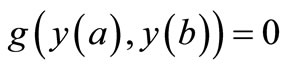 (28)
(28)
The approximate solution 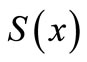 is a continuous function that is a cubic polynomial on each subinterval
is a continuous function that is a cubic polynomial on each subinterval 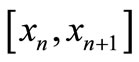 of a mesh
of a mesh . It satisfies the boundary conditions
. It satisfies the boundary conditions
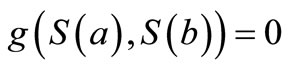 (29)
(29)
and it satisfies the differential equations (collocates) at both ends and the mid-point of each subinterval
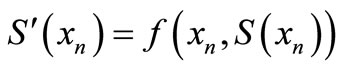 (30)
(30)
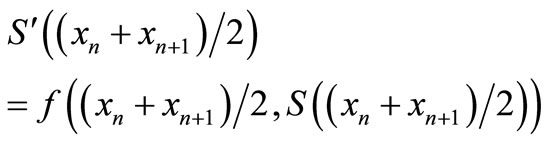 (31)
(31)
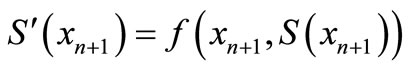 (32)
(32)
These conditions result in a system of nonlinear algebraic equations for the coefficients defining . The nonlinear algebraic equations are solved iteratively by linearization.
. The nonlinear algebraic equations are solved iteratively by linearization. 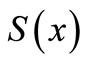 is a fourth order approximation to an isolated solution
is a fourth order approximation to an isolated solution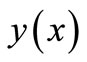 , i.e.,
, i.e., . Here h is the maximum of the step sizes
. Here h is the maximum of the step sizes 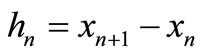 and
and 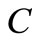 is a constant. For such an approximation, the residual
is a constant. For such an approximation, the residual 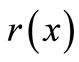 in the ODEs is defined by
in the ODEs is defined by
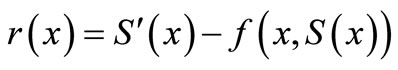 (33)
(33)
It is worth noting that the relative error tolerance on the residuals is 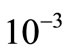 and the absolute error tolerance is
and the absolute error tolerance is . The calculations are done using MATLAB package (bvp4c). This code give an excellent guess for the mesh to minimize the number of mesh points to get an optimal convergent speed for the solution.
. The calculations are done using MATLAB package (bvp4c). This code give an excellent guess for the mesh to minimize the number of mesh points to get an optimal convergent speed for the solution.
We solved the problem again using Finite-difference method (we used NAG library for this purpose). As discussed above we write the ODEs as a system of first order ODEs, see Equation (27). Finite-difference equations are set up on a mesh of points and estimatedvalues for the solution at the grid points are chosen. Using these estimated values as starting values a Newton iteration is used to solve the Finite-difference equations. The accuracy of the solution is then improved by deferred corrections or the addition of points to the mesh or a combination of both. The technique used is described fully in [16]. The absolute error tolerance for this method is .
.
4. Results and Discussion
Equations (16) and (17) with the boundary conditions (18) and (19) are solved numerically for some values of the solid volume fraction of nanofluid 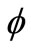 and the stretching plate parameter
and the stretching plate parameter . In order to test the accuracy of the present results, we have compared these results with those of Syakila et al. [9] when we neglect the effect of stretching plate parameter
. In order to test the accuracy of the present results, we have compared these results with those of Syakila et al. [9] when we neglect the effect of stretching plate parameter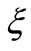 . We used two numerical methods to solve the governing equations (Collocation method and Finite-difference method) to ensure the accuracy of the calculations, as presented in Table 2. We noticed that the comparison shows an excellent agreement and the two methods almost give identical results. The range of nanoparticles volume fraction is
. We used two numerical methods to solve the governing equations (Collocation method and Finite-difference method) to ensure the accuracy of the calculations, as presented in Table 2. We noticed that the comparison shows an excellent agreement and the two methods almost give identical results. The range of nanoparticles volume fraction is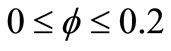 . The Prandtl number of the base fluid (water) is kept constant at 6.2. One type of nanoparticles is studied which is
. The Prandtl number of the base fluid (water) is kept constant at 6.2. One type of nanoparticles is studied which is . It is worth noting that for our calculations step
. It is worth noting that for our calculations step
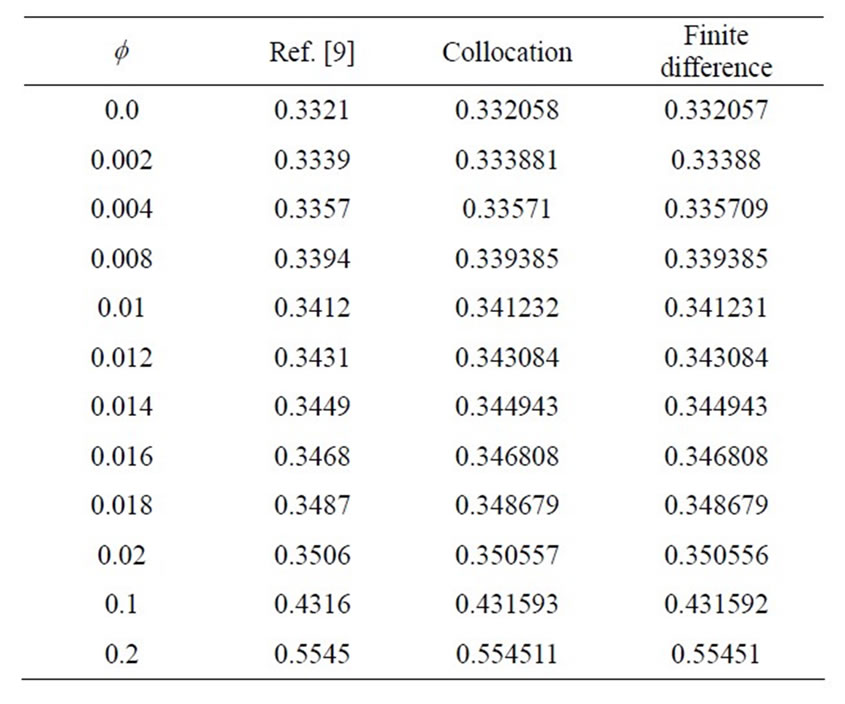
Table 2. Comparison of results for  or pr = 6.2,
or pr = 6.2, 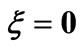 and various values of
and various values of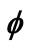 .
.
size of 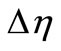 = 0.05 and
= 0.05 and 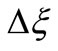 = 0.1 and
= 0.1 and  = 8.
= 8.
The effects of stretching plate parameter and volume fraction of nanoparticles 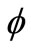 on the temperature profile are shown in Figure 1. It is obvious that for a constant value of stretching plate parameter the thickness of thermal boundary layer increased when the volume fraction of nanoparticles increased.
on the temperature profile are shown in Figure 1. It is obvious that for a constant value of stretching plate parameter the thickness of thermal boundary layer increased when the volume fraction of nanoparticles increased.
Figure 2 shows the temperature and velocity profiles for various values of stretching plate parameter. The figure reveals an increasing in velocity profile in the momentum boundary layer by increasing the stretching plate parameter, whereas the thickness of thermal boundary layer decreases which implies to increasing in heat gradient and then enhancing heat transfer rate through boundary layer.
Figures 3 and 4 show the variation of the skin friction and the local Nusselt number versus the stretching plate parameter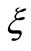 . It is obvious that the skin friction decreased when
. It is obvious that the skin friction decreased when  increased, whereas the local Nusselt number (heat transfer rate) increased for the increasing in
increased, whereas the local Nusselt number (heat transfer rate) increased for the increasing in , as we expected from Figure 2. So, from Figure 4 we concluded that the thickness of thermal boundary layer of nanofluid (
, as we expected from Figure 2. So, from Figure 4 we concluded that the thickness of thermal boundary layer of nanofluid (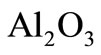 -water) is greater than it in water (when
-water) is greater than it in water (when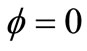 ). Thus, in the case of forced convection the heat transfer rate of water is better than the heat transfer rate of the nanofluid
). Thus, in the case of forced convection the heat transfer rate of water is better than the heat transfer rate of the nanofluid  -water. Further, Figure 3 depict the effect of the power law index
-water. Further, Figure 3 depict the effect of the power law index  for a regular fluid (
for a regular fluid (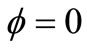 ) and
) and 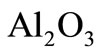 -water (
-water (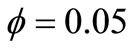 ) as working fluid. It is seen that the skin friction decreased with the increase of
) as working fluid. It is seen that the skin friction decreased with the increase of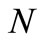 , but when
, but when  and
and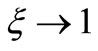 , the skin friction closed to zero and then reversed its direction and began to increase in the new direction. This is in agreement with the physical discussion that when the fast stretching plate is provided, the fluid slip velocity with
, the skin friction closed to zero and then reversed its direction and began to increase in the new direction. This is in agreement with the physical discussion that when the fast stretching plate is provided, the fluid slip velocity with
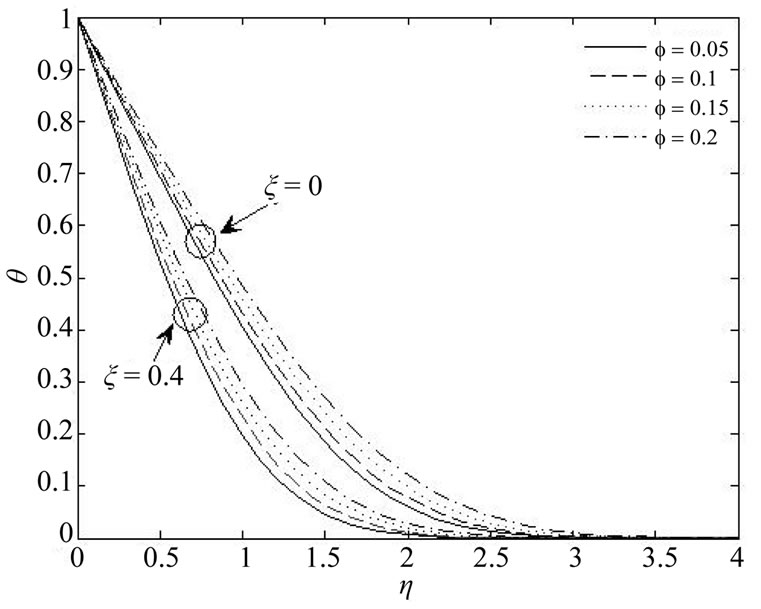
Figure 1. Temperature profiles for various values of 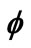 when
when 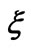 = 0, 0.4 and pr = 6.2.
= 0, 0.4 and pr = 6.2.
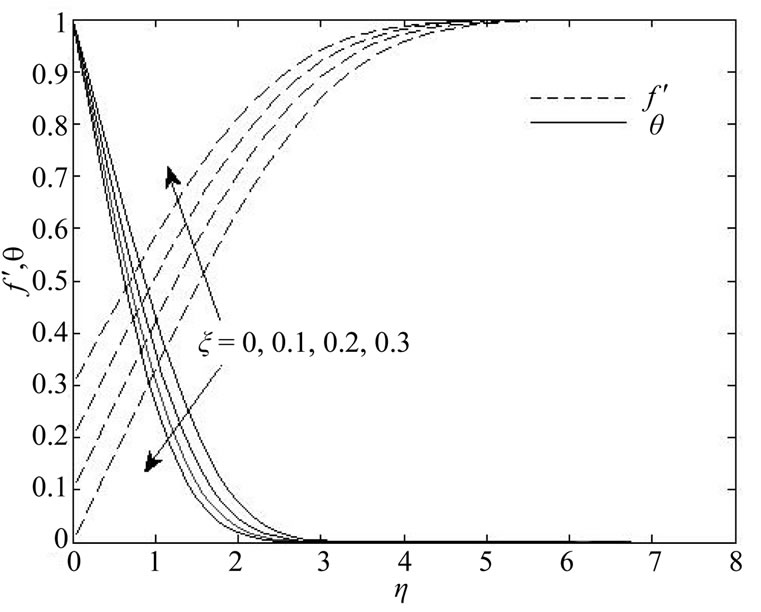
Figure 2. Temperature and velocity profiles for various values of  when pr = 6.2.
when pr = 6.2.
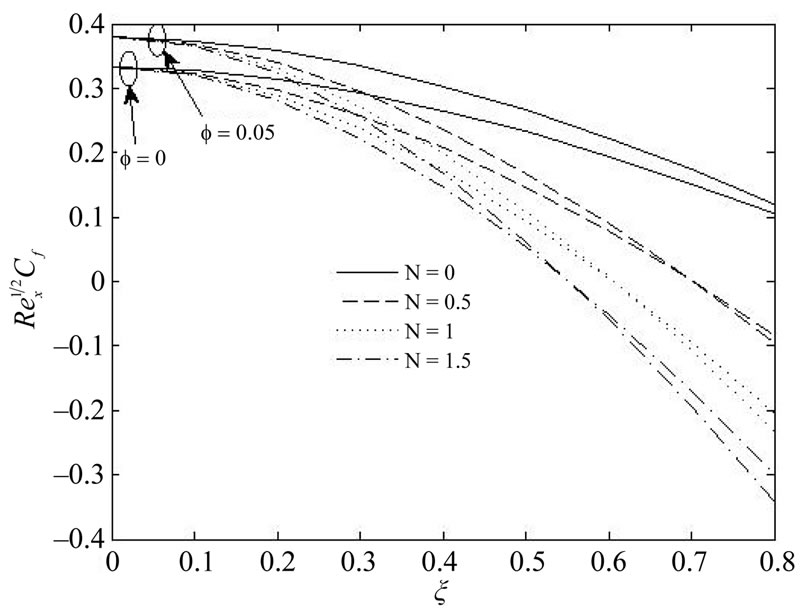
Figure 3. Variation of skin fraction for various values of  when
when 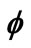 = 0, 0.5 and pr = 6.2.
= 0, 0.5 and pr = 6.2.
the plate will be inverse. On the other hand, the influence of the power law index N on the local Nusselt number
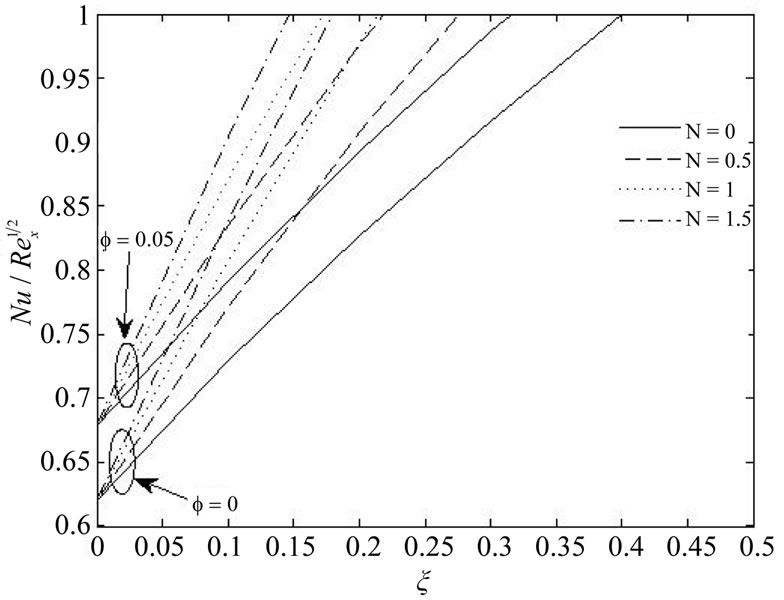
Figure 4. Variation of reduced Nusselt number for various values of  when
when  = 0, 0.5 and pr = 6.2.
= 0, 0.5 and pr = 6.2.
in the case of water ( ) and
) and  -water (
-water ( ) as working fluid is shown in Figure 4. It is obvious that the local Nusselt number or heat transfer rate increases with the increase of
) as working fluid is shown in Figure 4. It is obvious that the local Nusselt number or heat transfer rate increases with the increase of  in both the cases water and
in both the cases water and 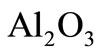 -water. However, we noticed that the value of local Nusselt number in
-water. However, we noticed that the value of local Nusselt number in  -water is greater than in the case of water for various values of
-water is greater than in the case of water for various values of , but this result is not expected because we concluded from Figure 1 the heat gradient in water case is greater than in nanofluid
, but this result is not expected because we concluded from Figure 1 the heat gradient in water case is greater than in nanofluid 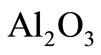 -water. This contradiction was observed experimentally by Pak and Cho [17] even though the Nusselt number increases, the heat transfer coefficient actually decreases by 3% - 12%. However, this may be due to the large increase in viscosity they observed.
-water. This contradiction was observed experimentally by Pak and Cho [17] even though the Nusselt number increases, the heat transfer coefficient actually decreases by 3% - 12%. However, this may be due to the large increase in viscosity they observed.
5. Conclusions
We have examined the influence of nanoparticles on steady forced convection boundary layer flow and heat transfer past a stretching horizontal plate, using a onephase model. In this study we have assumed the simplest possible boundary conditions, namely those in which both the temperature and the nanoparticle fraction are constant along the wall. This permits a nonsimilarity solution which depends on three dimensionless parameters, namely volume fraction of nanoparticles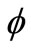 , a stretching plate parameter
, a stretching plate parameter 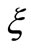 and the power law index
and the power law index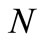 . Results for various parametric conditions are presented and discussed. We found some important points in the obtained results, such as:
. Results for various parametric conditions are presented and discussed. We found some important points in the obtained results, such as:
• the inclusion of 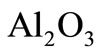 -nanoparticles into the base water fluid has produced an increase in the thickness of thermal boundary layer, skin fraction and Nusselt number;
-nanoparticles into the base water fluid has produced an increase in the thickness of thermal boundary layer, skin fraction and Nusselt number;
• in the case of stretching plats the temperature profile in boundary layer decreased whereas the velocity profile increased;
• the skin fraction and Nusselt number are affected seriously with stretching plat parameter;
• the skin friction decreased with the increase of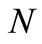 , but it reverse its direction for values of
, but it reverse its direction for values of  and large values of
and large values of ;
;
• the heat gradient in 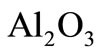 -water is greater than in the case of water for various values of
-water is greater than in the case of water for various values of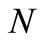 ;
;
• There is a gloomy picture in nanofluids in the case of forced convection, even though the heat gradient decreases through the boundary layer the Nusselt number increases.
As it has been mentioned by Muthtamilselvan et al. [16], the study of nanofluids is still at its developing stage so that it seems difficult to have a precise idea on the way the use of nanoparticles to understand the flow and heat transfer characteristics of nanofluids and identify new and unique applications for these fluids.
REFERENCES
- J. C. Maxwell, “A Treatise on Electricity and Magnetism,” 3rd Edition, Oxford University Press, London, 1892.
- S. Lee, S. U. S. Choi, S. Li and J. A. Eastman, “Measuring Thermal Conductivity of Fluids Containing Oxide Nanoparticles,” Journal of Heat Transfer, Vol. 121, No. 2, 1999, pp. 280-289. doi:10.1115/1.2825978
- J. A. Estman, S. U. S. Choi, S. Li, W. Yu and L. J. Thomson, “Anomalously Increased Effective Thermal Conductivities of Ethylene Glycol Based Nanofluid Containing Copper Nanoparticles,” Applied Physics Letters, Vol. 78, No. 6, 2001, pp. 718-720. doi:10.1063/1.1341218
- M. Shahi, A. H. Mahmoudi and F. Talebi, “Numerical Study of Mixed Convective Cooling in a Square Cavity Ventilated and Partially Heated from the Below Utilizing Nanofluid,” International Communications in Heat and Mass Transfer, Vol. 37, No. 2, 2010, pp. 201-213. doi:10.1016/j.icheatmasstransfer.2009.10.002
- J. Buongiorno, “Convective Transport in Nanofluids,” Journal of Heat Transfer, Vol. 128, No. 3, 2006, pp. 240-250. doi:10.1115/1.2150834
- A. Mahdy and F. M. Hady, “Effect of Thermophoretic Particle Deposition in Non-Newtonian Free Convection Flow over a Vertical Plate with Magnetic Field Effect,” Journal of Non-Newtonian Fluid Mechanics, Vol. 161, No. 1-3, 2009, pp. 37-41. doi:10.1016/j.jnnfm.2009.04.00
- D. A. Nield and A. V. Kuznetsov, “The Cheng-Minkowycz Problem for Natural Convective Boundary-Layer Flow in a Porous Medium Saturated by a Nanofluid,” International Journal of Heat and Mass Transfer, Vol. 52, No. 25-26, 2009, pp. 5792-5795. doi:10.1016/j.ijheatmasstransfer.2009.07.024
- A. V. Kuznetsov and D. A. Nield, “Natural Convective Boundary-Layer Flow of a Nanofluid Past a Vertical Plate,” International Journal of Thermal Sciences, Vol. No. 2, 49, 2010, pp. 243-247. doi:10.1016/j.ijthermalsci.2009.07.015
- S. Ahmed, A. M. Rohni and I. Pop, “Blasius and Sakiadis Problems in Nanofluids,” Acta Mechanica, Vol. 218, No. 3-4, 2011, pp. 195-204. doi:10.1007/s00707-010-0414-6
- H. F. Oztop and E. Abu-Nada, “Numerical Study of Natural Convection in Partially Heated Rectangular Enclosures Filled with Nanofluids,” International Journal of Heat and Fluid Flow, Vol. 29, No. 5, 2008, pp. 1326- 1336. doi:10.1016/j.ijheatfluidflow.2008.04.009
- R. K. Tiwari and M. K. Das, “Heat Transfer Augmentation in a Two-Sided Lid-Driven Differentially Heated Square Cavity Utilizing Nanofluids,” International Journal of Heat and Mass Transfer, Vol. 50, No. 9-10, 2007, pp. 2002-2018. doi:10.1016/j.ijheatmasstransfer.2006.09.034
- H. C. Brinkman, “The Viscosity of Concentrated Suspensions and Solutions,” Journal of Chemical Physics, Vol. 20, No. 4, 1952, pp. 571-581. doi:10.1063/1.1700493
- S. E. B. Maiga, S. J. Palm, C. T. Nguyen, G. Roy and N. Galanis, “Heat Transfer Enhancement by Using Nanofluids in Forced Convection Flows,” International Journal of Heat and Fluid Flow, Vol. 26, No. 4, 2005, pp. 530- 546. doi:10.1016/j.ijheatfluidflow.2005.02.004
- E. Abu-Nada, “Application of Nanofluids for Heat Transfer Enhancement of Separated Flows Encountered in a Backward Facing Step,” International Journal of Heat and Fluid Flow, Vol. 29, No. 1, 2008, pp. 242-249. doi:10.1016/j.ijheatfluidflow.2007.07.001
- V. Pereyra, “An Adaptive Finite-Difference Fortran Program for First Order Nonlinear, ordinary boundary Problems Codes for Boundary Value Problems in Ordinary Differential Equations,” Codes for Boundary-Value Problems in Ordinary Differential Equations, Lecture Notes in Computer Science, Vol. 76, 1979, pp. 67-88.
- M. Muthtamilselvan, P. Kandaswamy and J. Lee, “Heat Transfer Enhancement of Copper-Water Nanofluids in a Lid-Driven Enclosure,” Communications in Nonlinear Science and Numerical Simulation, Vol. 15, No. 6, 2010, pp. 1501-1510. doi:10.1016/j.cnsns.2009.06.015
- B. Pak and Y. I. Cho, “Hydrodynamic and Heat Transfer Study of Dispersed Fluids with Submicron Metallic Oxide Particle,” Experimental Heat Transfer, Vol. 11, No. 2, 1998, pp. 151-170. doi:10.1080/08916159808946559

