Applied Mathematics
Vol.3 No.10(2012), Article ID:23365,8 pages DOI:10.4236/am.2012.310163
Several New Types of Fixed Point Theorems and Their Applications to Two-Point Ordinary Differential Equations
1School of Applied Mathematics, Nanjing University of Finance and Economics, Nanjing, China
2Department of Mathematics, Shawnee State University, Portsmouth, USA
3Department of Mathematics, Nanjing University, Nanjing, China
Email: zcjyysxx@163.com, jli@shawnee.edu, recluseng@yahoo.com
Received November 1, 2010; revised September 3, 2012; accepted September 10, 2012
Keywords: Expansive Mapping; Cone Metric Space; Fuzzy Metric Space; Two-Point Ordinary Differential Equations
ABSTRACT
The present paper is mainly concerned with several new types of fixed point theorems in different spaces such as cone metric spaces and fuzzy metric spaces. By using these obtained fixed point theorems, we then prove the existence and uniqueness of the solutions to two classes of two-point ordinary differential equation problems.
1. Introduction
The theory of the fixed point has important applications in fields such as differential equations, equilibrium problems, variational inequality, optimization problems, maxmin problems etc. (cf. Klaus Deimling [1], Congjun Zhang [2] for example), which has attracted many scholars’ attention and became a hot topic in mathematics and applied mathematics field for a long time. In recent decades, many new types of fixed point theorems have been proposed (see [3-6] and the reference therein) and the generalizations of the existing ones have been dramatically developed in many ways. In [7], LongGuang Huang and Xian Zhang have introduced the notion of cone metric spaces and proved some fixed point theorems of contractive mappings on cone metric spaces. For fixed point theorems in fuzzy metric spaces, see [8-12]. In [13-16], some scholars have proved the fixed point theorem in partial order metric space, and applied them to prove the existence and uniqueness of the solution to the two-point ordinary differential equation problems. Inspired by the recent progress in this fields, we will study in the present paper the existence and uniqueness of the fixed point for some special mappings in cone metric spaces and fuzzy metric spaces as well as their applications to the following two-point ordinary differential equations.
Problem (1):

where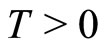 ,
,  is a continuous function satisfying some conditions which will be given explicitly later.
is a continuous function satisfying some conditions which will be given explicitly later.
Problem (2):

where ,
,  is a continuous function satisfying some conditions which will be given explicitly later.
is a continuous function satisfying some conditions which will be given explicitly later.
The paper is organized as follows. For the reader’s convenience, we recall in Section 2 some definitions and lemmas in cone metric spaces and fuzzy metric spaces that will be used in the sequel. Section 3 is devoted to the investigation on the existence and uniqueness of the fixed point for some special mappings in cone metric spaces and fuzzy metric spaces. In last section, two-point ordinary differential equation problems are studied by using the results obtained in Section 3 and the existence and uniqueness of the solutions to such equations is established.
2. Preliminaries and Abstract Results
We recall in this section some definitions and lemmas in cone metric spaces and fuzzy metric spaces that will be used in the sequel.
Definition 1 [6]. Let 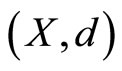 be a metric space and
be a metric space and  a mapping from
a mapping from 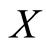 to
to  . For any
. For any 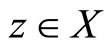 , define
, define 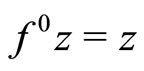 ,
, 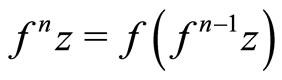 for
for 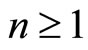 . The sequence
. The sequence  is called the orbit of f and
is called the orbit of f and  the n iterate of f.
the n iterate of f.
Definition 2. A function 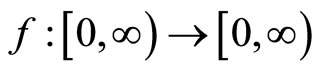 is called an ω-function if it is a monotone increasing function and satisfies that
is called an ω-function if it is a monotone increasing function and satisfies that 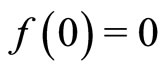 and for any
and for any  , there exists M > 0, such that
, there exists M > 0, such that 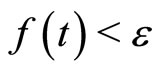 , for every
, for every 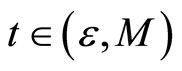 .
.
For example: , defined on
, defined on 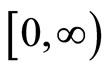 , is an ω-function.
, is an ω-function.
Definition 3 [7]. Let 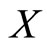 be a nonempty set. Let
be a nonempty set. Let 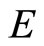 be a real Banach space,
be a real Banach space, 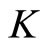 a cone of
a cone of 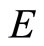 satisfying
satisfying 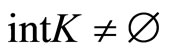 , where
, where 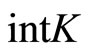 denotes the interior of
denotes the interior of 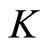 . Define a partial order
. Define a partial order  on
on 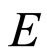 based on
based on 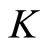 as follows: for any
as follows: for any  ,
,  if and only if
if and only if  , while
, while 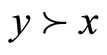 means
means  and
and 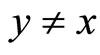 , and
, and 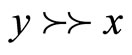 means
means 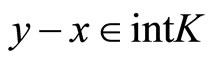 . And the following convention is assumed:
. And the following convention is assumed: 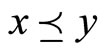 if and only if
if and only if  ,
, 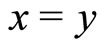 if and only if
if and only if 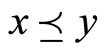 and
and 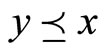 .
.
If a mapping  satisfies:
satisfies:
1)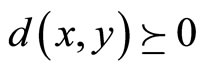 , for all
, for all 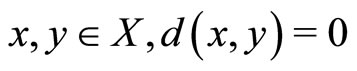 if and only if
if and only if 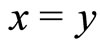 ;
;
2)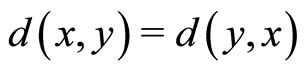 , for all
, for all 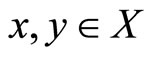 ;
;
3)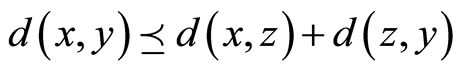 , for all
, for all 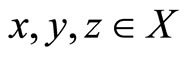 then
then  is called a cone metric on
is called a cone metric on 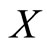 and
and 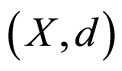 is called a cone metric space with respect to the Banach space
is called a cone metric space with respect to the Banach space  and the cone
and the cone 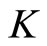 in
in 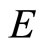 .
.
Definition 4 [2]. 1) A cone  in a Banach space
in a Banach space  is called normal, if there exists a number M > 0 such that for all
is called normal, if there exists a number M > 0 such that for all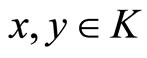 ,
,  implies
implies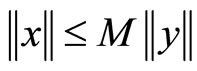 , where
, where 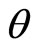 is the zero element of the Banach space
is the zero element of the Banach space . The smallest
. The smallest  satisfying that inequality is denoted by
satisfying that inequality is denoted by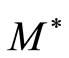 , and it is called the normal constant of
, and it is called the normal constant of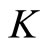 ; 2) A cone
; 2) A cone 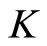 in a Banach space
in a Banach space 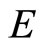 is called regular if every increasing sequence which is bounded from above is convergent. That is, if
is called regular if every increasing sequence which is bounded from above is convergent. That is, if 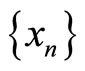 is sequence such that
is sequence such that 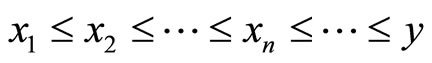 for some
for some , then there is
, then there is 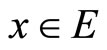 such that
such that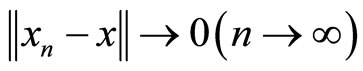 .
.
Remark 1. 1) For any normal cone 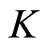 in a Banach space E, M* exists and
in a Banach space E, M* exists and 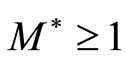 (see [2]); 2) Equivalently, a cone
(see [2]); 2) Equivalently, a cone 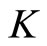 is regular if and only if every decreasing sequence which is bounded from below is convergent. It is well known that a regular cone is a normal cone.
is regular if and only if every decreasing sequence which is bounded from below is convergent. It is well known that a regular cone is a normal cone.
Definition 5 [7]. Let 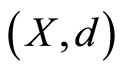 be a cone metric space with respect to a Banach space
be a cone metric space with respect to a Banach space 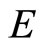 and a cone
and a cone 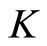 in
in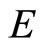 . Let
. Let  be a sequence in
be a sequence in  (see [7]).
(see [7]).
1)  is called a convergent sequence with limit
is called a convergent sequence with limit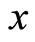 , if for any
, if for any , there exists
, there exists 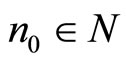 such that for every
such that for every ,
,  holds. In this case, we denote the limit of
holds. In this case, we denote the limit of  by
by , or
, or .
.
2) 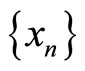 is called a Cauchy sequence on
is called a Cauchy sequence on , if for any
, if for any  with
with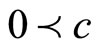 , there exists
, there exists 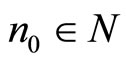 such that for each
such that for each 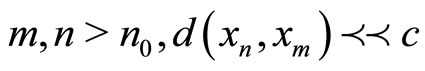 holds.
holds.
3) We call 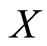 a complete cone metric space with respect to the Banach space
a complete cone metric space with respect to the Banach space 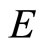 and the cone
and the cone 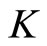 in
in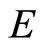 , if every Cauchy sequence is convergent in
, if every Cauchy sequence is convergent in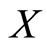 .
.
Remark 2. If K is a normal cone, then  converges to x if and only if
converges to x if and only if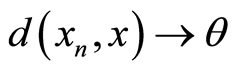 , as
, as .
.  is a Cauchy sequence on
is a Cauchy sequence on 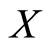 if and only if
if and only if 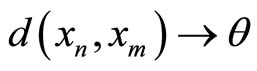 as
as 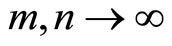 (see[7]).
(see[7]).
Definition 6 [7]. Let  be a cone metric space with respect to a Banach space
be a cone metric space with respect to a Banach space  and a cone
and a cone 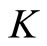 in
in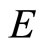 . If for any sequence
. If for any sequence 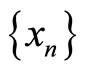 in
in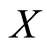 , there exists a subsequence
, there exists a subsequence 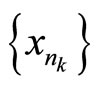 of
of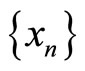 , such that
, such that  is convergent in
is convergent in . Then the cone metric space
. Then the cone metric space  is said to be sequentially compact.
is said to be sequentially compact.
Definition 7 [9,10]. A binary operation  is called a continuous t-norm, if the following conditions are satisfied: 1) * is associative and commutative; 2)
is called a continuous t-norm, if the following conditions are satisfied: 1) * is associative and commutative; 2)  is continuous; 3)
is continuous; 3) 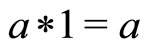 for all
for all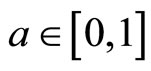 ; 4)
; 4) 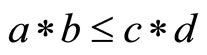 whenever
whenever 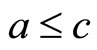 and
and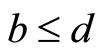 , for each
, for each . If it only satisfies conditions 1), 2) and 4), then it is called a t-norm.
. If it only satisfies conditions 1), 2) and 4), then it is called a t-norm.
Four typical examples of continuous t-norms are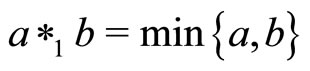 ,
, 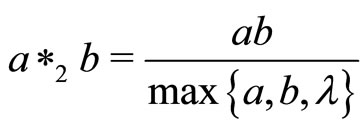 for
for and
and ,
,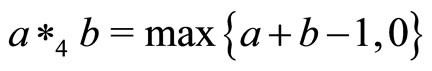 .
.
Definition 8 [9,10]. Let  be an arbitrary nonempty set. Let
be an arbitrary nonempty set. Let  be a continuous t-norm and M a fuzzy set on
be a continuous t-norm and M a fuzzy set on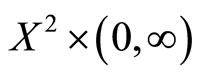 . If the following conditions satisfy:
. If the following conditions satisfy:
1)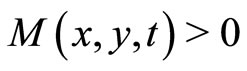 ;
;
2)  if and only if
if and only if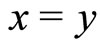 ;
;
3)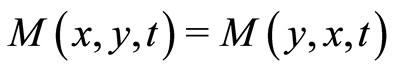 ;
;
4) ;
;
5) 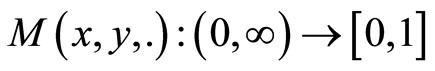 is continuous, for any
is continuous, for any 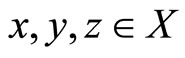 and
and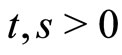 , then the 3-tuple
, then the 3-tuple 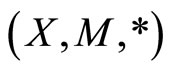 is called a fuzzy metric space.
is called a fuzzy metric space.
Remark 3. For any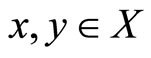 ,
, 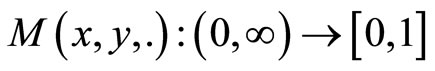 is a non-decreasing function (see [9,10]).
is a non-decreasing function (see [9,10]).
Definition 9 [9,10]. Let 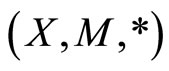 be a fuzzy metric space and M a fuzzy set on
be a fuzzy metric space and M a fuzzy set on .
. 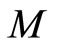 is said to satisfies the n-property on
is said to satisfies the n-property on 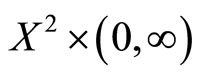 if
if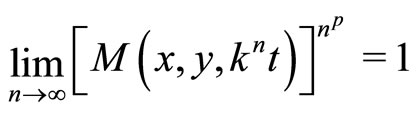 whenever
whenever  and
and .
.
Definition 10. Let 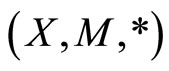 be a fuzzy metric space and
be a fuzzy metric space and 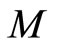 a fuzzy set on
a fuzzy set on .
. 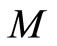 is said to satisfies the
is said to satisfies the 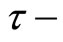 property on
property on 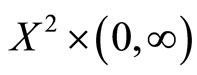 if
if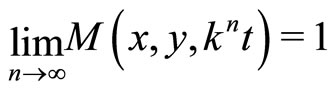 for all
for all  and
and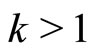 .
.
Definition 11 [11]. A function 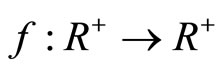 is said to satisfy
is said to satisfy 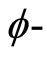 condition, if f is a strictly increasing function satisfying f(0) = 0 and
condition, if f is a strictly increasing function satisfying f(0) = 0 and  for any
for any , where
, where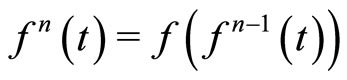 .
.
Remark 4. If a function 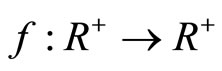 satisfies the
satisfies the 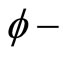 condition, then the following inequalities hold (see [11]):
condition, then the following inequalities hold (see [11]):
1)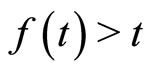 , for all
, for all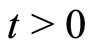 ;
;
2)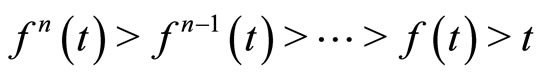 , for each
, for each 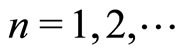 and for all
and for all .
.
Definition 12. Let 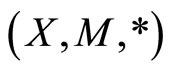 be a fuzzy metric space, the fuzzy set
be a fuzzy metric space, the fuzzy set 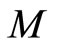 is said to have
is said to have 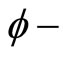 property whenever
property whenever for all
for all 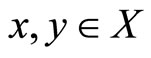 where
where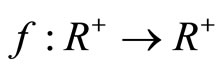 satisfying the
satisfying the 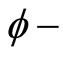 condition.
condition.
Definition 13 [9,10]. Let 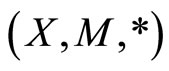 be a fuzzy metric space and
be a fuzzy metric space and 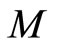 a fuzzy set on
a fuzzy set on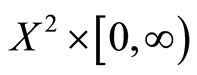 .
.
1) A sequence 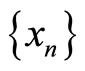 in
in 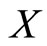 is said to fuzzy-convergent to a point
is said to fuzzy-convergent to a point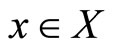 , if
, if 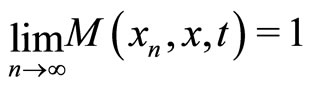 for all
for all .
.
2) A sequence 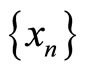 in
in 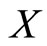 is called a fuzzy-Cauchy sequence, if for each
is called a fuzzy-Cauchy sequence, if for each  and
and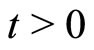 , there exists
, there exists , such that
, such that  for each
for each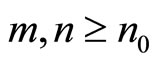 .
.
3) A fuzzy metric space is called fuzzy-complete, if every fuzzy-Cauchy sequence is fuzzy-convergent.
Definition 14 [9,10]. Let  be a fuzzy metric space. The fuzzy set
be a fuzzy metric space. The fuzzy set  is said to be fuzzy-continuous on
is said to be fuzzy-continuous on , whenever any
, whenever any  in
in  which fuzzy-converges to
which fuzzy-converges to 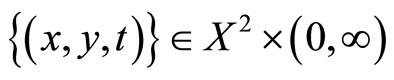 implies
implies
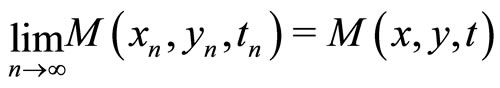 .
.
Remark 5. M is a continuous function on 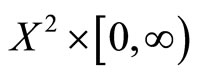 (see [9,10]).
(see [9,10]).
Definition 15 [12]. Let  be a fuzzy metric space and M the fuzzy set on
be a fuzzy metric space and M the fuzzy set on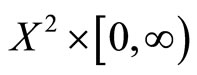 . Denote by
. Denote by  the set of all compact subsets of
the set of all compact subsets of  and define a function
and define a function 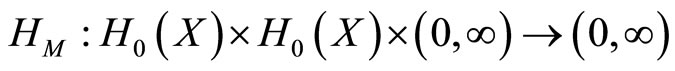 by
by
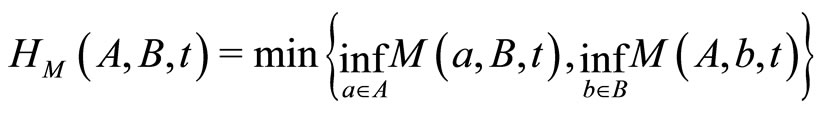
for any  and any
and any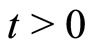 , where
, where
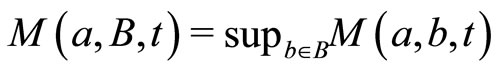 and
and
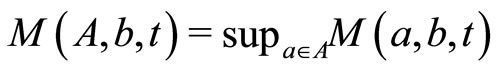 .
.
Lemma 1 [6]. Let 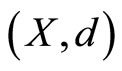 be a complete metric space,
be a complete metric space, 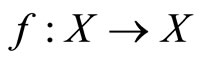 , for the
, for the 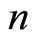 iterate of
iterate of 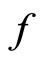
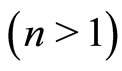 , the following statements hold:
, the following statements hold:
1) If  has a unique fixed point, then
has a unique fixed point, then 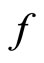 has a unique fixed point.
has a unique fixed point.
2) If there exists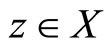 , such that the orbit of
, such that the orbit of 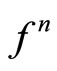 converges to
converges to , then the orbit of
, then the orbit of 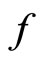 converges to
converges to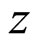 .
.
3) If the orbit of 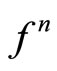 is a bounded sequence, then the orbit of
is a bounded sequence, then the orbit of 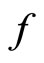 is a bounded sequence.
is a bounded sequence.
Lemma 2. Let  be a complete metric space and
be a complete metric space and 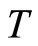 an expansive and surjective mapping on
an expansive and surjective mapping on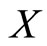 , then
, then 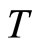 has a unique fixed point.
has a unique fixed point.
Proof. We claim first that 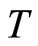 is injective. To show this claim, assume, by the way of contradiction, that there exist
is injective. To show this claim, assume, by the way of contradiction, that there exist 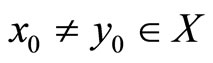 such that
such that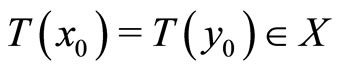 . Since
. Since , then
, then  holds. Since
holds. Since 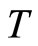 is an expansive mapping, it implies
is an expansive mapping, it implies 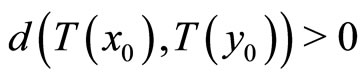 . It contradicts to
. It contradicts to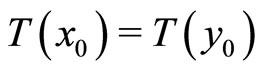 , that is,
, that is,  , which implies
, which implies  is a bijection. Hence T–1 exists and is a contraction mapping. By the contractive mapping priciple, there exists a unique
is a bijection. Hence T–1 exists and is a contraction mapping. By the contractive mapping priciple, there exists a unique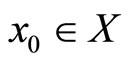 , such that
, such that , that is
, that is 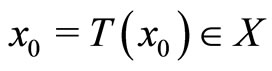 . The proof is complete.
. The proof is complete.
Lemma 3 [5]. Let  be a complete metric space and f a self mapping on X. If the following condition satisfies, for any
be a complete metric space and f a self mapping on X. If the following condition satisfies, for any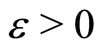 , there exists
, there exists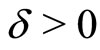 , such that
, such that 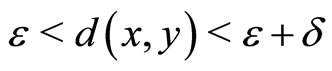 implies
implies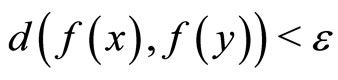 , then f has a unique fixed point
, then f has a unique fixed point  on
on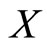 , and
, and for any
for any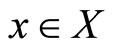 .
.
Lemma 4 [7]. Let  be a sequentially compact cone metric space with respect to a Banach space
be a sequentially compact cone metric space with respect to a Banach space 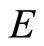 and a regular cone
and a regular cone 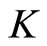 in
in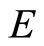 . Suppose a mapping
. Suppose a mapping  satisfies the contractive condition:
satisfies the contractive condition: 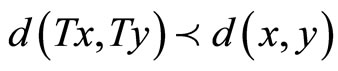 , for all
, for all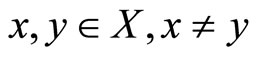 , then
, then 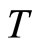 has a unique fixed point in
has a unique fixed point in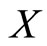 .
.
Lemma 5 [4]. Let 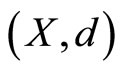 be a compact metric space and
be a compact metric space and 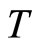 a self mapping on
a self mapping on . Assume that
. Assume that 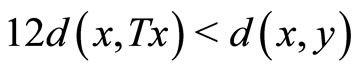 implies
implies 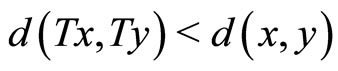 for any
for any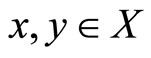 , then
, then  has a unique fixed point.
has a unique fixed point.
Lemma 6 [9,10]. Let  be a fuzzy metric space,
be a fuzzy metric space, 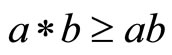 for all
for all 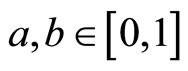 and M satisfy
and M satisfy 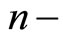 property. Let
property. Let 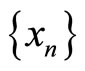 be a sequence in X such that for all
be a sequence in X such that for all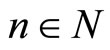 ,
, 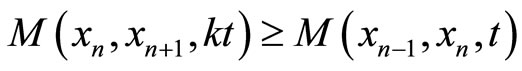 for every
for every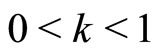 , then
, then 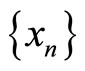 is a Cauchy sequence in X.
is a Cauchy sequence in X.
3. The Existence Theorem of Fixed Points
In this section, we apply the concepts and lemmas provided in Section 2 to prove some existence theorems of fixed points for some mappings. These results will be used in the following section.
Theorem 1. Let  be a complete metric space and
be a complete metric space and 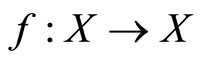 a surjective mapping. If there exist
a surjective mapping. If there exist 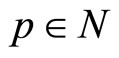 and
and 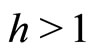 such that
such that

holds for any , then there exists a unique fixed point of f.
, then there exists a unique fixed point of f.
Proof. For each , since
, since  is a surjective, then there exists
is a surjective, then there exists , such that
, such that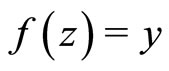 , in the same way, there exist
, in the same way, there exist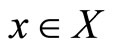 ,such that
,such that , i.e. there exists
, i.e. there exists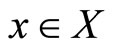 , such that
, such that . We deduce by induction that
. We deduce by induction that 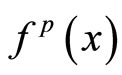 is also surjective, which combining (I) shows that
is also surjective, which combining (I) shows that 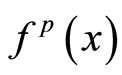 is an expansive mapping. By Lemma 2, there exists a unique fixed point of
is an expansive mapping. By Lemma 2, there exists a unique fixed point of , then we know by Lemma 1 that there exists a unique fixed point of f. The proof is complete.
, then we know by Lemma 1 that there exists a unique fixed point of f. The proof is complete.
Remark 6. It is obvious that we can get Lemma 2 from Theorem 1. An example satisfying Theorem 1 is given below.
Example 1. Define  by
by

it is clear that f is a surjective self-mapping on R and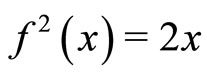 .
. 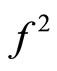 satisfies condition (I), i.e.
satisfies condition (I), i.e.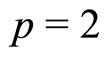 , then f has a fixed point, 0 is the fixed point in this example.
, then f has a fixed point, 0 is the fixed point in this example.
Theorem 2. Let 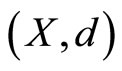 be a sequentially compact cone metric space with respect to a Banach space
be a sequentially compact cone metric space with respect to a Banach space 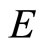 and a normal cone
and a normal cone  in
in 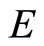 with normal constant
with normal constant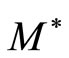 . Assume that
. Assume that 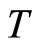 is a self mapping on
is a self mapping on 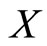 and satisfies for any
and satisfies for any ,
, 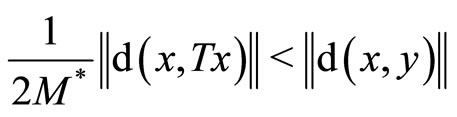 implies
implies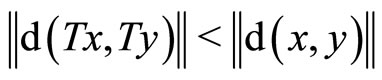 , then
, then 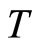 has a unique fixed point.
has a unique fixed point.
Proof. We claim first that 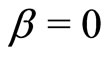 where
where 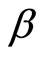 is defined by
is defined by

Using reduction to absurdity, we suppose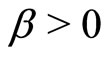 . Since
. Since  is sequentially compact, we deduce from the definition of
is sequentially compact, we deduce from the definition of  that there exists a sequence
that there exists a sequence 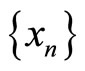 such that
such that
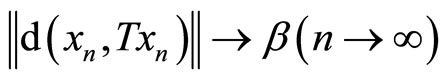
and
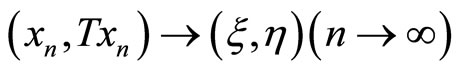
for some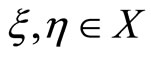 . Observe that the normal constant
. Observe that the normal constant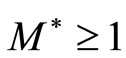 , there exists
, there exists 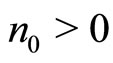 such that for any
such that for any  the inequality
the inequality
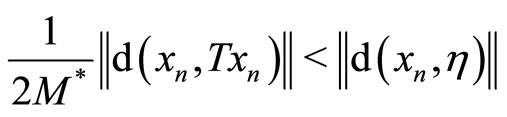
holds, which combining the given conditions shows that for any ,
,
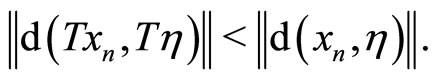
By calculations we then have
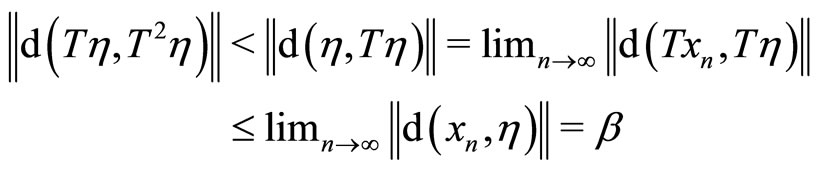
which contradicts to the definition of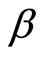 .
.
We prove next that T has a fixed point. We proceed once more by using reduction to absurdity and suppose that T has no fixed point. Then for each ,
,
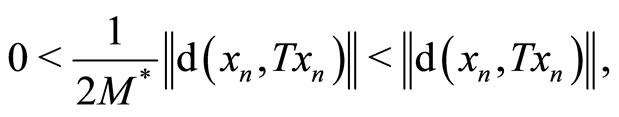
which implies that for each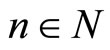 ,
,
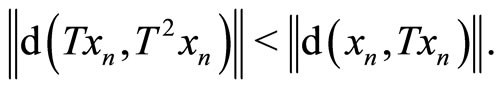
By the triangle inequality in cone metric spaces, we have
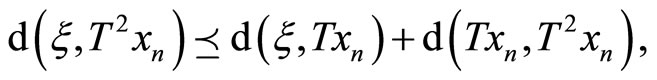
then,

We claim that at least one of the following two inequalities should be hold:

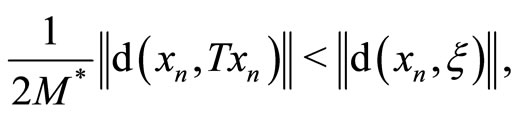
otherwise, we reach a contradiction by the following calculations:

If the first inequality of the above two holds, then
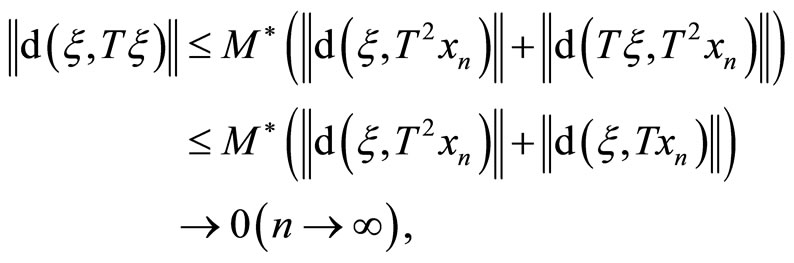
if the the other one holds, then
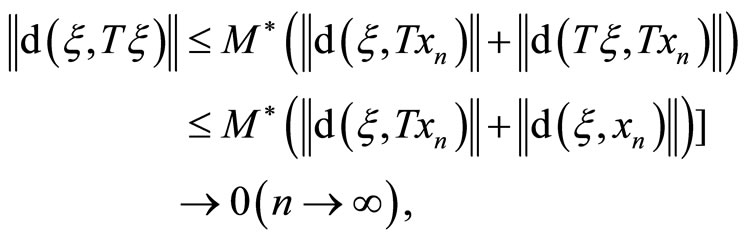
which show that 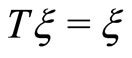 in each case, and the proof of the existence of the fixed point is complete.
in each case, and the proof of the existence of the fixed point is complete.
We finally prove the uniqueness of the fixed point. Suppose 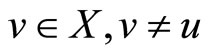 and
and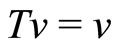 . Since
. Since , then
, then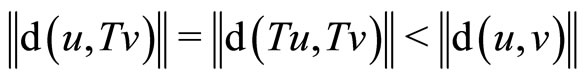 , we reach a contradiction which completes the proof.
, we reach a contradiction which completes the proof.
Remark 7. In [7], Long-Guang Huang and Xian Zhang have established a fixed point theorem in a sequentially compact cone metric space with respect to a Banach space 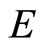 and a regular cone
and a regular cone  in
in  (see Lemma 4), where the mapping
(see Lemma 4), where the mapping 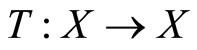 satisfies the contractive condition. In [4], Tomonari Suzuki has established a fixed point theorem in a compact metric space where the mapping T satisfying a condition similarly to condition (II) of theorem 2 (see Lemma 5). Observe that any regular cone is always normal, Theorem 2 is established under a different and weaker condition when comparing with Lemma 4 and generalize the results of Lemma 5 from compact metric spaces to sequentially compact cone metric spaces.
satisfies the contractive condition. In [4], Tomonari Suzuki has established a fixed point theorem in a compact metric space where the mapping T satisfying a condition similarly to condition (II) of theorem 2 (see Lemma 5). Observe that any regular cone is always normal, Theorem 2 is established under a different and weaker condition when comparing with Lemma 4 and generalize the results of Lemma 5 from compact metric spaces to sequentially compact cone metric spaces.
Theorem 3. Let 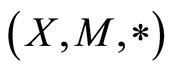 be a complete fuzzy metric space, where
be a complete fuzzy metric space, where  is defined by
is defined by  for any
for any 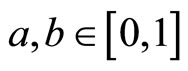 and M a fuzzy set on
and M a fuzzy set on 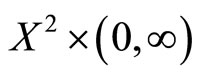 satisfying
satisfying 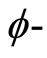 property. For a surjective function
property. For a surjective function , if for any
, if for any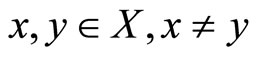 , the following inequality holds
, the following inequality holds
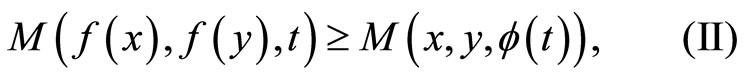
then 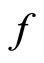 has a fixed point on
has a fixed point on . If inequality (II) is strict, then
. If inequality (II) is strict, then 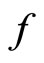 has a unique fixed point on
has a unique fixed point on .
.
Proof. By choosing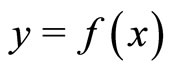 , we deduce from (II) that for any
, we deduce from (II) that for any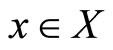 ,
,

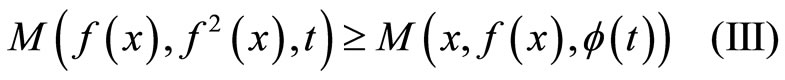
Proceed by introduction on n, we have for any 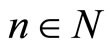
For any , we have
, we have
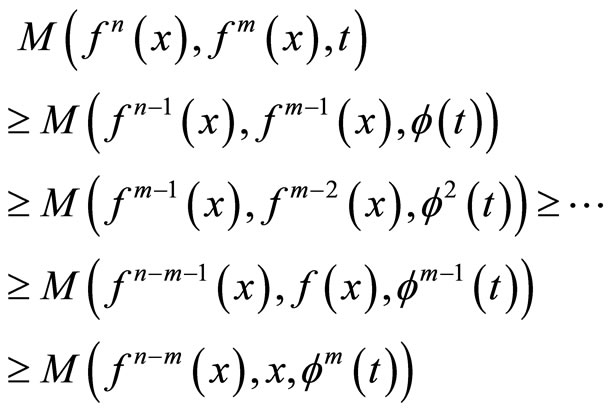
Observe that 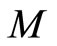 satisfies
satisfies 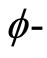 property, then
property, then
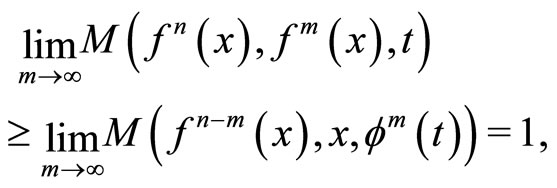
which shows that 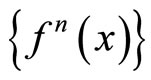 is a fuzzy-Cauchy sequence. Since
is a fuzzy-Cauchy sequence. Since 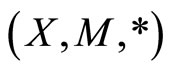 is complete, there exists
is complete, there exists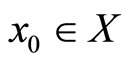 , such that
, such that
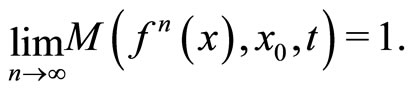
Then by (II) and the nondecreasing property of M, we have

for any . Since
. Since
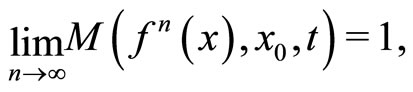
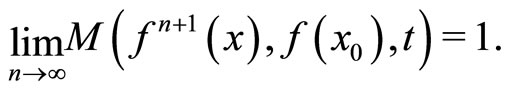
We therefore deduce
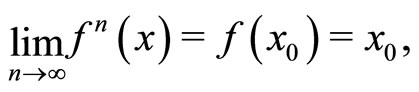
which shows 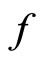 has a fixed point on
has a fixed point on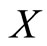 .
.
If there exist 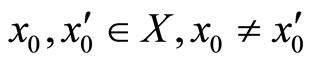 such that
such that 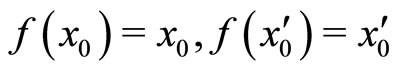 , then by condition (II),
, then by condition (II),
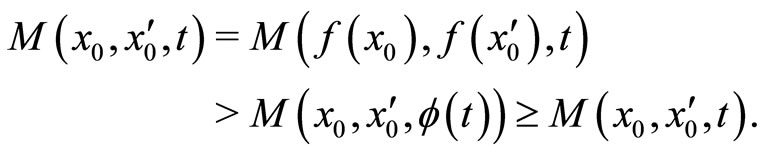
It is a contradiction, hence . We have now proved the uniqueness which complete the proof.
. We have now proved the uniqueness which complete the proof.
Corollary 1. Let  be a complete fuzzy metric space and
be a complete fuzzy metric space and 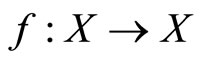 a bijective mapping, where * is defined by
a bijective mapping, where * is defined by  for any
for any 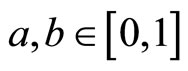 and M a fuzzy set on
and M a fuzzy set on 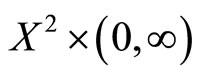 satisfying
satisfying 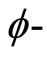 property. If for any
property. If for any 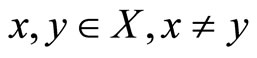 ,
,
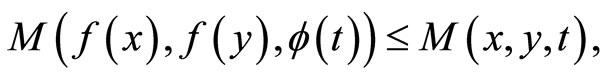
then f has a fixed point on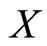 . If the above inequality is strict, then f has a unique fixed point on
. If the above inequality is strict, then f has a unique fixed point on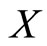 .
.
Proof. Since f is bijective, 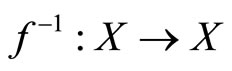 exists and satisfies for any
exists and satisfies for any  ,
,

By Theorem 3, we know 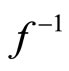 has fixed point, and the fixed point of
has fixed point, and the fixed point of 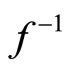 is the same as that of f, then f has fixed point on
is the same as that of f, then f has fixed point on  . If the inequality is strict, then the proof is the same as that in Theorem 3.
. If the inequality is strict, then the proof is the same as that in Theorem 3.
Corollary 2. Let 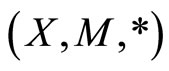 be a complete fuzzy metric space, where
be a complete fuzzy metric space, where  is defined by
is defined by 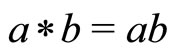 for any
for any 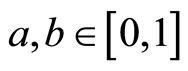 and M a fuzzy set on
and M a fuzzy set on  satisfying
satisfying 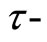 property, and
property, and 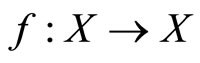 a surjective mapping satisfying
a surjective mapping satisfying

for any ,
, 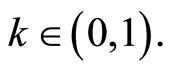 Then f has a fixed point on
Then f has a fixed point on  . If the inequality is strict, then f has a unique fixed point on
. If the inequality is strict, then f has a unique fixed point on 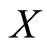 .
.
Proof. Let ,
,  , then by Theorem 3 we can easily propose the results of Corollary 2. We omit the details.
, then by Theorem 3 we can easily propose the results of Corollary 2. We omit the details.
Example 2. Assume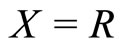 ,
,  , and define M by
, and define M by

clearly M satisfies 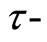 property. For any f satisfies the conditions of Corollary 2, i.e.
property. For any f satisfies the conditions of Corollary 2, i.e.
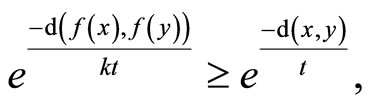
we have 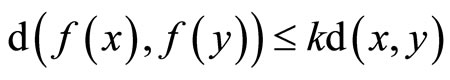 for any
for any 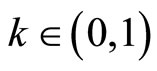 , hence
, hence 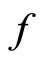 is a contraction mapping which has a fixed point on
is a contraction mapping which has a fixed point on 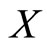 .
.
In the following, we show an example to demonstrate the conditions in Corollary 2 are only sufficient condition, not necessary conditions.
Example 3. Assume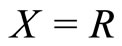 ,
,  , and define M by
, and define M by
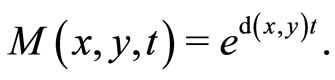
Obviously 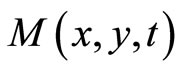 is a fuzzy set which doesn’t have
is a fuzzy set which doesn’t have 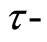 property, hence it can’t be judged by Corollary 3. But if
property, hence it can’t be judged by Corollary 3. But if 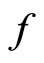 is a contraction mapping, a fixed point still exist on
is a contraction mapping, a fixed point still exist on 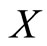 .
.
Theorem 4. Let 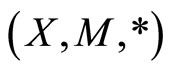 be a complete fuzzy metric space, where
be a complete fuzzy metric space, where  is defined by
is defined by 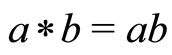 for any
for any 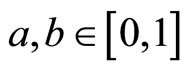 and
and 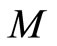 a fuzzy set on
a fuzzy set on 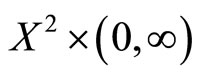 satisfying
satisfying 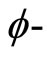 property.
property.  is a compact setvalued mapping, satisfies for any
is a compact setvalued mapping, satisfies for any 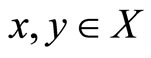 ,
,

then 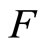 has a fixed point on
has a fixed point on  .
.
Proof. By the choice axioms (see [6]), there exists a single-valued function , such that
, such that 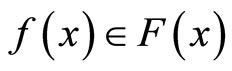 for any
for any 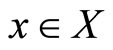 . Then for each
. Then for each  , there exist
, there exist 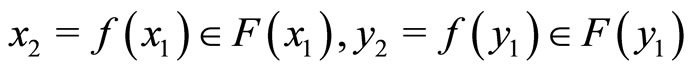 . By the definition of
. By the definition of 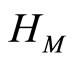 , we have
, we have

Theorem 3 shows that  has a fixed point
has a fixed point 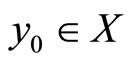 , i.e .
, i.e .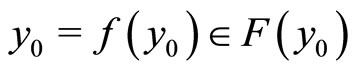 , which is also a fixed point of
, which is also a fixed point of  on
on  .
.
Corollary 3. Let 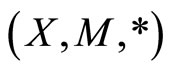 be a complete fuzzy metric space and
be a complete fuzzy metric space and 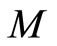 a fuzzy set on
a fuzzy set on  satisfying
satisfying  property.
property.  is a compact setvalued mapping satisfying for every
is a compact setvalued mapping satisfying for every 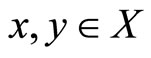 ,
,
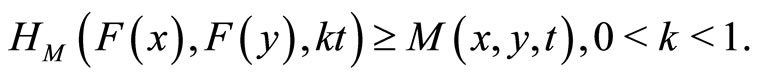
Then 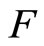 has a fixed point on
has a fixed point on  .
.
4. Applications to Differential Equations
This section is concerned with the proof of the existence and uniqueness of the solutions to the two-point ordinary differential equations by using the fixed point theorems obtained in Section 3. The following are the main results.
Theorem 5. Assume that 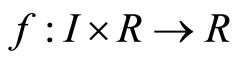 is a continuous function. If there exists
is a continuous function. If there exists 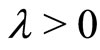 such that the following inequalities
such that the following inequalities

hold for any 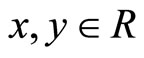 with
with  , where
, where 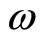 is an ω-function, then Problem(1) has a unique solution.
is an ω-function, then Problem(1) has a unique solution.
Proof. Problem (1) is equivalent to the integral equation

where

Define
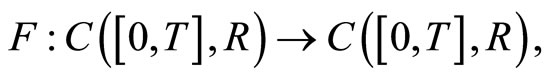
by
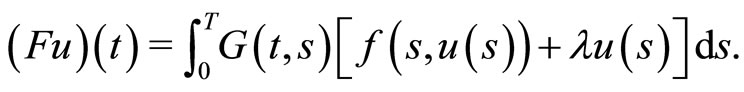
Note that if 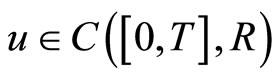 is a fixed point of
is a fixed point of 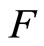 , then
, then 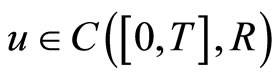 is a solution to Problem (1). Define a order relation in
is a solution to Problem (1). Define a order relation in 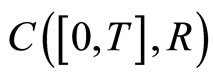 by
by 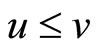 if and only if
if and only if 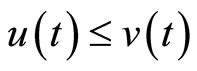 for every
for every 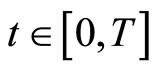 , for every
, for every 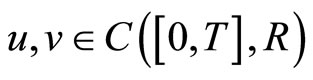 . Denote by
. Denote by
 for any
for any
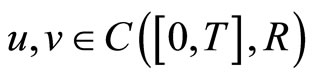 the distance in
the distance in 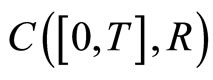 . For each
. For each 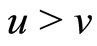 , by the left side of (IV),
, by the left side of (IV), 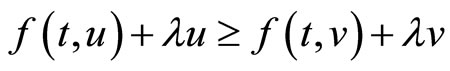 . Since
. Since 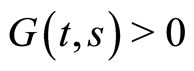 , for each
, for each  ,
,

which shows that 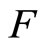 is monotone increasing. For any
is monotone increasing. For any 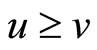 , if
, if 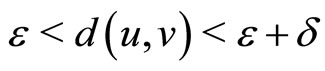 , then
, then
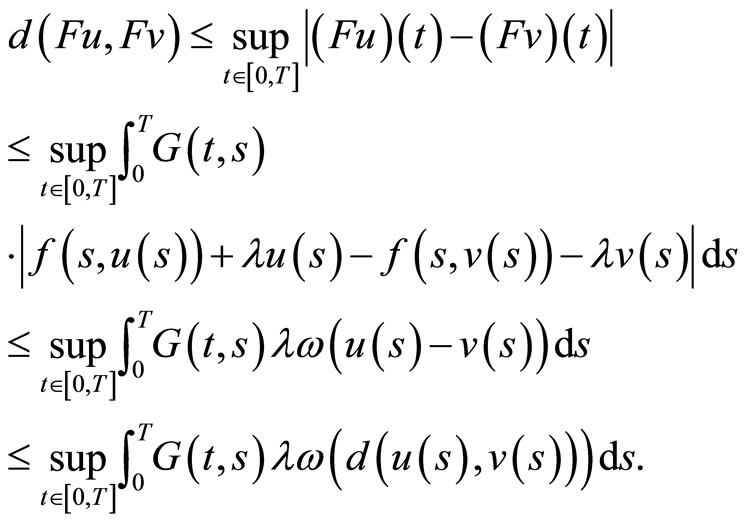
Since 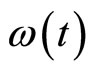 is a increasing function, then
is a increasing function, then
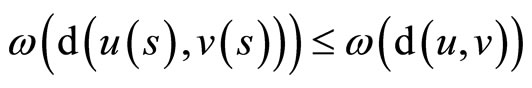 for
for 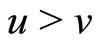 , and
, and
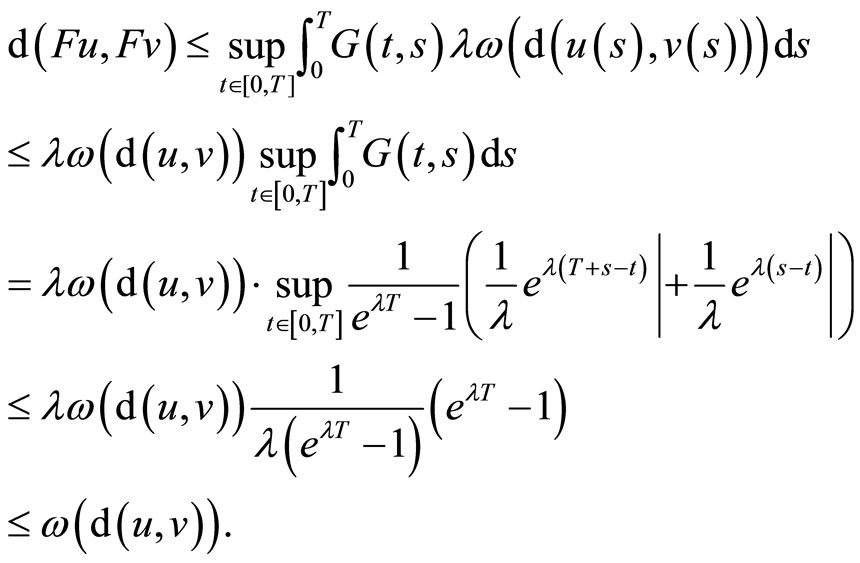
By the definition of 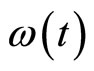 , for each
, for each  , there exists
, there exists 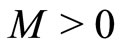 such that
such that
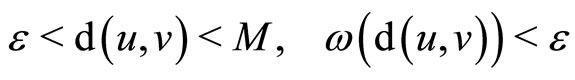 , let
, let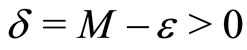
hence  . It demonstrates
. It demonstrates 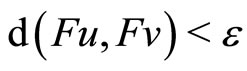 . By Lemma 3, F has a unique fixed point, and
. By Lemma 3, F has a unique fixed point, and 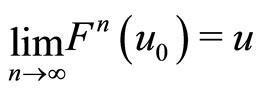 for each
for each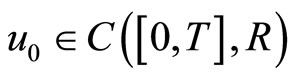 ,
,  is the fixed point of
is the fixed point of  , i.e. the solution of Problem (1).
, i.e. the solution of Problem (1).
Assume  is a lower solution of Problem (1), we can prove as Theorem 3.1 in [13] to obtain the uniqueness of the solution.
is a lower solution of Problem (1), we can prove as Theorem 3.1 in [13] to obtain the uniqueness of the solution.
Remark 8. Contrasted with some related results in [13-15], the conditions in Theorem 5 is relatively clearer.
Theorem 6. Assume that 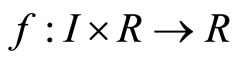 is a continuous function. If there exists
is a continuous function. If there exists 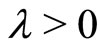 such that for any
such that for any 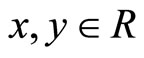 with
with 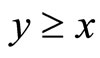 , the following inequalities
, the following inequalities
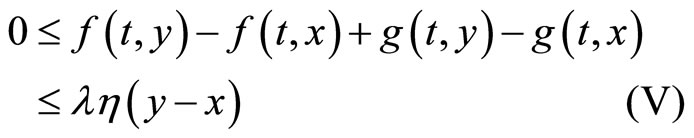
hold, where  is an ω-function, then the solution of Problem (2) exists.
is an ω-function, then the solution of Problem (2) exists.
Proof. Problem (2) is equivalent to the following integral equation
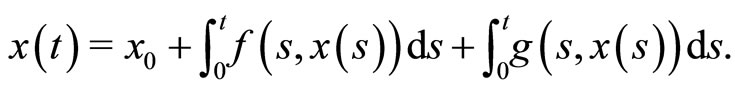
Define
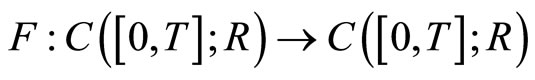
by
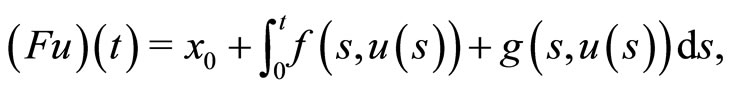
for any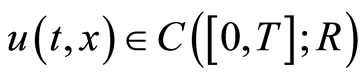 . Note that
. Note that is a fixed point of
is a fixed point of 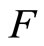 , then
, then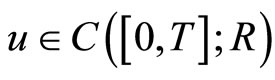 is a solution of Problem (2). For
is a solution of Problem (2). For , we define
, we define  if and only if
if and only if 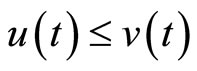 for any
for any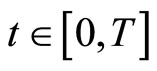 . Denote
. Denote
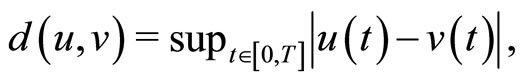 for
for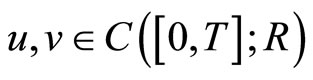 .
.
Then by (V), for any 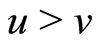 ,
,
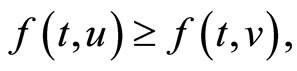

which implies
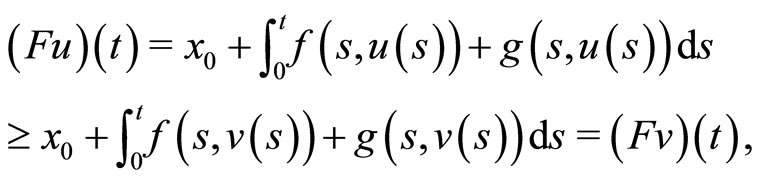
and
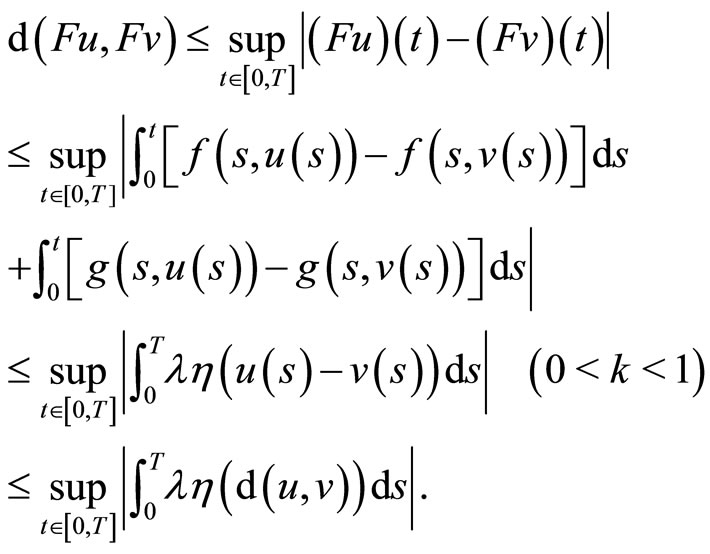
By the definition of function 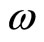 , let
, let 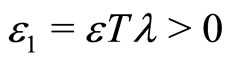 , there exists
, there exists  , such that
, such that  , there exists
, there exists , such that
, such that 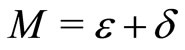 , then
, then 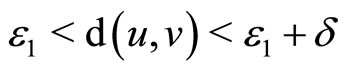 ,
, 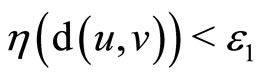 and
and
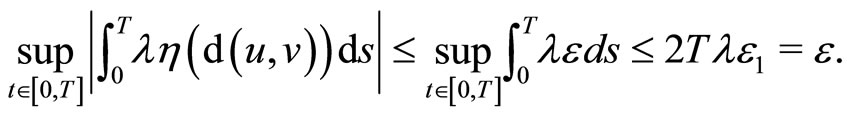
By Lemma 3, 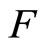 has a unique fixed point, and
has a unique fixed point, and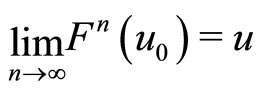 for any
for any 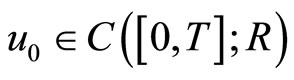 , u is a fixed point of
, u is a fixed point of 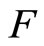 , which is also a solution of Problem (2). The proof is complete.
, which is also a solution of Problem (2). The proof is complete.
Define 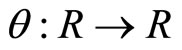 satisfying for any
satisfying for any
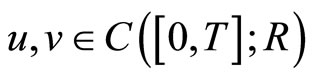 ,
,
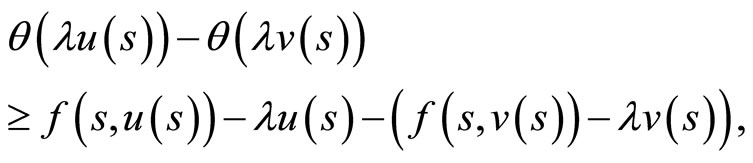
then we have the following theorem:
Theorem 7. Let  be a complete fuzzy metric space,
be a complete fuzzy metric space,  . If the following conditions hold:
. If the following conditions hold:
1) For any ,
, 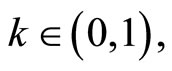

2) For any 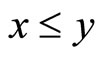 ,
,

then the solution of Problem (1) is unique.
Proof. By example 2, while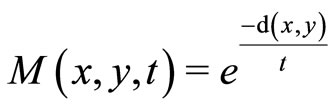 , a mapping satisfying the above conditions is a contraction mapping, i.e.
, a mapping satisfying the above conditions is a contraction mapping, i.e. 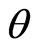 is a contraction mapping. Then we can proceed the proof with the same arguments as that in Theorem 5.
is a contraction mapping. Then we can proceed the proof with the same arguments as that in Theorem 5.
Remark 9. If we replace condition (1) by the inequality in Example 2 or Example 3 as well as the corresponding expression of M, then Theorem 7 can also make sure the uniqueness of t he solution of Problem (1).
Define 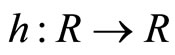 satisfying for any
satisfying for any
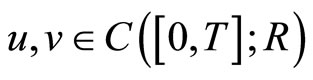 ,
,
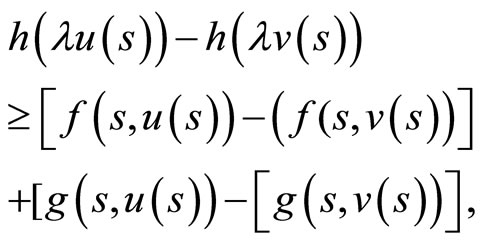
then we have the following theorem:
Theorem 8. Let  be a complete fuzzy metric space,
be a complete fuzzy metric space, 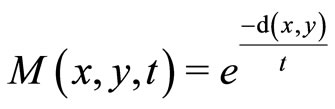 . If the following two conditions hold:
. If the following two conditions hold:
1) for any 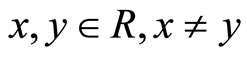 and
and 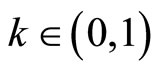 ,
,

2) for any 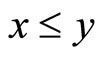 ,
,
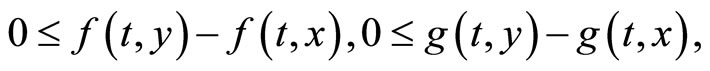
then the solution of Problem (2) exists.
Proof. By Example 2, while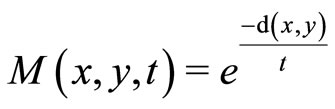 , a mapping satisfying the conditions above is a contraction mapping, hence h is a contraction mapping. Then we can proceed the proof with the same arguments as that in Theorem 6 and complete the proof.
, a mapping satisfying the conditions above is a contraction mapping, hence h is a contraction mapping. Then we can proceed the proof with the same arguments as that in Theorem 6 and complete the proof.
5. Conclusion
The paper is devoted to several new types of fixed point theorems in different spaces such as cone metric spaces and fuzzy metric spaces together with their applications. We have also proved the existence and uniqueness of the solutions to two classes of two-point ordinary differential equation problems by using these obtained fixed point theorems.
6. Acknowledgements
The authors of this paper would like to appreciate the referee’s helpful comments and valuable suggestions which have essentially improved this paper. This work is supported by the National Natural Science Foundation (11071109) of People’s Republic of China.
REFERENCES
- K. Deimling, “Nonlinear Functional Analysis,” SpringerVerlag, Berlin, 1985. doi:10.1007/978-3-662-00547-7
- C. J. Zhang, “Set-Valued Analysis and Its Applications to Economics,” The Science Press, Beijing, 2004.
- W. Walter, “Remarks on a Paper by F. Browder about Contraction,” Nonlinear Analysis, Vol. 5, 1981, pp. 21-25. doi:10.1016/0362-546X(81)90066-3
- T. Suzuki, “A New Type of Fixed Point Theorem in Metric Spaces,” Nonlinear Analysis, Vol. 71, 2009, pp. 5313- 5317. doi:10.1016/j.na.2009.04.017
- A. Meir and E. Keeler, “A Theorem on Contraction Mappings,” Journal of Mathematical Analysis and Applications, Vol. 28, 1969, pp. 326-329. doi:10.1016/0022-247X(69)90031-6
- T. Cardinali and P. Rubbioni, “An Extension to Multifunctions of the Keeler-Meir’s Fixed Point Theorem,” Fixed Point Theory, Vol. 7, No. 1, 2006, pp. 23-36.
- L.-G. Huang and X. Zhang, “Cone Metric Spaces and Fixed Point Theorems of Contractive Mappings,” Journal of Mathematical Analysis and Applications, Vol. 332, No. 2, 2007, pp. 1468-1476.
- A. George and P. Veeramani, “On Some Result in Fuzzy Metric Space,” Fuzzy Sets and Systems, Vol. 64, 1994, pp. 395-399. doi:10.1016/0165-0114(94)90162-7
- S. Sedghi, I. Altunb and N. Shobe, “Coupled Fixed Point Theorems for Contractions in Fuzzy Metric Spaces,” Nonlinear Analysis, Vol. 72, 2010, pp. 1298-1304. doi:10.1016/j.na.2009.08.018
- X.-H. Zhu and J.-Z. Xiao, “Note on ‘Coupled Fixed Point Theorems for Contractions in Fuzzy Metric Spaces’,” Nonlinear Analysis, Vol. 74, 2011, pp. 5475-5479. doi:10.1016/j.na.2011.05.034
- S. S. Zhang, “Fixed Point Theorems of Mappings on Probabilistic Metric Spaces with Applications,” Scientia Sinca (Series A), Vol. 11, 1983.
- J. Rodriguez-Lopez and S. Romaguera, “The Hausdorff Fuzzy Metric on Compact Sets,” Fuzzy Sets and Systems, Vol. 147, No. 2, 2004, pp. 273-283.
- A. Amini-Harandi and H. Emami, “A Fixed Point Theorem for Contraction Type Maps in Partially Ordered Metric Spaces and Application to Ordinary Differential Equations,” Nonlinear Analysis, Vol. 72, 2010, pp. 2238-2242. doi:10.1016/j.na.2009.10.023
- T. G. Bhaskar and V. Lakshmikantham, “Fixed Point Theorems in Partially Ordered Metric Spaces and Applications,” Nonlinear Analysis, Vol. 65, 2006, pp. 1379- 1393. doi:10.1016/j.na.2005.10.017
- J. Harjani and K. Sadarangani, “Generalized Contractions in Partially Ordered Metric Spaces and Applications to Ordinary Differential Equations,” Nonlinear Analysis, Vol. 72, 2010, pp. 1188-1197. doi:10.1016/j.na.2009.08.003
- J. Harjani and K. Sadarangani, “Fixed Point Theorems for Weakly Contractive Mappings in Partially Ordered Sets,” Nonlinear Analysis, Vol. 71, 2009, pp. 3403-3410. doi:10.1016/j.na.2009.01.240

