Advances in Bioscience and Biotechnology
Vol.5 No.2(2014), Article ID:42409,11 pages DOI:10.4236/abb.2014.52013
Assessing spatial genetic structure from molecular marker data via principal component analyses: A case study in a Prosopis sp. forest
1Statistics and Biometry, Faculty of Agricultural Sciences, National University of Córdoba-CONICET, Córdoba, Argentina
2Centro de Investigaciones Agropecuarias, Instituto Nacional de Tecnología Agropecuaria, Córdoba, Argentina
Email: ingridteich@gmail.com
Copyright © 2014 Ingrid Teich et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Ingrid Teich et al. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received 5 November 2013; revised 16 December 2013; accepted 3 January 2014
KEYWORDS
Multivariate Analysis; Forests; Molecular Markers; Spatial Genetics; sPCA
ABSTRACT
Advances in genotyping technology, such as molecular markers, have noticeably improved our capacity to characterize genomes at multiple loci. Concomitantly, the methodological framework to analyze genetic data has expanded, and keeping abreast with the latest statistical developments to analyze molecular marker data in the context of spatial genetics has become a difficult task. Most methods in spatial statistics are devoted to univariate data whereas the nature of molecular marker data is highly dimensional. Multivariate methods are aimed at finding proximities between entities characterized by multiple variables by summarizing information in few synthetic variables. In particular, Principal Component analysis (PCA) has been used to study genetic structure of geo-referenced allele frequency profiles, incorporating spatial information with a posteriori analysis. Conversely, the recently developed spatially restricted PCA (sPCA) explicitly includes spatial data in the optimization criterion. In this work, we compared the results of the application of PCA and sPCA in the study of the spatial genetic structure at fine scale of a Prosopis flexuosa and P. chilensis hybrid swarm. Data consisted in the genetic characterization of 87 trees sampled in Córdoba, Argentina and genotyped at six microsatellites, which yielded 72 alleles. As expected, principal components explained more variance than sPCA components, but were less spatially autocorrelated. The maps obtained by the interpolation of sPC1 values allowed a better visualization of a patchy spatial pattern of genetic variability than the PC1 synthetic map. We also proposed a PC-sPC scatter plot of allele loadings to better understand the allele contributions to spatial genetic variability.
1. INTRODUCTION
Advances in molecular biology have led to the introduction of many new types of molecular markers, which provide cheap and high-throughput methods to characterize genomes at multiple loci. However, the amount of available information in biological studies has increased dramatically not only at the molecular level but also at other levels of organization and nowadays molecular marker data are often complemented with other covariates, like spatial and temporal coordinates. The joint analysis of genetic and spatial data can lead to a better understanding of evolutionary and ecological processes, such as drift, population expansions, bottlenecks, and selection and mutation regimes [1,2] and it is rapidly becoming the norm in population genetics. Spatial genetic structure (SGS) in natural populations, i.e. the nonrandom spatial distribution of genotypes, is expected to occur frequently at fine spatial scales within continuous plant populations [3]. SGS can result from different processes, including selection pressures or historical events. At a fine spatial scale, however, the most prevalent cause is the formation of local pedigree structures as a result of limited gene dispersal. In this context, genetic similarity is expected to be higher among neighbors (positive autocorrelation) than among more distant individuals, and the theory of isolation by distance [4,5], predicts the expected pattern of SGS at drift-dispersal equilibrium. Many empirical studies have investigated fine-scale SGS within plant populations from molecular marker data, often using spatial autocorrelation coefficients [6].
Regarding the statistical framework to study genetic variability from genetic data with known sampling site positions, spatial statistical genetics has become a rapidly evolving field. When implementing a spatially explicit approach to analyze georreferenced molecular marker data, it is important to consider that different statistical methods provide different types of information. The statistical dependence between geographic and genetic distances is usually carried out using the Mantel test, a permutational procedure to test the statistical significance of the correlation between matrices [7]. A common approach to quantify autocorrelation is the Moran index I [8], which has been extensively used and in genetic studies has been frequently applied to test the spatial structure of single alleles. Many methods for the analysis of SGS have been developed for single-locus, diploid genotypic data such as the one provided by isozymes [9]. However, genetic data are highly multidimensional and it is currently obtained from multiple loci with molecular markers. To deal with multivariate molecular data, dimension reduction techniques have proven to be useful [10-13].
Principal Components Analysis (PCA) [14] is one dimension reduction technique that can be applied to summarize molecular marker profiles into a few uncorrelated components. It finds an orthogonal basis for the data in such a way that the first axis of the new spanned space is along the direction of greatest variation of the original data, providing a set of eigenvectors and their corresponding eigenvalues. Eigenvectors contain the weight coefficients to build the linear combinations, which indicate the relative importance of variables to explain variability among the biological entities (e.g. trees) on each axis. Once the synthetic variables (principal components) of interest have been chosen, they can be used to give scatter plots of observations with optimal properties to study the underlying variability among entities. One advantage of the use of synthetic variables is that they collapse the multidimensional genetic characterization of individuals, allowing the construction of synthetic maps of genetic variability. For mapping purposes, individual scores on the principal components can be interpolated, by the prediction of the variable (PC) in spatial points. This technique allows visualizing the spatial pattern of genetic variability [15-18]. Plotting the values of the resulting synthetic variables (components) onto a geographic map as a way to explore the spatial structure of genetic variance, has been pioneered by Cavalli-Sforza [10] for the reconstruction of the early history of human populations. The power of PCA with large spatial genomic data sets became evident in Novembre et al. [19], who observed a very high correlation between the positions in a PCA plot and human geographic origin, showing that Single Nucleotide Polymorphisms (SNPs) were spatially structured. However, PCA was not properly designed to investigate spatial patterns and consequently spatial information was used as the posteriori analysis. The first principal components explain variance among observations rather than autocorrelation and therefore PCA may fail to detect spatial structuring if this is not associated with the most pronounced genetic differentiation.
For a more complete characterization of spatial structures in genomic data, the analysis of the principal components has to focus on the part of the multidimensional variance that is spatially structured. This can be accomplished using the spatial information within the optimization criterion used to find the synthetic variables. This issue was previously tackled in the context of ecological data by Thioulouse et al. [20], who built on the work of Wartenberg [21] to test the statistical significance of spatial structures in the context of multivariate analyses. The main concept was to introduce the neighboring relationship between sampling units in the analysis. Jombart et al. [22] developed a spatial Principal Component Analysis (sPCA) suitable for genetic allelic frequency data which relied on a modification of PCA such that not only the variance of the synthetic variables, but also their spatial autocorrelation, was optimized. The spatial information is stored inside a spatial weighting matrix which contains positive terms corresponding to some measurement (often binary) of spatial proximity among entities. Such terms can be derived from a connection network, or a neighboring graph, which is created by connecting the neighboring observations on a map [23]. For example, the Delaunay neighboring graph [24] is suited to evenly distributed observations, but may also connect unrelated peripheral observations, whereas the Gabriel neighboring graph [25] is a subset of the Delaunay graph without peripheral connections. In sPCA this spatial weighing, matrix is used to compute the spatial autocorrelation using the Moran’s index statistic. The optimization criterion defined in the sPCA allows us to take into account both the spatial structure and the variability of the data. The eigenvalues provided by the sPCA are highly positive when the synthetic variables have a large variance and exhibit positive autocorrelation; and conversely, sPCA eigenvalues are largely negative when the spatial principal components have a high variance and display negative autocorrelation.
In this work, we attempt to clarify the use of PCA to tackle the study of spatial genetic patterns from molecular marker data. To achieve this, we compare the results of the application of PCA and sPCA on microsatellite data in the study of the SGS of a tree species. We also propose a PC-sPC scatter plot of allele loadings to better understand the allele contributions to spatial genetic variability. The value of the simultaneous use of both types of principal component analysis is demonstrated for a hybrid swarm between Prosopis chilensis and P. flexuosa, two arboreal species with economic and ecological importance in Argentina.
2. METHODS
2.1. Data
The data [26] contains the genetic characterization of geo-referenced trees (observations) of a hybrid swarm between Prosopis chilensis and Prosopis flexuosa. The study was carried out in a 4700 m2 plot included in a continuous forest located in the Natural Reserve Chancaní, in Córdoba, Argentina (Lat. 31˚23'S, Long. 65˚27'W). In the study plot, a total of 87 flowering Prosopis trees (adult population) were identified as P. flexuosa, P. chilensis or hybrid using a taxonomic key based on quantitative characters [27]. The position of each tree in the plot was measured in the field using polar coordinates (distances and angles) and then converted to Cartesian coordinates. Genetic structure and variation was characterized in the adult population using six polymorphic microsatellites (SSR) originally developed for P. chilensis [28]. The total number of alleles found over all individuals was 72 and the number of alleles per locus ranged from 3 to 16. Allelic frequencies were calculated and centered by subtracting the mean allele frequency from all observations. Therefore, all analyses were performed on an 87 × 72 data matrix, corresponding to the 87 trees and 72 alleles.
2.2. Univariate Analysis
To better interpret the multivariate output, we evaluated the variance and the spatial autocorrelation of each allele independently. To estimate autocorrelation, we first built two spatial weighting matrices, one using Gabriel neighboring graph and the other using Delaunay’s triangulation, with the choose CN function of adegenet [29] library in R software [30]. The number of neighbors for each individual obtained with both methods were compared through their frequency distribution. Each allele’s spatial autocorrelation was estimated with the Moran Index and both spatial weighing matrices, using the function moran.test of spdep library [31] in R software. Finally, we plotted the Moran Index of each allele against its corresponding variance. On this plot we identified the four alleles with higher variances and the four alleles with more autocorrelation. We focused our analysis on the spatial structures with positive autocorrelation.
2.3. Application of PCA and sPCA
Both PCA and sPCA were performed on the 87 × 72 allele frequency data matrix using R software. For PCA the dudi.pca function in ade4 library [32] was applied and sPCA was run with the spca function in the adegenet library using Gabriel’s Graph connection network. A number of components which explain a relevant amount of genetic variance were analyzed. To select the number of components we considered not only the variance they explained but also its distribution among eigenvalues in a screeplot. Additionally, biplots for both analyses were obtained with InfoStat software [33]. In the biplots the individuals were identified as P. chilensis, P. flexuosa or hybrid.
2.4. Comparison Criteria
The results obtained with both PCA and sPCA were compared by three criteria. First we contrasted the variance and spatial autocorrelation explained by the Principal Components (PC) and the spatial Principal Components (sPC). For this purpose we calculated the autocorrelation of the PCs and sPCs with the Moran Index using the spatial weighing matrix obtained by Gabriel Graph with the moran.test function of spdep library of R software. The Moran Index of each PC and each sPC against their corresponding variance were plotted. On this plot we identified the PCs and sPCs with the highest variances and autocorrelation. Secondly, we compared the maps of genetic variability built with the first synthetic variables yielded by both methods. To achieve this we plotted the PC1 and sPC1 scores of each tree positioned by its spatial coordinates. In this map the different sizes of the used symbols (squares) represent different absolute values of the synthetic variables: trees with large black squares are well differentiated from trees with large white squares and observations represented with small squares are less differentiated among them. This type of map was performed using the s.value function in ade 4. We also generated a surface using a local interpolation of principal component scores (function s.image in library ade 4), using grey levels and contour lines. The closer the contour lines are from each other, the steepest the genetic differentiation is. Finally, we compared the allele’s contribution to the PCA and sPCA axes. To achieve this we proposed to build a PC-sPC scatter plot of the allele loadings of both synthetic variables and identify those alleles with high inertia in one axis (e.g. PC) and low inertia in the other (e.g. sPC).
3. RESULTS AND DISCUSSION
3.1. Univariate Analysis
The connection networks used to calculate the Moran Index of each allele (CN) are shown in Figure 1. With the Delaunay CN the total number of connections was 492, with an average number of 5.6 neighbors per individual, higher than with the Gabriel’s CN, which rendered an average of 3.5 links per individual and a total of 310 connections. The most connected individual in the Delaunay CN had 9 neighbors and all individuals had 3 or more neighbors, whereas with the Gabriel CN, two individuals had the maximum number of links, which was 7 and 17 individuals had less than 3 neighbors. As shown in Figure 1 the most frequent number of links was 5 for Delaunay CN and 4 with Gabriel CN. The frequency distributions suggest that a higher number of neighbors per individual will be used to estimate spatial autocorrelation with Delaunay Triangulation than with Gabriel Graph.
Among the 72 alleles, only four explained more than 6% of total variance each (Figure 2). These were L1.3, L5.10, L1.2 and L4.03, which together explained 25% of total variance. Among these alleles, L4.03 showed the highest spatial autocorrelation, with a Moran’s I of 0.081. In general, spatial autocorrelation was higher when calculated with Gabriel CN. Nevertheless, the four alleles with the highest positive autocorrelation are the same using both connection networks. The allele with highest Moran Index was L5.04 with a Moran I of 0.25 or 0.1 if calculated with Gabriel CN or Delaunay CN, respectively. Alleles L6.05, L5.05 and L3.04 also showed relatively high Moran Indexes. The alleles with more spatial autocorrelation did not account for high proportions of the total variance (5.6%).
As Figure 1 shows, many peripherical connections are included with Delaunay CN, connecting individuals which may not be actual neighbors in space. When there is information regarding the actual connectivity among the biological entities, such information should be used to choose or build a connection network. For example, in some data sets it might be better to adapt the connection network manually in order to exclude contacts across geographical barriers or to include long-range contacts which for biological reasons might have genetic exchange. When this information is not available, an algorithm has to be used to build it [23]. The R software provides many tools to perform this task though they are spread through different packages. For our case study we preferred to use the Gabriel CN.
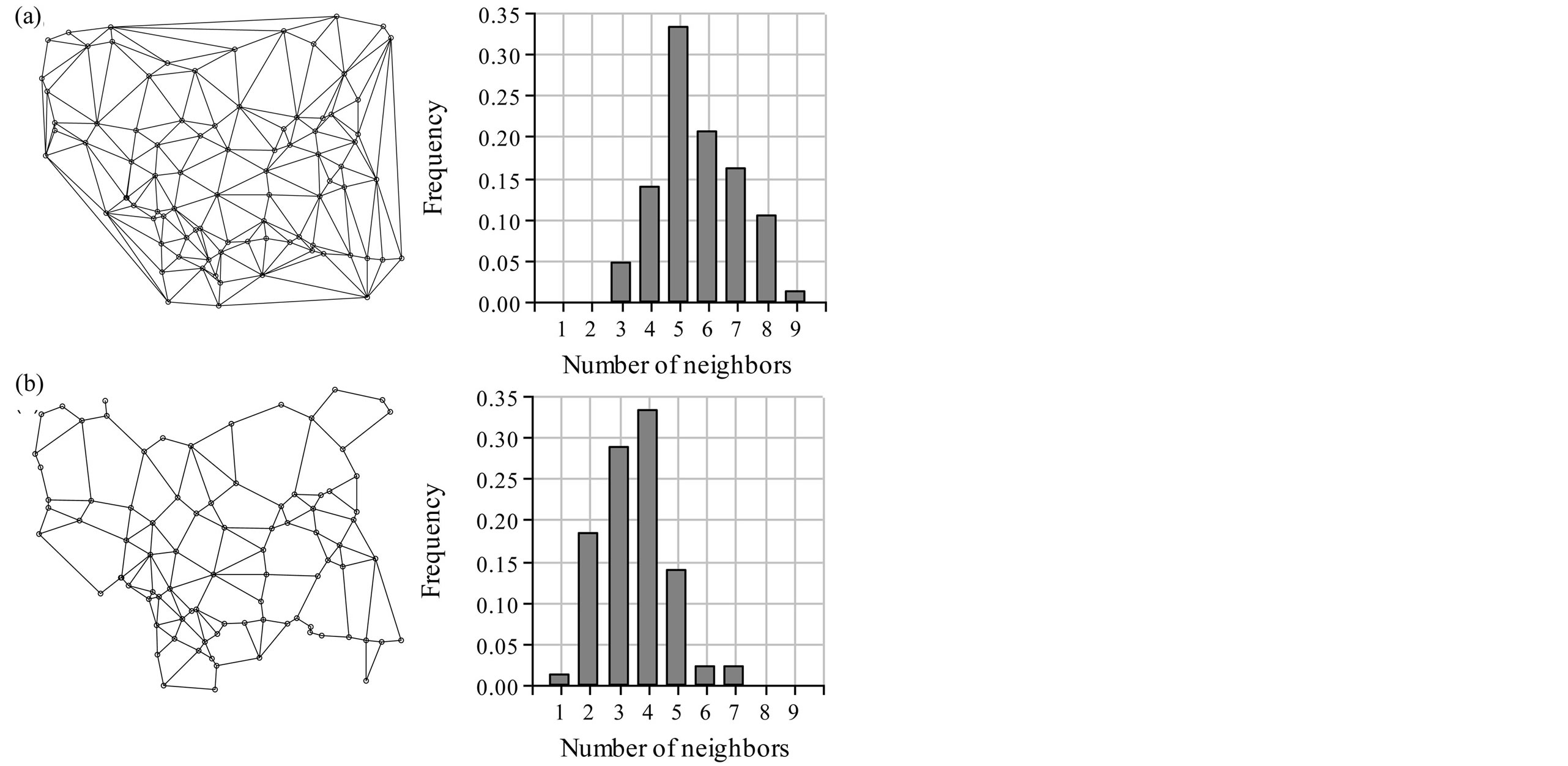
Figure 1. Connection networks for spatial analyses calculated using (a) Delaunay triangulation and (b) Gabriel’s Graph. Bar plots indicate the frequency of individuals with each neighborhood size expressed as number of neighbors.
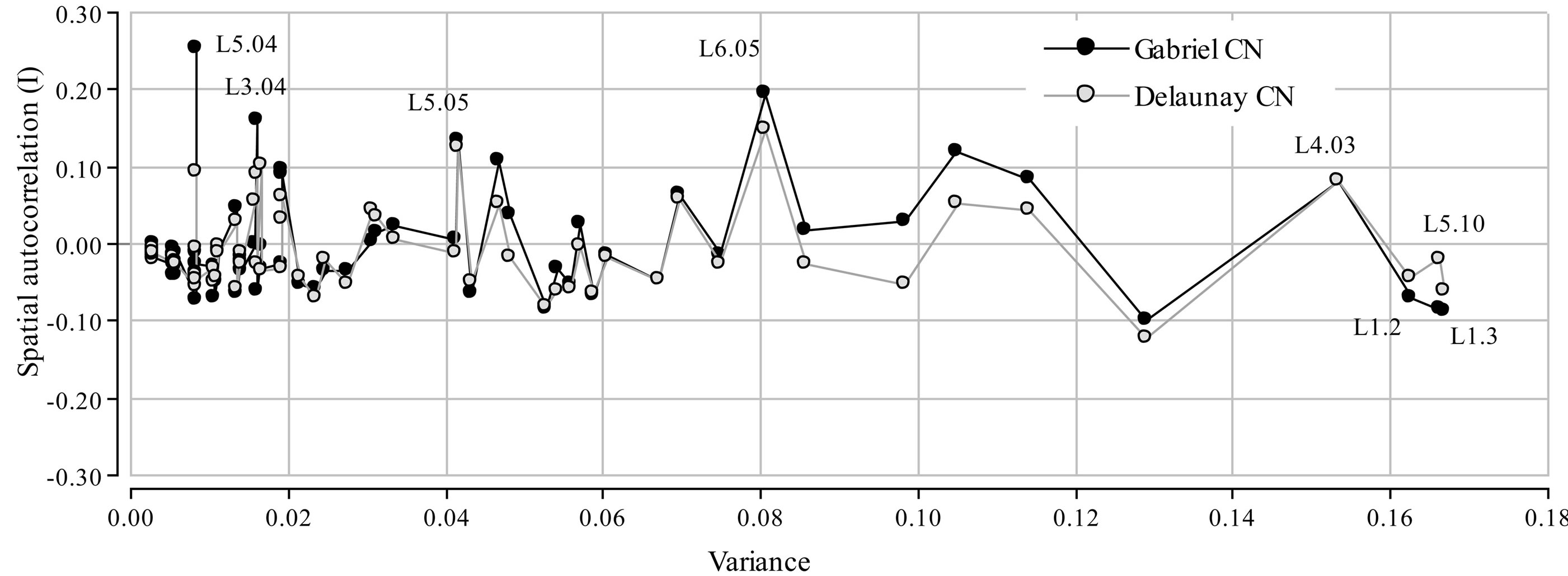
Figure 2. Spatial Moran’s index of each allele plotted against the corresponding variances. Results correspond to the two connection networks: Delaunay triangulation and Gabriel’s Graph.
3.2. Analysis of the Genetic Variability with PCA
The first synthetic variable of PCA (PC 1) had a variance of 0.42 and PC 2 had a variance of 0.36, accounting for 16.1% and 13.7% of the total genetic variability, respectively. With highly dimensional data, such as the provided by molecular markers, which are not necessarily linked among each other, PC1 and PC2 should not be expected to explain a high percentage of the total variance. For example, Novembre et al. [19] analyzed population SGS measured by 500,568 SNP loci on the space generated by a PC1 and a PC2 which explained 0.30% and 0.15%, respectively. However, the SGS of the populations was evident in the synthetic space. In our case study set, in which 72 allele’s frequencies were analyzed, a first plane explaining 29.8% of total genetic variance was regarded as sufficient to explain the main pattern of alleles (co)-variability. In addition, the screeplot (Figure 3(b)) shows a sharp decay between PC2 and PC3, indicating that most of the variance in the data can be explained with the first two synthetic variables. The screeplot is a complementary tool to the axis variances and both should be used to decide the number of synthetic variables to be analyzed. Jombart et al. [11] cites two contrasting studies illustrating the need of using both indicators. In one study [34], the first two PC explaining a high percentage (80%) of total genetic variability of yak (Poephagus grunniens) populations were not as much informative in terms of genetic differentiation as in another study [35] in which they explained 10% of total variability, providing insights about the phylogeny of different maize subspecies. In our study, the analysis was performed using the first two PCs and the difference between species was clearly visible in the biplot.
As showed in the PCA biplot (Figure 3(a)) PC 1 separates P. flexuosa individuals from the hybrids and P. chilensis individuals. These trees show higher allelic frequencies of allele 3 in locus 4 (L4.03) and lower frequencies of allele 5 in locus 10 (L5.10). Alleles 3 and 2 of locus 1 (L1.3 and L1.2) are the alleles with more contribution in PC2 variability, which is not associated with a between species variance. The group with higher within genetic variability was P. flexuosa and these individuals were the most separated on the PC2 axis. As expected, the four alleles identified with higher variances in the univariate analysis (Figure 2) are the four alleles with more contribution in the first two PCA synthetic variables. In the biplot, the length of the arrows representing the alleles is proportional to the amount of genetic variability explained by the allele. Allele frequencies were centered but not scaled, maintaining the inherent variance of the alleles. This approach allows identifying the alleles that contribute most to the total genetic variability even in high dimensional data sets. Centering of allele frequencies is common but their scaling is discussed [36]. Scaling allele frequencies could mask differences in the genetic variability contained by informative and non-informative markers, ultimately hiding structures in the data [11]. Many studies that apply PCA on genetic data represent either the entities in the variables (alleles) space or the alleles in the space spanned by the observations. Here we used the biplot representation of the allele frequencies data which is useful because both the alleles and the trees can be visualized in the same plot. Different types of biplots have been used to graphically represent genetic variability from molecular markers profiles [12,37].

Figure 3. Results obtained by principal component analysis. (a) Biplot of first and second axis of PCA, individuals are colored according to classification in P. chilensis, P. flexuosa and hybrid and segment lines represent the alleles; (b) Screeplot of PCA eigenvalues.
3.3. Analysis of Genetic Variability with sPCA
The first synthetic variable (sPC 1) had a variance of 0.26 accounting for 10% of the total inertia. The first two principal components of sPCA explained 14% of the data structure. Similar levels of total inertia explained by the first two spatial principal components (sPC) were accounted for other genetic studies [22,38]. Analogous to the classical biplot used to represent PCA results, we built a symmetrical biplot from the two sPCs. The sPCA biplot (Figure 4(b)) shows that sPC 1 also allows to separate P. flexuosa individuals from the hybrids and P. chilensis. The sPCA screeplot shows a sharp decay between the first and the second eigenvalue, indicating that the analysis of sPC1 variability may be enough to explain SGS in this Prosopis hybrid swarm. Although sPCA was also applied on centered and not scaled allele frequencies, the lengths of the vectors representing the alleles are similarly distributed. sPCA is related to multivariate spatial correlation [21] but it allows alleles to have different variances. Scaling allele frequency data in sPCA has the same negative effect discussed above for PCA.
The allele with the highest contribution in sPC1 is L4.03 and allele L6.05 is the second allele with a relatively high loading in sPC1. This allele is one of the four alleles with high spatial autocorrelation and from these four, the one with most variance (Figure 2). When sPCA is performed, negative eigenvalues, which account for negative autocorrelation structure, arise. In our study case the highest negative eigenvalue explained less percentage of total variance than the first positive eigenvalue. In addition there is no evidence of a sharp decay between two negative eigenvalues in the sPCA screeplot (Figure 4(b)). For this reason we only analyzed the SGS related to positive autocorrelation.
3.4. Comparison of PCA and sPCA Results
PCA eigenvalues were larger in magnitude and much less spatially autocorrelated (Figure 5). The first two PCs, which account for 16% and 14% of total genetic variance, had no spatial autocorrelation, with low and not statistically significant Moran’s Indexes (I1PCA = 0.05, I2PCA = −0.07, p > 0.05) (Table 1). On the contrary, the variance of the first two sPCs was much lower (10% and 3.8% of total variance) but they had higher and significant Moran Indexes (I1sPCA = 0.29, I2sPCA = −0.39, p < 0.05). The spatial principal component with most positive spatial auto

Table 1. Variance and spatial autocorrelation of the first 2 PCA and sPCA eigenvalues.

Figure 4. Results obtained by spatial principal component analysis (sPCA). (a) Biplot of first and second axis of sPCA, individuals are colored according to classification in P. chilensis, P. flexuosa and hybrids; (b) Screeplot of sPCA eigenvalues.
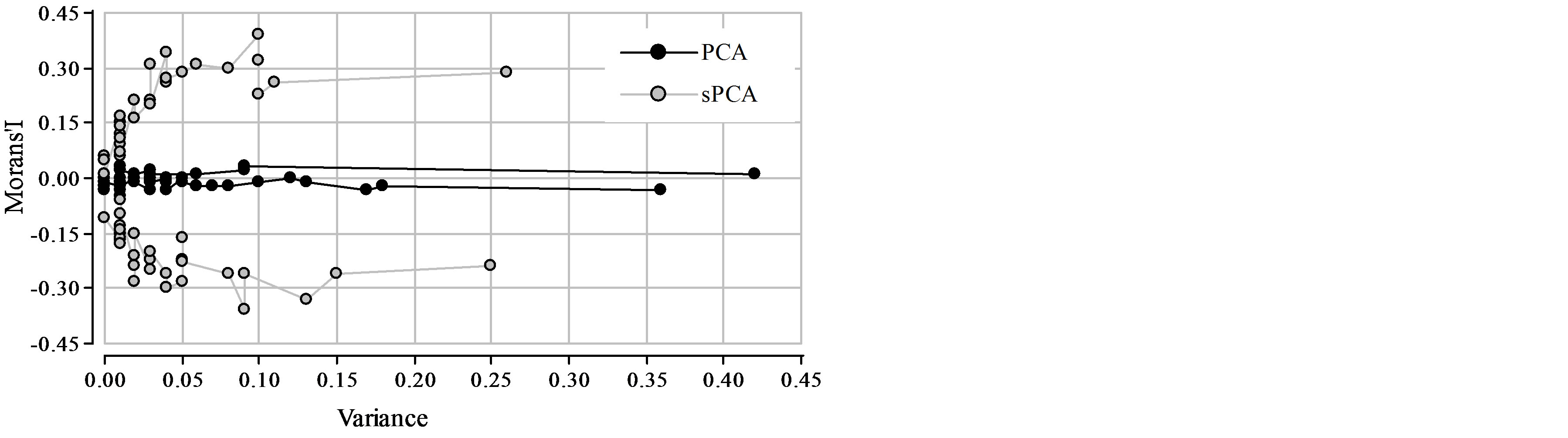
Figure 5. Spatial Moran’s index of sPCA and PCA eigenvalues plotted against the corresponding variances.
correlation was sPC 2 (I2sPCA = 0.39) and the PC with most positive spatial autocorrelation was PC 9 (I9PCA = 0.22). These results show that the first principal components are associated with alleles that explain variance instead of spatial correlation. PCA axes, which spatial autocorrelation was very low, might fail to identify relevant spatial patterns in this Prosopis hybrid zone. On the contrary, sPCA detects additional spatially structured components. As discussed by Jombart et al. [22], the variance associated to the first axis in sPCA was lower than the variance of PC1, however, it captures a spatial pattern associated to the spatially structured genetic differentiation. The relative value of sPCA over PCA depends on the nature of the structure underlying the data. When the spatially genetic variability is not associated to the alleles with higher variability among entities, the relative sPCA value increases. In our study case the alleles with most spatial autocorrelation were not those with highest variances. Therefore sPCs provide new information to the study of SGS. In other cases, when the most spatially structured alleles also have the higher variances, the first sPCs correspond to the first coordinates of the unrestricted PCA [38].
As both principal component analyses suggest, the spatial pattern of genetic variability in this hybrid swarm shows at least two patches of genotypes in space (Figure 6). One patch is constituted by individuals with high positive scores (black) on the principal components and the other with high negative scores (white). In both types of maps the spatial structure is clearer with sPC1 scores than with PC1 scores. In the interpolated maps, contour lines are closer together in the sPC1 map, indicating that the magnitude of the gradient is larger. Therefore, the sPC1 allows a better visualization of a patchy spatial pattern of genetic variability in our study case. As higher scores of sPC1 are associated to hybrids and P. chilensis, the darker patch is associated to them, whereas the lighter patch is associated to P. flexuosa.
Our results are in concordance with the findings of Bessega et al. [39], who studied the genetic structure of P. alba, a very similar species. They conclude that pollen

Figure 6. Spatial analysis of PCA and sPCA results. Scores of the first principal components obtained with PCA (above) and sPCA (below). Left: Each square corresponds to the score of an individual and it is positioned by its spatial coordinates. Right: Map of the scores, values obtained by the interpolation of the principal components.
and seed dispersion is limited, estimating the average pollen dispersal distance to be between 5.36 and 30.92 m. Their findings explain the strong genetic structure of the P. alba population, which was studied through its mating system, but not through the spatial distribution of the genotypes.
To visually identify those alleles that contribute most to the structures captured by the both the PC1 and the sPC1, as well as those alleles that either have a lot of inertia in one axis but not on the other, we built a scatter plot of the allele loadings in PC1 and sPC1 (Figure 7). Statistical validation of identified markers was carried out through comparison of variance and Moran Index between both types of principal components (Table 2). In the PC-sPC scatter plot, three types of areas are identified by different colors. These areas were defined using the mean ± a standard deviation of the allele loadings in a synthetic variable. For all synthetic variables, loadings have a mean of 0 and standard deviation of 0.12 because of the normalization of eigenvectors. The white square in the middle of the PC1-sPC1 scatter plot corresponds to loadings that range between −0.12 and 0.12 in both the sPC1 and the PC1; the alleles that belong to this area do not have much inertia in either the PC1 or the sPC1.
Therefore, these alleles do not contribute much to the SGS. On the contrary, the four light grey squared areas correspond to alleles that have high inertia in both PC1
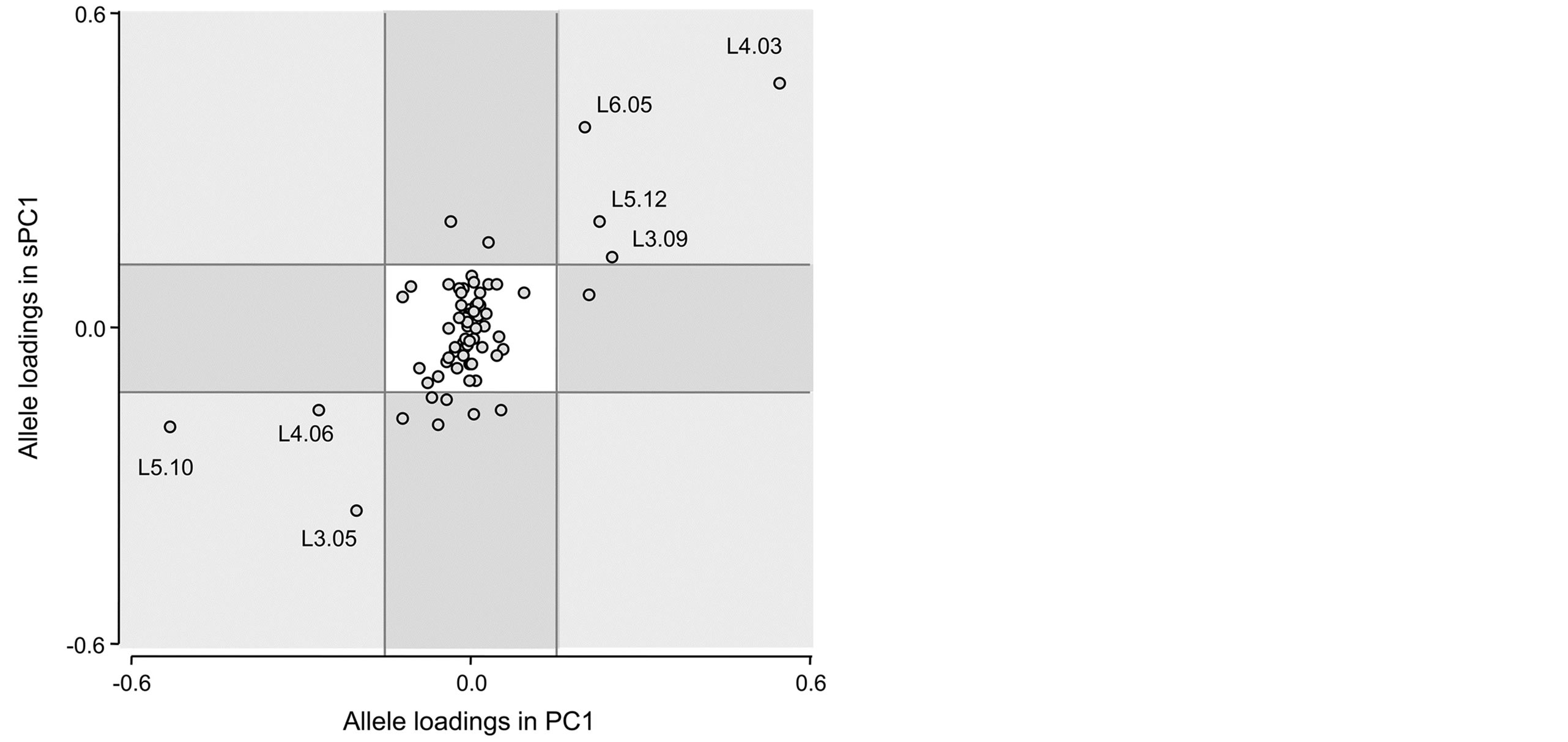
Figure 7. PC-sPC scatter plot: allele loadings of the first sPCA axis vs. PCA axis.
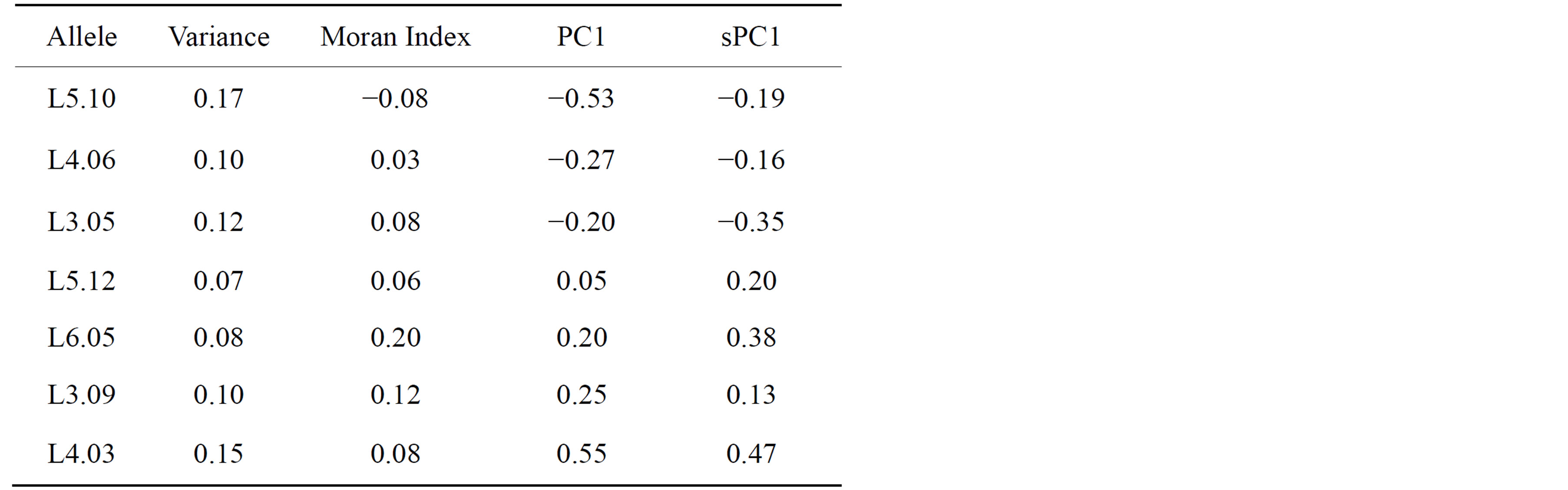
Table 2. Variance, Moran Index and loadings in the first PC and sPC of identified alleles.
and sPC1. These alleles explain variability between species as shown in the biplots (Figures 3 and 4) and their variances were relatively high (Table 2). The four remaining darker areas correspond to alleles with a high contribution in one synthetic variable and a low inertia in the other. The horizontal dark rectangles correspond to alleles with high loadings in PC1 and low loadings in sPC1. Only one allele falls in this category (L5.09). This allele is important in terms of between species variability but is associated to a type of variability that is not spatially structured. The vertical dark grey rectangles correspond to areas of high loadings in sPC1 and low loadings in PC1. In our study eight alleles were found in these areas, corresponding to alleles that do not contribute much to the main axis of genetic differentiation between species but that their variability is spatially structured. However, the interpretation is not simple in these cases, as it is important to consider that high loadings in a sPC are associated to alleles with a relatively high product between their variances and their spatial autocorrelation.
The sPCA biplot (Figure 4(a)) shows that allele’s loadings have a more uniform distribution than in PCA. This fact is probably associated with the lower variability of the product between allele’s variance and Moran Index than the variability of allele’s variances, which are the optimization criteria of sPCA and PCA, respectively. The cut-off values of 0.12 and −0.12 which were used as selection criterion for groups of contributing allele markers will have effects on the outcome of the biological results. In other words different cutoffs can render different biological results. Therefore the whole process was performed with several others cut-offs on the first 2 PCs. This analysis showed that the cut-off based on one standard deviation of allele loadings highlighted markers which have either high variance and/or high autocorrelation (data not shown).
Our results show that to effectively understand the relative contribution of alleles to spatial genetic structure, the joint application of both principal component analyses is useful. However, the results shown before were obtained by applying the combination of PCA and sPCA on all available markers. To explore the results of both PCA and sPCA when performed on the selected subset of markers we applied both methods on the 16 alleles outside the white square of the PC1-sPC1 scatter plot. As expected, the results show that the main pattern of species differentiation was no different from the overall effects present in the whole dataset. This is another way to validate the interpretation of the allele contributions in the PC-sPC scatter plot.
Both techniques, PCA and sPCA, have been applied in studies of the SGS of animals, such as the Scandinavian brown bear (Ursus arctus) and domestic ruminants in Europe [22,38]. As compared to most animal species, adults from plant species do not move and plants’ propagules, i.e. pollen and seeds, often show moderate to strong spatial restriction in their dispersal leading to strong SGS. In particular, the study of these structures in forests provides vital information for their conservation and management. This is of utmost importance in Argentina, where 70% of forest cover has been lost and forest emergency has recently been declared (National Law 26.331). Among other native tree species, the genus Prosopis constitute a very important natural resource for dry zones that need strong conservation actions [40]. Although the genus Prosopis presents no difficulty of identification, individual species are in some cases difficult to determine due to the occurrence of many natural hybrid combinations within the genus [41-43]. Because frequent events of interspecific natural hybridization with fertile hybrid production in areas of sympatry occur, isolation mechanisms between Prosopis species seem to be weak or incomplete [26,44]. Natural interspecific hybridization has been recognized as playing an important role in plant evolution and hybrid zones are viewed as active sites of evolutionary change that constitute sources of new recombinant types [45-47]. Hybrid zones are characterized by a continuous variation in morphological and genetic traits and the loss of differentiation of pure species. Therefore, cryptic and continuous patterns of spatial genetic variability are expected even at small spatial scales, which might be difficult to identify and characterize. In this case, recovery plans and management of forests can particularly benefit from the joint use of both type of principal component analysis of spatial molecular marker data. They provide a useful insight into the problem of selecting founding populations and particularly, in selecting individuals within populations, where sometimes the spatial genetic structure is overlooked. Spatial analysis techniques provide a suitable framework to integrate the knowledge derived from genetic, demographic and ecological approaches to species conservation, allowing the formulation of management strategies that take into account different considerations.
4. CONCLUSION
After the application of PCA and sPCA and visual inspection of the allele contribution to both types of synthetic variables, interesting markers to investigate genetic spatial structure can be selected. The combination of PCA and sPCA, as demonstrated here, is a valuable tool in forests molecular marker data analysis because more information is available on the allele contributions to the spatial genetic structure. The PC-sPC scatter plot can be used to split and visualize the different components of genetic variability yielded by molecular markers. Considering the spatial genetic structure of the studied Prosopis sp. hybrid swarm, two groups of tree genotypes (corresponding to different Prosopis species) were distinguished at a small spatial scale. The patchy spatial pattern observed could be explained by the existence of a patchy spatial structure of available safe sites for the establishment of the different genotypes and by limited gene dispersal.
ACKNOWLEDGEMENTS
We thank Martin Mottura for providing the Prosopis sp. data set. I.T. is a recipient of a postdoctoral fellowship of the National Council of Technical and Scientific Research (CONICET), respectively.
REFERENCES
- Keitt, T.H., Bjørnstad, O.N., Dixon, P.M. and CitronPousty, S. (2002) Accounting for spatial pattern when modeling organism-environment interactions. Ecography, 25, 616-625. http://dx.doi.org/10.1034/j.1600-0587.2002.250509.x
- Vucetich, J. and Waite, T. (2003) Spatial patterns of demography and genetic processes across the species’ range: Null hypotheses for landscape conservation genetics. Conservation Genetics, 4, 639-645. http://dx.doi.org/10.1023/A:1025671831349
- Vekemans, X. and Hardy, O.J. (2004) New insights from fine-scale spatial genetic structure analyses in plant populations. Molecular Ecology, 13, 921-935. http://dx.doi.org/10.1046/j.1365-294X.2004.02076.x
- Wright, S. (1943) Isolation by distance. Genetics, 28, 114-138.
- Wright, S. (1946) Isolation by distance under diverse systems of mating. Genetics, 31, 39-59.
- Epperson, B.K. (1993) Spatial and space-time correlations in systems of subpopulations with genetic drift and migration. Genetics, 133, 711-727.
- Mantel, N. (1967) The detection of disease clustering and a generalized regression approach. Cancer Research, 27, 209-220.
- Moran, P.A.P. (1950) Notes on continuous stochastic phenomena. Biometrika, 37, 17-23.
- Smouse, P.E. and Peakall, R. (1999) Spatial autocorrelation analysis of individual multiallele and multilocus genetic structure. Heredity (Edinb), 82, 561-573. http://dx.doi.org/10.1038/sj.hdy.6885180
- Cavalli-Sforza, L.L. (1966) Population structure and human evolution. Proceedings of the Royal Society of London. Series B, Biological Sciences, 164, 362-379. http://dx.doi.org/10.1098/rspb.1966.0038
- Jombart, T., Pontier, D. and Dufour, A.B. (2009) Genetic markers in the playground of multivariate analysis. Heredity (Edinb), 102, 330-341.
- Balzarini, M., Teich, I., Bruno, C. and Peña, A. (2011) Making genetic biodiversity measurable: A review of statistical multivariate methods to study variability at gene level. Revista de la Facultad de Ciencias Agrarias de la Universidad Nacional de Cuyo, 43, 261-275.
- Wang, C., Zöllner, S. and Rosenberg, N.A. (2012) A quantitative comparison of the similarity between genes and geography in worldwide human populations. PLoS Genetics, 8, e1002886. http://dx.doi.org/10.1371/journal.pgen.1002886
- Hotelling, H. (1933) Analysis of a complex of statistical variables into principal components. Journal of Educational Psychology, 24, 417-441. http://dx.doi.org/10.1037/h0071325
- Manel, S., Joost, S., Epperson, B.K., Holderegger, R., Storfer, A., Rosenberg, M.S., et al. (2010) Perspectives on the use of landscape genetics to detect genetic adaptive variation in the field. Molecular Ecology, 19, 3760- 3772. http://dx.doi.org/10.1111/j.1365-294X.2010.04717.x
- Manel, S., Schwartz, M.K., Luikart, G. and Taberlet, P. (2003) Landscape genetics: Combining landscape ecology and population genetics. Trends in Ecology & Evolution, 18, 189-197. http://dx.doi.org/10.1016/S0169-5347(03)00008-9
- Manel, S. and Segelbacher, G. (2009) Perspectives and challenges in landscape genetics. Molecular Ecology, 19, 1821-1822. http://dx.doi.org/10.1111/j.1365-294X.2009.04151.x
- Storfer, A., Murphy, M.A., Evans, J.S., Goldberg, C.S., Robinson, S., Spear, S.F., et al. (2007) Putting the “landscape” in landscape genetics. Heredity (Edinb), 98, 128- 142. http://dx.doi.org/10.1038/sj.hdy.6800917
- Novembre, J., Johnson, T., Bryc, K., Kutalik, Z., Boyko, A.R., Auton, A., et al. (2008) Genes mirror geography within Europe. Nature, 456, 98-101. http://dx.doi.org/10.1038/nature07331
- Thioulouse, J., Chessel, D. and Champely, S. (1995) Multivariate analysis of spatial patterns: A unified approach to local and global structures. Environmental and Ecological Statistics, 2, 1-14. http://dx.doi.org/10.1007/BF00452928
- Wartenberg, D. (1985) Multivariate spatial correlation: A method for exploratory geographical analysis. Geographical Analysis, 17, 263-283. http://dx.doi.org/10.1111/j.1538-4632.1985.tb00849.x
- Jombart, T., Devillard, S., Dufour, A.B. and Pontier, D. (2008) Revealing cryptic spatial patterns in genetic variability by a new multivariate method. Heredity (Edinb), 101, 92-103. http://dx.doi.org/10.1038/hdy.2008.34
- Legendre, P. and Legendre, L. (1998) Numerical ecology. Elsevier Science B.V., Amsterdam.
- Upton, G.J.G. and Fingleton, B. (1985) Spatial data analysis by example. Wiley, Chichester/New York.
- Gabriel, K.R. and Sokal, R.R. (1969) A new statistical approach to geographic variation analysis. Systematic Biology, 18, 259-278.
- Mottura, M.C. (2006) Development of microsatellites in Prosopis spp. and their application to study the reproduction system. Library of Lower Saxony State and GeorgAugust University of Göttingen, Göttingen.
- Verga, A. (2000) Clave para la identificación de híbridos entre Prosopis chilensis y P. flexuosa sobre la base de carcateres cuantitativos. Multequina, 9, 17-22.
- Mottura, M.C., Finkeldey, R., Verga, A.R. and Gailing, O. (2005) Development and characterization of microsatellite markers for Prosopis chilensis and Prosopis flexuosa and cross-species amplification. Molecular Ecology Notes, 5, 487-489. http://dx.doi.org/10.1111/j.1471-8286.2005.00965.x
- Jombart, T. (2008) Adegenet: A R package for the multivariate analysis of genetic markers. Bioinformatics, 24, 1403-1405. http://dx.doi.org/10.1093/bioinformatics/btn129
- R Development Core Team, R. (2011) R: A language and environment for statistical computing. Vienna, Austria.
- Bivand, R., Altman, M., Anselin, L., Assunção, R., Berke, O., Bernat, A., et al. (2011) Spdep: Spatial dependence: weighting schemes, statistics and models. R package version 0.5-31.
- Dray, S. and Dufour, A.B. (2007) The ade4 package: Implementing the duality diagram for ecologists. Journal of Statistical Software, 22, 1-20.
- Di Rienzo, J.A., Casanoves, F., Balzarini, M.G., Gonzalez, L., Tablada, M. and Robledo, C.W. (2011) InfoStat.
- Xuebin, Q., Jianlin, H., Lkhagva, B., Chekarova, I., Badamdorj, D., Rege, J.E.O., et al. (2005) Genetic diversity and differentiation of Mongolian and Russian yak populations. Journal of Animal Breeding and Genetics, 122, 117-126. http://dx.doi.org/10.1111/j.1439-0388.2004.00497.x
- Matsuoka, Y., Vigouroux, Y., Goodman, M.M., Sanchez G., J., Buckler, E. and Doebley, J. (2002) A single domestication for maize shown by multilocus microsatellite genotyping. Proceedings of the National Academy of Sciences, 99, 6080-6084.
- Weir, B.S. (1996) Genetic data analysis II: Methods for discrete population genetic data. Sinauer Associates, Sunderland.
- Demey, J.R., Vicente-Villardón, J.L., Galindo-Villardón, M.P. and Zambrano, A.Y. (2008) Identifying molecular markers associated with classification of genotypes by External Logistic Biplots. Bioinformatics, 24, 2832-2838. http://dx.doi.org/10.1093/bioinformatics/btn552
- Laloë, D., Moazami-Goudarzi, K., Lenstra, J.A., Marsan, P.A., Azor, P., Baumung, R., et al. (2010) Spatial trends of genetic variation of domestic ruminants in Europe. Diversity, 2, 932-945. http://dx.doi.org/10.3390/d2060932
- Bessega, C., Pometti, C.L., Ewens, M., Saidman, B.O. and Vilardi, J.C. (2012) Strategies for conservation for disturbed Prosopis alba (Leguminosae, Mimosoidae) forests based on mating system and pollen dispersal parameters. Tree Genetics & Genomes, 8, 277-288. http://dx.doi.org/10.1007/s11295-011-0439-6
- Pasiecznik, N.M., Felker, P., Harris, P.J.C., Harsh, L.N., Cruz, G., Tewari, J.C., et al. (2001) The Prosopis juliflora-Prosopis pallida complex: A monograph. HDRA, Coventry.
- Palacios, R. (1998) Taxonomía numérica (Descriptores). Prosopis en la Argentina. Facultad de Ciencias Agrarias, Universidad Nacional de Córdoba, Argentina, 91-96.
- Saidman, B.O., Bessega, C.F., Ferreira, L.I., Julio, N. and Vilardi, J. (2000) The use of genetic markers to assess population structure and relationships among species of the genus Prosopis (Leguminosae). Boletín de la Sociedad Argentina de Botánica, 35, 315-324.
- Ferreyra, L., Vilardi, J., Verga, A., López, V. and Saidman, B. (2013) Genetic and morphometric markers are able to differentiate three morphotypes belonging to Section Algarobia of genus Prosopis (Leguminosae, Mimosoideae). Plant Systematics and Evolution, 299, 1157- 1173. http://dx.doi.org/10.1007/s00606-013-0786-x
- Verga, A.R. (1995) Genetische untersuchungen an Prosopis chilensis und P. flexuosa (Mimosaceae) im trockenen Chaco Argentiniens. Göttingen Research Notes in Forest Genetics. Abteilung für Forstgenetik und Forstpflanzenzüchtung der Universität Göttingen, 19, 1-96.
- Harrison, R.G. (1990) Hybrid zones: Windows on evolutionary process. Oxford Surveys in Evolutionary Biology, 7, 59.
- Barton, N.H. (2001) The role of hybridization in evolution. Molecular Ecology, 10, 551-568. http://dx.doi.org/10.1046/j.1365-294x.2001.01216.x
- Soltis, P.S. and Soltis, D.E. (2009) The role of hybridization in plant speciation. Annual Review of Plant Biology, 60, 561-588. http://dx.doi.org/10.1146/annurev.arplant.043008.092039

