Received 30 April 2015; accepted 5 June 2015; published 8 June 2015

ABSTRACT

The paper deals with the optimal proportional reinsurance in a collective risk theory model involving two classes of insurance business. These classes are dependent through the number of claims. The objective of the insurer is to choose an optimal reinsurance strategy that maximizes the expected exponential utility of terminal wealth. We are able to derive the evolution of the insurer surplus process under the assumption that the number of claims of the two classes of the insurance business has a Poisson bivariate distribution. We face the problem of finding the optimal strategy using the dynamic programming approach. Therefore, we determine the infinitesimal generator for the surplus process and for the value function, and we give the Hamilton Jacobi Bellmann (HJB) equation. Under particular assumptions, we obtain explicit form of the optimal reinsurance strategy on correspondent value function.

Keywords:

Collective Risk Theory, Optimal Proportional Reinsurance, Dynamic Programming

1. Introduction

The classical Cramer-Lundberg risk model assumes that the stochastic process 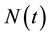denotes the number of claims up to time t and the random variables X_j, the claim size of the j-th claim. In this model, 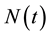is independent of the claim sizes and the claim sizes are independent and identically distributed; however, this assumption is too restrictive at times. Several authors have proposed models with dependence between the risks. Among the various types of dependence models proposed, in this paper we refer to the case where the dependency is obtained assuming that the insurer has 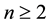correlated classes of insurance business, where is the number of claims of the i-th class;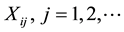, is the claim sizes of the j-th claim of the i-th class and the numbers 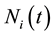are dependent claim count processes. Models of this type are proposed in [1] -[6] . In [3] [4] , a risk model involving two dependent classes of insurance business is considered in a given period of time and the expected utility of the insurer wealth is maximized by the determination of optimal retention limits of Unlimited or Limited Excess of Loss reinsurance.

In this paper, we consider an optimal proportional reinsurance problem of an insurer whose surplus process is generated by two dependent classes of insurance business. The objective is to choose an optimal reinsurance strategy; in order to maximize the insurer’s expected exponential utility of terminal wealth we use the dynamic programming approach.

The paper is organized as follows. In Section 2, we present the risk model. In Section 3, we find the surplus evolution and the conditional expected utility of the insurer’s terminal surplus, define the problem and give the corresponding value function. In Section 4, using the infinitesimal generator, we derive the HJB equation and justify the form of the value function. Finally, in Section 5, we discuss the solution giving an explicit solution in a particular framework.

2. The Model

In the finite time horizon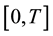, , 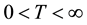we consider a model that involves two risks that may represent two classes of insurance business dependent through the number of claims. Let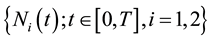, are the arrival processes of the respective claims. We denote by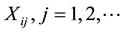, the random variable claim size of the risk i, i = 1, 2, assuming that these random variables have respectively the same distribution function F_i, with 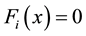for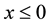, and mean values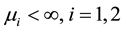. Moreover, we assume that the moment generating function of the random variables 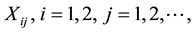exists. Finally, we assume that the random variables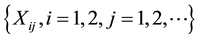, are mutually independent, and independent of. We denote by, , the aggregate claims amounts of the risk i, i = 1, 2. We assume that the processes, are Poisson processes defined as follows:

(1)

where are Poisson random variables that are mutually independent having positive mean, in the time unit, respectively. It follows that has a Poisson bivariate distribution and that and are correlated by; in fact, it results:

(2)

In the following, we will use the variables X_i, i = 1, 2, identically distributed to

We denote by c, i = 1, 2 the premium rate, for the time unit, assuming that the premium calculation principle is the expected value principle with loading coefficient, that is:

(3)

We introduce a proportional reinsurance: the reinsurer pays, , of each claim of the type i, i = 1, 2 and he receives from the insurer the reinsurance premium. We denote by, i = 1, 2, the reinsurance premium and we get

for which it is

(4)

Note that the condition linked to the positivity of the security loading is not assumed, as it may or may not be satisfied.

3. The Problem

We denote by the proportion insured at time t, , where is therefore the risk exposure of insurer at time t. We assume that, at every time t, , the insurer can choose the risk exposure, according to the observable information about the insurance risk processes up to time t. There- fore, i = 1, 2, are the insurer’s control parameters; let be the set of all admissible policies. The objective for the insurer is to choose an optimal reinsurance strategy that maximize the expected exponential utility of terminal wealth. We will make use of the HJB theory to face the problem. After the reinsurance the total claim amount charged to the insurer is

(5)

We denote by the surplus process of the insurer adopting the reinsurance strategy process. The surplus evolves over time as:

(6)

We recall that and are defined by (1), then the process has a bivariate Poisson distribution. This fact, noting that the process has stationary increments (see [7] ) and using results in [8] , allows us to determine the following joint probabilities:

From previous result it follows

(7)

where X_i are identically distributed to X_ij,.

We consider an utility function, , strictly increasing and concave (that is and). For each control strategy, , given, , we define the following conditional expected utility of the insurer’s terminal surplus:

(8)

As previously stated, the insurer’s goal is to determine an optimal reinsurance strategy so as to maximize the expected utility of the terminal surplus (8). We therefore consider the following problem

(9)

It follows that the insurer has to find the optimal strategy and the corresponding value function such that:

(10)

with the usual boundary condition (see [9] [10] )

(11)

4. The HJB Equation and the Value Function

We can find the infinitesimal generator for the process and for the function V. The procedure is similar to that one used in [11] and in [12] .

Theorem 1. Let be defined by (9) and (10) and let. Therefore, V satisfies the following HJB equation:

(12)

Proof. We derive the following infinitesimal generator for the process and for the function V:

(13)

it allows us to write the HJB Equation (12).

We recall that, by (6) and (7) it results in

therefore we have, remembering the independence between X_i and N_i, i = 1, 2:

Therefore V must satisfy Equation (12). ■

We introduce the following utility function

(14)

With the purpose to write (9) we observe that:

1) from (6) and remembering that Poisson processes have stationary increments, we obtain:

(15)

with, as previously stated,;

2) in Section 2 we have assumed that the moment generating functions of random variables, , and therefore of random variables, exist.

We denote those functions by, and we observe that;

3) according to [7] and from the probability generating function of the bivariate Poisson distribution (see [8] , p. 126), it results in:

(16)

4) from the previous considerations, we have:

(17)

Because of these considerations, we assume that the value function V, defined by (10) with the condition (11) has the form

(18)

with the condition

(19)

5. Possible Solutions

We consider the assumptions (18); it results in:

Therefore, (12) becomes

with; hence, remembering that, it results in:

(20)

with.

Assuming the particular case where the insurer’s risk exposure is the same for the two classes of the insurance business; that is the control parameter is (resulting in), and (20) becomes:

(21)

with. The problem of the determination of the optimal control can be easily solved, as we will see in the following.

For simplicity, we write (21) as follows

observing that

(22)

from which we obtain:

1) by (3) and (4), from which we deduce that is an increasing function in and therefore;

2)

;

3)

From the previous results it follows that is equal to zero in a single point and:

if and therefore;

if and therefore;

if and therefore

being

(23)

We therefore obtain the following results.

If it results in and by (21) we have:

with, from which we obtain

(24)

then the resulting value function (18) is:

If it results in such that. Therefore, remembering (22), it results in

(25)

and by (21):

with. From the previous, with a procedure analogous to that followed in the case, it is possible to find and the resulting value function.

Acknowledgements

We thank the Editor and the Referees for their comments.

References