Modern Economy
Vol.4 No.9A(2013), Article ID:35999,7 pages DOI:10.4236/me.2013.49A002
Irrelevance of Conjectural Variation in a Private Duopoly with Consistent Conjectures: The Relative Performance Approach and Network Effects*
College of Economics, Nihon University, Tokyo, Japan
Email: yasuhiko.r.nakamura@gmail.com
Copyright © 2013 Yasuhiko Nakamura. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received July 16, 2013; revised August 10, 2013; accepted August 16, 2013
Keywords: Relative Profit Maximization; Conjectural Variation; Consistent Conjecture; Network Effects
ABSTRACT
This paper explores the equilibrium market outcomes in the contexts of both quantity-setting and price-setting private duopolies with the consistent conjectures of two private firms, wherein they maximize the weighted sum of their own profits and their respective opponent firm’s profit. Similar to the private duopoly without network effects wherein the two private firms maximize their genuine relative profits, in the private duopoly with network effects such that both firms maximize the weighted sum of their own profits and their respective opponent firm’s profit, we show that the equilibrium outcomes in the quantity-setting competition with the consistent conjectures of both firms are equivalent to those in the price-setting competition with the consistent conjectures of both firms.
1. Introduction
This paper tackles the problem of whether or not the consistent conjectures of two relative profit maximizing private firms yield the same equilibrium outcomes between a quantity-setting competition and a price-setting competition in the context of a private duopolistic market with differentiated and substitutable goods and with network effects. Conjectural variations in oligopolistic markets have been investigated for a long time. For example, Bresnahan [1], Perry [2], Boyer and Moreaux [3], Tanaka [4], and Tanaka [5] considered the effects of the conjectural variations of firms on equilibrium market outcomes in several economic contexts1. More recently, in private duopoly with the linear demand function and constant marginal cost functions composed of two symmetric private firms, Tanaka [6] showed that their equilibrium output and price levels in the Cournot equilibrium under their relative profit maximization are equal to those in the Bertrand equilibrium under their relative profit maximization2.
As indicated in Matsumura et al. [8], the performances of firms’ managers are often based on their relative performance and outperforming managers often obtain good positions in the management job markets. Taking the importance of the relative performance approaches into account, the relative profit approaches employed in this paper have been adopted in the modern many theoretical oligopolistic works. In the context of evolutionary economics à la Schaffer [9], Vega-Redondo [10] found that each firm’s adoption of its relative profit maximizing behavior yields the Walrasian equilibrium in the general equilibrium framework. Furthermore, Lundgren [11] presented a new economic method for preventing incentives for collusion by making managerial compensation which depends on relative profits rather than absolute profits. Kockesen et al. [12] derived the condition that the firm with interdependent preferences (i.e., the relative profit preference) obtains a strictly higher profit than the independent (i.e., the absolute profit preference) firm in any equilibrium. Moreover, Matsumura and Matsushima [13] investigated the relationship between the degree of competition and the stability of collusive behavior by introducing the element of relative performance into the objective functions of the firms and showed that an increase in the degree of competition destabilizes collusion.
In this paper, we consider the equilibrium market outcomes between the quantity-setting competition and the price-setting competition in a private duopoly with network effects by adopting the maximization of the weighted sum of their own profit and the profit of their respective opponent firm including the case of their genuine relative profit maximization (the “extended” relative profit). The network effects that we consider in this paper were introduced in Katz and Shapiro [14] and applied in Hoernig [15], Nakamura [16], and Nakamura [17]. These effects reflected a simple mechanism where the surplus obtained by a firm’s client increases directly with the number of other clients of this firm. Then, taking into account the network effects and the maximization of the extended relative profit of the private firms, in this paper, we confirm the robustness of the result on the coincidence of the equilibrium market outcomes in the contexts of both the quantity-setting competition and price-setting competition in the private duopoly.
Except for the question of whether or not there exists the presence of network effects à la Katz and Shapiro [14], the difference between the settings of Tanaka [6] and Tanaka [7] and this paper is whether or not to allow the private firm to maximize the weighted sum of its own profit and its opponent firm’s profit. Tanaka [6] and Tanaka [7] considered the situation wherein the private firm maximizes the genuine relative profit, which is equal to the difference between its own profit and its opponent firm’s profit. In this paper, we focus on the influence of the parameter of the degree of importance of each private firm’s relative performance on the equilibrium market outcomes in the contexts of both the quantity-setting competition and price-setting competition3. In this paper, we show that even if we take into account both the network effects and the possibility of the weighted sum of each firm’s profit and its opponent firm’s profit, the equilibrium market outcomes in the quantity-setting competition are equivalent to those in the price-setting competition. Thus, the equivalence of Cournot and Bertrand equilibria in the private duopoly with differentiated and substitutable goods still holds against the introduction of network effects à la Katz and Shapiro [14] and the possibility of maximization of the weighted sum of the profit of the private firm and its opponent firm’s profit.
The remainder of this paper is organized as follows: in Section 2, we formulate the basis model employed in this paper. In Section 3, we derive the equilibrium outcomes in both the quantity-setting competition and price-setting competition with differentiated and substitutable goods in the private duopoly with network effects à la Katz and Shapiro [14] wherein the private firms maximize the weighted sum of their own profits and their respective opponent’s profit. Section 4 concludes with several remarks.
2. Model
We formulate a private duopolistic model with differentiated and substitutable goods and consistent conjectures composed of two extended relative profit-maximizing private firms with an additional term that reflects the network effects introduced in Katz and Shapiro [14] and applied by Hoernig [15], Nakamura [16], and Nakamura [17]. Similar to Hoernig [15], Nakamura [16], and Nakamura [17], firm i faces a linear demand of the following form:
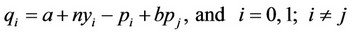 (1)
(1)
where 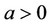 and
and 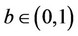 are demand parameters4.
are demand parameters4.  indicates the strength of network effects, and
indicates the strength of network effects, and 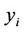 is consumers’ expectations of firm
is consumers’ expectations of firm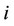 ’s equilibrium market share. The ordinary demand function for the good of firm
’s equilibrium market share. The ordinary demand function for the good of firm 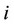 is obtained from the inverse demand function given in Equation (1) as follows:
is obtained from the inverse demand function given in Equation (1) as follows:
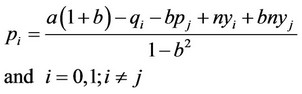 (2)
(2)
As explained in Hoernig [15], Nakamura [16], and Nakamura [17], the above demand system can be derived from the following quasi-linear concave utility function of a representative consumer:
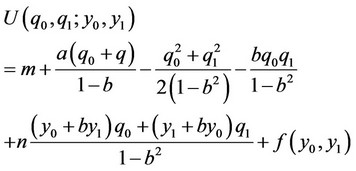
where m denotes the income of the representative consumer and 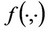 represents some symmetric function of expectations. In this paper, in the same manner as in Hoernig [15], Nakamura [16], and Nakamura [17], we suppose that
represents some symmetric function of expectations. In this paper, in the same manner as in Hoernig [15], Nakamura [16], and Nakamura [17], we suppose that
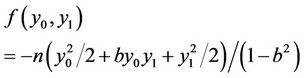 5.
5.
We consider a private duopolistic market composed of two extended relative profit maximizing private firms (firms 0 and 1). We use 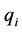 and
and 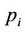 to represent firm
to represent firm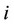 ’s output and price levels, respectively,
’s output and price levels, respectively,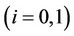 . We adopt the constant marginal cost function, where
. We adopt the constant marginal cost function, where 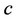 is a common marginal cost between firms 0 and 1, similar to Hoernig [15], Nakamura [16], and Nakamura [17] 6. The marginal cost of production of both firms 0 and 1 is commonly assumed to be
is a common marginal cost between firms 0 and 1, similar to Hoernig [15], Nakamura [16], and Nakamura [17] 6. The marginal cost of production of both firms 0 and 1 is commonly assumed to be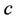 . The profit function of firm
. The profit function of firm 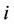 is given by
is given by
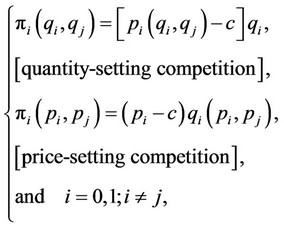
where 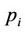 is given in Equation (1) and
is given in Equation (1) and  is given in Equation (2). Consumer surplus is expressed as the representative consumer’s utility as follows:
is given in Equation (2). Consumer surplus is expressed as the representative consumer’s utility as follows: 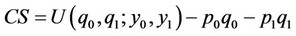 , whereas producer surplus is given by the sum of the profits of both firms 0 and 1,
, whereas producer surplus is given by the sum of the profits of both firms 0 and 1,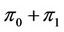 . Finally, we suppose that social welfare is defined as the sum of consumer surplus and producer surplus. We consider the “rational expectations” subgame perfect Nash equilibrium by imposing the rational expectations condition that
. Finally, we suppose that social welfare is defined as the sum of consumer surplus and producer surplus. We consider the “rational expectations” subgame perfect Nash equilibrium by imposing the rational expectations condition that 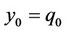 and
and  à la Katz and Shapiro [14], Hoernig [15], Nakamura [16], and Nakamura [17].
à la Katz and Shapiro [14], Hoernig [15], Nakamura [16], and Nakamura [17].
3. Equilibrium Analysis
In this section, we derive the equilibrium market outcomes with firms 0 and 1 in the contexts of both the quantity-setting competition and price-setting competition with their consistent conjectures in the private duopoly with differentiated and substitutabled goods wherein they maximize the extended relative profit.
3.1. Quantity-Setting Framework
In this subsection, we consider the situation wherein the strategic variables of firms 0 and 1 are their output levels. The objective functions of firms 0 and 1 are given as follows:
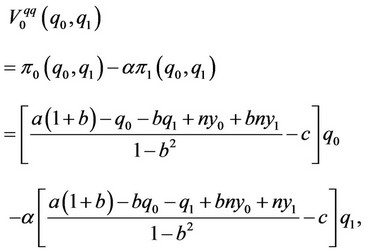
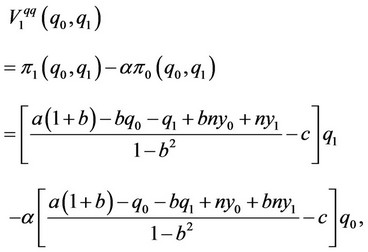
where 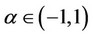 7.
7.
Firm 0 decides its output level in order to maximize 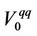 assuming that the reaction of the output level of firm 1 to the output level of firm 0 is given as follows:
assuming that the reaction of the output level of firm 1 to the output level of firm 0 is given as follows:
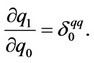
On the other hand, firm 1 decides its output level in order to maximize 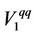 assuming that the reaction of the output level of firm 0 to the output level of firm 1 is given as follows:
assuming that the reaction of the output level of firm 0 to the output level of firm 1 is given as follows:
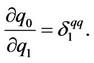
The first-order conditions of firms 0 and 1 in the quantity-setting market competition are given, and their real reaction functions of firms are obtained as follows8:

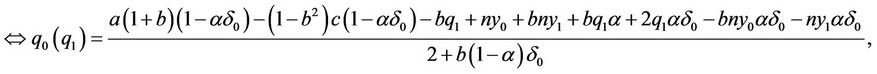
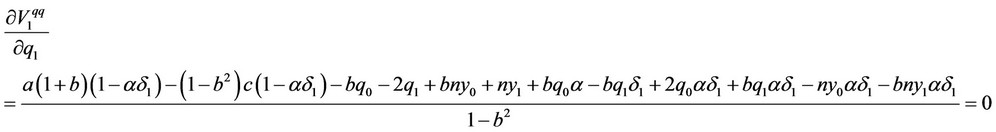
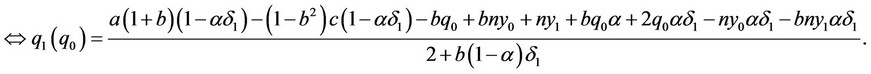
From the real reaction function of the output level of firm 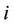 to the output level of firm
to the output level of firm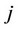 , we obtain the following result
, we obtain the following result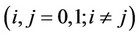 :
:
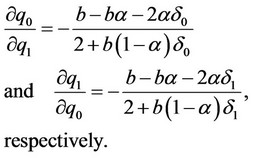
The conditions of the consistency of the conjectural variations of firms 0 and 1 are, respectively,
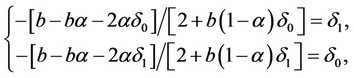
yielding

From the symmetry of firms 0 and 1, we notice that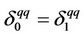 . The above values of firms 0 and 1 are the equilibrium consistent conjectures in the quantity-setting competition under the assumption that
. The above values of firms 0 and 1 are the equilibrium consistent conjectures in the quantity-setting competition under the assumption that 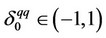 and
and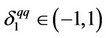 . Thus, by substituting the rational expectations assumption that
. Thus, by substituting the rational expectations assumption that 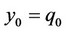 and
and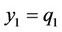 , the equilibrium output levels and price levels of firms 0 and 1 under the assumption that
, the equilibrium output levels and price levels of firms 0 and 1 under the assumption that 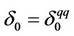 and
and  are obtained as follows:
are obtained as follows:
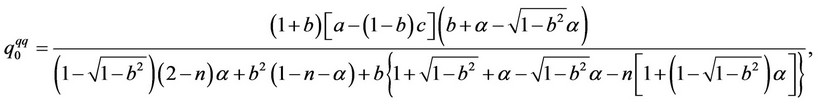
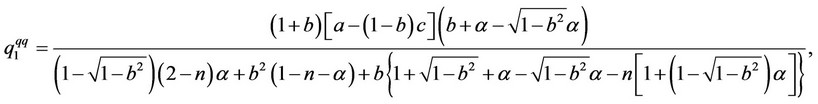
and
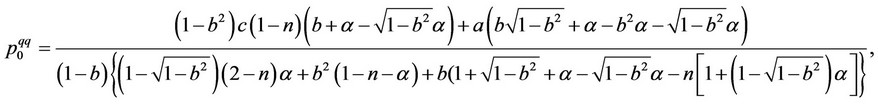
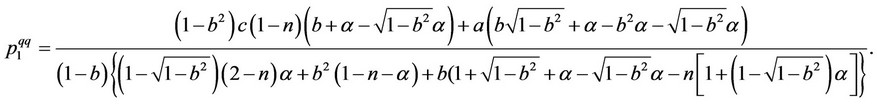
3.2. Price-Setting Framework
In this subsection, we consider the situation wherein the strategic variables of firms 0 and 1 are their price levels. The objective functions of firms 0 and 1 are given as follows:
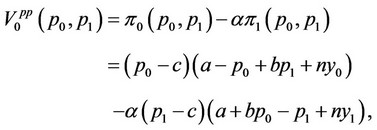
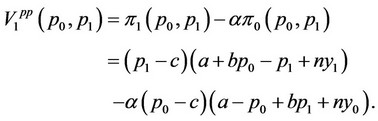
Firm 0 decides its price level in order to maximize 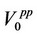 assuming that the reaction of the price level of firm 1 to the price level of firm 0 is given as follows:
assuming that the reaction of the price level of firm 1 to the price level of firm 0 is given as follows:
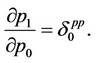
On the other hand, firm 1 decides its price level in order to maximize 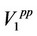 assuming that the reaction of the price level of firm 0 to the price level of firm 1 is given as follows:
assuming that the reaction of the price level of firm 0 to the price level of firm 1 is given as follows:
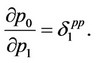
The first-order conditions of firms 0 and 1 in the price-setting competition are given, and the real reaction functions of firms are obtained as follows9:
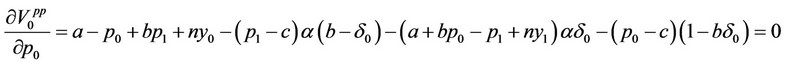
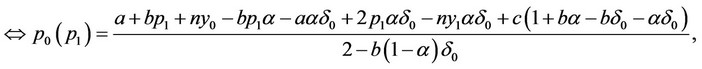
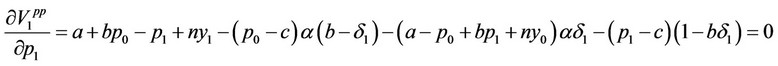
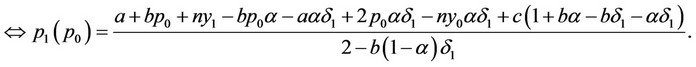
From the real reaction of the price level of firm 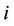 to the price level of firm
to the price level of firm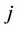 , we obtain the following result
, we obtain the following result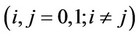 :
:
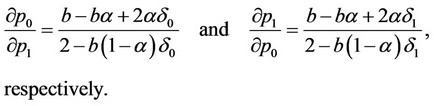
The conditions of the consistency of the conjectural variations of firms 0 and 1 are, respectively,
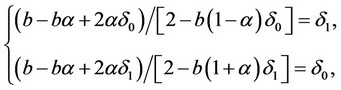
yielding
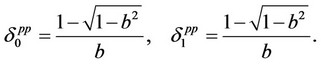
The above values of firms 0 and 1 are the equilibrium consistent conjectures in the price-setting competition under the assumption that 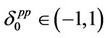 and
and 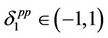 . Note that each firm’s consistent conjectural variation in the price-setting competition is different from that in the quantity-setting competition10. Thus, by substituting the rational expectations assumption that
. Note that each firm’s consistent conjectural variation in the price-setting competition is different from that in the quantity-setting competition10. Thus, by substituting the rational expectations assumption that 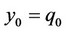 and
and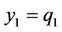 , the equilibrium price level and output level under the assumption that
, the equilibrium price level and output level under the assumption that 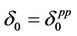 and
and 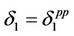 are obtained as follows:
are obtained as follows:
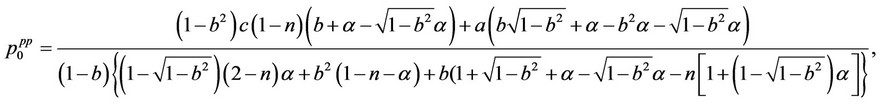
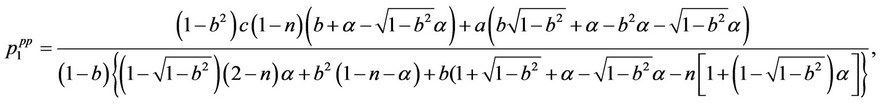
and
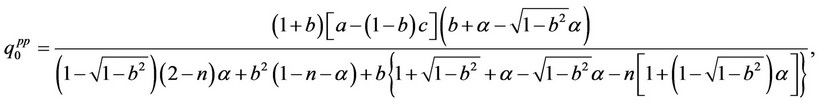
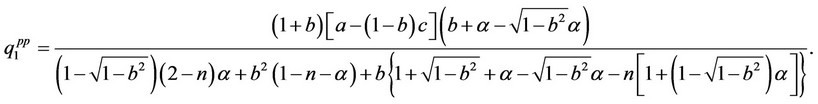
Thus, we have the result that  and
and 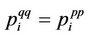 ,
, . Summing up the rational expectations equilibrium market outcomes with consistent conjectures including the output and price levels of firms 0 and 1 between the quantity-setting competition and pricesetting competition, we obtain the following proposition:
. Summing up the rational expectations equilibrium market outcomes with consistent conjectures including the output and price levels of firms 0 and 1 between the quantity-setting competition and pricesetting competition, we obtain the following proposition:
Proposition 1 In the private duopoly with consistent conjectural variations composed of the two extended relative profit maximizing private firms, the rational expectations equilibrium outcomes including their output and price levels, profit, consumer surplus, and social welfare in the quantity-setting competition are equivalent to those in the price-setting competition.
Note that the statement of Proposition 1 is relevant to the private duopoly composed of extended relative profitmaximizing private firms that is without network effects à la Katz and Shapiro [14] since it includes the case of . On the other hand, the statement of Proposition 1 is relevant to the private duopoly with the network effects à la Katz and Shapiro [14] composed of the absolute profit-maximizing private firms since it includes the case of
. On the other hand, the statement of Proposition 1 is relevant to the private duopoly with the network effects à la Katz and Shapiro [14] composed of the absolute profit-maximizing private firms since it includes the case of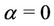 .
.
4. Concluding Remarks
In this paper, we considered the equilibrium market outcomes in a private duopoly with differentiated and substitutable goods and with an additional term that reflects network effects in the fashion of Katz and Shapiro [14], Hoernig [15], Nakamura [16], and Nakamura [17], wherein the private firms maximize the weighted sum of their own profits and their respective opponent firm’s profit. Similar to the private duopoly without network effects composed of two absolute profit maximizing firms and of two relative profit maximizing firms investigated in Tanaka [6], we show that the equilibrium outcomes in the quantitysetting competition are equivalent to those in the price-setting competition even in the private duopoly with network effects à la Katz and Shapiro [14], wherein the two private firms maximize their extended relative profits, which are equal to the weighted sum of the firm’s own profit and its opponent firm’s profit. In this paper, we also showed that in the above private duopolistic market, the equilibrium market outcomes in the quantity-setting competition are the same as those in the price-setting competition. Thus, the above so-called irrelevance result that the equilibrium market outcomes are the same between the quantity-setting competition and price-setting competition is robust against the introduction of both network effects à la Katz and Shapiro [14] and the presence of the weighted relative profit-maximizing private firms.
Finally, we identify several topics to be addressed in our future research. In a symmetric private duopoly with differentiated and substitutable goods wherein two private firms maximize their genuine relative profits, Tanaka [7] showed that the choice of the strategic variables of the two firms is irrelevant to the outcome of the game in the sense that since their equilibrium output, price levels, and profits are the same in all situations, any combination of their strategy choices comprises a subgame perfect equilibrium in the game on the endogenous selections of their strategic variables. Then, as one of our future studies, we will consider the two-stage game on the endogenous selections of each firm’s strategic variable in a private duopoly with differentiated and substitutable goods and with network effects wherein two private firms maximize the weighted sum of their own profits and their respective opponent firm’s profit. Second, as indicated in Tanaka [6] and Tanaka [7], as one of our future studies, we should check the robustness of the results obtained in this paper against the general numbers of the existing private firms and the general demand function.
REFERENCES
- T. Bresnahan, “Duopoly Models with Consistent Conjectures,” American Economic Review, Vol. 71, No. 5, 1981, pp. 934-945.
- M. Perry, “Oligopoly and Consistent Conjectural Variations,” Bell Journal of Economics, Vol. 13, No. 1, 1982, pp. 197-205. doi:10.2307/3003440
- M. Boyer and M. Moreaux, “Consistent versus NonConsistent Conjectures in Duopoly Theory: Some Examples,” Journal of Industrial Economics, Vol. 32, No. 1, 1983, pp. 97-110. doi:10.2307/2097988
- Y. Tanaka, “Consistent Conjectures in Free Entry Oligopoly,” Economics Letters, Vol. 17, No. 1-2, 1985, pp. 15-18. doi:10.1016/0165-1765(85)90118-1
- Y. Tanaka, “On Multiplicity of Consistent Conjectures in Free Entry Oligopoly,” Economics Letters, Vol. 28, No. 2, 1985, pp. 109-115. doi:10.1016/0165-1765(88)90099-7
- Y. Tanaka, “Equivalance of Cournot and Bertrand Equilibria in Differentiated Duopoly under Relative Profit Maximization with Linear Demand,” Economics Bulletin, Vol. 33, No. 2, 2013, pp. 1479-1486.
- Y. Tanaka, “Irrelevance of the Choice of Strategic Variables in Duopoly under Relative Profit Maximization,” Economics and Business Letters, Vol. 2, No. 2, 2013, pp. 75-83.
- T. Matsumura, N. Matsushima and S. Cato, “Competitiveness and R&D Competition Revisited,” Economic Modelling, Vol. 31, 2013, pp. 541-547. doi:10.1016/j.econmod.2012.12.016
- M. E. Schaffer, “Are Profit Maximizers the Best Survivors?” Journal of Economic Behavior and Organization, 12, 1, 1989, 29-45. doi:10.1016/0167-2681(89)90075-9
- F. Vega-Redondo, “The Evolution of Walrasian Behavior,” Econometrica, Vol. 65, No. 2, 1997, pp. 375-384. doi:10.2307/2171898
- C. Lundgren, “Using Relative Profit Incentives to Prevent Collusion,” Review of Industrial Organization, Vol. 11, No. 4, 1996, pp. 533-550. doi:10.1007/BF00157777
- L. Kockesen, E. A. Ok and R. Sethi, “The Strategic Advantage of Negatively Interdependent Preferences,” Journal of Economic Theory, Vol. 92, No. 2, 2000, pp. 274- 299. doi:10.1006/jeth.1999.2587
- T. Matsumura and N. Matsushima, “Competitiveness and Stability of Collusive Behavior,” Bulletin of Economic Research 64, Supplement, Vol. 64, Suppl. 1, 2012, pp. 22- 31. doi:10.1111/j.1467-8586.2012.00439.x
- M. Katz and C. Shapiro, “Network Externalities, Competition, and Compatibility,” American Economic Review, Vol. 75, No. 3, 1985, pp. 424-440.
- S. Hoernig, “Strategic Delegation under Price Competition and Network Effects,” Economics Letters, Vol. 117, No. 2, 2012, 487-489. doi:10.1016/j.econlet.2012.06.045
- Y. Nakmaura, “Social Welfare under Quantity Competition and Price Competition in a Mixed Duopoly with Network Effects: An Analysis,” Theoretical Economics Letters, Vol. 3, No. 4, 2013, pp. 211-215. doi:10.4236/tel.2013.34035
- Y. Nakmaura, “Endogenous Timing in Price-Setting Private and Mixed Duopoly with Network Effects,” 2013, Mimeo.
- Y. Nakamura and M. Saito, “Capacity Choice in a Mixed Duopoly: The Relative Performance Approach,” Theoretical Economics Letters, Vol. 3, No. 2, 2013, pp. 124- 133. doi:10.4236/tel.2013.32020
- Y. Nakamura and M. Saito, “Capacity Choice in a PriceSetting Mixed Duopoly: The Relative Performance Approach,” Modern Economy, Vol. 4, No. 4, 2013, pp. 273- 280. doi:10.4236/me.2013.44031
- Y. Nakamura, “Price versus Quantity in a Mixed Duopoly: The Case of Relative Profit Maximization,” 2013, Mimeo.
- F. Y. Edgeworth, “Mathematical Physics,” P. Kegan, London, 1881.
- R. M. Cyert and M. H. de Groot, “An Analysis of Cooperation and Learning in a Duopoly Context,” American Economic Review, Vol. 63, No. 1, 1973, pp. 24-37.
- Y. Tanaka, “Irrelevance of Conjectural Variation in Duopoly under Relative Profit Maximization and Consistent Conjectures,” 2013, Mimeo.
NOTES
*We are grateful for the financial support of KAKENHI (25870113). Any remaining errors are our own.
1In particular, Perry [2] showed that when the number of firms is fixed, their competitive behaviors are consistent in the case wherein their marginal costs are constant, but that when marginal costs are rising, the consistent conjectural variation will be between competitive and Cournot behavior. Furthermore, they found that when we allow free entry of firms, only their competitive behaviors will be consistent.
2In addition, Tanaka [7] found that in private duopoly with the linear demand and constant marginal cost functions, when the two symmetric private firms maximize their genuine relative profits, the choices of their strategic variables are irrelevant to the outcome of the game in the sense that the equilibrium outcomes are the same in all three types of market structures. Any combination of choices of the strategic variables by the private firms composes a subgame perfect equilibrium in the two stage game.
3A number of existing works have used relative performance approaches in the context of a mixed duopoly with one social welfaremaximizing public firm and one extended relative profit-maximizing private firm, Nakamura and Saito [18] investigated each firm’s capacity choice in a quantity-setting competition, whereas Nakamura and Saito [19] considered each firm’s capacity choice in a price-setting competition.
4The value of 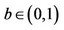 indicates that the relation between the goods of firms 0 and 1 is substitutable. Moreover, the assumption that
indicates that the relation between the goods of firms 0 and 1 is substitutable. Moreover, the assumption that 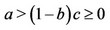 is made to ensure the non-negativity of all equilibrium outcomes.
is made to ensure the non-negativity of all equilibrium outcomes.
5This assumption in the form of 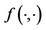 implies that the representative consumer’s utility is highest with respect to the consumption vector of the goods produced by the two private firms,
implies that the representative consumer’s utility is highest with respect to the consumption vector of the goods produced by the two private firms, 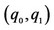 , when expectations are rational and correct.
, when expectations are rational and correct.
6In their theoretical model, Tanaka [6], Tanaka [7], and Nakamura [20] adopted the genuine relative profit that is equal to the difference between each firm’s absolute profit and its opponent firm’s absolute profit.
7As indicated in Matsumura and Matsushima [13], parameter 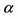 is closely related to the “coefficient of effective sympathy” defined by Edgeworth [21] and the “coefficient of cooperation” defined by Cyert and de Groot [22].
is closely related to the “coefficient of effective sympathy” defined by Edgeworth [21] and the “coefficient of cooperation” defined by Cyert and de Groot [22].
8The second-order conditions of firms 0 and 1 are satisfied.
9The second-order conditions of firms 0 and 1 are satisfied.
10In Tanaka [23], in a private duopoly composed of two absolute profit maximizing firms, it is shown that their consistent conjectural variations in the quantity-setting competition are also different from those in the price-setting competition.

