Journal of Biophysical Chemistry
Vol.05 No.04(2014), Article ID:51532,8 pages
10.4236/jbpc.2014.54015
Volume Change of the Random Coil to Folded Conformational Transition of Thermomyces lanuginosus Xylanase at 24˚C and pH = 7.0 via Application of the Clausius-Clapeyron Equation
Heather N. H. Wilks, Tara M. Arrington, Billy Mark Britt
Department of Chemistry and Biochemistry, Texas Woman’s University, Denton, Texas, USA
Email: mbritt@twu.edu
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 September 2014; revised 13 October 2014; accepted 12 November 2014
ABSTRACT
A partial phase diagram characterizing the conformational change that occurs in Thermomyces lanuginosus xylanase as it is slowly heated in 150 mM sodium phosphate (pH = 7.0) has been constructed from slow-scan-rate differential scanning calorimetry measurements. The Clausius-Cla- peyron equation was applied to determine an associated volume change of −205 L∙mol−1 at 24˚C, the equilibrium transition temperature at 1.0 atm pressure. This value is in excellent agreement with that predicted using a previously published [1] empirical equation for calculating the hydrodynamic radius if the transition is regarded as from a random coil to a functional, folded state and with the assumption that the hydrodynamic radius is a good approximation of the true random coil radius. The existence of a low-temperature random coil is confirmed by circular dichroism and dynamic light scattering measurements. Thus, at 24˚C and 1.0 atm pressure the enzyme appears to fold from a random coil to a functional, folded form as it is slowly heated.
Keywords:
Clausius-Clapeyron, Conformational Change, Slow-Scan-Rate Differential Scanning Calorimetry, Thermomyces lanuginosus Xylanase, Volume Change

1. Introduction
The purpose of this investigation is to determine whether application of the Clausius-Clapeyron equation to an enzyme system may be of value in characterizing volume changes associated with conformational changes. The Clausius-Clapeyron equation, which may be written in the form
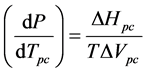 (1)
(1)
is generally applicable to a phase change of a pure, single component. The equation describes the phase boundary
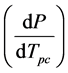 , experimentally determined from the pressure dependence of the observed phase change transition
, experimentally determined from the pressure dependence of the observed phase change transition
temperature Tpc, in terms of the enthalpy ΔHpc and volume ΔVpc changes associated with the conformational change at a particular temperature T of interest. A phase change may be defined as a change in physical state of a substance when the chemical nature of the substance remains unaltered. Enzyme conformational changes may be considered phase changes if the few ionizable groups that may alter protonation states between conformations are ignored. We are unaware of an application of this type of the Clausius-Clapeyron equation.
Our laboratory’s current emphasis is in detecting and characterizing nondenaturational enzyme conformational changes. We have previously detected conformational changes that occur at moderate temperatures in several enzymes using slow-scan-rate differential scanning calorimetry (ssrDSC) [2] -[6] . For each enzyme studied we detected evidence for a non-unfolding change in the enzyme between the temperature where the enzyme crystal was formed for X-ray structure determination and the optimal physiological temperature of the organism from which the enzyme is isolated. The data further suggest that the low-temperature structure is more compact than the physiological-temperature structure. An obvious implication of these findings is the crystal structures for these enzymes cannot be the physiological structures as is generally assumed. As the enzymes studied were all from mesophilic organisms, we thought that it would be interesting to investigate a thermophilic enzyme to see if the same behavior is exhibited. Instead, we found evidence that at pH = 7.0 the thermophilic enzyme undergoes a transition from a random coil to a folded form as it is slowly heated with the transition occurring at 24˚C at 1.0 atm pressure.
For this study we chose the enzyme Thermomyces lanuginosus xylanase (TLX) [7] . The enzyme is isolated from a thermophilic fungus with an optimal thriving temperature of around 50˚C [8] and is commercially available. Xylanases are often used in the feed, food, pulp, and paper industries. TLX is most commonly used in chlorine-free bleaching paper mills and is ideal because of its stability and tolerance to extreme temperatures and pH values. The enzyme is monomeric, consists of 194 amino acid residues, and has a molecular weight of 21.312 kDaltons. An X-ray structure determined at room temperature from crystals grown at pH = 4.0 and 4˚C is available [9] .
Our approach is to first establish that TLX may undergo a low-temperature conformational change using ssrDSC. Having established this, we determine the pressure dependence of the transition temperature and construct a partial phase diagram describing the low-temperature to physiological-temperature conformational change. With a value of ΔHpc obtained from analysis of the ssrDSC data we then calculate a value of ΔVpc. This value is then reconciled with possible conformational states which are subsequently confirmed by circular dichroism and dynamic light scattering measurements.
2. Materials and Methods
Thermomyces lanuginosus xylanase (product number X2753) and the sodium phosphate buffer components were obtained from Sigma Aldrich. The components of the succinic acid buffer (product number A7710) were obtained from GFS Chemicals.
Differential scanning calorimetry measurements were performed on a Calorimetry Sciences Corporation Nano DSC III calorimeter. Initial enzyme solutions were prepared at 2.0 mg/mL in enzyme (with correction for mass of sample attributable to salt) and were prepared in either 150 mM sodium phosphate buffer (pH = 7.0) or 250 mM succinic acid buffer (pH = 4.0). Samples were dialyzed against a 1000-fold volume excess of buffer for at least 8 hours at 4˚C using Thermo Scientific Slida-A-Lyzer dialysis cassettes (MWCO = 3500). Any change in volume of the sample was noted and the sample concentration corrected accordingly. The concentrations of the solutions measured were 2.0 ± 0.1 mg/mL. DSC runs were performed at scan rates from 0.020 K∙min−1 to 0.050 K∙min−1 from 15˚C to 60˚C at total applied pressures of 1.0 to 5.0 atm. All runs were then baseline corrected from runs of dialysate versus dialysate at the same scan rate, pressure, and range of temperature as that of the enzyme solutions.
Evidence of a conformational change is revealed in the appearance of an exothermic transition from 26˚C to 42˚C, the exact temperature being dependent upon scan rate. Apparent enthalpy changes associated with the transitions at 1.0 atm total applied pressure were calculated by standard integration techniques. This analysis also revealed the apparent transition temperature as the temperature where the difference between baseline and data was the greatest.
CD measurements. Circular dichroism measurements were performed on an Olis RSM 1000 Spectrophotometer. Enzyme solutions were 1.0 mg/mL in either 150 mM phosphate (pH 7.0) or 250 mM succinic acid (pH 4.0). Spectra were obtained in a 10.0 cm path-length cell. Spectra were deconvolved into theoretical major secondary structural component content using instrument software (namely, the CDSSTR, CONTINILL, and SELCON 3 algorithms). Samples were equilibrated overnight at either 14˚C or 34˚C.
DLS measurements. Dynamic light scattering measurements were performed on a Malvern Instruments Zetasizer μV instrument using polystyrol/polystyrene disposable cuvettes. Samples were 1.0 mg/mL prepared in the pH = 7.0 buffer, filtered with Whatman Anotop 10, 0.02 μm filters to removed dust particles, and equilibrated overnight at the temperature of interest, either 14˚C or 34˚C.
3. Results and Discussion
First, it is established that TLX may undergo a nondenaturational conformational change at low temperature. This is achieved by ssrDSC which employs scan rates as low as 0.010 K∙min−1 [2] . DSC is an ideal choice since the technique measures relative changes in heat capacity between reference and sample and enzyme conformational changes are likely to be accompanied by heat capacity changes due to the concomitant net binding or release of water molecules. Such slow scan rates allow for detection of events that may be under kinetic control and therefore not observed at conventional scan rates of around 1 K∙min−1.
Figure 1 shows a representative raw ssrDSC run at a scan rate of 0.030 K∙min−1 of a 2.0 mg∙mL−1 solution of TLX in 150 mM sodium phosphate buffer (pH = 7.0) and at 1.0 atm pressure. An exothermic transition at ~32˚C is observed. We have previously observed such transitions in other enzymes where we demonstrated, via the construction of protein stability curves, that this signal may be indicative of a global, nondenaturational conformational change [2] -[6] . When scans are made at the conventional scan rate of 1.0 K∙min−1 no such signal is observed. The process observed in Figure 1 is reversible in the sense that a nearly identical scan is obtained after the sample is recovered and stored at 4˚C for three days.
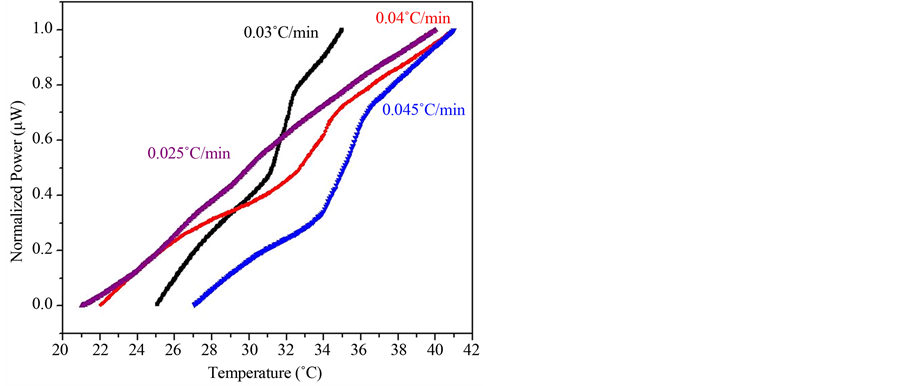
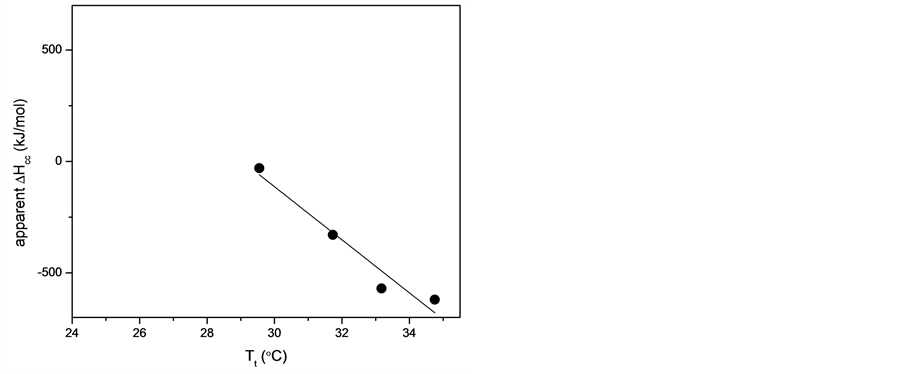
Figure 2 shows baseline-corrected, ssrDSC scans of TLX solutions at 1.0 atm total pressure. It is observed that the apparent temperature of the putative conformation change decreases with decreasing scan rate. Also, the transition enthalpy change becomes less negative with decreasing scan rate and even appears to become slightly positive at the scan rate of 0.025 K∙min−1.
The true, or equilibrium, transition temperature at 1.0 atm total applied pressure is obtained from a plot of the
Figure 1. Screen capture of data obtained in a ssrDSC run of a 2.0 mg/mL sample of TLX in 150 mM sodium phosphate buffer (pH = 7.0) and at total applied pressure of 1.0 atm. Scan rate is 0.030 K∙min−1. Run is not baseline corrected.
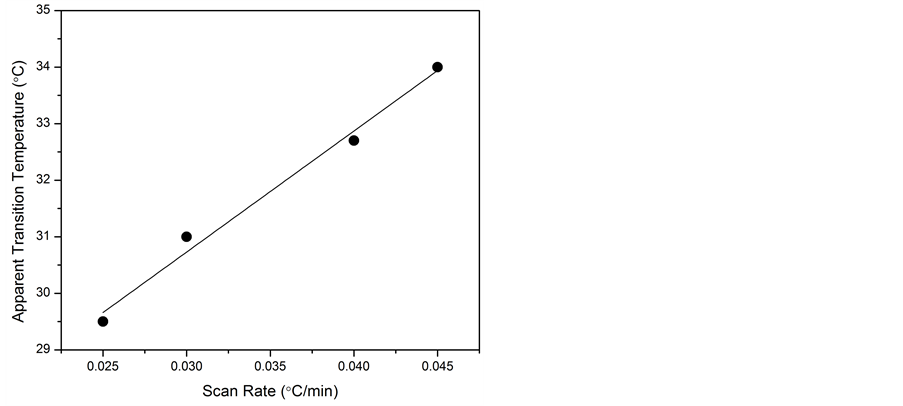
apparent transition temperature vs. scan rate obtained from analysis of the runs in Figure 2 (Figure 3). The trend is well modeled by a line. At 1.0 atm total applied pressure, TLX appears to undergo a conformational change at 24˚C.
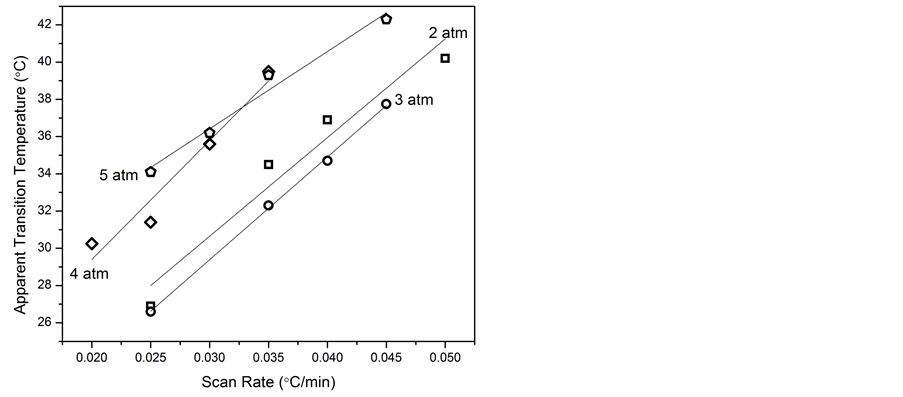
Other ssrDSC measurements were also made at total applied pressures of 2.0, 3.0, 4.0, and 5.0 atm and the data similarly analyzed to give apparent transition temperatures. These temperatures again depended linearly upon scan rate and gave the equilibrium temperatures shown in Figure 4.
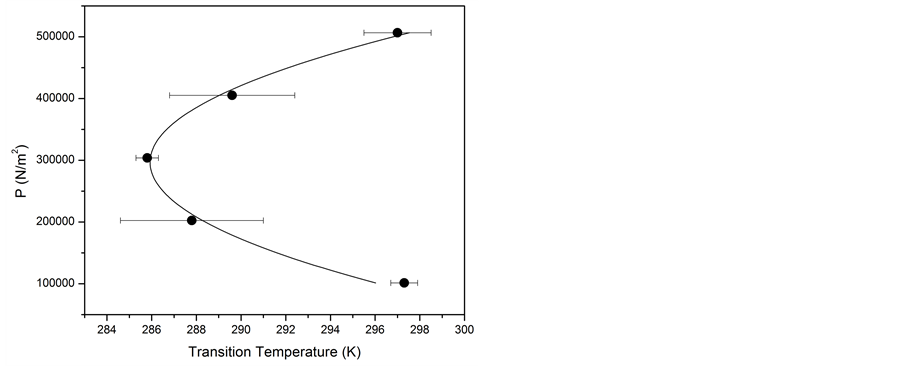
With this data, a partial phase diagram is constructed (Figure 5). This diagram gives the pressure dependence of the transition temperature between the presently uncharacterized low- to physiological-temperature conformational change. The shape of the curve is elliptical, characteristic of a transformation involving an unfolded state [10] [11] .
The slope at p = 101325 N∙m−2 (1 atm) is calculated to be −9.87 × 103 kg∙m−1∙s−2∙K−1. This value was calcu-
Figure 2. Normalized (with respect to instrument power output), baseline-corrected ssrDSC measurements of 2.0 mg∙mL−1 samples of TLX in 150 mM sodium phosphate buffer (pH = 7.0, p = 1.00 atm). Scan rates are indicated.
Figure 3. Apparent transition temperatures of the exothermic DSC transitions at 1.0 atm as function of instrument scan rate. Extrapolation to zero scan rate yields 24.3˚C ± 0.6˚C as the equilibrium transition temperature.
Figure 4. Linear extrapolations to zero scan rate of the apparent transition temperatures of TLX as function of scan rate and total pressure to give the equilibrium transition temperatures. These temperatures are used to construct the partial phase diagram. Tt for 2.0 atm data (squares) = 14.8˚C ± 3.2˚C, 3.0 atm (circles) = 12.8˚C ± 0.5˚C, 4.0 atm (diamonds) = 16.6˚C ± 2.8˚C, and 5.0 atm (pentagons) = 24.0˚C ± 1.5˚C.
Figure 5. Phase diagram characterizing the low- and physiological-temperature conformation equilibrium of TLX at pH = 7.0. The trend line is a quadratic fit to an x/y transpose of the data. Error bars are the uncertainty in the equilibrium unfolding temperatures expressed as uncertainty in the y-intercepts of plots from Figure 4.
lated by first fitting the x/y transpose of the data to a quadratic equation, approximating the quadratic fit with a line in the region corresponding T = 297 K (24˚C) and p = 1.0 atm, obtaining the mathematical inverse of this li-
near fit to give  and then solving for the slope.
and then solving for the slope.
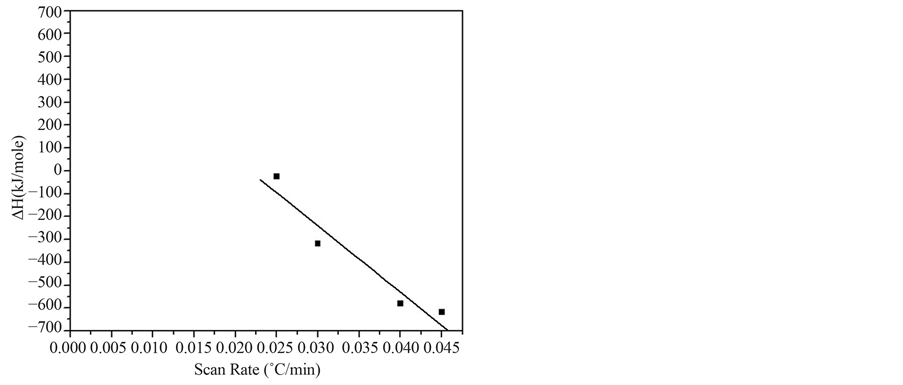
The final piece of information required for the application of Equation (1) to determine the volume change associated with the transition is the value of ΔHpc at 1.0 atm. We compare two methods for its evaluation (Fig- ure 6). When the calculated apparent enthalpy changes are plotted as a function of scan rate the data are observed
Figure 6. Methods for the evaluation of ΔHpc. A plot of the observed enthalpy changes vs. scan rate yields a value of 6.3 × 102 ± 2.1 × 102 kJ∙mol−1 (left) and vs. apparent temperature of the transition yields 6.0 × 102 ± 1.1 × 102 kJ∙mol−1.
to be adequately modeled by a line. A rather uncertain equilibrium value of ΔHpc = 6.3 × 102 ± 2.1 × 102 kJ∙mol−1 is obtained from extrapolation to zero scan rate. Alternatively, when the evaluated enthalpy changes are plotted as a function of the temperature at which they were determined the trend is again observed to be linear but with a better fit. Evaluation of the enthalpy change at the equilibrium temperature of 24˚C yields a value of ΔHpc = 601 ± 97 kJ∙mol−1. The good agreement between the two methods tends to validate the result. For the calculations, we will use the latter, apparently more precise, value.
Next we calculate a value of ΔVpc—the calculated change in volume upon transitioning from the low-tem- perature conformation to the physiological-temperature conformation—using Equation (1) in the form
 (2)
(2)
ΔVpc = −205 ± 33 L∙mol−1.
An X-ray structure determination of the enzyme was performed on crystals grown at pH = 4.0 [9] . The dimensions of a single molecule are reported as 40 × 38 × 35 Å and the enzyme is thus ellipsoid in shape with a molecular volume of 2.78 × 104 Å3 or 18 L∙mol−1. We assume that although the crystals were formed at a very different pH from that employed here the folded volume is roughly the same. The Clausius-Clapeyron analysis strongly suggests the conformational species that exists below 24˚C is an open structure. Two possible general structures are the molten globule and the random coil.
Lorna J. Smith and coworkers have examined a number of proteins in both their native and nonnative states and derived empirical relationships for calculating hydrodynamic radii. Their work reveals for a highly unfolded structure the hydrodynamic radius Rh is predicted to be
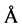 (3)
(3)
where N is the number of amino acid residues constituting the protein. With N = 194 for TLX, the hydrodynamic radius for the fully unfolded TLX is calculated to be 44.5 Å corresponding to a unfolded molar volume 222 L∙mol−1. The hydration radius of a protein is defined as the radius of a hard sphere that diffuses at the same rate as the measured molecule and should therefore be regarded as only an approximation of the true radius. However, it is reasonable to assume the random coil is largely spherical in shape and that the calculated hydration radius is a good approximation of the actual radius. To confirm the low-temperature form of TLX exists as a random coil, we investigate its circular dichroism. This technique is the spectroscopic method of choice for identifying the secondary structural content of the enzyme.
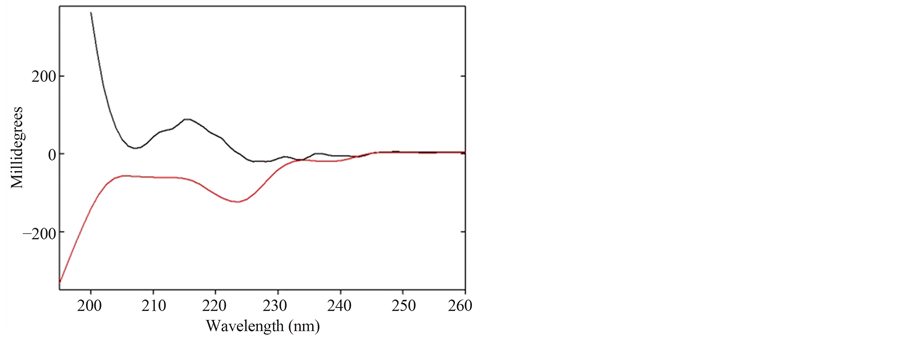
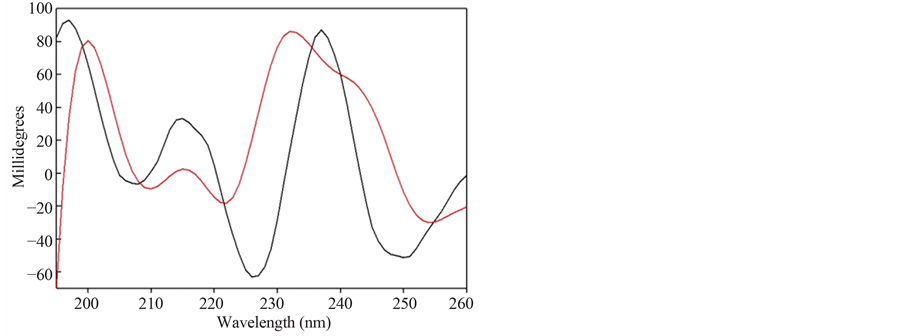
Figure 7 shows the CD spectra of the protein at 14˚C and at 34˚C. These temperatures are 10˚C on either side of the transition temperature where it is assumed, due to the phase change nature of the transition, the enzyme is completely in one conformation or the other. Analysis was done of each scan using the SELCON 3 algorithm which resulted in the lowest standard deviation values. At 14˚C the protein apparently consists of ~85% unordered structure and 0% alpha helix, 5% beta sheet and 9% turns. Conversely, at 34˚C the enzymeis 40% alpha helix, 36% unordered, and 23% turns. These values strongly suggest that a conformational change occurs between these two temperatures and that the low-temperature conformation is a random coil.
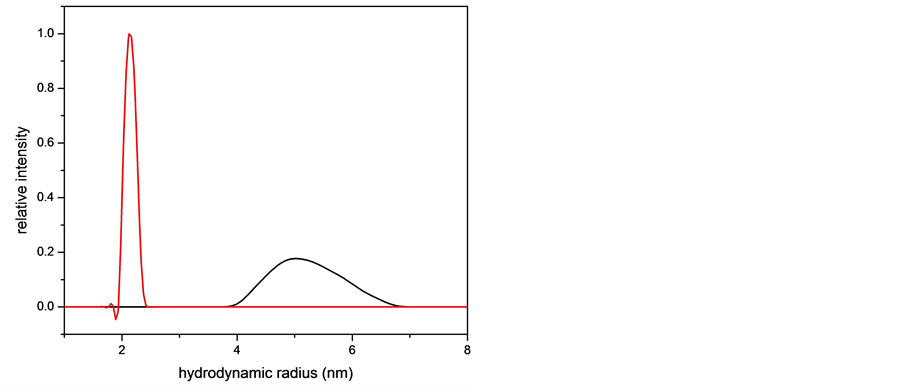
Figure 8 shows our determinations of the hydrodynamic radius as a function of temperature using dynamic light scattering. At 14˚C a broader peak is observed with an apparent hydrodynamic radius Rh = 48.9 ± 5.3 Å. This value agrees with that obtained by Equation (3) which predicts that the TLX random coil to be 44.5 Å. At 34˚ a single peak at Rh = 21.3 ± 0.9 Å is observed. Smith and coworkers also derived an empirical formula to give the hydration radius of the folded, functional protein as
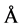 (4)
(4)
where again N is the number of amino acid residues in the protein [1] . This formula predicts Rh = 21.9 Å for native TLX. This value agrees well with the value we determined.
Finally, we reconcile our findings with the reported crystal structure where a folded form was observed in the temperature range where we instead detect an apparent random coil structure [9] . The crystal structure was determined under conditions that are 1000× more acidic than the data presented here. We made ssrDSC measure-
Figure 7. CD spectra of TLX at pH 7.0, 14˚C (black) and 34˚C (red).
Figure 8. Dynamic light scattering graph of TLX at pH = 7.0 at 14˚C (black) and 34˚C (red).
Figure 9. CD spectra of TLX at pH 4.0 and 14˚C (black) and 34˚C (red).
ments at pH = 4.0 but found no evidence for a predenaturational conformational change. Likewise, CD measurements at pH = 4.0 made in a similar fashion as those at pH = 7.0 showed no evidence for a major low-tem- perature-induced conformational change including no evidence for the existence of an unfolded structure (Figure 9). We therefore conclude that the reported structure has no direct bearing on the present studies and may not be physiologically relevant.
4. Conclusion
The data presented here make a strong case for the existence of TLX as a random coil below 24˚C in 150 mM sodium phosphate buffer (pH = 7.0). We are not aware of a previous report of a cold temperature-induced formation of a random coil structure from a native enzyme under normal, physiological conditions (no extremes of pH or pressure). Furthermore, the application of the Clausius-Clapeyron for the purposes of calculating volume changes appears valid.
Acknowledgements
We thank the Robert A. Welch Foundation for a departmental grant which funded this work.
References
- Wilkins, D.K., Grimshaw, S.B., Receveur, V., Dobson, C.M., Jones, J.A. and Smith, L.J. (1999) Hydrodynamic Radii of Native and Denatured Proteins Measured by Pulse Field Gradient NMR Techniques. Biochemistry, 38, 16424-16431. http://dx.doi.org/10.1021/bi991765q
- Bodnar, M.A. and Britt, B.M. (2006) Transition State Characterization of the Low- to Physiological-Temperature Nondenaturational Conformational Change in Bovine Adenosine Deaminase by Slow-Scan-Rate Differential Scanning Calorimetry. Journal of Biochemistry and Molecular Biology, 39, 167-170. http://dx.doi.org/10.5483/BMBRep.2006.39.2.167
- Younvanich, S.S. and Britt, B.M. (2006) The Stability Curve of Hen Egg White Lysozyme. Protein and Peptide Letters, 13, 769-762. http://dx.doi.org/10.2174/092986606777841163
- Hollowell, H.N., Younvanich, S.S., McNevin, S.L. and Britt, B.M. (2007) Thermodynamic Analysis of the Low- to Physiological-Temperature Nondenaturational Conformational Change of Bovine Carbonic Anhydrase. Journal of Biochemistry and Molecular Biology, 40, 205-211. http://dx.doi.org/10.5483/BMBRep.2007.40.2.205
- McNevin, S.L., Nguyen, D.T. and Britt, B.M. (2008) Partial Phase Diagram of Aqueous Bovine Carbonic Anhydrase: Analyses of the Pressure-Dependent Temperatures of the Low- to Physiological-Temperature Nondenaturational Conformational Change and of Unfolding to the Molten Globule State. Journal of Biomolecular Structure & Dynamics, 26, 263-272. http://dx.doi.org/10.1080/07391102.2008.10507242
- Ijeoma, O., Hollowell, H.N., Bodnar, M.A. and Britt, B.M. (2008) Thermodynamic Analysis of the Nondenaturational Conformational Change of Baker’s Yeast Phosphoglycerate Kinase at 24˚C. Archives of Biochemistry and Biophysics, 478, 206-211. http://dx.doi.org/10.1016/j.abb.2008.07.005
- Singh, S., Madlala, A.M. and Prior, B.A. (2006) Thermomyces lanuginosus: Properties of Strains and Their Hemicellulases. FEMS Microbiology Reviews, 1, 3-16.
- Azad, K., Hossain, F. and Halim, M.A. (2013) Screening of Cellulase, Pectinase and Xylanase Activities and Optimization of Radial Mycelial Growth of Two Thermophilic Fungi. Bangladesh Journal of Botany, 42, 207-213.
- Gruber, K., Klintschar, G., Hayn, M., Schlacher, A., Steine, W. and Kratky, C. (1998) ThermophilicXylanase from Thermomyces lanuginosus: High-Resolution X-Ray Structure and Modeling Studies. Biochemistry, 37, 13475-13485. http://dx.doi.org/10.1021/bi980864l
- Meersman, F., Smeller, L. and Heremans, K. (2006) Protein Stability and Dynamics in the Pressure-Temperature Plane. Biochimica et Biophysica Acta (BBA)—Proteins and Proteomics, 1764, 346-354. http://dx.doi.org/10.1016/j.bbapap.2005.11.019
- Winter, R. and Dzwolak, W. (2004) Temperature-Pressure Configurational Landscape of Lipid Bilayers and Proteins. Cellular and Molecular Biology, 50, 397-417