Psychology
Vol.05 No.18(2014), Article ID:51663,11 pages
10.4236/psych.2014.518200
A Procedure for Diagnostically Modeling Extant Large-Scale Assessment Data: The Case of the Programme for International Student Assessment in Reading
Jinsong Chen1*, Jimmy de la Torre2
1Department of Psychology, Sun Yat-sen University, Guangzhou, China
2Department of Educational Psychology, Rutgers, The State University of New Jersey, New Brunswick, USA
Email: *jinsong.chen@live.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 17 September 2014; revised 12 October 2014; accepted 8 November 2014
ABSTRACT
Cognitive diagnosis models (CDMs) are psychometric models developed mainly to assess examinees’ specific strengths and weaknesses of a set of skills or attributes within a domain. Recently, several methodological developments have been added to the CDM literature, which include the development of general and reduced CDMs, various absolute and relative fit measures at both the test and item levels, and a general Q-matrix validation procedure. Building on these developments, this research proposes a systematic procedure to diagnostically model extant large-scale assessment data. The procedure can be divided into four phases: construction of initial attributes and Q-matrices, construction of final attributes and Q-matrix, evaluation of reduced CDMs, and cross- validation of the selected model. Working with language experts, we use data from the PISA 2000 reading assessment to illustrate the procedure.
Keywords:
CDM, Q-Matrix, Large-Scale Assessment, Fit Measures, PISA

1. Introduction
Cognitive diagnosis models (CDMs) are psychometric models developed mainly to assess examinees’ specific strengths and weaknesses, or mastery or nonmastery of a given set of skills or attributes within a domain. Different from conventional unidimensional item response models (IRMs) that rank examinees along a proficiency continuum, CDMs with latent classes are employed for the purpose of diagnosing the presence or absence of multiple fine-grained attributes. In conjunction with an appropriate Q-matrix (Tatsuoka, 1983) , CDMs can be applied to different assessments for diagnostic purposes, thereby facilitating a more precise measurement of student learning and aiding in the design of better instruction. Recently, several methodological developments have been added to the CDM literature. Among others, these developments include the generalization of highly constrained models like the deterministic inputs, noisy “and” gate (DINA; Haertel, 1989; Junker & Sijtsma, 2001 ) model and the deterministic inputs, noisy “or” gate (DINO; Templin & Henson, 2006 ) model to saturated models such as the log-linear CDM (Henson, Templin, & Willse, 2009) and the generalized DINA (G-DINA; de la Torre, 2011 ) model; different reduced CDMs like the additive CDM (A-CDM; de la Torre, 2011 ), the linear logistic model (LLM; Maris, 1999 ), and the reduced reparameterized unified model (R-RUM; DiBello, Roussos, & Stout, 2007; Hartz, 2002 ); general CDM for expert-defined polytomous attributes (Chen & de la Torre, 2013) ; various model-data misfit measures (Chen, de la Torre, & Zhang, 2013; de la Torre & Chen, 2011; de la Torre & Lee, 2010; Kunina-Habenicht, Rupp, & Wilhelm, 2012) for absolute or relative fit evaluation on the test or item levels; and a general Q-matrix validation procedure (de la Torre, 2008; de la Torre & Chiu, 2010) .
Compared to the methodological developments, however, empirical applications of CDMs are still limited. The usefulness of these developments is best reflected by the breadth and depth of their applications across substantive areas. Although empirical examples were usually provided when developing the above methodologies, they were largely limited to the mathematics domain, particularly the subtraction fraction data by Tatsuoka (1990) . However, if used in a systematic way, these developments can allow non-diagnostic assessments to be adapted for diagnostic purposes. We found that large-scale assessments like the Programme for International Student Assessment (PISA), Trends in International Mathematics and Science Study (TIMSS), or the National Assessment of Educational Progress (NAEP) can be adapted. Considering the large amount of resources that have been invested in developing the assessments, it would be cost-effective if these assessments can be used for other purposes such as drawing fine-grained inferences about what students can and cannot do.
In this research, we proposed a systematic procedure of modeling extant large-scale assessments for diagnostic purpose by capitalizing on and integrating recent CDM developments. By working with language experts, we used the PISA reading assessment to demonstrate the procedure in practice. A domain different from mathematics was chosen for a wider application of the developments. We expect that a similar procedure is applicable to other large-scale assessments and/or other subject matters. It is worth noting that the PISA reading domain is somewhat different from conventional reading in that it does not focus on text decoding or literal comprehension (OECD, 1999, 2006a) . Instead, PISA reading emphasizes the understanding of reading literacy under the context of daily activities. As a result, we found attributes well beyond the scope of the traditional reading domain (e.g., number sense). In light of this, comparisons between this research and those of the diagnostic assessments in the conventional reading domain (e.g., Jang, 2009; Lee & Sawaki, 2009; von Davier, 2008 ) should be done with caution. In the rest of this research, we will first summarize the methodological background required for the modeling procedure. After the description of the PISA reading assessments and released items, we will illustrate the four phases of the modeling procedure. The paper concludes with a discussion of the results and some implications of this work.
2. Background
2.1. Q-Matrix and Required Attributes
For any assessment to provide useful diagnostic information, the Q-matrix plays an important role, as it provides the specification of attributes for the items. As in, the Q-matrix describes the relationship between the items and the attributes being measured. Let qjk denote the element in row j and column k of a J × K Q-matrix, where J and K represent the numbers of items and attributes, respectively. The element qjk is specified to be one if the kth attribute is required to answer item j correctly, and zero otherwise. The jth row of the Q-matrix (i.e., qj・) is called
the jth q-vector, which gives the attribute specification of item j.  is used to denote the number of required attributes for item j. For notational convenience, let the first
is used to denote the number of required attributes for item j. For notational convenience, let the first  attributes be required for item j. The required attributes for item j can be represented by the reduced vector
attributes be required for item j. The required attributes for item j can be represented by the reduced vector , where
, where . By adopting the concept of required attributes we can simplify the model because the number of attribute vectors to be considered for item j reduces from
. By adopting the concept of required attributes we can simplify the model because the number of attribute vectors to be considered for item j reduces from  to
to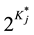 . The probability that examinees with reduced vector
. The probability that examinees with reduced vector 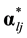 will answer item j correctly is denoted as
will answer item j correctly is denoted as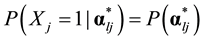 .
.
2.2. Saturated and Reduced CDM
When there is only one required attribute for item j, there is no need to distinguish between the general and re-
duced CDM, because both will have two different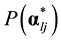 , corresponding to the two reduced vectors. In prac-
, corresponding to the two reduced vectors. In prac-
tice however, it is highly likely that each item measures more than one attribute. For a multiple-attribute item j, the saturated form of its item response function (IRF) in the identity link is
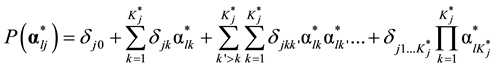
which has 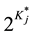 item parameters (i.e.,
item parameters (i.e.,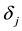 ). Using different link functions (e.g., logit or log) we can get differ-
). Using different link functions (e.g., logit or log) we can get differ-
ent saturated forms that are linear in the parameters, all of which theoretically provide identical model-data fit (de la Torre, 2011) .
By constraining the parameters of the saturated forms, we can obtain different reduced CDMs. In this research, five commonly used reduced CDMs were considered: The DINA model has two parameters per item, and assumes incremental probability only when all the required attributes have been simultaneously mastered; the DINO model also has two parameters per item, and assumes incremental probability when at least one required
attribute has been mastered; the other three CDMs (i.e., A-CDM, LLM, and R-RUM) all have  parameters for item j, and assume additive contributions of the parameters to
parameters for item j, and assume additive contributions of the parameters to  based on different link functions.
based on different link functions.
Specifically, the identity, logit and log link is adopted by the A-CDM, LLM, and R-RUM, respectively. More technical details about the above saturated and reduced CDMs can be found in de la Torre (2011) and de la Torre and Chen (2011) .
2.3. Model-Data Fit Evaluation
For inferences from any CDM applied on the assessment to be valid, it is important to evaluate the model-data fit. Two types of misfit are of major concern under the context of diagnostic assessment: Q-matrix and CDM misspecifications. Based on simulation study from Chen, de la Torre, and Zhang (2013) , we can separate the fit evaluation process into two steps: evaluating the appropriateness of the Q-matrix based on a saturated CDM, and then evaluating the appropriateness of reduced CDMs given an appropriate Q-matrix. To detect possible Q-ma- trix misspecification, we can evaluate the ρ statistics (residual between the observed and predicted Fisher- transformed correlation of item pairs) and the l statistics (residual between the observed and predicted log-odds ratios of item pairs). In addition to evaluate the whole Q-matrix, we also found that these two statistics can give hints about the problematic q-vectors in case Q-matrix misspecifications exist. Given that an appropriate Q-ma- trix can be identified based on a saturated CDM, the next step is to find appropriate reduced CDMs. Using the above ρ and l statistics, we can similarly evaluate the fit of the reduced CDMs in the absolute sense. The conventional Akaike’s information criterion (AIC; Akaike, 1974 ) and Bayesian information criterion (BIC; Schwarzer, 1976 ) can be also used to compare different CDMs. Finally, a likelihood ratio test (LRT) based on χ2 distribution can be conducted to compare two nested Q-matrices or models.
2.4. Systematic Modeling of Large-Scale Assessment
To model extant assessments for diagnostic purposes, we need to address four critical issues: 1) defining a set of meaningful attributes; 2) constructing an appropriate Q-matrix; 3) obtaining appropriated reduced CDMs; and 4) validation of the fit results. It is understood that the first and second issues cannot be fully separated with extant assessments. Large-scale assessments have an assessment framework that is designed by content experts and has been field-tested. Used with the released items, we can readily construct different initial attributes and Q-ma- trices for evaluation in the first phase. The above absolute (i.e., ρ and l) and relative (i.e., AIC, BIC and LRT) fit measures can be used to ascertain model-data fit. In this phase, if the absolute fit results are generally poor, the relative fit results can give us directions for possible adjustment of the attributes and Q-matrices.
In the second phase, we can redefine the attributes and change the Q-matrix specifications based on the findings of the initial set of attributes. It is possible to construct different Q-matrices based on different initial attributes we choose. Although the different Q-matrix could be equally appropriate, they would result in different interpretation of the final attributes. Many initial attributes based on the assessment framework are intended to be exclusive in that they are defined so that each item can measure a single attribute only. One way to improve absolute fit is to redefine the attributes so that each item can measure multiple attributes. Another way is to combine some initial attributes based on conceptual understanding. Both ways can also lower the typically high interrelations among the initial attributes. In doing so, the attributes can provide more diagnostic information. After fixing the attribute definitions, we can re-specify the Q-matrix and fine-tune individual q-vectors using item-level indices. This fine-tuning is performed until the Q-matrix is acceptable, say, at a significance level of α = 0.05. In the third phase, the selected Q-matrix can be used to evaluate the appropriateness of reduced CDMs using the similar absolute or relative fit measures.
Finally, to ensure that the selected Q-matrix and CDMs are applicable beyond the current data, the above fit results need to be validated using different data. For international assessments like PISA, data from a different country or region with similar culture can be used to validate the fit of the Q-matrix and reduced CDMs. For a national assessment like NAEP or when the sample size is sufficient large (e.g., N > 2000), the original dataset can be separated into two subsets, where one subset can be used for the analysis phases, and the other for the validation phase.
3. Data Description
To provide meaningful diagnostic information using large-scale assessments, released items are needed to construct Q-matrices based on well-defined attributes. We chose PISA 2000 reading assessment because of the large number of released items associated with the assessment (OECD, 2006b) . PISA reading assessment is an international assessment measuring 15-year-old students’ reading achievement, with a focus on students’ ability to apply what they learned in school to their daily activities (OECD, 1999, 2006a) . Booklet 8 and 9 of the assessment are adopted, which consist of 26 released items from six independent articles. Among all participating countries and regions, we found the largest number of examinees in the United Kingdom (UK) using these two Booklets, which will be used for the analysis. Examinees from the United States (US) were chosen to validate the fit results, due to the cultural similarity between these two countries. To ensure the adequacy of the diagnostic information, we remove examinees that missed half or more items on the test, resulting in a sample of 2012 and 802 examinees for the UK and the US, respectively. All data and related technical documents are publicly available in the PISA official web site (http://www.oecd.org/pisa/). We converted the partial-credit items to dichotomous items by considering full credit as successful, and the remaining scores as failure. Table 1 gives a summary of examinees’ responses to the 26 released items for the UK. Response patterns of the US examinees are similar and are omitted to save space.
A salient feature of the response data was the large percentage of missing responses towards the end of the test. To have a clearer picture, a visualization of Table 1 is given in Figure 1. It can be seen that the trends between the missing and failure patterns are remarkably similar towards the end of the test, especially when we exclude multiple-choice items (i.e., Item 19, 20 and 24). Such a pattern suggests that the missing responses near the end are neither ignorable nor uninformative. Additional discussion of the missing responses is given below.
3.1. Modeling Phase One: Initial Attribute Definition and Q-Matrices Construction
An important component of diagnostic modeling is to construct an appropriate Q-matrix based on defined attributes. As a starting point, our language experts employed the five processes (aspects) of reading under the PISA assessment framework (OECD, 1999: pp. 28-32, 2006a: pp. 48-52) as initial attributes. According to the framework, these five interrelated processes are necessary for the full understanding of texts and provided guidance for item design. Table 2 presents their definitions and how they were operationalized during item development. If we treat each process as one attribute, we can obtain a Q-matrix with five attributes and 26 single- attribute items from the released item manual (OECD, 2006b) , which will be called Q1 (see α1 - α5 in Table 3).
Figure 1. Distribution of item responses.
Table 1. Summary of examinees’ responses to the 26 items for the UK.
Notes: M = multiple choice; CR = constructed response; CM = complex multiple choice; %M = missing%; %F = failing%; %S = successful%.
Table 2. Definitions of the five reading processes in pisa reading.
Notes: Summarized from the PISA assessment framework (OECD, 1999: pp. 28-32, 2006a: pp. 48-52) .
Table 3. Eight initial attributes and corresponding item specifications.
Notes: α1 - α5: see Table 2; α6 = related to test speededness; α7 = interpreting non-continuous texts; α8 = number sense.
In addition to the five processes, the PISA framework defined text format like information sheets, tables, diagrams, charts, and graphs as non-continuous texts (OECD, 2006a: pp. 47-48) , of which the first three articles (i.e., R040, R077, and R088) were largely consisted. Hence, our language experts defined an additional initial attribute to interpret non-continuous texts. Furthermore, we noticed that the first and third articles were rich in numbers, and defined another initial attribute as number sense. Lastly, as shown in Table 1 and Figure 1, both the missing and failure patterns tended to increase towards the end of the test. Taking into account that items towards the end are not necessarily increasingly difficult, it suggests that some examinees simply needed more time to answer those items correctly. Accordingly, our language experts created another attribute related to test speededness, which means that the examinees who master the attribute have the ability to fully consider all items within the test time. Assuming that the examinees finish the items in order, the attribute would be required to answer the last seven items in the last two articles successfully. Altogether, we constructed eight initial attributes with their item specifications shown in Table 3.
Based on these attributes, we created five additional Q-matrices for evaluation, all of which contain Q1 as a subset, as shown in Table 4. Conceptually, these six Q-matrices can be divided into three hierarchical layers: 1) Q1 (first five attributes); 2) Q2, Q3, and Q4 (adding one attribute); and 3) Q5 and Q6 (adding two attributes). Note that α7 and α8 were not used together in the same Q-matrix because the latter is just a subset of the former with the current set of released items. With these Q-matrices, we can evaluate the model-data fit using the saturated model and corresponding fit statistics as discussed in the Background Section. Table 4 presents the fit results using these Q-matrices. As expected, none of the Q-matrices can be accepted at 0.01 significant level based on either the r or l statistics. In addition, the number of items with poor fitting values is not small for any Q-ma- trix. However, we can see the direction of improvement from the first to the third layer based on relative fit results (i.e., AIC, BIC). Based on their nested relationships and the LRT, we found that: 1) any of Q2, Q3, or Q4 was significantly better than Q1; 2) Q5 was significantly better than Q2 or Q3; and 3) Q6 was significantly better than Q2 or Q4 (p ≈ 0 in all cases). Based on the above results, we can choose either Q5 or Q6 as a basis to finalize the attribute definitions and Q-matrix specifications in the next phase.
Table 4. Model-data fitting results for Q1 to Q6.
Note: −2LL: −2 × log-likelihood; df: degree of freedom; Max. z(r) & Max. z(l): maximum z score for r and l; #z(r) & #z(l): number of items with Max. z(ρ) and Max. z(l) at p < 0.01; critical z score = 4.17 for α = 0.01 (with the Bonferroni correction of 26 × 25 comparisons).
3.2. Modeling Phase Two: Final Attribute Definition and Q-Matrix Construction
The only difference between Q5 and Q6 is the use of either α7 or α8. Our language experts found that either one can help to construct an appropriate Q-matrix, but will result in different attribute interpretations. In this research we select Q6 because α8 can help to interpret the final attributes in a more straightforward way. Specifically, we noticed that α8 can be conceptually incorporated into α4, because number sense is exactly one type of external knowledge that is needed to interpret the article. By combining α4 and α8 (i.e., α4 + α8 >1) together as new α4, we transformed Q6 into a six-attribute Q-matrix Q7. The relative fit for Q7 was worse than that for Q6 based on LRT (p ≈ 0) or the BIC, and the absolute fit for Q7 was even further away from an acceptable value compared with Q6 (Table 5). But we did find one improvement: In Q6 the first five attributes were highly interrelated (Table 6), which implied that limited diagnostic information on these five attributes can be obtained because mastering any of them suggests a large chance of mastering them all. In Q7, α4 was separated out from the other four attributes with lower values in the correlation matrix (Table 6).
To improve the absolute fit of Q7, our language experts adjusted the definitions of the first five attributes. We redefined α4 to focus on number sense only, and extended α5 to cover both the form and content of a text. Attributes α1 to α3 were also adjusted and the revised definitions are given in Table 7. One major change was to make the original definitions less exclusive so that the items could measure multiple attributes. With these adjustments, the absolute fit of the adjusted Q-matrix was much closer to the acceptable value. After that, we utilized suggestions from the item-level ρ and l statistics to fine-tune the Q-matrix. We also found that items with large guessing parameters (i.e., P(0)) can provide useful hints to adjust specific q-vectors. Note that we adopted suggestions or hints to change the corresponding q-vectors only if they were consistent with the adjusted definitions. The specifications of the resulting Q-matrix Q8 can be found in Table 8.
The final fit results are given in Table 5, which suggest that the model is above a 5% significance level based on either ρ or l. As shown in Table 9, the correlations of attribute mastery are more reasonable (0.46 - 0.8). It is interesting to see that α4 is the most difficult attribute to master (i.e., lowest prevalence), whereas α1 is the easiest one. Meanwhile, 40% of examinees failed to master α6 (i.e., need more time to fully consider all items). Table 10 presents the estimates of item parameters based on Q8. The difference in the probabilities of success between examinees who have all the required attributes and those who have none, as in, P(1) - P(0), was at least 0.35 for all items and at least 0.5 for 21 items, with a mean difference of 0.59. These results indicate that the items in the test are relatively diagnostic. Item 13 and 26 are the most difficult items, with a P(1) of 0.4 or lower. It can be seen that the guessing (i.e., P(0)) for some items (i.e., Item 1, 4, 6, 14, 16, 17, and 19) are rather large. It should not be surprising to find out that the large guessing parameters are mostly associated with multiple- choice items, except for 14, which is a complex multiple-choice item.
3.3. Modeling Phase Three: Reduced CDM Evaluation
In this phase we attempted to obtain more interpretable reduced CDMs for the released items based on Q8. Test-level relative and absolute fit results are presented in Table 11. The LLM had both the best relative and absolute fit whereas the DINO model had the worst. It is worth noting that the DINA model, which is the most widely used CDM, was only second to the worst. But none of the reduced CDMs can be accepted for the entire
Table 5. Model-data fitting results for Q7 to Q8.
Note: critical z score = 3.61, 3.78, and 4.17 for α = 0.1, 0.05, and 0.01, respectively (with the Bonferroni correction).
Table 6. Correlations of attribute mastery for Q6 and Q7.
Notes: Upper diagonal for Q6; lower diagonal for Q7.
Table 7. Adjusted definitions for α1 - α5.
Table 8. Attribute specifications for Q8.
Notes: α1 - α5: see Table 6; α6 = related to test speededness; underscored entries are different from Q1.
Table 9. Attribute mastery correlations and prevalence for Q8.
Notes: AP = attribute prevalence.
Table 10. Items’ probability of success for different reduced attribute vectors.
Table 11. Test-level reduced model fitting.
Note: critical z score = 4.17 for α = 0.01 (with the Bonferroni correction).
test at a 0.01 significance level, although the LLM was relatively close. This implied that the test might consist of items that were appropriate with different reduced CDMs, and possibly a saturated CDM. More specific item- level fit evaluation might be needed to determine appropriate reduced models for each item, which is beyond the scope of this paper.
3.4. Modeling Phase Four: Cross-Validation
In this phase, we cross-validated the fit results of the final Q-matrix and reduced CDMs using different data. Examinees from the US were used, and the fit results based on the final Q-matrix are shown in Table 12. Considering the differences of the sample size and educational system between the UK and US, the results can be considered quite similar. Specifically, for both countries: 1) the final Q-matrix based on the saturated model can be accepted at 0.05 significance level; and 2) the test-level fit of the reduced CDMs based on either relative or absolute fit measures followed a similar ranking (i.e., the LLM is better than the R-RUM or A-CDM, both of which are better than the DINA or DINO model).
4. Discussions
This research proposed a systematic procedure for modeling extant large-scale assessments for diagnostic purposes. The procedure can be divided into four phases, namely, initial attribute definition and Q-matrices construction, final attribute definition and Q-matrix construction, reduced CDM evaluation, and cross-validation. In the procedure, we adopted and integrated recent methodological developments in cognitive diagnosis modeling, including the development of general and reduced CDMs, various absolute and relative fit measures, and a general Q-matrix validation procedure. The PISA reading assessment was employed to demonstrate the modeling procedure in practice, which resulted in attributes with meaningful definitions and an appropriate Q-matrix. The modeling procedure can be generalized to other large-scale assessments like NAEP or TIMSS and/or other domain areas like mathematics or science, provided that adequate initial attributes and released items can be found. The current dichotomous attributes can be also extended to expert-defined polytomous attributes (Chen & de la Torre, 2012) based on the five-level reading processes in the PISA assessment framework (OECD, 2006a: p. 61) to provide more useful diagnostic information, given that more item information is available. We have a note of caution in determining the Q-matrix specification: if we only rely on the indices to adjust the q-vectors, it is possible to obtain a Q-matrix which has an acceptable absolute fit but is theoretically incorrect (i.e., the attribute specifications for some items are not consistent with the attribute definitions). Accordingly, it is important for researchers to also exercise subjective judgment and not solely rely on objective criteria to make sure that the changes in the attribute specifications are always consistent with how the attributes have been defined.
In addition to some practical implications, this research also highlights a few issues that, when adequately addressed, can improve existing CDM methodologies. First, here we estimate the joint distribution of all attributes, which would be cumbersome as the number of attributes becomes large. Finding a more efficient way to estimate the attribute distributions could help us to detect the attributes’ relationship more easily. Second, the number of items is important for CDMs in providing accurate classification of the examinees. To accommodate more released items from large-scale assessments, design issues such as missing data across multiple booklets and varying sampling weights need to be addressed. This would require modifying existing CDM procedures (e.g., calibration, Q-matrix validation) to effectively handle these issues.
Table 12. Q-matrix and reduced CDMs fitting for the US.
Note: critical z score =3.61, 3.78, and 4.17 for α = 0.1, 0.05, and 0.01, respectively (with the Bonferroni correction).
To the extent possible, large-scale assessment data should be harnessed to provide information of additional practical value, considering the sizeable amount of resources invested in collecting them. With the recent CDM developments, we are in a better position to utilize extant large-scale data for diagnostic purpose. However, most large-scale assessments are still designed based on unidimensional IRM. Although current CDM developments allow them to be retrofitted more effectively compared to a few years ago, we are cognizant that retrofitting of any CDM to data that were not originally designed to provide diagnostic information will always provide less than ideal results. With the maturation of CDM methodologies, it appears that now is a propitious time to incorporate these methodologies into the development of large-scale assessments so that the assessments can provide optimal diagnostic information.
Acknowledgements
This research was supported by Sun Yat-sen University Start-Up Grant No. 26000-18801031.
Cite this paper
JinsongChen,Jimmy de laTorre, (2014) A Procedure for Diagnostically Modeling Extant Large-Scale Assessment Data: The Case of the Programme for International Student Assessment in Reading. Psychology,05,1967-1978. doi: 10.4236/psych.2014.518200
References
- 1. Akaike, H. (1974). A New Look at the Statistical Identification Model. IEEE Transactions on Automated Control, 19, 716-723.
http://dx.doi.org/10.1109/TAC.1974.1100705 - 2. Chen, J., & de la Torre, J. (2012). An Extension of the G-DINA Model for Polytomous Attributes. Paper Presented at the Annual Meeting of American Educational Research Association, Vancouver.
- 3. Chen, J., & de la Torre, J. (2013). A General Cognitive Diagnosis Model for Expert-Defined Polytomous Attributes. Applied Psychological Measurement, 37, 419-437.
http://dx.doi.org/10.1177/0146621613479818 - 4. Chen, J., de la Torre, J., & Zhang, Z. (2013). Relative and Absolute Fit Evaluation in Cognitive Diagnosis Modeling. Journal of Educational Measurement, 50, 123-140.
http://dx.doi.org/10.1111/j.1745-3984.2012.00185.x - 5. de la Torre, J. (2008). An Empirically-Based Method of Q-Matrix Validation for the DINA Model: Development and Applications. Journal of Educational Measurement, 45, 343-362.
http://dx.doi.org/10.1111/j.1745-3984.2008.00069.x - 6. de la Torre, J. (2011). The Generalized DINA Model Framework. Psychometrika, 76, 179-199.
http://dx.doi.org/10.1007/s11336-011-9207-7 - 7. de la Torre, J., & Chen, J. (2011). Estimating Different Reduced Cognitive Diagnosis Models Using a General Framework. Paper Presented at the Annual Meeting of the National Council on Measurement in Education, New Orleans.
- 8. de la Torre, J., & Chiu, C.-Y. (2010). A General Method of Empirical Q-Matrix Validation Using the G-DINA Model Discrimination Index. Paper Presented at the Annual Meeting of the National Council on Measurement in Education, Denver.
- 9. de la Torre, J., & Lee, Y.-S. (2010). Item-Level Comparison of Saturated and Reduced Cognitive Diagnosis Models. Paper Presented at the Annual Meeting of the National Council on Measurement in Education, Denver.
- 10. DiBello, L., Roussos, L., & Stout, W. (2007). Cognitive Diagnosis Part I. In C. R. Rao, & S. Sinharay (Eds.), Handbook of Statistics (Vol. 26): Psychometrics (pp. 979-1030). Amsterdam: Elsevier.
- 11. Haertel, E. H. (1989). Using Restricted Latent Class Models to Map the Skill Structure of Achievement Items. Journal of Educational Measurement, 26, 301-321.
http://dx.doi.org/10.1111/j.1745-3984.1989.tb00336.x - 12. Hartz, S. (2002). A Bayesian Framework for the Unified Model for Assessing Cognitive Abilities: Blending Theory with Practicality. Unpublished Doctoral Dissertation, University of Illinois at Urbana-Champaign.
- 13. Henson, R. A., Templin, J., & Willse, J. (2009). Defining a Family of Cognitive Diagnosis Models Using Log-Linear Models with Latent Variables. Psychometrika, 74, 191-210.
http://dx.doi.org/10.1007/s11336-008-9089-5 - 14. Jang, E. E. (2009). Cognitive Diagnostics Assessment of L2 Reading Comprehension Ability: Validity Arguments for Fusion Model Application to Langu Edge Assessment. Language Testing, 26, 31-73.
http://dx.doi.org/10.1177/0265532208097336 - 15. Junker, B. W., & Sijtsma, K. (2001). Cognitive Assessment Models with Few Assumptions, and Connections with Non-Parametric Item Response Theory. Applied Psychological Measurement, 25, 258-272.
http://dx.doi.org/10.1177/01466210122032064 - 16. Kunina-Habenicht, O., Rupp, A. A., & Wilhelm, O. (2012). The Impact of Model Misspecification on Parameter Estimation and Item-Fit Assessment in Log-Linear Diagnostic Classification Models. Journal of Educational Measurement, 49, 59-81.
http://dx.doi.org/10.1111/j.1745-3984.2011.00160.x - 17. Lee, Y., & Sawaki, Y. (2009). Application of Three Cognitive Diagnosis Models to ESL Reading and Listening Assessments. Language Assessment Quarterly, 6, 239-263.
http://dx.doi.org/10.1080/15434300903079562 - 18. Maris, E. (1999). Estimating Multiple Classification Latent Class Models. Psychometrika, 64, 187-212.
http://dx.doi.org/10.1007/BF02294535 - 19. OECD (1999). Measuring Student Knowledge and Skills: A New Framework for Assessment. Paris: Organization for Economic Cooperation and Development.
- 20. OECD (2006a). Assessing Scientific, Reading and Mathematical Literacy: A Framework for PISA 2006. Paris: Organization for Economic Cooperation and Development.
- 21. OECD (2006b). PISA Released Items: Reading.
http://www.oecd.org/pisa/38709396.pdf - 22. Schwarzer, G. (1976). Estimating the Dimension of a Model. Annals of Statistics, 6, 461-464.
http://dx.doi.org/10.1214/aos/1176344136 - 23. Tatsuoka, K. K. (1983). Rule Space: An Approach for Dealing with Misconceptions Based on Item Response Theory. Journal of Educational Measurement, 20, 345-354.
http://dx.doi.org/10.1111/j.1745-3984.1983.tb00212.x - 24. Tatsuoka, K. K. (1990). Toward an Integration of Item-Response Theory and Cognitive Error Diagnosis. In N. Frederiksen, R. Glaser, A. Lesgold, & M. Safto (Eds.), Diagnostic Monitoring Skills and Knowledge Acquisition (pp. 453-488). Hillsdale, NJ: Erlbaum.
- 25. Templin, J., & Henson, R. A. (2006). Measurement of Psychological Disorders Using Cognitive Diagnosis Models. Psychological Methods, 11, 287-305.
http://dx.doi.org/10.1037/1082-989X.11.3.287 - 26. von Davier, M. (2008). A General Diagnostic Model Applied to Language Testing Data. British Journal of Mathematical and Statistical Psychology, 61, 287-307.
http://dx.doi.org/10.1348/000711007X193957
NOTES
*Corresponding author.




