Wireless Engineering and Technology
Vol.06 No.03(2015), Article ID:58036,10 pages
10.4236/wet.2015.63006
Wireless Power Transmission into Metallic Tube Using Axial Slit for Infrastructure Diagnostics
Kohei Shimamura1, Kimiya Komurasaki2
1Department of Engineering Mechanics and Energy, University of Tsukuba, Tsukuba, Japan
2Department of Aeronautics and Astronautics, The University of Tokyo, Tokyo, Japan
Email: shimamura@kz.tsukuba.ac.jp, komurasaki@al.t.u-tokyo.ac.jp
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 5 June 2015; accepted 12 July 2015; published 16 July 2015
ABSTRACT
Wireless power transfer (WPT) using a metallic tube with axial slits was attempted to demonst- rate WPT using magnetic resonance coupling to the diagnostics infrastructure. The transmission efficiency was measured at various distances using the transmission and receiver resonator in the tube. Furthermore, the transmission and receiver resonator were set respectively outside and inside of the tube. Experiment results were assessed computationally using the finite-difference time-domain (FDTD) simulation. As a result, the transmission efficiency of the transmitter and receiver resonators in the metallic slit tube was higher than that of the case without a metallic tube in the range of the normalized transmission-distance of x/d > 0.4. In the simulation, the current density on the metallic tube around both transmitter and receiver coil were connected. These results reveal that the slit on the tube plays a role of the relay coil.
Keywords:
Wireless Power Transmission, Magnetic Resonance Coupling, Infrastructure Diagnostics

1. Introduction
In recent years, accidents caused by the collapsed or damaged infrastructure facilities have been observed in economically developed countries [1] . In Japan, large-scale collapse accidents might occur in the future because most infrastructure facilities installed during the high economic growth era had a 40 - 50-year designed lifetime. Equipment maintenance to prevent accidents has come to present financial and technical difficulties [2] . To maintain the old infrastructure and to prevent large-scale accidents, automated inspection techniques using wireless power transmission technology have been considered. For example, Tsuno et al. proposed a system to monitor tunnel deformation by installing wireless sensors [3] . Kuroda et al. examined wireless power transmission to an inspection robot in a power plant pipe [4] .
Benefits of wireless power transmission include non-destructive inspection and lack of interference with existing infrastructure posed by cables, in addition to measurement and inspection of multiple points of the huge infrastructure. An electromagnetic induction type charger has a sensing device for metallic obstacles and a function to stop the power transmission automatically. Zangl et al. conducted power transmission experiments using electromagnetic induction through metal with 50 Hz power source, which has a long penetration depth into metal [5] . For this experiment, the transmission efficiency and power were not high because the excitation frequency was non-resonant.
The magnetic resonant coupling techniques are useful for the non-contact and non-destructive infrastructure investigation of concrete and its internal reinforcement. Using 10 kHz frequency, transmission in a space of 10 cm is possible at high efficiency using conventional electromagnetic induction. Wireless power transmission via magnetic resonant coupling can achieve power transmission by several meters with high efficiency [6] [7] . Since 2007, magnetic resonance coupling techniques have been actively applied to electric vehicles and mobile phones [8] -[12] .
Effects of metal on magnetic resonant coupling have been investigated to improve the transmission efficiency [13] [14] . Ishida et al. have used frequencies of 60 Hz power transmission through reinforced concrete walls [15] . Our previous studies demonstrated that power transmission efficiency of 43% was achieved through a 1.0 mm SUS plate and of 10% into a 5.0-mm-thick metal plate using magnetic resonance coupling at AC frequency of 50 Hz [16] . Transmission efficiency of the magnetic resonant coupling system in the high-frequency band is widely used in much research because it is superior to other frequency bands.
To investigate the infrastructure diagnosis by wireless power transmission technology using a high-frequency band, we proposed a power transmission system to a closed metal space containing a non-dielectric slit. Because it is difficult to transmit power through the metal tube at a high-frequency band, a slit shape was introduced into the metal tube, which served as the relay coil. Relay coils have been studied widely for use in extending the transmission distance [17] -[19] .
It is possible to replace a slit shape pipe proposed for the present study with a part of the existing pipe. The power can be transmitted without contact to the measuring instruments in the pipe. As presented in Figure 1, long-term operation without a battery can be achieved because the infrastructure-diagnostic device can be charged from the input spot. To replace the conventional tube to these input spots, a pipe structure with a reinforced plastic slit can be regarded as a non-dielectric slit in the metal tube.
Figure 1. Application of the wireless power transfer in the metal tube with axial slit.
For this study, we obtained a design guideline of the slit metal tube with changing of the metallic material, the length and diameter of the tube, and the resonators. Then, the current density was evaluated using numerical calculations of FDTD to investigate the difference between the presence and absence of the slit on the metallic tube.
2. Experimental and Numerical Condition
2.1. Power Transmission System
The transmitter and receiver resonator in the tube were made from a 3-mm-diameter copper-rod and a 470 pF mica-capacitor, which is compatible with high frequencies. The diameter of these resonators was 115 mm. The resonant frequency, shape, diameter, and capacitance of the capacitor were the same for the pick-up and excitation coil. Furthermore, the transmitter resonator made from 200 pF capacitor had diameter of 215 mm outside the tube. The configuration of the excitation coil outside of the tube was identical to that of the resonator.
The Q-factor and the resonance frequency were measured using a vector network analyzer (DG85AQ; SDR- Kits, Inc.) and a one-turn inductive coil with inductance that was much smaller than that of the resonator. The diameter and radius of the inductive coil cross-section were, respectively, 120 mm and 1.0 mm. The resonator was put between two inductive coils at even intervals. The inductive coils were then connected to the vector network analyzer. The Q-factor was obtained using Q = f0/(f2 − f1), where f2 − f1 is the FWHM of the resonant curve [20] .
Table 1 and Table 2 present specifications of the transmitter and receiver resonator with and without slits, and without the metal tube. Without the metal tube, the resonance frequency and Q-factor of the transmitter and receiver resonators were, respectively, 13.712 and 13.695 MHz, and 332 and 322. These values were almost identical as the estimated values. The transmission efficiency is expressed as the product of the resonator Q- value and the coupling coefficient k between the resonators as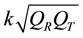 . A high Q-factor and coupling coefficient are necessary to obtain high transmission efficiency. For the slit tube, the resonance frequency was shifted to 14.1 MHz. The Q-factor of transmitter and receiver resonator was 190, which was less than that of the test without the metallic tube because the outer metallic tube served as a dielectric: it affected the resonator electric field. The resonance curve was impossible to measure with a slit-free metallic tube.
. A high Q-factor and coupling coefficient are necessary to obtain high transmission efficiency. For the slit tube, the resonance frequency was shifted to 14.1 MHz. The Q-factor of transmitter and receiver resonator was 190, which was less than that of the test without the metallic tube because the outer metallic tube served as a dielectric: it affected the resonator electric field. The resonance curve was impossible to measure with a slit-free metallic tube.
2.2. Transmission Efficiency and S Parameter Measurement
Transmission efficiency was calculated from the S-parameters obtained by the network analyzer. The output port and input port of the network analyzer were connected to the transmission and receiver side of the resonator,
Table 1. Specifications of Transmitter (TX) and receiver (RX) resonator in the tube.
Table 2. Transmitter resonator outside of the tube.
respectively. The transmission efficiency η was determined with measured S21,
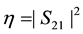 (1)
(1)
Figure 2 shows a schematic of the two power transmission systems. In Figure 2(a), both resonators were put in the metallic tube. In Figure 2(b), the transmitter resonator is put outside of the metallic tube; the receiver resonator was put in the tube. A 0.1-mm-thick stainless steel sheet (SUS304, containing nickel and chromium of 8% - 10.5% and 18% - 20%, respectively) was used because high-frequencies such as 13.70 MHz cannot penetrate the metal [21] . The outer diameter and slit width of the metallic tube were, respectively, 180 and 10 mm. The resonators in the tube were fixed on an acrylic disk. The distance between the pick-up coil and the resonator and between the excitation coil and the resonator was 5 mm. The resonator outside of the tube was fixed on the polystyrene plate. The large resonator was 10 mm distant from the excitation coil. To ascertain the transmission efficiency, the transmission distance between the two resonators was normalized by the resonator diameter.
2.3. Numerical Method and Condition
The effects of the presence or absence of the slit on the current-density distribution on the surface of the tube and coil were evaluated using the FDTD method with FEMTET® (Murata Mfg. Co. Ltd.). Figure 3 shows the boundary and experimental condition of the FDTD calculation. The calculation configuration was identical to that of the experiment. The metallic tube and the coil were made respectively of stainless steel and copper. The metallic tube was surrounded by a large dry-air sphere. The absorbing boundary condition was applied to the air sphere. The input and output ports of the high-frequency wave were put on the resonators. To simplify the electromagnetic calculation, the configuration of calculation conditions was 15 times larger than that of the experiment. The capacitance at 20.65 pF was put on the coil for the lumped-constant to be set as 13.70 MHz. The normalized distance x/d between two resonators was fixed at 0.9 for both experiments.
The pick-up and excitation coils as presented in Figure 2 were eliminated in the calculation with the appropriate boundary condition. To set the Q-factor as a high value eliminating the effect of the instruments and the termination load on the resonator, excitation and pick-up coils were necessary. The calculation conditions from
Figure 2. Schematics of wireless power transfer (a) in the metallic tube with a slit and (b) from outside to inside of the tube.
Figure 3. Calculation conditions: the boundary condition and materials.
outside to inside were identical to those of the transmission in the tube. To investigate the coil and metal tube diameter effects on the resonance frequency and Q-factor, the dependence of the frequency on S21 at normalized distance x/d = 0.9 was compared between the experiment and calculation in Figure 4. The resonance frequency on the experiment and calculation were 14 MHz. For the calculation, S21 and the efficiency in the experiment were reproduced, respectively, within 1 dB and 10%.
3. Power Transmission System Design
3.1. Distance between the Resonator and the Tube D/d
Figure 5(a) portrays the dependence of the normalized diameter D/d on the transmission efficiency η and the resonance frequency f0, where D stands for the metallic tube diameter. The transmission distance and slit width were fixed, respectively, at 115 mm and 10 mm. The stainless steel metallic tube was used.
The transmission efficiency decreased with increasing normalized diameter. At D/d = 2.0, the transmission efficiency was 0.3, which was identical to the experiment without the metallic tube. The resonance frequency was shifted from 13.70 MHz with decreasing D/d. At D/d = 1.25, the resonance frequency was 15.10 MHz. As with η, f0 approached to the designed value with increasing D/d. Also, f0 was 13.53 MHz in the range of D/d > 2.0. As a result of η and f0, the metallic tube has no effect on the power transmission in the range of D/d > 2.0. To design a high-efficiency power transmission system, D/d should be as small as possible.
3.2. Slit Width δ
Figure 5(b) presents the effect of slit width δ on the transmission efficiency at D/d = 1.6 and x/d = 1.0 using the stainless steel tube. This figure shows the slit angle θ instead of the slit width. The slit width only slightly affects the transmission efficiency. η was 0.5 for θ < 90. With increasing θ, η decreased slightly; η was 0.3 without the metallic tube.
3.3. Metallic Material
Figure 5(c) portrays the effects of the metallic material on the transmission efficiency using the magnetic
Figure 4. Verification of the FDTD simulation compared with the experimental results. Normalized distance x/d = 0.9.
Figure 5. Effects of (a) distance between a resonator and metal tube; (b) slit width; and (c) metal difference on the transmission efficiency and resonance frequency.
(stainless steel) and non-magnetic (aluminum and copper) materials with D/d = 1.6, x/d = 1.0, and δ = 10 mm. The aluminum, copper, and stainless steel are often used in the piping of structures. The metallic sheet in this experiment was 0.1-mm thick because the respective penetration depths of the copper, aluminum, and stainless were 65, 83, and 12 μm at 1 MHz frequency. No differences were observed among metallic materials. η of non-magnetic materials was slightly higher than that of magnetic materials.
4. Axial Slit Effects on the Current Density Distribution on the Metal Tube Surface
4.1. Characteristics of the Frequency on the S Parameter
Figure 6 presents the measurement results of S21 (solid line) and S11 (dotted line) of the two experimental conditions using the vector network analyzer. This figure shows the condition without a metallic tube, with a metallic tube, and with a metallic tube using the axial slit. The black, blue, and red lines respectively portray x/d = 0.3, 0.4, and 0.9.
As S11 shows in Figure 6, the critical coupling condition was observed at x/d = 0.4. The characteristic of the resonant curve was shifted from diphasic to monomodality. When the two peaks of resonance frequency were observed (tightly coupled state), it was possible to transfer the power at 90% efficiency [12] . However, the transmission efficiency decreased markedly with increasing transmission distance when the single peak of the resonance frequency was observed. Without a metallic tube, the resonance frequency was almost equal to the designed frequency at 13.70 MHz. Using the metallic tube with and without slits, the respective resonance frequencies were 14.1 and 14.4 MHz. The efficiency using the metallic slit tube was slightly lower with increasing distance than without using the metallic tube.
Figure 7 shows S11 and S21 curves in the power transmission from outside to inside. The same tendency as that of Figure 6 was observed in Figure 7. Using the metallic non-slit tube, S21 was −30 dB at x/d = 0. Using the metallic slit tube, S21 was slightly lower than that shown in Figure 6.
Figure 6. In the tube experiment, the power transmission S21 and reflection S11 parameter as a function of the frequency in the case of (upper) normal condition (without the metal tube), (middle) the metal tube with axial slit and (lower) the metal tube without axial slit.
Figure 7. From outside to inside experiment, power transmission S21 and reflection S11 parameter as a function of the frequency in the case of (upper) normal condition (without the metal tube), (middle) the metal tube with axial slit and (lower) the metal tube without axial slit.
4.2. Relation between the Transmission Efficiency and Distance
Figure 8 presents the measurement result of the transmission efficiency for a non-metal tube, the slit metal tube, and the non-slit metal tube. The transmission efficiency was obtained using η = |S21|2. In Figure 8(a), η was 80% - 90%, independent of the presence of the metallic tube for x/d < 0.4. For the non-slit tube, η was decreased markedly in the range of x/d > 0.4 and was 0 at x/d = 1. Without the metallic tube, η was slightly decreased up to x/d = 1.5. However, η was 40% at x/d = 1.5 for the metallic slit tube; it was higher than that of the non-metallic tube.
In Figure 8(b), high η was observed for x/d < 0.2, but η was 0 at x/d = 0 for the non-slit tube. As shown in Figure 8(a), η of the slit metal tube was higher than that of the case of the non-slit metal tube because the metallic tube served as a relay coil. This effect was observed markedly with increased transmission distance. The current was decreased because of the radiation and conductor loss of the metal surface. Therefore, η of the slit metal tube was lower than that of the case the non-slit tube for x/d < 0.4. In Figure 8(b), η of the non-slit metal tube was almost 0 because the penetration depth of the high frequency at 13.7 MHz on the metal surface was less than the metal tube thickness (0.1 mm).
4.3. Calculation Results of the Current Density Distribution
To investigate the power transmission mechanism in the case of the slit metal tube, the current density was calculated using the FDTD method, as shown in Figure 9 and Figure 10. The cases of (a) and (b) respectively show calculations for tubes with and without slits. The color change in the figure corresponds to the value of the logarithmic color bar. The current density is expressed as a vector with magnitude shown as the magnitude of arrows. The transmitter and receiver coils were put, respectively, on the lower and upper side of figure.
As shown in Figure 9(a), the induced current flow around the tube surface of each coil was observed in the circumferential direction. The current flow around the coil was connected through the tube slit. However, in
Figure 8. Transmission efficiency vs. transmission distance: Wireless power transfer (a) in the tube and (b) from outside to inside tube.
Figure 9. Density distribution of the magnetic current on the tube surface (a) with the axially slit and (b) without slit. Wireless power transfer in the tube.
Figure 9(b), coupling between the coils was canceled by demagnetization of the induced current around the tube surface.
Similar behaviors between the induced current and coupling phenomena are shown in Figure 10(a) and Figure 10(b). The induced current was not observed in Figure 10(b) because the 13.7 MHz high frequency signal
Figure 10. Density distribution of the magnetic current on the tube surface (a) with the axially slit and (b) without slit. Wireless power transfer from outside to inside of the tube.
was unable to pass through the metal of about 0.1 mm thickness.
Results reveal that the coupling coefficient between the resonators was increased by the current flow through the axial slit in the metal tube. Consequently, the axial slit serves as a relay coil. The experiment using the metal tube without the slit, however, shows the strong magnetic field on the center axis because of the induced current of the tube surface. The magnetic field cancels out the effects of coupling between the resonators. Therefore, the transmission efficiency using the slit metal tube was higher than that without the tube for x/d > 0.4 because the metallic tube serves as the relay coil.
5. Conclusions
The influence of the slit width and metallic materials on the transmission efficiency was small. The transmission efficiency and the resonance frequency were investigated with changing transmission distance and distance between the resonator diameter and the metal tube diameter. Results show that the transmission efficiency increased with the decrease of the transmission distance. Furthermore, the transmission efficiency without the metal tube was equal to that of the case in which the metal tube diameter was twice as large as the resonator. Furthermore, the transmission efficiency of the transmitter and receiver resonators in the metallic slit tube was higher than that of the case without a metallic tube in the range of the normalized transmission-distance of x/d > 0.4.
Calculation results show that the induced electric current flowing through the tube surface around the transmitter and receiver resonator was connected through the slit in the case of the metallic slit tube. The transmission distance and efficiency are attributable to the metallic tube, which serves as a relay coil. The power transmission in the tube and into the tube using the metallic tube without a slit was slight because the magnetic field generated by the strong induced electric current reduces the coupling effect between the resonators.
Acknowledgements
This work is supported by the research grant of the Obayashi Foundation.
Cite this paper
KoheiShimamura,KimiyaKomurasaki, (2015) Wireless Power Transmission into Metallic Tube Using Axial Slit for Infrastructure Diagnostics. Wireless Engineering and Technology,06,50-60. doi: 10.4236/wet.2015.63006
References
- 1. Inoue, M. and Fujino, Y. (2010) Study of Social Impact of the I-35W Bridge Collapse in Minneapolis. Journal of Construction Management and Engineering, 66F, 14-26. (In Japanese). http://dx.doi.org/10.2208/jscejf.66.14
- 2. Maruyama, H. (2010) Requirements for Enhancement of Durability and Elongation of Lifetime of Infrastructure. Journal of Prestressed Concrete, Japan, 52, 34-37. (in Japanese)
- 3. Tsuno, K., Kamachi, H. and Nakanishi, Y. (2009) Monitoring System for Deformed Tunnel Using Wireless Sensor Network. Proceedings of Tunnel Engineering, 19, 245-249. (in Japanese)
- 4. Kuroda, T. (2010) Creation of High-Performance Ultra-Low-Power Short-Rage Wireless Mobile Information Systems. IPSJ Magazine, 51, 861-869. (in Japanese)
- 5. Zangl, H., Fuchs, A., Bretterklieber, T., Moser, M.J. and Holler, G. (2010) Wireless Communication and Power Supply Strategy for Sensor Applications within Closed Metal Walls. IEEE Transactions on Instrumentation and Measurement, 59, 1686-1692. http://dx.doi.org/10.1109/TIM.2009.2026602
- 6. Kurs, A., Karalis, A., Moffatt, R., Joannopoulos, J.D., Fisher, P. and Soljacic, M. (2007) Wireless Power Transfer via Strongly Coupled Magnetic Resonances. Science, 317, 83-86. http://dx.doi.org/10.1126/science.1143254
- 7. Kurs, A., Moffatt, R. and Soljacic, M. (2010) Simultaneous Mid-Range Power Transfer to Multiple Devices. Applied Physics Letters, 96, Article ID: 044102. http://dx.doi.org/10.1063/1.3284651
- 8. Komaru, T., Koizumi, M., Komurasaki, K., Shibata, T. and Kano, K. (2012) Compact and Tunable Transmitter and Receiver for Magnetic Resonance Power Transmission to Mobile Objects. In: Tech Wireless Power Transfer—Principles and Engineering Explorations, 133-150. http://dx.doi.org/10.5772/28068
- 9. Koizumi, M., Komurasaki, K., Mizuno, K. and Arakawa, Y. (2012) Wireless Power Feeding with Strongly Coupled Magnetic Resonance for a Flying Object. Wireless Engineering and Technology, 3, 86-89. http://dx.doi.org/10.4236/wet.2012.32014
- 10. Yamakawa, M., Shimamura, K., Komurasaki, K. and Koizumi, H. (2014) Demonstration of Automatic Impedance Matching and Constant Power Feeding to and Electric Helicopter via Magnetic Resonance Coupling. Wireless Engineering and Technology, 5, 45-53. http://dx.doi.org/10.4236/wet.2014.53006
- 11. Sample, A.P., Meyer, D.A. and Smith, J.R. (2011) Analysis, Experimental Results, and Range Adaption of Magnetically Coupled Resonators for Wireless Power Transfer. IEEE Transactions on Industrial Electronics, 58, 544-554. http://dx.doi.org/10.1109/TIE.2010.2046002
- 12. Imura, T. and Hori, Y. (2011) Maximizing Air Gap and Efficiency of Magnetic Resonant Coupling for Wireless Power Transfer Using Equivalent Circuit and Neumann Formula. IEEE Transactions on Industrial Electronics, 58, 4746-4752. http://dx.doi.org/10.1109/TIE.2011.2112317
- 13. Yu, X.F., Sandhu, S., Beiker, S., Sassoon, R. and Fan, S.H. (2011) Wireless Energy Transfer with the Presence of Metallic Planes. Applied Physics Letters, 99, Article ID: 214102. http://dx.doi.org/10.1063/1.3663576
- 14. Lee, W.S., Jang, H.S., Oh, K.S. and Yu, J.W. (2013) Close Proximity Effects of Metallic Environments on the Antiparallel Resonant Coil for Near-Field Powering. IEEE Transactions on Antennas and Propagation, 61, 3400-3403. http://dx.doi.org/10.1109/TAP.2013.2247553
- 15. Ishida, H. and Furukawa, H. (2015) Wireless Power Transmission through Concrete Using Circuits Resonating at Utility Frequency of 60 Hz. IEEE Transactions on Power Electronics, 30, 1220-1229. http://dx.doi.org/10.1109/TPEL.2014.2322876
- 16. Yamakawa, M., Mizuno, Y., Ishida, J., Komurasaki, K. and Koizumi, H. (2014) Wireless Power Transmission into a Space Enclosed by Metal Walls Using Magnetic Resonance Coupling. Wireless Engineering and Technology, 3, 86-89.
- 17. Kim, J.W., Son, H.C., Kim, K.H. and Park, Y.J. (2011) Efficiency Analysis of Magnetic Resonance Wireless Power Transfer with Intermediate Resonant Coil. IEEE Antennas and Wireless Propagation Letters, 10, 1609. http://dx.doi.org/10.1109/LAWP.2011.2178876
- 18. Zhang, F., Hackworth, S.A., Fu, W., Li, C., Mao, Z. and Sun, M. (2011) Relay Effect of Wireless Power Transfer Using Strongly Coupled Magnetic Resonance. IEEE Transactions on Magnetics, 47, 1478-1481. http://dx.doi.org/10.1109/TMAG.2010.2087010
- 19. Moon, S., Kim, B.C., Cho, S.Y., Ahn, C.H. and Moon, G.W. (2014) Analysis and Design of a Wireless Power Transfer System with an Intermediate Coil for High Efficiency. IEEE Transactions on Industrial Electronics, 61, 5861-5870. http://dx.doi.org/10.1109/TIE.2014.2301762
- 20. Pozar, D.M. (2011) Microwave Engineering. 4th Edition. Wiley, New York.
- 21. Balanis, C.A. (2005) Antenna Theory: Analysis and Design. 3rd Edition, Wiley-Interscience, New York.












