Wireless Engineering and Technology
Vol.05 No.04(2014), Article ID:50344,6 pages
10.4236/wet.2014.54013
Analysis and Impact of Surface Acoustic Wave Filter in-Band Ripple on Testing and Measurement of High Data Rate Communications
Taher Al Sharabati
Al-Ahlyya Amman University, Amman, Jordan
Email: sharabat@email.sc.edu
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 July 2014; revised 19 August 2014; accepted 5 September 2014
ABSTRACT
In this paper, we present a background and theory of the effect of Surface Acoustic Wave (SAW) Filter Module (SFM) in-band ripple on high data rate communications parameters such as the Error Vector Magnitude (EVM). In addition, we present analyses and statements for the choice of unbalanced S-parameters set of the SFM over balanced S-parameters set of the SFM in measurements and Agilent’s Advance Design System (ADS) Ptolemy simulations. A test and measurement setup using Agilent’s equipment will be presented.
Keywords:
SAW Filters, EVM, ADS, S-Parameters, Baluns, 3 GPP, In-Band Ripple, High Speed Data Packet Access (HSDPA)

1. Introduction
SAW filters play an important role in today’s front-end radio frequency designs of wireless communications. Requirements by mobile phones like increased data rates make it stringent on RF filters to satisfy these conditions. RF SAW filters meet the demands of increased bandwidth, frequency and higher data rates [1] . Their high stop band rejection and in band insertion loss make their applications span across a variety of commercial and military products. In addition, their low cost make them an attractive choice for high volume products. They are based on acoustic wave technology where information is carried on the surface of the piezoelectric crystal.
As said above, SAW filter technologies are based on piezoelectric substrate as shown in Figure 1 where the
Figure 1. Basic SAW filter structure on a piezoelectric substrate.
metal is printed on the piezoelectric crystal substrate [2] .
SAW filters are used in mobile handsets due to their low cost, small size, which save PCB area, and their sharp cut off frequencies. They also provide high attenuation of unwanted signals [3] . An example of SAW filter characteristics is shown in Figure 2. It is proven from the high stop band rejection performance for this filter in this figure. Its in-band insertion loss ranges, nominally, from 0.8 to 1.3 dB.
EVM is an important parameter of the modulation of the received signal and is measured in percentage (%). It is a measurement of transmitter as well as receiver demodulator quality performance in the presence of noise. EVM has become the standard of the demodulator fidelity, especially in high data rate systems; and it is an essential measurement in today’s testing equipment geared towards high data rates measurements. As a matter of fact, it is a specification in many standards, product performance, quality and even passive components (such as SFMs) data sheets and requirements. For example, for NodeB transmitter tests, 3 GPP TS 25.141 specifies EVM to be less that 12.5% due to the 16Q AM modulation scheme used on HS-PDSCH.
Figure 3 best defines EVM. Ideally, the measured IQ vector should be a, but due to perturbations, the measured vector becomes the IQ Constellations. Therefore, a resultant vector called Error Vector along with its phase
error 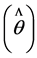 emerge.
emerge.
EVM is stipulated as a part of a body of standards such as the standard of 3 GPP. It is carried out in test equipment such as the Agilent’s N9020A or Rode Schwartz’s R & S FSV instruments. It is carried out after the received symbol passes through two paths; one produces the measured waveform and another produces the reference waveform. Both symbols are produced after being processed by the filtering operation.
2. Analysis
Assume the filter response has a magnitude attenuation, an attenuation (insertion loss) α(f) with root-mean- square (rms) magnitude ripple Δαrms(f) and phase Φ(f) with rms phase ripple ΔΦ(f), then the EVM can be calculated using the following equation [4] ,
 (1)
(1)
where [4] ,
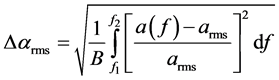
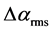 is the effective rms magnitude ripple of the filter attenuation;
is the effective rms magnitude ripple of the filter attenuation;
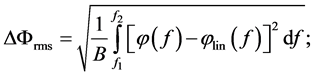
 is the rms phase ripple;
is the rms phase ripple;
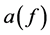 is the magnitude attenuation;
is the magnitude attenuation;
Figure 2. Typical Murata saw filter measured power spec- trum characteristics.
Figure 3. Definition of EVM.
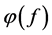 is the unwrapped phase;
is the unwrapped phase;
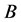 is the filter bandwidth and is equal to
is the filter bandwidth and is equal to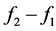 .
.
Figure 4 shows a simulation block diagram of how EVM could be measured by using ADS 3 GPP High Speed Data Packet Access (HSDPA) library of component blocks. It consists of a 3 GPP downlink RF source and a 3 GPP EVM measurement block. Parameters and variables are specified to suit a particular need. This figure is intended to show how, in general, EVM can be measured.
As well known, the S-parameters describe any N port network as they relate incident voltages to reflected voltages at RF and microwave frequencies [5] . This relation is through the S matrix as shown in Equation (2):
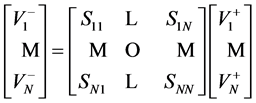 (2)
(2)
S-parameters can be measured using network analyzers and stored as files for later processing and simulation. The file extension convention SnP is used to designate the file as an S-parameters file where n is the number of ports in the network. For example, S2P designate a file extension of measured S-parameters for a two-port network. Figure 5 shows a sample setup of how a 2-port S-Parameters measurement file could be accessed and used in the simulation in Agilent’s ADS.
A balanced input/output has two input/output connectors that are 180˚ out of phase [6] . They are also called differential inputs/outputs. If one input or output is 0˚, then the other input or output has the same amplitude but 180˚ phase shift. While the unbalanced input/output would have only one connector for the input/output signal and the other connector would be connected to ground, as shown in the Figure 6.
With the proper design, transformers are used to transform single ended (unbalanced) to double ended (balanced) connections and vice versa. Other components may be used with the balun to achieve matching. Figure 7 shows a setup of 3-port S-Parameters measurement file and how it could be accessed and used in the simulation in a 100 ohm balanced transformer. In this figure, it is seen how the transformer (TF1) is used to transform the double-ended measured based filter file block (S3P) to a single-ended 100 Ω output port.
Figure 4. Measuring EVM using Agilent’s ADS.
Figure 5. Accessing 2-port measurements in a 50-ohm circuit.

Figure 6. Balanced (a) vs. unbalanced (b) inputs balanced (c) vs. unbalanced (d) inputs.
Figure 7. Accessing and simulating 3-port S-parameters measurements in a 100-ohm balanced transformer.
Figure 8 gives a sample procedure of how a 2-port S-Parameters measured based filter file block (S2P) could be accessed and used in the simulation of EVM in HSDPA environment.
3. SAW Filter EVM Measurements
Figure 9 shows a typical measurement setup for EVM measurements. EVM measurements can be carried out using specialized equipment such as the Agilent’s N5182A Signal Generator shown below and Agilent’s N9020A Vector Signal Analyzer. The SAW filter design would be placed in a prototype PCB for evaluation. However, the signal generator itself has EVM internally generated as shown in Figure 10 [8] , which will affect the SAW filter EVM measurements. Care must be taken to account for the internally generated EVM and factor it in the measurement of the SAW filter total EVM measurements. For example, as Figure 10 shows, a typical value for the EVM out of the instrument for EDGE is 0.7%.
In order to measure the EVM performance of the SAW filter, the SAW filter may need a balun and matching components, to interface it with the 50 Ω instruments and circuits. The balun and matching components will have ripple in the pass band. The ripple will produce EVM as explained in the theory part. Therefore, the balun and the matching components will have their own contributions to the EVM measurement or simulations of SAW filter. Any EVM measurements due to SAW filter parameters should, also, take into consideration the effects of the external elements interfacing the SAW filter prototype to the instruments used. To avoid this, one could end up having to assess EVM performance with unbalanced over balanced measurements.
4. Conclusions
In this review, a background and theory was presented for SAW filters, EVM and the relationship between them. Some specifications of the EVM from the instrument manufacturer as well as the 3 GPP standard were given. The background for balanced-unbalanced terminations was presented. With EVM assessment of unbalanced SAW filters, the use of baluns and matching elements may affect EVM simulations or measurements due to their in band ripple.
This paper gives the designer and the reader insights on the different scenarios of assessing SAW filters when it comes to performance due to the in-band ripple. Of these scenarios is the EVM generated internally by the instruments. Other scenarios are the ripple of the balun and matching components used in the measurement procedure. All of these scenarios will skew off and/or distort the EVM measurements of the SAW filter and hence it will be difficult to give an accurate EVM assessment and specification of the SAW filter performance due to the in band ripple. One solution to this is to ignore the measurement process and resort to ADS Ptolemy simulations
Figure 8. Accessing 2-port measurements file for EVM simulations [7] .
Figure 9. A typical measurement setup for EVM measurements.
Figure 10. Agilent’s N5182A EVM specifications [8] .
using SAW filter measurement based file to do the EVM assessment as shown in Figure 8 [7] .
References
- Satoh, Y., Ikata, O., Miyashita, T. and Ohmori, H. (2011) RF SAW Filters. Fujitsu Labrorites Ltd., Kanagawa.
- Campbell, C.K. (1998) Understanding Surface Acoustic Wave (SAW) Devices for Mobile and Wireless Applications and Design Techniques, Chapter 2. Academic Press, Boston.
- Browne, J. (2008) Understanding SAW Technology for Filters. Penton Media, Inc., New York. http://mwrf.com/components/understanding-saw-technology-filters
- Weigel, R., Schmidt, M., Pimingsddorfer, D. and Maurer, L. On the Role of SAW Devices in Current and Future Radio Systems. Institute for Electronics Engineering, University of Erlangen-Nuremberg, Erlangen and Nuremberg.
- Pozar, D.M. (1998) Microwave Engineering, Chapter 4. 2nd Edition, John Wiley & Sons, Hoboken.
- Sayre, C.W. (2001) Complete Wireless Design, Chapter 8. 2nd Edition, McGraw-Hill, New York.
- Murata (2007) EVM Actual Measurements Data/Simulation. Motorola and Murata Joint Effort Internal Document.
- Agilent Technologies (2012) Agilent N5182A MXG and N5162A MXG ATE Vector Signal Generators Data Sheet. Agilent Technologies, Inc., Santa Clara.










