Wireless Engineering and Technology
Vol.4 No.4(2013), Article ID:37190,10 pages DOI:10.4236/wet.2013.44024
Performance Assessment for LTE-Advanced Networks with Uniform Fractional Guard Channel over Soft Frequency Reuse Scheme
![]()
1Network Planning Department, National Telecommunication Institute, Cairo, Egypt; 2Department of Electrical Engineering, Alazhar University, Cairo, Egypt; 3Department of Electronics and Computer Engineering, HIT, Egypt.
Email: mahammad.safwat@gmail.com, heshamelbadawy@ieee.org, ahmed_yahya_1@yahoo.com, hosni.motaafy@gmail.com
Copyright © 2013 Mahammad A. Safwat et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received July 10th, 2013; revised August 18th, 2013; accepted August 29th, 2013
Keywords: Soft Frequency Reuse; Queuing; Uniform Fractional Guard Channel
ABSTRACT
Dropping probability of handoff calls and blocking probability of new calls are two important Quality of Service (QoS) measures for LTE-Advanced networks. Applying QoS for Cell edge users in soft frequency reuse scheme in LTE system is a challenge as they already suffer from limited resources. Assigning some resources for handover calls may enhance dropping probability but this is in price of degradation in the blocking probability for new calls in cell-edge. Uniform Fractional Guard Channel (UFGC) is a call admission policy that provides QoS without reserving resources for handover calls. In this paper, the performance of Soft Frequency Reuse (SFR) in presence of Uniform Fractional Guard Channel (UFGC) will be investigated using queuing analysis. The mathematical model and performance metrics will be deduced in this assessment. The impact of UFGC will be evaluated in edge and core part separately. Then the optimal value for the parameter of UFGC will be obtained to minimize the blocking probability of new calls with the constraint on the upper bound on the dropping probability of handoff calls.
1. Introduction
In cellular mobile systems, spectrum available for communication is limited. Hence, efficient utilization of the scarce spectrum allocated for cellular communication is a major challenge in cellular system design [1]. This limitation means that the radio resources have to be reused as much as possible in order to support a numerous number of simultaneous calls that may arise in many typical mobile networks. By reusing frequency more and more times, a scarce spectrum can be used many times and an efficient utilization for the spectrum is achieved. Many frequency reuse schemes have been introduced in the literature [2-4]. A comparison of different frequency reuse schemes is introduced in [5] in terms of outage probability, network throughput, spectral efficiency, and average cell edge user Signal to Interference plus Noise Ratio (SINR). Soft frequency Reuse has been introduced as one of the most promising frequency reuse schemes and it is introduced to be used in LTE-Advanced networks [6]. The SFR scheme divides UEs within each cell into two groups, cell core UEs and cell edge UEs, depending on which type of bandwidth they have access to. Cell-edge users are confined to cell-edge Resource blocks (RBs) while cell-core users can access the cell-core RBs and can also access the cell-edge RBs but with less priority than cell-edge users.
Handover is a key element in wireless cellular networks in order to sustain the provided QoS to the users and to support users’ mobility. There are two QoS parameters in these networks: new call blocking probability and handover call dropping probability. The probability of assigning no channel to handover call is defined as handover call dropping probability PD. The probability of assigning no channel to new call is defined as new call blocking probability PB. There is a trade-off between PB and PD. Call Admission Control (CAC) schemes are some strategies to keeping this parameters under desired level. From user point of view, blocking a new call is less annoying than dropping a handover one [7].
So Handover prioritization schemes result in a decrease of handover dropping probability and in an increase of new call blocking probability that, in turn, reduces the total admitted traffic. The concept of these strategies is to reserve a number of channels called guard channels (GC) exclusively for handovers [1]. More handover attempts can be admitted by buffering process [8].
When applying this strategy in soft frequency reuse, the blocking probability of new call at edge part will increase dramatically as they already suffer from resources availability. Providing suitable QoS for handover users while keeping blocking probability fairly acceptable, is a challenge especially, users in the edge part of the cell. In order to overcome this problem different schemes have been proposed: fractional guard channel (FGC), limited fractional guard channel (LFGC) and the uniform fractional guard channel (UFGC) schemes. General call admission FGC schemes have been studied in [9,10] and are used to improve the call blocking probability. This policy depends on acceptance of new call with a certain probability that depends on the current channel occupancy and acceptance of handover calls as long as channels are available. [11,12] explained LFGC and UFGC schemes, which are particular examples of FGC scheme. LFGC scheme controls communication service quality by effectively varying the average number of reserved channels by a fraction of one where as UFGC accepts new calls with an admission probability independent of channel occupancy.
In [13], an analytical approach for the performance analysis and optimization of FGC and UFGC in wireless cellular networks is developed for which different types of calls are prioritized based on a channel reservation scheme.
In [9], an algorithm for finding the optimal value of new call acceptance probability is deduced; this algorithm minimizes the blocking probability of new calls with the constraint on the upper bound on dropping probability of handover calls.
The current work assists the performance of SFR with UFGC in terms of blocking and dropping probability. In addition, using an algorithm in [12], [14] an optimal acceptance probability 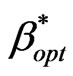 is obtained to provide minimum new call blocking probability in presence of constrained handover dropping probability Ph.
is obtained to provide minimum new call blocking probability in presence of constrained handover dropping probability Ph.
In [15], a good model for representing SFR using queuing analysis is introduced, this model is modified to suit UFGC, and a set of linear balance equations are deduced from the queuing model. A successive over relaxation (SOR) as an iterative algorithm is used to solve these balance equations to get steady state probabilities.
This paper is organized as follows: In section II, the system model for SFR with UFGC is presented. An iterative algorithm to get steady state probability is introduced in section III, and Numerical results and analysis are provided in section IV. Finally, conclusion is presented in section V.
2. Model Description
A homogeneous multi-cellular system is assumed that has the same traffic patterns. This allows considering only one cell for performance study and all other cells catch the interaction through handoff call arrival process.
A two dimension Markov chain is used to model SFR with UFGC considered. Horizontal axis stands for the number of RBs used by cell-core users and vertical axis represents the number of RBs used by cell-edge users.
2.1. Model Assumptions
In this paper the following assumption are considered:
• The basic resource element considered in this paper is the physical resource block (PRB) which spans both frequency and time dimensions.
• N is the number of available PRBs that can be used for transmission in each transmission time interval (TTI) in the cell. The maximum number of PRB that can be assigned to the edge-users and core-users is E and C respectively; the ratio of cell-edge PRBs to the total number of PRBs each cell is η, so E = η N where E + C = N.
• Users are uniformly distributed in a cell. A new call follows a Passion process with the mean arrive rate λ. The effective distance between users to eNodeB in a cell is the dominant parameter to be considered. The target cell can be modeled by two queues with the mean arrival rates λc= ξc λ and λe = ξe λ respectively, where ξc represents the ratio of cell-core area to the whole cell area, while ξe represents the ratio of celledge area to the whole cell area. λh is call arrival rate for handover calls.
• The FG policy uses a vector 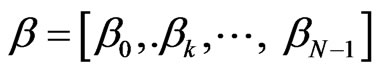 to accept the new calls, where 0 ≤ βk ≤ 1 (for
to accept the new calls, where 0 ≤ βk ≤ 1 (for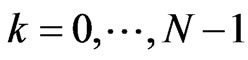 ). This policy accepts new calls with probability βk when k channels are busy. The UFGC can be obtained from FG by setting βk = β*.
). This policy accepts new calls with probability βk when k channels are busy. The UFGC can be obtained from FG by setting βk = β*.
• The cell-edge PRB is available for both of cell-edge users (with acceptance probability β*) and handover users and if there are none of them, it can be occupied by cell-core users.
• A cell-edge user may be blocked if all cell-edge PRBs in the cell is occupied by cell-edge users or handover users. A cell-core user may be blocked if there is no more cell-core PRBs or cell-edge PRBs in target cell.
• An ongoing handover call may be dropped if all celledge PRBs in the target cell is occupied by cell-edge users or handover users.
• System may force the cell-core call which has already connected to the networks to be terminated if the cellcore call has occupied cell-edge PRBs and a new celledge user initialized a new call simultaneously or an ongoing handover call entered the cell.
• The service rate of a cell-core user, a cell-edge user and handover users are negative exponentially distributed with μ and for simplicity it is assumed to be equal for three users.
2.2. Queuing Model
The queuing model is used in order to tackle and investigate the contention problem. This problem is a raised due to the limitation of the available radio resources. Figure 1 explains the state diagram in SFR with UFGC. In this figure, the cell is characterized as two dimensional Markov chain. Horizontal axis stands for the number of PRBs used by cell-core users and is denoted by i while vertical axis stands for the number of PRBs used by celledge users or handover users and is denoted by j. Then, a two dimensional state space Γ can be defined as:
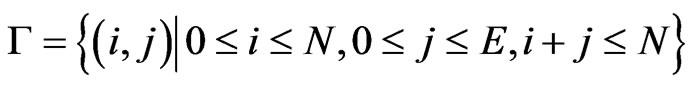 (1)
(1)
Let 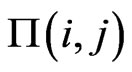 be the steady state probability for a valid state
be the steady state probability for a valid state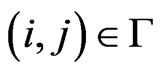 .
.
The steady state probabilities should satisfy the normalization constraint.
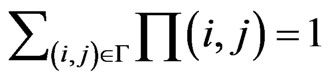 (2)
(2)
In the following, based on the state diagram shown, the set of global balance equations are introduced:
For the state 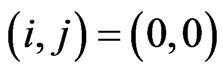
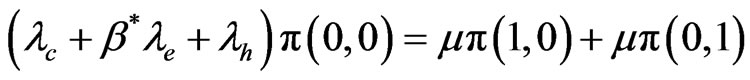 (3)
(3)
For states 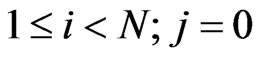
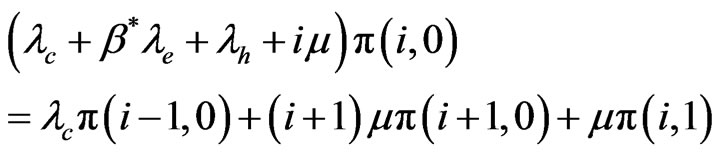 (4)
(4)
For states 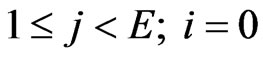
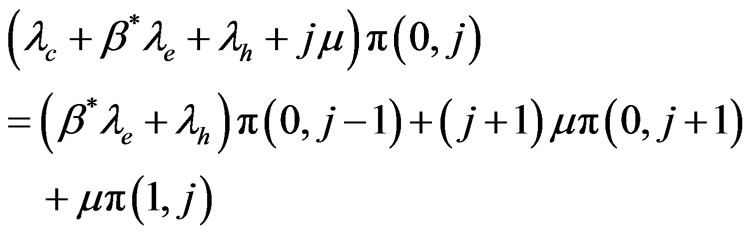 (5)
(5)
For states 
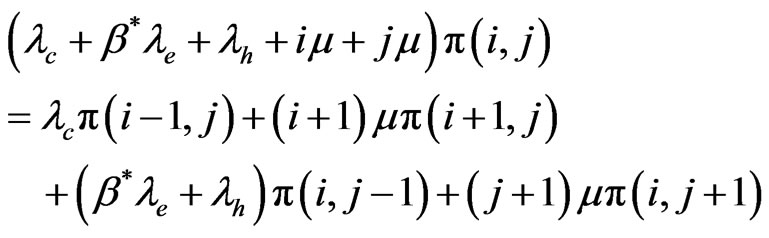 (6)
(6)
For the state 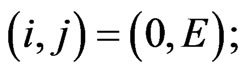
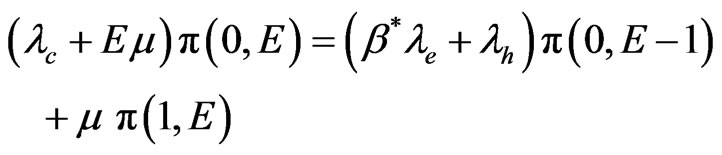 (7)
(7)
For the states 
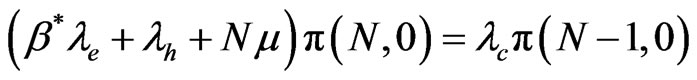 (8)
(8)
For states 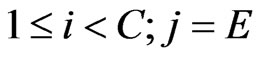
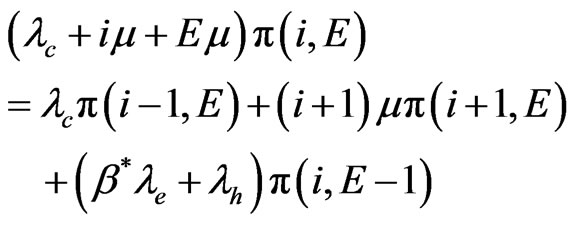 (9)
(9)
For states 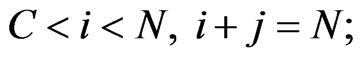
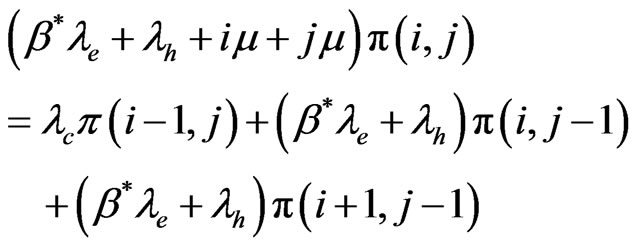 (10)
(10)
For the state 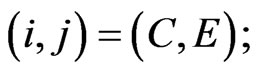
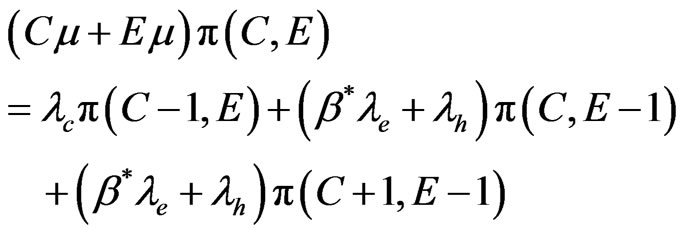 (11)
(11)

Figure 1. The state diagram of SFR with UFGC.
3. Assessment Criteria
In this section, the proposed queuing model will solved using successive over relaxation method to get steady state probability for each state. Performance metrics can be obtained from this steady state probability.
3.1. Successive over Relaxation
The successive over relaxation is an iterative method [15], [16] that used to solve the set of linear equation; the successive over-relaxation (SOR) is a variant of the Gauss-Seidel method for solving a linear system of equations, resulting in faster convergence.
In this method, a new set of equations, called SOR equations, are deduced from balance equation, the left hand side of these equations is a new value of steady state probability which is obtained iteratively using previous value for steady state probability on the right hand side. The speed of convergence is determined by relaxation factor ω, the choice of relaxation factor is not necessarily easy, and depends upon the properties of the coefficient matrix. For symmetric, positive-definite matrices it can be proven that 0 < ω < 2 will lead to convergence, but we are generally interested in faster convergence rather than just convergence.
The set of SOR equation is obtained as follow:
For the state 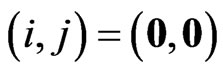
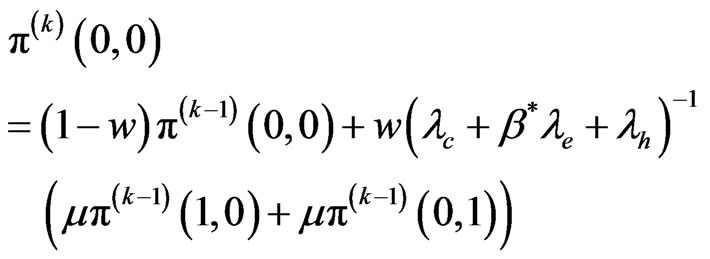 (12)
(12)
For states 
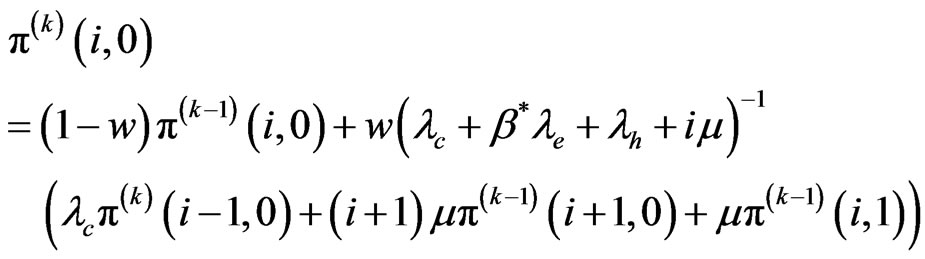 (13)
(13)
For states 
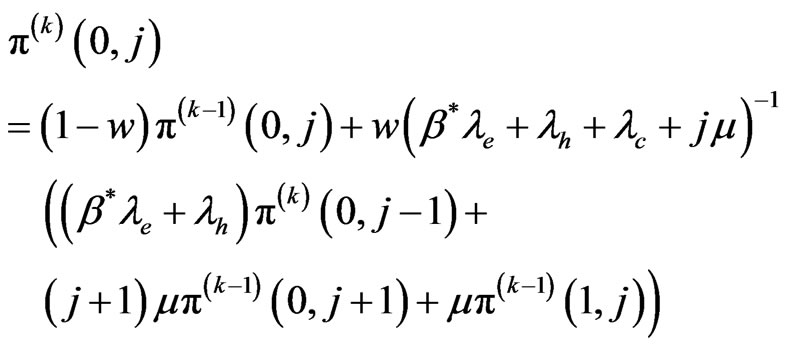 (14)
(14)
For states  (see Equation (15) below)
(see Equation (15) below)
For the state 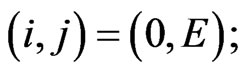
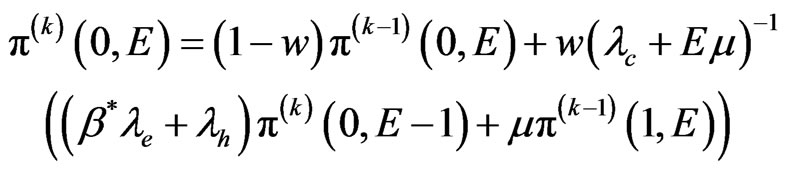 (16)
(16)
For the state 
 (17)
(17)
For states 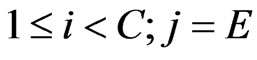
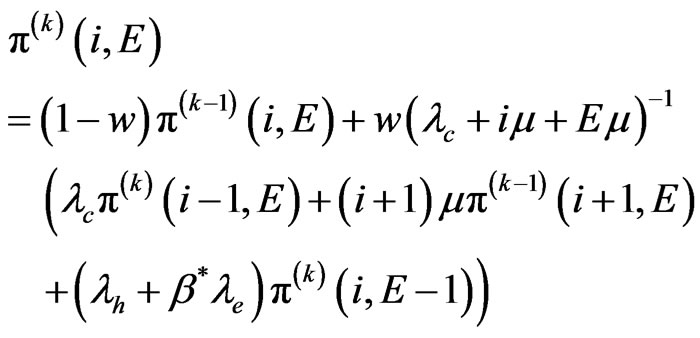 (18)
(18)
For states 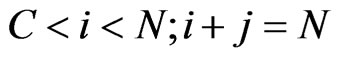
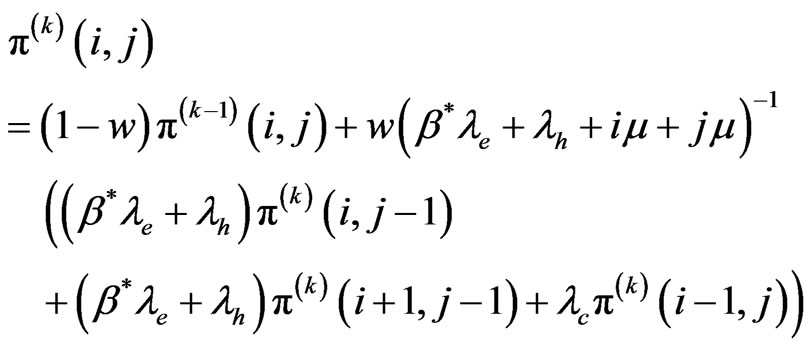 (19)
(19)
For the state 
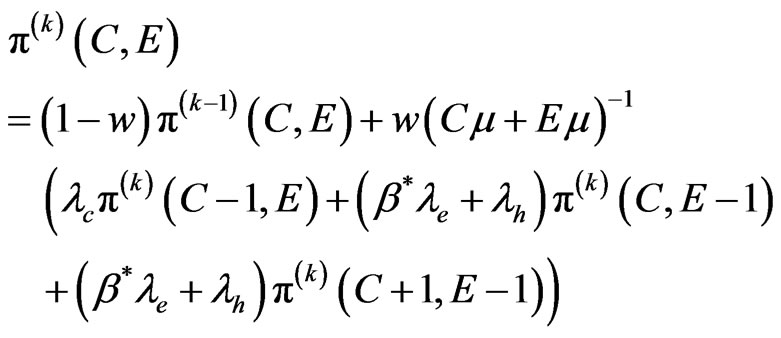 (20)
(20)
Figure 2 explains the SOR algorithm which comprises three main parts. First, all equations are started using initial valid state probability distribution and convergence criteria and relaxation factor. Second, we iterate SOR equations aforementioned until the steady probability distribution satisfies the convergence condition or iterations exceed 1000. This equation should solve in sequence as some of it values depends on the values from the former equation. Finally, performance metrics can be obtained if the algorithm could acquire the steady state probability corresponding with the convergence condition [15].
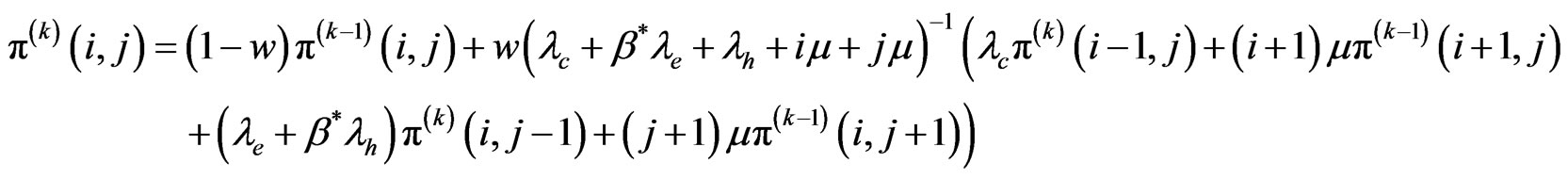 (15)
(15)
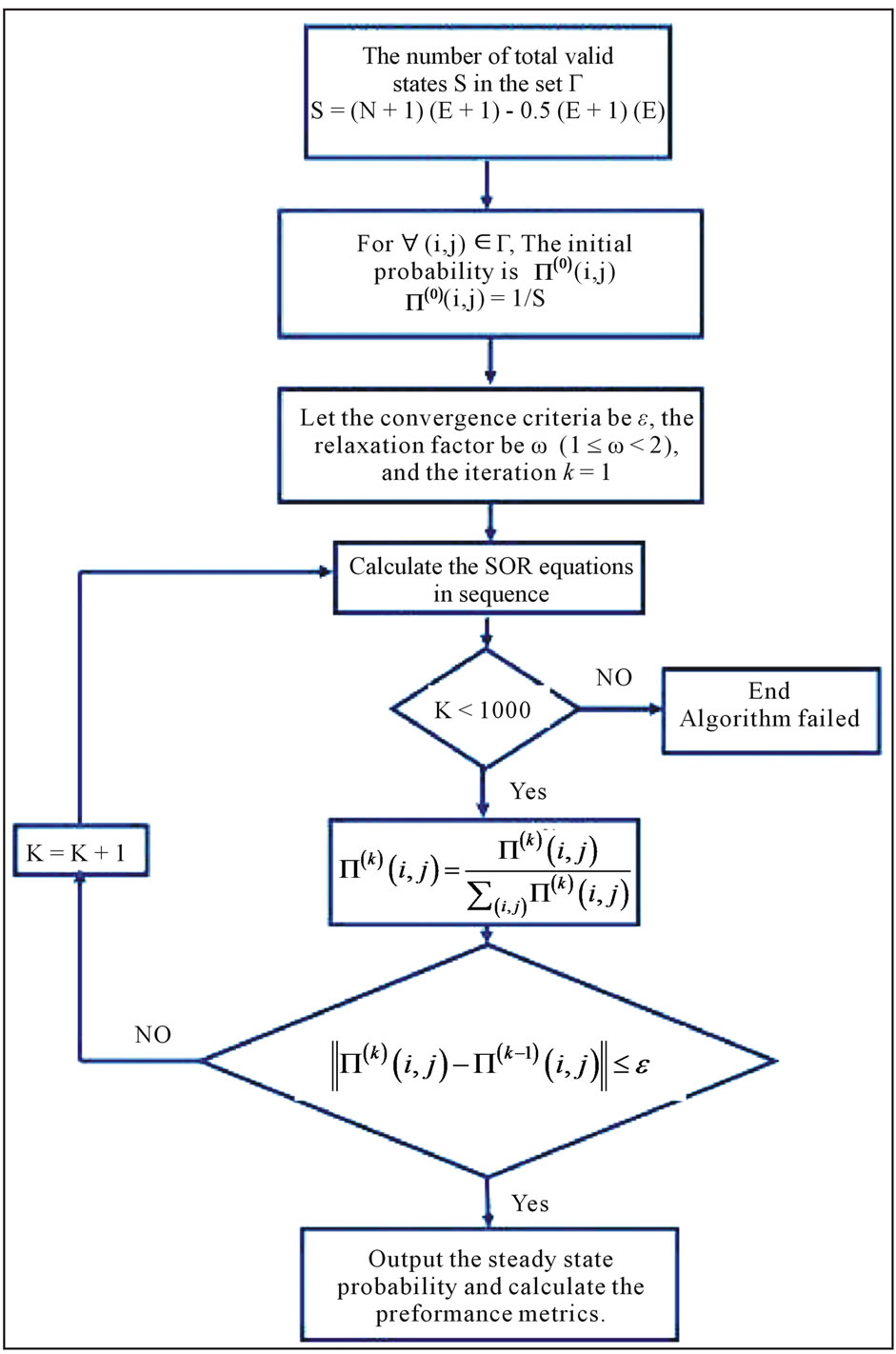
Figure 2. Flow chart for SFR algorithm.
3.2. Performance Metrics
The performance of the current model will be evaluated by determine of blocking probability (PB) as well as dropping probability (PD). Cell blocking probability is the probability that a new arriving cell-core user and a cell-edge user are blocked. Let ψbc and ψbe be the subsets of states where a new arriving cell-core user and a celledge user are blocked respectively.
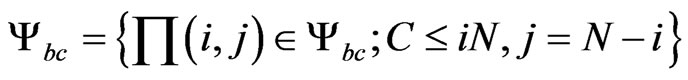
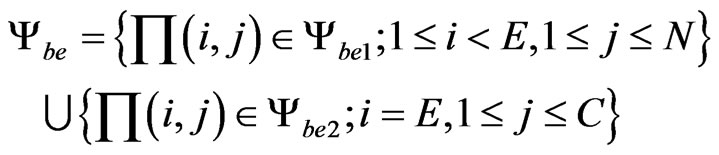 (21)
(21)
Then the blocking probability is calculated as [12]:
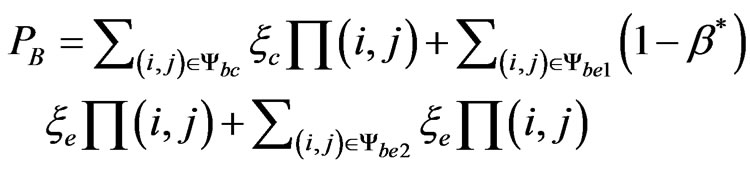 (22)
(22)
Finally let ψd be the subsets of states where the system forces to terminate the ongoing handover call.
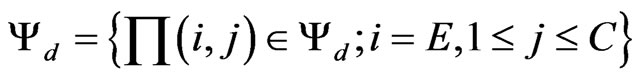 (23)
(23)
Then the cell dropping probability is calculated as:
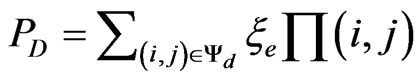 (24)
(24)
3.3. Optimization of New Call Acceptance Probability 
The objective of this part is to obtain the optimal value of new call acceptance probability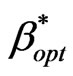 . This will minimize the new call blocking probability subjected to a hard constraint on handover dropping probability or minimize PB such that PD ≤ Ph.
. This will minimize the new call blocking probability subjected to a hard constraint on handover dropping probability or minimize PB such that PD ≤ Ph.
The presented algorithm in [12] will be used to find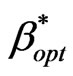 . This algorithm is given in Figure 3 and can be described as follows. At the beginning, the algorithm considers two cases: the first case when all channels are exclusively used for handover calls. If the exclusive use of channels for handover calls does not satisfy the level of QoS, then the number of allocated channels to the cell is not sufficient and the algorithm terminates; the second case when all channels are shared between handover and new calls. If the complete sharing satisfies the level of QoS, then the algorithm considers that
. This algorithm is given in Figure 3 and can be described as follows. At the beginning, the algorithm considers two cases: the first case when all channels are exclusively used for handover calls. If the exclusive use of channels for handover calls does not satisfy the level of QoS, then the number of allocated channels to the cell is not sufficient and the algorithm terminates; the second case when all channels are shared between handover and new calls. If the complete sharing satisfies the level of QoS, then the algorithm considers that 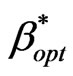 =1 and the algorithm terminates; otherwise the algorithm searches for the optimal value of
=1 and the algorithm terminates; otherwise the algorithm searches for the optimal value of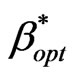 . The search method used in this algorithm is binary search.
. The search method used in this algorithm is binary search.
4. Numerical Analysis and Results
In this section, the performance of SFR scheme in presence of UFGC is analyzed and evaluated using queuing model. The aforesaid performance metric of blocking

Figure 3. Algorithm for obtaining optimal value of new call acceptance probability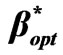 .
.
probability PB and dropping probability PD is used for evaluation. The effect of new call acceptance probability β* and handover arrival rate λh in the blocking and dropping probability is studied. For more depicted analysis, the blocking probability is studied in cell-edge and cellcore separately.
The queuing model parameters for the presented results are as follow: the available PRB in the cell 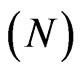 is 48; the mean service period
is 48; the mean service period 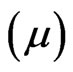 is 90 seconds. The SOR parameters are ω = 1.05, ε = 10−5 and k = 1000.
is 90 seconds. The SOR parameters are ω = 1.05, ε = 10−5 and k = 1000.
4.1. The Blocking Probability PB
Figures 3 to 6 illustrate the effect of handover arrival rate λh and new call acceptance probability β* on blocking probability for both of cell-edge and cell-core part.
The SFR parameters setting for the presented results are: ξ = 1/2 and η = 1/3. These parameters are in consistence with Huawei proposal [6]. For practical consideration and system sustainability, the values of handover arrival rate λh are chosen to be less than the arrival rate of new call for cell-edge user λe.
The new call acceptance probability β* is 0.5 in the obtained results in Figures 3 & 4 and the handover arrival rate λh is 0.25 λe in the obtained results in Figures 5 & 6.
The effect of handover arrival rate λh on blocking probability of cell-edge and cell-core users is introduced in Figures 4 & 5 respectively.
As illustrated in Figures 4 & 5, the increasing of λh will leads to have more blocking for new calls. This may be happened as a result of the increasing of radio resources competition by the handover traffic.
These results may be used as an evidence for the stability and sustainability of the proposed model.
The system behavior in Figure 4 is more degraded than that in Figure 5. This may be explained due to the shortage of the edge to resources that are allocated for new and handover call. The effect on the core is less than that in the edge due to there are many opportunities for the allocation of new calls.
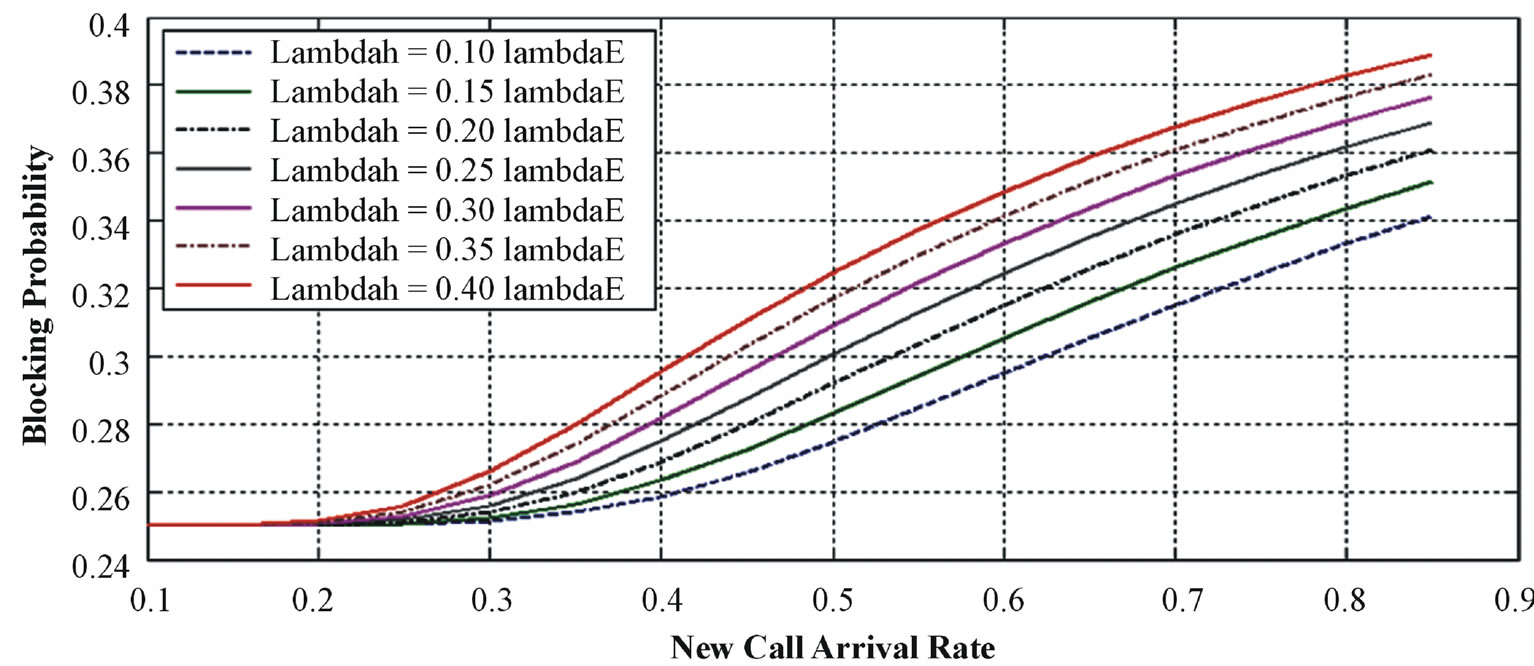
Figure 4. Blocking probability for cell-edge user with different λh.
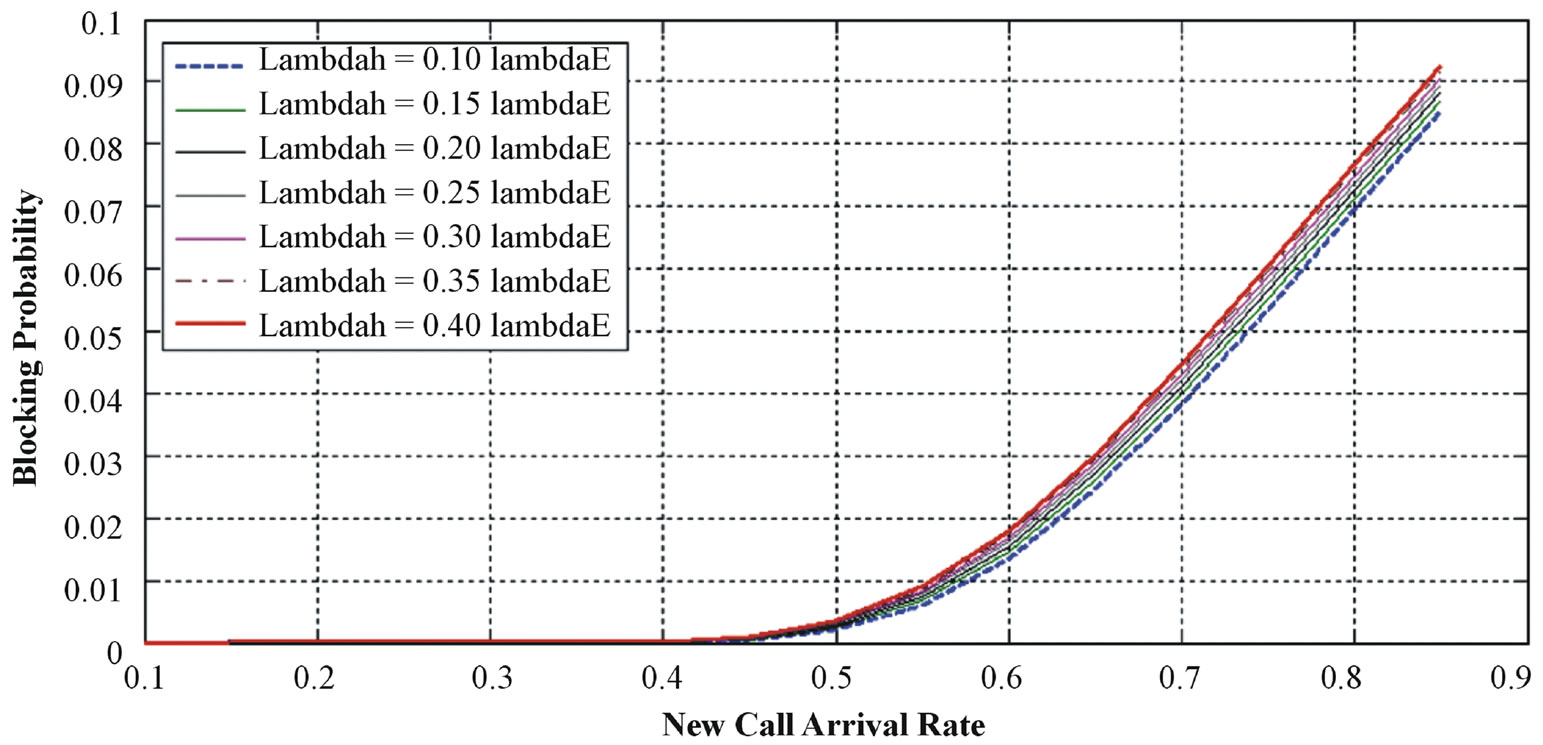
Figure 5. Blocking probability for cell-core user with different λh.
Figure 6 explains the noticeable effect of new call acceptance probability β* in blocking probability for celledge users and it is compared with the system without UFGC.
It can be noticed that the increase of blocking probability when using UFGC as a results of reducing the resources permitted to new call request.
It is clear from Figure 6 that the blocking probability decreases while β* is increased as more resources are admitted for new calls. In addition, It can be noticed that the impact of β* on blocking probability differs with regard to traffic load. This can be interpreted as follow:
In heavy traffic region there are more and more new call requests, so more resources are occupied, hence blocking probability for more new calls will increase. So the blocking probability in this region is due to increaseing of arrival rate of new call rather than the effect of acceptance probability. On the other hand, when new call arrival rate is becoming light, there is a little call requests and a lot of available resources. Consequently, the blocking (if happened) will be occurred as a result of the lack of the available resources admitted for new calls.
So the dominant factor that affect on blocking is traffic load. In heavy traffic region blocking will be mainly influenced by λ. whereas, in the light traffic region block will be controlled mainly by β*.
Figure 7 explains the impact of β* on blocking probability for cell-core users. This impact is a result of accessing of the core users the edge resources when there are no edge or handover users (some sort of resource borrowing from edge to serving the core customers). This impact is limited in comparison with cell-edge case; this is due to blocking of new call in cell-core part is occurred as a result of full usage of the resources. Consequently, the effect of acceptance probability is limited. On the contrary of Figure 6, the blocking probability in Figure
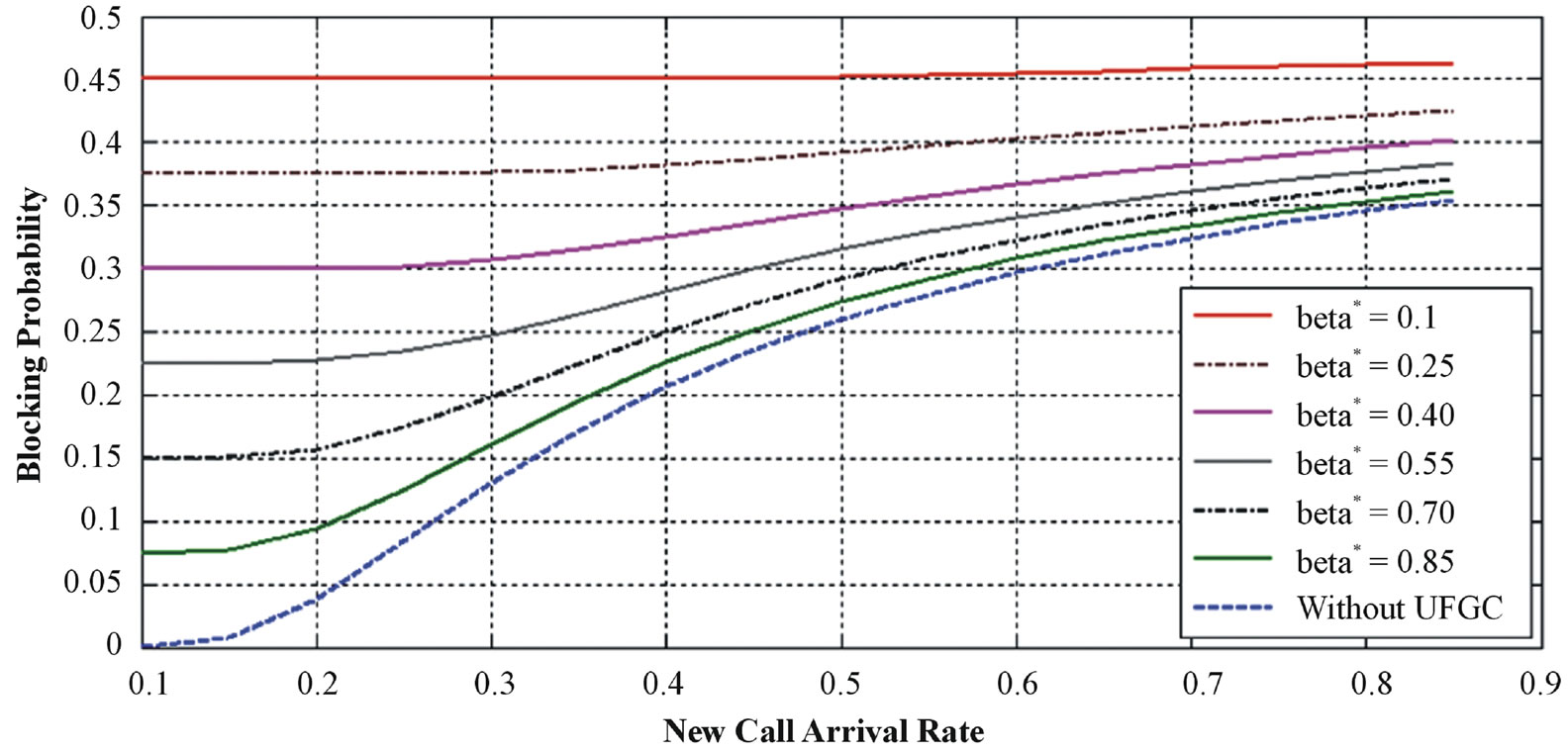
Figure 6. Blocking probability for cell-edge user with different β*.

Figure 7. Blocking probability for cell-core user with different β*.
7 increases as β* is increasing. This is because of new call arrival rate is always greater than handover arrival rate, consequently with large values of β*, the system is permitted to admit new call requests more than handover requests. This leads to more overall call requests and more resources occupation and probability of blocking increases. On the other hand Figure 6 shows the improvement of blocking probability for cell-core users when using UFGC. This occurred as a result of some resources is admitted for handover call which have lower rate. So the overall service request decreases and provides cell-core users more available resources. But, without UFGC whole resources is admitted for new call of edge users, this leads to higher overall service requests. So the system starves to serve cell-core users.
4.2. The Dropping Probability PD
In the following subsection, the effect of handover arrival rate λh as well as new call acceptance probability β* on dropping probability PD are investigated. These effects are presented in Figures 8 and 9 respectively.
The new call acceptance probability β* is 0.5 in the obtained results in Figure 8 and the handover arrival rate λh is 0.25 λe in the obtained results in Figure 9.
Figure 8 explains the effect of handover arrival rate on dropping probability. It is shown that by having more handover request, more resources are occupied. Then, the probability for serving handover calls is reducing.
The impact of new call acceptance probability β* is illustrated in Figure 9. Large values of acceptance probability means more new call admitted than handover call.
This leads to increasing in the overall arrival rate, so the system will be fully occupied faster. Consequently, handover call will suffer from more dropping due to the limitation of the available resources.
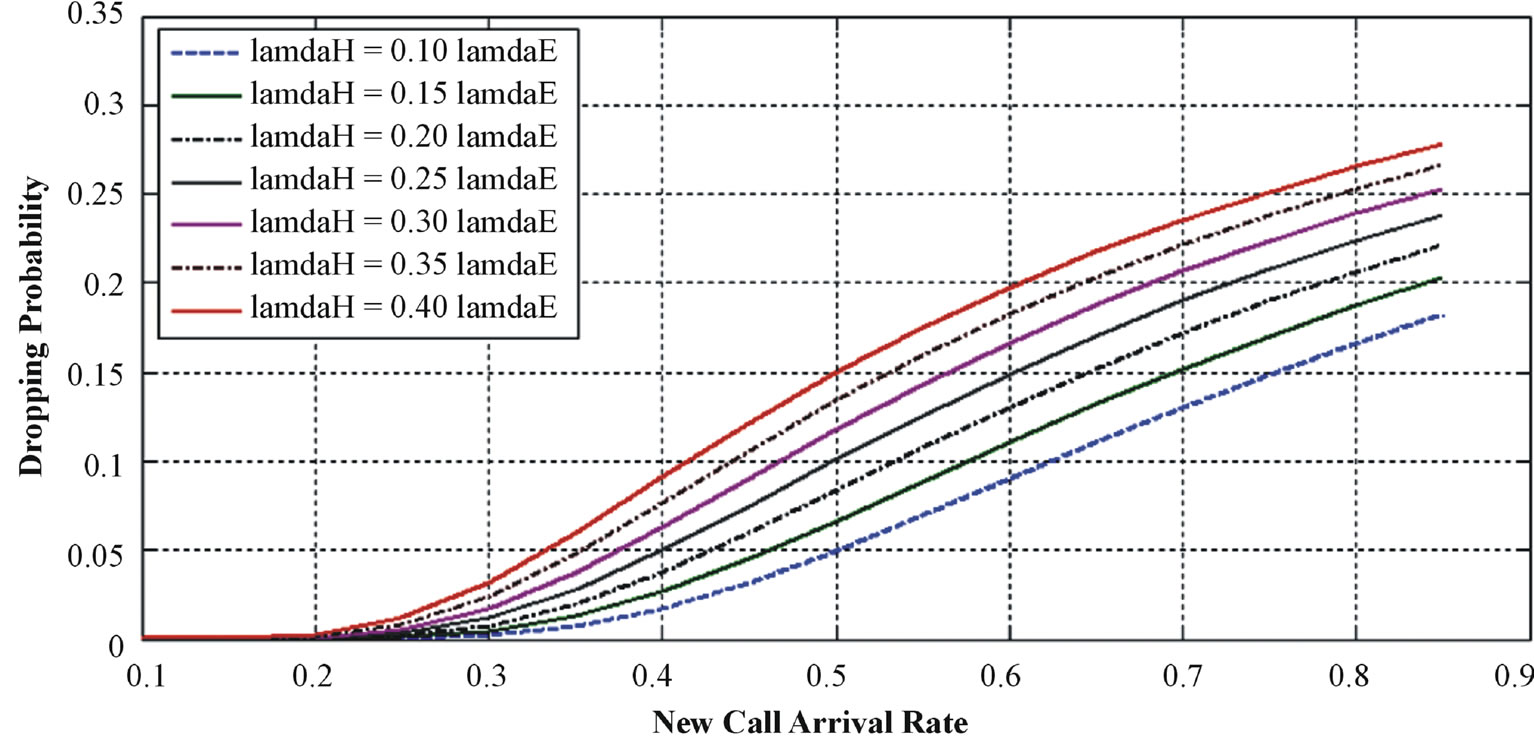
Figure 8. Dropping probability with different λh.
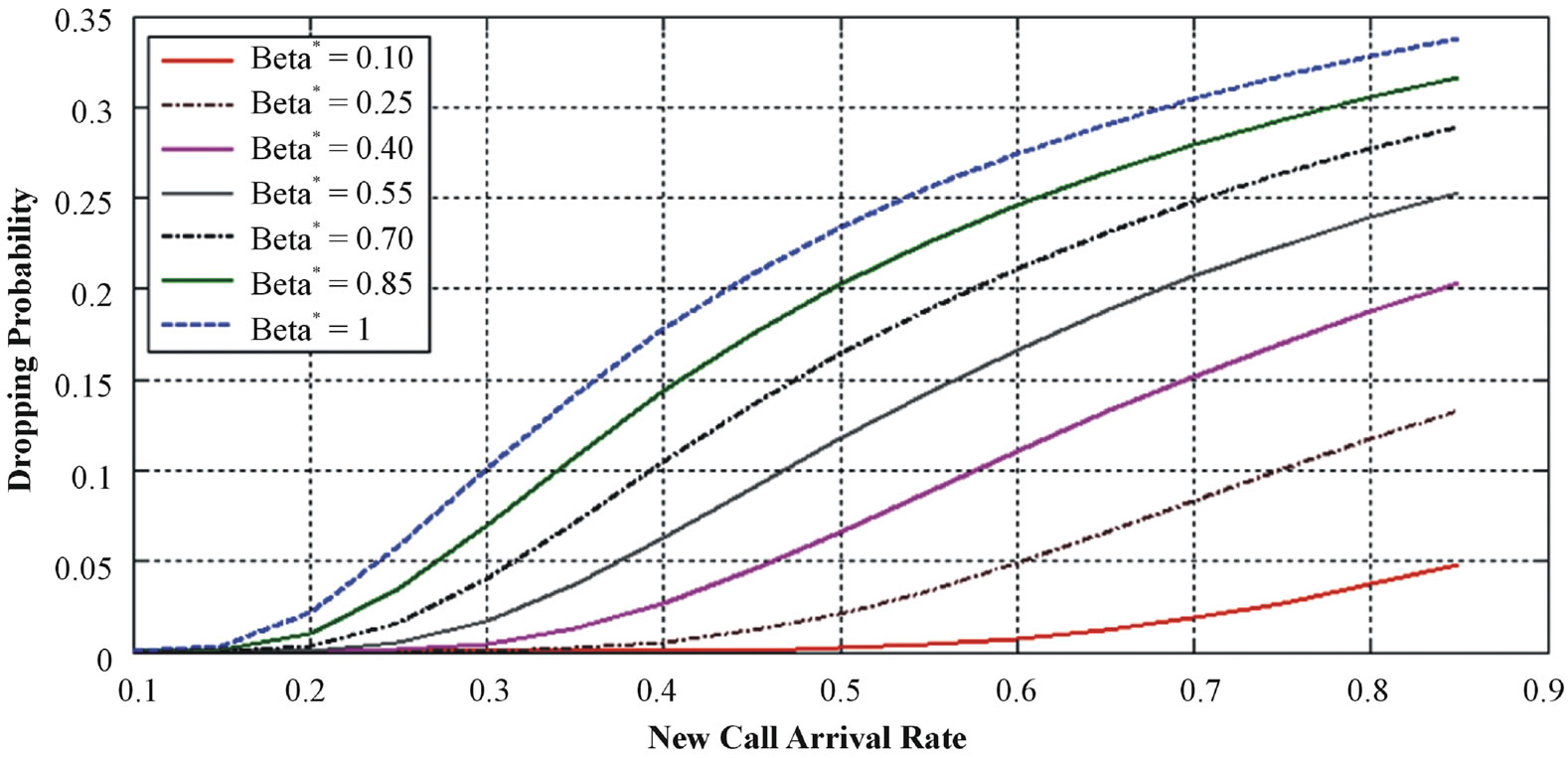
Figure 9. Dropping probability with different β*.

Figure 10. Blocking and dropping probability as a function of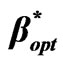 .
.
4.3. Optimization of New Call Acceptance Probability 
In order to find out the most optimized value of acceptance probability 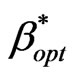 that provides hard constraint of dropping probability Ph, we will follow Figure 3 algorithm.
that provides hard constraint of dropping probability Ph, we will follow Figure 3 algorithm.
Figure 10 is illustrating the optimized values of 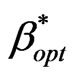 that provide a hard constraint PD ≤ Ph (for 0.008 £ Ph ≤ 0.2). Following algorithm of Figure 3,
that provide a hard constraint PD ≤ Ph (for 0.008 £ Ph ≤ 0.2). Following algorithm of Figure 3, 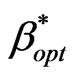 may be determined satisfying the condition PD ≤ Ph. At each point of
may be determined satisfying the condition PD ≤ Ph. At each point of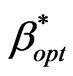 , the equivalent value of dropping probability PD and blocking probability PB are determined. The new call arrival rate λ and handover arrival rate λh is taken to be 0.5 and 0.05 respectively. So, the shown results in Figure 10 may be used as design curve to give the minimum blocking probability for a given Ph. As an example, the required Ph to be taken as 0.05 (as a QoS measure), the optimized
, the equivalent value of dropping probability PD and blocking probability PB are determined. The new call arrival rate λ and handover arrival rate λh is taken to be 0.5 and 0.05 respectively. So, the shown results in Figure 10 may be used as design curve to give the minimum blocking probability for a given Ph. As an example, the required Ph to be taken as 0.05 (as a QoS measure), the optimized 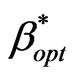 will be 0.4 which provide blocking probability of 0.33.
will be 0.4 which provide blocking probability of 0.33.
5. Conclusion
In this paper, the effect of uniform fractional guard channels in resources availability of SFR is investigated using queuing model. A steady state probability is deduced using successive over relaxation method. Through numerical results and analysis the following can be deduced: the blocking probability of edge users can be controlled by varying new call acceptance probability. On the hand the acceptance probability and handover arrival rate has a tremendous impact on blocking probability and dropping probability of edge users. In addition, the core users affected, but to a lesser extent, by acceptance probability and handover arrival rate. Finally, the optimal value of acceptance probability that provides minimum blocking probability under hard constraint on handover dropping probability is obtained.
REFERENCES
- V. Goswami and P. K. Swain, “Analysis of Finite Population Limited Fractional Guard Channel Call Admission Scheme in Cellular Networks,” Procedia Engineering, Vol. 30, No. 2012, pp. 759-766. http://dx.doi.org/10.1016/j.proeng.2012.01.925
- X. Zheng and B. Walke, “Frequency Reuse Techniques for Attaining Both Coverage and High Spectral Efficiency in OFDMA Cellular Systems,” 2010 IEEE Wireless Communications and Networking Conference (WCNC), Sydney, 18-21 April 2010, pp. 1-6.
- C. Lei and D. Yuan, “Generalizing and Optimizing Fractional Frequency Reuse in Broadband Cellular Radio Access Networks,” EURASIP Journal on Wireless Communications and Networking 2012, Vol. 2012, 2012, pp. 1-15.
- M. L. Qian, et al., “Inter-Cell Interference Coordination through Adaptive Soft Frequency Reuse in LTE Networks,” 2010 IEEE Wireless Communications and Networking Conference (WCNC), Shanghai, 1-4 April 2012, pp. 1618-1623.
- T. Novlan, J. G. Andrew, S. Illsoo, R. K. Ganti and A. Ghosh, “Comparison of Fractional Frequency Reuse Approaches in the OFDMA Cellular Downlink,” 2010 IEEE Global Telecommunications Conference (GLOBECOM 2010), Miami, 6-10 December 2010, pp. 1-5.
- “R1-050507, Soft Frequency Reuse Scheme for UTRAN LTE,” Huawei 3GPP TSG RAN WG1 Meeting No.41, Athens, May 2005.
- Z. Firouzi and H. Beigy, “A New Call Admission Control Scheme Based on New Call Bounding and Thinning II Schemes in Cellular Mobile Networks,” IEEE International Conference on Electro/Information Technology, 2009, Windsor, 7-9 June 2009, pp. 40-45.
- M. Jain, G. C. Sharma and R. Mittal, “Performance Analysis of Prioritized Call Admission Control Schemes for Integrated Traffic in Wireless Network,” International Journal of Electronics Communication and Computer Engineering, Vol. 4, No. 1, 2013, pp. 283-291.
- R. Ramachandran, D. Towsley and R. Nagarajan, “On Optimal Call Admission Control in Cellular Networks,” Wireless Networks, Vol. 3, No. 1, 1997, pp. 29-41. http://dx.doi.org/10.1023/A:1019172226345
- J. Vazquez-Avila, F. A. C. Cruz-Perez and L. Ortigoza-Guerrero, “Performance Analysis of Fractional Guard Channel Policies in Mobile Cellular Networks,” IEEE Transactions on Wireless Communications, Vol. 5, No. 2, 2006, pp. 301-305.
- H. Beigy and M. R. Meybodi, “Uniform Fractional Guard Channel Policy,” Proceedings of the 6th SCI’2002, Vol. 15, Orlando, July 2002.
- H, Beigy and M. R. Meybodi, “A New Fractional Channel Policy,” Journal of High Speed Networks, Vol. 13, No. 1, 2004, pp. 25-36.
- H. Kim, et al., “An Analytical Approach to the Analysis of Guard-Channel-Based Call Admission Control in Wireless Cellular Networks,” Journal of Applied Mathematics, Vol. 2012, 2012, Article ID: 676582.
- H. Beigy and M. R. Meybodi, “Adaptive Uniform Fractional Channel Algorithms,” Iranian Journal of Electrical and Computer Engineering, Vol. 3, No. 1, 2004, pp. 47-53.
- S. Li, X. Wen, Z. Liu, Z. Wei and Y. Sun, “Queue Analysis of Soft Frequency Reuse Scheme in LTE-Advanced,” 2nd International Conference on Computer Modeling and Simulation, Vol. 1, Sanya, 22-24 January 2010, pp. 248- 252.
- Y. Zhang, Y. Xiao and H. H. Chen, “Queueing Analysis for OFDM Subcarrier Allocation in Broadband Wireless Multiservice Networks,” IEEE Transactions on Wireless Communication, Vol.7, No. 10, 2008, pp. 3951-3961.

