Wireless Engineering and Technology
Vol.4 No.3(2013), Article ID:34176,5 pages DOI:10.4236/wet.2013.43020
Spectrum Sensing and AM-FM Decomposition through Synchrosqueezing
![]()
Department of Electronics and Communication Engineering, Amrita Vishwa Vidyapeetham, Coimbatore, India.
Email: aswin_mssa@ymail.com, divyakotireddy@gmail.com, chinchu.varma@gmail.com, sowmyareddy1992@gmail.com, k.vandhu@gmail.com, ka_narayanankutty@yahoo.com.
Copyright © 2013 K. Vandhana et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received April 23rd, 2013; revised May 30th, 2013; accepted June 16th, 2013
Keywords: Cognitive Radio; Synchrosqueezing; AM-FM; Spectrum Sensing; Time-Frequency Reassignment; Empirical Mode Decomposition
ABSTRACT
In this paper we have accomplished one of the tasks of cognitive radio i.e. dynamic spectrum sensing by using wavelet based Synchrosqueezing transform [1], a novel technique, which was proposed to analyze a signal in time-frequency plane. The distinctive feature of this transform compared to other techniques is that it enables us to decompose amplitude and frequency modulated signals and allows individual reconstruction of these components. The objective is also to separate the occupied band into amplitude modulated and frequency modulated bands.
1. Introduction
The tremendous growth of wireless data use in our dayto-day life piloted the problem of spectrum scarcity. Recent developments in the line of wireless networks have resulted in huge leap which diminishes underutilization of spectrum. Cognitive radio (CR) [2] originates as an alluring solution to this issue. Yesteryears had witnessed fixed allocation of bands but modern methods in cognitive radio have resulted in dynamic allocation of the unused licensed bands. Prime concern of cognitive radio is spectrum sensing.
Spectrum Sensing
Spectrum sensing in cognitive radio ensures the efficient utilization of spectral holes in the licensed frequency band. This feature enables a secondary (unlicensed) user to avail the spectrum holes without causing interference to a primary (licensed) user. It has got additional functions which find the bandwidth, waveform, modulation and carrier frequency of the signal that occupied the spectrum. There are three different approaches in which spectrum sensing can be done namely:
1) Transmitter detection: Detects the existence of a signal in a particular spectrum. e.g. Energy based sensing, matched filtering.
2) Cooperative detection: Detects primary users through the information obtained from various cognitive radios. e.g. Centralized sensing, Distributed sensing.
3) Interference based detection: Interference temperature level restricts the coexistence of secondary and primary users in a CR system.
The second half of the paper handles the decomposition of amplitude modulated and frequency modulated signals. Previous works done [3,4] on AM-FM decomposition deal with separating AM and FM harmonics presented in audio signals which contribute to applications like audio coding, singer segregation etc. On the other hand, we have realized AM or FM modulated schemes used by the primary users and also their corresponding bandwidths.
The overall essence of this paper is to appraise the concept of cognitive radio’s spectrum sensing, and specifically, on the establishment of an innovative Synchrosqueezing transform on this particular spectrum. This fetches us a more appropriate conclusion that shows the distinction in AM and FM signal, from which we can deduce the range of bandwidth of AM and FM signals. The contents are arranged as follows. Section 2 deals with brief history in spectrum sensing, Section 3 deals with Synchrosqueezing transform and its algorithm, Section 4 shows the results of spectrum sensing and AM-FM decomposition, Section 5 includes discussion of the scope of the concept and conclusion.
2. Spectrum Sensing through Ages [5]
Spectrum sensing can be done on the basis of several methods. Let us take a peep on the methods through the ages. Initially Energy based Detection was popular as it required no information about primary users. The detection was performed by comparing the output of energy detector with a previously set threshold value. Energy based detection method faces problems in deciding the threshold, its incapability to discriminate between primary user and noise. This method is not favorable when the noise is nonstationary. Cyclostationarity paved the way in utilizing the features like periodicity of received signals. Channel fading influences cyclostationarity approach on a large scale making it prone to offsets and losing cyclostationary features of received signals. In matched filter it obtains an optimal solution for signal detection where the transmitted signal is known. This method requires information regarding operating frequency, bandwidth, modulation type etc. But implementing receivers for all those signal types make it complex and impractical. Hilbert Huang Transform is a combination of EMD [6] (Empirical Mode Decomposition) and HSA (Hilbert Spectral Analysis) for decomposing a signal and obtaining its instantaneous frequency for non-stationary and nonlinear data. Major limitation in this method is that it cannot distinguish different components in narrow band signals. To overcome this limitation a new concept of Synchrosqueezing Transform (SST) method of timefrequency analysis, where it can differentiate closely spaced components in frequency domain. The following section gives us an insight to the SST.
3. Synchrosqueezing Transform [1,7]
Analysis of time series data primarily aims at separating meaningful components, and knowing the structure and to extrapolate for predictions. Nonstationary real time signals that are observed in the application of any scientific work are analyzed using time-frequency transforms such as the short-time Fourier transform (STFT), the Wigner-Ville distribution [8], and the continuous wavelet transform (CWT) [9]. To comprehend more clearly about the signal, the classical Empirical mode decomposition is used. Although EMD helps us to understand this concept, and able to deal with nonstationary signals, its basic mathematical explanations are fuzzy. This is where Synchrosqueezing comes in handy, as Synchrosqueezing algorithm extracts and explains the constituent oscillatory components obtained by the decomposition of the signal. This transform comes under the clan of time-frequency reassignment (TFR) techniques, but its uniqueness is that reassignment is done in frequency domain unlike other TFR techniques basically used in time domain.
Given any signal, s(t), which is always a sum of amplitude modulated and frequency modulated signals. i.e.,
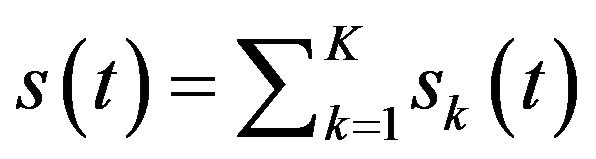 (1)
(1)
where,  (2)
(2)
is an intrinsic mode type function (IMF) with an amplitude Ak(t) and frequency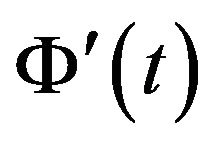 . These IMFs are well separated in frequency domain and are obtained by means of Synchrosqueezing.
. These IMFs are well separated in frequency domain and are obtained by means of Synchrosqueezing.
Algorithm
a) Compute the CWT of the signal s(t).
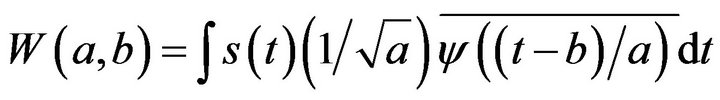 (3)
(3)
where ψ(t) is mother wavelet chosen, a is scaling factor of mother wavelet, b is the translating factor in time axis.
b) In order to convert time-scale plane to time-frequency plane, candidate instantaneous frequency is obtained by,
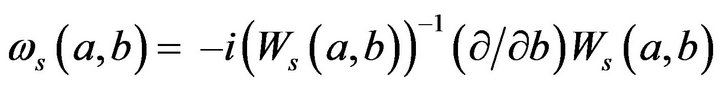 (4)
(4)
where ωs(a,b) is the instantaneous frequency.
c) The obtained instantaneous frequencies are divided into different frequency regions such that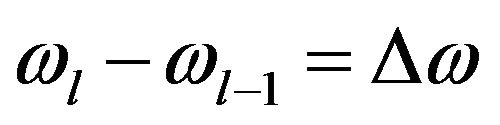 , where ωl is the center frequency. Synchrosqueezed transform is obtained by assigning the net contributions of ωs(a,b) in these frequency regions to its corresponding center frequencies.
, where ωl is the center frequency. Synchrosqueezed transform is obtained by assigning the net contributions of ωs(a,b) in these frequency regions to its corresponding center frequencies.
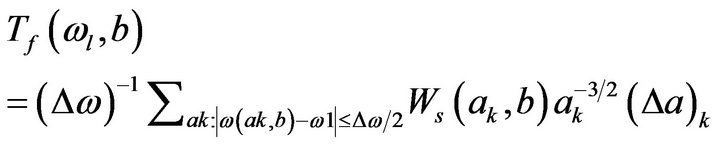 (5)
(5)
where ak’s are discrete values of a for which the transform values are calculated and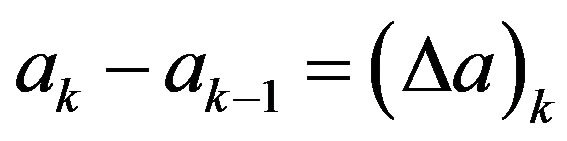 .
.
Hence time-scale plane is converted to time-frequency plane by this reassignment technique thereby enhancing the resolution of TF plane which facilitates the easy extraction of the IMF components.
The primary requirement in demodulation of a signal is to get amplitude, phase and instantaneous frequency information. Synchrosqueezing takes advantage of its reassignment principle to overcome the noise interfereence of signal (non-linear and non-stationary). In the reassignment mode, Synchrosqueezing uses superposition of a class of functions that slowly varies with respect to the instantaneous frequencies.
Reference [10] summarizes a bi-dimensional version of Synchrosqueezing transform on images, this enables to decompose its AM-FM harmonics. This paper focuses on separation of AM-FM components of 1-D signal. Decomposition can be done in either of the two categories where AM and FM modulated signals co-exist or exist in different bands.
4. Results
4.1. Spectrum Sensing
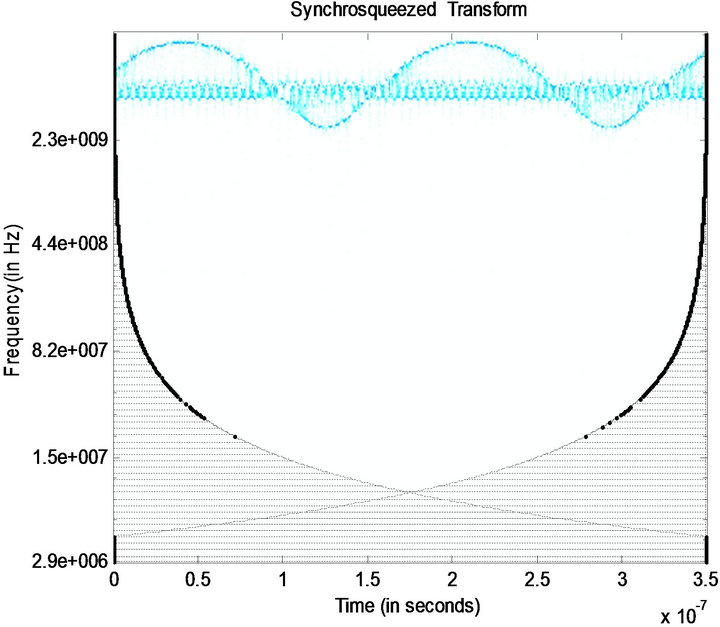
In this paper we have taken a wideband signal of bandwidth 2.5 GHz ranging from 750 MHz to 3.25 GHz with a noise power of −3 db as input signal shown in Figure 1. Applying Synchrosqueezing transform on this signal yields a sharpened TF plot as shown in Figure 2. It is evident from this figure that Synchrosqueezing transform gives us finite thread like instantaneous frequency curves in spite of the noise presented in the signal. Figure 3 depicts the presence and absence of frequencies in the signal as 1 representing the former and 0 representing the latter.
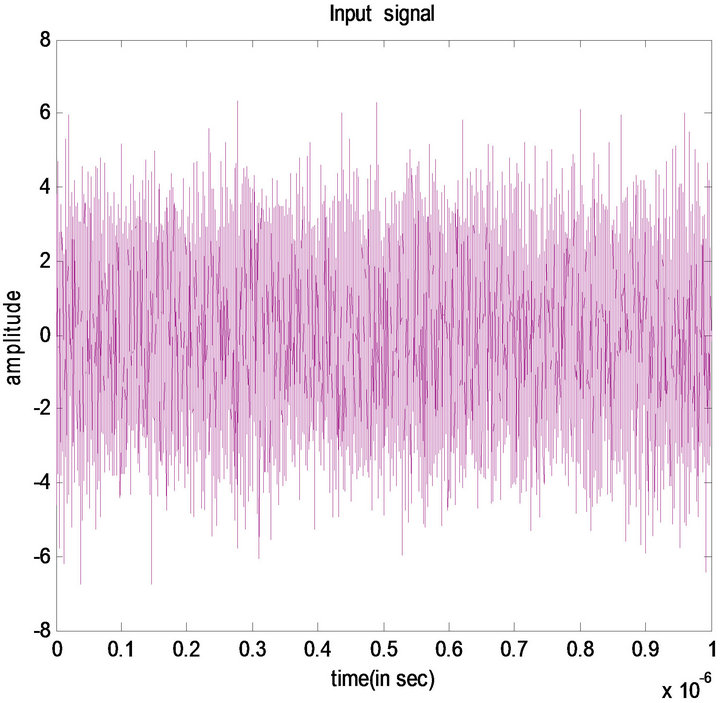
Figure 1. Input signal with noise power of −3 dB.
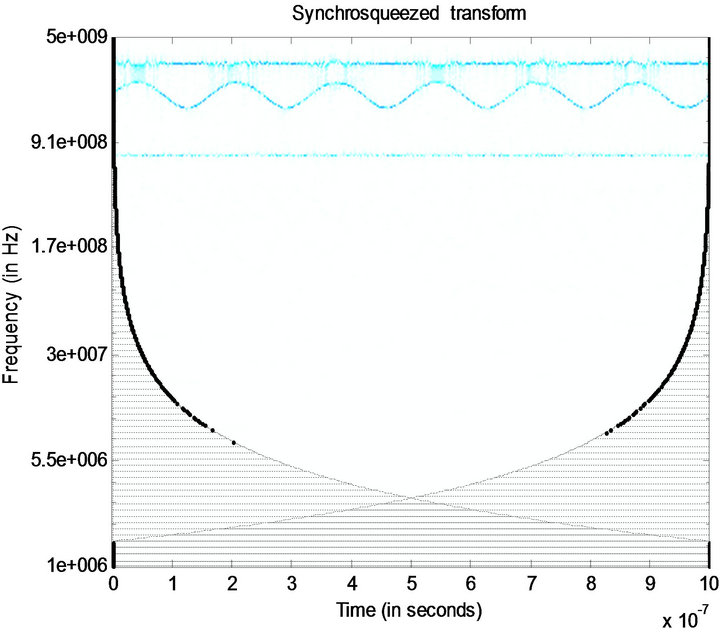
Figure 2. Synchrosqueezed transform of the input signal.
4.2. AM-FM Decomposition
1) Non Overlapping Case:
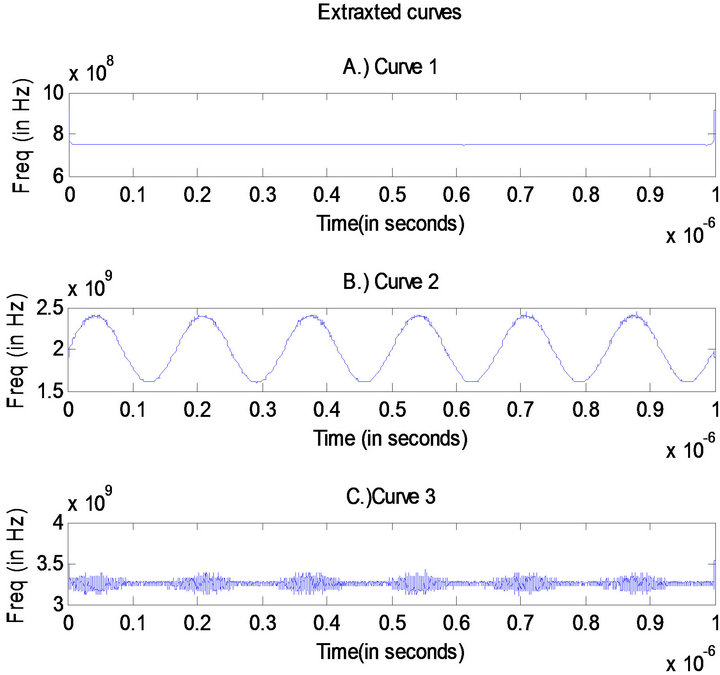
The input signal taken here is same as that of spectrum sensing (Figure 1) which consists of AM and FM band. In Figure 3 the wider band corresponds to FM modulated components and the other two bands correspond to AM modulated components. Extraxcted curves (Figure 4) from Figure 2 portray the IMFs presented in the signal. Figures 4(a) and (c) represent AM components and Figure 4(b) represents FM component in the signal. Figure 5 shows the occupancy of FM band (1.5 - 2.4 GHz) and Figure 6 shows the occupancy of AM band (750 MHz & 3.25 GHz).
2) Overlapping Case:
This is the worst case scenario of AM-FM decomposi-
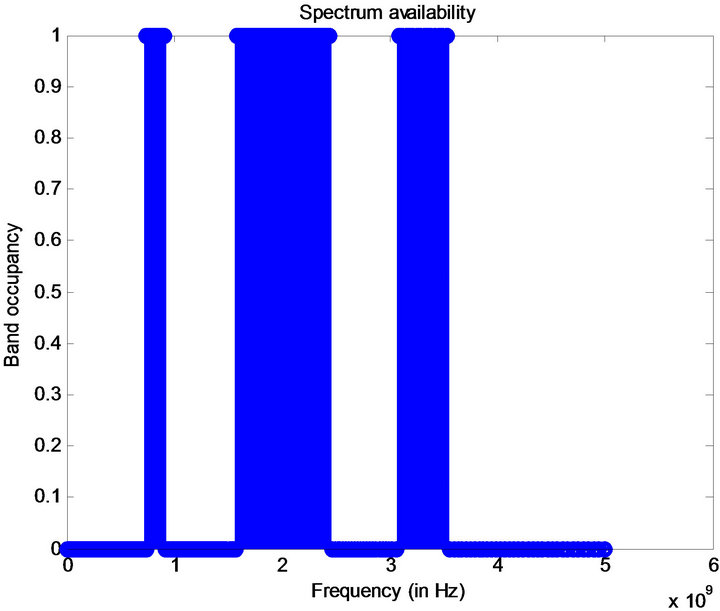
Figure 3. Spectrum occupied of the input for efficient usage.
tion. Despite the hindrance, we can still distinguish AM and FM components. The bandwidth of the input signal (Figure 7) is 8 GHz ranging from 2.8 GHz to 10.8 GHz. The results of this case are shown in Figures 8-11.
5. Conclusion
The crux of this paper reveals us an interesting develop ment in time-frequency reassignment technique, which is in Synchrosqueezing. The involvement of Synchrosqueezing in spectrum sensing delivers us with sharpened TF image of the signal. Co-existence of FM and AM signals in a specific domain can enhance the value of spectral utility. The paper also reveals the present status of AM-FM decomposition where it will be beneficial for future references and for more complex modulation
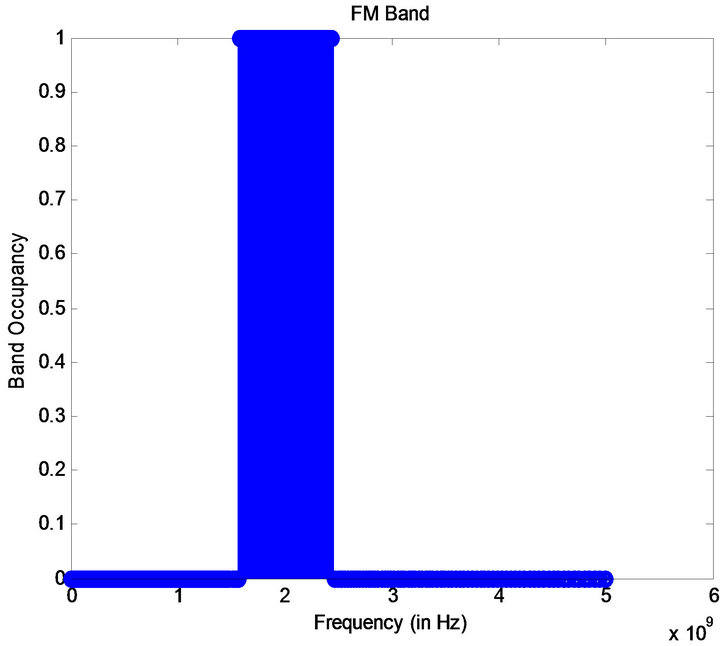
Figure 5. Bandwidth occupied by FM.
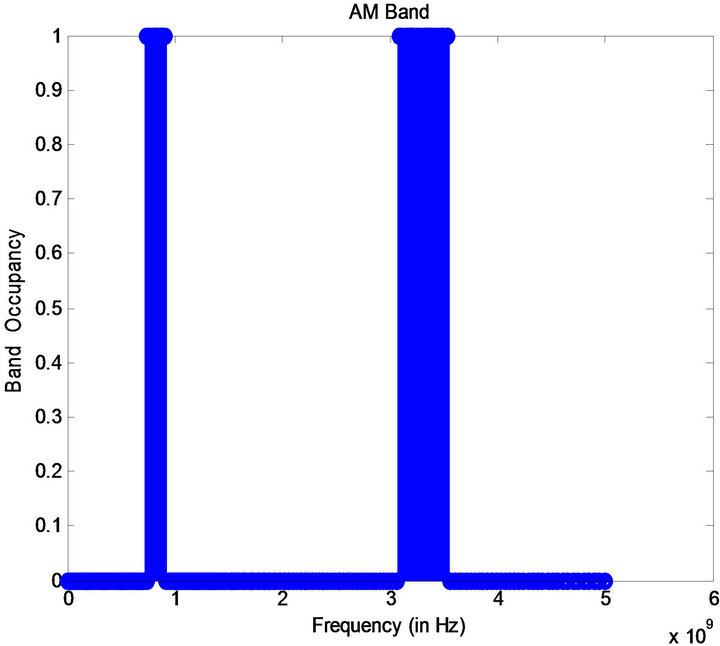
Figure 6. Bandwidth occupied by AM.
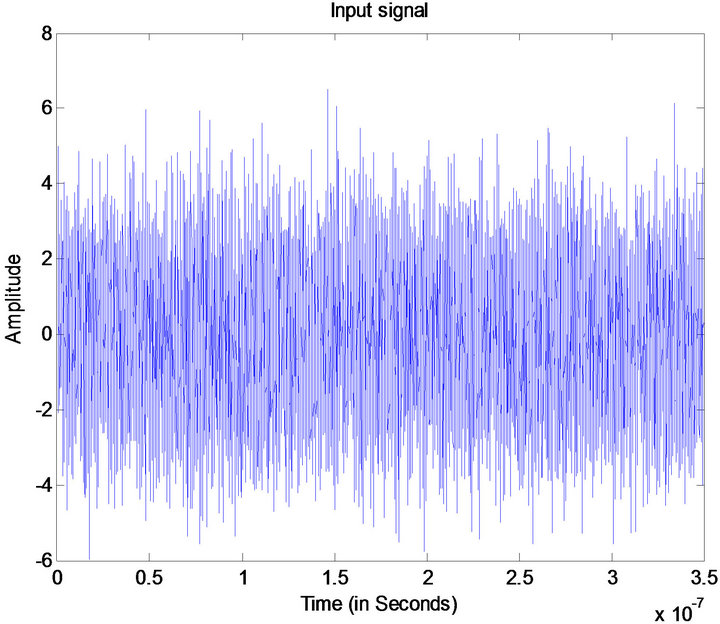
Figure 7. Input signal with noise power −3 dB (for overlapping case).
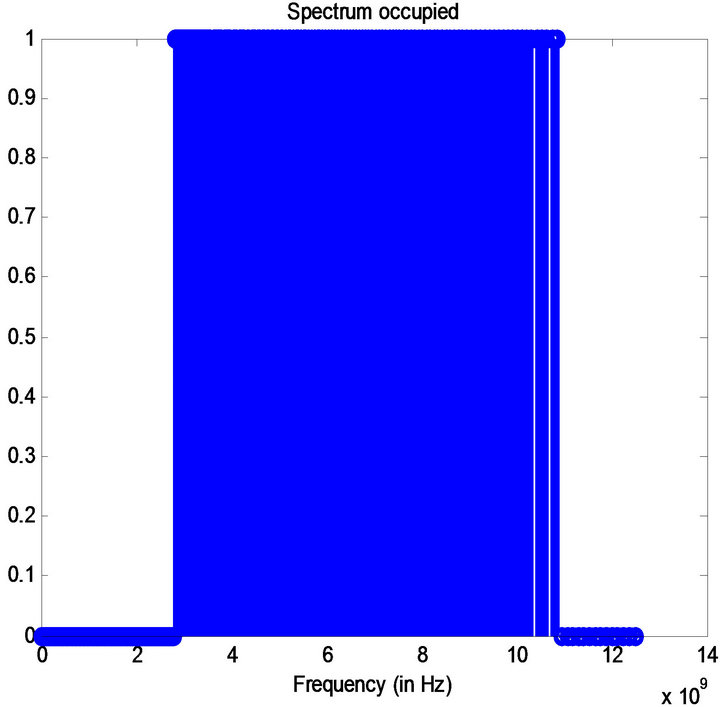
Figure 9. Spectrum occupied by input signal.
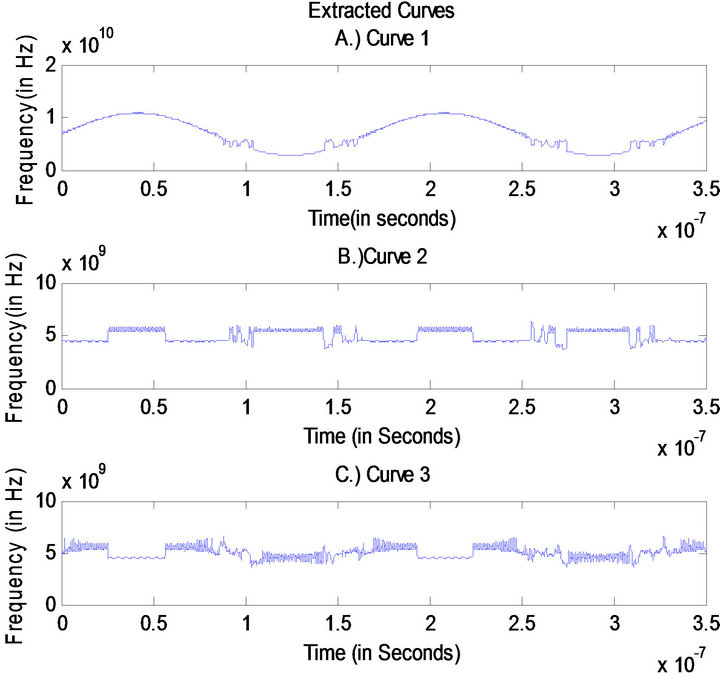
Figure 10. Extracted curves from synchrosqueezed transform.
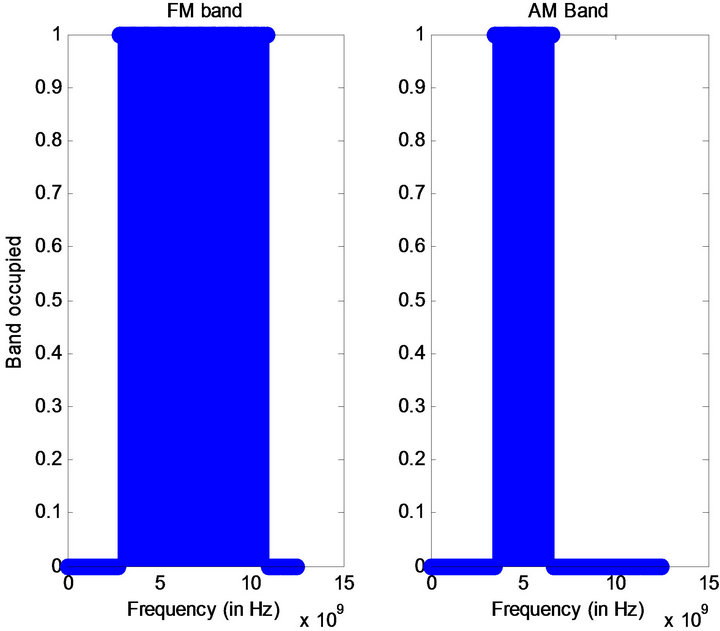
Figure 11. Spectrum occupied by FM (left) of band 2.8 - 10.8 GHz and AM (right) of band 4.5 - 5.5 GHz.
techniques. This also can act as evidentiary support for futuristic cognitive radio ideas in areas of research and development.
REFERENCES
- I. Daubechies, J. F. Lu1 and H.-T. Wu, “Synchrosqueezed Wavelet Transforms: An Empirical Mode Decomposition-Like Tool,” 25 July 2010.
- S. Haykin and L. Fellow, “Cognitive Radio: Brain Empowered Wireless Communications,” IEEE Journal, Vol. 23, No. 2, 2005.
- Gianfelici, F. Biagetti, G. Crippa and P. Turchetti, “AMFM Decomposition of Speech Signals: An Asymptotically Exact Approach Based on the Iterated Hilbert Transform,” IEEE Conference Publication, July 2005, pp. 333- 338.
- T. Backstrom, “Parametric AM/FM Decomposition for Speech and Audio Coding,” IEEE Conference Publication, October 2009, pp. 333-336.
- T. Yucek and H. Arslan, “A Survey of Spectrum Sensing Algorithms for Cognitive Radio Applications,” IEEE Communication Surveys & Tutorials, Vol. 11, No. 1, 2009. doi:10.1109/SURV.2009.090109
- S. Meignen and V. Perrier, “A New Formulation for Empirical Mode Decomposition Based on Constraint Optimization,” 2007. http://www-ljk.imag.fr/membres/Valerie.Perrier/PUBLI/EMD-optim07.pdf
- G. Thakur, E. Brevdo, N. S. Fuˇckar and H.-T. Wu, “The Synchrosqueezing Algorithm for Time-Varying Spectral Analysis: Robustness Properties and New Paleoclimate Applications,” 2012. arXiv:1105.0010v2[math.CA]
- P. Flandrin, “Time-Frequency/Time-Scale Analysis,” Academic Press, San Diego, 1999.
- A. Graps, “An Introduction to Wavelets,” IEEE Computational Science and Engineering, Vol. 2, No. 2, 1995. doi:10.1109/99.388960
- M. Clausel, T. Oberlin1 and V. Perrier, “The Monogenic Synchrosqueezed Wavelet Transform: A Tool for the Decomposition/Demodulation of AM-FM Images,” 2012. http://arxiv.org/abs/1211.5082