Wireless Engineering and Technology
Vol.3 No.4(2012), Article ID:24179,4 pages DOI:10.4236/wet.2012.34028
Reducing Peak-to-Average Power Ratio of a Turbo Coded OFDM
![]()
Physics Department, University of Ioannina, Ioannina, Greece.
Email: schrono@cc.uoi.gr, me00168@cc.uoi.gr, gtatsis@grads.uoi.gr, kostarakis@uoi.gr
Received May 15th, 2012; revised June 13th, 2012; accepted June 24th, 2012
Keywords: Orthogonal Frequency Division Multiplexing; Peak to Average Power Ratio; μ-Law; μLaCP; μLaIF; Parallel Concatenated Convolutional Codes; A Posteriori Probability; Cyclic Prefix; Zero Padding; Peak Ratio; Bit Error Rate
ABSTRACT
Peak to Average Power Ratio (PAPR) is defined as the instantaneous power (maximum value) to the average power ratio. PAPR is considered to be a major problem in OFDM systems. This problem can cause radical unexpected behavior of the signal fluctuation. This fluctuation is constituted by a large number of power states. The enormous number of these states leads to an additional complexity of ADCs and DACs. This research addresses the previous problem in OFDM systems utilizing Turbo Codes. μLaCP technique is employed for the purpose of decreasing PAPR. Moreover, our OFDM system was simulated in the presence of an AWGN channel with four types of codes (without the presence of ADCs and DACs). These were constituted of PCCC (typical and new), SCCC, and Convolutional Codes. Our Turbo Coded OFDM exhibited unchanged BER performance before and after the use of μLaCP technique. This was accomplished by modifying our previous PAPR reduction technique without sacrificing greatly its attributes.
1. Introduction
Many promising technologies which utilize or participate in high speed data systems are OFDM [1], UWB [2], MIMO [3], Tunable antennas [4], etc. The field of multiplexing technique (OFDM—Orthogonal Frequency Division Multiplexing) offers excellent annotation to channel fading but it also suffers from high fluctuation of the produced signal power. This fluctuation is measured, simulated or estimated as a ratio of Peak Power to Average Power and is usually expressed in dB. If the previous problem won’t be addressed properly, then various problems can emerge. Power amplifiers won’t work adequately as a larger operation region is needed. Also, Digital-to-Analog converters must be very complex. This happens because their function must be more accurate in detecting more Power states due to the fact of the previous magnitude fluctuation. The problem of PAPR has already been researched. Its bibliography exhibits various schemes which provide very interesting approaches of restricting the aforesaid undesirable effects. Clipping [5, 6], root companding transformation [7], combined interleaving and companding [8] and the reacquisition of the clipped part of the signal [9] belong to the PAPR research field. The previous schemes show some drawbacks even if they succeed in their purpose. These draw backs are relevant either to complexity, or undesirable radiation or reduced performance or the combination of all previous when they are compared to μLaCP technique [10]. This technique will be analyzed later in brief.
Our OFDM simulation platform used Turbo codes, specifically a new scheme. This scheme is based on Parallel Concatenated Convolutional Codes (PCCC). Generally, this innovative design boosts the performance of a system according to various selected block sizes [11]. Our previous technique introduces many differences in design level compared to typical PCCC. Three convolutional encoders are concatenated in parallel instead of two. This produces a higher code rate of 1/4. The decoding part is consisted of more puncturing procedures. More procedures are needed as the information stream contains four (instead of three) outputs of convolutional encoders. In turn, new data sequences are produced and inserted to the appropriate A Posteriori Probability (APP) decoders. These decoders participate in an iterative function with the purpose of reevaluating the estimated information for further boosting the system’s performance.
Our research included after the enhancement of an OFDM system with our two new PAPR reduction techniques (μLSR and μLaCP), a further development (in simulation level) in terms of BER. This development was a new PCCC design which was inserted in our system and simulated. The results were excellent verifying that the new Turbo Coded OFDM system exhibited low probability of errors. In turn, this research is the next stage to our previous efforts. This was accomplished with the utilization and modification of the best of our techniques which is an altered version of μLaCP (μLaIF) for decreasing PAPR. Consequently, the simulated project was consisted of our Turbo Coded OFDM [12] along with the presence of μLaIF. The purpose was to conduct an extensive research in the new Turbo Coded OFDM system taking into consideration the effects of PAPR. We verified with the insertion of the modified scheme that no deterioration would appear in the system performance. Moreover, we verified that the system would not exhibit large power fluctuations. Accordingly, we can assume that no further deterioration in system performance would take place in the possible future use of ADCs or DACs.
This paper is consisted of four sections. In the second section the complete system will be presented containing OFDM, Turbo codes and the PAPR reduction technique. Third section is dedicated to simulation procedures and results. Fourth section presents very useful conclusions along with the future scopes of this study.
2. Overview of the Turbo Coded OFDM System with Reduced PAPR
The following paragraphs present an overview of the proposed system. Paragraph 2.1 is a short description of our Parallel Turbo scheme while 2.2 mentions in brief the Coded OFDM architecture. Finally in 2.3 is discussed our μLaIF (modified μLaCP) scheme which was combined with all previous to form an efficient OFDM system in terms of BER and reduced PAPR.
2.1. Turbo Codes
Turbo codes can be split into two topologies. These are characterized by the concatenation type. If the concatenation is conducted as a parallel join of convolutional codes, then this scheme is known as Parallel Concatenated Convolutional Codes (PCCC). If serial association of convolutional codes is employed, then this technique is named as Serial Concatenated Convolutional Codes (SCCC). Typical SCCC and PCCC systems are mentioned in [13-15]. Our Parallel Turbo Codes [11] were developed in order to be part of an OFDM system [12]. This system is discussed in the following paragraphs.
Three convolutional encoders and two random interleavers [16] form a Parallel Turbo encoder. This new scheme is shown in Figure 1. The original sequence of randomly generated data enters only one of the three encoders while its interleaved versions are the inputs of the
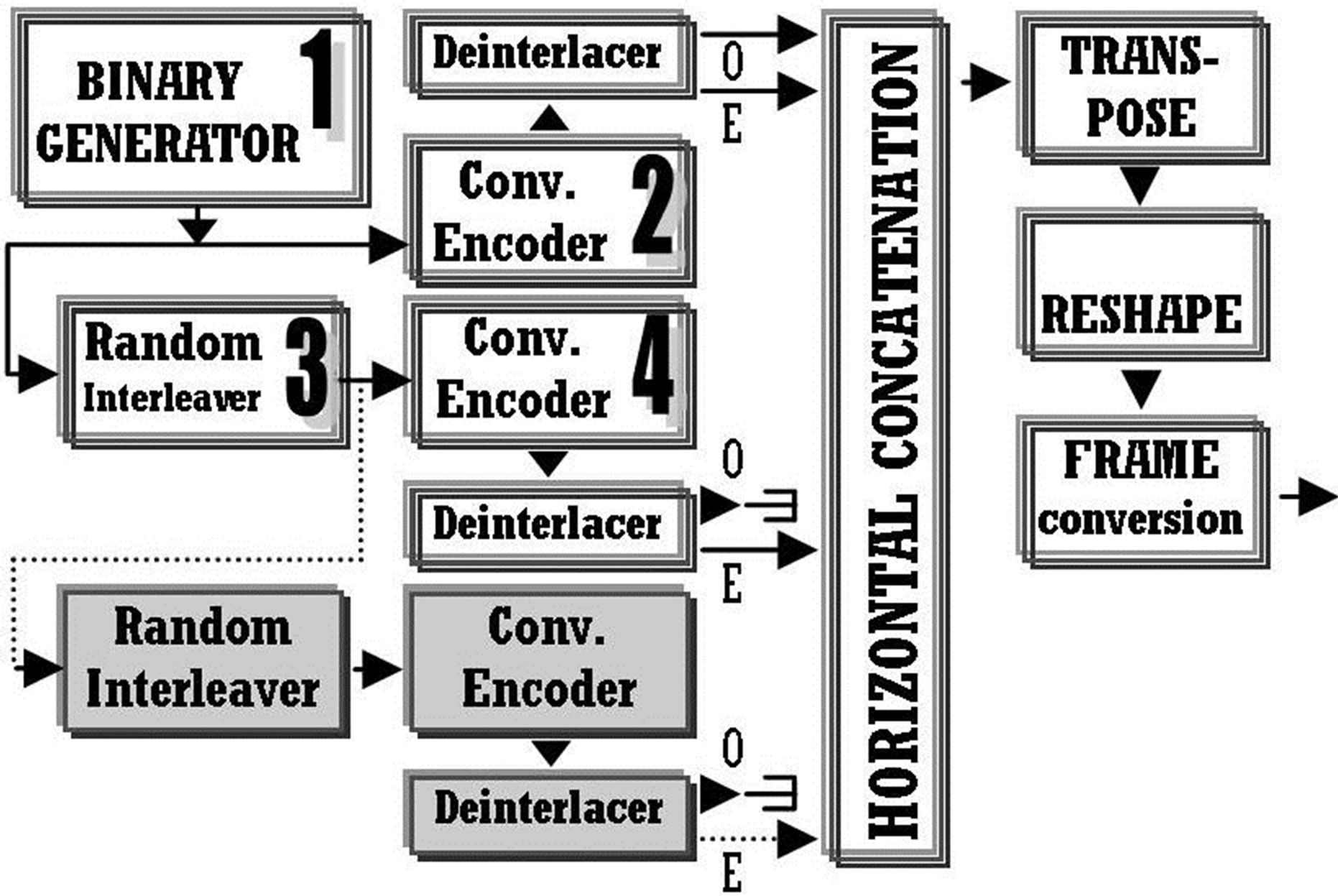
Figure 1. Parallel Turbo encoder (blocks with gray colors must be added to a typical PCCC. Moreover, the sequence 1->2->3->4 represents an SCCC encoder).
other two. Interleaving is conducted in order to decorrelate the three inputs of convolutional encoders for the purpose of accomplishing the best possible system performance. Moreover one of the encoders provides in its outputs the systematic and the recursive version of the input signal. All others produce only the recursive stream with the use of deinterlacers. The decoding procedure is constituted from two stages. The first stage (Figure 2) contains puncturing procedures in order to acquire independently each recursive or systematic version of the original signal which has passed through an AWGN channel. Then, the recursive versions are interlaced with systematic versions (by using Random interleavers) of the signal. The final produced signals are in fact the original outputs of every parallel concatenated convolutional encoder with the difference that they contain Additive White Gaussian Noise (AWGN). In turn, these streams must be decoded. This will provide the best possible version of the primary produced information stream. Taking into consideration all previous, the second stage (Figure 3) was designed in order to contain three APP decoders operating in an iterative manner. More iterations provide better estimation of the primary information with the drawback of the additional delay [17]. So, a rational number of iterations was selected. This will be mentioned again in the simulations’ section.
2.2. OFDM System
Orthogonal frequency division multiplexing is a technique which splits a stream of information to substreams. These substreams are then transmitted with the use of orthogonal frequency carriers. The previous function is conducted using Inverse Fast Fourier Transform in transmitter’s part. Various safety precautions must be utilized notwithstanding this technique is immune to channel fading. Cyclic prefix (CP) [18] must be used in order to increase every symbol’s duration for avoiding

Figure 2. First decoding stage is accomplished by adding grey blocks to a typical PCCC system.
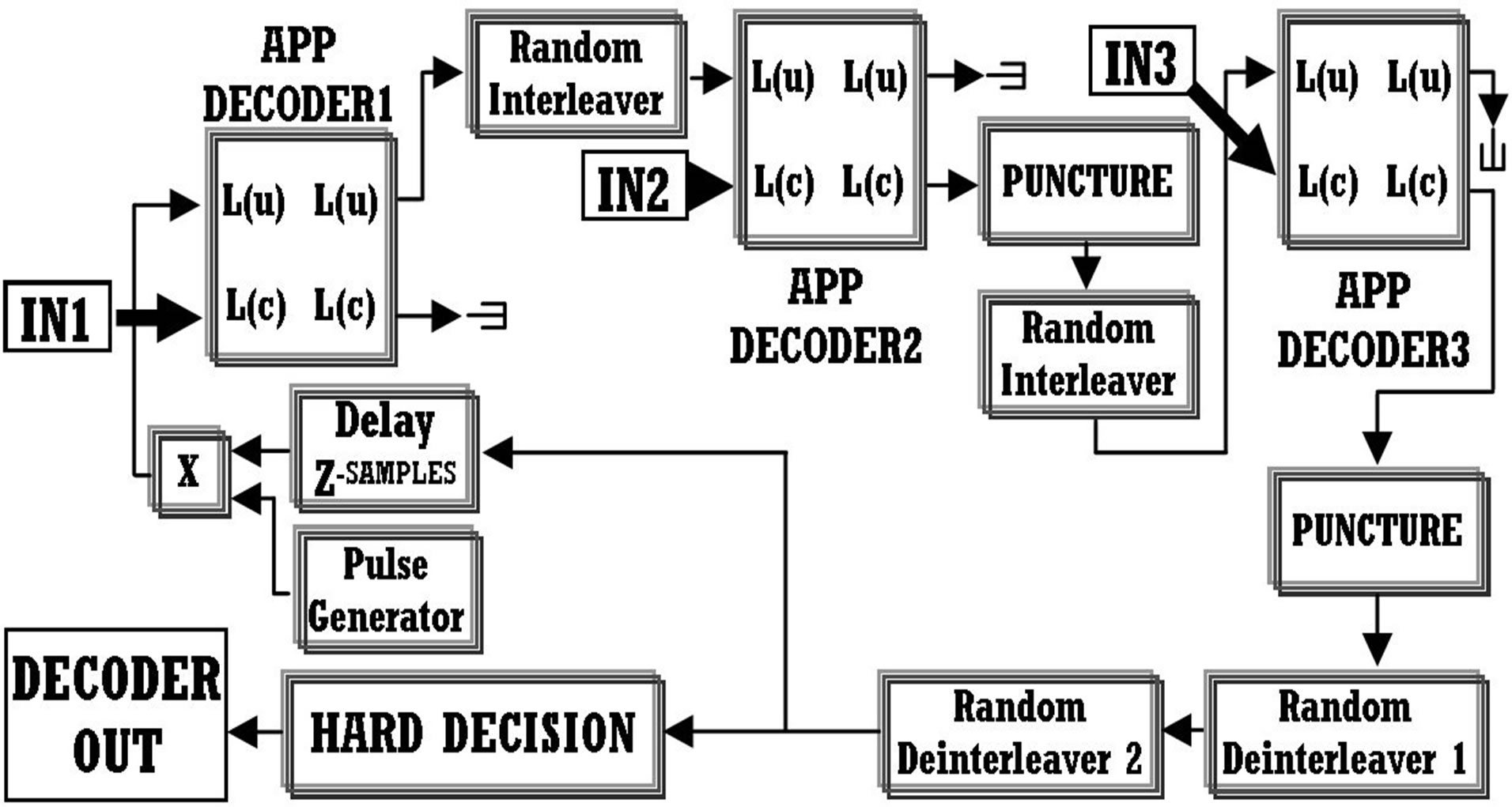
Figure 3. Second decoding stage of our PCCC system.
intersymbol interference. Another alternative to CP is Zero padding (ZP) which is considered to be better but with drawbacks [19]. These two schemes were combined for assuring the best possible performance of our Turbo Coded OFDM system.
Figure 4 presents the Turbo Coded OFDM system [12] with a new feature. This feature is μLaCP technique [10] which has been modified to μLaIF. The system is formed in such a way that gives the capability to the final user of simulating different block sizes, different number of iterations, various numbers of produced carriers (in IFFT output) PAPR parameter (will be discussed later) and the adjustment of an additional factor. This factor must be changed according to the block size for certifying that the same amount of information has been transmitted. The encoder and decoder blocks refer to the selected type of scheme (PCCC, SCCC, new scheme and Convolutional encoding with Viterbi decoder). Zero Padding is applied before IFFT input and it corresponds to the 25% of total produced carriers. In turn Cyclic Prefix is fixed to 25% of IFFT output. Then, OFDM signal passes through an AWGN channel and reaches receiver’s part. The reverse procedures are applied for the purpose of acquiring the information signal.
All previous procedures are not conducted at once. So, various delays are produced which must be taken into consideration for the final BER estimation. The various delays are shown in Table 1 [12]. Moreover, the block named “μLaIF” is the technique of reducing PAPR and is analyzed in the following paragraph. μLSR has not been
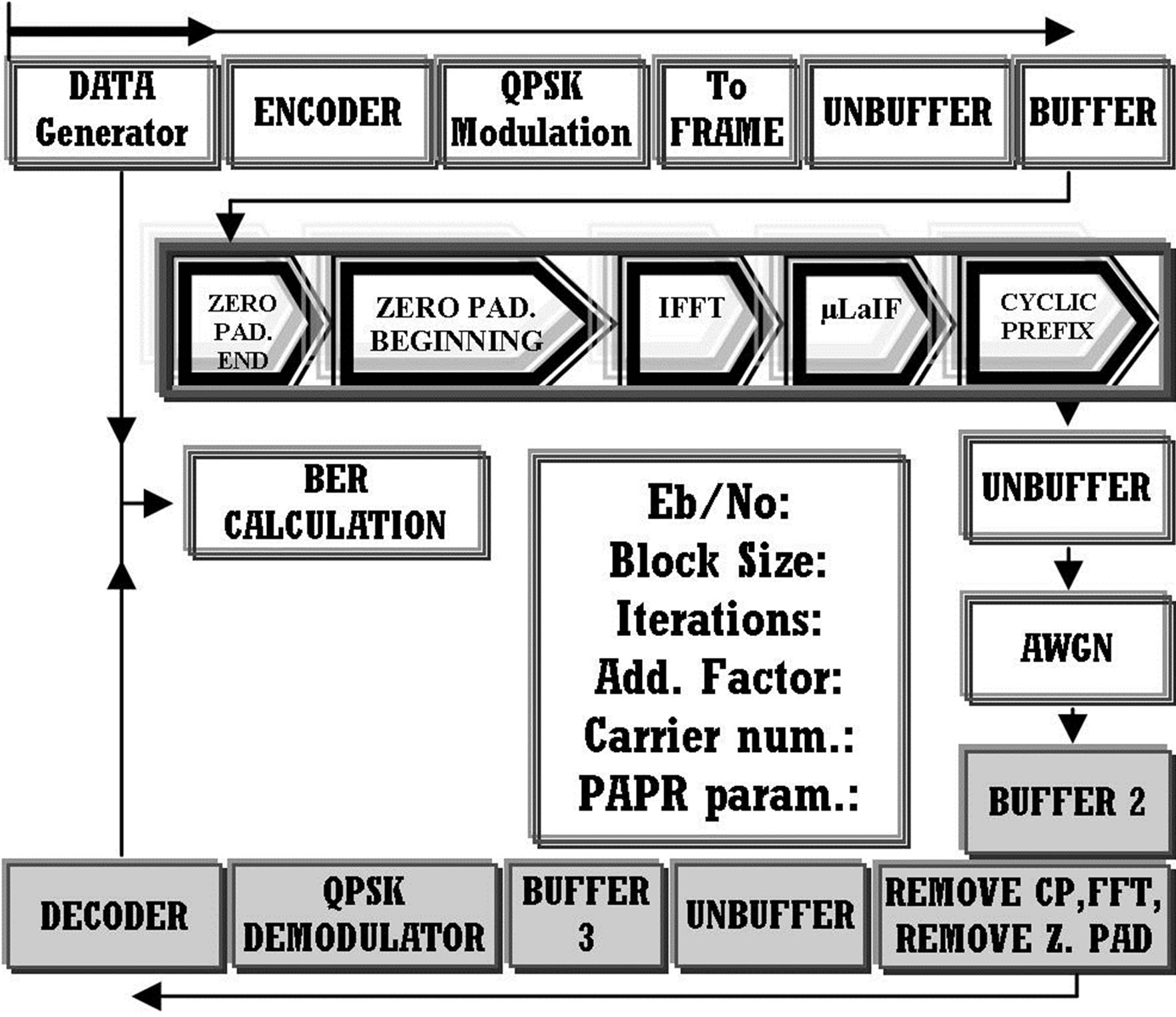
Figure 4. Schmematic of OFDM simulation platform with μLaIF.

Table 1. Produced delays due to coding type.
applied to the Coded OFDM as it exhibits worst performance than that of μLaCP [10].
2.3. μLaIF Scheme
The PAPR reduction scheme which is called “μ-Law output subtracting IFFT output” is applied in the OFDM simulation platform. It originates from μLaCP [10]. The idea behind the mechanism is the same. The input of μ-Law block is subtracted from its output (Figure 5). The different approach in this case is based on the location where this subtraction is applied. It is found through simulations that μLaIF is slightly better than μLaCP. This has a profound effect in the system’s performance. If PR= √2 and μ = 3 is applied in this system then PAPR will be dramatically reduced but BER deterioration will be imminent (without ADC and DAC). In accordance to the previous fact, we had to accept the idea of applying a larger-μ-number which would deteriorate the PAPR performance. So, it was convenient the increased performance that μLaIF had to offer, with the need of finding larger-μ-values. Equations (1) and (2) express the idea of the proposed subtraction.
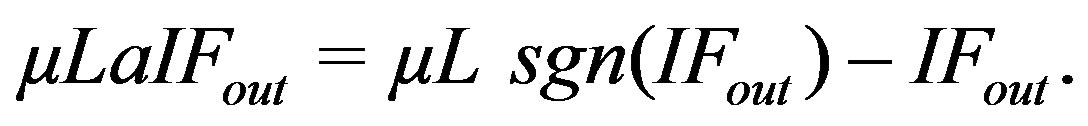 (1)
(1)
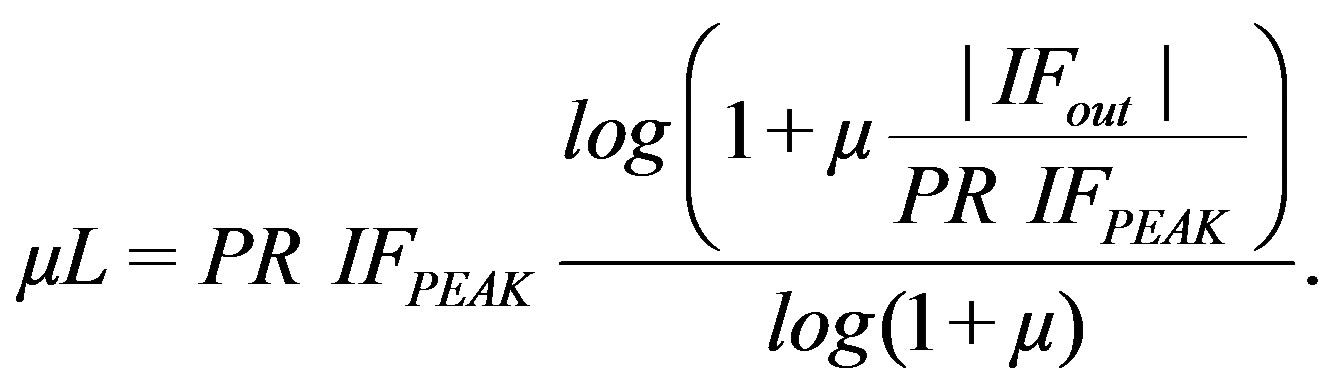 (2)
(2)

Figure 5. Function of μLaIF.
where IFout is the output of IFFT, IFPEAK is the maximum peak amplitude in the output of IFFT, PR is the Peak ratio [20] and μ represents the compression parameter.
3. Simulation Procedures and Results
The OFDM simulation platform used various kinds of frame sizes (64, 128, 256 and 512) and thus it was configured in order to sustain four types of coding schemes. These schemes were previously mentioned. They included two types of Convolutional codes. One type had a rate of 1/2, constraint length of 3, memory of 2 and generator polynomials 78 and 58. The other type had a rate of 2/3 and memory of 4. Only convolutional codes with rate 1/2 used in Parallel Turbo coding schemes while the two types were present only in the case of SCCC [12]. The stages of decoders were constituted of APP decoders (Turbo techniques) and Viterbi decoder (Convolutional Coding). These APP decoders utilized log-Map algorithm [21]. Also, noise characteristics of the selected AWGN channel were adjusted through the applied noise variance. This factor included the parameters of modulation type (QPSK with M = 4), Code rates (1/2 or 1/3 or 1/4), Es and Eb/No [11]. Moreover, important simulations settings relevant to our developed system are summarized in Table 2.
Peak to Average Power Ratio is an important characteristic of an OFDM system. Precautions must be taken in order to reduce this fluctuation. PAPR is known as a ratio of the maximum occurring power to the average power and is expressed usually in terms of dB.
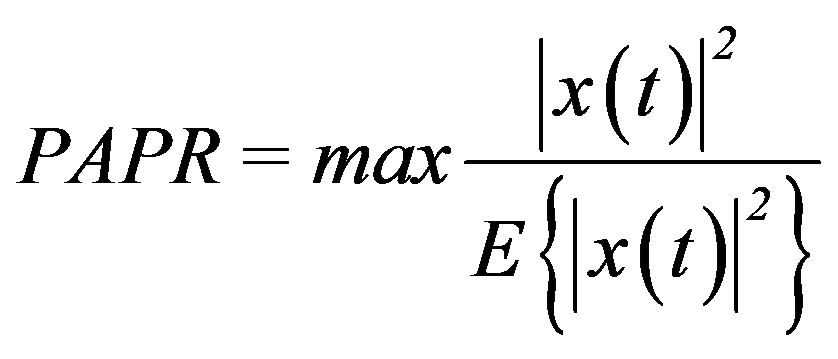 (3)
(3)
BER analysis is very helpful for understanding system performance at a first glance. If the previous research doesn’t include ADCs’ and DACs’ in simulation level then PAPR must be the next step of the study. The golden mean is found by producing a lower PAPR, using the appropriate technique, without reducing greatly the BER performance. The previous idea was applied in this research. Our Turbo scheme presented in [11] exhibited the best performance compared to other Coding techniques. Figure 6 shows BER performance for five iterations. Moreover, the main goal of this study was to identify if μLaIF (formerly known as μLaCP) could be applied in the best coding scheme. Simulations proved that
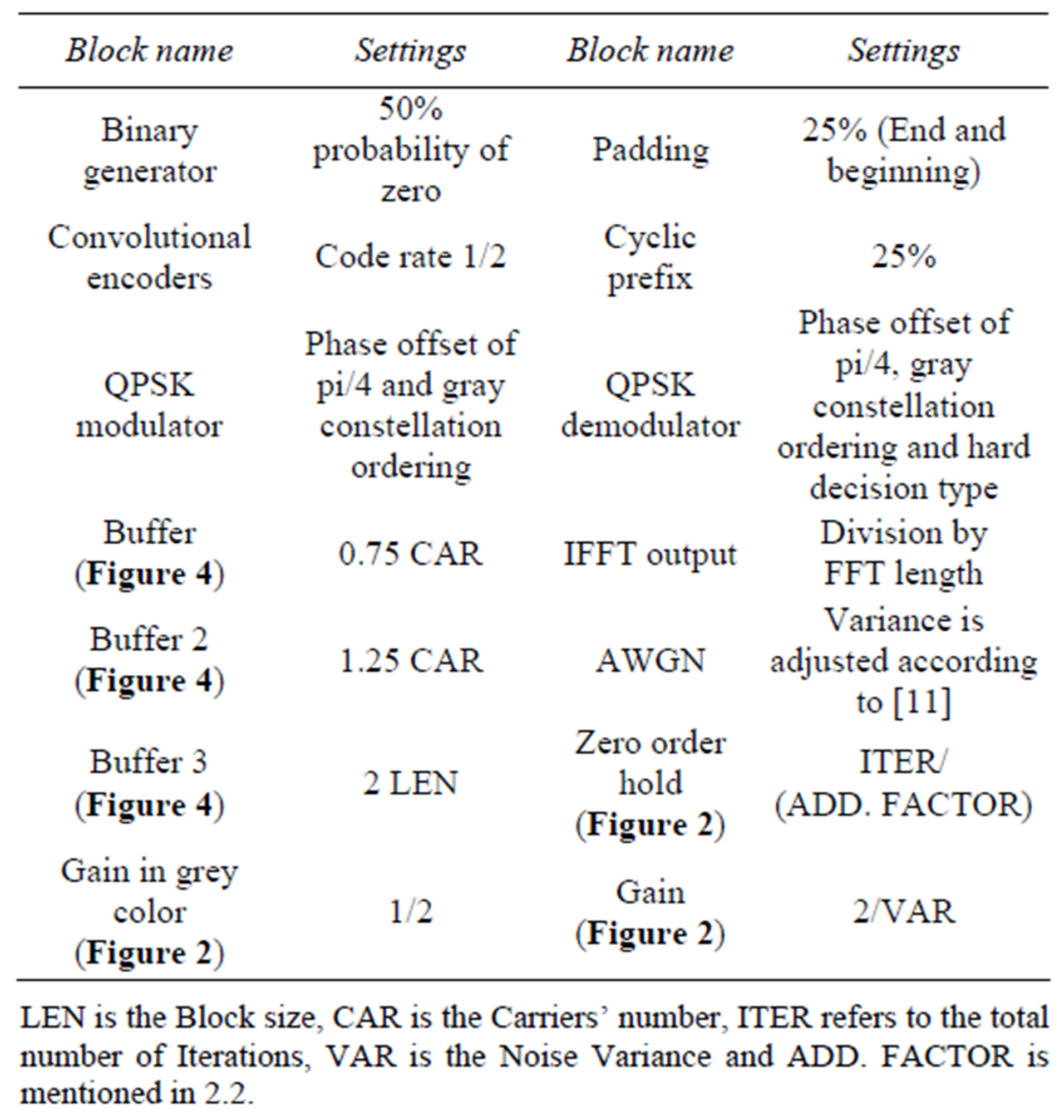
Table 2. Simulations settings of OFDM (PCCC, Rc = 1/4).
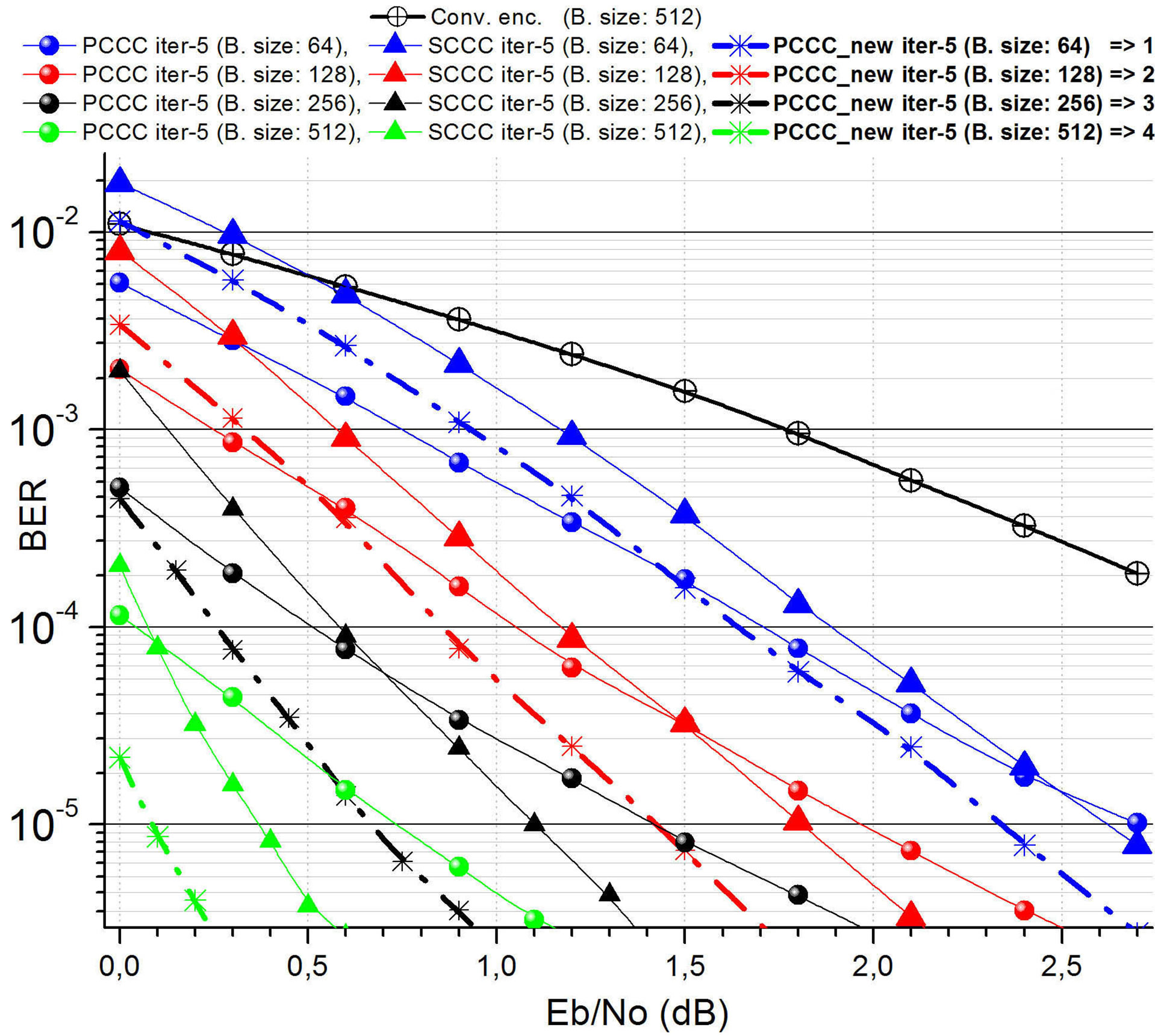
Figure 6. BER Performance without companding scheme (for block size 256 and 5 iterations).
this was feasible with the use of Complementary Cumulative Distribution (CCDF) function.
CCDF plot is a tool intended to acquire important information relevant to the Signal Power of various components such as mixers, amplifiers, filters and other devices. CCDF presents the time during which, a signal has the specific or greater than this power state. Specifically, this type of curve shows in probability terms the time that signal’s level is found above the average power. Both axes of the previous figures are expressed logarithmically [22-24]. “PAPR parameter” which is shown in Figure 4, is the maximum observed PAPR. This value differs each time for different block size and carriers number. We adjusted the Peak Ratio (PR) to [25], using the previous factor (taking into consideration in our calculations the mean power). Moreover various values of μ (or else stated as mu) were tested. The best results were definitely those for mu = 3. This is shown in Figure 7 for 4096 OFDM carriers, various frame sizes and mu (with values of 3, 4, 5). Even, if PAPR performance was superior for mu = 3 this was not the case for BER performance. We checked the feasibility of mu = 3 through BER simulations and the results were disappointing, so we concluded in checking also mu = 4,5. The best results in relevance to BER performance were those for mu = 5. In Figure 8 is presented the CCDF plot for fixed block size (256), for various carriers and different mu values. Also, the system with PAPR reduction technique is compared to systems without μLaIF. Even with the use of mu = 5 the PAPR (dB) is almost the half compared to those without PAPR reduction technique. Moreover BER performance of mu = 5 outperforms that of mu = 4 and at the same time it reaches almost the primary performance (without compander). All previous are shown in Figures 6 and 9 (for up to five iterations). Finally, Figure 10
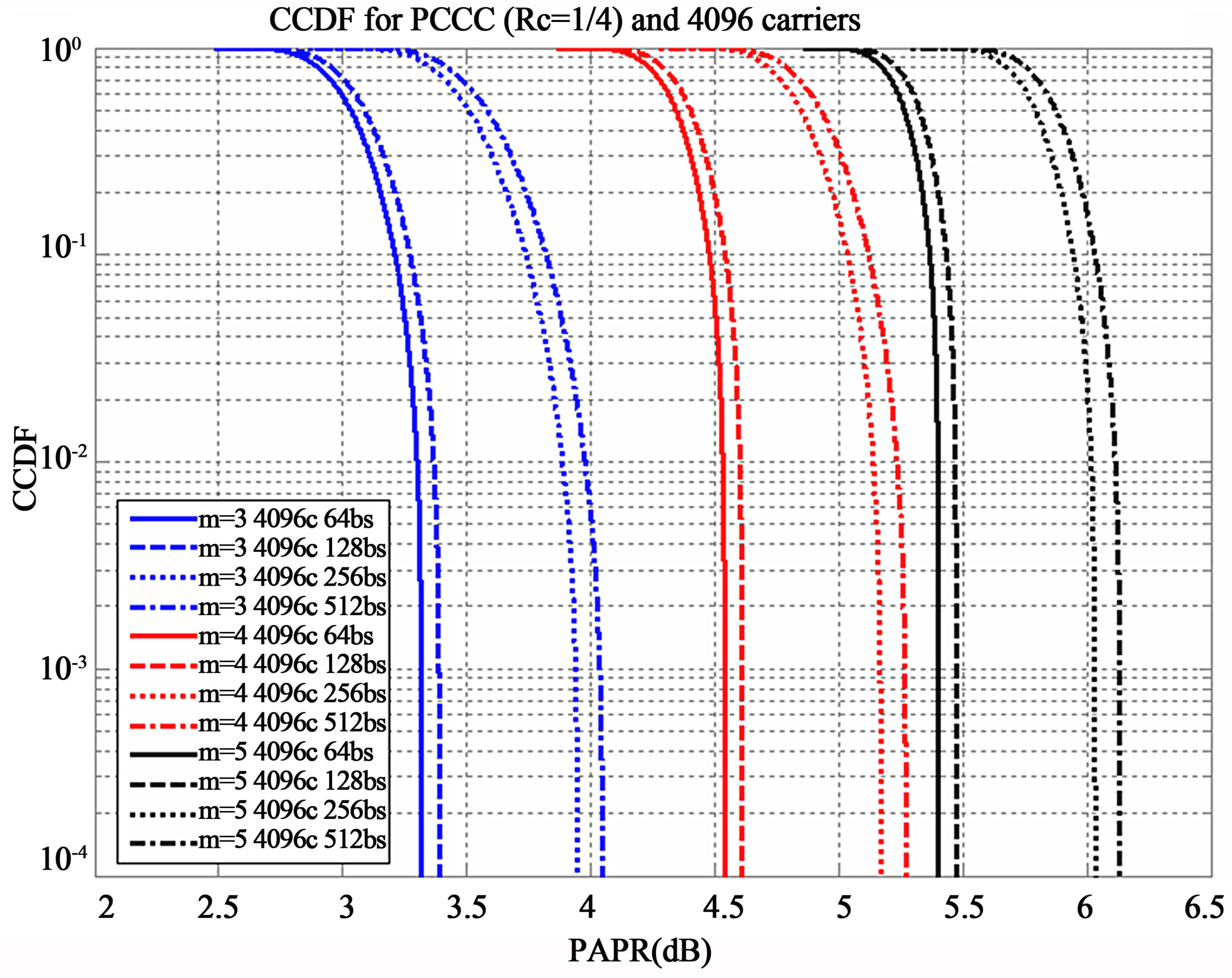
Figure 7. PAPR Performance for fixed number of carriers.
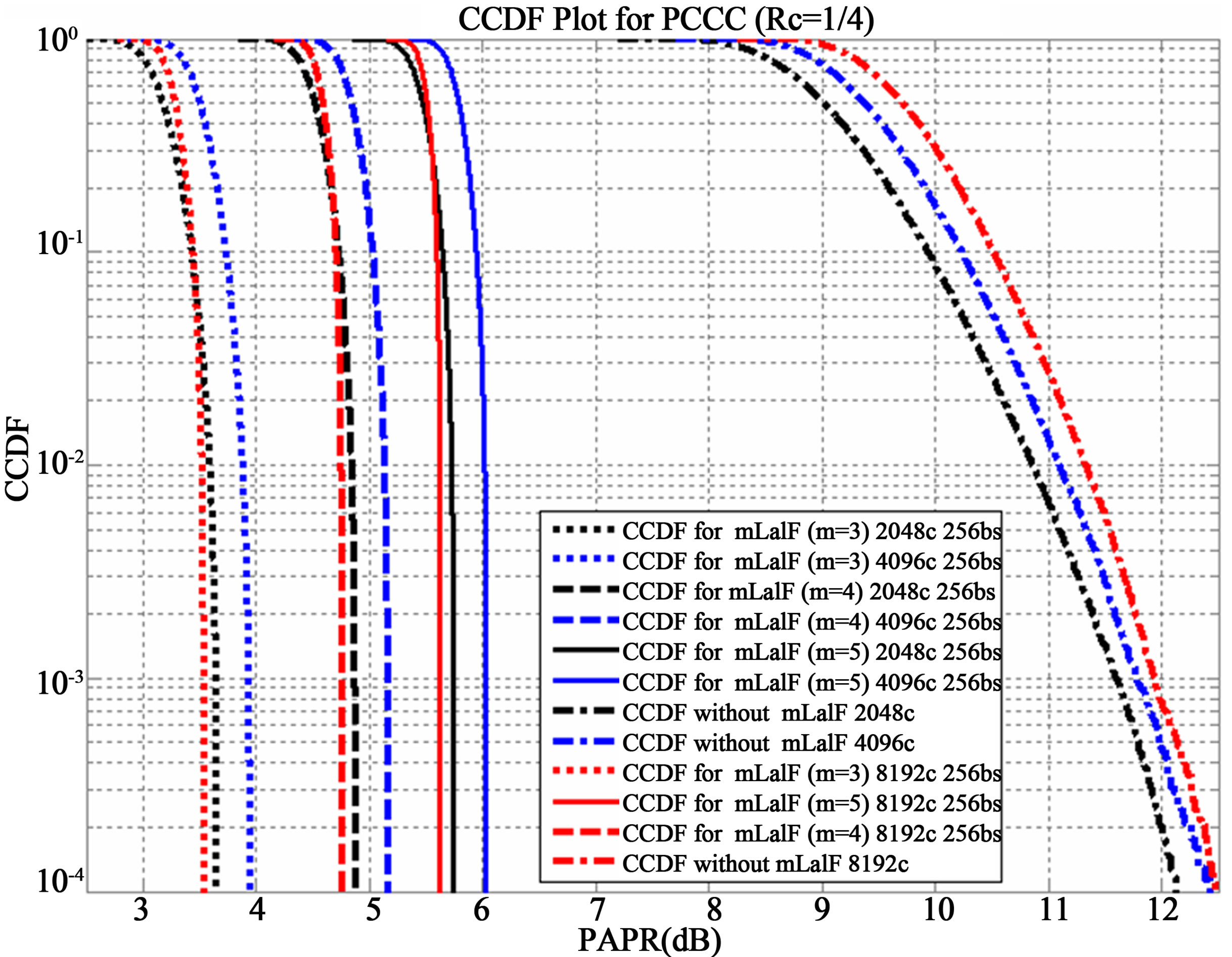
Figure 8. PAPR performance for fixed block size.
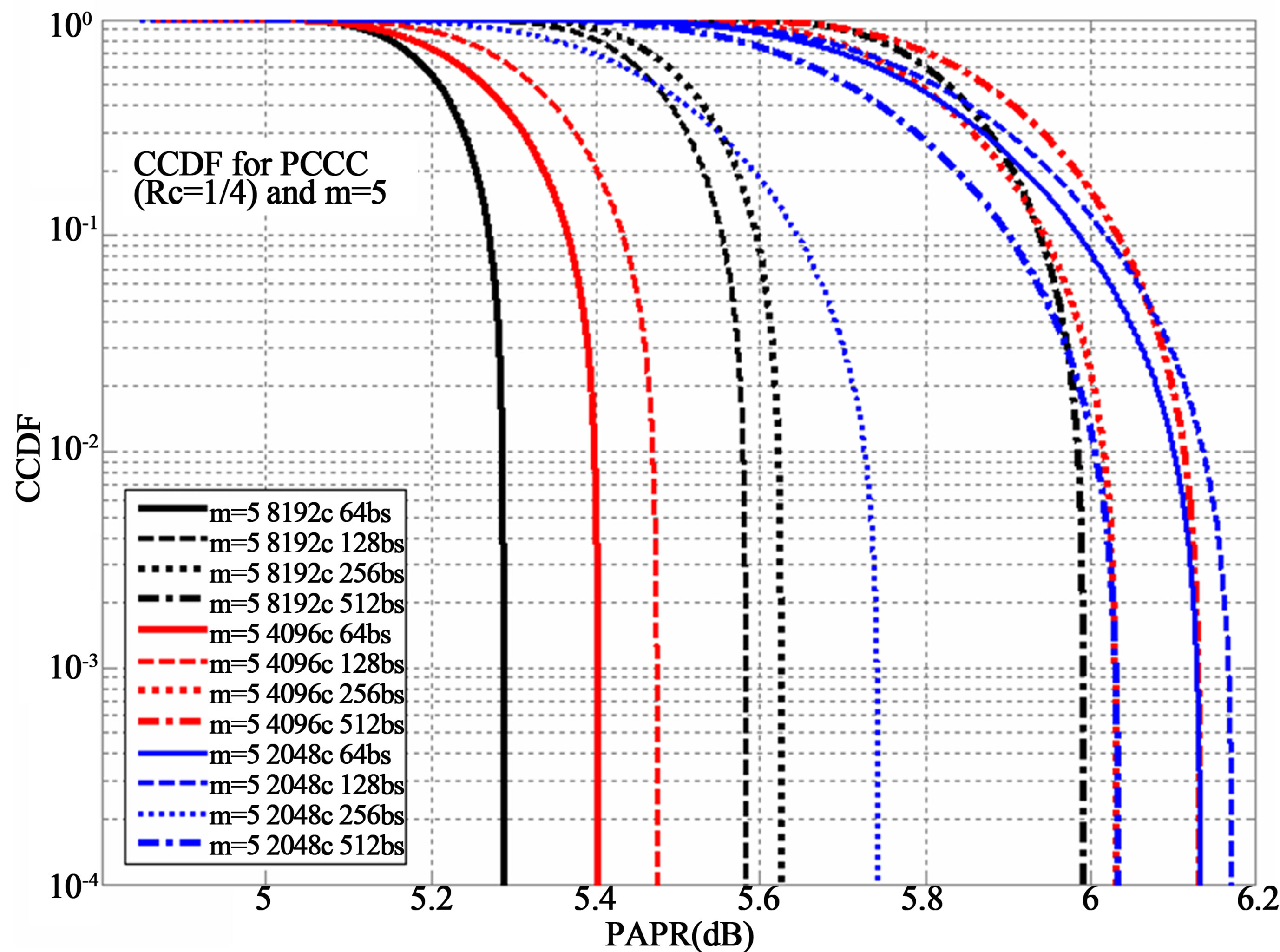
Figure 10. PAPR performance for mu = 5 (proposed value).

Figure 9. BER performance of best coding technique for mu = 4, 5 and for various iterations.
presents the system performance in terms of PAPR for fixed mu value, which is the proposed value of 5.
4. Conclusions
This research was focused on reducing PAPR in a Turbo Coded OFDM system which employed the best Coding technique compared to others. The selected companding technique is one of the best techniques. This scheme was modified in order to reduce PAPR along with sustaining unchanged BER performance (without the presence of ADCs and DACs). The results were excellent exhibiting a PAPR (dB) decrease of almost 50%.
Future scope of this research is the proposed system to be implemented in a DSP [26]. Furthermore, it could include or to be part of emerging technologies such as UWB [27], MIMO [28], Tunable antennas [29], etc. Also, our intention is this research to be conducted taking into consideration the presence of ADCs and DACs [30].
5. Acknowledgements
This research has been co-financed by the European Union (European Social Fund—ESF) and Greek national funds through the Operational Program “Education and Lifelong Learning” of the National Strategic Reference Framework (NSRF)—Research Funding Program: Heracleitus II. Investing in knowledge society through the European Social Fund.
REFERENCES
- S. K. Chronopoulos, C. Votis, V. Raptis, G. Tatsis and P. Kostarakis, “In Depth Analysis of Noise Effects in Orthogonal Frequency Division Multiplexing Systems, Utilising a Large Number of Subcarriers,” Proceedings of the 7th International Conference of the Balkan Physical Union, Alexandroupolis, 9-13 September 2009, pp. 967-972. doi:10.1063/1.3322592
- G. Tatsis, C. Votis, V. Raptis, V. Christofilakis, S. K. Chronopoulos and P. Kostarakis, “Performance of UWBImpulse Radio Receiver Based on Matched Filter Implementation with Imperfect Channel Estimation,” Proceedings of the 7th International Conference of the Balkan Physical Union, Alexandroupolis, 9-13 September 2009, pp. 573-578. doi:10.1063/1.3322512
- C. Votis and P. Kostarakis, “Design and Analysis of a Multiple-Input Receiver for Mimo Wireless Applications,” International Journal of Communications, Network and System Sciences, vol. 3, no. 7, 2010, pp. 593- 601. doi:10.4236/ijcns.2010.37079
- V. Raptis, C. Votis, G. Tatsis, S. K. Chronopoulos, V. Christofilakis and P. Kostarakis, “Active Tuning Antennas for Wireless Communication,” Proceedings of the 7th International Conference of the Balkan Physical Union, Alexandroupolis, 9-13 September 2009, pp. 1058-1062. doi:10.1063/1.3322310
- S. I. Hernandez, “Simulation and Evaluation of a DVB System Using Simulink (Vol. I),” Master Thesis, Linkopings Universitet, Linkoping, 2005.
- F. Zbynek and S. Vladimir, “Reduction of PAPR in OFDM by Clipping,” Proceedings of 15th International Czech-Slovak Scientific Conference Radioelektronika, Brno, May 2005, pp. 474-477.
- P.-H. Chang, S.-S. Jeng and J.-M. Chen, “Utilizing a Novel Root Companding Transform Technique to Reduce PAPR in OFDM Systems,” International Journal of Communication Systems, Vol. 23, No. 4, 2010, pp. 447- 461.
- H. Sakran, M. Shokair and A. A. Elazm, “Combined Interleaving and Companding for PAPR Reduction in OFDM Systems,” Progress in Electromagnetics Research C, Vol. 6, 2009, pp. 67-78.
- I. I. Al-kebsi, M. Ismail, K. Jumari and T. A. Rahman, “Eliminate the Effects of Clipping Technique on the SER Performance by Recovering the Clipped Part of the OFDM Signal,” International Journal of Computer Science and Network Security (IJCSNS), Vol. 9, No. 7, 2009, pp. 37-45.
- S. K. Chronopoulos, G. Tatsis, V. Raptis and P. Kostarakis, “Enhanced PAPR in OFDM without Deteriorating BER Performance,” International Journal of Communications, Network and System Sciences, Vol. 4, No. 3, 2011, pp. 164-169. doi:10.4236/ijcns.2011.43020
- S. K. Chronopoulos, G. Tatsis and P. Kostarakis, “Turbo Codes―A New PCCC Design,” Communications and Network, Vol. 3, No. 4, 2011, pp. 229-234. doi:10.4236/cn.2011.34027
- S. K. Chronopoulos, G. Tatsis and P. Kostarakis, “Turbo Coded OFDM with Large Number of Subcarriers,” Journal of Signal and Information Processing (JSIP), Vol. 3, No. 2, 2012, in press.
- S. Shah and V. Sinha, “Iterative Decoding vs. Viterbi Decoding: A Comparison,” Proceedings of the 14th National Conference on Communications NCCC 2008, Mumbai, 1-3 February 2008, pp. 491-493.
- W. Xie, G.-J. Hu and Q. Deng, “Application of Turbo Codes in Optical OFDM Multimode Fiber Communication System,” Optics Communications, Vol. 281, No. 5, 2008, pp. 1118-1122. doi:10.1016/j.optcom.2007.10.84
- I. S. Raad and M. Yakan, “Implementation of a Turbo Codes Test Bed in the Simulink Environment,” Proceedings of the Eighth International Symposium on Signal Processing and Its Applications ISSPA’05, Sydney, 28-31 August 2005, pp. 847-850. doi:10.1109/ISSPA.2005.1581071
- S. Rekh, S. S. Rani and A. Shanmugam, “Optimal Choice of Interleaver for Turbo Codes,” Academic Open Internet Journal, Vol. 15, 2005.
- S. Choudhury, “Modeling and Simulation of a Turbo Encoder and Decoder for Wireless Communication Systems,” 2002. http://users.ece.utexas.edu/~bevans/courses/ee382c/projects/spring02/index.html
- W. Henkel, G. Taubock, P. Odling, P. O. Borjesson, N. Petersson and A. Johansson “The Cyclic Prefix of OFDM/ DMT—An Analysis,” Proceedings of 2002 International Zurich Seminar on Broadband Communications: AccessTransmission-Networking, Zurich, 19-21 February 2002, p. 22. doi:10.1109/IZSBC.2002.991762
- B. Muquet, Z. Wang, G. B. Giannakis, M. De Courville and P. Duhamel, “Cyclic Prefixing or Zero Padding for Wireless Multicarrier Transmissions?” IEEE Transactions on Communications, Vol. 50, No. 12, 2002, pp. 2136-2148. doi:10.1109/TCOMM.2002.806518
- A. Vallavaraj, B. G. Stewart and D. K. Harrison, “An Evaluation of Modified μ-Law Companding to Reduce the PAPR of OFDM Systems,” AEU—International Journal of Electronics and Communications, Vol. 64, No. 9, 2010, pp. 844-857. doi:10.1016/j.aeue.2009.07.013
- P. Robertson, P. Villebrun and P. Hoeher, “A Comparison of Optimal and Sub-Optimal MAP Decoding Algorithms Operating in the Log Domain,” Proceedings of IEEE International Conference on Communications, Seattle, 18- 22 June 1995, pp. 1009-1013. doi:10.1109/ICC.1995.524253
- Agilent, “Fundamentals of RF and Microwave Power Measurements (Part 2)—Power Sensors and Instrumentation,” Application Note, 2006, pp. 55-56.
- Anritsu, “CCDF Measurements MS269xA—Signal Analyzer,” Application Note, 15 April 2008.
- L. Angrisani, A. Langella and M. Vadursi, “New Digital Signal-Processing Approaches for Measuring Power CCDF Curves,” 13th Symposium on Measurements for Research and Industrial Applications, 9th Workshop on ADC Modeling and Testing (TC4), Athens, 2004.
- A. Vallavaraj, B. G. Stewart, D. K. Harrison and F. G. McIntosh, “Reduction of Peak to Average Power Ratio of OFDM Signals Using Companding,” Proceedings of the 9th IEEE International Conference on Communications Systems, Singapore, 6-8 September 2004, pp. 160-164. doi:10.1109/ICCS.2004.1359359
- M. F. Sabir, R. Tripathi, B. L. Evans and A. C. Bovik, “A Real-Time Embedded Software Implementation of a Turbo Encoder and Soft Output Viterbi Algorithm Based Turbo Decoder,” Record of the 36 ACSC, Pacific Grove, 3-6 November 2002, pp. 1099-1103. doi:10.1109/ACSSC.2002.1196954
- G. Tatsis, C. Votis, V. Raptis, V. Christofilakis, S. K. Chronopoulos and P. Kostarakis, “Design and Implementation of Ultra-Wideband Impulse Radio Transmitter,” Proceedings of the 7th International Conference of the Balkan Physical Union, Alexandroupolis, 2009, pp. 579- 584. doi:10.1063/1.3322513
- C. I. Votis, P. Kostarakis and L. P. Ivrissimtzis, “Design and Measurements of A Multiple-Output Transmitter for MIMO Applications,” Journal of Circuits, Systems, and Computers (JCSC), vol. 20, no. 3, 2011, pp. 515-529. doi:10.1142/S0218126611007426
- V. Raptis, C. Votis, G. Tatsis, S. K. Chronopoulos, V. Christofilakis and P. Kostarakis, “Tuning Techniques for Planar Antennas in Wireless Communication,” Proceedings of the 7th International Conference of the Balkan Physical Union, Alexandroupolis, 2009, pp. 1053-1057. doi:10.1063/1.3322309
- V. N. Christofilakis, A. A. Alexandridis, P. Kostarakis and K. P. Dangakis, “Software Defined Radio Implementation Aspects Related to the ADC Performance,” Proceedings of the 6th International Multiconference on Circuits, Systems, Communications and Computers, Crete, 7-11 July 2002, pp. 3231-3239.

