Wireless Engineering and Technology
Vol.3 No.3(2012), Article ID:21462,4 pages DOI:10.4236/wet.2012.33017
Throughput Maximizing Frequency and Power Scheduling for Wireless Ad-Hoc Networks in the Low-SINR Regime
![]()
Division of Engineering and Applied Sciences, Harvard University, Cambridge, USA.
Email: nahid@deas.harvard.edu
Received January 18th, 2012; revised February 22nd, 2012; accepted February 28th, 2012
Keywords: Ad-Hoc Networks; Cognitive Networks; Optimization; Mixed Zero-One Linear Problem; Zero-One Nonlinear Problem
ABSTRACT
We study the problem of frequency and power allocation and scheduling at a time-slotted cognitive ad-hoc wireless network, where cognitive nodes share a number of frequency bands and frequency reuse is allowed. In such a network the throughput maximization problem generally results in a mixed zero-one nonlinear non-convex problem. Interestingly, in the low-SINR regime, the power allocation policy that maximizes the total throughput follows an “on/off” strategy with maximum power usage in the “on” state. In this paper we show that the on/off strategy in the low-SINR regime is also optimal with respect to throughput when scheduling users over time and frequency subject to minimum SINR requirements. We show that these additional constraints will not change the optimum strategy, but may affect the set of “on” or “off” transmitters. Also we present an approach that transforms the mixed zero-one nonlinear problem to an equivalent mixed zero-one linear problem at the expense of extra variables.
1. Introduction
We study optimal resource allocation techniques when a number of cognitive radios and primary users share the same spectral white spaces. Cognitive radios have the ability to sense the radio spectrum environment and to switch to the available frequency bands so that they do not interfere with the high priority primary users. The question of how the sensed resources should best be allocated is a fundamental question which has received a fair amount of attention in closely related ad-hoc and cognitive network communities. Depending on the type and the design objectives of the network, the optimal solution can be defined as an allocation that maximizes the total throughput in the network [1], or the one that minimizes the power consumption [2,3] while satisfying some quality of service requirements.
The problem of transmission scheduling and assigning power and frequency in a centralized fashion in order to maximize the throughput in a wireless ad hoc network where frequency reuse is allowed is a non-linear nonconvex problem. To overcome the complexity of the problem distributed algorithms [1,3-5] and approximation methods [1,4,6-10] have been introduced. To further simplify the problem the authors of [11] have focused on maximizing the number of transmissions as a measure of the throughput, and the authors of [5] considered minimizing the interference instead of maximizing the throughput. In the above references communicating nodes and/or their occupied frequency bands are known in advance. The problem considered in this paper assumes that communicating nodes and their occupied frequency bands are not given and must be determined such that the total throughput of the network is maximized. We also strive on determining the optimal power allocation for a maximum throughput transmission.
In this paper we focus on centralized throughput maximization in the low-SINR regimes. In [12] we investigated a similar problem in the high-SINR regime and proposed an approach based on the concept of Geometric Programming. In the low-SINR regime, we prove that the on/off strategy maximizes the throughput under the additional constraint on the minimum SINR required for a successful transmission.
The contribution of this paper lies in suggesting a mathematical method for finding optimum solutions to the throughput maximization problem in an ad-hoc network where power, frequency and scheduling are to be determined by a central controller. This problem is approached more rigorously than in the past, where the solutions were either approximate or based on relaxing one of the scheduling, power allocation or frequency allocation requirements.
In what follows we start by describing our assumptions and problem formulation. In Section 3 we prove that the optimal solution to our throughput maximization problem allocates either zero or maximum power to each transmitter. We also prove that the throughput maximization in low-SINR regime which is a mixed zero-one nonlinear optimization problem has an equivalent nonlinear optimization problem with real variables. We also show how our mixed zero-one non-linear problem can be transformed to an equivalent mixed zero-one linear problem. Finally, we conclude the paper in Section 4.
2. Assumptions and Problem Formulation
We consider a centralized cognitive network operating in the low-SINR regime composed of 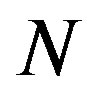 nodes and
nodes and  available frequencies, over which the communicating pairs seek to transfer data. The objective is to determine the optimal time scheduling, and frequency and power allocation such that the total throughput is maximized. We assume that Every node has access to every frequency band and a central scheduler determines which frequencies can be occupied by each cognitive pair. We also assume that frequency reuse is allowed under the condition that SINR is sufficiently large to guarantee a successful transmission. Figure 1 shows a possible frequency allocation for a network of cognitive users which have access to at most 5 frequency bands. The allocation of frequency bands is subject to a number of constraints dictated by the abilities of the transmitter and receiver technologies, as well as the physical layer protocol governing the network. We assume the following model for communication: Network is composed of
available frequencies, over which the communicating pairs seek to transfer data. The objective is to determine the optimal time scheduling, and frequency and power allocation such that the total throughput is maximized. We assume that Every node has access to every frequency band and a central scheduler determines which frequencies can be occupied by each cognitive pair. We also assume that frequency reuse is allowed under the condition that SINR is sufficiently large to guarantee a successful transmission. Figure 1 shows a possible frequency allocation for a network of cognitive users which have access to at most 5 frequency bands. The allocation of frequency bands is subject to a number of constraints dictated by the abilities of the transmitter and receiver technologies, as well as the physical layer protocol governing the network. We assume the following model for communication: Network is composed of 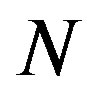 cognitive nodes and
cognitive nodes and 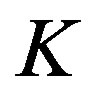 available frequency bands to be used by cognitive users. The objective is to identify the best selection of cognitive transmitter-receiver pairs, allocate frequency bands to them, and define their optimal power consumptions such that the overall throughput is maximized. Frequency reuse is allowed in the network as long as the SINR is greater than a given threshold
available frequency bands to be used by cognitive users. The objective is to identify the best selection of cognitive transmitter-receiver pairs, allocate frequency bands to them, and define their optimal power consumptions such that the overall throughput is maximized. Frequency reuse is allowed in the network as long as the SINR is greater than a given threshold , where
, where  is fixed. Each node cannot transmit and receive on the same frequency band. Every transmitter (receiver) can send to (receive from) at most one receiver (transmitter) at the same frequency the power consumption per frequency per node at each time-slot cannot exceed
is fixed. Each node cannot transmit and receive on the same frequency band. Every transmitter (receiver) can send to (receive from) at most one receiver (transmitter) at the same frequency the power consumption per frequency per node at each time-slot cannot exceed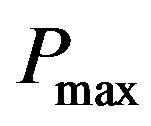 . The received signal at each frequency band at node
. The received signal at each frequency band at node  is subject to additive white Gaussian noise (AWGN) of power
is subject to additive white Gaussian noise (AWGN) of power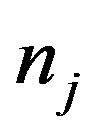 .
.
Based on these assumptions the joint scheduling, frequency and power allocation problem is formulated as Problem 1. All logarithms are in base 2, and equations with unspecified indices such as (3) for example, is meant to represent a set of equations which hold for all unspecified indices (such as  and
and  in (3)). The variables are defined in Table 1.
in (3)). The variables are defined in Table 1.
 (1)
(1)

Figure 1. Visualization of a possible frequency allocation during one time-slot for an ad-hoc network of cognitive users with at most 5 available frequency bands. The arrows show a connection between a transmitter and a receiver on a specific frequency band. The narrow lines indicate a partial mesh wireless network, where a node can communicate with other nodes within its accessibility range, given the resources are available. For a node i we say a given nodes j is accessible, if .
.

Table 1. Algorithms variables and parameters.
 (2)
(2)
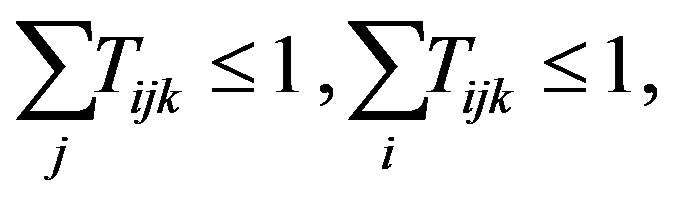 (3)
(3)
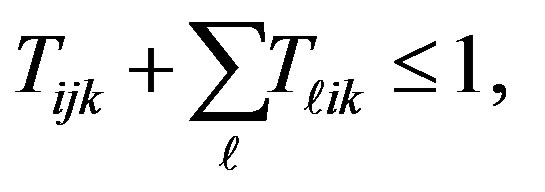 (4)
(4)
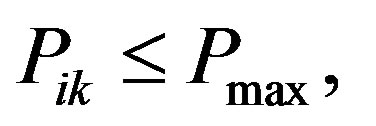 (5)
(5)

where 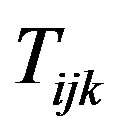 is a binary variable which indicates whether or not node
is a binary variable which indicates whether or not node 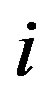 is transmitting to node
is transmitting to node  over frequency band
over frequency band 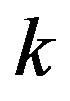 and
and 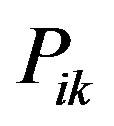 is a real variable which denotes the amount of allocated power to node
is a real variable which denotes the amount of allocated power to node  on frequency
on frequency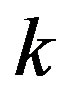 . If node
. If node  is not transmitting to any node on frequency
is not transmitting to any node on frequency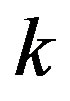 , then
, then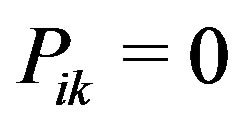 .
.  is the signal to interference plus noise ratio defined as
is the signal to interference plus noise ratio defined as
 where
where  defines transmission gain from node
defines transmission gain from node 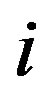 to node
to node  on frequency
on frequency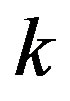 . Equation (2) corresponds to assumption 3. Equations (3) and (4) correspond to assumptions 4 and 5 for scheduling constraints. Equation (5) corresponds to assumption 6 which sets an upper bound on the power allocated to each transmitter.
. Equation (2) corresponds to assumption 3. Equations (3) and (4) correspond to assumptions 4 and 5 for scheduling constraints. Equation (5) corresponds to assumption 6 which sets an upper bound on the power allocated to each transmitter.
3. Scheduling and Power Control in Low-SINR Regime
In contrast to our prior work [12], where Problem 1 was approached in the high-SINR regime, we aim to simplify the non-convex non-linear optimization problem in the low-SINR regime. This regime is particularly relevant in networks where the number of frequency bands is large and frequency reuse is common. The throughput maximization problem in this case is simplified by approximating the Shannon capacity with its first order Taylor series around zero SINR. That is, we approximate the objective function 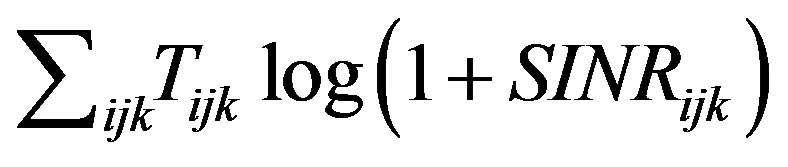 at low-SINR with
at low-SINR with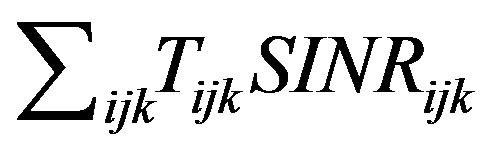 , keeping the remaining constraints on
, keeping the remaining constraints on  and
and  the same. We determine the optimum solution to this approximation to the desired problem in a number of steps:
the same. We determine the optimum solution to this approximation to the desired problem in a number of steps:
1) In Section 3.1 we first determine a solution for the relaxation to the problem subject only to constraints on the variable domains 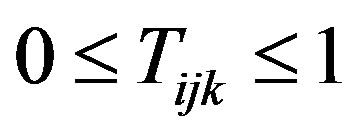 and
and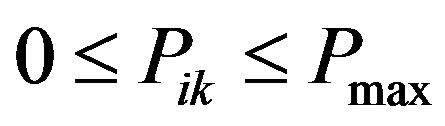 ,
, 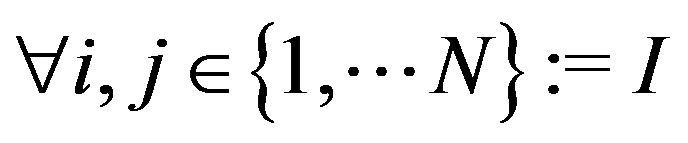 and
and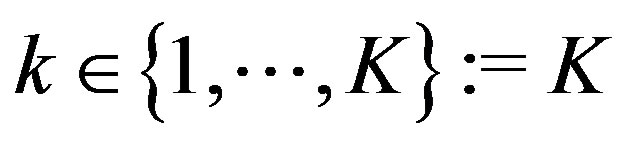 .
.
2) Next, in Section 3.2 we determine the solution for P matrix when the minimum SINR constraints 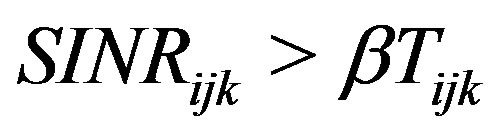 are added,
are added,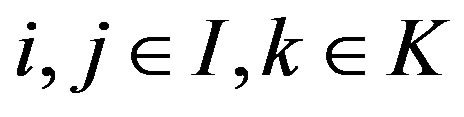 .
.
3) In Section 3.3 we incorporate all the scheduling constraints in (3) and (4) and show that 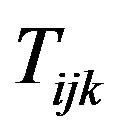 will be binary using a suitable penalty function.
will be binary using a suitable penalty function.
4) Finally, in Section 3.4 we introduce new variables which transform the non-linear optimization problem to a linear one.
The main conclusions to be drawn are that the optimal signaling strategy follows an on/off strategy, and that the optimization may be turned into an easily solvable linear program at the expense of increasing the number of variables from 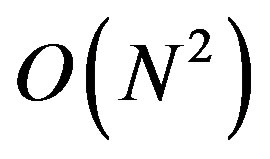 to
to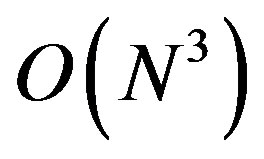 . The core insight follows from the work of Ebrahimi et al. [10], where the authors proved that in a similar problem without frequency allocation, if the transmission power is constrained by
. The core insight follows from the work of Ebrahimi et al. [10], where the authors proved that in a similar problem without frequency allocation, if the transmission power is constrained by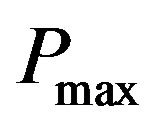 , the power allocation strategy which maximizes
, the power allocation strategy which maximizes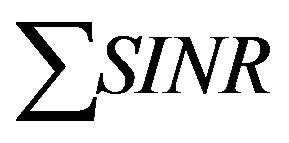 , assigns either a power of 0 or
, assigns either a power of 0 or 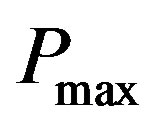 to each transmitter. This is called the on/off strategy. Using a similar approach we prove that the on/off strategy also maximizes the objective function of the form
to each transmitter. This is called the on/off strategy. Using a similar approach we prove that the on/off strategy also maximizes the objective function of the form 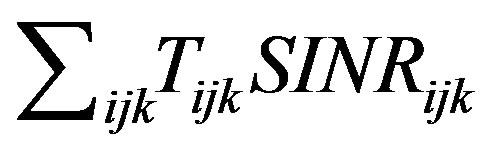 subject to additional frequency and SINR constraints.
subject to additional frequency and SINR constraints.
3.1. Relaxed, Unconstrained Throughput Maximization
We begin by removing most of the constraints from Problem 1 and relaxing the domains of .
.
Theorem 1. Consider the following optimization problem:
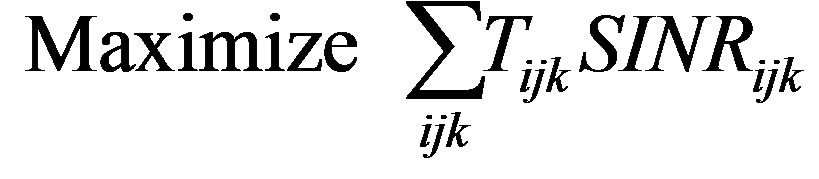
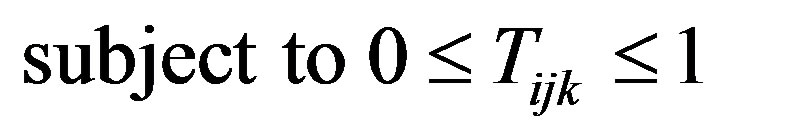
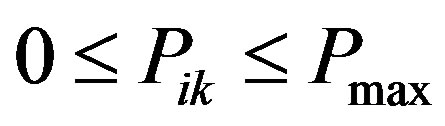
1) The optimum solution to this problem allocates either 0 or 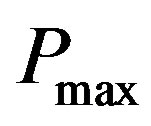 power to every node.
power to every node.
2) The optimum solution results in binary values for the 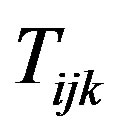 variables.
variables.
Proof. A proof by contradiction was provided for the first part of the theorem by Ebrahimi et al. [10]. Using a similar argument we provide the proof for the second part. It can be seen that 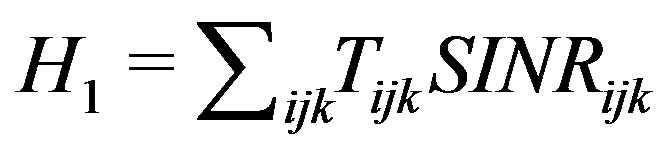 is convex with respect to each
is convex with respect to each 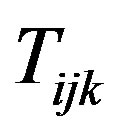 since
since 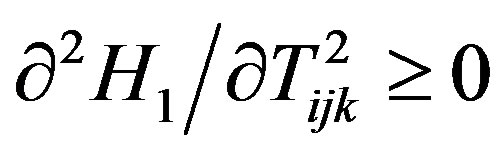 (see Appendix). Thus, the maximum of
(see Appendix). Thus, the maximum of 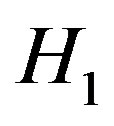 will happen at the boundaries of the variable domains. To see this, assume that the optimum solution corresponds to a set
will happen at the boundaries of the variable domains. To see this, assume that the optimum solution corresponds to a set  with at least one non-binary element;
with at least one non-binary element; . Since
. Since 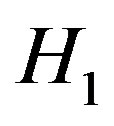 is convex with respect to
is convex with respect to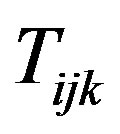 , then by keeping the rest of the variables constant and moving
, then by keeping the rest of the variables constant and moving 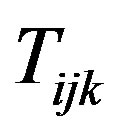 to the boundaries (0 or 1) one can find a larger amount for
to the boundaries (0 or 1) one can find a larger amount for 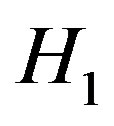 and hence the set
and hence the set  with non-binary element cannot be the optimum solution. Therefore,
with non-binary element cannot be the optimum solution. Therefore,  must hold for all
must hold for all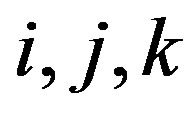 .
.
3.2. Throughput Maximization with SINR Constraints
The only constraint in the problem addressed in previous section are on the domains of the  and
and 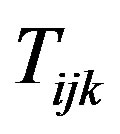 variables. When the SINRs are required to exceed a minimal value it is not clear if/how the optimal power allocation changes. Now we prove that adding the SINR constraint may change the set of “on” or “off” transmitters, but the on/off power allocation is still optimal. The proof is a direct result of the Generalized Lagrange Multiplier (GLM) Technique proposed by Everette [13]. Using GLM technique it can be shown that for a specific class of constrained problems, one can generate a lagrangian function of the problem such that the solution to the maximization of the lagrangian is a solution to the constrained problem. We state the needed result of [13] for clarity.
variables. When the SINRs are required to exceed a minimal value it is not clear if/how the optimal power allocation changes. Now we prove that adding the SINR constraint may change the set of “on” or “off” transmitters, but the on/off power allocation is still optimal. The proof is a direct result of the Generalized Lagrange Multiplier (GLM) Technique proposed by Everette [13]. Using GLM technique it can be shown that for a specific class of constrained problems, one can generate a lagrangian function of the problem such that the solution to the maximization of the lagrangian is a solution to the constrained problem. We state the needed result of [13] for clarity.
Proposition 1. Consider a constrained optimization problem of the form:
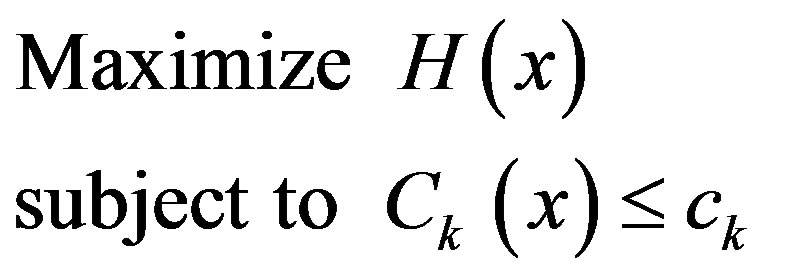 (6)
(6)
If the objective function 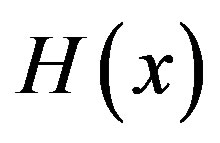 of a constrained optimization problem given by Equation (6) is concave with respect to the constraint functions
of a constrained optimization problem given by Equation (6) is concave with respect to the constraint functions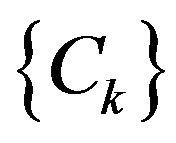 , then it can be guaranteed that there is a set of non-negative lagrange multipliers
, then it can be guaranteed that there is a set of non-negative lagrange multipliers 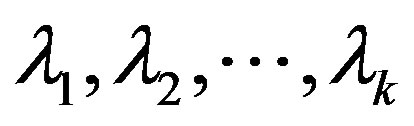 for the lagrangian of this problem,
for the lagrangian of this problem, 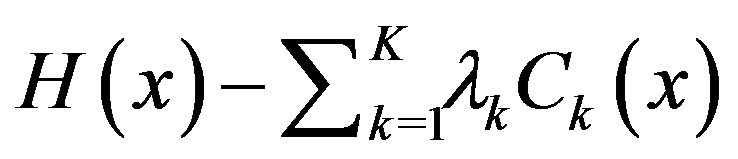 , such that the solution to the constrained optimization in Equation (6) and the solution to its lagrangian are identical [13].
, such that the solution to the constrained optimization in Equation (6) and the solution to its lagrangian are identical [13].
We use this proposition directly in our throughput maximization to show that the on/off power strategy still holds when a constraint on each active link’s SINR is enforced. Since we only define the optimum solution for 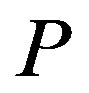 matrix, we assume that the
matrix, we assume that the  matrix is given and hence SINR is only a function of
matrix is given and hence SINR is only a function of . Define Problem 4:
. Define Problem 4:
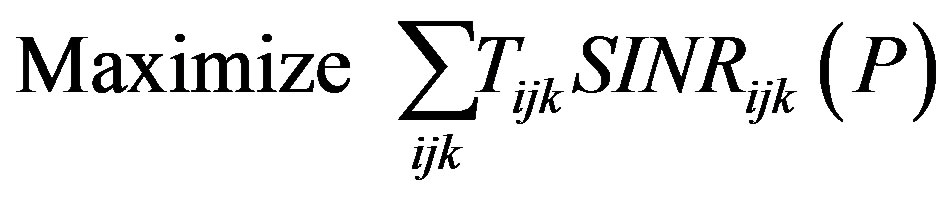


We apply this Proposition to Problem 4 in the following theorem.
Theorem 2. The optimum solution to Problem 4 allocates either 0 or 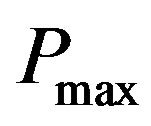 power to each transmitter in the network.
power to each transmitter in the network.
Proof. To apply Proposition 1 we must show that H is concave with respect to C, where C = [ ]. In this problem
]. In this problem 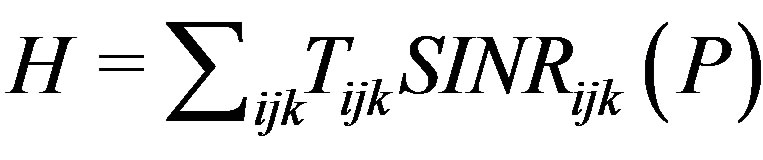 and
and .
.
Define  the set of possible solutions for
the set of possible solutions for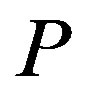 . Suppose that we map every feasible matrix
. Suppose that we map every feasible matrix  into a point in the space of H and C. Since
into a point in the space of H and C. Since 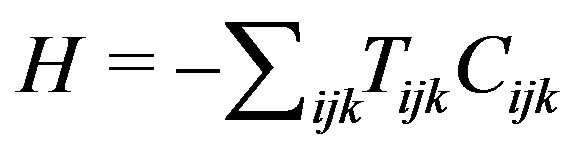 is a hyperplane in the H and C space, then it is both convex and concave. Note that based on our assumption
is a hyperplane in the H and C space, then it is both convex and concave. Note that based on our assumption  s are constants and define the slope of the hyperplane in the H and C space. Similar to the proof of Theorem 1 it can be shown that the Lagrangian corresponding to Problem 4,
s are constants and define the slope of the hyperplane in the H and C space. Similar to the proof of Theorem 1 it can be shown that the Lagrangian corresponding to Problem 4,
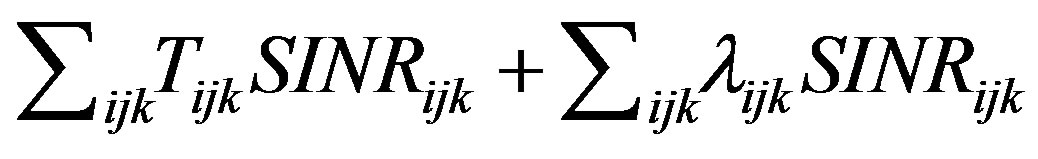 is convex with respect to every
is convex with respect to every . Therefore, for any non-negative set of
. Therefore, for any non-negative set of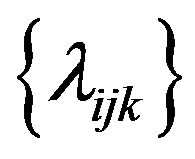 , the solution to the unconstrained Lagrangian problem follows an on/off strategy (i.e.,
, the solution to the unconstrained Lagrangian problem follows an on/off strategy (i.e.,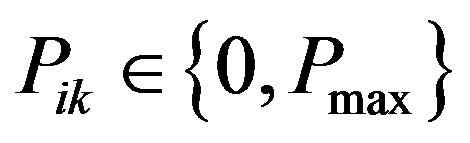 ). By Proposition 1, the optimal solution to the unconstrained problem is equal to that of the the constrained problem, hence the solution to Problem 4 follows an on/off strategy.
). By Proposition 1, the optimal solution to the unconstrained problem is equal to that of the the constrained problem, hence the solution to Problem 4 follows an on/off strategy.
3.3. Adding Scheduling Constraints to the Optimization Problem
The last set of constraints that must be added to the problem are the scheduling constraints which are ,
,  , and
, and . These additional constraints violate the optimum zero-one solution for the
. These additional constraints violate the optimum zero-one solution for the  matrix. However, we can easily limit the solution to zero-one by adding a penalty function (i.e.,
matrix. However, we can easily limit the solution to zero-one by adding a penalty function (i.e., 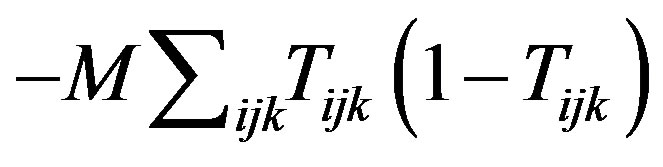 to the objective function, where
to the objective function, where  is a very large constant. This penalty function will take a very large value if any of the
is a very large constant. This penalty function will take a very large value if any of the 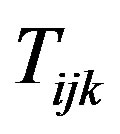 s has a non-binary value. Therefore the solution is directed towards a zeroone solution. Based on this discussion we state the last theorem of this section as follows:
s has a non-binary value. Therefore the solution is directed towards a zeroone solution. Based on this discussion we state the last theorem of this section as follows:
Theorem 3. The solution to the nonlinear real-valued optimization problem defined as Problem 5:

subject to Equations (2)-(5)
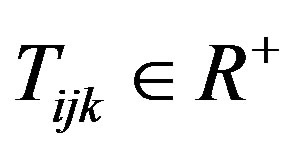
is a zero-one solution which is also the optimum solution to this zero-one optimization problem defined as Problem 6:
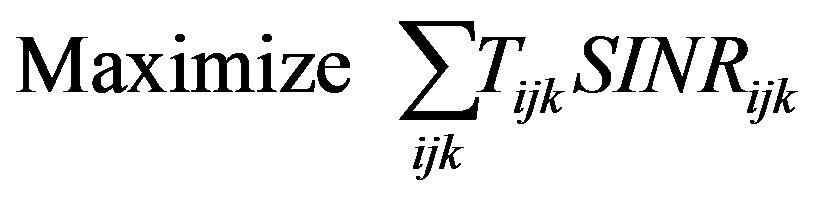
subject to Equations (2)-(5)

Proof. For large enough  the optimum solution to Problem 5 is a zero-one solution, since the penalty function added to the objective function limits the solution to only zero and one values. On the other hand the solution is a maximizer for Problem 6 as it maximizes the first term in Problem 5 for binary values of
the optimum solution to Problem 5 is a zero-one solution, since the penalty function added to the objective function limits the solution to only zero and one values. On the other hand the solution is a maximizer for Problem 6 as it maximizes the first term in Problem 5 for binary values of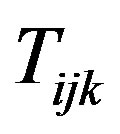 . Note that Equations (2)-(5) includes all scheduling constraints as well as the
. Note that Equations (2)-(5) includes all scheduling constraints as well as the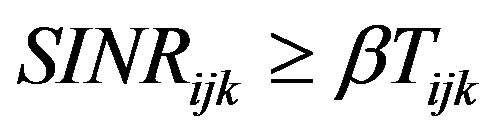 .
.
Discussion. With Theorems 2 and 3 we proved that the solution to Problem 6 with zero-one variables (i.e.,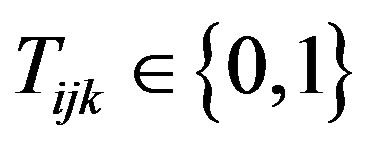 ), is the same as the solution to Problem 5 with real variables. This significantly reduces the complexity of our problem from a mixed integer non-linear problem to a regular non-linear problem. With Theorem 2 we proved that the optimum solution to Problem 6 results in 0 or
), is the same as the solution to Problem 5 with real variables. This significantly reduces the complexity of our problem from a mixed integer non-linear problem to a regular non-linear problem. With Theorem 2 we proved that the optimum solution to Problem 6 results in 0 or 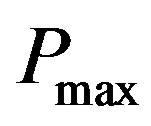 solutions for
solutions for 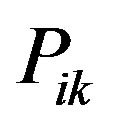 s. This finding helps us introduce an approach for linearizing Problem 6 in Section 3.4.
s. This finding helps us introduce an approach for linearizing Problem 6 in Section 3.4.
3.4. Transforming the Throughput Maximization to a Mixed Zero-One Linear Problem
The throughput maximization problem is a non-linear problem. However, in low-SINR regime when the transmitters follow an on/off power allocation strategy (based on Theorem 2), the problem can be transformed to a linear problem with the cost of additional variables. In the maximization problem both the objective function and the SINR constraint are non-linear. But both can be linearized using a variation of Balas method [14]. With the assumption of binary values for 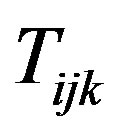 s and also 0 or
s and also 0 or 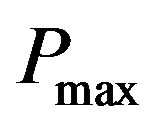 values for
values for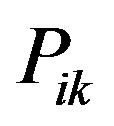 , the objective function
, the objective function 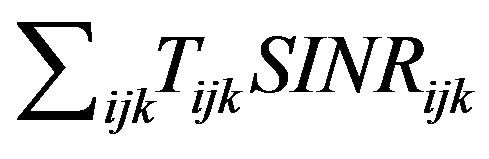 is transformed to:
is transformed to:
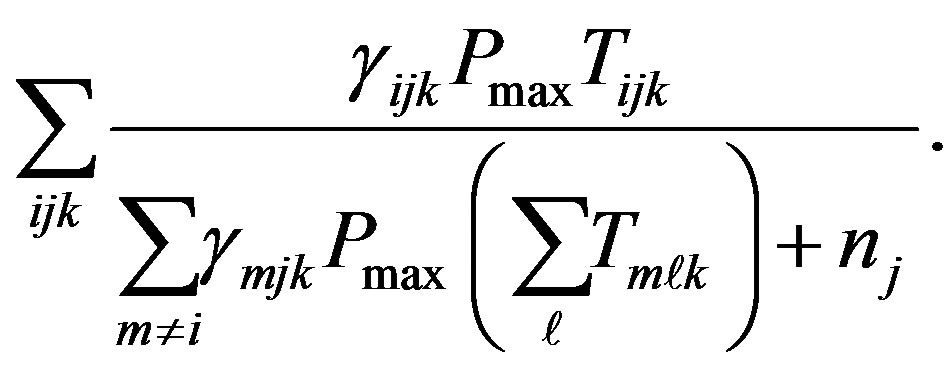 (7)
(7)
Note that if 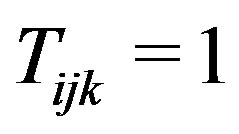 then
then 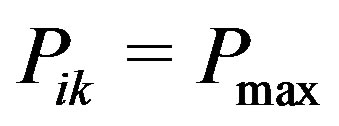 and so
and so 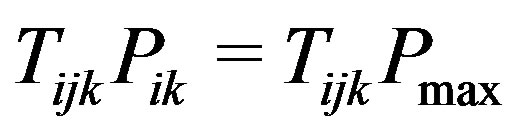 holds. Also if
holds. Also if , regardless of the value of
, regardless of the value of 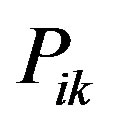
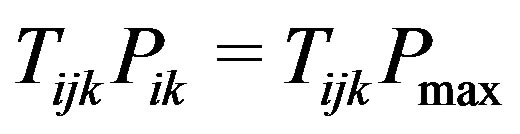 holds. A similar argument can be used to explain
holds. A similar argument can be used to explain 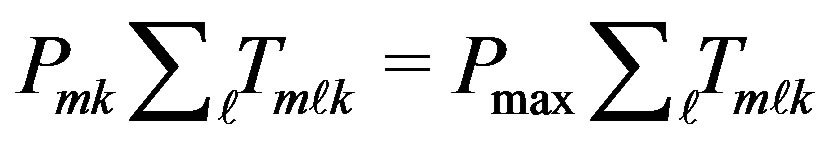 in the denominator. Equation (7) is a non-linear function of binary variables
in the denominator. Equation (7) is a non-linear function of binary variables . Without loss of generality we assume that
. Without loss of generality we assume that  and
and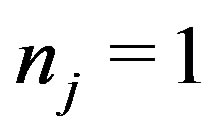 . Also define variables
. Also define variables
 . Therefore the objective function is transformed to
. Therefore the objective function is transformed to , with an additional constraint defining
, with an additional constraint defining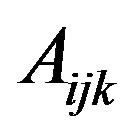 . After crossing multiplication we obtain:
. After crossing multiplication we obtain:
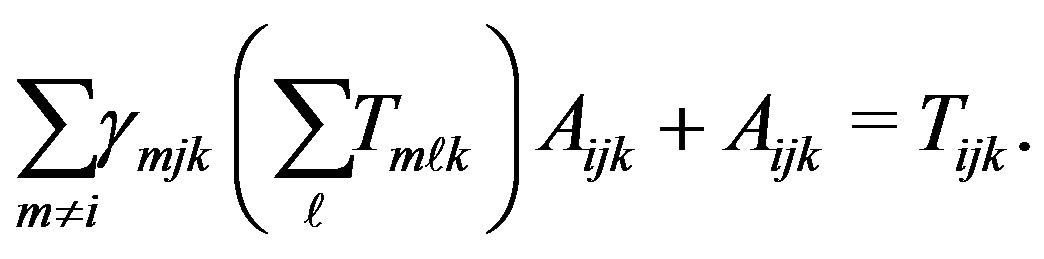 (8)
(8)
Even though 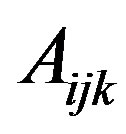 is not a binary variable, since it is smaller than 1, we still can use the Balas approach to linearize its multiplication with a binary variable. Note that
is not a binary variable, since it is smaller than 1, we still can use the Balas approach to linearize its multiplication with a binary variable. Note that  can only take values 0 or 1 due to our scheduling constraints. Let’s define
can only take values 0 or 1 due to our scheduling constraints. Let’s define . Then Equation (8) is transformed to a linear constraint and using Balas method we only need to add a number of linear inequalities to the problem:
. Then Equation (8) is transformed to a linear constraint and using Balas method we only need to add a number of linear inequalities to the problem:
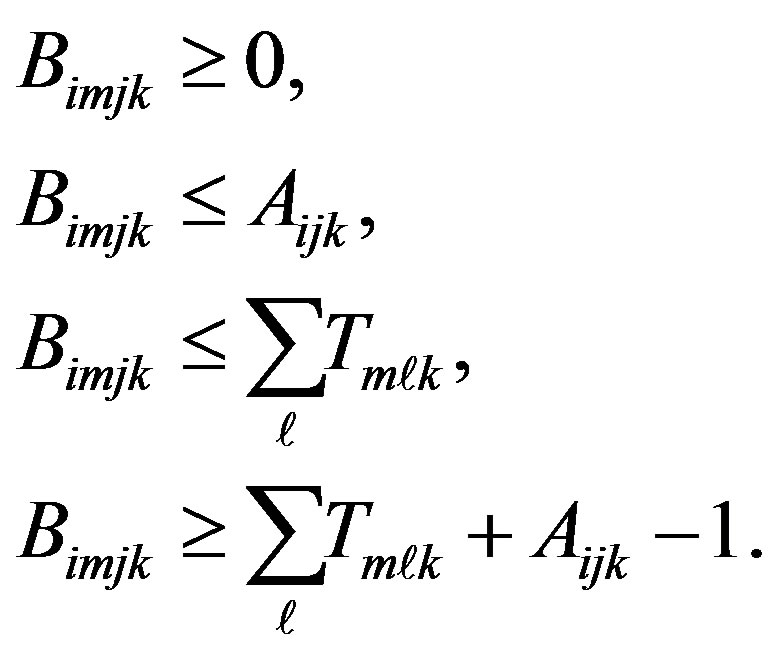
To transform the non-linear SINR constraint to a linear one we consider the fact that if  then regardless of the value of
then regardless of the value of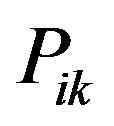 , the constraint
, the constraint 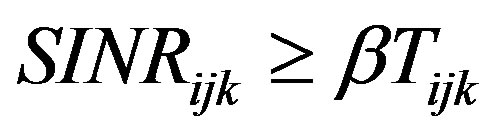 is satisfied. Also if
is satisfied. Also if 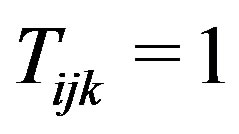 then
then 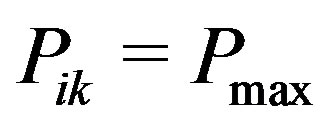 and so we can replace
and so we can replace 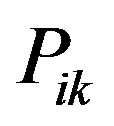 in the numerator of
in the numerator of  in this constraint with
in this constraint with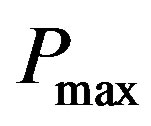 . We introduce additional variables
. We introduce additional variables  to transform this constraint to a linear one. Therefore, the linear constrained optimization problem to be solved is:
to transform this constraint to a linear one. Therefore, the linear constrained optimization problem to be solved is:

subject to
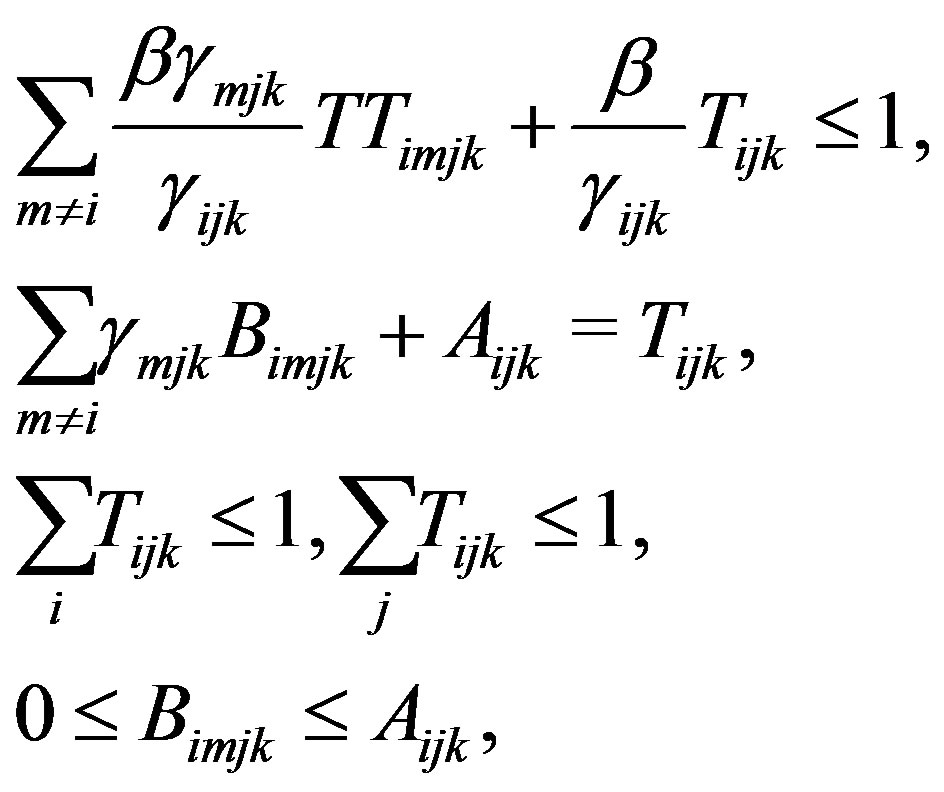

This problem is a mixed zero-one linear problem with binary variables  and real variables
and real variables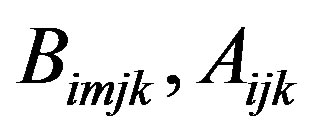 . This problem can be solved using standard methods for solving mixed-integer linear problems. Note that we did not use any approximation to transform Problem 6 (nonlinear non-convex problem) to a linear one, but the cost that we pay for this transformation is an increase in the number of variables from
. This problem can be solved using standard methods for solving mixed-integer linear problems. Note that we did not use any approximation to transform Problem 6 (nonlinear non-convex problem) to a linear one, but the cost that we pay for this transformation is an increase in the number of variables from  to
to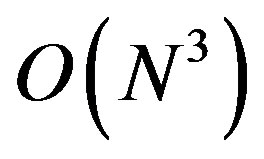 . This complexity compared to the number of possible solutions in an exhaustive search which is the only reliable solution to the non-linear problems of this type is very low. The complexity of a search method for Problem 6 is
. This complexity compared to the number of possible solutions in an exhaustive search which is the only reliable solution to the non-linear problems of this type is very low. The complexity of a search method for Problem 6 is
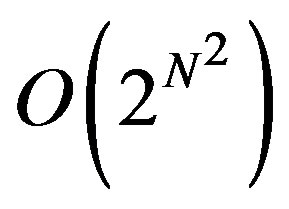 which is much higher than the complexity of our linear problem, especially for large values of N.
which is much higher than the complexity of our linear problem, especially for large values of N.
4. Conclusion
In this paper we presented methods for obtaining optimal solutions for throughput maximization in centralized cognitive networks operating in the low-SINR regime. The optimal solutions define the set of optimum communicating pairs as well as the optimum power levels and frequency allocated to the transmitters. We showed that in the low-SINR regime the mixed zero-one non-linear problem can be solved with an equivalent non-linear optimization problem. Also we proved that the optimal solution allocates 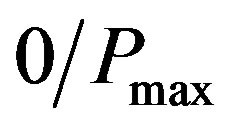 powers to the transmitters. Using this result we transformed the mixed zero-one nonlinear problem to an equivalent mixed zero-one linear problem, which can be solved efficiently using the standard methods for solving mixed integer linear problems. The centralized optimum solution presented in this paper serves as a benchmarks for suggesting new distributed algorithms and evaluating approximation algorithms for both centralized and distributed methods.
powers to the transmitters. Using this result we transformed the mixed zero-one nonlinear problem to an equivalent mixed zero-one linear problem, which can be solved efficiently using the standard methods for solving mixed integer linear problems. The centralized optimum solution presented in this paper serves as a benchmarks for suggesting new distributed algorithms and evaluating approximation algorithms for both centralized and distributed methods.
REFERENCES
- J. Bazerque and G. Giannakis, “A Distributed Scheduling and Resource Allocation for Cognitive OFDMA Radios Bazerque,” Proceedings of International IEEE Conference on Cognitive Radio Oriented Wireless Networks and Communications, Orlando, 3 August 2007, pp. 343-350.
- R. Cruz and A. Santhanam, “Optimal Routing, Link Scheduling and Power Control in Multi-Hop Wireless Net-Works,” Proceedings of IEEE INFOCOM, San Francisco, 1-3 April 2003, pp. 702-711.
- G. Foschini and Z. Miljanic, “A Simple Distributed AuTonomous Power Control Algorithm and Its Convergence,” IEEE Transactions on Vehicular Technology, Vol. 42, No. 4, 1993, pp. 641-646. doi:10.1109/25.260747
- M. Chiang, C. W. Tan, D. Palomar, D. O’Neill and D. Julian, “Power Control by Geometric Programming,” IEEE Transactions on Wireless Communications, Vol. 7, 2007, pp. 2640-2651. doi:10.1109/TWC.2007.05960
- B. Babadi and V. Tarokh, “A Distributed Asynchronous Algorithm for Spectrum Sharing in Wireless Ad-Hoc NetWorks,” Proceedings of 42nd Annual Conference on Information Sciences and Systems, Princeton, 19-21 March 2008. doi:10.1109/CISS.2008.4558635
- R. Urgaonkar and M. J. Neely, “Opportunistic Scheduling with Reliability Guarantees in Cognitive Radio Networks,” Proceedings of IEEE INFOCOM, Phoenix, 13-18 April 2008.
- Y. Y. T. Hou, Y. Shi and H. Sherali, “Optimal Spectrum Sharing for Multi-Hop Software Defined Radio Networks,” Proceedings of IEEE INFOCOM, Anchorage, 6-12 May 2007.
- Y. Yuan, P. Bahl, R. Chandra, T. Moscibroda and Y. Wu, “Allocating Dynamic Time-Spectrum Blocks in Cognitive Radio Networks,” Proceedings of IEEE/ACM MobiHoc, Montreal, 9-14 September 2007.
- C. Peng, H. Zheng and B. Y. Zhao, “Utilization and Fairness in Spectrum Assignment for Opportunistic Spectrum Access,” ACM Mobile Networks and Applications, Vol. 11, No. 4, 2006, pp. 555-576. doi:10.1007/s11036-006-7322-y
- M. Ebrahimi, M. A. Maddah-Ali and A. K. Khandani, “Throughput Scaling Laws for Wireless Networks with Fading Channels,” IEEE Transactions on Information Theory, Vol. 113, No. 2-3, 2007, pp. 4550-4554.
- J. Tang, G. Xue, C. Chandler and W. Zhang, “Link Scheduling with Power Control for Throughput EnhanceMent in Multihop Wireless Networks,” IEEE Transactions on Vehicular Technology, Vol. 55, No. 3, 2006, pp. 733-742. doi:10.1109/TVT.2006.873836
- N. Saberi and N. Devroye, “Geometric Programming for High-SINR Resource Allocation in Wireless Ad-Hoc Networks,” IEEE Communications Letters, in Press.
- H. Everett, “Generalized Lagrange Multiplier Method for Solving Problems of Optimum Allocation of Resources,” Operations Research, Vol. 11, No. 3, 1963, pp. 399-417. doi:10.1287/opre.11.3.399
- E. Balas, “An Additive Algorithm for Solving Linear ProGrams with Zero-One Variables,” Operations Research, Vol. 13, No. 4, 1965, pp. 517-546.
Appendix
Proof of .
.
We have . Without loss of generality we consider a given element of matrix
. Without loss of generality we consider a given element of matrix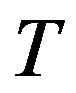 , say
, say , and rewrite
, and rewrite 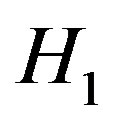 as:
as:

The first partial differentiation is obtained as:

The second partial differentiation is obtained as:
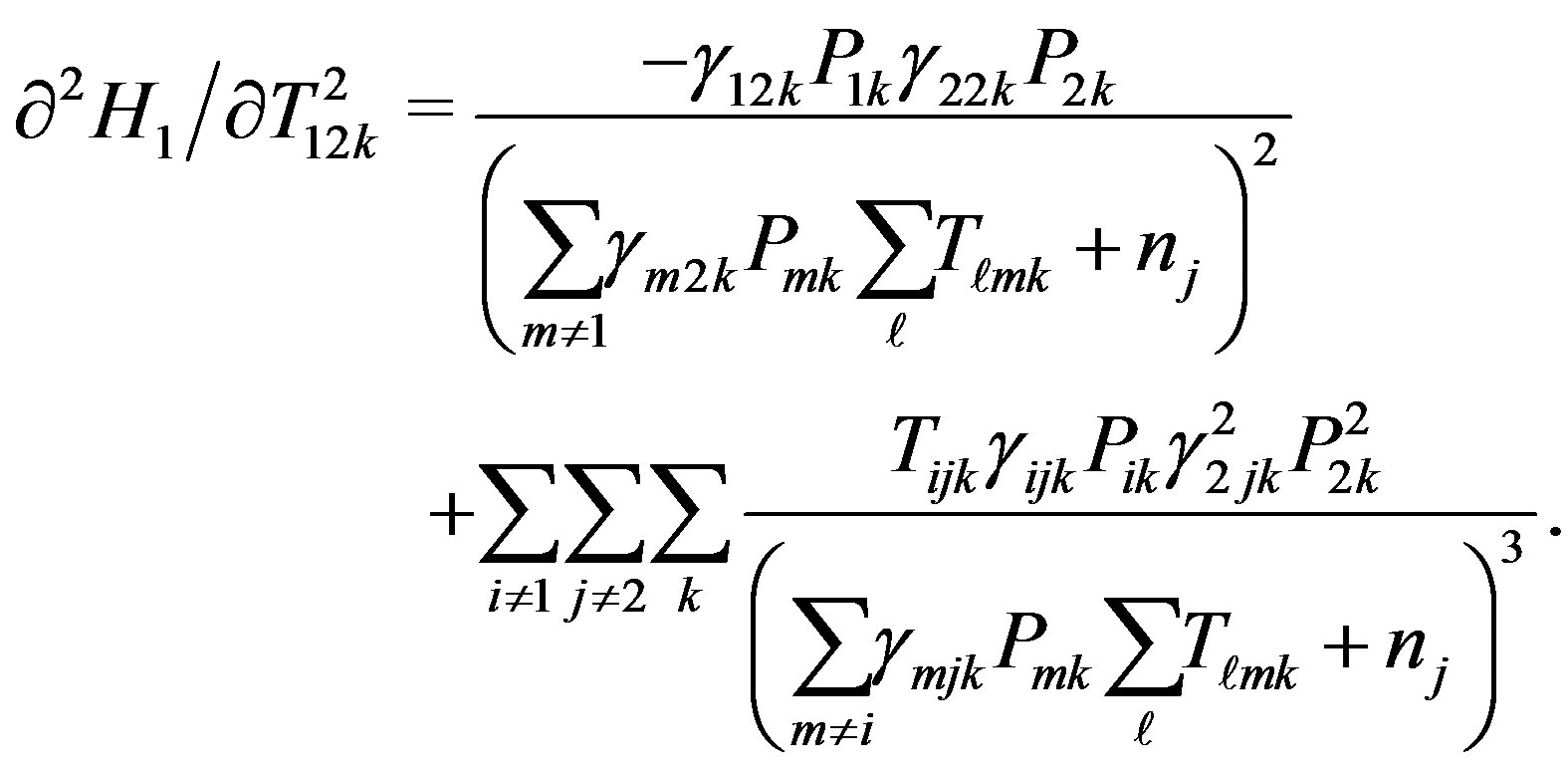
Since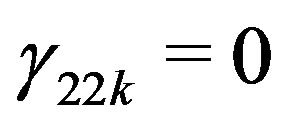 , the first term in the last equation is zero, and the second term is always positive. Therefore,
, the first term in the last equation is zero, and the second term is always positive. Therefore, 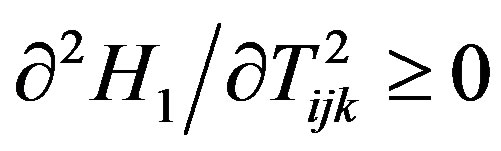 always holds.
always holds.

