Wireless Engineering and Technology
Vol.1 No.1(2010), Article ID:2336,4 pages DOI:10.4236/wet.2010.11002
The Performance Gain of Cognitive Radio in Adaptive Modulation Scheme
![]()
National Kapodistrian University of Athens, Department of Informatics and Telecommunications, Ilisia Athens, Greece.
Email: foukalas@di.uoa.gr
Received December 24th, 2009; revised January 25th, 2010; accepted March 30th, 2010.
Keywords: Cognitive Radio, Adaptive Modulation, Performance Gain
ABSTRACT
Cognitive radio is considered as one of the main enablers for provisioning dynamic and flexible spectrum/channel allocation in wireless communications. The reliable data transmission over cognitive radio should employ modulation, coding etc. and thus the performance of such a new communication system should be realized. In this paper, we provide the performance analysis of adaptive modulation over a cognitive radio system in order to study the potential gain of cognitive radios in terms of spectral efficiency. The results obtained show that the performance gain of cognitive radio in adaptive modulation is remarkable.
1. Introduction
The Cognitive Radio (CR) concept brought the idea to exploit the spectrum holes which result from the underutilization of the electromagnetic spectrum in wireless communications. This fact is corroborated by the Spectrum Policy Task Force of the Federal Communications Commission (FCC) which ascertains that the legacy regulation on spectrum availability begets snags in potential spectrum access by users. More precisely, it was identified that spectrum bands seems to be unoccupied most of the time and some of them seems to be occupied partially by the primary (or licensed) users [1]. There are two types of cognitive radio systems namely opportunistic spectrum access or spectrum pooling and spectrum sharing or spectrum underlay [2]. Due to the fact that an OSA model presents a significant potential for studying the design aspects of spectrum utilization in CRNs with minimal deployment requirements, we have chosen it as the cognitive radio system in this work. In the following text, we provide the details of an OSA-based CRN model and its performance in terms of capacity achieved over Rayleigh fading channels. To this end, we assume a spectrum pooling system with cognition capabilities. Such a system is capable to reliably sense the spectrum range. Moreover, considering that the frequency carrier is divided into subbands then the mobile users are being served in a multi-band context. In such a context, the task of detecting holes in spectrum bands could be performed for instance by a ‘listen-before-talk’ strategy [3].
By assuming such a cognitive radio system we should be able to assess the performance of reliable transmission that us taking place at the physical layer. To this direction, we have chosen to study the performance analysis of adaptive modulation over such a cognitive radio system [4]. More specific, since the channel allocation in spectrum pooling systems employs optimum power control policy, we study the variable rate variable power case of adaptive modulation which also follows such a transmission policy [5]. In order to make an objective performance analysis and evaluation, we present first the performance of cognitive radio system over a particular fading propagation environment. Thus, we calculate the capacity of such a system over a flat fading channel with Rayleigh coefficients [6] . We conclude this paper with the numerical results of this performance analysis and evaluation of adaptive modulation over cognitive radio.
2. Background
2.1 Spectral Efficiency of Cognitive Radio in Rayleigh Fading Channels
In spectrum pooling systems, the spectrum or channel allocation technique gives priority to primary users. Subsequently, the secondary users are assigned the detected spectrum holes. These holes are assumed voids in subband range. Thus, secondary users fill these voids as long as they achieve the desirable transmit power level. More specific, the spectrum is divided into N sub-bands and each user l is trying to transmit by using an optimum power control policy. The system’s operation is considered to be under a wide-band context. Hence, the N sub-bands of the cognitive radio channel extend to infinite (N → ∞). The channel is assumed with fading components that are varying slowly in time, i.e. the receiver is able to sense and track the channel fluctuations. The channel fluctuations represent the channel gains hl for each user l and are assumed over a block fading length in order to be able to retain their values constant during the processed block. Under these assumptions, the average capacity of user l in bits/sec/Hz obtained by the following equation:
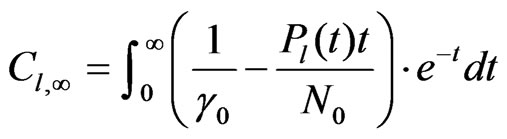 (1)
(1)
for  that is the number of users being served by the cognitive system with N sub-bands. However, the channel allocation for each user is performed in order to maximize the transmission rate when the optimal power is achieved. Hence, the power of
that is the number of users being served by the cognitive system with N sub-bands. However, the channel allocation for each user is performed in order to maximize the transmission rate when the optimal power is achieved. Hence, the power of  is subject to the average constraint:
is subject to the average constraint:
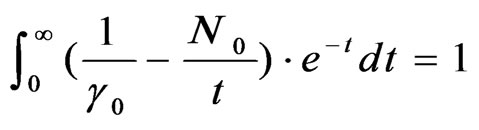 (2)
(2)
This technique for optimal power and rate adaptation is relied on water-filling algorithm and the corresponding SNR cut-off levels. In our case, the cut-off SNR levels are equal to 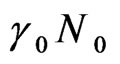 that denote the values of the channel gain above which a user can transmit on a sub-band. The term
that denote the values of the channel gain above which a user can transmit on a sub-band. The term 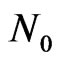 denotes the additive Gaussian noise at the receiver, while the
denotes the additive Gaussian noise at the receiver, while the 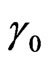 is calculated by keeping the aforementioned transmit power constraint expressed by equation (2). However, in order to obtain the performance of adaptive modulation over cognitive radio, we keep below the formulation of Rayleigh channel fading model [6]. More specific, the capacity per unit bandwidth is expressed as follows when optimal power and rate adaptation is considered
is calculated by keeping the aforementioned transmit power constraint expressed by equation (2). However, in order to obtain the performance of adaptive modulation over cognitive radio, we keep below the formulation of Rayleigh channel fading model [6]. More specific, the capacity per unit bandwidth is expressed as follows when optimal power and rate adaptation is considered
 (3)
(3)
In this case, the cut-off level is related to average SNR 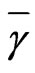 values.
values.
In previous analysis, we keep on purpose the notation of the first user as  since the spectral efficiency over cognitive radio is related to the average capacity of the primary user and the band factor gain of the cognitive radio itself. The band factor gain
since the spectral efficiency over cognitive radio is related to the average capacity of the primary user and the band factor gain of the cognitive radio itself. The band factor gain 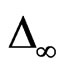 of a cognitive radio system is defined as the spectrum band, which is being sensed as void from user l to user l + 1 over the total bandwidth W. This gain is obtained as follows:
of a cognitive radio system is defined as the spectrum band, which is being sensed as void from user l to user l + 1 over the total bandwidth W. This gain is obtained as follows:
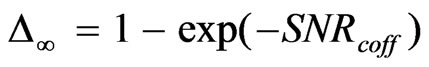 (4)
(4)
where 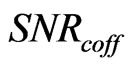 denotes the cut-off level in the corresponding SNR values. Taking into account the aforementioned formulas for the Rayleigh fading channel, we can note that the SNR cut-off value for the Rayeligh fading channel is equal to
denotes the cut-off level in the corresponding SNR values. Taking into account the aforementioned formulas for the Rayleigh fading channel, we can note that the SNR cut-off value for the Rayeligh fading channel is equal to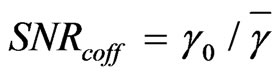 . In case of the whole radio system, the sum spectral efficiency is considered which is obtained as follows [3]
. In case of the whole radio system, the sum spectral efficiency is considered which is obtained as follows [3]
 (5)
(5)
Figure 1 shows the spectral efficiency achieved in cognitive radio and the one achieved in conventional radio systems. The numerical results derived from the aforementioned analysis are dedicated to Rayleigh channels. More specific, the line with cross marker type illustrates the spectral efficiency of optimal power and rate adaptation using the closed-form (3). The line with square marker type depicts the sum spectral efficiency of cognitive radio using the combination of closed-forms (3-6). It is evident that the propagation over cognitive radio yields an increase in capacity that has a considerable value in low average SNR regions that is ranged between 0.2-0.3 bits/sec/Hz. For comparison purposes, we also depict the sum spectral efficiency of cognitive radio when only the primary user is considered that is in fact the capacity of user 1 over Rayleigh fading channel model.
2.2 Spectral Efficiency of Adaptive Modulation
Although, adaptive modulation was introduced in [5] studying both variable rate and variable power (VRVP)
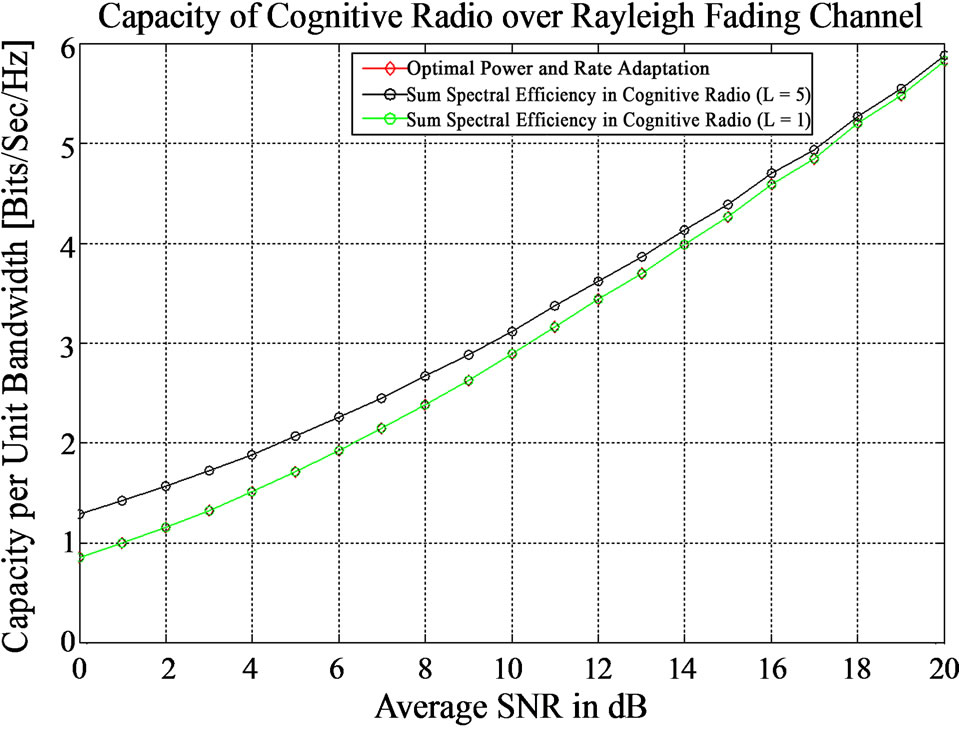
Figure 1. Capacity of cognitive radio over Rayleigh fading channel
modulations, it was followed with the analysis of variable-rate and constant-power (VRCP) case presented in [4]. The VRVP instead of VRCP uses power adaptation that is relied on optimal power control policy that we mention above. On the other hand, the achievable performance of cognitive radio depends on the band factor gain which relies on the corresponding channel allocation technique. As specified in [3], this capability is related to the frequency variation that is expressed by the channel fading distribution. Since power control policy is employed, the frequency variation depends on the cut-off fade level. The obvious inference is that we use the VRVP case for studying the performance of adaptive modulation over cognitive radio, since the cognitive radio system employs such an optimal power control policy for allocating channels to each user. To this end, we should rely on the performance of VRVP case of adaptive modulation and its spectral efficiency in particular [5].
The VRVP scheme deploys MQAM constellations denoted as the set 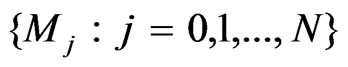 that can be chosen according to the instantaneous signal-to-noise ratio γ during the symbol period. Throughout this set, the
that can be chosen according to the instantaneous signal-to-noise ratio γ during the symbol period. Throughout this set, the 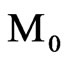 choice means no data transmission. Particularly, each constellation is associated with a fading region that is emerged by the division of the range
choice means no data transmission. Particularly, each constellation is associated with a fading region that is emerged by the division of the range  into
into 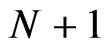 regions known as fading regions. Thus, when the fading level is set in the
regions known as fading regions. Thus, when the fading level is set in the 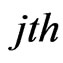 region then the constellation Mj is chosen. Consequently, the current data rate of the adaptable system is
region then the constellation Mj is chosen. Consequently, the current data rate of the adaptable system is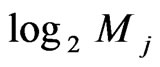 . However, since the transmit power
. However, since the transmit power 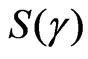 should also be adapted in order to retain the average power constraint
should also be adapted in order to retain the average power constraint 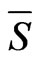 and therefore the received SNR is equal to
and therefore the received SNR is equal to . Thus, the adaptive scheme should be able to decide by which rate should transmit in the next period and which will be the transmit power either. Both rate and power are controlled under the required BER value (target BER) which should be retained at the physical layer.
. Thus, the adaptive scheme should be able to decide by which rate should transmit in the next period and which will be the transmit power either. Both rate and power are controlled under the required BER value (target BER) which should be retained at the physical layer.
Afterwards, the aim of such a system with power control policy is to maximize the spectral efficiency subject to the power constraint

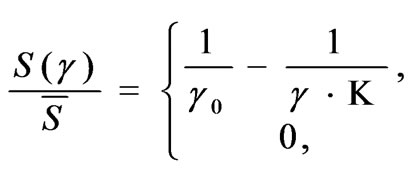 (6)
(6)
It is obvious that the cut-off level is equal to  where K is in relation with the target BER (
where K is in relation with the target BER (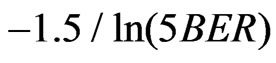
 ). Denoted the
). Denoted the 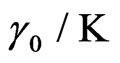 as
as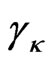 , the data rates are fallen in the fading region with optimum power allocation expressed as
, the data rates are fallen in the fading region with optimum power allocation expressed as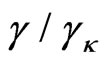 . Afterwards, the spectral efficiency of VRVP is the sum of data rates multiplied by the probability that the fading level falls in that region
. Afterwards, the spectral efficiency of VRVP is the sum of data rates multiplied by the probability that the fading level falls in that region
 (7)
(7)
3. Adaptive Modulation over Cognitive Radio
As described above, the achievable performance of cognitive radio depends on the band factor gain. Therefore, the band factor of the VRVP adaptive modulation, is expressed as follows
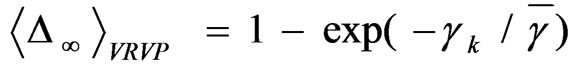 (8)
(8)
Taking into account the sum spectral efficiency of cognitive radio system, we derive the sum spectral efficiency of VRVP adaptive modulation over cognitive radio which obtained as follows
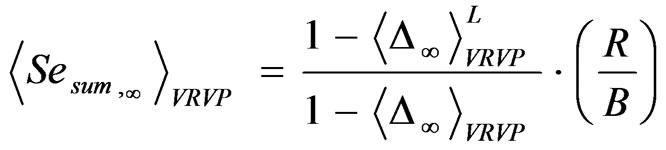 (9)
(9)
3.1 Numerical Results
1) Sum Spectral efficiency: Figure 2 shows the numerical results of adaptive modulation shceme over cognitive radio.
We keep as reference the numerical results derived in [5]. The regions denote the number of constellation that the system employs i.e. the number of deployed M-QAM at the physical layer. It is obvious the performance gain of cognitive radio at the lower average SNR regions while the gain is negigible at the higher average SNR regions. More specific, when 5 regions are considered then the performance gain in terms of bits per second per symbol period is approximately 0.2 in the average SNR region below 10 dB. In case of 4 regions, this gain seems to be smaller than 0.2 bps/Hz while in 3 regions is follows the same scaling procedure i.e. decrease. However, the decrease is more evident in average SNR regions higher that 10 dB.
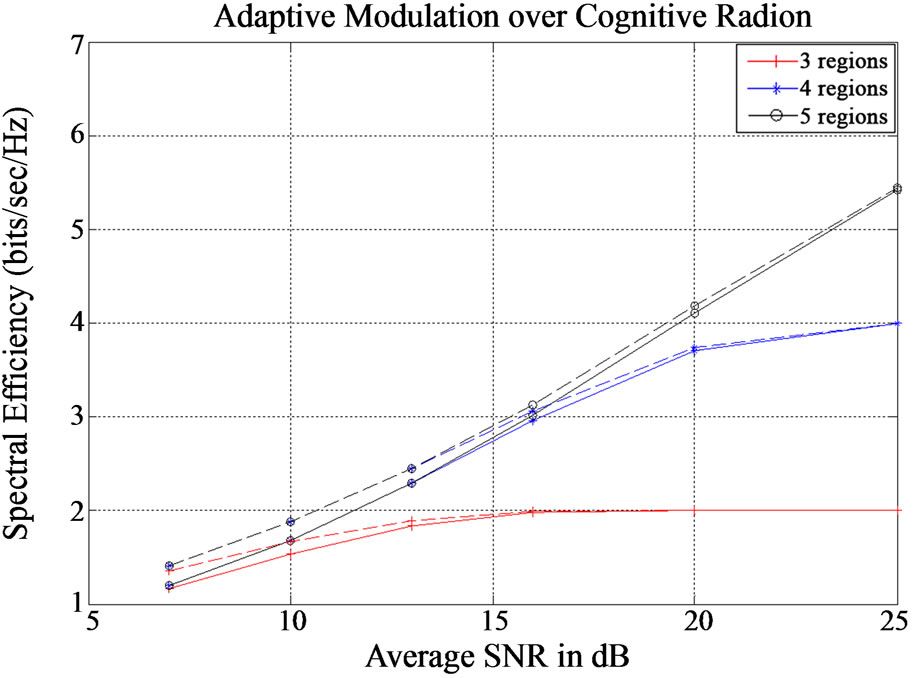
Figure 2. The spectral efficiency of adaptive modulation over cognitive radio
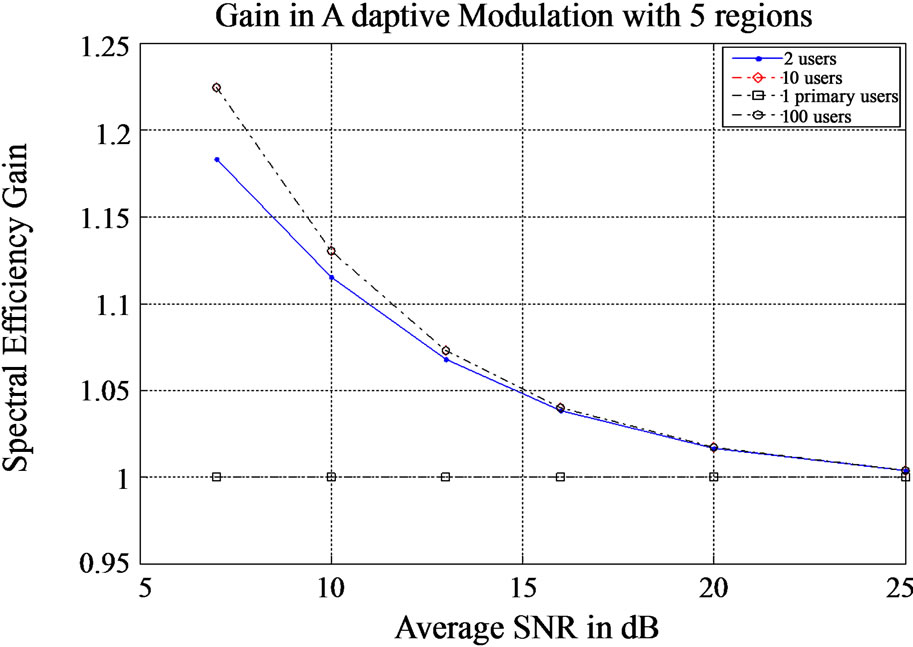
Figure 3. The performance gain of cognitive radio in adaptive modulation
2) Performance Gain: Figure 3 shows the performance gain in adaptive modulation with 5 regions. We depict the results using L users. It is obvious from the results that the increase in number of users leads to increase in the performance gain. However, the increase is getting negligible when the number of users is getting increased either. For instance, above 10 users the performance gain is approximately equal to that achieved with 10 users precisely. Moreover, this figure corroborates the performance gain of cognitive radio in low average SNR regions. We should remind that we have resulted in the same conclusion for the capacity of cognitive radio over fading channel illustrated in Figure 1, where the results are related to instantaneous received SNR. Afterwards, it can be noted that the performance gain of cognitive radio at the physical layer in general, is remarkable at low fading regions and is retained at the same level for more than a small number of users.
REFERENCES
- S. Haykin, “Cognitive Radio: Brain-Empowered Wireless Communications,” Selected Areas in Communications, IEEE Journal on, Vol. 23, No.23, No. 2.2,(07 February 2005), pp 7 February 2005, pp. 201-220.201-220.
- Q. Zhao and B. M. Sadler, “A Survey of Dynamic Spectrum Access: Signal Processing, Networking, and Regulatory Policy,” IEEE Signal Processing Magazine: Special Issue on Resource-Constrained Signal Processing, Communications, and Networking, May 2007, pp. 79-89.
- M. Haddad, A. Hayar and M. Debbah, “Spectral Efficiency of Spectrum-Pooling Systems,” Communications, Institution of Engineering and Technology, July 2008, Vol. 2, No. 6, pp. 733-741.
- M. Alouini and A. J. Goldsmith, “Adaptive Modulation over Nakagami Fading Channels,” Wireless Personal Communications, Vol. 13, No. 1-2, 2000, pp. 119-143.
- J. Goldsmith and S.-G. Chua, “Variable-Rate Variable-Power MQAM for Fading Channels,” IEEE Transactions on Communications, vol. 45, No. 10, October 1997, pp. 1218-1230.
- M. Alouini and A. J. Goldsmith, “Capacity of Rayleigh Fading Channels Under Different Adaptive Transmission and Diversity-Combining Techniques,” IEEE Transactions on Vehicular Technology, Vol. 48, No. 4, July 1999, pp. 1165-1181.

