Journal of Environmental Protection
Vol.4 No.6(2013), Article ID:33105,6 pages DOI:10.4236/jep.2013.46060
Formation of Glaciation Epochs
![]()
1Geotechnical Engineering Research Division, Korea Institute of Construction Technology, Goyang City, South Korea; 2Rudolf W. Gunnerman Energy and Environment Laboratory, University of Southern California, Los Angeles, USA; 3Geodynamics and Paleo-Oceanology Laboratory, Oceanology Institute, Russian Academy of Sciences, Moscow, Russia; 4Seismology and Geodynamics Laboratory, Oceanology Institute, Russian Academy of Sciences, Moscow, Russia.
Email: *scott@kict.re.kr
Copyright © 2013 Sanghee Shin et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 20th, 2013; revised April 22nd, 2013; accepted May 21st, 2013
Keywords: Earth’s Precession; Glaciation Epochs; Climate Evolution; Climate Change; Global Warming; Global Cooling
ABSTRACT
The effect of Earth precession angle on a climate is presented here. It is shown that the glaciation epochs occurred only when the precession angle was low. After the continental glaciation formed in the Northern hemisphere, Earth’s spherecal symmetry was disrupted and its precession angle increased drastically. As a result, a drastic and rapid climate warm-up occurred, the glaciers melted down and an interglacial stadial1 began. Subsequently, affected by the Lunar-Solar gravity pull on the Earth’s equatorial swelling, the precession angle gradually decreased and a new cooling-down phase occurred. As a result, there was nonlinear oscillation of Earth’s climate with periods on the order of 100 - 120 MY.
1. Introduction
The emergence of Earth’s glaciation epochs is an oscillatory process as the periods of significant cooling-down are followed by appreciable warm-ups (interglacial stadials) which, in turn, are followed by cooling-down periods. For this reason it is practically impossible to explain this oscillatory process by smooth climatic changes (such as declinein the atmospheric pressure due to bacterial activity). In this case, it is important to consider to the behavior of the revolving Earth precession, which emerges in association with deflections of the Earth’s mass distribution from the spherical symmetry. Such deflections from symmetry are caused first of all by the Earth’s crust nonuniformity in its continental and oceanic segments (i.e., the position of continents and oceans on the Earth’s surface); the other reason is the potential density nonuniformity of mantle [1].
The average period of the Earth’s axis to go over the total precession circle is presently τ ≈ 25.7 - 26 thousand years [2]. The precession motions are superposed by smaller short-period nutation (“nodding”) fluctuations. They are perceived as the pole motions apparently caused by the tidal disturbances, movements of the internal Earth’s core and by the Earth-Moon system revolution around the common barycenter. A result is rather complex pattern of the Earth’s axis rotation [3-5].
2. Formation of the Glaciation Epochs
The shape of Earth is very close to that of the revolution ellipsoid of a liquid body with the equatorial inertial swelling. The Earth’s equatorial radius (Re = 6378.2 km) is greater than the polar radius Rp = 6356.8 km by 21.4 km, which corresponds to the compression
 . That is the reason why a greater excess mass is concentrated at the equator and can have the gravity interaction with the other celestial bodies. These interactions tend to turn Earth so that her equatorial plane would coincide with the rotation plane of the disturbing body. Still, only the gravity pull by Moon and Sun play the main role in decreasing the precession angle (see Figure 1).
. That is the reason why a greater excess mass is concentrated at the equator and can have the gravity interaction with the other celestial bodies. These interactions tend to turn Earth so that her equatorial plane would coincide with the rotation plane of the disturbing body. Still, only the gravity pull by Moon and Sun play the main role in decreasing the precession angle (see Figure 1).
The gravitational pull of the Moon and Sun acts simultaneously on both sides of the Earth’s equatorial swelling tending to turn its revolution axis in the opposite directions. But the gravity action on the swelling side facing the Moon or Sun is slightly greater than on the opposite side (see Figure 1).
To determine the mass of the Earth’s equatorial swelling, it is necessary to determine its volume. The volume of the equatorial swelling is equal to the difference between the Earth’s revolution ellipsoid volume and the volume of a sphere inscribed in it:
 (1)
(1)
Then the mass of the equatorial swelling is equal to:

where Vswell (≈2.8 g/cm3) is the average density of the swelling accounting for the oceanic water layer about 3 - 4 km deep and the underlying layer of the oceanic crust and the upper mantle (about 17 km). One half of this equatorial swelling is facing Moon, whereas the other half is on the opposite side of Earth (see Figure 1). Thus, the effective mass of each half is about 2 times smaller, just mswell/2 ≈ 1 × 1024 g. Then, the difference of the Lunar gravity forces acting on these halves 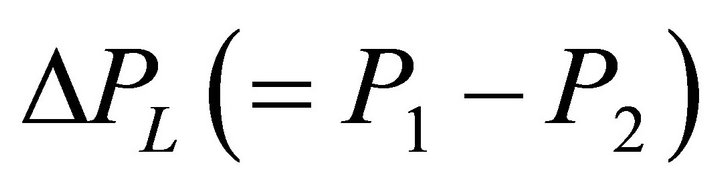 is:
is:
 (2)
(2)
where γ (=6.67 × 10−8 сm3/g∙s2) is the gravitational constant; mL (=7.35 × 1025 g) is the Lunar mass; LL (=3.844 × 1010 сm) is the distance between the Earth’s and Moon’s centers of mass; R (=6.371 × 108 сm) is the average radius of Earth; Ψ is the precession angle (present value of Ψ = 23.44˚); λ (≈5˚) is the angle between Moon-aroundEarth rotation plane and the plane of the ecliptics.
Thus, ΔPL ≈ 1.3725 × 1021 сm∙g/s2.
Similarly, the difference in the Sun gravitational forces acting on the equatorial swellings is:
 (3)
(3)
where 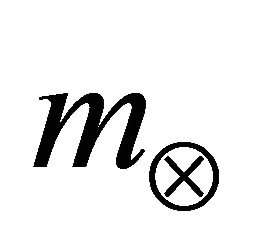 (=1.99 × 1033 g) is the mass of Sun;
(=1.99 × 1033 g) is the mass of Sun; 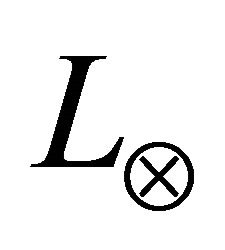 (≈ 1.496 × 1013 сm) is the distance between the Sun and Earth mass centers. Then,
(≈ 1.496 × 1013 сm) is the distance between the Sun and Earth mass centers. Then, 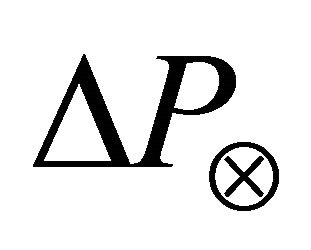 ≈ 0.6088 × 1021 cm∙g/s2.
≈ 0.6088 × 1021 cm∙g/s2.
The lunar and solar gravitational forces must be applied to the center of mass of each half of the equatorial swelling. Each half is similar to a convex dome with the center of gravity from the center of the Earth at a distance of about 2/3 Earth’s radius (Figure 2). Therefore,
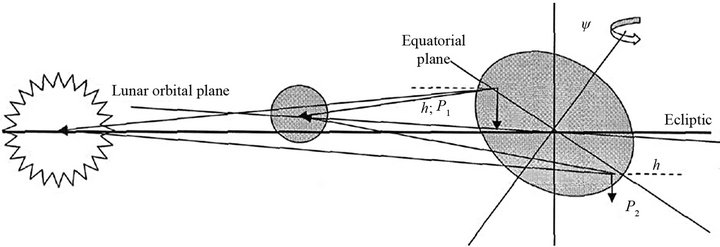
Figure 1. Schematic diagram of the effect of Lunar-Solar gravitational pull on the Earth’s equatorial inertial swelling resulting in Earth’s equatorial plane approach to Lunar revolution plane and to the ecliptics, i.e., in a decline of Earth’s precession angle (not to scale).

Figure 2. Center of gravity of Earth’s equatorial swelling in the cross-section facing Moon: (а) In equatorial plane; (b) In meridional plane.
 , (4)
, (4)
The difference of the momentums of force applied from the lunar side to the Earth’s equatorial swelling (see Figure 2) is equal to ML = PL∙h = 3.71 × 1029 g∙сm2/s2. From the solar side, ΔMS = ΔPS∙h = 1.72 × 1029 g∙сm2/s2. The combined effect gravitational pull of the Moon and Sun is Δ(ML + MS) = 5.43 × 1029 g∙сm2/s2.
Besides the effect of Moon and Sun, the Earth’s precession is influenced by the asymmetry of continental positions on the globe’s surface. The combined mass of the continents mcont is equal to approximately 2.25 × 1025 g [6], the average thickness of the continental crust is Hcont = 40 km = 4 × 106 сm and their average elevation (stand) above sea level is Δh = 875 m = 8.75 × 104 cm. The effect of continents on the Earth’s asymmetry is due to their centers of mass being positioned slightly above the center of mass of the mantle matter displaced by the continents. Under the continents’ isostatic equilibrium the mass of the displaced mantle mmant is equal to the mass of the continents mcont = 2.25 × 1025 g. Judging from the elevation of continent, the continents’ center of mass is above the center of mass of the displaced mantle by h ≈ 500 - 600 m. Thus, the continental crust excess mass is Δmcont ≈ mcont∙h/Hcont ≈ 3.38 × 1023 g. With the centrifugal acceleration gctrf = Ω2∙R∙cosφ, where Ω = 7.27 × 10−5 rad/s is the Earth’s revolution angular velocity and is the latitude of the continents’ center of mass. At φ = 30˚, gctrf = 2.9 сm/s2 and ΔPcont = Δmcont∙gctrf ≈ 9.8 × 1023 g∙сm/s2. Depending on the distance between the center of mass of the entire continental ensemble and the Earth’s center, the value ΔMcont is between 1029 and 1030 - 1031 g∙сm2/s2. The mantle is non-uniform, especially with respect to the positions of the lighter ascending mantle flows and the heavier descending ones. Besides, the nonuniformity is added by the core surface topography. The result is that the combined effect of all these factors is not clear. An indirect estimate, based on a comparison of the theoretical temperature climate fluctuations in Pleistocene with the isotopic temperatures of the Antarctic ice cover (see Figure 3), shows that the present-day ΔMcont+m is equal approximately to (0.2 tо 0.6) × 1029 сm2∙g/s2.
Using the theory of free gyroscopes the authors determined the average rate of the revolution of Earth’s axis rotation around the intersection line of the equatorial plane with the lunar orbit plane around Earth and the Earth orbit plane around Sun:
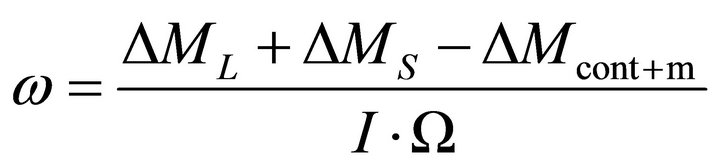 , (5)
, (5)
where I (=8.04 × 1044 g∙сm2) is the Earth’s moment of inertia; Ω = 7.27 × 10−5 rad/s) is the angular velocity of the Earth’s revolution. The present-day Earth’s rotation rate, with the precession angle of 23.44˚, is ω ≈ 4.83 × 10−12 rad/s or 1.53 × 10−4 rad/year (rotation by 1˚ takes approximately 716.5 years). The Earth rotation from the present precession angle of 23.44˚ to the lunar orbit inclination angle to the ecliptics occurs asymptotically and gradually approaches 5.1˚. This takes millions of years. Thus, the function of Earth’s rotation rate vs. the precession angle is quite nonlinear. The Earth rotation time may be found from the following equation:
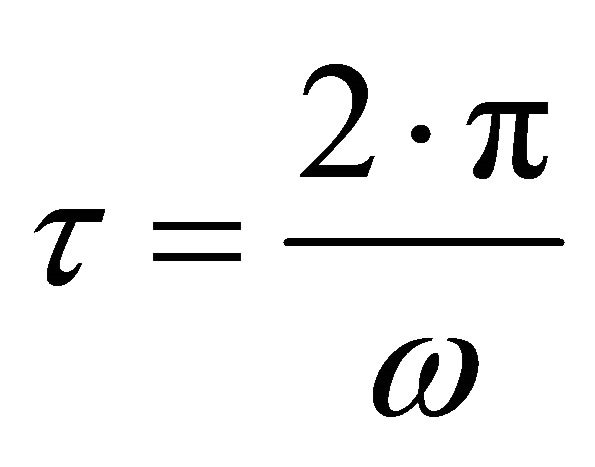 (6)
(6)
Inasmuch as the ω = dψ/dt, the precession angle correlation vs. time is (Figure 4)
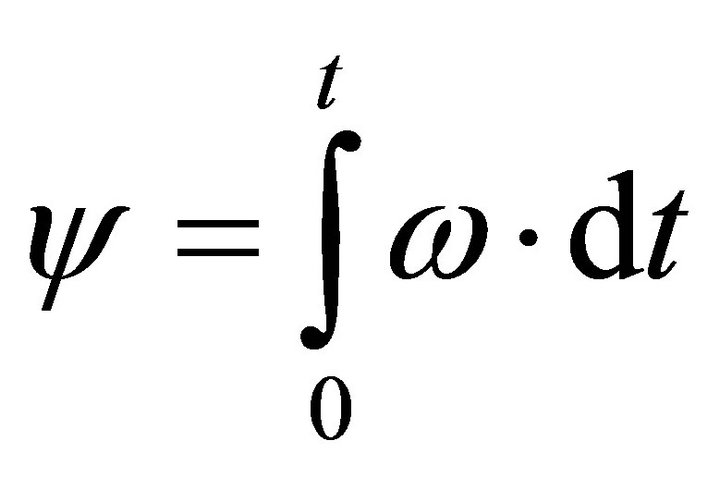 , (7)
, (7)
At the equilibrium of Lunar-Solar gravity pull on the Earth equatorial swelling with the effect of the continents and mantle,
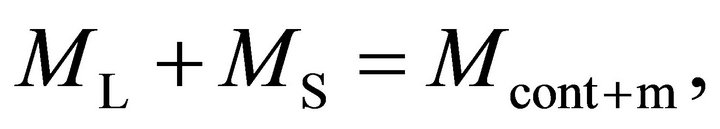 (8)
(8)
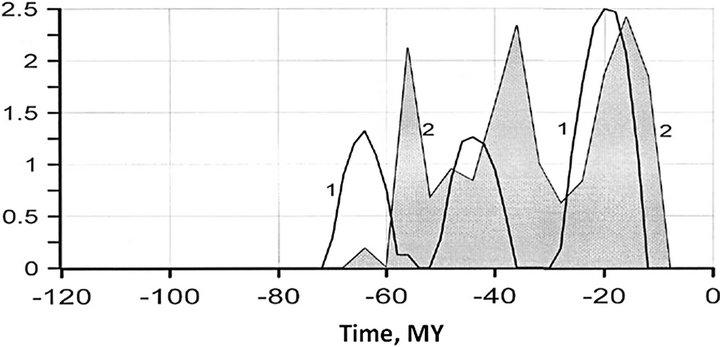
Figure 3. Distribution of glaciations in the northern continents determined from the theoretical temperature curve of the latest (Wurm) Pleistocene precession climatic cycle (Curve 1). Average Earth surface temperature of 10˚ was assumed as the threshold of the beginning of glaciation. Shaded area of curve 2 represents averaged glaciations distribution in Canada and USA determined from the positions of border moraines in North America (Imbrie and Imbrie, 1979 [2]) (arbitrary vertical scale on both diagrams).
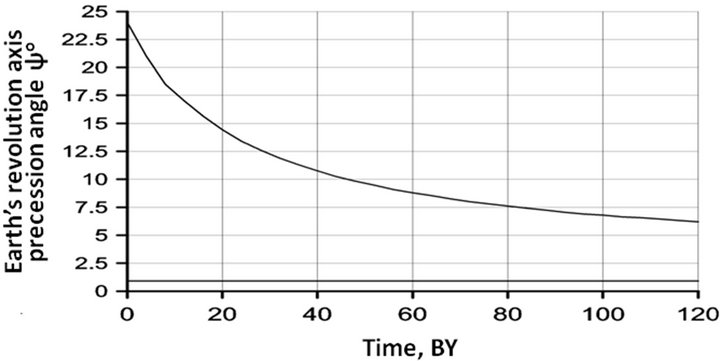
Figure 4. Variation of Earth’s precession angle with time as affected by Lunar-Solar tides and asymmetric locayion of continents on the Earth’s surface. As an example, the initial precession angle is assumed to be 24˚. Minimal precession angle is determined by asymmetry of the continents’ position on the Earth’s surface its current value is about 2.5˚.
ω = 0, and the precession angle acquires its equilibrium value at t → ∞. For the present-day positions of the continents, ψ∞ ≈ 2.5˚ (Figure 4). Currently, the precession angle declines at a rate of about 6 × 10−4 deg/year.
On assuming that the Earth’s albedo А = 0.3, the value of Earth’s effective temperature Те = 263.6 К. Then, the tropospheric temperature (including the surface temperature) can be expressed as planet’s effective temperature:
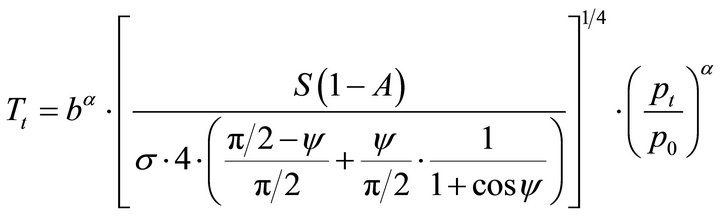 (9)
(9)
According to the empirical calculations, the presentday average near-surface Earth temperature at р = р0 = 1 atm and ψ = 23.44˚ is approximately equal to: Ts ≈ 288 Кor +15˚ Сassuming Ts = 288.2 К. The proportionality coefficient at ψ = 23.44˚, Те = 263.6 К and Ts = 288.2 K, and at ψ = 0˚, Те = 255 К and Ts = 278.6 К. Then, within a wide range of the precession angles for the Earth, bα = 1.093.
Using Equation (9), one can establish the correlation of the near-surface temperature vs. time (Figure 5).
As the plane of the Earth’s equator approaches the plane of the lunar orbit around Earth and the ecliptics, the Moon’s and Sun’s external influence on the Earth’s equatorial swelling substantially decreases. According to Equation (9), a noticeable cooling of climate occurs as the result. As soon as the average near-surface temperature reaches some critical level, glaciations begin on the highlatitude continents (for the northern region, the critical value of the Earth average temperature will to be close to 9˚C - 10˚C).
Indeed, the emergence of ice sheets and growth in the polar areas unavoidably disrupts the Earth’s revolution equilibrium and leads to a renewed rapid increase of the

Figure 5. Changes in the Earth’s surface average temperature as affected by the gravity pull from Moon and Sun on the equatorial swelling and by the asymmetry of the continents’ positions on the Earth’s surface. As the precession angle monotonously declines from 24˚, the temperature curve asymptotically approaches its minimum value of Т∞ ≈ 6.5˚C (classical value of temperature of absolutely black body at Earth distance to Sun being equal to 278.6 К = 5.4˚C).
precession angle. To determine the direction of the action of ice sheets on the Earth’s revolution regime, the glaciations in both Northern and Southern hemispheres must be accounted for (Figure 6).
However, the Antarctic ice mass increment was limited by the finite size of the underlying continent and mostly occurred in the nearshore areas and in the West Antarctic where humid cyclone penetration was common. The Eastern Antarctic ice dome has a high stand (up to 4 km). For this reason, it is dominated by anticyclones and the snow mass increment in its central areas is mostly due to the hoar-frost precipitation out of a relatively dry air. This increment is almost totally compensated by the plastic flow of ice from the central areas to the shores. Besides, Antarctic (the main ice accumulator in the southern hemisphere) is almost symmetrical relative to the South Pole and does not cause substantial disruptions in the Earth’s axial symmetry.
The main ice mass in the Northern Hemisphere was accumulated over the Canadian Shield. Thus, two force momentums, directed against each other must have been acting on the body of Earth in Late Pleistocene. One was
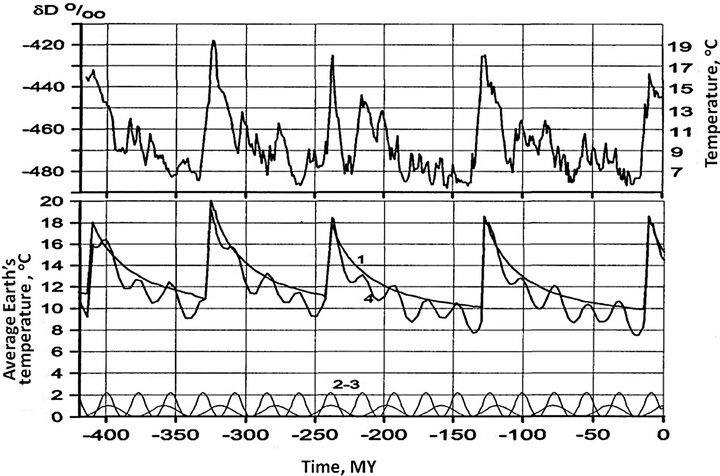
Figure 6. Correlation of the theoretical changes in Earth’s average temperature during Pleistocene (lower diagram) with the experimental values of isotope temperatures determined in the Antarctic ice cover (upper diagram). The experimental data have been obtained in the ice cover at the Vostok station (Kotlyakov, 2000). Based on Kotlyakov’s calculations, the last peak in the isotopic temperature, which occurred about 10 - 20 thousand years ago, corresponded with 8˚C. The previous temperature transition from 140 tо 130 thousand years ago corresponded with 10˚C (the oldest fourth cycle is apparently distorted by the near-ocean-floor ice flows). The theoretical curve in the lower graph is plotted accounting for the Milankovitch cycles. 1—temperature fluctuations caused by changes in Earth’s precession angle (the maxima of curve 1 are superposed on maximum values of the experimental data). 2 and 3—temperature fluctuations caused by the precession of the orbit of Earth-around-Sun revolution (two major harmonics with periods of about 40 and 22 thousand years are the Milankovitch cycles). 4—composite temperature change as affected by all causes.
caused by the Canadian glaciation and the other, by the West Antarctic glaciation as shown in Figure 7. The momentum of force from the Northern Hemisphere clearly prevailed.
In estimating the effect of ice sheet on the Earth’s precession angle, the glacier masses positioned symmetrically with respect to the poles may be disregarded as they mutually balance each other and do not have any significant effect on the Earth’s revolution regime.
According to our estimate, the excess mass of the ice sheets (taking the southern glaciers into account) in Late Pleistocene was located at about 70˚N over Canada and was approximately 2 × 1022 g. The centrifugal acceleration at 70˚ latitude is equal to about gstrf ≈ 1.15 сm/s2. In this case, ΔPglacier ≈ 2.3 × 1022 g·сm/s2, and the distance between center of gravity of the excess mass and the North Pole was close to hglacier ≈ 2.2 × 108 cm or 2200 km. Then the additional momentum of force attached to Earth is equal to ΔМ = ΔРglacier·h ≈ 5.1 × 1030 g∙сm2/s2. Then, using Equation (7), ω ≈ 7.9 × 10−11 rad/s and the characteristic warming time τ ≈ 2500 years. This, of course, is a very approximate estimate, but it provides the order of a characteristic warming and glaciers degrading time of about a few thousand years, which was actually observed. Quoting Kotlyakov [7], “the disintegration of a giant Pleistocene glaciation in the Northern Hemisphere occurred very rapidly, just over a few thousand years”.
To calculate temperature climate change, it is necessary to estimate how it is affected by the Earth’s orbit precession during its rotation around the Sun (Milankovitch cycles). Main harmonics of the Milankovitch cycles have periods of about 41,000 and 23,000 years [8]. Their effect causes temperature changes on the order of ±2˚C to ±3˚C. The average Late Pleistocene temperature considering such fluctuations and in comparison with the isotopic temperature of the Antarctic ice at the Vostok Station is shown in Figure 6.
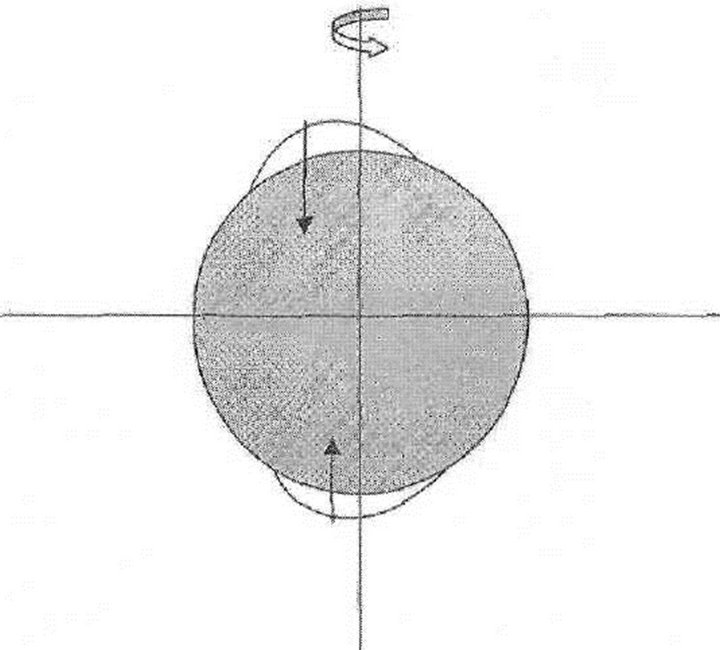
Figure 7. Effect of inertia forces from the excess mass of ice sheets in the Northern and Southern hemispheres on the turning of the Earth’s rotation axis.
It should be noted here that the isotope temperatures within the Antarctic ice describe not the ice cover formation temperature but the average World ocean surface water temperature; their evaporation preserved the deuterium/hydrogen isotope ratios typical of these waters. After having been precipitated in the Antarctic these ratios were remembered by the corresponding layers of the ice cover.
As shown in Figure 6, correlation of the theoretical temperature curves with the experimental data is quite good although the theoretical curves are somewhat smoothed.
Cycle and the independent geologic data on the ice sheet distribution in Canada and the US as presented in 1988 by Imbry and Imbry (Figure 3).
Both curves are similar, with slight deviations in ages and scales. Our curve is tied with the age scale of the Antarctic temperature fluctuations. It is also possible that some glacier traces (end moraines) of somewhat earlier glaciation phases (for instance, the phases about 70,000 years ago) were obliterated by the last-phase glaciation, which substantially overlaid the area of earlier glacier phases.
The shape of the theoretical curve depends substantially on 1) the phase relationships between the main cycles of the Lunar-Earth and “glacier” temperature fluctuitions; 2) precession cycles of the Earth-around-Sun revolution orbit; and 3) precession of the Earth own revolution. Based on these, the writers selected the best fit between the theory and experimental isotope temperature determinations in the Antarctic ice sheet from the phase shift of the component climatic fluctuations. Thus, the future climate changes can be forecast (as an example of such forecast see Figure 8).
The Pleistocene/Holocene boundary (we are living in Holocene) is usually drawn at the boundary between the latest and most significant phase of the Wurm (Valday) glaciation and the present-day interglacial stadial. Based on the data in Figure 8 (tied-in with the age determinations of temperature fluctuations in the Antarctic ice cover at the Vostok station) the age of this boundary is
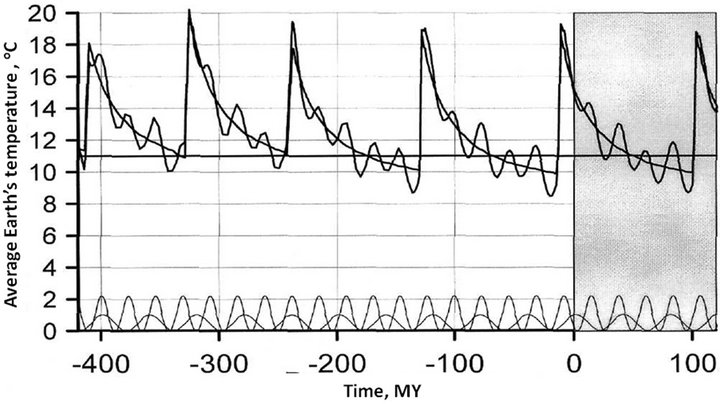
Figure 8. Temperature forecast for the next 120 thousand years is presented by the shaded area of the graph.
approximately 12,000 - 11,000 years. The later values are close to the value of 10,000 years determined by the INKVA Holocene commission [9].
On the other hand, the warm climate during the second half of Mesozoic was due to the formation at that time of the supercontinent Pangaea and to the accelerated oxygen generation caused by the explosion of flowering plants, which temporarily compensated the decline in the nitrogen partial pressure. After Pangaea began to break down and oxygen pressure stabilized, a new cooling phase started in Cenozoic despite a slight increase in the solar luminosity. The authors estimate that the average surface temperature at the end Mesozoic reached +18˚C to +19˚C (the present-day value is +15˚C).
3. Conclusion
As a result of the Moon-Earth interaction, slow but regular climate cooling episodes periodically occurred in Pleistocene. Every one reached 8˚C to 10˚C and lasted 100 to 120 thousand years. After the emergence of thick ice sheets there was a rapid, within just a few thousand years, climate warming by the same 8˚C - 10˚C, with equally rapid degradation of glaciers. Therefore, the Moon-Earth connections in combination with the Earth’s glaciations initiated substantially nonlinear self-oscillatory climatic processes so typical of the entire Late Pleistocene. The future climatic forecast is cooling, probably, the most severe of all preceding cooling episodes. According to Sorokhtin et al., 2010, cooling occurs due to life activity of the nitrogen-consuming bacteria, which continuously lowers the partial pressure of nitrogen and subsequently the general atmospheric pressure. The atmospheric pressure decline leads to the Earth’s climate cooling (see Equation (9)).
REFERENCES
- J. Imbrie and K. P. Imbrie, “Ice Ages Solving the Mystery,” Hillside, New Jersey, 1979, 264 p.
- W. M. Kaula, “An Introduction to Planetary Physics,” The Terrestrial Planets, J. Wiley and Sons Inc., New York, 1968, 492 p.
- O. G. Sorokhtin, “Evolution and Forecast of Changes in Earth’s Global Climate,” Institute of Computer Studies, Izhevsk, Moscow, 2006, 88 p.
- O. G. Sorokhtin, G. V. Chilingar and L. F. Khilyuk, “Global Warming and Global Cooling: Evolution of Climate on Earth,” Developments in Earth and Environmental Sciences, Elsevier, Amsterdam, 2007, 313 p.
- O. G. Sorokhtin, G. V. Chilingarian and N. O. Sorokhtin, “Evolution of Earth and Its Climate. Elsevier Science,” Developments in Earth and Environmental Sciences, Elsevier, Amsterdam, 2011, 763 p.
- A. B. Ronov and А. А. Yaroshevsky, “Chemical Composition of the Earth’s Crust and of Her Shells,” In: V. V. Belousov, Ed., Tectonosphere of Earth, Nedra, Moscow, 1978, pp. 376-402.
- V. M. Kotlyakov, “In the World of Snow and Ice,” Vol. 5, Nauka, Moscow, 2002, 384 p.
- V. А. Bolshakov, “New Concept of Orbital Theory of Paleoclimate,” Taurus, Moscow, 2003, 256 p.
- D. Q. Bouen, “Quaternary Geology, a Stratigraphic Framework for Multidisciplinary Work,” Pergamon Press, Moscow, 1978, 272 p.
NOTES
*Corresponding author.
1A stadial is a period of lower temperatures during an interglacial (warm period) separating the glacial periods of an ice age. Such periods are of insufficient duration or intensity to be considered glacial periods. Notable stadials include the Older Dryas and Younger Dryasstadials and the Little Ice Age. An interstadial is a warm period during a glacial period of an ice age that is of insufficient duration or intensity to be considered an interglacial (http://en.wikipedia.org/wiki/Stadial)
The Russian definition of the stadial (http://www.kroka.ru/html/s/stadial.html): Stadial is a relatively shortlasting cooling down within a glaciation epoch causing the glacier edge to stop in place. http://www.ruswiki.org/index.php/term/6,2288.xhtml).

